OpenMM: A Hardware Independent Framework for Molecular Simulations

Abstract

The wide diversity of computer architectures today requires a new approach to software development. OpenMM is a framework for molecular mechanics simulations, allowing a single program to run efficiently on a variety of hardware platforms.

Introduction

Computer architectures today are in a period of rapid advancement and diversification. A decade ago, most programs were run on conventional, single core processors capable of executing one thread at a time. In the last ten years, those simple CPUs have been replaced by an array of multi-core CPUs,¹ dedicated accelerators such as the Cell Broadband Engine,² and so-called Graphics Processing Units that are actually capable of powerful, general purpose computation.³ This trend is likely to continue in the future. It is difficult to predict what architectures will be available as little as five years from now, or what programming models will be best suited to exploiting them.

This creates a dilemma for all programmers, but especially for those in science and engineering. On the one hand, their computing needs are often extreme, involving simulations or other types of calculations that can only be run on enormous supercomputing clusters. On the other hand, their resources for developing software are usually quite limited. Writing and optimizing all the necessary software for a single architecture is a challenge. Repeating the task for several widely differing architectures is completely out of the question.

In some ways, this situation is analogous to the early days of the computer industry when programs were written in each computer’s native machine language. Different processors had different instruction sets, so porting a program to a new computer required completely rewriting it. Compilers solved this problem by introducing an abstraction layer between the programmer and the hardware: programs could be written in terms of higher level instructions, and those could automatically be transformed into the machine language of any processor desired.

This scheme works well as long as the processors involved are all fundamentally similar in their capabilities and operating models. When the processors differ too much, it ceases to work. For example, it is unreasonable to expect a single piece of source code to be compiled efficiently for both a single core CPU and a massively parallel GPU. These architectures require fundamentally different algorithms to perform the same calculation efficiently, and that is beyond the scope of any existing compiler.

What is really required is another abstraction layer to isolate the programmer from the hardware their code is running on; not just its instruction set, but its fundamental capabilities. One should be able to express the problem to solve using high level concepts appropriate to the problem at hand without needing to specify what particular algorithms to use. The abstraction layer should then automatically select an implementation of those concepts most appropriate to the currently available hardware. This approach has been used successfully in a number of cases, two of the most prominent examples being LAPACK⁴ for linear algebra and OpenGL⁵ for 3D graphics.

The Design of OpenMM

To address this goal within the specific domain of molecular simulation, we have developed OpenMM, a library for performing molecular mechanics on high performance computing architectures.⁶ It allows programmers to write their programs using a high level, hardware independent API. Those programs can then run without modification on any hardware that supports the API. In principle, that could be anything from a single CPU core at the low end, up to a large supercomputing cluster with multiple CPU cores and GPUs on each node.

To be successful, any abstraction layer of this sort must satisfy three basic requirements:

1. It must allow users to express their problem at an appropriate level of detail.

2. It must permit efficient implementations on all targeted hardware platforms.

3. It must incorporate modularity and extensibility as fundamental aspects of the API.

Let us consider each of these requirements in detail, and see how they are implemented in OpenMM.

Level of Abstraction

In any interface, it is critical to choose the right level of abstraction. The goal is to identify which aspects of the problem should be determined by the user, and which should be left to the library to determine. Too high a level of abstraction will make the library useless: there are certain aspects of the problem description that the user genuinely cares about, and if the interface does not allow them to precisely describe those aspects, they cannot use it. On the other hand, too low a level of abstraction restricts the library’s ability to implement the problem efficiently on a variety of hardware. If the user is required to specify implementation details that are not actually important to them, such as specific algorithms for performing calculations, there is no longer an option to automatically pick a different algorithm better suited to the available hardware.

In molecular mechanics, the user typically wants to describe the problem to solve in terms of potential functions, constraints, time integrations, temperature coupling methods, etc. They should be able to specify those without having to describe, for example, what method to use for evaluating the potential function. To express it in a slightly different way, the user cares about equations, not algorithms. An ideal interface should allow the user to specify the mathematical system they want to model, while leaving the library free to numerically evaluate that system in an appropriate way.

Permitting Efficient Implementation

Even if the interface does not explicitly define how the calculations are to be implemented, it can easily restrict the range of implementations that are practical. Great care is needed to ensure that no feature of the API will unnecessarily restrict the hardware platforms it can be used on.

An example of this from OpenMM is in the mechanism for accessing state information. A molecular mechanics simulation involves various data about the current state of the system being simulated: the positions and velocities of atoms, the forces acting on them, etc. Traditionally, simulation codes have represented these values as arrays in memory. When a program needs to examine the position of an atom, for example, it simply looks at the appropriate array element. To a developer accustomed to using such a code, a natural and obvious API for accessing atom positions would be a routine that takes an atom index and returns “the current position of that atom”.

Unfortunately, that API would be impossible to implement efficiently on many architectures. When doing calculations on a GPU, for example, the atom positions are stored in device memory, and transferring them to host memory is a relatively expensive operation. The problem is even worse for a cluster, where atom positions are distributed between many different computers across a network. Any program that assumes it has fast, random access to atom positions at all times is guaranteed to run very slowly on these systems.

OpenMM addresses this by explicitly not giving direct access to state data. Instead, the user invokes a routine to create a State object, specifying in advance all information that should be stored in that object. This has two advantages. First, because OpenMM knows in advance the full set of information the user is going to request, it can efficiently collect that information with a few bulk operations. Second, the user is aware they are performing an expensive operation, and therefore will give careful thought to when and how they access state data. They are not misled by seemingly trivial API calls (e.g. “get the position of atom 5”) that actually are expensive.

Modularity and Extensibility

If a library of this sort is to be successful, it must incorporate the division between interface and implementation as a fundamental aspect of its design. The author of a program should not need to specify what implementation to use. When the program is run, it should automatically select whatever implementation is most appropriate to the available hardware. At the same time, it should also allow the program to query the available implementations and manually select which one to use. For example, the user of a program might sometimes want to perform calculations on the main CPU and other times on a GPU.

Equally important is extensibility. As new hardware becomes available, new implementations will be necessary. It is impossible to enumerate all possible implementations, and the interface must not attempt to do so. It must be designed to be extensible, so new implementations can be written independently of the main library and existing programs can use them without modification.

OpenMM accomplishes this by means of a plugin architecture. Each implementation (or “Platform”) is distributed as a dynamic library and installed simply by placing it in a particular directory. At runtime, all libraries in that directory are loaded and made available to the program.

It also provides extensibility of a different sort: plugins are able not only to implement new Platforms, but also to add new features to existing Platforms. It is important to understand that OpenMM is not merely a library for performing certain calculations; it is an architectural framework designed to unify an entire problem domain. While the library comes with particular features built in (e.g. particular potential functions and integration methods), it also permits other features to be added by plugins. The goal is to provide a framework within which nearly any molecular mechanics calculation can be implemented.

Architecture

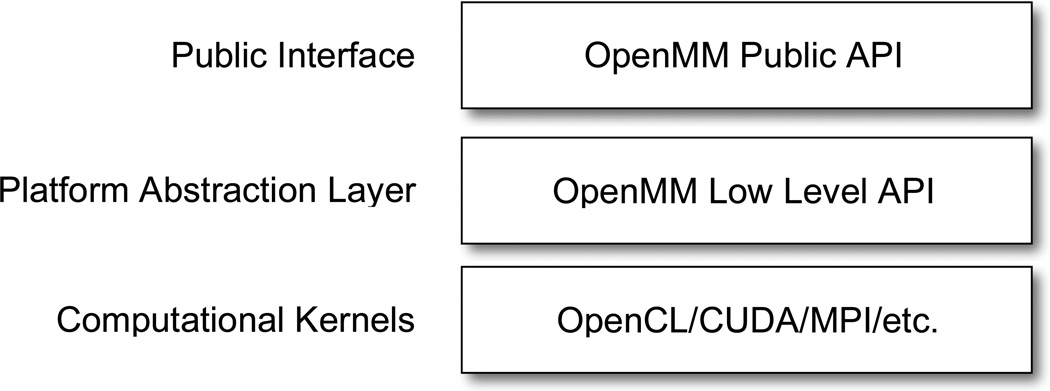
We now consider how to create an architecture that meets these goals. OpenMM is based on a layered architecture, as shown in Figure 1. At the highest level is the public API, which developers program against when using OpenMM in their own applications. In any such library, the public API must express concepts in terms relevant to the problem domain (e.g. molecular mechanics) without reference to how those concepts are implemented. In the case of OpenMM, those concepts are particles, forces, time integration methods, etc. For example, a Force object specifies the mathematical form of an interaction between particles, but does not dictate a particular algorithm for computing it.

Figure 1.

The architecture of OpenMM.

The public API is implemented through calls to a lower level API that serves as an interface between the platform-independent problem description and platform-dependent computational kernels. OpenMM represents this low level API as a set of abstract C++ classes, each defining a particular computation to be done. Note the very different roles played by these two interfaces: the public API is implemented by the core OpenMM library and is invoked by users; the low level API is implemented by plugins and is invoked by the core OpenMM library.

At the lowest level of the architecture are the actual implementations of the computational kernels. These may be written in any language and use any technology appropriate for the hardware they execute on. For example, they might use a technology such as CUDA or OpenCL to implement GPU calculations, Pthreads or OpenMP to implement parallel CPU calculations, MPI to distribute work across nodes in a cluster, etc.

This leaves the critical task of selecting and invoking an implementation of the low level API. In the case of OpenMM, this means instantiating a concrete subclass of the abstract class defining each kernel. This task is coordinated by a Platform object, which acts as a factory for computational kernels. Each class of the public API queries the Platform to get a concrete instance of each kernel it requires, then uses that instance to perform its calculations. The choice of what implementation to use thus consists entirely of choosing which Platform to use. A program may also elect not to specify a Platform, in which case one is chosen automatically based on the available hardware.

Actually, the arrangement is slightly more complicated. A Platform does not create kernels directly, but instead delegates the task to one or more KernelFactory objects. That is how a plugin can add new features to an existing Platform: it defines a computational kernel, creates a KernelFactory that can create instances of the kernel, and adds the factory to the Platform. When the Platform is later asked to create an instance of that kernel, it uses the new KernelFactory to do so.

How This Architecture Works in Practice

We now consider a concrete example of how this architecture works in practice: the computation of nonbonded interactions between atoms in a molecular system. This accounts for the bulk of the processing time in most simulations, so it is very important that it be well optimized.

In conventional codes designed to run on CPUs, there are well established techniques for doing this efficiently.⁷ One begins by building a neighbor list that explicitly enumerates every pair of atoms that are close enough to interact with each other. By using voxel based methods, this can be done in O(N) time. One then loops over all atom pairs in the neighbor list and computes the interaction between them. OpenMM’s reference Platform, which is written to run on a single CPU thread, works in exactly this way.

Unfortunately, neighbor lists are very inefficient on a GPU due to the need for indirect memory access. For each neighbor list entry, one must load information about the two atoms involved (position, charge, etc.). The indices of the atoms processed by successive threads need not follow any pattern, so the memory access cannot be coalesced.

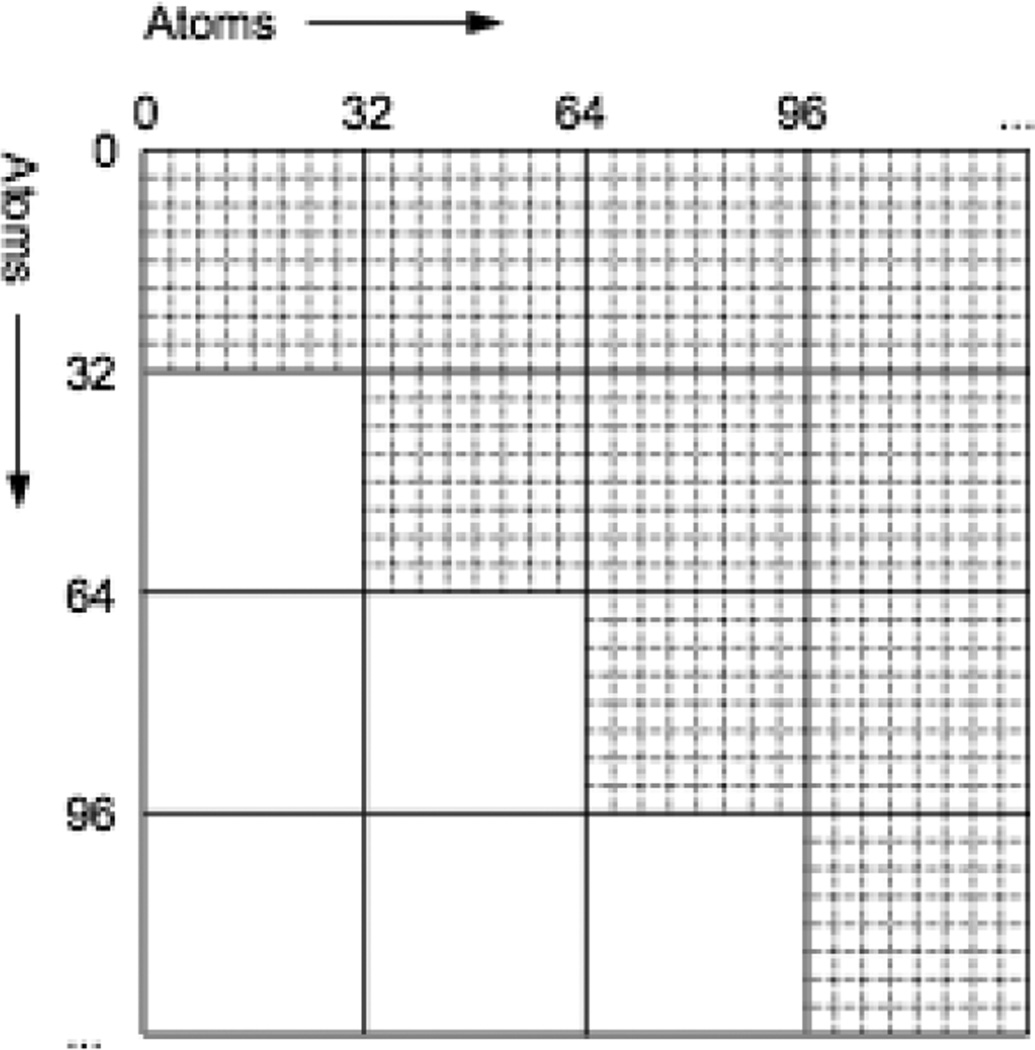
We therefore have developed an alternate method better suited to running on a GPU.⁸ We divide the full set of atoms into blocks of 32. The set of N² interactions then divides into (N/32)² tiles as shown in Figure 2, each involving the interactions between two blocks of atoms. To process a tile, we load the data for the 64 atoms involved into shared memory, compute all 1024 interactions between them, and finally write out the resulting forces and energies to global memory. In place of a conventional neighbor list, we use a list of which tiles contain interactions: effectively, a neighbor list specifying which blocks of 32 atoms interact. Other researchers have also developed algorithms for computing nonbonded interactions on GPUs.^9–11

Figure 2.

Atoms are divided into blocks of 32, which divides the full set of N² interactions into (N/32)² tiles, each containing 32² interactions. Tiles below the diagonal do not need to be calculated, since they can be determined from symmetry.

Our method was designed for use on Nvidia GPUs, and the size of each block (32 atoms) was chosen to match the SIMD width of those processors. Adapting it to other types of processors, even other GPUs, requires modifications to the algorithm. For example, some AMD GPUs have a SIMD width of 64, so threads must be distributed between tiles in a different way to obtain maximum efficiency.

We therefore need several fundamentally different algorithms to efficiently implement the same calculation on different hardware. Significantly, however, the choice of algorithm depends only on the hardware, not on the precise form of the force being calculated. Many different mathematical forms are used to represent nonbonded interactions in molecular simulations, differing in how they model van der Waals interactions, smoothing of cutoffs, solvent screening effects, etc. These are important differences that scientists genuinely care about when running simulations. Ideally, programmers should be able to choose the functional forms of the interactions and still have them calculated using the most efficient algorithm for the available hardware. The user should specify the equations to use, and the library should determine how best to evaluate those equations.

OpenMM accomplishes this goal through its CustomNonbondedForce class. This class allows the user to specify an arbitrary mathematical function for the pairwise energy between atoms. That function may depend on an arbitrary set of atomic parameters and tabulated functions, as well as a variety of standard mathematical functions. For example, the following lines of code create a CustomNonbondedForce to calculate a Lennard-Jones 12-6 interaction:

CustomNonbondedForce nb("4*epsilon*((sigma/r)^12-(sigma/r)^6);"
    "sigma=0.5*(sigma1*sigma2); epsilon=sqrt(epsilon1*epsilon2)");
nb.addPerParticleParameter("sigma");
nb.addPerParticleParameter("epsilon");

The first line specifies the energy of the interaction as a function of the distance r:

$$E(r)=4\epsilon ({\left(\frac{\sigma }{r}\right)}^{12}-{\left(\frac{\sigma }{r}\right)}^6)$$

where the parameters from two interacting atoms are merged using Lorentz-Bertelot combining rules: the arithmetic mean of the sigmas and the geometric mean of the epsilons. The next two lines specify that the parameters “sigma” and “epsilon” should be associated with each atom.

OpenMM now has the task of implementing this efficiently on a variety of hardware platforms. It begins by parsing the user-specified expressions and analytically differentiating the energy to determine an expression for the force. Each expression is then converted to a sequence of instructions. To evaluate an expression, the reference and CUDA implementations loop over the instructions and perform each one, effectively acting as an interpreter for an internal language.

For the OpenCL based implementation, a better solution is possible. Because OpenCL allows programs to be compiled from source code at run time,¹² it is possible to synthesize a kernel with the user-defined mathematical expression inserted into the appropriate hardware-specific algorithm. That kernel is then compiled down to the device’s machine code, eliminating the cost of interpreting the expression and yielding nearly as fast performance as if the entire kernel had been written by hand.

We stress that this approach allows for a great deal of flexibility in our code, permitting the powerful combination of rapid development (i.e. one can change the key underlying equations for interactions between particles easily) and yet still retaining rapid execution (since the underlying optimizations, especially with OpenCL, allows for minimal overhead). This opens the door to new uses of our code, especially in terms of the rapid development of novel methods for simulating particle interactions, such as novel implicit solvent models for molecular simulation.

Features and Performance

We have implemented Force classes corresponding to all the most widely used energy terms in molecular simulations: a variety of bonded forces, Lennard-Jones and Coulomb forces for nonbonded interactions, Ewald summation and Particle Mesh Ewald for long range Coulomb forces, and a Generalized Born implicit solvent model. OpenMM also includes several methods of time integration and the ability to enforce distance constraints. These features are implemented in three different Platforms: a reference Platform written in C++, a CUDA based Platform for Nvidia GPUs, and an OpenCL based Platform for a variety of GPUs and CPUs.

We have previously published benchmarks for the CUDA implementation when simulating a variety of proteins.^{6, 8} Speeds range from 5 ns/day when simulating a 318 residue protein in explicit solvent (73,886 atoms total) up to 576 ns/day when simulating a 33 residue protein in implicit solvent (544 atoms total). We also compared it to the single CPU core performance of several widely used molecular dynamics packages when simulating an 80 residue protein in explicit solvent. It was found to be 6.4 times faster than Gromacs, 28 times faster than NAMD, and 59 times faster than AMBER. (GPU calculations were run on an Nvidia GTX280, and CPU calculations were run on a 3.0 GHz Intel Core 2 Duo.)

The newest feature of OpenMM is custom forces that let the user specify an arbitrary algebraic expression for the form of their force. In addition to the CustomNonbondedForce described above, there is also a CustomBondForce for bonded interactions, CustomExternalForce for forces applied independently to each atom, and CustomGBForce which supports a wide range of implicit solvent models. These are most useful with the OpenCL platform, since it allows them to be used with very little performance penalty. In preliminary testing, we have found that Coulomb and Lennard-Jones forces implemented with CustomNonbondedForce are only about 4% slower than the standard, hand coded implementations. This means that a scientist with no GPU programming experience can still implement arbitrary functional forms for their nonbonded interactions, and get nearly as good performance as hand tuned GPU code.

Conclusions

Rapid, ongoing changes to computer architecture require a new approach to software development. Fundamentally different algorithms are required to perform the same calculation on a multi-core CPU, a GPU, a Cell processor, and a CPU cluster. The processors available five years from now will likely require still different algorithms to get optimal performance. A program written specifically for one architecture will quickly become out of date and be difficult to adapt to new hardware.

This problem can be solved by introducing a domain specific abstraction layer. Although this idea is not new, it has not been widely applied in scientific computing. The rapid evolution in hardware is making it increasingly important, and it is likely to remain so for the foreseeable future. Traditional approaches to development that mix the definition of the scientific problem to solve with algorithmic details of how to solve it are very difficult to maintain and support across a wide range of hardware architectures.

Introducing an abstraction layer results in a clean separation between the hardware specific and hardware independent aspects of the program. As hardware changes, new versions of the computational kernels can be written and distributed as plugins. Any program that uses the public interface will then work on the new hardware and make optimal use of it with no need for modification of any sort.

To be successful, any such abstraction layer will necessarily be domain specific, and the design must be based on a thorough understanding of the problem domain. On the one hand, it must give users full control over all aspects of the calculation that are scientifically relevant. On the other hand, it must hide as many details as possible, so those details can be optimized automatically for specific hardware. In the case of OpenMM, this means giving users complete freedom to choose the mathematical form of the forces acting on their system, while not exposing any details of how those forces are to be calculated. By doing so, it can simultaneously satisfy three goals that often conflict with each other: enabling rapid development of applications, allowing a high level of flexibility, and providing very high performance on a variety of hardware platforms.

Biographies

Peter Eastman, Clark Center, Stanford University, Stanford, CA 94305, peastmanstanford.edu

Peter Eastman is a software engineer in the Bioengineering Department at Stanford University. His work focuses on the physical simulation of biological systems, particularly the development of novel algorithms for high performance computing architectures. He has a Ph.D. in Applied Physics from Stanford University.

Vijay Pande, Clark Center, Stanford University, Stanford, CA 94305, pandestanford.edu

Prof. Pande is currently an Associate Professor of Chemistry and (by courtesy) of Structural Biology and of Computer Science at Stanford University. Prof. Pande received a BA in Physics from Princeton University in 1992 and PhD in physics from MIT in 1995. Prof. Pande’s current research centers on the development and application of novel grid computing simulation techniques to address problems in chemical biology. In particular, he has pioneered novel distributed computing methodology to break fundamental barriers in the simulation of kinetics and thermodynamics of proteins and nucleic acids.