Abstract
The hematocrit of a thrombus is a key factor associated with the susceptibility to thrombolysis. Ultrasonic imaging is currently the first-line screening tool for thrombus examinations. Different hematocrits result in different acoustical structures of thrombi, which alter the behavior of ultrasonic backscattering. This study explored the relationships among thrombolytic efficiencies, hematocrits, and ultrasonic parameters (the echo intensity and backscattered statistics). Porcine thrombi with different hematocrits, ranging from 0% to 50%, were induced in vitro. An ultrasonic scanner was used to scan thrombi and acquire raw image data for B-mode (echo intensity measurements) and Nakagami imaging (backscattered statistics analysis). Experiments on thrombolysis were performed using urokinase to explore the effect of the hematocrit on thrombolytic efficiency. Results showed that the weight loss ratio of thrombi exponentially decreased as the hematocrit increased from 0% to 50%. Compared with the echo intensity obtained from the conventional B-scan, the Nakagami parameter predicts the weight loss ratio, increasing from 0.6 to 1.2 as the weight loss ratio decreased from 0.67 to 0.26. The current findings suggest that using Nakagami imaging characterizing thrombi provides information of backscattered statistics, which may be associated with the thrombolytic efficiency.
Thrombi represent a critical problem in modern society because they are associated with arterial occlusion (myocardial infarction and stroke) and venous thromboembolism (deep-vein thrombosis and pulmonary embolism). Each year, approximately 1.8 million people in the United States experience acute myocardial infarction and stroke1,2. The estimated annual incidence of venous thromboembolism in the United States is more than 250 thousand, and more than 100 thousand patients die because of pulmonary embolism3,4. Thrombolytic therapy with thrombolytic agents has gained worldwide recognition for treating myocardial infarction5,6 and ischemic stroke7. Thrombolytic agents are also valuable for treating hemodynamically significant pulmonary emboli8,9. Because thrombolytic therapy carries the risk of bleeding1,10, assessing the susceptibility of thrombi to lysis before treatment is vital.
Thrombi are primarily composed of red blood cells (RBCs) and platelets entrapped in a fibrin mesh11,12. The fibrin structure affects thrombolytic susceptibility because it determines the pore size and fiber diameter. Thrombi with large pore sizes and thick fibers are susceptible to lysis13,14,15,16,17,18. The volume percentages of RBCs in the thrombi (hematocrit) also influence lysability. Several previous studies have indicated that a high RBC concentration in a blood clot confers lytic resistance because of the decreasing fiber diameter and pore size19,20. Contradictory evidence was observed in other studies reporting that the accumulation of RBCs in a thrombus may facilitate thrombolysis21,22. The hematocrit of a thrombus is a key factor associated with the susceptibility to thrombolysis; however, the exact mechanism through which the hematocrit affects thrombolysis remains undetermined. Noninvasively detecting the hematocrit of a thrombus before thrombolytic treatments will provide opportunities to predict the thrombolytic response for possible treatment planning.
In clinical situations, medical imaging techniques have been widely used to screen and examine thrombi. Among all possibilities, ultrasonic imaging is the first-line screening tool because of its nonionizing radiation, relatively simple signal processing, and real-time capability. The primary scatterers in a thrombus are RBCs, which are smaller than the wavelengths of ultrasound used clinically (approximately 2–10 MHz). Thus, the echoes received from a thrombus are actually formed by ultrasonic scattering between scatterers and the incident wave. It has been shown that the received backscattered signals can provide useful clues regarding tissue properties23,24. Ultrasonic backscattering and its coefficients or intensity-related parameters have been used in detecting different hematocrits25,26,27,28,29. Different hematocrits may result in different concentrations and arrangements of scatterers (RBCs), causing the behavior of backscattered ultrasonic signals and the corresponding statistical distributions to depend on the acoustical structures of scatterers in the thrombi. Hence, analyzing the statistical distribution of backscattered ultrasonic signals may also be a potential method for differentiating thrombi on the basis of hematocrits.
To investigate the feasibility of using ultrasonic imaging in the pretreatment evaluation of thrombi, this study (i) examined ultrasonic parameters (the echo intensity and backscattered statistics) of thrombi as a function of the hematocrit and (ii) analyzed the relationships among thrombolytic efficiencies, hematocrits, and ultrasonic parameters. The following section demonstrates that susceptibility to thrombolysis depends on the hematocrit, which can be quantified using the echo intensity and backscattered statistics. The proposed strategy has potential in the pretreatment evaluation of thrombi in the future.
Results
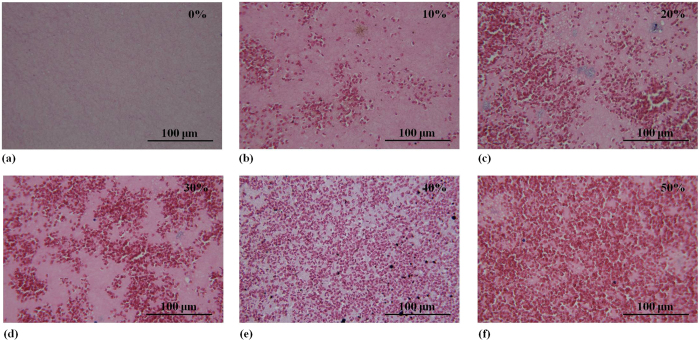
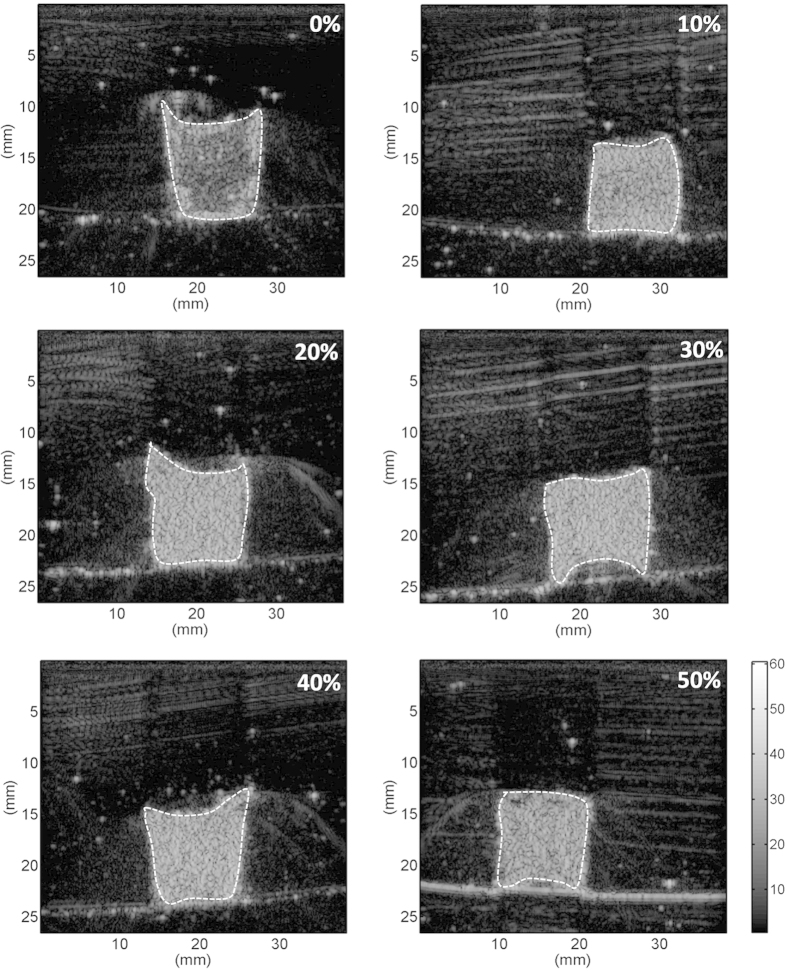
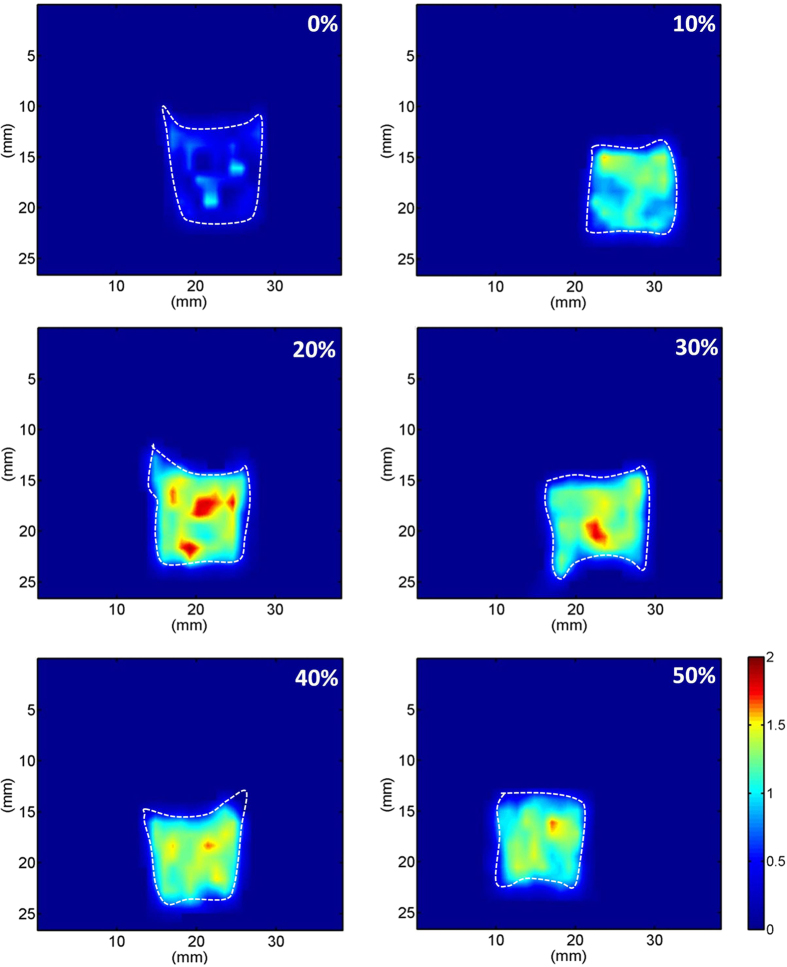
Figure 1 shows hematoxylin and eosin (H&E)-stained images prepared from thrombus samples with various hematocrits. With an increasing hematocrit, the RBC number increases in the background of the thrombus. Figure 2 shows ultrasonic B-mode images obtained from thrombi with different hematocrits. The average echo intensities obtained from whole blood and thrombi increased with the hematocrit and then decreased when the hematocrit was >20%, as shown in Fig. 3. Similar to the B-scan, the Nakagami images of thrombi appeared brighter with an increasing hematocrit, as shown in Fig. 4. This finding is supported by Fig. 5, which shows that the Nakagami parameters obtained from the whole blood and thrombi increased with the hematocrit and slightly decreased when the hematocrit was >20%. Figure 6 shows that the weight loss ratio was approximately proportional to the lysis time for each hematocrit, and Fig. 7 further indicates that thrombi with lower hematocrits have higher weight loss ratios. An exponential decay function with an equation form y = y0 + ae−bx was used to fit the data in Fig. 7; the result suggests that the weight loss ratio exponentially decreases with the hematocrit (correlation coefficient r = 0.86; probability value p <0.01). The weight loss ratio of thrombi was found to decrease exponentially with an increasing intensity (r = 0.68; p < 0.01) and Nakagami parameter (r = 0.83; p < 0.01) (Figs 8 and 9). The results show that thrombi with lower intensities and Nakagami parameters have higher thrombolytic efficiencies.
Figure 1. Hematoxylin and eosin-stained images of thrombi with different hematocrits ranging from 0% to 50%.
With an increasing hematocrit, the number of red blood cells increased in the background of the thrombus.
Figure 2. Ultrasonic B-mode images of thrombi with different hematocrits.
The brightness of the B-mode images increased as the hematocrit increased from 0% to a maximum of 20%. Beyond the hematocrit of 20%, the brightness of the B-mode images decreased slightly. Whole blood samples were liquid; hence, no images are available.
Figure 3. Echo intensities of whole blood and thrombi as a function of the hematocrit.
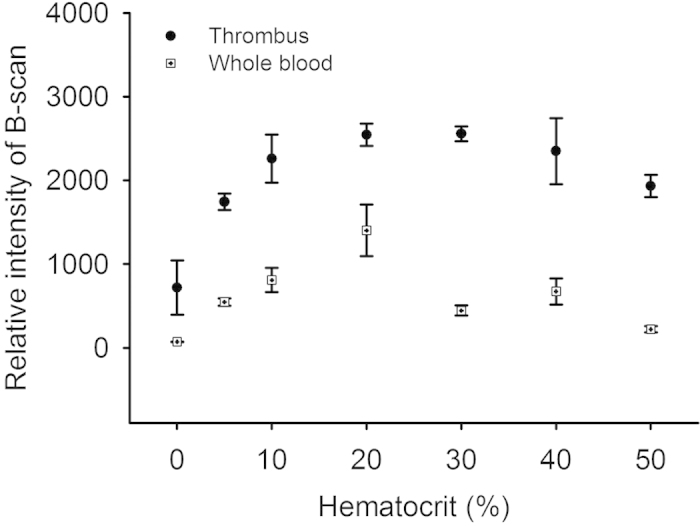
The average echo intensity obtained from whole blood increased from 70.96 to 1401.52 when the hematocrit increased from 0% to 20%, and then decreased to 221 when the hematocrit increased to 50%. The intensity measured from thrombi also increased to a maximal value of 2546.15 at a hematocrit of 20% and decreased to 1931.93 when the hematocrit increased to 50%.
Figure 4. Nakagami images of thrombi with different hematocrits.
The shading of the Nakagami image of the thrombi increased as the hematocrit increased from 0% to a maximum of 20%; however, beyond the hematocrit of 20%, the shading of the Nakagami image of the thrombi decreased slightly.
Figure 5. Nakagami parameters measured from whole blood and thrombi as a function of the hematocrit.
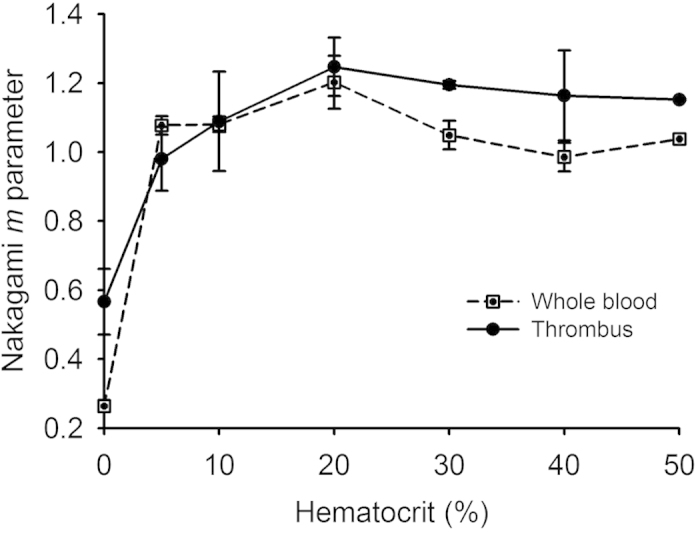
The pair of Nakagami parameters obtained from the whole blood and thrombi (m blood, m thrombus) varied from 0.26 and 0.59 to 1.20 and 1.25, respectively, when the hematocrit increased from 0% to 20%, and slightly decreased to 1.03 and 1.15 when the hematocrit increased to 50%.
Figure 6. Weight loss ratios of thrombi with different hematocrits as a function of the lysis time.
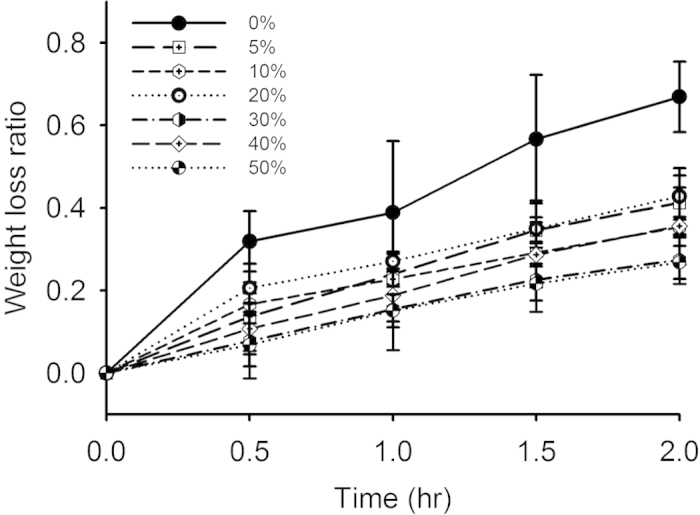
The weight loss ratio was approximately proportional to the lysis time for each hematocrit. The largest ratio of weight loss was observed at a hematocrit of 0% (%: the volume percentage of RBCs in a thrombus).
Figure 7. Curve of the weight loss ratio as a function of the hematocrit measured after thrombolysis for 2 h.
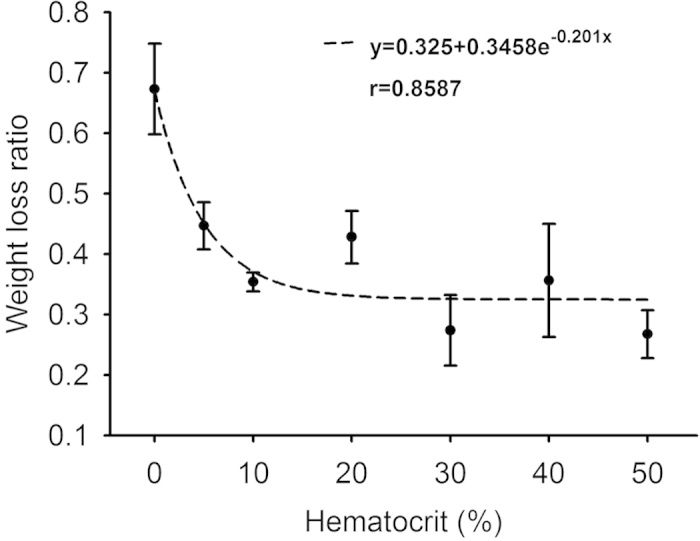
The weight loss ratio exponentially decreased from approximately 0.67 to 0.26 as the hematocrit increased from 0% to 50%. An exponential fitting suggests that the weight loss ratio is an exponentially decreasing function of the hematocrit (correlation coefficient r = 0.86).
Figure 8. Weight loss ratio as a function of the echo intensity obtained from B-scan imaging.
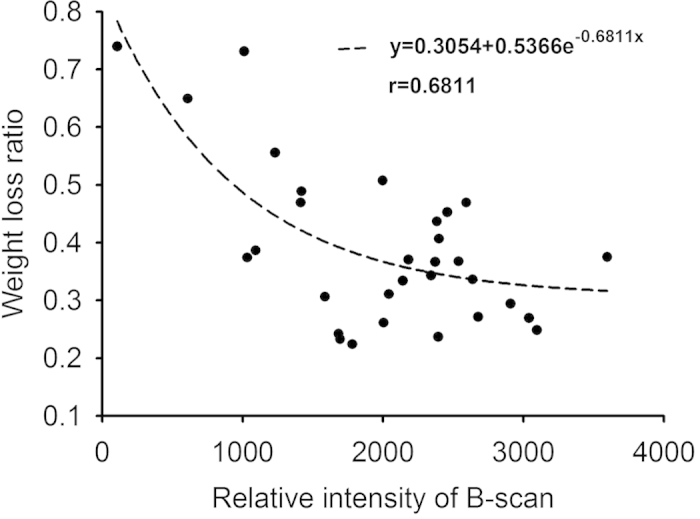
The weight loss ratio of a thrombus exponentially decreased from 0.7 to 0.3 as the intensity increased. The correlation coefficient obtained using the exponential decay function between the weight loss ratio and echo intensity was 0.68.
Figure 9. Weight loss ratio as a function of the Nakagami parameter obtained from Nakagami imaging.
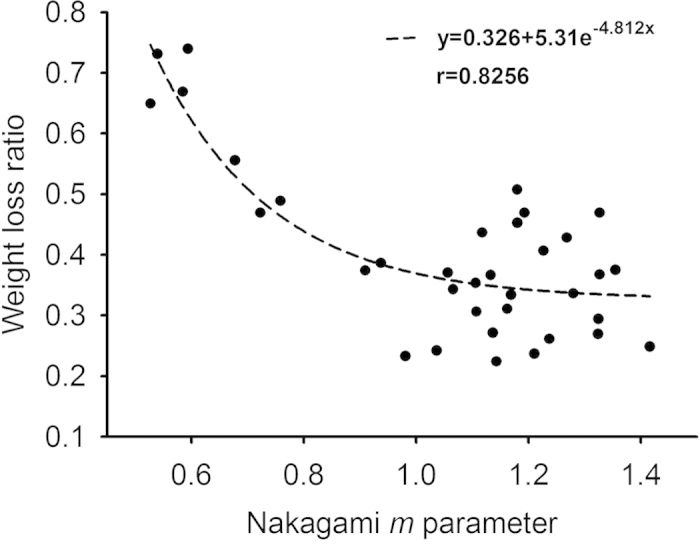
The weight loss ratio of thrombi exponentially decreased from 0.7 to 0.3 as the Nakagami parameter increased. Compared with the echo intensity, the Nakagami parameter has a higher correlation with the weight loss ratio (correlation coefficient = 0.83).
Discussion
Significance of this study
The experimental findings are summarized as follows: (i) the echo intensity and Nakagami parameter can differentiate various hematocrits in the range of 0% to 20%; (ii) a thrombus with a low hematocrit is more sensitive to treatment with a thrombolytic agent because of a high weight loss ratio; (iii) the weight loss ratio of a thrombus following treatment with a thrombolytic agent depends on the measures of the echo intensity and Nakagami parameter. This study is the first to demonstrate that parameters of ultrasonic backscattering (measured before thrombolytic treatments) may reflect the thrombolytic efficiency.
Effect of the hematocrit on the echo intensity
The trend of the echo intensity as a function of the hematocrit obtained from whole blood (Fig. 3) was consistent with the findings in previous studies on blood27,30. The echo intensities of thrombi are higher than those of whole blood. The differences in echogenicity between blood and thrombi may be contributed by fibrin fibers, which act as stronger scatterers (compared with RBCs) to increase the strength of ultrasonic backscattering measured from thrombi.
Effect of the hematocrit on backscattered statistics
The behaviors of the Nakagami parameter as a function of the hematocrit of whole blood and thrombi were similar (Fig. 5). The Nakagami parameters measured from thrombi were greater than those measured from whole blood, although the difference in the Nakagami parameter between whole blood and thrombi was not as significant as that in the echo intensity. The Nakagami parameter is a shape parameter, which is less affected by the signal amplitude and mainly depends on the statistical distribution of backscattered data. Therefore, the effect of the hematocrit on the Nakagami parameters of whole blood and thrombi should be discussed by considering the arrangements and concentrations of scatterers in the scattering medium.
In whole blood, RBCs are the primary scatterers that determine the statistical distribution of backscattered data. It is well known that backscattered statistics obey the Rayleigh distribution when the numbers of scatterers in the resolution cell of the ultrasonic transducer are higher than 1031,32,33. The resolution cell used in our experiments was at a level of cubed millimeters, and the mean volume of a RBC is approximately 63 μm3 for pigs30. Except at a hematocrit of 0%, the whole blood samples had many RBCs randomly distributed in the resolution cell, causing backscattered statistics to follow the Rayleigh distribution and the corresponding Nakagami parameters to approximate 1. A high number of RBCs in whole blood may still have an aggregation effect to some degree; hence, the Nakagami parameters corresponding to the hematocrits larger than 20% varied between 1 and 1.2. Similar results have been obtained in previous studies27,34.
At least two types of scatterers should be considered in thrombi: RBCs and fibrin fibers. A hematocrit of 0% indicates that no RBCs in a thrombus contribute echoes. In this condition, the fibrin fibers, which exhibit diverse shapes, sizes, and scatterer spacings, become the dominant scatterers and generate a scattering environment with a high degree of variances in the scattering cross sections of scatterers. Hence, the backscattered statistics tend to follow a pre-Rayleigh distribution in accordance with the Nakagami parameters lower than 1. With an increasing hematocrit, RBCs gradually replace the fibrin fibers to become the primary scatterers dominating the formation of backscattered signals, changing the acoustical structure of a thrombus from a relatively nonuniform medium (a mixture of fibrin fibers and RBCs) to a more uniform arrangement of fibers embedded with a large number of randomly distributed scatterers21. As long as the acoustical structure of a thrombus is based on a high number of scatterers, the backscattered statistics remain close to the Rayleigh distribution, and the Nakagami parameter is approximately 1.
Effect of the hematocrit on thrombolysis
The current results demonstrated that the susceptibility of a thrombus to lysis depends on the hematocrit. The weight loss ratio of a thrombus as a function of the lysis time for each hematocrit follows an approximately linear relationship (Fig. 6). This result conformed to the distance run by the fibrin boundary layer of a thrombolytic agent19 and the fiber lysis rate according to plasma thrombi (thrombi with 0% hematocrit)15. The overall thrombolytic efficiency after 2-h lysis indicated that RBCs increase lytic resistance. As shown in Fig. 7, the weight loss ratios of thrombi decreased from 0.67 to 0.26 with increasing the hematocrit from 0% – 30%, and those corresponding to the hematocrits >30% varied in a limited range between 0.25 and 0.35. This may be explained by two reasons. First, the occlusion of pores in fibrin networks by RBCs reduces the pore size20, influencing permeability35,36, which is the most crucial mode of enzyme transport from the outside to the inside of thrombi35,37. Second, RBC fibrinogen receptors cause fibers to thin19,38 and, thus, have fewer binding sites for thrombolytic agents, limited access for thrombolytic agents to the binding sites, or a combination of both13. This reduces the interaction between fibrin fibers and thrombolytic agents, and hence reduces the thrombolytic efficiency.
Potential of backscattered statistics in thrombolysis evaluation
Note that clinical thrombolytic treatment carries the hazard of secondary hemorrhage1,10, and thus it would be valuable to know in advance whether the offending thrombus is susceptible or inherently resistant to thrombolytic treatment. Our proposed concept, based on the analysis of ultrasonic backscattering statistics, may enable evaluating the outcome of thrombolysis before treatment. The results in Figs 8 and 9 indicated that the weight loss ratio of a thrombus following treatment with thrombolytic agents appears to be an exponential decay function of the ultrasonic parameters (the echo intensity and Nakagami parameter). In particular, the Nakagami parameter, based on backscattered statistics, has a stronger correlation with the weight loss ratio of thrombi according to the correlation coefficient obtained from curve fitting. The experimental findings based on the current data suggest that ultrasound Nakagami imaging can characterize thrombi to provide information of backscattered statistics, which may be associated with the thrombolytic efficiency.
Future work
Some concerns must be clarified for future clinical applications: (i) the properties of thrombi obtained in in vitro and in vivo environments are different. The spatial distribution of RBCs in thrombi produced in vivo is relatively nonuniform compared to that produced in in vitro samples. Unlike in vitro thrombi mainly composed of uniform fibrin and RBCs, the structures of in vivo thrombi also include platelets, fibrin-platelet patterns39, or platelet aggregations40. The distribution of platelets in a thrombus is actually an important factor in thrombolysis. For instance, the laminations of coalescent platelets mixed with the fibrin network (known as Zahn lines41,42) in in vivo thrombi may result in a stronger resistance to thrombolysis43. For these reasons, the performance of using Nakagami imaging to evaluate the lysis of thrombus in vivo should be investigated using animal models. (ii) The thrombus age is also a factor that affects the efficiency of thrombolysis. Thrombi with different ages have different degrees of fibrin cross-bridging. It has been shown that aged (retracted) thrombi have a stronger resistance to thrombolysis44,45. The dependencies of the Nakagami parameter on the weight loss ratios of thrombi with different ages should also be established. (iii) The susceptibility to thrombolysis depends not only on the thrombus composition but also on the flow and systemic factors. Flow dynamics may vary according to different vessel locations, velocities, diameters, and branching anatomies, causing the permeability of thrombi to change to influence the susceptibility to thrombolysis16,35,46. Systemic factors such as blood glucose and plasminogen activator levels may also influence the activity of thrombolytic agents47. The aforementioned concerns require clinical measurements to clarify.
Conclusion
This study used an in vitro model to perform ultrasonic B-mode and Nakagami parametric imaging of thrombi with different hematocrits for comparison between the weight loss ratios of thrombi following treatment with thrombolytic agents and ultrasonic parameters. The experimental results demonstrated that the hematocrit of a thrombus affects the material structure and corresponding response to thrombolysis. Compared with the echo intensity obtained from the conventional B-scan, the Nakagami parameter estimated from ultrasonic Nakagami imaging improves the differentiation of various hematocrits and correlates well with the weight loss ratios of thrombi. The current findings suggest that using ultrasonic Nakagami imaging characterizing a thrombus provides information of backscattered statistics, which may be associated with the thrombolytic efficiency.
Materials and Methods
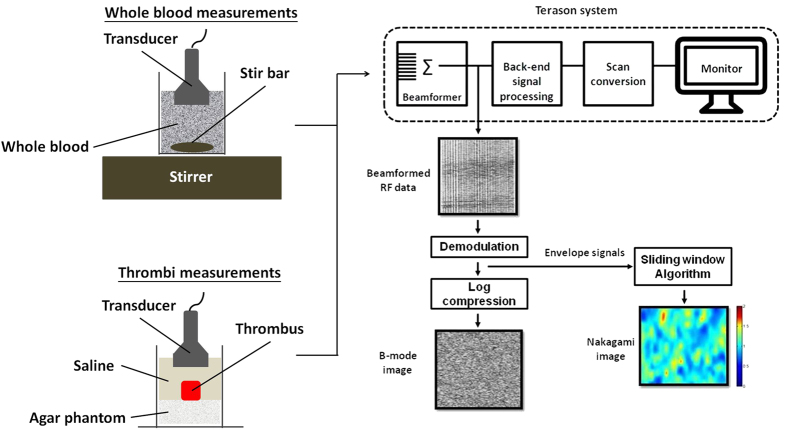
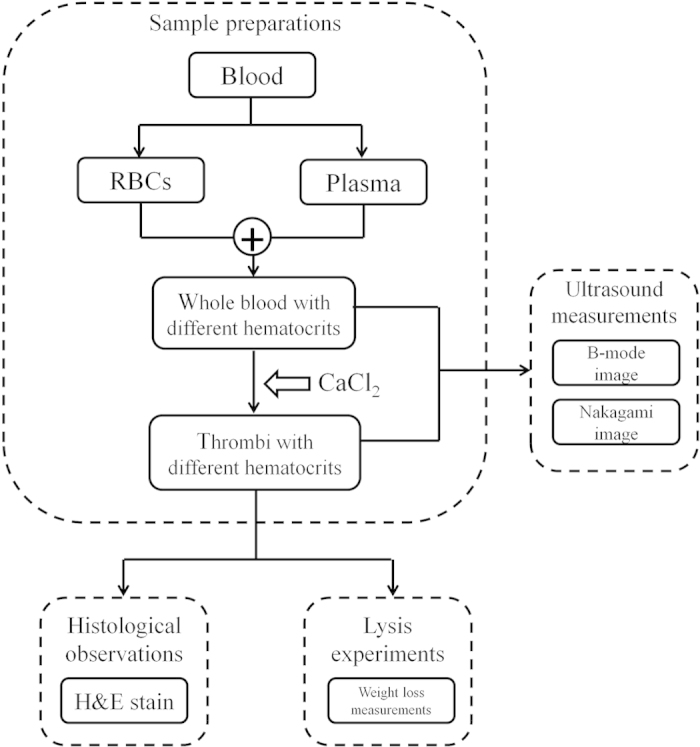
The experimental design is illustrated in Fig. 10 and includes sample preparations, ultrasonic measurements, histological observations, and experiments on thrombolysis.
Figure 10. Flowchart of the experiments, including sample preparations, ultrasonic measurements, histological observations, and experiments on thrombolysis.
Sample preparations: whole blood
Fresh porcine blood containing a 15% acid citrate dextrose anticoagulant solution was collected from a local slaughterhouse, and no specific permission was required. Porcine blood is a suitable material for fundamental research because of its availability and biochemical similarity to human blood48. Ultrasonic backscattering depends on the dimensions of scatterers. Because the dimensions of porcine RBCs (63 μm3) are close to those of human RBCs (87 μm3)30, the generated backscattered echoes in porcine blood may behave like those of humans. The blood was passed through a sponge to filter out impurities and was discarded whenever coagulation was observed. The blood was centrifuged at room temperature for 15 min at 1500 rpm to separate RBCs from the plasma. Whole blood was prepared by adding RBCs to plasma to obtain hematocrits of 0%, 5%, 10%, 20%, 30%, 40%, and 50%. For each hematocrit, 10 samples were prepared (total n = 70).
Sample preparations: thrombi
To induce thrombi in vitro, whole blood for each hematocrit was added to a container, which was placed on a stirrer to be stirred for 15 min and bathed in water at 37.3 °C for 20 min while being exposed to room air for equilibrating the gas content. Thrombi coagulation was initiated by adding 0.5 M CaCl2 at a ratio of 1:1049,50, and the coagulum was molded in a 6-mL syringe. The syringes were incubated at 37.3 °C for 3 h during coagulation. The average volume of thrombi was approximately 1 cm3. Ten animals were used to induce thrombi for each hematocrit (total n = 70).
Ultrasonic measurements of whole blood and thrombi
Figure 11 explains how we performed ultrasonic measurements and analyzed the echo intensities and statistical distributions of backscattered signals. Prior to experiments on thrombi, evaluating whole blood (without fibrin structures) for echo intensities and backscattered statistics as a function of the hematocrit is necessary to clarify the effects of RBCs and fibrin structures on ultrasonic signals. In whole blood, rouleaux formation or RBC aggregation occurs, resulting in the nonuniform distribution of scatterers51. For whole blood measurements, an ultrasonic transducer was immersed in blood, which was stirred using a magnetic stirrer at a rotational speed of 200 rpm to randomly distribute RBCs in the plasma.
Figure 11. Illustration of how we performed ultrasonic measurements and analyzed the echo intensity and statistical distribution of backscattered signals.
For thrombotic measurements, each thrombus sample was placed on an agar phantom in an acrylic case filled with a saline solution. An agar phantom was used as a bottom layer to prevent the overlap of strong reflection signals from the bottom of the case with backscattered signals from the thrombi.
Both whole blood and thrombus samples were imaged using a clinical ultrasonic scanner (Model 3000, Terason, Burlington, MA, USA) equipped with a 7.5-MHz linear array transducer (Model 10L5, Terason) to acquire raw beamformed radiofrequency (RF) data consisting of 256 scan lines of backscattered signals. The focal zone was adjusted to the center of the samples to reduce the effect of beam diffraction. The time gain compensation was not used. The pulse length of the transducer and the sampling rate of RF signals were 0.7 mm and 30 MHz, respectively. In total, five independent scans of each sample were performed. The system settings remained the same for all image data acquired.
For each image RF datum, each scan line was demodulated using the absolute value of Hilbert transform52 to construct an envelope image for ultrasonic B-mode (echo intensity calculation) and Nakagami imaging (backscattered statistics analysis).
Ultrasonic B-mode and Nakagami imaging
The ultrasonic B-mode image was formed using a logarithm-compressed envelope image (dynamic range = 60 dB). Ultrasonic Nakagami imaging was used to measure the backscattered statistics. The Nakagami image is a well-established ultrasonic parametric image based on the Nakagami parameter m used for backscattered statistics analysis53,54,55,56,57,58,59. The Nakagami parameter is a shape parameter of the Nakagami statistical model and can be estimated as follows:
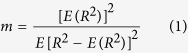 |
where R is the envelope of backscattered ultrasonic signals60. In general, the backscattered statistics of the envelopes received from biological tissues can be divided into three distribution types61,62: (i) the Rayleigh distribution caused by a high number of randomly distributed scatterers in the resolution cell of the transducer; (ii) the pre-Rayleigh distribution (with a phase lead compared to Rayleigh statistics) caused by a low scatterer concentration or the presence of scatterers in the resolution cell with randomly varying scattering cross sections with a high degree of variance; and (iii) the post-Rayleigh distribution (with a phase lag compared with Rayleigh statistics) caused by a resolution cell containing periodically located scatterers in addition to randomly distributed scatterers. A study showed that the variation of the Nakagami parameter from 0 to 1 corresponds to a change in the envelope statistics from pre-Rayleigh to Rayleigh distributions; Nakagami parameters higher than 1 indicate that the statistics of the backscattered signal conform to post-Rayleigh distributions60. Consequently, the Nakagami distribution is a general model for ultrasonic backscattering.
The details of the algorithm for ultrasonic Nakagami imaging can be found in previous studies62,63,64,65. In brief, the Nakagami image is based on the Nakagami parametric map, which is constructed using a square sliding window to process the envelope image (without logarithmic compression). This involves two main steps: (i) a square window within the envelope image is used to collect local backscattered envelopes for estimating the local Nakagami parameter, which is assigned as the new pixel located in the center of the window; and (ii) the window is allowed to move throughout the envelope image in one-pixel steps, and Step 1 is repeated to construct the map of the local Nakagami parameter. Previous studies have suggested that the side length of the square window that can simultaneously satisfy the image resolution and stable parameter estimation is three times the pulse length of the transducer63. In this study, we used a square window with a side length of 2.1 mm, corresponding to three times the transducer pulse length, to construct the Nakagami image.
Image data analysis
For each sample, the average echo intensity and Nakagami parameter were calculated using the envelope and Nakagami images, respectively. A region of interest with a size of 5 × 5 mm2 was used to acquire the corresponding image pixel data for averaging. The curves of the relative intensity (i.e., envelope amplitude) and Nakagami parameter as functions of the hematocrit were plotted. Data are expressed as means ± standard deviation (SD).
Histological observations
To confirm the change in the number of RBCs with an increasing hematocrit, each thrombus was processed using H&E staining. Each thrombus was immersed in a 10% formaldehyde-buffered solution for 24 h. Thrombi were then paraffin-embedded, cut into 5-μm sections, and stained with H&E. Histological images of whole thrombi (400 × magnification) were photographed using a Leica DM759 bright-field microscope with a color digital camera (Canon EOS600D).
Experiments on thrombolysis
After ultrasonic measurements, experiments on thrombolysis were performed to examine the effect of the hematocrit on the thrombolytic efficiency. Each thrombus was placed in an acrylic case filled with a thrombolytic agent solution, which was incubated at 37.3 °C. The thrombolytic agent solution was prepared by dissolving commercial lyophilized urokinase powder (250000 IU, Green Cross Co. Ltd., Taipei, Taiwan) in 25 mL of normal saline, according to the manufacturer’s instructions. The thrombolysis efficiency obtained using urokinase is almost the same as that of other thrombolytic agents (e.g., streptokinase or tissue-type plasminogen activator)66,67. However, urokinase is suggested for in vitro tests only because of a poor fibrin specificity1. During experiments, the ratios of weight loss for thrombi with hematocrits were measured every 30 min to 2 h. The ratios of weight loss (data are expressed as means ± SD) as a function of time were plotted to evaluate the thrombolytic efficiencies at different hematocrits. Measuring weight loss is a simple experimental technique that is minimally susceptible to intersample variability58.
Statistical analysis
According to observations on the relationships between the weight loss of a thrombus and ultrasonic parameters (the echo intensity and Nakagami parameter), nonlinear curve fitting in an equation of the form y = y0 + ae−bx was carried out using the SigmaPlot software (Version 9.0, Systat Software, Inc., CA, USA) to calculate the correlation coefficient r and the probability value (p-value).
Additional Information
How to cite this article: Fang, J. and Tsui, P.-H. Evaluation of thrombolysis by using ultrasonic imaging: an in vitro study. Sci. Rep. 5, 11669; doi: 10.1038/srep11669 (2015).
Acknowledgments
This work was supported by the Ministry of Science and Technology (Taiwan) under Grant No. MOST 103-2221-E-182-001-MY3 and the Chang Gung Memorial Hospital (Linkou, Taiwan) under Grant Nos. CMRPD3E0241, CIRPD1E0021, and CMRPD1C0661.
Footnotes
Author Contributions J.F. and P.H.T. wrote the manuscript text and performed data analysis. J.F. performed experiments and prepared figures. All authors reviewed the manuscript.
References
- Khan I. A. & Gowda R. M. Clinical perspectives and therapeutics of thrombolysis. Int. J. Cardiol. 91, 115–127 (2003). [DOI] [PubMed] [Google Scholar]
- Roger V. L. et al. Heart disease and stroke statistics–2012 update: a report from the American Heart Association. Circulation 125, e2–e220 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Augustinos P. & Ouriel K. Invasive approaches to treatment of venous thromboembolism. Circulation 110, 27–34 (2004). [DOI] [PubMed] [Google Scholar]
- McRae S. J. & Ginsberg J. S. Initial treatment of venous thromboembolism. Circulation 110, 3–9 (2004). [DOI] [PubMed] [Google Scholar]
- Pashos C. L. et al. Trends in the use of drag therapies in patients with acute myocardial infarction: 1988 to 1992. J. Am. Coll. Cardiol. 23, 1023–1030 (1994). [DOI] [PubMed] [Google Scholar]
- Ouriel K., Veith F. J. & Sasahara A. A. A comparison of recombinant urokinase with vascular surgery as initial treatment for acute arterial occlusion of the legs. N. Engl. J. Med. 338, 1105–1111 (1998). [DOI] [PubMed] [Google Scholar]
- Sekoranja L. et al. Intravenous Versus Combined (Intravenous and Intra-Arterial) Thrombolysis in Acute Ischemic Stroke A Transcranial Color-Coded Duplex Sonography–Guided Pilot Study. Stroke 37, 1805–1809 (2006). [DOI] [PubMed] [Google Scholar]
- Goldhaber S. et al. Alteplase versus heparin in acute pulmonary embolism: randomised trial assessing right-ventricular function and pulmonary perfusion. Lancet 341, 507–511 (1993). [DOI] [PubMed] [Google Scholar]
- Konstantinides S., Geibel A., Heusel G., Heinrich F. & Kasper W. Heparin plus alteplase compared with heparin alone in patients with submassive pulmonary embolism. N. Engl. J. Med. 347, 1143–1150 (2002). [DOI] [PubMed] [Google Scholar]
- Hirschl M., Gwechenberger M., Zehetgruber M. & Weber H. Severe complications following thrombolytic therapy of an acute thrombosis of a prosthetic mitral valve. J. Clin. Invest. 72, 466–469 (1992). [DOI] [PubMed] [Google Scholar]
- Cadroy Y. & Hanson S. R. Effects of red blood cell concentration on hemostasis and thrombus formation in a primate model. Blood 75, 2185–2193 (1990). [PubMed] [Google Scholar]
- Kurz K., Main B. & Sandusky G. Rat model of arterial thrombosis induced by ferric chloride. Thromb. Res. 60, 269–280 (1990). [DOI] [PubMed] [Google Scholar]
- Gabriel D. A., Muga K. & Boothroyd E. M. The effect of fibrin structure on fibrinolysis. J. Biol. Chem. 267, 24259–24263 (1992). [PubMed] [Google Scholar]
- Weisel J. Structure of fibrin: impact on clot stability. J. Thromb. Haemost. 5, 116–124 (2007). [DOI] [PubMed] [Google Scholar]
- Collet J. et al. Influence of fibrin network conformation and fibrin fiber diameter on fibrinolysis speed dynamic and structural approaches by confocal microscopy. Arterioscler. Thromb. Vasc. Biol. 20, 1354–1361 (2000). [DOI] [PubMed] [Google Scholar]
- Rijken D. & Sakharov D. Molecular transport during fibrin clot lysis. Fibrinolysis Proteol. 14, 98–113 (2000). [Google Scholar]
- Weisel J. W., Veklich Y., Collet J. P. & Francis C. W. Structural studies of fibrinolysis by electron and light microscopy. Thromb. Haemost. 82, 277–282 (1999). [PubMed] [Google Scholar]
- Lord S. T. Molecular mechanisms affecting fibrin structure and stability. Arterioscler. Thromb. Vasc. Biol. 31, 494–499 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wohner N. et al. Lytic resistance of fibrin containing red blood cells. Arterioscler. Thromb. Vasc. Biol. 31, 2306–2313 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Varin R. et al. Whole blood clots are more resistant to lysis than plasma clots-greater efficacy of rivaroxaban. Thromb. Res. 131, e100–e109 (2013). [DOI] [PubMed] [Google Scholar]
- Gersh K. C., Nagaswami C. & Weisel J. W. Fibrin network structure and clot mechanical properties are altered by incorporation of erythrocytes. Thromb. Haemost. 102, 1169–1175 (2009). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Carr M. E. Jr. & Hardin C. L. Fibrin has larger pores when formed in the presence of erythrocytes. Am. J. Physiol. 253, 1069–1073 (1987). [DOI] [PubMed] [Google Scholar]
- Bamber J. & Hill C. Acoustic properties of normal and cancerous human liver—I. Dependence on pathological condition. Ultrasound Med. Biol. 7, 121–133 (1981). [DOI] [PubMed] [Google Scholar]
- Insana M. F., Wagner R. F., Brown D. G. & Hall T. J. Describing small‐scale structure in random media using pulse‐echo ultrasound. J. Acoust. Soc. Am. 87, 179–192 (1980). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shung K. K., Sigelmann R. A. & Reid J. M. Scattering of ultrasound by blood. IEEE Trans. Biomed. Eng. 23, 460–467 (1976). [DOI] [PubMed] [Google Scholar]
- Shung K. K. On the ultrasound scattering from blood as a function of hematocrit. IEEE Trans. Sonics Ultrason. 29, 327–330 (1982). [Google Scholar]
- Mo L. Y. L., Kuo I. Y., Shung K. K., Ceresne L. & Cobbold R. S. C. Ultrasound scattering from blood with hematocrits up to 100%. IEEE Trans. Biomed. Eng. 41, 91–95 (1994). [DOI] [PubMed] [Google Scholar]
- Huang C. C. & Wang S. H. Statistical variations of ultrasound signals backscattered from flowing blood. Ultrasound Med. Biol. 33, 1943–1954 (2007). [DOI] [PubMed] [Google Scholar]
- Huang C. C. High-frequency attenuation and backscatter measurements of rat blood between 30 and 60 MHz. Phys. Med. Biol. 55, 5801–5815 (2010). [DOI] [PubMed] [Google Scholar]
- Shung K. K. & Thieme G. A. Ultrasonic scattering in biological tissues (CRC Press, Boca, Raton, 1992). [Google Scholar]
- Oosterveld B., Thijssen J. & Verhoef W. Texture of B-mode echograms: 3-D simulations and experiments of the effects of diffraction and scatterer density. Ultrason. Imaging 7, 142–160 (1985). [DOI] [PubMed] [Google Scholar]
- Tuthill T., Sperry R. & Parker K. Deviations from Rayleigh statistics in ultrasonic speckle. Ultrason. Imaging 10, 81–89 (1988). [DOI] [PubMed] [Google Scholar]
- Zagzebski J. A., Chen J. F., Dong F. & Wilson T. Intervening attenuation affects first-order statistical properties of ultrasound echo signals. IEEE Trans. Ultrason,. Ferroelect., Freq. Contr. 46, 35–40 (1999). [DOI] [PubMed] [Google Scholar]
- Cloutier G. et al. Non-Gaussian statistics and temporal variations of the ultrasound signal backscattered by blood at frequencies between 10 and 58 MHz. J. Acoust. Soc. Am. 116, 566–577 (2004). [DOI] [PubMed] [Google Scholar]
- Diamond S. L. & Anand S. Inner clot diffusion and permeation during fibrinolysis. Biophys. J. 65, 2622–2643 (1993). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Anand S., Kudallur V., Pitman E. B. & Diamond S. L. Mechanisms by which thrombolytic therapy results in nonuniform lysis and residual thrombus after reperfusion. Ann. Biomed. Eng. 25, 964–974 (1996). [PubMed] [Google Scholar]
- Blinc A. et al. Dependence of blood clot lysis on the mode of transport of urokinase into the clot–a magnetic resonance imaging study in vitro. Thromb. Haemost. 65, 549–552 (1991). [PubMed] [Google Scholar]
- Carvalho F. A. et al. Atomic force microscopy-based molecular recognition of a fibrinogen receptor on human erythrocytes. ACS Nano 4, 4609–4620 (2010). [DOI] [PubMed] [Google Scholar]
- Marder V. J. et al. Analysis of thrombi retrieved from cerebral arteries of patients with acute ischemic stroke. Stroke 37, 2086–2093 (2006). [DOI] [PubMed] [Google Scholar]
- Tratar G. et al. Characterization of pulmonary emboli ex vivo by magnetic resonamce imaging and ultrasound. Thromb. Res. 120, 763–771 (2007). [DOI] [PubMed] [Google Scholar]
- Wessler S., Reiner L., Freiman D. G., Reimer S. & Lertzman M. Serum-induced thrombosis studies of its induction and evolution under controlled conditions in vivo. Circulation 20, 864–874 (1959). [DOI] [PubMed] [Google Scholar]
- Lee R., Adlam D., Clelland C. A. & Channon KM. Lines of Zahn in coronary artery thrombus. Eur. Heart. J. 33, 1039 (2012). [DOI] [PubMed] [Google Scholar]
- Vidmar J. et al. An MRI study of the differences in the rate of thrombolysis between red blood cell‐rich and platelet‐rich components of venous thrombi ex vivo. J. Magn. Reson. Im. 34, 1184–1191 (2011). [DOI] [PubMed] [Google Scholar]
- Kramer M. C. A. et al. Presence of older thrombus is an independent predictor of long-term mortality in patients with ST-elevation myocardial infarction treated with thrombus aspiration during primary percutaneous coronary intervention. Circulation 118, 1810–1816 (2008). [DOI] [PubMed] [Google Scholar]
- Holland C. K., Vaidya S. S., Datta S., Coussios C. C. & Shaw G. J. Ultrasoundenhanced tissue plasminogen activator thrombolysis in an in vitro porcine clot model. Thromb. Res. 121, 663–673 (2008). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Anand S., Kudallur V., Pitman E. B. & Diamond S. L. Mechanisms by which thrombolytic therapy results in nonuniform lysis and residual thrombus after reperfusion. Ann. Biomed. Eng. 25, 964–974 (1997). [PubMed] [Google Scholar]
- Ribo M. et al. Acute hyperglycemia state is associated with lower tPA-induced recanalization rates in stroke patients. Stroke 36, 1705–1709 (2005). [DOI] [PubMed] [Google Scholar]
- Sutton J. T., Ivancevich N. M., Perrin S. R., Vela D. C., & Holland C. K. Clot retraction affects the extent of ultrasound-enhanced thrombolysis in an ex vivo porcine thrombosis model. Ultrasound Med. Biol. 39, 813–824 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Huang C. C. & Wang S. H. Assessment of blood coagulation under various flow conditions with ultrasound backscattering. IEEE Trans. Biomed. Eng. 54, 2223–2230 (2007). [DOI] [PubMed] [Google Scholar]
- Huang C. C., Shih C. C., Liu T. Y. & Lee P. Y. Assessing the viscoelastic properties of thrombus using a solid-sphere-based instantaneous force approach. Ultrasound Med. Biol. 37, 1722–1733 (2011). [DOI] [PubMed] [Google Scholar]
- Shung K. & Reid J. Ultrasonic instrumentation for hematology. Ultrason. Imaging 1, 280–294 (1979). [DOI] [PubMed] [Google Scholar]
- Azhari H. Basics of biomedical ultrasound for engineers. (Wiley-IEEE Press, Hoboken, New Jersey, 2010). [Google Scholar]
- Gu X., Wei M., Zong Y., Jiang H. & Wan M. Flow Quantification with Nakagami Parametric Imaging for Suppressing Contrast Microbubbles Attenuation. Ultrasound Med. Biol. 39, 660–669 (2013). [DOI] [PubMed] [Google Scholar]
- Ho M. C. et al. Using ultrasound Nakagami imaging to assess liver fibrosis in rats. Ultrasonics 52, 215–222 (2012). [DOI] [PubMed] [Google Scholar]
- Lin Y. H., Huang C. C. & Wang S. H. Quantitative assessments of burn degree by high-frequency ultrasonic backscattering and statistical model. Phys. Med. Biol. 56, 757–773 (2011). [DOI] [PubMed] [Google Scholar]
- Yang X. et al. Noninvasive evaluation of vaginal fibrosis following radiotherapy for gynecologic malignancies: A feasibility study with ultrasound B-mode and Nakagami parameter imaging. Med. Phys. 40, 022901-1-022901-7 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhang S. et al. Feasibility of using Nakagami distribution in evaluating the formation of ultrasound-induced thermal lesions. J. Acoust. Soc. Am. 131, 4836–4844 (2012). [DOI] [PubMed] [Google Scholar]
- Larrue A. & Noble J. A. Nakagami imaging with small windows. IEEE International Symposium on Biomedical Imaging, Chicago, Illinois (doi: 10.1109/ISBI.2011.5872546) (2011, March 30).
- Ho M. C. et al. Using ultrasound Nakagami imaging to assess liver fibrosis in rats. Ultrasonics 52, 215–222 (2012). [DOI] [PubMed] [Google Scholar]
- Shankar P. M. A general statistical model for ultrasonic backscattering from tissues. IEEE Trans. Ultrason., Ferroelect., Freq. Contr. 47, 727–736 (2007). [DOI] [PubMed] [Google Scholar]
- Shankar P. M. et al. Classification of eltrasonic B-mode images of breast masses using Nakagami distribution. IEEE Trans. Ultrason., Ferroelect., Freq. Contr. 48, 569–580 (2001). [DOI] [PubMed] [Google Scholar]
- Tsui P. H. Minimum requirement of artificial noise level for using noise-assisted correlation algorithm to suppress artifacts in ultrasonic Nakagami images. Ultrason. Imaging. 34, 110–124 (2012). [DOI] [PubMed] [Google Scholar]
- Tsui P. H. & Chang C. C. Imaging local scatterer concentrations by the Nakagami statistical model. . Ultrasound Med. Biol. 33, 608–619 (2007). [DOI] [PubMed] [Google Scholar]
- Tsui P. H., Yeh C. K. & Chang C. C. Microvascular flow estimation by contrast-assisted ultrasound B-scan and statistical parametric images. IEEE Trans. Inf. Technol. Biomed. 13, 360–369 (2009). [DOI] [PubMed] [Google Scholar]
- Tsui P. H. et al. Ultrasound temperature estimation based on probability variation of backscatter data. Med. Phys. 39, 2369–2385 (2012). [DOI] [PubMed] [Google Scholar]
- Sabovic M. & KeberIn D. In-vitro synergism between t-PA and scu-PA depends on clot retraction. Fibrinolysis 9, 101–105 (1995). [Google Scholar]
- Sabovic M. & Keber D. Factors influencing the lysis of ex vivo human thrombi. Fibrinolysis 2, 103–109 (1996). [Google Scholar]