Human Representation of Visuo-Motor Uncertainty as Mixtures of Orthogonal Basis Distributions

Abstract

In many visuo-motor decision tasks subjects compensate for their own visuo-motor error, earning close to the maximum reward possible. To do so they must combine information about the distribution of possible error with values associated with different movement outcomes. The optimal solution is a potentially difficult computation that presupposes knowledge of the probability density function (pdf) of visuo-motor error associated with each possible planned movement. It is unclear how the brain represents such pdfs or computes with them. In three experiments, we used a forced-choice method to reveal subjects’ internal representations of their spatial visuo-motor error in a speeded reaching movement. While subjects’ objective distributions were unimodal, close to Gaussian, their estimated internal pdfs were typically multimodal, better described as mixtures of a small number of distributions differing only in location and scale. Mixtures of a small number of uniform distributions outperformed other mixture distributions including mixtures of Gaussians.

Introduction

Think about a baseball game. The batter has to decide whether and how to hit the incoming pitch. He needs to judge the position and speed of the ball—given his own visual uncertainty—in order to estimate the probability of a successful swing—given his own visuo-motor uncertainty.

Visuo-motor decisions like this are common in everyday life and have been studied in a rich and increasing body of laboratory tasks^1–3. Human subjects are frequently found to compensate for their own sensorimotor uncertainty in ways that approximate an ideal Bayesian observer who maximizes expected reward^4–11. While plausible neural representations have been proposed for the combination of probabilistic information^12,13, little is known about representations of probability density functions (pdfs) that capture visuo-motor error¹⁴.

Bayesian movement planning

In the framework of Bayesian decision theory² the visuo-motor uncertainty associated with a possible reaching movement is summarized as a probability density function (pdf) on possible movement outcomes in space or time. The pdf is often close to Gaussian in form (blue curve in Fig. 1a, drawn as 1-D for convenience) and is centered on the point that the subject aims for. Suppose now that the subject can gain a reward if she reaches to and hits a small target. A plot of the reward associated with each possible outcome is called the gain function G(x) and here is either 0 (outside the target) or the promised reward (inside the target). If the subject aims at location a then her expected gain on each attempt would be EG = ∫ G(x)f(x − a) dx, the integral of the product of the pdf with a gain function². In Figure 1b we illustrate the computation of expected gain when the subject is aiming at the center of the target.

Figure 1.

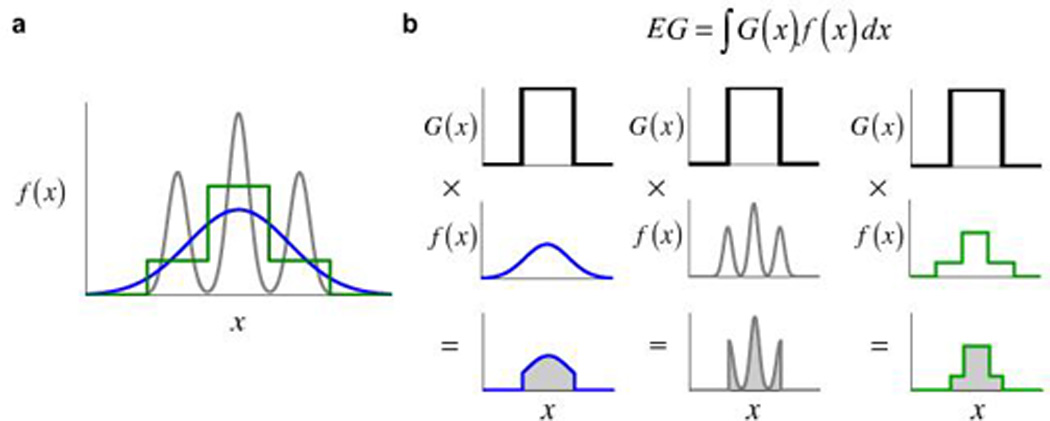
Computation of expected gain. (a) Three examples of probability density functions (pdfs). Gaussian distribution (blue), an mG-mix mixture distribution (gray), and a U-mix mixture distribution (green). (b) The computation of expected gain (EG) for each. G(x) denotes the gain function, f(x) denotes the pdf. The areas of the shaded regions in the plots of G(x) times f(x) correspond to EG = ∫G(x)f(x) dx.

Discrete mixture distributions

The computation involved is potentially demanding and a possible way to reduce the computational load is to use additive weighted mixtures of a fixed set of basis distributions b₁(x),…,b_n(x) to approximate the objective pdfs¹⁵:

$$f(x)\approx \sum _{i=1}^n{w}_i{b}_i(x)$$ (1)

Two examples of a discrete mixture distribution are shown in Figure 1a, the first based on non-overlapping uniform basis distributions, the second on Gaussian distributions that all share a common variance but differ in location. The Gaussian basis functions overlap but—if they are sufficiently widely separated—then they are effectively orthogonal for our purposes. We refer to such mixtures of a finite number of orthogonal or nearly orthogonal functions as discrete mixture distributions.

In three experiments, we estimated the internal pdfs used by human subjects in planning speeded reaching movements (method described below) and compared them to their objective pdfs. We found that (1) subjects’ choice behavior was better described by (Bayesian-optimal) decisions based upon a mixture of discrete distributions than by single Gaussian distributions or other unimodal distributions, even though their actual motor error distributions were close to Gaussian; (2) the mixture of non-overlapping uniform distributions (i.e. U-mix, Fig. 1a) outperformed other discrete mixture distributions including mixture of Gaussians. We will show that the number of basis functions in the discrete mixture representation needed to account for human performance is remarkably small, roughly 2–6.

Discrete weighted mixture representations can speed computation of expected gain: if the expected gain for each basis function can be computed, the expected gain associated with alternative targets or movement plans would be reduced to weighted linear summation of the contributions from each basis distribution. The use of mixtures of distributions is also relevant to Bayesian model averaging, models based upon mixtures of experts, and hierarchical formulations of motor control (e.g. hierarchical MOSAIC¹⁶).

Estimating internal pdfs

Each experiment consisted of two phases, training and choice. The results of the training phase allowed us to estimate subjects’ objective pdfs; the results of the choice phase allowed us to estimate their internal pdfs.

Figure 2 illustrates the task and design of Experiment 1. Human subjects were first trained to repeatedly reach to a specific target on the screen within a time limit (Fig. 2a). Typically, their endpoints had a distribution close to bivariate Gaussian (Fig. 2b).

Figure 2.

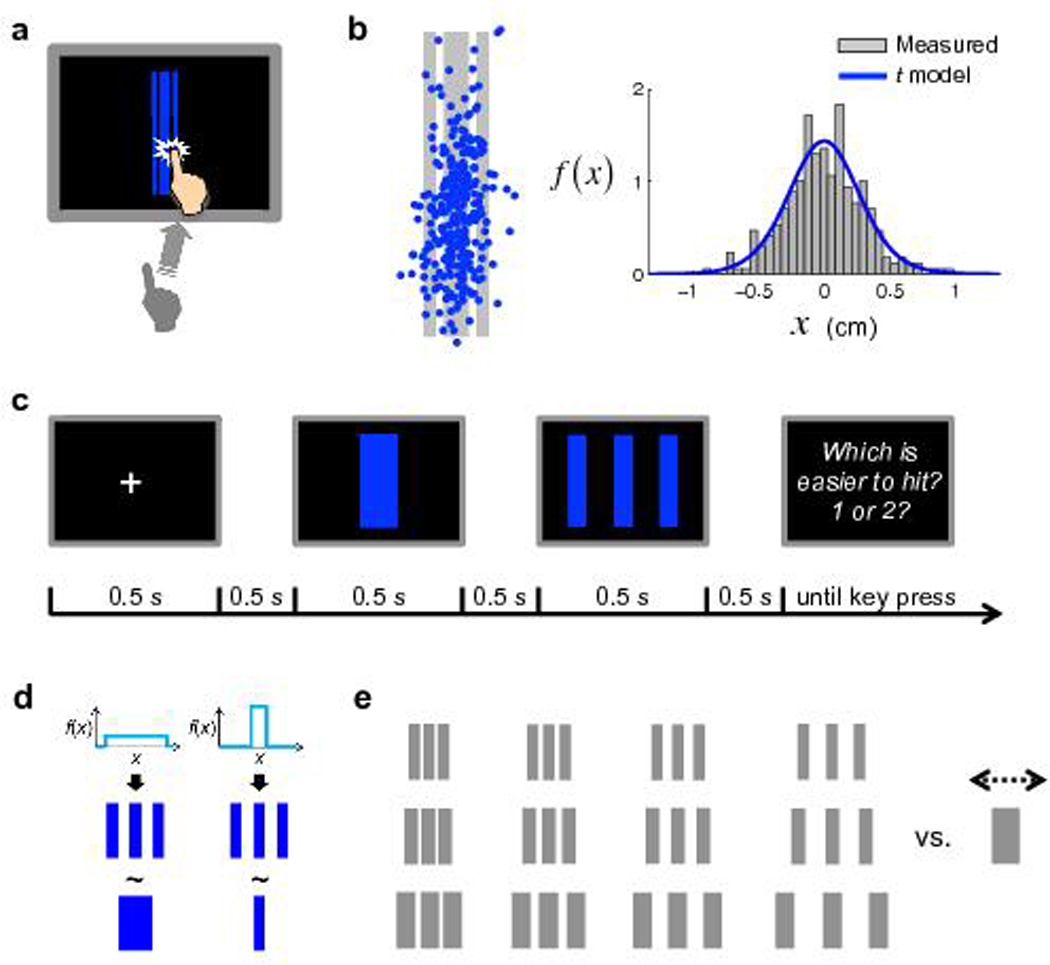
Task and design of Experiment 1. (a) The reaching task. Subjects were required to hit the target (blue regions) at the center of the screen within 400 msec for each of 300 trials. (b) One subject’s visuo-motor error distribution in the reaching task. Left: The endpoint of each trial (blue dot) is marked on the target (gray regions). Right: The distribution of horizontal visuo-motor error fits to a scaled Student’s t distribution. (c) Time course of the choice task. On each trial, subjects chose between a Triple (an array of three rectangles) and a Single (one rectangle) the target that they perceived to be easier to hit. The subject did not reach to hit the target; she only chose a preferred target. (d) Rationale of the choice task. We illustrate two extreme cases. Left: When the subject’ internal pdf of visuo-motor error is a uniform distribution that is wide enough to contain the whole Triple, the subject would be indifferent (denoted by ~) between the two targets when the width of the Single equals the total width of the three rectangles in the Triple. Right: In contrast, when the subject’s model is a uniform distribution that covers only the central rectangle of the Triple, the equivalent Single would be merely as wide as the central rectangle. (e) Design of the choice task. Twelve different Triples were used, for each of which, the width of its paired Single was adjusted by an adaptive procedure for 70 trials.

In a second phase, subjects viewed two virtual targets differing in width and configuration and chose the target they preferred to try later for monetary rewards (Fig. 2c). We assumed subjects’ choice was generated by a softmax function based on their estimates of the expected utilities of the two targets (Methods online), which, under our reward structure (hit = fixed reward; miss = nothing), were reduced to the probabilities of hit. Thus subjects’ choices were determined by their internal pdfs, integrated over the target regions (illustrated in Fig. 2d). Conversely, we could re-construct approximations of subjects’ internal pdfs from their choices¹⁷.

The targets were vertically elongated so that only horizontal error affected reward. On each trial, one target was a Triple (three identical, equally-gapped rectangles) and the other was a Single (one rectangle). We chose the Triple target as a convenient way to explore the distribution of probability mass in the tails of the internal pdfs by varying the gap between the outer rectangles and the inner (Fig. 2e).

Results

Experiment 1: objective pdf

We ignore the irrelevant vertical direction and describe the horizontal statistics only. Subjects’ endpoints in the reaching task (Fig. 2b for one typical subject) had a Gaussian-like distribution symmetric around the target center. The distribution of all but one subject’s visuo-motor error (endpoints’ deviation from the mean endpoint) had a kurtosis higher than that of Gaussian—by 0.04–1.78, median 0.44—indicating a more peaked center or heavier tail. We modeled each subject’ visuo-motor error as a scaled Student’s t distribution with a scale parameter and a shape parameter (Methods online), for which the Gaussian distribution is a limiting case. The t model captured individual subjects’ visuo-motor error in standard deviation (Pearson’s r = 1.0, p < 0.001) and kurtosis (Pearson’s r = 0.82, p = 0.004). We refer to the t distribution estimated in a subject’s reaching task as the subject’s objective visuo-motor error distribution, or objective pdf.

Experiment 1: internal pdf

We first visualized subjects’ internal pdfs from their choices, assuming a Gaussian-process prior (Methods online) which results in a smoothed estimate of the pdf; it assumes only a weak correlation between adjacent locations on the pdf and allows for the possibility that the underlying distribution is multimodal.

Some technical notes: First, the resulting fits are effectively smoothed and any abrupt changes in the pdf may be lost in this analysis. Second, because of the choice of stimuli in Experiment 1, we cannot reliably estimate the probability density in a small interval at the center of the pdf (Methods online; we remove this limitation in Experiment 2) and we replaced it by a horizontal bar.

For the single subject’s data shown in Figure 3a, there appear to be multiple discrete modes (peaks) or possibly steps (marked with red circles). The presence of such modes is inconsistent with the unimodal form of the objective pdf (i.e. t distribution). Results for all subjects are shown in Supplementary Figure 1 online.

Figure 3.

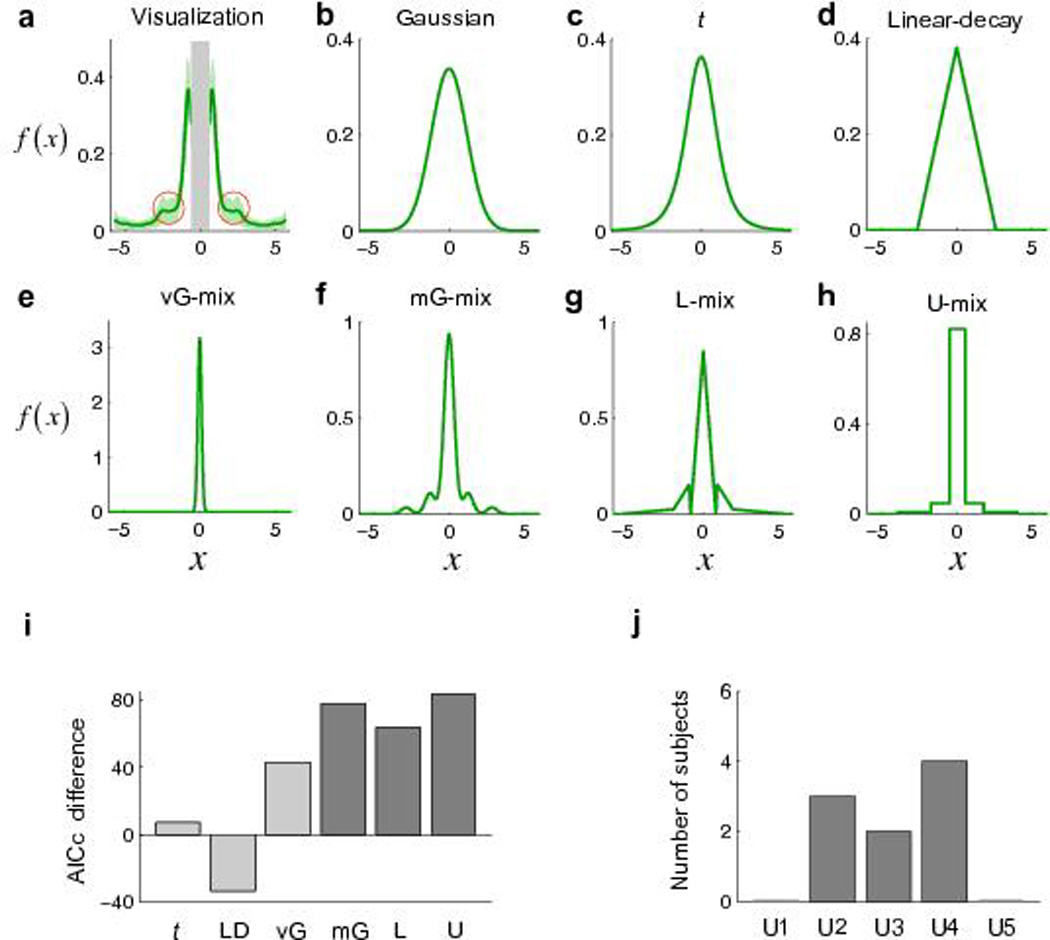
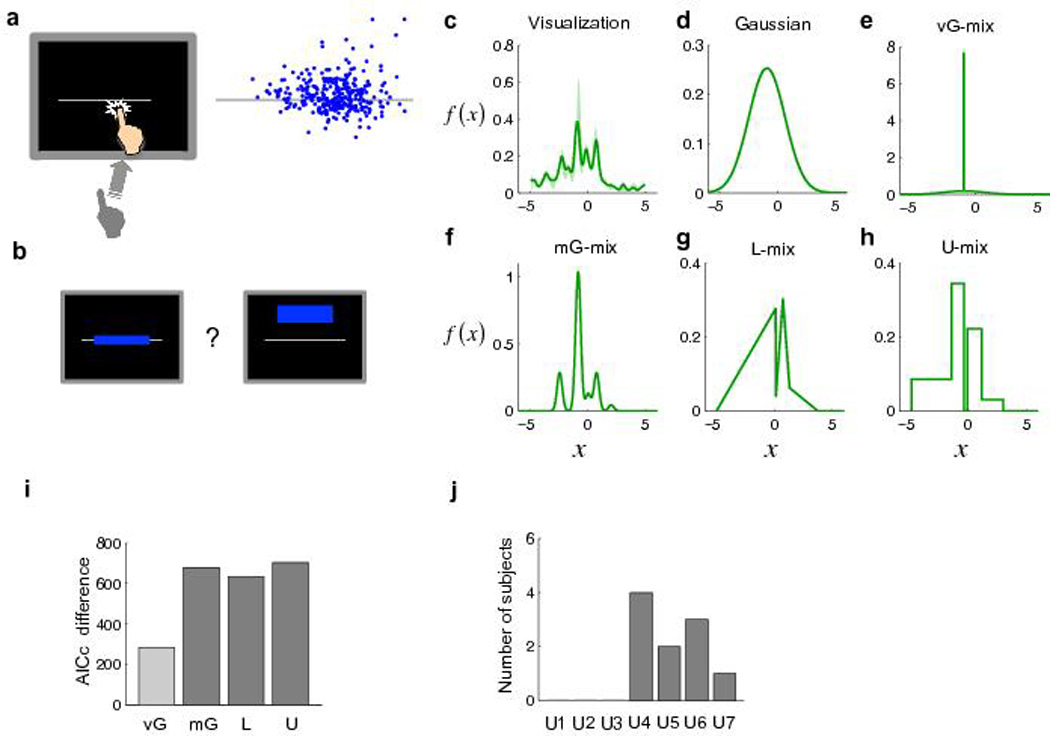
Internal pdfs in the choice task of Experiment 1. (a) Non-parametric visualization of the internal pdf for one subject. Green-shaded regions denote ±SEM. x is in the unit of the subject’s horizontal standard deviation estimated from the reaching task. The gray-shaded central range of [−0.6, 0.6] could not be reliably estimated in Experiment 1 (Methods online) and therefore the visualization gives information about the pdf only away from the origin. Two regions of interest are marked by red circles. The visualizations for all subjects are to be found in Supplementary Figure 1. (b–h) Internal pdfs estimated from different models for the same subject. (i) AICc difference between the Gaussian model and the other six models summed over the 9 subjects. The unimodal models (including vG-mix) and mixture models are respectively coded in light gray and dark gray. Positive difference indicates better fit. LD denotes linear-decay. (j) Number of subjects best fit by each U-mix model.

The results of this analysis suggest—but do not demonstrate—that subjects’ internal pdfs are multimodal. We used a model comparison procedure to further explore the form of the internal pdf.

We compared seven different classes of models of the internal pdf—three unimodal distributions, a mixture distribution which is always unimodal, and three mixture distributions that could be multimodal (Methods online). The Akaike information criterion with a correction for sample sizes (AICc)^18,19 was used for model selection.

Unimodal distributions

The first and the baseline model was the Gaussian model, whose variance was fitted as a free parameter. The second model was the t model, whose scale and shape parameters were free. In a third model, the linear-decay model, we assumed that the probability density functions in subjects’ internal pdfs were continuous but took the simple linear form of a triangular distribution, with variance as a free parameter.

Mixture distributions

We next considered four classes of mixture distributions (including the unimodal mixture distribution). One class was the linear combination of multiple uniform distributions (i.e. uniform mixtures, abbreviated as U-mix) whose ranges abutted one another. We assumed symmetry for the current problem: a U-mix model with n components was composed of n pairs of uniform distributions symmetric around 0 (i.e. two symmetric uniform distributions were counted as one component). The U-mix distributions shown in Figure 1, for example, had two components. For each subject, we constructed 5 levels of U-mix models with increasing number of components, denoted U1–U5, and fit them to the subject’s choices. The ranges (spatial extent) and weights (heights of the components) of the uniform components were free parameters.

Two classes of mixtures of Gaussian distributions were modeled: the vG-mix model was a linear combination of Gaussian distributions with the same mean but different variances; the mG-mix is a linear combination of Gaussian distributions with the same variance but different means. The mean(s), variance(s), and weights of the Gaussian components were fitted as free parameters. The vG model, described amongst mixture distributions for convenience, was classified as a unimodal model.

A vG-mix or mG-mix with n components had the same number of free parameters as a U-mix with n components. Similar to U-mix, we constructed 5 levels of vG-mix and mG-mix and obtained the best-fit vG-mix and mG-mix. Last, we reported a mixture model composed of piecewise linear components, denoted as L-mix.

The probability density function estimated from each model is plotted for one subject in Figure 3b–h. The AICc differences between the baseline (Gaussian) and the other six models (summed over the 9 subjects) are shown in Figure 3i. Two conclusions could be reached. First, all the mixture distribution models fit better to subjects’ choice patterns than any of the unimodal distributions. The unimodal distribution models tend to smooth over any abrupt changes in subjects’ choice patterns while the mixture distribution models, with their multiple discrete modes or steps, can capture them (Supplementary Fig. 2).

Second, the U-mix model outperformed the other mixture models

According to the group-level Bayesian model selection²⁰, among the seven models, the probability for the U-mix model to be the best model was 65.7%; the probability was 1.3% for Gaussian, 1.0% for linear-decay, 1.0% for t, 1.3% for vG-mix, 28.0% for mG-mix, 1.7% for L-mix.

The underlying Bayes factors provide only weak evidence favoring the uniform mixture model over the Gaussian mixture model. However, we will see later, in the third experiment (when considering two-dimensional basis functions), that there is stronger evidence for uniform over Gaussian mixtures.

Model fits of all subjects’ internal pdfs are shown in Figure 4 for the mG-mix and U-mix models. The U-mix models are evidently discrete mixture representations, as defined in the Introduction. The “runner up” mG-mix models were also discrete mixture representations: the basis pdfs in the mG-mix models had, on average, an overlap of only 8.0% in probability density (Methods online), i.e., they were close to non-overlapping, orthogonal.

Figure 4.

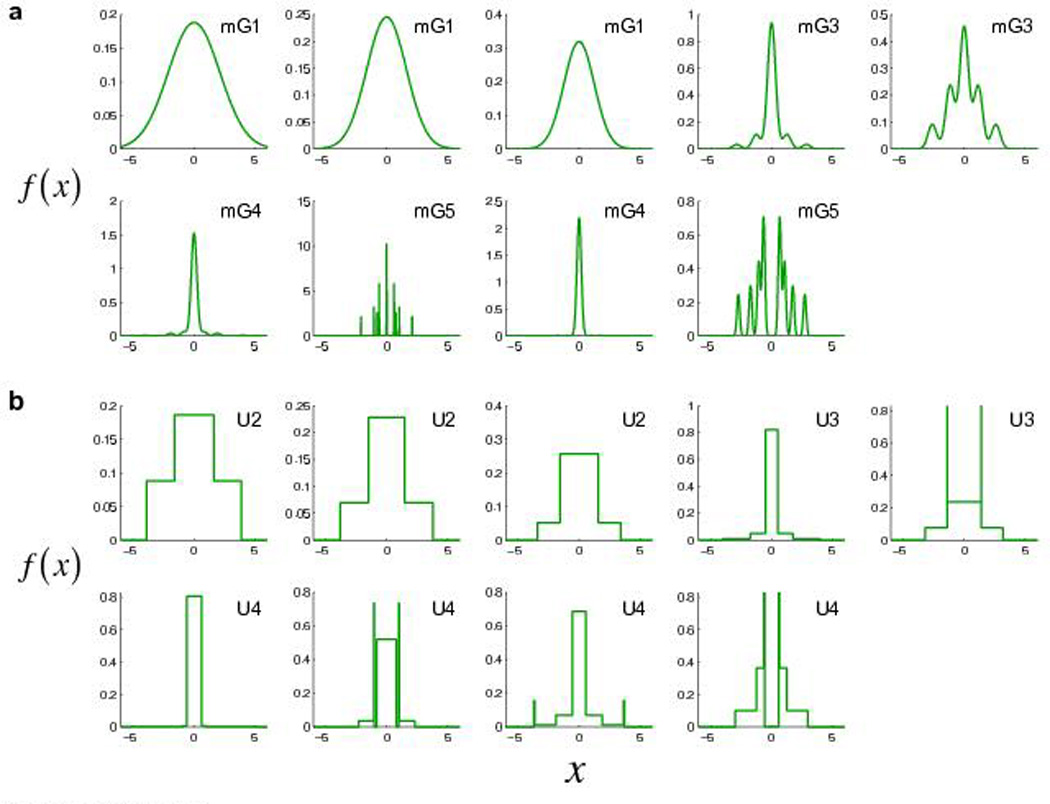
Model fits of all subjects’ internal pdfs in Experiment 1. (a) mG-mix model. (b) U-mix model. Each panel is for the probability density function of one subject. x is in the unit of the subject’s horizontal standard deviation estimated from the reaching task. Subjects are in the same order as in Supplementary Figure 1.

According to AICc comparisons, the U-mix models that best fit subjects’ choices contained only a small number of components (Fig. 3j): all subjects were best fit by U2–U4. The best-fit U-mix model for one subject shown in Figure 3h was, for example, U3.

Experiment 2

We wanted to show that the discrete mixture representation of visuo-motor uncertainty was not somehow a result of the particular stimuli we used in Experiment 1. Could the Triples, in particular, have somehow led the subject to choose a discrete mixture representation that she might otherwise never make use of?

In a second experiment, we trained subjects to touch a line within a time limit (Fig. 5a). The distribution of each subject’s endpoints was close to Gaussian. Instead of an all-or-none reward, the amount subjects received on each trial could be any integer between 0 and 100, decreasing with the distance of their endpoint to the target line. In the subsequent choice phase, subjects chose between a central rectangular region and a peripheral rectangular region (Fig. 5b and Methods online).

Figure 5.

Experiment 2. (a) The reaching task. Left: The task. Same as Experiment 1 except that a horizontal line was used as the target. Right: The endpoints for one subject. (b) The choice task. Similar to Experiment 1 but each pair of targets consisted of a rectangle on the line and a rectangle off the line. (c) Non-parametric visualization of the internal pdf for one subject. Shaded regions denote ±SEM. x is in the unit of the subject’s vertical standard deviation estimated from the reaching task. (d–h) Internal pdfs estimated from different models for the same subject. (i) AICc difference between the Gaussian model and the other four models summed over the 10 subjects. The unimodal models (including vG-mix) and mixture models are respectively coded in light gray and dark gray. Positive difference indicates better fit. (j) Number of subjects best fit by each U-mix model.

The analyses of Experiment 2 were similar to those of Experiment 1, except that the design of the experiment allowed us to include asymmetric distributions among the candidates for subjects’ internal pdfs and there is no restriction on estimating the pdf near its center as there was in Experiment 1 (Methods online). The visualization and model fits for one subject are shown in Figure 5c and Figure 5d–h (see Supplementary Figs. 3 and 4 online for other subjects). Again, all the mixture models were superior to the Gaussian and the U-mix model was superior to the other mixture models in AICc (Fig. 5i, summed over the 10 subjects). Not only the U-mix models but also the mG-mix models were discrete mixture representations: the basis pdfs in the mG-mix models had, on average, an overlap of only 9.2% in probability density. They were close to non-overlapping, orthogonal. According to group-level Bayesian model selection²⁰, among the five models, the probability for the U-mix model to be the best model was 63.4%; the probability was 0.7% for Gaussian, 22.3% for vG-mix, 12.7% for mG-mix, 0.9% for L-mix. The best-fit U-mix models for most subjects were U4–U6 (Fig. 5j).

Experiment 3

We applied the tests developed above to the 2-D choice data of Experiment 1 in Zhang, Daw, and Maloney²¹ and present it as Experiment 3. Its task and design was the same as that of Experiment 1 with the following exceptions (Fig. 6a–c). The target of the reaching task was a circle and subjects’ visuo-motor error had a bivariate Gaussian distribution. The pair of targets in the choice task was a rectangle and a circle.

Figure 6.

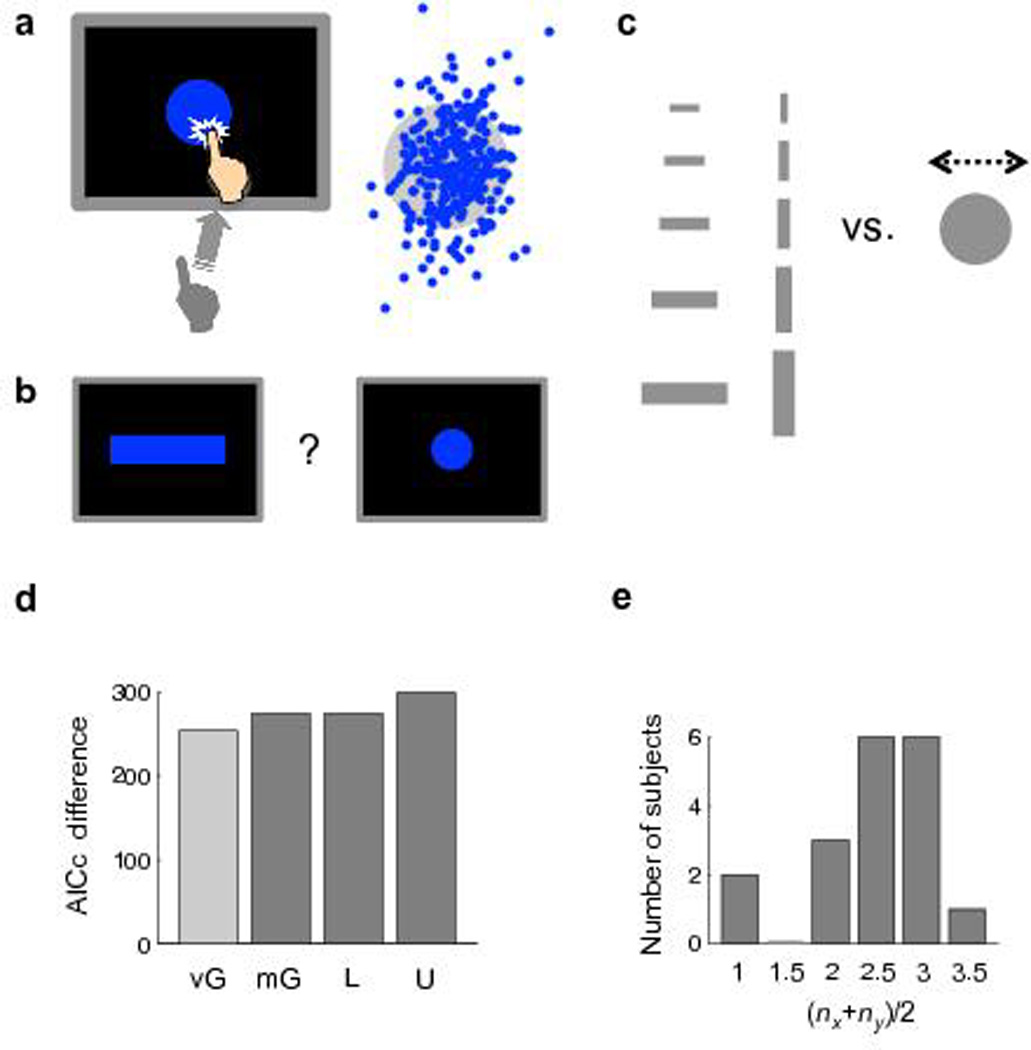
Experiment 3. (a) The reaching task. Left: The task. Same as Experiment 1 except that a circular target was used. Right: The endpoints for one subject. (b) The choice task. Same as Experiment 1 except that each pair of targets was a rectangle and a circle. (c) Design of the choice task. Ten different rectangles were used, for each of which the radius of its paired circle was adjusted by adaptive procedures for 100 trials. (d) AICc difference between the Gaussian model and the other four models summed over the 18 subjects. The unimodal models (including vG-mix) and mixture models are respectively coded in light gray and dark gray. Positive difference indicates better fit. (e) Number of subjects best fit by each U-mix model.

We modeled subjects’ internal pdfs in the horizontal and vertical directions separately and considered the Gaussian, vG-mix, mG-mix, L-mix, and U-mix models (Methods online). As in Experiments 1 and 2, the mixture models were superior to the Gaussian model and the U-mix model was superior to the other mixture models in AICc (Fig. 6d, summed over the 18 subjects). Not only the U-mix models but also the mG-mix models (Supplementary Figs. 5 and 6 online) were discrete mixture representations: the basis pdfs in the mG-mix models had, on average, an overlap of only 17% in probability density. According to group-level Bayesian model selection²⁰, among the five models, the probability for the U-mix model to be the best model was 97.6%; the probability was 0.02% for Gaussian, 0.3% for vG-mix, 0.5% for mG-mix, 1.6% for L-mix.

For a mixture model that had n_x components in the horizontal direction and n_y components in the vertical direction, define its number of components as $\frac{n_x+n_y}{2}$. The best-fit U-mix model for most subjects had 2–3 components (Fig. 6e).

Discussion

We estimated human subjects’ internal model of their own visuo-motor error in a speeded reaching task and compared it to their objective visuo-motor error. Subjects’ actual visuo-motor error distributions (objective pdfs) were in all cases unimodal, close to a Gaussian in many cases and to a t-distribution in the remainder. However, the distributions implicit in their choices (internal pdfs) were very different from their actual distributions.

We found, first of all, that multimodal mixture distributions (e.g. U-mix, mG-mix) provided a better fit to subjects’ choice patterns than any single Gaussian or the alike. Second, among the mixture models tested, a model consisting of a mixture of non-overlapping uniform distributions with 2 to 6 non-zero steps performed best.

Both results are unexpected. The first and broader conclusion—that subjects’ internal pdfs were mixtures of basis distributions—was well supported by our data. Moreover, the basis distributions in the mixtures either had no overlaps (e.g. U-mix) or just slight overlaps (e.g. mG-mix). We refer to such mixtures of local distributions as discrete mixture representations. The subjects’ representations of their own visuo-motor error were discrete.

It is less clear what the form of the basis distributions was: the mG-mix fits came close to the U-mix in both goodness-of-fit and overall appearance. While fits to the data favored uniform basis distributions over Gaussian, there could well be a third candidate that would dominate both.

There are two possible advantages of using uniform rather than Gaussian mixtures to represent probability mass. First, we can “tile” the space of events in an orthogonal (sparse) fashion, without any bias to a particular location. Second, the probability assigned to each event (here, endpoint) depends only on the tile it is in. That is, we can estimate the constant probability density of each tile by simply counting events within the tile.

Relationship to previous measures

A few studies have reconstructed human subjects’ representation of sensory probability distributions based on their decisions. In one study, Körding and Wolpert⁷ found subjects’ internal pdf of a Gaussian prior distribution closely followed the objective prior (their Figure 2d), which seemingly disagrees with a discrete mixture representation of probability distributions. However, what Körding and Wolpert⁷ showed is that subjects computed a weighted average of the mean of a prior distribution and the mean of a likelihood. While such averaging is consistent with Bayesian inference based on Gaussians it is unclear how to infer from their data that subjects actually maintained and multiplied specifically Gaussian distributions²². Interestingly, a second condition in the same study demonstrated that subjects successfully represented a bimodal prior distribution, a capability which is, broadly, consistent with our finding that the brain employs mixture distributions. Of course, a formal test whether behavior in such a setting is best fit by particular forms of mixture, such as our U-mix, remains for future work.

One surprising feature of the discrete mixture representation we found is that it was multimodal, though the true distribution was unimodal. While this outcome was unexpected, it is not completely unprecedented: subjects’ representation of temporal prior distributions inferred by Acerbi, Wolpert, and Vijayakumar²³ (their Figures 7–9) appear to have more than one mode.

Discrete representation and near-optimal motor decisions

Our finding that subjects’ internal pdfs of their own visuo-motor error distribution were discrete—thus deviating systematically from the objective distribution—does not necessarily conflict with near-optimal human performance in previous studies^4–10 (see Ref. 11 for an example of a binary choice task). Many tasks may simply be insensitive to systematic deviations in subjects’ internal pdfs: For example, Zhang, Daw, and Maloney²¹ demonstrated that a virtual subject who has a Gaussian error distribution but who mistakenly assumes it is a uniform distribution of the same variance would still be able to achieve near-optimal performance in the visuo-motor decision task of Trommershäuser et al⁸. A discrete mixture representation with 2 to 6 non-zero steps, as we found in our experiments, enables even better approximations to the objective distribution and can therefore lead to near-optimal performance as well.

Simplifying probabilistic calculation

Psychologists and neuroscientists modeling biological computation have encountered the computational problems that arise when manipulating high-dimensional or continuous distributions in many guises. Broadly speaking, tractable solutions require approximating the exact computation with some simpler, sparser form. The discrete mixture representation we propose is one example, and shares its essential feature of sparseness with many other approaches such as approximating distributions with a reduced rank form²⁴ or a kernel density estimator²⁵, with Monte Carlo approximations that substitute a few samples for a random variable^26–29 or with the use of linear models to approximate surface spectral reflectance density functions³⁰. Since these approaches share many essential similarities, it is possible that all arise from the same neural solution to complexity.

An important question for future work is whether U-mix (or other mixture) distributions we observe are the only internal representations of the distribution of visuo-motor error available to the visuo-motor system or whether they are transient representations—derived from a more accurate representation—that vary with the task imposed. That is, the neural system could maintain a high-resolution representation of visuo-motor error but use simplified representations in carrying out specific computational tasks, just as most common programming languages make use of a variety of numerical representations.

Discrete representation as explanation for decision biases

The U-mix representation may be used to approximate any arbitrary probability distribution. One example is a sensorimotor decision task by Körding and Wolpert³¹ (a different study from Ref. 7 discussed earlier), in which, for skewed error distributions, they found a deviation of subjects’ aim point from the mean towards the median. Körding and Wolpert³¹ estimated subjects’ internal loss functions that would lead to this bias. However, in a close examination of their data (black symbols in Fig. 7b), we noticed an unexplained away-from-median bias (i.e. towards the longer or fatter tail) in the middle range of skewness—the U-shaped curve trends below zero. The coexistence of the towards-median and away-from-median biases could not be explained by any of the loss functions proposed by Körding and Wolpert³¹ and it is not obvious whether there exists such a loss function that is non-negative.

Figure 7.

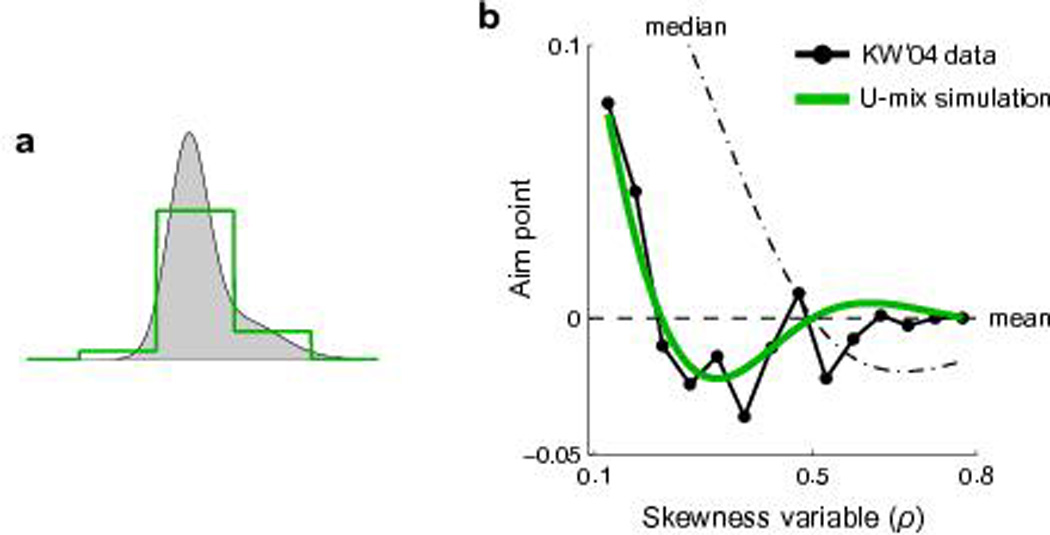
U-mix simulation for Körding and Wolpert³¹. We simulated a virtual subject in the task of Körding and Wolpert³¹. We assumed that the subject had a quadratic loss function but that she approximated the skewed distributions with a U-mix with 3 non-zero probability categories (Methods online). (a) Illustration of the discrete mixture representation. The U-mix is centered on the median of the to-be-represented distribution. The half of its total width is 3.3 times of the standard deviation of the distribution. (b) Simulated aim points vs. data. The simulated aim points (green curve) agreed well with their data (black curve, re-plot from their Figure 2B, noninverted trials). Note the U-shaped trend below zero—a deviation from the mean (dashed line) but towards the inverse direction of the median (dot-dashed line)—could not be explained the model of Körding and Wolpert³¹.

However, if we assume subjects had a quadratic internal loss function^32–34 but employed a discrete mixture representation (U-mix) of their error distribution, we can reproduce the pattern of Körding and Wolpert’s³¹ data—both the towards-median and away-from-median biases—with satisfying precision (Fig. 7, see Methods online). Intuitively, the two opposite biases stem from two complementary effects: First, discretization trims the skewed tail outside the discrete range, leading to the underweighting of large errors; second, discretization homogenizes the density within each tile, effectively moving the probability mass away from the shorter tailed side towards the longer tailed side.

An mG-mix could lead to a similar effect as U-mix does (Supplementary Fig. 7 online). However, since a mixture of two Gaussians is exactly the error distribution used by Körding and Wolpert, we had to choose a mixture of two Gaussians that differed from the actual mixture to get the pattern of biases present in the human data.

The discrete mixture representation we proposed for sensorimotor error can serve as a general framework for human representation of probability distributions and can potentially explain a range of known biases in human choices. For example, humans exhibit a “skewness preference”, a well-documented phenomenon in economics and finance^35–38: they prefer reward distributions with positive skewness to those with zero or negative skewness when the mean and variance of the distributions are the same, exhibiting the pattern we found in Körding and Wolpert’s³¹ experiment which was consistent with a U-mix representation.

Online Methods

Ethics Statement

The experiments were approved by the University Committee on Activities Involving Human Subjects of New York University. Informed consent was given by each subject prior to the experiment.

Subjects

There were respectively 10 (1 male), 12 (4 male), and 18 (8 male, 4 left-handed) subjects, aged 18–40, participating the three experiments. All subjects used the index finger of their dominant hand for the reaching movement. Subjects received US$12 per hour plus a performance-related bonus.

Apparatus and stimuli

Stimuli were presented in a dimly lit room on a 17” (33.8×27 cm) Elo touch screen mounted vertically on a Unistrut frame, controlled using the Psychophysics Toolbox^39,40. Subjects were seated at a viewing distance of 30 cm. In the reaching task, the starting position, a stabilized key, was 28 cm away in depth and 20.5 cm below the screen center. The touch screen recorded the endpoints.

Procedure and design

The three experiments had common task structures: reaching and choice. We detail the procedure and design of Experiment 1 and describe the differences in Experiment 2. See Zhang et al²¹ for Experiment 3.

Experiment 1: Reaching

The reaching task served to reveal each subject’s objective visuo-motor error distribution to us and to the subject. Subjects were required to touch a target at the center of the screen (with a horizontal and vertical random jitter within ±1 cm) within 400 milliseconds. The target (Fig. 2a) was consisted of three vertical rectangles: One 0.4-cm-wide central rectangle and two 0.2-cm-wide flankers, separated by 0.13-cm-wide gaps. They were 5 cm high, therefore large enough to render subjects’ vertical errors inconsequential (only 0–5.2%, median 0.70% of subjects’ endpoints fell outside the vertical boundaries). Only the horizontal errors of the endpoints would be of interest to us and to the subjects. Subjects’ constant errors (mean deviation from the center) were negligible (0.0065–0.45 [median 0.18] of the standard deviation).

Subjects held down the starting key to trigger the next target. The timer started when they released the key. If they reached the screen within the time limit, a dot would appear on the target to echo the endpoint. An additional message indicated hit, miss, or time-out.

There were 50 warm-up trials and 300 formal trials. Subjects received financial rewards for hitting the target. At the end of the task, eight bonus trials would be randomly drawn from the 300 reaching trials they had performed. Each bonus trial delivered US$1 for hit, zero for miss, or incurred a penalty of US$2 for time-out.

Experiment 1: Choice

The choice task was designed to estimate the visuo-motor error distribution subjects assumed in planning their own reaching movements. Subjects chose between two targets, selecting the one they judged to be easier to hit (Fig. 2c). Subjects were instructed to imagine hitting the targets from the same starting position and under the same time limit as they had in the earlier reaching task, but no actual reaching attempts were allowed.

On each trial, one target was a row of three equally-spaced, identical rectangles (“Triple”); the other target was a single rectangle (“Single”). Each target was presented at the center of the screen for 0.5 second and they were separated by a duration of 0.5 second. Subjects were prompted to respond, “Which is easier to hit? 1^st or 2^nd?” by key press.

The heights of the targets were the same as those of the reaching task. The widths of the targets were tailored for each subject based on the standard deviation of her horizontal visuo-motor error, σ₀, estimated from the reaching task (0.23–0.38 cm across subjects). There were 12 combinations of Triples (Fig. 2e), whose width of rectangles was σ₀, 1.5σ₀, or 2σ₀, and whose gap widths were 0.4, 0.6, 0.9, or 1.35 times the width of the corresponding rectangles. The width of the Single paired with each Triple was adjusted by a 1-up/1-down staircase procedure that terminated after 70 trials. All 12 staircases were interleaved.

The 12×70=840 formal choice trials were preceded by 20 warm-up trials. Trials were self-initiated by key press. Similar to the reaching task, a monetary incentive was applied to encourage subjects to choose the target associated with a higher probability of hit. Subjects were instructed that, at the end of the experiment, eight targets would be randomly selected from those they had preferred in the formal choice trials. They would attempt to hit these bonus targets and be rewarded for hits just as in the reaching task.

Experiment 2

Three settings were different from Experiment 1. First, the target in the reaching task was an 8-cm-long line (Fig. 5a) that delivered graded instead of all-or-none rewards. For any trial completed within the time limit and the span of the line, subjects received a reward between 100 and 0 points (5000 points = US$1), decreasing as a logistical function of the endpoint-to-line distance. Second, in the choice task subjects chose between two rectangular regions (Fig. 5b), one on the target line (“Central”), the other off the target line (“Side”). Subjects were instructed to choose the region that was more likely to catch their endpoints in the previous reaching task. Two trials would be selected at random as bonus trials at the end of the experiment, for each of which subjects could win US$5 if they were correct. Third, staircase procedures were not used. Denote σ₀ as the standard deviation of the subject’s vertical visuo-motor error (0.45–0.71 cm across subjects). The Central had 5 possible heights, 0.2σ₀, 0.4σ₀, 0.6σ₀, 0.8σ₀, σ₀. The Side had 6 possible heights, 0.4σ₀, 0.8σ₀, 1.2σ₀, 1.6σ₀, 2σ₀, 2.4σ₀, and must be greater in height than its paired Central. The Side could be above or below the target line by 10 possible distances, 0.25σ₀, 0.5σ₀, 0.75σ₀, …, 2.5σ₀. A full combination of these conditions times 2 repetitions resulted in 960 trials, presented in random order.

Exclusion of trials or subjects

Reaching

Time-out trials, 2.7%–15% (median 4.3%) for Experiment 1, 2.6–27% (median 9.2%) for Experiment 2, 1.3%–21% (median 9.0%) for Experiment 3, and outlier trials beyond 8σ₀ were excluded. In Experiment 2, endpoints outside the ends of the target line (no more than one trial for each subject) were also excluded; time-out trials and outside trials were replaced during the experiment.

Choice

In Experiment 1, one subject was excluded due to violation of dominance: The subject consistently preferred the Single even when the Single could be contained in the Triple. In Experiment 2, two subjects were excluded. One of them chose the Central in 99% trials; the other chose the upper region in 97% trials.

Discrete mixture representations

A discrete mixture representation is specified by first designating a partition of part of the real line a₀ < a₁ < a₂ < … < a_n. Each interval of the partition [a_i−1,a_i] is paired with a basis distribution f_i(x) as follows. Let c_i = (a_i + a_i−1)/2 be the location of the interval and s_i = (a_i − a_i−1)/2 its scale. Then for some choice of seed distribution f(x) that is non-zero outside the interval [−1, 1] define

$$f_i(x)=\frac{1}{s_i}f\left(\frac{x-c_i}{s_i}\right),i=1,\dots ,n.$$ (2)

The basis distributions f_i(x) are part of a location-scale family and they are orthogonal.

Let w₁,…,w_n be non-negative weights with $\sum _{i=1}^n{w}_i=1$. Then—for any choice of w₁,…,w_n —the mixture distribution

$$\phi (x)=\sum _{i=1}^n{w}_i{f}_i(x)$$ (3)

is a discrete mixture representation based on the seed distribution f(x) and the partition a₀ < a₁ < a₂ < … < a_n.

U-mix is an example of a discrete mixture representation based on a uniform seed distribution. For convenience, we treat mixtures of Gaussians as a discrete mixture representation with the assumption that almost all of the probability density is confined to one interval of the partition: we ignore the overlap.

Data fitting and model comparison

All the data fitting procedures were conducted on the individual level using maximum likelihood estimates. We used fminsearchbnd (Author: John D'Errico), a function based on fminsearch in MATLAB® (Mathworks, Natick, MA) to search for the parameters that minimized minus log likelihood. To verify that we had found the global minimum, we repeated the search process using different starting points.

Equivalent width (radius)

In Experiment 1 (Experiment 3), for each specific Triple (rectangle), subjects’ probability of choosing the Single (circle) was modeled as a two-parameter (location and slope) sigmoidal psychometric function of the logarithm of the width of the Single (the radius of the circle). The psychometric functions of the 12 Triples (10 rectangles) were assumed to have different locations but the same slope. The equivalent width (radius) corresponded to the point on the psychometric function where the probability of choosing the Single (circle) was 0.5.

Linking subjects’ internal pdfs to their choices

We assume a specific subject’s choice between the two targets (T₁ and T₂) on a specific trial is generated as follows. First, probabilities of hit are computed for the two targets based on the subject’s internal pdf, which, in the 1-D case, is:

$$p_1=\underset{T_1}{\int }f(x)dx,$$ (4)

$$p_2=\underset{T_2}{\int }f(x)dx.$$

where f(x) denotes the internal pdf. Subjects would receive a fixed positive value (whose utility is denoted v) for hit and 0 for miss. The expected utilities for the two targets are thus p₁v and.p₂v.

The subject’s choice, T₁ or T₂, is generated as a Bernoulli random variable, with the probability of choosing T₂ determined by p₁ and p₂ following the normalized expected utility model⁴¹ in the form of a softmax function:

$$\text{Pr}(T_2)=\frac{1}{1+e^{(p_{1}v-p_{2}v)/(\tau D)}}$$ (5)

where τ > 0 is a temperature parameter determining the randomness of the choice, and D = p₁(1 − p₂)v + p₂(1 − p₁)v is a normalization term. Note that v cancels out in the equation. For each distribution model (e.g. Gaussian, U-mix), we fit Pr(T₂) to subjects’ choices to estimate its free parameters and τ.

Visualization of subjects’ internal pdf

For each subject, we visualized the internal pdf implicit in the subject’s choices using a Bayesian inference procedure as follows. First, we generated 1,000,000 pdfs by sampling from a Gaussian-process prior⁴² in log space and normalizing each sample (to guarantee the area under any pdf equals one). The length scale of the Gaussian process was 0.3σ₀. In Experiment 1, we required the pdfs to be symmetric around 0 and spanned the stimuli range [−5.7σ₀, 5.7σ₀]. We arbitrarily set the densities within the central range of [−0.6σ₀, 0.6σ₀] to be constant, because the central width of the smallest Triple was σ₀, leaving the central densities underdetermined. In Experiment 2, asymmetry was allowed and the pdfs spanned the stimuli range [−4.9σ₀, 4.9σ₀]. Second, for each sample pdf, we computed its likelihood of generating the subject’s choices. The temperature parameter τ in Eq. 5 was chosen to be the same as the subject’s τ fitted in the Gaussian model. Third, with each sample pdf’s likelihood serving as its weight in importance sampling, we obtained the posterior distribution of the subject’s internal pdf and accordingly its mean±SEM (i.e. 68% confidence interval).

t model

The probability density function is in the form of a scaled Student’s t distribution:

$$f(x|\kappa ,\nu )=\frac{\mathrm{\Gamma }\left(\frac{\nu +1}{2}\right)}{\kappa \sqrt{\nu \pi }\mathrm{\Gamma }\left(\frac{\nu }{2}\right)}{\left(\frac{\nu +\frac{x^2}{{\kappa }^2}}{\nu }\right)}^{-(\nu +1)/2}$$ (6)

where κ > 0 is a scale parameter and v ≥ 4 is a shape parameter (x/κ has a standard Student’s t distribution of v degrees of freedom), Γ(․) is the gamma function. The Gaussian distribution is a limiting case of the scaled Student’s t distribution with v → ∞.

Linear-decay model

The probability density function is in the form of a triangular distribution:

$$f(x|\xi )=\{\begin{array}{cc}\hfill \frac{\xi +x}{{\xi }^2},\hfill & \hfill -\xi \le x\le 0;\hfill \\ \hfill \frac{\xi -x}{{\xi }^2},\hfill & \hfill 0<x\le \xi ;\hfill \\ \hfill 0,\hfill & \hfill x<-\xi \text{or}x>\xi .\hfill \end{array}$$ (7)

where ξ > 0 is the free parameter, denoting the boundary of the regions with non-zero probability density.

Mixture models

Denote w_i as the weight for the i-th component (or pair of components) of an n-component mixture model, which satisfies 0 ≤ w_i ≤ 1 and $\sum _{i=1}^n{w}_i=1$. The Gaussian model is a special case of mixture models vG-Mix or mG-Mix with n = 1.

vG-mix is a linear combination of Gaussian distributions with the same mean but different variances:

$$f(x|\mu ,{\sigma }_i,w_i)=\sum _{i=1}^n{w}_i\frac{1}{\sqrt{2\pi }{\sigma }_i}{e}^{\frac{{(x-\mu )}^2}{2{\sigma }_i^2}},i=1,2,\dots ,n.$$ (8)

where σ_i and w_i are free parameters, μ = 0 in Experiment 1 and is a free parameter in Experiment 2.

mG-mix is a linear combination of Gaussian distributions with the same variance but different means. In Experiment 1, the Gaussian distributions are in pairs symmetric around 0:

$$f(x|{\mu }_i,\sigma ,w_i)=\sum _{i=1}^n{w}_i(\frac{1}{2\sqrt{2\pi }\sigma }{e}^{-\frac{{(x-{\mu }_i)}^2}{2{\sigma }^2}}+\frac{1}{2\sqrt{2\pi }\sigma }{e}^{-\frac{{(x-{\mu }_i)}^2}{2{\sigma }^2}}),i=1,2,\dots ,n.$$ (9)

where μ₁ = 0, μ_i (i > 1), σ and w_i are free parameters. In Experiment 2, symmetry is not assumed:

$$f(x|{\mu }_i,\sigma ,w_i)=\sum _{i=1}^n{w}_i\frac{1}{\sqrt{2\pi }\sigma }{e}^{-\frac{{(x-{\mu }_i)}^2}{2{\sigma }^2}},i=1,2,\dots ,n.$$ (10)

where μ_i, σ and w_i are free parameters.

L-mix is a distribution whose probability density function is a piecewise linear function. In Experiment 1, the distribution is symmetric around 0:

$$f(x|b_i,h_i)=\{\begin{array}{cc}\hfill \frac{(h_1-h_0)|x|+h_0{b}_1-h_1{b}_0}{b_1-b_0},\hfill & \hfill \mathit{\text{if}}{b}_0\le |x|<b_1;\hfill \\ \hfill \frac{(h_2-h_1)|x|+h_1{b}_2-h_2{b}_1}{b_2-b_1},\hfill & \hfill \mathit{\text{if}}{b}_1\le |x|<b_2;\hfill \\ \hfill \dots \hfill & \hfill \hfill \\ \hfill \frac{(h_n-h_{n-1})|x|+h_{n-1}{b}_n-h_n{b}_{n-1}}{b_n-b_{n-1}},\hfill & \hfill \mathit{\text{if}}{b}_{n-1}\le |x|<b_n;\hfill \\ \hfill 0,\hfill & \hfill \mathit{\text{if}}|x|\ge b_n.\hfill \end{array}i=0,1,2,\dots ,n.$$ (11)

where b_i > 0, h_i > 0 are free parameters except that b₀ = 0, h_n = 0. In Experiment 2, symmetry is not assumed:

$$f(x|b_i,h_i)=\{\begin{array}{cc}\hfill \frac{(h_1-h_0)x+h_0{b}_1-h_1{b}_0}{b_1-b_0},\hfill & \hfill \mathit{\text{if}}{b}_0\le x<b_1;\hfill \\ \hfill \frac{(h_2-h_1)x+h_1{b}_2-h_2{b}_1}{b_2-b_1},\hfill & \hfill \mathit{\text{if}}{b}_1\le x<b_2;\hfill \\ \hfill \dots \hfill & \hfill \hfill \\ \hfill \frac{(h_n-h_{n-1})x+h_{n-1}{b}_n-h_n{b}_{n-1}}{b_n-b_{n-1}},\hfill & \hfill \mathit{\text{if}}{b}_{n-1}\le x<b_n;\hfill \\ \hfill 0,\hfill & \hfill \mathit{\text{if}}x\ge b_n\text{or}x<b_0.\hfill \end{array}i=0,1,2,\dots ,n.$$ (12)

where b_i, h_i > 0 are free parameters except that h₀ = 0, h_n = 0. b_i and h_i satisfy ∫ f(x|b_i,h_i) dx = 1.

U-mix is a linear combination of uniform distributions that are adjacent to each other. Let u(a,b) denote the probability density function of the uniform distribution on the range [a,b]. In Experiment 1, the uniform distributions are in pairs symmetric around 0:

$$f(x|{\theta }_i,{\theta }_{n+1},w_i)=\sum _{i=1}^n{w}_i(\frac{1}{2}u({\theta }_i,{\theta }_{i+1})+\frac{1}{2}u(-{\theta }_{i+1},-{\theta }_i)),i=1,2,\dots ,n.$$ (13)

where θ₁ = 0, 0 ≤ θ₂ ≤ θ₃ ≤ … ≤ θ_n+1 and w_i are free parameters. In Experiment 2, symmetry is not assumed:

$$f(x|{\theta }_i,{\theta }_{n+1},w_i)=\sum _{i=1}^n{w}_{i}u({\theta }_i,{\theta }_{i+1}),i=1,2,\dots ,n.$$ (14)

where θ₁ ≤ θ₂ ≤ … ≤ θ_n+1 and w_i are free parameters.

Bivariate Gaussian model

The probability density function of the bivariate Gaussian model has the form:

$$\psi (x,y|{\sigma }_x,{\sigma }_y)=\frac{1}{2\pi {\sigma }_x{\sigma }_y}{e}^{-(\frac{x^2}{2{\sigma }_x^2}+\frac{y^2}{2{\sigma }_y^2})}$$ (15)

where σ_x and σ_y are free parameters. The probability of hitting a specific target is computed as the integral of ψ(․) over the region of the target.

1-D-times-1-D assumption

We considered the possibility that subjects might model their 2-D errors as two independent 1-D distributions and that they then computed the probability of hitting a 2-D region as the product of probabilities of hitting the two 1-D ranges. This 1-D-times-1-D assumption, when applied to the Gaussian model, led to a much higher goodness-of-fit to subjects’ choices in Experiment 3 than the bivariate Gaussian model—the median AICc difference across subjects was 22. In the model comparison of Experiment 3, the Gaussian and all mixture models were based on the 1-D-times-1-D assumption.

2-D mixture models

A 2-D mixture model (vG-mix, mG-mix, L-mix, or U-mix) in Experiment 3 consists of two 1-D mixtures separately for the horizontal and vertical directions, f(x) and g(y), modeled in the same way as the corresponding models in Experiment 1. The number of components, n, is counted as the mean of components in the two directions, $\frac{n_x+n_y}{2}$. Only models with |n_x − n_y| ≤1 were considered. The 2-D Gaussian model is a special case of 2-D mixture models vG-Mix or mG-Mix with n = 1.

The probability of hitting a rectangular target of width 2a and height 2b is computed as the product of two 1-D probabilities:

$$\text{Pr}(T_{\mathit{\text{rect}}})=({\int }_{-a}^{a}f(x)dx)({\int }_{-b}^{b}g(y)dy)$$ (16)

The probability of hitting a circular target of radius R is also computed as the product of two 1-D probabilities:

$$\text{Pr}(T_{\mathit{\text{circle}}})=({\int }_{-\eta R}^{\eta R}f(x)dx)({\int }_{-\eta R}^{\eta R}g(y)dy)$$ (17)

where $\frac{1}{\sqrt{2}}\le \eta \le 1$ is a discounting parameter for the radius so that the probability of hitting the circle is no less than the probability of hitting its inscribed square and no greater than the probability of hitting its circumscribed square.

Overlap of basis distributions in probability density

For an mG-mix pdf with n Gaussian components (n > 1), we divided the spatial axis into n intervals using the middle points of the centers of adjacent components. That is, each interval was owned by one and only by one Gaussian basis distribution. The probability mass in each interval also came from the tails of other Gaussians. We computed the percentage of probability mass contributed by the owner Gaussian for each interval and averaged the percentage across intervals. One hundred minus the resulting percentage was defined as the percentage of overlap.

U-mix simulation for Körding & Wolpert³¹

The subject’s task was to use her finger to control the horizontal position of a virtual pea-shooter to hit a vertical target line. The position of each pea x was drawn from a skewed distribution whose mean was determined by their aim point m and whose skewness was determined by one single parameter ρ:

$$f(x|m,\rho )=(1-\rho )N(m-0.2,0.2\sqrt{2})+\rho N(m-0.2+0.2/\rho ,0.2{(1+{(1/\rho -1)}^2)}^{0.5})$$ (18)

where N(μ,σ) is a Gaussian centered at μ with the standard deviation σ. If a subject assumed a loss function where the cost increases quadratically with error, she should align the mean of her error distribution with the target. Körding & Wolpert found the deviation of subjects’ aim point from the mean varied systematically with ρ (Fig. 7b). They concluded that subjects’ loss functions were quadratic for small errors but less than quadratic for large errors.

For Figure 7, we simulated a virtual subject who had a quadratic loss function—and thus would aim for the mean—but who approximated her error distribution with a U-mix of 3 non-zero probability categories. For a specific ρ, the categories centered at the median of the error distribution and evenly partitioned the range of [−3.3σ_ρ, 3.3σ_ρ], where σ_ρ is the standard deviation of the error distribution. The probability density of each category was computed as the mean density of the error distribution within the range with the area under the u-mix scaled to be one.

For Supplementary Figure 7, we simulated a second virtual subject who was similar to the virtual subject above but who approximated her error distribution with an mG-mix with 3 components. The standard deviation of each component was 0.28. For each specific ρ, the three components were centered in the same way as the U-mix components above. Their weights were estimated as free parameters to minimize the sum of squared differences between the error distribution and the mG-mix approximation.

In the experiment, the error distribution was manipulated to be right-skewed in half of the trials (“noninverted trials”) and was inverted in the other half. Figure 2B of Körding & Wolpert³¹ showed subjects’ aim point as a function of ρ for the noninverted trials and all trials. The two curves were similar, both having the towards-median and away-from-median biases. But we noticed that the all-trials curve significantly deviated from the mean when the error distribution was symmetric (ρ = 0.5), an anomaly that could not be explained by any loss functions or probability distortions without introducing an asymmetry between left and right, and which was probably due to unknown visuo-motor biases subjects had with respect to pointing to left or right. For this reason, we used the curve for noninverted trials as the data to account for in our simulation.

Summary of statistical tests

No statistical methods were used to pre-determine sample sizes but our choice of sample size was based on previous work including Zhang et al²¹. AICc^18,19 and group-level Bayesian model selection²⁰ were used in all experiments. Pearson’s correlation was used in Experiment 1. We verified the assumptions of all of the statistical tests used. A supplementary methods checklist is available.