Automated Recognition of Obstructive Sleep Apnea Syndrome Using Support Vector Machine Classifier

Abstract

Obstructive sleep apnea (OSA) is a common sleep disorder that causes pauses of breathing due to repetitive obstruction of the upper airways of the respiratory system. The effect of this phenomenon can be observed in other physiological signals like the heart rate variability, oxygen saturation, and the respiratory effort signals. In this study, features from these signals were extracted from 50 control and 50 OSA patients from the Sleep Heart Health Study database and implemented for minute and subject classifications. A support vector machine (SVM) classifier was used with linear and second-order polynomial kernels. For the minute classification, the respiratory features had the highest sensitivity while the oxygen saturation gave the highest specificity. The polynomial kernel always had better performance and the highest accuracy of 82.4% (Sen: 69.9%, Spec: 91.4%) was achieved using the combined-feature classifier. For subject classification, the polynomial kernel had a clear improvement in the oxygen saturation accuracy as the highest accuracy of 95% was achieved by both the oxygen saturation (Sen: 100%, Spec: 90.2%) and the combined-feature (Sen: 91.8%, Spec: 98.0%). Further analysis of the SVM with other kernel types might be useful for optimizing the classifier with the appropriate features for an OSA automated detection algorithm.

I. Introduction

Sleep apnea is a common sleep disorder that causes pauses of breathing during sleep. A sleep apnea episode is defined as the cessation or near cessation of airflow for 10 s or more in an adult. In obstructive sleep apnea syndrome (OSAS), the pause of breathing is due to the obstruction of the upper airways of the respiratory system. It affects around 4% of men and 2% of women of the general population [1]. Sleep studies (polysomnography) are the traditional methods for assessment of breathing disorders during sleep. Polysomnography has recordings of around 16 signals, including ECG, EEG, respiratory effort, and airflow that are collected over a whole night. This method is expensive, time consuming, and it is challenging for subjects to be connected to all these instruments in sleep laboratories for whole nights. Portable polysomnography devices with fewer signals are also available. Several other methods have been proposed for diagnosing or screening sleep apnea. Time and frequency analysis of heart rate variability (HRV), ECG-derived respiration, photoplethysmography, and other signals were proposed for minute-by-minute apnea classification algorithms for the whole night of sleep [2]–[5].

In this study, we evaluate features from the magnitude and phase of the thoracic and abdominal respiratory effort signals for OSA detection. This is based on the physiological fact that during normal breathing the abdominal and thoracic efforts happen simultaneously. This makes the two signals approximately in common phase. In OSAS, as the airway becomes obstructed, the phase difference between the abdominal and thoracic movement increases, and at total obstruction, these two signals get into counterphase in a situation called paradoxical breathing. This is due to the fact that, during an obstructive apnea, the air volume in the lung remains constant but the motion of the diaphragm continues. Then, during an obstructed inhalation attempt, the abdomen grows in circumference while the thorax reduces in circumference. Therefore, the grade of airway obstruction and hence the seriousness of the corresponding episode of OSA can be characterized by the phase difference between the abdominal and the thoracic excursion signals. The magnitudes of both respiratory efforts drop to very low values in OSA and central sleep apnea compared to normal breathing. Várady et al. showed that phase difference between the thoracic and abdominal respiratory signals has 80–90% accuracy in classifying selected 1-min segments from OSA and control subjects [6]. Cross correlation between the two respiratory effort signals showed 66% accuracy compared with respiratory distress index for the whole night of sleep [7].

The goal of this study is to evaluate classification of whole-night normal and apneic epochs using extracted features from the phase and magnitude of the respiratory efforts signals, compared and combined with some other features from HRV and oxygen saturation signals. The main phase feature studied in this paper is the phase-locking value (PLV). PLV is a nonlinear measure of synchronization between two signals and was introduced by Hoke et al. [8] in 1989 when studying magnetoencephalo-grams, and used in studying synchrony between EEG signals by Lachaux et al. [9] and Mormann et al. [10]. The PLV is a statistical quantity bounded between 0 and 1. A PLV value of zero means that the two signals are not coupled at all while a PLV of one means that the two signals are perfectly coupled because of the constant phase difference between the two signals over all time sample. Compared to other synchronization measures, PLV shows simplicity, yet it keeps the same informational level as the more complex measures [11].

II. Methods

Polysomnographic data for 50 OSA patients (AHI = 36.86 ± 24.32) and 50 control subjects (AHI = 1.1 ± 1.48) were selected from the Sleep Heart Health Study (SHHS) [12]. The selected group includes 24 severe apnea (AHI > 30), 14 moderate apnea (30 ≥ AHI > 15), and 12 mild apnea (15 ≥ AHI > 5) patients. Ten subjects had AHI between 4.5 and 5.5. No other demographic data were provided by the source. The thoracic and abdominal respiratory effort signals, ECG, and oxygen saturation signals (sampled at 10, 250, and 1 Hz, respectively) were extracted for the whole night. These records were divided into segments of 1-min length. Using the provided starting time and duration of every apnea/hypoapnea event, each segment i was labeled with its apnea type as follows:

• If D_O (i) ≥ 5 s label(i) is: Obstructive Apneic

• else if D_M (i) ≥5 s label(i) is: Mixed Apneic

• else if D_C (i) ≥5 s label(i) is: Central Apneic

• else if D_H (i) ≥5 s label(i) is: Hypoapneic

where D_O, D_M, D_C, and D_H are durations of obstructive, mixed, central, and hypoapnea in each segment, respectively. All the apnea/hypoapnea labeled segments are then annotated as apneic, while the remaining unlabeled segments are annotated as normal.

To compute the PLV between the two effort signals, the instantaneous phases of the two signals are first computed using the Hilbert transform. Given a function x(t), the analytical signal z(t) is defined as follows:

$$z\left(t\right)=x\left(t\right)+i\tilde{x}\left(t\right)$$ (1)

where $\tilde{x}\left(t\right)$ is the Hilbert transform of x(t) and is computed as follows:

$$\tilde{x}\left(t\right)=\frac{1}{\pi }p.v.{\int }_{-\infty }^{+\infty }\frac{x\left(t\right)}{t-\tau }d\tau$$ (2)

where p.v. denotes that the integral is taken in the sense of Cauchy principal value, and the instantaneous phase is calculated as follows:

$${\theta }_x\left(t\right)=\arctan \left(\frac{\tilde{x}\left(t\right)}{x\left(t\right)}\right).$$ (3)

The PLV is then computed as follows:

$${\mathrm{PLV}}_t=\mid {\langle e^{i\Delta \theta \left(t\right)}\rangle }_t\mid$$ (4)

where ${\langle \cdot \rangle }_t$ is the operator of averaging over time and Δθ(t) is the instantaneous phase difference. For discrete signals, the PLV is calculated as follows:

$$\mathrm{PLV}=\mid \frac{1}{N}\sum _{n=1}^N{e}^{i\Delta \theta \left(n\right)}\mid .$$ (5)

In our application, Δθ(n) is instantaneous phase difference between the thoracic and abdominal respiratory efforts and N is the number of samples in each 1-min segment (N = 600). The Hilbert transform was computed using the built-in MATLAb function “hilbert,” which implements the discrete-time Fourier transform to compute the analytical signal. PLV is a normalized number that varies between zero and one. The other features extracted from the respiratory signals are the mean of the phase difference Δθ_m , the standard deviation of the phase difference Δθ_std, the standard deviation of the thoracic effort T_std, and the standard deviation of the abdominal effort A_std, all computed for the 1-min segments.

RR intervals were extracted from the ECG signals using the Pan–Tompkins algorithm [13]. Premature ventricular contractions (PVC) were detected by using a discriminator based on the five-point median of the RR interval. A PVC is detected if:

$$R{R}_i=0.75\ast mRR,\text{and}R{R}_{i+1}=1.25\ast mRR$$ (6)

where mRR is the median of the normal five RR intervals preceding RR_i. The corrected RR_i and RR_i+1 were computed using linear interpolation. The RR intervals were evaluated at every heartbeat. Cubic-spline interpolation was used to resample the signal as a function of time (in seconds) with a sampling frequency of 1 Hz. The RR signal was then divided into segments of 1-min length. The Power Spectral Density was computed using a 256-point FFT. The mean and standard deviation of the RR intervals, the absolute and normalized powers in the VLF, LF, and HF bands, and the ratio of LF power over the HF power (LHR) were all computed. The 1-min means and standard deviations of the oxygen saturation (SaO2_m and SaO2_std) were also computed. For epoch classification, support vector machine (SVM) classifiers were used [14]. SVM classifiers have shown better performance over linear discriminant and neural network classifiers in OSA recognition [15]. SVM constructs a hyper plane or a set of hyper planes in a high-dimensional space where the n-dimensional input vector is mapped into a K-dimensional feature space via a nonlinear mapping φ(x). The equation of hyper plane separating two different classes is given by the relation

$$y\left(x\right)=W^T\phi \left(X\right)=\sum _{j=1}^K{\omega }_j{\phi }_j\left(x\right)+{\omega }_0=0$$ (7)

where W = [ω₀, ω₁, . . . , ω_K] is the weight vector of the network. All training and testing operations are done using kernel functions. The most commonly used kernels are linear, polynomial, and Gaussian. In this study, linear and second-order polynomial functions were selected as kernels with different values of the regularization parameter C (C = 0.1, 1, 5, 10), which is a constant that determines the tradeoff between the maximum margin and minimum classification error. A high C can minimize training error but will also compromise margin separation. Due to the long training time, one-tenth of the normal and apneic epochs were used to train the classifiers. The classification was done for the respiratory effort, HRV, and oxygen saturation features separately then, a classification using all these features was performed. In this study, the overall accuracy is defined as the percentage of total epochs correctly classified. The sensitivity is defined as the percentage of apneic epochs correctly classified and the specificity is the percentage of normal epochs correctly classified. For subject classification, the total number of apneic minutes per hour of sleep (m-AHI) was computed for each subject and a threshold value to maximize the subject classification accuracy was found. Here, the sensitivity is defined as the percentage of OSA subject correctly classified while the specificity is defined as the percentage of control subject correctly classified.

III. Results

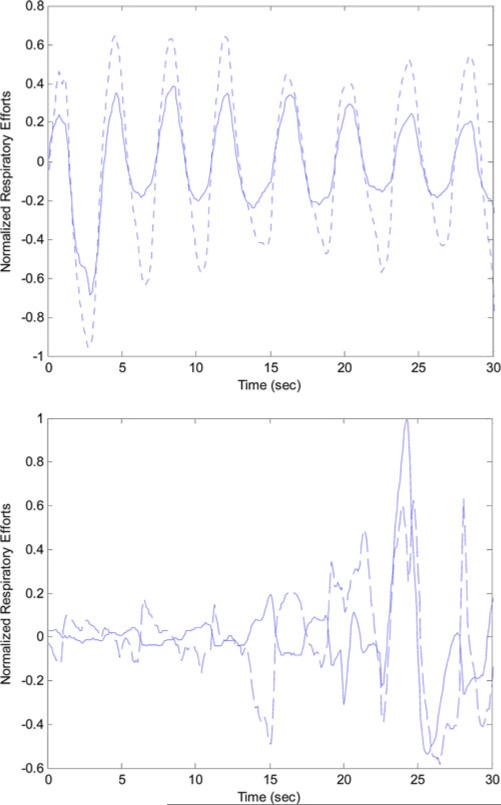
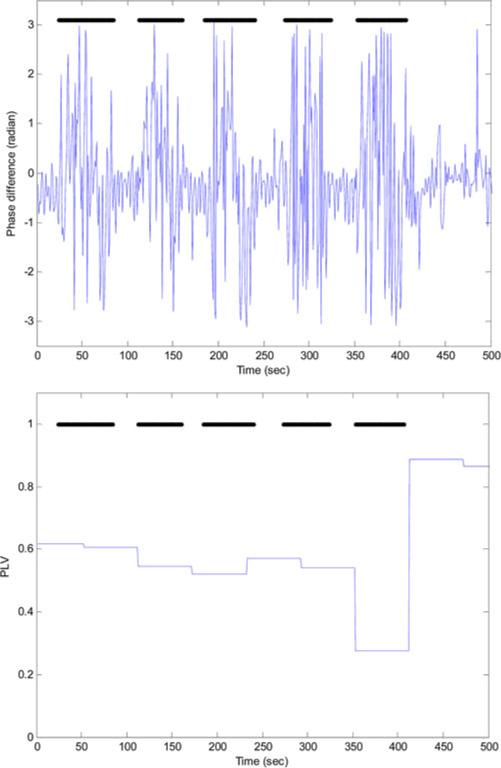
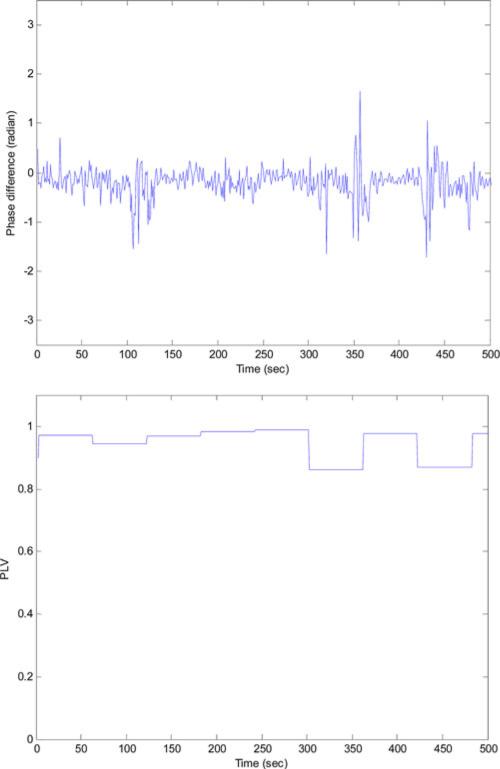
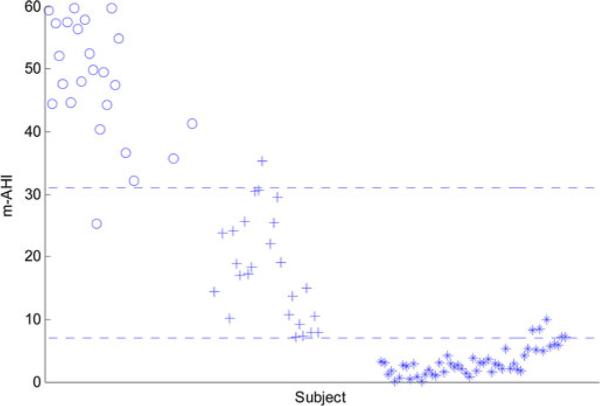
The total number of the 1-min segments for the 100 subjects was 39575: 22908 annotated as normal while 16 667 annotated as apneic. Among the apneic minutes; 5462 were labeled as obstructive, 4 as mixed, 656 as central, and 10 545 as hypoapnea. Fig. 1 shows the synchrony between the thoracic and abdominal respiratory efforts during normal breathing and the paradoxical breathing during OSA. Fig. 2 shows the instantaneous phase difference and the PLV of an OSA patient during OSA and Fig. 3 shows these features during normal breathing for the same OSA patient. During obstructive apnea, the phase difference between the two respiratory signals increases that results in lowering the corresponding PLV. During normal breathing, the phase difference decreases and PLV increases toward one. Table I shows the mean ± std and one-way ANOVA p-value for the respiratory effort, HRV, and oxygen saturation features that showed significant differences between the control and OSA groups. To evaluate any influence of rapid eye movement (REM) sleep on increasing the OSA epochs, variation in the respiratory phase features (PLV, Δθ_m , Δθ_std) between REM and non-rapid eye movement (NREM) sleep was tested. However, no significant difference was found in any of these features between these two sleep stages. The extracted features were implemented to classify the normal and apneic epochs using the SVM classifier. Table II shows the minute classification results of the respiratory effort, HRV, and oxygen saturation signals separately and the combination of all these signals. The polynomial kernel always gave higher accuracy than the linear kernel classification. Also, the combined-signal classifier always had the highest accuracy compared to the separate signal classifiers. Among the three signals, oxygen saturation always had the highest specificity (up to 98%), while the respiratory efforts had the highest sensitivity (up to 72%). There was an interesting increase in the oxygen saturation sensitivity from 25% (using the linear kernel) to 60% (using the polynomial kernel). This caused an improvement in its overall accuracy to reach 80%. Generally speaking, the accuracy increases as C increases where the maximum accuracy achieved at C = 5 or 10 except for the oxygen-saturation linear classification where the accuracy decreases as C increases. The maximum minute accuracy (Acc: 82.4%, Sen: 69.9%, Spec: 91.4%) was achieved with the combined-signal classifier, implementing a second-order polynomial kernel with C = 5. Table III shows the subject classification results. Here again, the polynomial classifier showed better accuracy except for the respiratory efforts where it had a slight drop. Also, the combined classifier gave the best results: Acc: 92%, Sen: 89.8%, Spec: 94.1%, C = 1 for the linear kernel and Acc: 95%, Sen: 91.8%, Spec: 98.1%, C = 0.1, 1 and 5 for the polynomial kernel. Interestingly, the best oxygen-saturation classifier had the same accuracy even with 100% sensitivity but with a lower specificity of 90.2%. Fig. 4 shows the m-AHI for the 100 subjects computed by the best oxygen-saturation classifier. The lower dashed line (m-AHI = 7) represents the threshold that gives the highest apnea classification accuracy. All the OSA patients were correctly classified with this threshold while five control subjects were falsely classified as patients. Among these five subjects, three were on the borderline (their AHI > 4.5). The upper dashed line (m-AHI = 31) represents the threshold that gives the highest accuracy for apnea severity classification, where one severe apnea was falsely classified as moderate and one moderate apnea was classified as severe. To test the agreement between the AHI and m-AHI, the Bland–Altman method was used [16]. Any subject with AHI ≥ 60 was removed from the analysis since m-AHI saturates at 60. Again, the oxygen saturation classifier gave the best results. The mean bias was −1.06 and the upper and lower limits were 7.99 and −10.11, respectively. The difference between the AHI and m-AHI tends to increase as the apnea severity increases. When severe OSA patients were removed from the analysis, the upper and lower limits were lowered to 2.03 and −5.8, respectively, and the mean bias was − 1.89.

Fig. 1.

Thoracic effort (dashed curve) and abdominal effort (solid curve) during normal breathing (top) and OSA (bottom).

Fig. 2.

Phase difference (top) and PLV (bottom) during OSA. OSA epochs are represented with the dark horizontal lines at the top of the plots.

Fig. 3.

Phase difference (top) and PLV (bottom) during normal breathing.

TABLE I.

Average and Standard Deviation of Respiratory,HRV, and Oxygen-Saturation Features for Control and OSA Groups

Feature	Control	OSA	ANOVA
Δθm (rad)	0.56 ± 0.38	1.05 ± 0.54	p<10−5
Δθstd (rad)	0.37 ± 0.17	0.82 ± 0.41	p<10−9
PLV	0.86 ± 0.14	0.64 ± 0.20	p<10−8
Astd	0.13 ± 0.07	0.22 ± 0.14	p<0.0001
Tstd	0.13 ± 0.06	0.16 ± 0.08	p<0.05
VLF (sec2)	0.25 ± 0.25	0.53 ± 0.58	p<0.005
LF (sec2)	0.20 ± 0.20	0.50 ± 1.08	p<0.05
NVLF	0.34 ± 0.08	0.42 ± 0.13	p<0.005
NHF	0.29 ± 0.10	0.24 ± 0.12	p<0.05
RRstd (sec)	0.04 ± 0.02	0.06 ± 0.05	p<0.005
SaO2m(%)	95.53 ± 1.66	93.34 ± 1.78	p<10−8
SaO2std(%)	0.82 ± 0.58	2.12 ± 1.09	p<10−10

TABLE II.

Minute Classification Using SVM

Kernel	C	HRV Features			Respiratory Features			Oxygen Saturation Features			Combined Features
		Acc%	Sen%	Spec%	Acc%	Sen%	Spec%	Acc%	Sen%	Spec%	Acc%	Sen%	Spec%
Linear	0.1	62.2	19.2	93.4	69.0	59.1	76.2	67.5	26.5	97.3	71.5	63.0	77.6
	1	64.1	26.8	91.1	69.1	59.1	76.4	65.5	21.4	97.6	72.2	62.4	79.2
	5	68.6	49.1	82.7	69.2	59.6	76.2	59.1	5.4	98.2	72.3	57.4	83.1
	10	68.8	51.6	81.4	69.2	59.5	76.3	58.0	2.6	98.3	72.6	57.9	83.4
2-nd order Polynomial	0.1	66.6	38.5	87.1	69.7	69.3	69.9	79.1	57.3	94.9	82.0	67.9	92.2
	1	69.1	51.6	81.8	69.8	72.4	68.0	80.0	60.4	94.3	82.3	69.0	92.0
	5	69.4	54.3	80.3	69.9	72.3	68.1	80.1	60.9	94.1	82.4	69.9	91.4
	10	69.5	54.8	80.1	69.9	72.1	68.2	80.0	60.3	94.3	82.1	70.9	90.2

TABLE III.

Subject Classification Using SVM

Kernel	C	HRV Features			Respiratory Features			Oxygen Saturation Features			Combined Features
		Acc%	Sen%	Spec%	Acc%	Sen%	Spec%	Acc%	Sen%	Spec%	Acc%	Sen%	Spec%
Linear	0.1	64.0	46.9	80.4	89.0	85.7	92.2	87.0	77.6	96.1	90.0	89.8	90.2
	1	69.0	57.1	80.4	88.0	83.7	92.2	86.0	75.5	96.1	92.0	89.8	94.1
	5	79.0	79.6	78.4	88.0	83.7	92.2	70.0	63.3	76.5	91.0	85.7	96.1
	10	77.0	79.6	74.5	88.0	83.7	92.2	60.0	42.9	76.5	88.0	91.8	84.3
2-nd order Polynomial	0.1	74.0	61.2	86.3	88.0	87.8	88.2	95.0	98.0	92.2	95.0	91.8	98.0
	1	77.0	71.4	82.4	86.0	87.8	84.3	95.0	100	90.2	95.0	91.8	98.0
	5	78.0	67.3	88.2	87.0	87.8	86.3	95.0	100	90.2	95.0	91.8	98.0
	10	78.0	67.3	88.2	87.0	87.8	86.3	95.0	100	90.2	93.0	91.8	94.1

Fig. 4.

m-AHI computed from the best oxygen saturation classifier for the 100 subjects (*:control; +:mild/moderate apnea, o: severe apnea subjects).

IV. Discussion

Paradoxical respiration is a well-known respiratory pattern in OSA syndrome. It is observed in our dataset, as all the respiratory phase features were significantly different between the control and OSA groups. The absence of significant differences in these features between the NREM and REM sleep stages supports the results that show the respiratory disturbance is not greatly affected by sleep stages, in contrast to the studies that suggest that OSA is a REM-predominant phenomenon [17]. The high sensitivity of the respiratory features compared to the HRV and oxygen-saturation features in the minute classification shows that the phase difference between the thoracic and abdominal efforts is better in capturing the obstructive apnea event. However, the sensitivity was in the 70% range. Including the central apnea epochs in the total apneic epochs helped in lowering the sensitivity as no respiratory efforts are observed during central apnea; however, the contribution of these epochs is small since they represent less than 4% of the total apneic epochs. Hypoapnea epochs on the other hand, (63% of the apneic epochs) had greater effect in lowering the sensitivity, as the changes in the amplitude and phase difference between the respiratory efforts are smaller than the OSA epochs. Also, the sampling rate used in the SHHS for the respiratory efforts was 10 Hz. This is reasonable for normal breathing that varies between 12–20 breaths/min; however, it might not be enough to capture detailed phase variation during apnea. The increase of the sympathetic tone (observed as increase in the LF power of HRV) and the cyclic variation of the heart rate (observed as increase in the VLF power of HRV) are well known behaviors associated with sleep apnea [18], [19]. However, the cyclic alternating pattern, which is the natural arousal rhythm of the NREM sleep, is associated with significant increase of the LF and decrease of HF spectral components of the HRV in normal subjects [20]. Also, the frequency resolution using the 1-min time window is low (around 0.017 Hz). This reduces the accuracy of the estimated power in VLF band (0.003–0.04 Hz). Enlarging the time-window will improve the frequency resolution; however, it will affect the time resolution and will reduce the accuracy of the minute classification. This explains the low sensitivity of the HRV classifier. On the other hand, the oxygen saturation classifier showed interesting results. Oxygen saturation is known to have low sensitivity and high specificity as many OSA patients displayed normal oximetry [21] and our results from the linear classifier were consistent with this. Using second-order kernel caused a big improvement in the sensitivity as the specificity stayed high. There is no clear explanation of this improvement; however, it is most likely related to the advantage of the polynomial kernel in separating the normal and apneic planes. Further analysis using higher order polynomials and other kernel types needs to be implemented to determine the optimum kernel type for best classification accuracy. A disadvantage of the SVM is its long training time especially with long dataset (around 40 000 points in our case). However, new algorithms are proposed to improve the training speed and even improve the overall accuracy [22].

V. Conclusion

The respiratory phase and magnitude features showed high sensitivity in the apnea minute classification compared to the other features. This is expected since OSA is associated with phase asynchrony between the two respiratory efforts. Oxygen saturation features were more accurate in classifying the normal epochs. Implementing second-order polynomial kernel had a clear improvement on the oxygen-saturation accuracy in the minute and subject classification. These features can be incorporated into automatic algorithms for portable OSAmonitoring using the available respiratory and oxygen saturation devices.

Biography

Haitham M. Al-Angari received the Ph.D. degree in electrical engineering from Northwestern University, Evanston, IL, in 2005.

He is currently a Visiting Scholar at Northwestern University. His research interests include biomedical instrumentation and signal processing, finite element modeling, and sleep apnea detection and treatment.

Alan V. Sahakian (S'84–M'84–SM'94–F'07) received the Ph.D. degree in electrical engineering from the University of Wisconsin, Madison, in 1984.

In 1984, he joined Northwestern University, Evanston, IL, where he is currently a Professor and the Chair in the Department of Electrical Engineering and Computer Science, and a Professor in the Department of Biomedical Engineering, and is also a Member of the Academic Affiliate Staff of North Shore University Health System (Evanston Hospital, Evanston, IL). He is the author or coauthor of approx imately 200 papers, abstracts, patents, and book sections. His current research interests include the areas of cardiac electrophysiology, RF, microwave and millimeter-wave imaging and remote sensing and patient monitoring methods, and irreversible electroporation methods for tumor ablation.

Dr. Sahakian has served as the Vice-President for Publications and Technical Activities for the Engineering in Medicine and Biology Society. He is a Fellow of the American Institute for Medical and Biological Engineering.