Probabilistic brains: knowns and unknowns

Abstract

There is strong behavioral and physiological evidence that the brain both represents probability distributions and performs probabilistic inference. Computational neuroscientists have started to shed light on how these probabilistic representations and computations might be implemented in neural circuits. One particularly appealing aspect of these theories is their generality: they can be used to model a wide range of tasks, from sensory processing to high-level cognition. To date, however, these theories have only been applied to very simple tasks. Here we discuss the challenges that will emerge as researchers start focusing their efforts on real-life computations, with a focus on probabilistic learning, structural learning and approximate inference.

Uncertainty is an intrinsic part of neural computation, whether for sensory processing, motor control or cognitive reasoning. For instance, it is impossible to determine with certainty the age of a person on the basis of a photo, but it is possible to make a reasonable guess, and even to estimate the uncertainty associated with that guess. Similarly, motor behavior is inherently variable and uncertain. As any golfer or tennis player can attest, repeating the same movement twice is impossible. However, just as we can estimate the confidence associated with a guess about the age of a person, we also have a sense of how much variability corrupts our movements. Thus, a right-handed player would know right away that there would be less variability when playing with her right hand compared with playing with her left. At the cognitive level, we are also constantly faced with decisions in the presence of uncertainty; for instance, whether we should invest our money in the stock market or in a house.

An efficient, and under some circumstances optimal, way to perform tasks involving uncertainty is to represent knowledge with probability distributions and to acquire new knowledge by following the rules of probabilistic inference. Indeed, Cox’s theorem¹ tells us that probability theory provides the only sensible and coherent way to reason under uncertainty, whereas the Dutch Book theorem² explicitly demonstrates the hazards of acting on beliefs that violate the rules of probabilistic calculus (at least for gamblers). The idea that the brain performs probabilistic reasoning is commonly referred to as the Bayesian approach, as it relies on the so-called Bayes’ rule³. However, Bayes did not suggest that human knowledge is acquired through probabilistic inference; his focus was purely on the laws of probability. The idea was alluded to by Richard Price in his introduction (and appendix) to Bayes’ paper, but it was most clearly stated by the mathematician Pierre Simon Laplace, who wrote two centuries ago, “One may even say, strictly speaking, that almost all our knowledge is only probable; and in the small number of things that we are able to know with certainty, the principle means of arriving at the truth—induction and analogy—are based on probabilities”⁴. This deep, and prescient, insight explains the use of probabilistic in the title of this article, as opposed to the more common term Bayesian (we could have used the term Laplacian, but feared the consequences of violating Stigler’s Law⁵, which states that “no scientific discovery is named after its original discoverer”).

Mach⁶ and Helmholtz⁷ were among the first to apply this idea to sensory perception, but strong experimental evidence in support of this notion has emerged only over the last two decades. These experiments have shown that human behavior is highly consistent with probabilistic reasoning not only in the sensory domain^8–12, but also in the motor^13–15 and cognitive^16–22 domains.

In the last domain, cognitive reasoning, probabilistic inference has been applied to a wide variety of problems²³. Consider, for example, inductive reasoning¹⁶. Suppose you are told that chimpanzees and gorillas share a particular gene. How likely is it that seals carry that gene as well? Or ants? Recent studies¹⁸ strongly suggest that humans use probabilistic inference to answer such questions. Moreover, they appear to rely on prior knowledge (in this example, knowledge of animal evolutionary development). Other cognitive functions, such as semantic memory²⁰, theory-based causal reasoning¹⁹, language comprehension²¹ and language production²², have also been formalized in this framework.

Although it is well-established that humans and monkeys (and other animals) perform probabilistic inference, it is less clear how inference is implemented at the level of neural circuits. Recently, however, neural theories of probabilistic inference have started to emerge, along with new experimental tests. Here we briefly review these advances and discuss some of the main challenges.

Probabilistic inference for multisensory integration

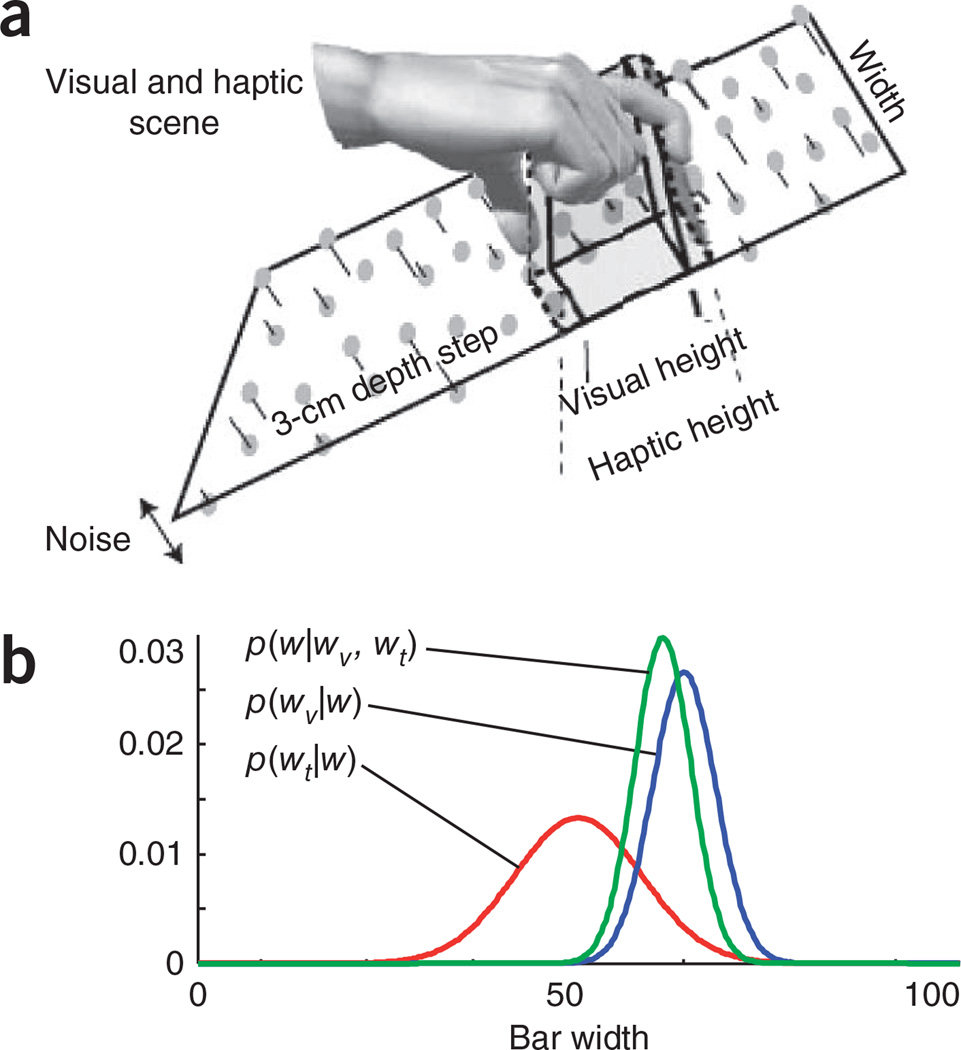
Multisensory integration provides one of the best illustrations of the power of the probabilistic approach. For instance, Ernst and Banks studied how human subjects estimate the width of an object by looking at it and touching it (Fig. 1a)¹¹. One could imagine several ways to solve this problem. A non-probabilistic approach could involve the following steps. First, look at the image and extract a measurement of the width of the bar. Second, do the same for touch. Finally, use the average of the visual and tactile estimates. The problem, however, is that equal weights are given to both modalities, which is rarely appropriate. For instance, in complete darkness, any estimate based on vision would reflect only noise and should be ignored altogether. Thus, rather than equal weights, each cue should contribute to the final estimate in proportion to its reliability. This is precisely what would happen if we adopted a probabilistic approach and, rather than estimating a value, we recovered the probability distribution over the width of the bar given visual and tactile information. This distribution, denoted p(w|w_v,w_t) (w is the true width of the object and w_v and w_t are the width measurements obtained from vision and touch, respectively), can be obtained by applying Bayes’ rule:

$$p(w|w_v,w_t)=\frac{p(w_v,w_t|w)p(w)}{p(w_v,w_t)}=\frac{p(w_v|w)p(w_t|w)p(w)}{p(w_v,w_t)}$$ (1)

The second equality is based on the assumption that the noise corrupting the visual and tactile measurements are independent (Fig. 1b). If that is the case, and the noise distributions are Gaussian and unbiased (that is, if the visual and tactile measurements, w_v and w_t, are equal to the true width, w, plus Gaussian noise with variance ${\mathbf{\sigma }}_v^2\text{and}{\mathbf{\sigma }}_t^2$) and the prior distribution (p(w); Box 1) is flat, one can show that p(w|w_v ,w_t) is also Gaussian, with mean and variance given by

$${\mu }_{\mathit{\text{vt}}}=\frac{1/{\mathbf{\sigma }}_v^2}{1/{\mathbf{\sigma }}_v^2+1/{\mathbf{\sigma }}_t^2}{w}_v+\frac{1/{\mathbf{\sigma }}_t^2}{1/{\mathbf{\sigma }}_v^2+1/{\mathbf{\sigma }}_t^2}{w}_t$$ (2)

$${\mathbf{\sigma }}_{\mathit{\text{vt}}}^2=\frac{{\mathbf{\sigma }}_v^2{\mathbf{\sigma }}_t^2}{{\mathbf{\sigma }}_v^2+{\mathbf{\sigma }}_t^2}$$ (3)

Equation (2) captures our initial intuition: the mean of the posterior distribution (Box 1) is a compromise between the mean obtained from vision and the mean obtained from touch, but weighted by the inverse of the variance (that is, the precision) of each cue. Equation (3) states that the combined variance is smaller than both the visual and the tactile variance—as it should, given that combining cues increases the information.

Figure 1.

The visuo-haptic multisensory experiment of Ernst and Banks¹¹. (a) Subjects were asked to estimate the width of a bar that they could see and touch. Subjects did not see an actual bar, but saw a set of dots floating above the background, as if glued to an otherwise invisible bar. In addition, the background dots did not all appear at the same depth, but followed a Gaussian distribution with a mean equal to the mean depth of the background. The same applied to the dots corresponding to the bar. The reliability of the visual input was controlled by the variance of the Gaussian distributions in depth. This variance varied from trial to trial and acted as a nuisance parameter. Adapted from ref. ¹¹. (b) The posterior distribution over the width (p(w|w_v, w_t), green curve) is proportional to the product of the visual (p(w_v|w), blue curve) and haptic (p(w_t|w), red curve) likelihood functions. Note that the posterior distribution is shifted toward the more reliable cue (the one with the smaller variance; in this case, vision).

Box 1 Terms and definitions.

Posterior distribution

Suppose you record the activity of a population of neurons in area MT in response to a visual stimulus moving in direction s. The posterior distribution, denoted p(s|r), is the function that tells us the probability of each direction given the observed pattern of activity r. This function is obtained via Bayes’ rule, by multiplying the likelihood function with the prior and normalizing; for example, see equation (4) (but note that r is replaced by I).

Likelihood function

The likelihood function of s is the function p(r|s) that tells us the probability of the observed pattern of activity r given stimulus s. As in the above example, r could be the activity in area MT and s the direction of motion. Notably, when we refer to p(r|s) as the likelihood function, we are keeping r constant and varying s. Note that the function p(r|s) can also be treated as a function of r, in which case it is not referred to as the likelihood function of s, but as the conditional distribution of r given s.

Prior distribution

The prior distribution over a stimulus, denoted p(s), is the probability distribution before receiving any evidence, that is, before observing neural activity r. In our area MT example, p(s) is the prior over direction of motion and is usually taken to be uniform (all directions of motion are equally likely). Uniform priors, however, are not the norm. For example, in natural environments, most objects don’t move, and when they do move, they are more likely to move slowly than rapidly; in that case, the prior would explicitly favor lower speeds. In general, the prior should refect the frequencies of different values of s in natural environments.

Marginalization

Typically marginalization refers to ‘integrating out’ variables from a joint distribution. For instance, computing p(x) from p(x,y), which is done via the integral p(x) = ∫ p(x,y)dy, is known as marginalization. Here we expand that notion so that marginalization includes computing p(f(x,y)) from p(x,y). To see that this can be cast as a marginalization, let p(x,y,z) = p(x,y)δ(z – f(x,y)), where δ(·) is the Dirac delta function. Then, p(f(x,y)) = p(z) = ∫ p(x,y,z)dxdy.

Cost function

A cost function is a function that specifies the costs and benefits associated with decisions. It is a critical ingredient for turning probabilities into decisions. For instance, imagine finding a mushroom that, on the basis of appearance, has a 99% chance of being a Volvariella volvacea and a 1% chance of being a Amanita phalloides. Should you eat it? If you like Volvariella volvacea (which is widely used in Asian cooking and is very tasty), you’d probably be tempted to, but you might reconsider your dinner option once you find out that Amanita phalloides is highly toxic. Thus, although it is likely that the mushroom will be both tasty (a benefit) and non-toxic (also a benefit), eating it is not necessarily the right decision given that a mistake could result in liver failure (a cost). In general, decisions should be based on a combination of probabilities and costs.

As this example illustrates, the probabilistic approach allows us to derive explicit rules for combining evidence. These rules can, in turn, be used to probe the extent to which animals use probabilistic reasoning. What Ernst and Banks¹¹ (and several prior studies^12,24,25) found is that human behavior is consistent with equations (2) and (3), providing evidence that humans properly take into account uncertainty on a trial-by-trial basis, an integral part of probabilistic reasoning.

A unified framework

Multisensory integration is just one area of application of the probabilistic approach. In all areas, however, the goal is the same: compute probability distributions over variables of interest s given sensory measurements I and prior knowledge p(s). In probabilistic models, the variable s is referred to as a latent variable (the width of the bar in the previous example) or, more generally, a set of latent variables; a terminology we use throughout the paper. Note that latent variable is a broad term and need not refer to concrete quantities in the outside world. In motor control, s can be a goal (for example, reaching an object at a particular location), and, in the cognitive domain, it can be relational structures, such as who in our circle of friends gets along with whom. In the latter case, the sensory measurements, I, can go back a long time, possibly many years.

Probabilistic inference starts with the generative model, a statistical model of how the measurements, I, are generated (which has to be learned by the animal). The generative model consists of a prior distribution p(s) and a distribution p(I|s) (known as the likelihood function when viewed as a function of s; Box 1). In the previous example, the prior, p(w), was assumed to be flat, and the likelihood functions corresponded to the functions p(w_v|w) and p(w_t|w). Bayes’ rule then provides a recipe for formulating beliefs about s, in the form of the posterior distribution

$$p(s|I)=\frac{p(I|s)p(s)}{p(I)}$$ (4)

The denominator, p(I), ensures that the posterior distribution integrates to 1.

The fact that the techniques for doing inference (for computing the right-hand side of equation (4)) are the same regardless of domain has important implications for computational work. It means that there is hope for the emergence of general theories of neural computation that could transfer across domains. It also implies that it is worthwhile spending time and effort on general models, rather than domain-specific ones. For instance, there are numerous models of decision-making based on the drift-diffusion model^26–28. Although these models have provided us with a great deal of insight into binary decision-making, it’s not clear how well they generalize to more complex decisions, such as ones in which the reliability of the evidence changes over time, or to motor control or visual processing. However, because making a decision is inherently probabilistic, one could use more general probabilistic inference algorithms. Similarly, the probabilistic approach can be used for motor control, some aspects of visual processing, such as tracking moving objects, and even the general problem of determining which set of actions will maximize future rewards^29,30. Thus, understanding the neural basis of probabilistic inference might put us in a position to discover general theories of neural computation.

Encoding probabilities with neurons

Before discussing how animals perform probabilistic inference using neural circuits, we consider the issue of representation. How do populations of neurons represent probability distributions? Until fairly recently, the classical assumption was that they didn’t. Instead, neural activity was thought to encode a single value, such as the direction of motion of an object or the identity of an object (the latent variable). For instance, the activity of neurons in V1 is typically interpreted as encoding orientation, whereas neurons in area MT are thought to encode direction of motion. Over the last two decades, however, several groups have proposed that neural activity encodes functions of latent variables, as opposed to single values. In the probabilistic framework, these functions are either probability distributions or likelihood functions. If this is the case, then neural computations must manipulate whole functions, and must do so according to the rules of probabilistic inference. To understand how this is done at the neural level, we first need to discuss the format of these neural codes; that is, how whole probability distributions (or likelihood functions) are represented. Here we briefly review the more common proposals.

Probably the most straightforward schemes for encoding probability distributions are those that map activity directly onto probability. For instance, Barlow³¹ proposed that the response of a neuron tuned to a particular image feature, such as the orientation of a contour, is proportional to the log of the probability that the feature is present in the neuron’s receptive field (also see ref. ³²). More recently, Anastasio³³ proposed that neuronal responses are proportional to the probability rather than to its log (also see refs. ^34–37). Several groups have explored a variation of these ideas in which, rather than coding for the log probability that a feature is present, neurons code for the log probability that a feature takes on a particular value^38–42. When s is a binary variable, a similar coding scheme assumes that the neural response is proportional to the log odds (r ∝ log p(s = 1)/p(s = 0))⁴³. We refer to these types of code as log probability codes. Although the distinction between a code that uses probability versus one that uses log probability may seem arcane, it has important ramifications for probabilistic inference: for a code that uses probability, adding probabilities is easy, whereas, for one that uses log probabilities, multiplying them is easy. As both addition and multiplication are key steps in probabilistic inference, neither code has an obvious advantage over the other.

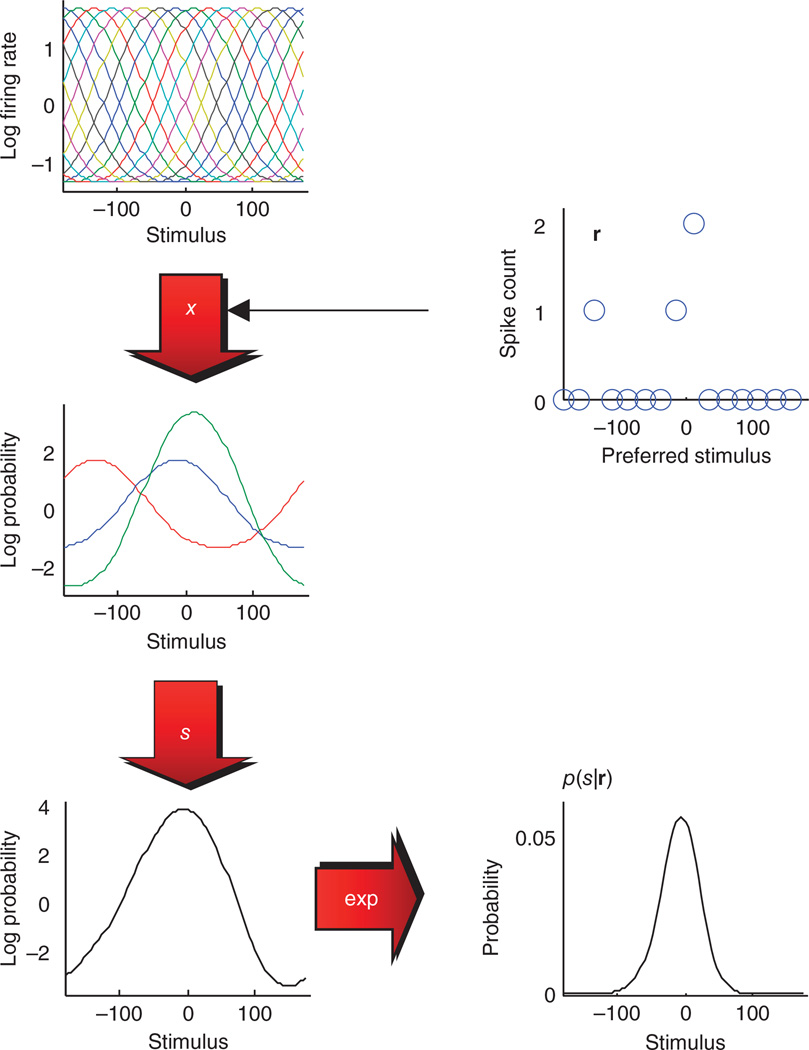
Other investigators have exploited the fact that probability distributions are functions, and, as such, can be encoded using a variety of techniques^44,45. A common one is to express functions as the sum of other functions, in this context called basis functions. For instance, one might use radial basis functions⁴⁶. This is analogous to what is done in Fourier analysis, where a function is expressed as a linear combination of sines and cosines. With the basis function approach, probability distributions would be represented as a set of coefficients^44,45 and the coefficients would be encoded by neural activity. Note that this scheme also works for the log of the probability and has been proposed by several groups^47–50 (Fig. 2). More specifically, log p(s|r) would be represented as

$$\text{log}p(s|\mathbf{r})=\mathbf{\sum }_i{r}_i{h}_i(s)+\text{constant}$$ (5)

where h_i(s) are the basis functions and the constant is needed to ensure proper normalization. When the basis functions are derived from the likelihood function, log p(r|s) (equation (6)), the result is a linear probabilistic population code^47,48, and when the basis functions h_i(s) are Dirac delta-functions, probabilistic population codes reduce to log probability codes.

Figure 2.

Probabilistic population code using a basis function decomposition of the log probability. Top left, the basis functions, for this example the log of the tuning curve, of 15 neurons to a periodic stimulus whose value varies from −180 to 180. Top right, pattern of spike counts, calculated over a 200-ms interval, across the same neuronal population in response to a stimulus whose value is 0. The spike counts were drawn from a Poisson distribution with means specified by the tuning curves. To turn spike counts into log probability, we first multiply each basis function by its corresponding spike count. Given that only three neurons are active on this trial, only three basis functions remain (center left, scaled by spike counts). The scaled basis functions are then summed to yield the log probability (up to a constant). Bottom left, the un-normalized log probability. Bottom right, the probability (properly normalized). Note that the two plots on the right (spike count versus stimulus and probability versus stimulus) represent the same probability distribution, but with a different format, just as a function can be represented directly or by its Fourier transform.

Which code or set of codes the brain uses is an open experimental question. However, there is experimental evidence for the scheme given in equation (5). Assuming a flat prior, Bayes’ rule tells us that

$$p(s|\mathbf{r})\propto p(\mathbf{r}|s)$$ (6)

where p(r|s) is the distribution of neural variability: the variability in spike counts in response to repeated presentations of the same stimulus. This implies that the code for the posterior distribution, p(s|r), can be deduced from the form of the neural variability, p(r|s)⁴⁷. Experimental data^51,52 suggest that p(r|s) belongs to a family of distributions known as the exponential family with linear sufficient statistics⁴⁷, leading to the code shown in equation (5) if the prior is flat. Thus, linear probabilistic population codes have the advantage that they are consistent with the statistics of neural responses. Moreover, as the h_i(s) can be any set of functions of s, equation (5) can represent virtually any posterior distribution, p(s|r).

Finally, some groups have proposed that the brain may represent probability distributions by the values of a set of samples drawn from the encoded distribution^34,36,53,54. Spikes, for example, could represent samples from a distribution over binary random variables, whereas the value of the membrane potential could represent samples from a probability distribution over real-valued random variables. Whether this type of code is mutually exclusive or complementary to other codes is still being debated, but this is clearly an interesting and important proposal.

Neural implementation of probabilistic inference

The neural implementation of probabilistic inference has received increasing attention over the last several years. Although a thorough review of this literature is beyond the scope of the present perspective, we provide a brief overview, with a particular emphasis on models using linear probabilistic population codes.

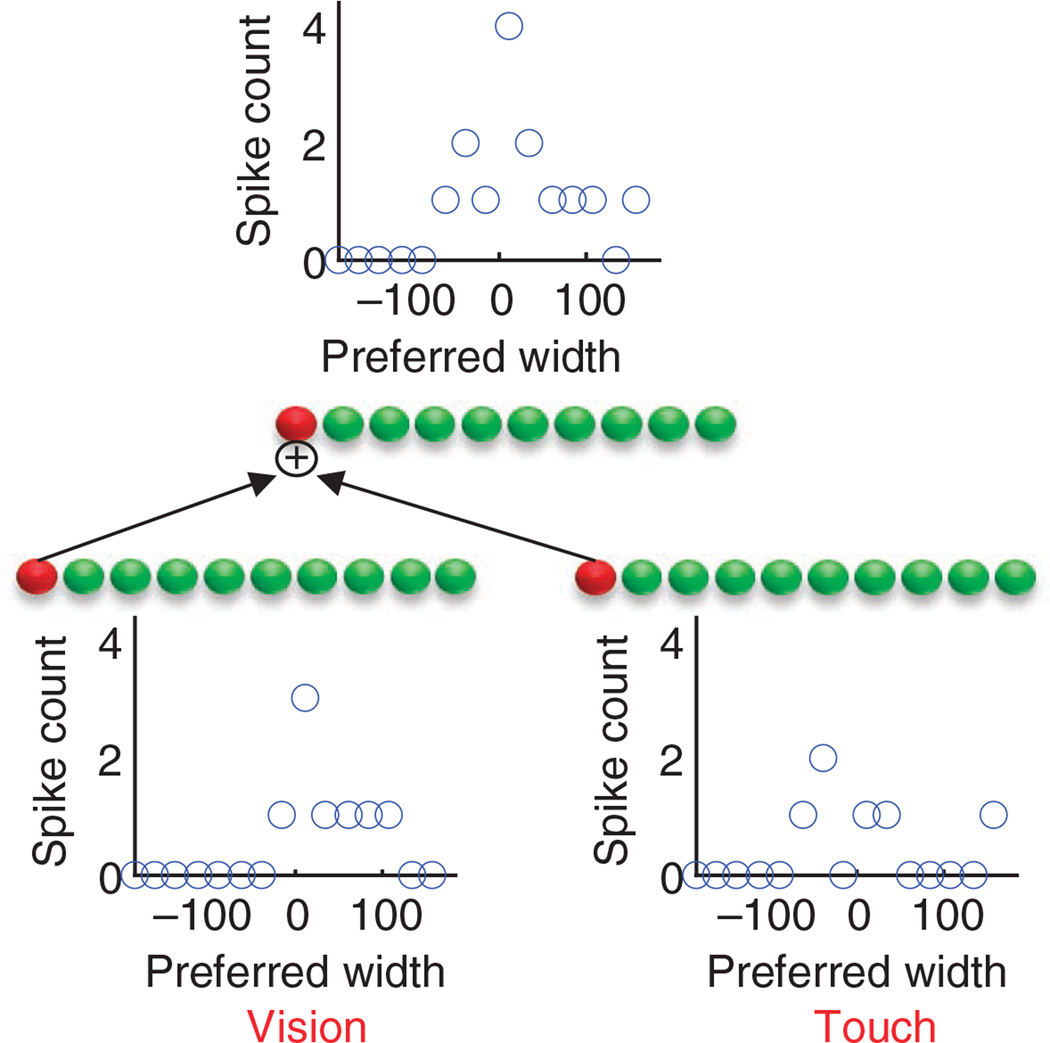
One particularly common form of inference involves combining multiple sources of information, as was the case for the multisensory experiment that we considered earlier (Fig. 1). The posterior distribution over the width of the bar is obtained by taking the product of the visual and haptic likelihood functions, as in equation (1). For a probabilistic population code, this product can be implemented at the neural level by simply taking linear combinations of neural activity (Fig. 3). This is because activity is proportional to the log of the probability (equation (5)), and logs turn products into sums. Experimental results in a multisensory integration task involving the visual and vestibular systems are consistent with this prediction⁵⁵. This approach can be generalized to the related problem of accumulating evidence over time in decision-making. In this case, instead of combining information across sensory modalities, the information is combined across time. Mathematically, this still requires a product of likelihood functions, but over time instead of across modalities. Thus, at the neural level, neurons need to sum their inputs over time; that is, to behave like neural integrators. This predicts that neurons involved in computing the posterior distribution over a variable given all the evidence up to the present time should linearly integrate their inputs⁵⁶. This is consistent with the responses of neurons in areas such as lateral intraparietal cortex when they are accumulating information about direction of motion^27,57.

Figure 3.

Taking a product of likelihood functions with probabilistic population codes. Bottom panels, probabilistic population codes for the two likelihoods shown in Figure 1b (the blue and red curves). Summing the two population codes (neuron by neuron) yields a population code (top) for the product of the two likelihoods (the green curve in Fig. 1b), as required for optimal multisensory integration (equation (1)).

Another important form of inference is known as marginalization, an operation found at the heart of almost all probabilistic reasoning. Marginalization typically refers to recovering the distribution over a variable x, p(x), from a joint distribution over x and other variables, for example, p(x,y,z). For instance, suppose you are interested in the orientation of a moving bar. The visual information about that bar depends on other quantities, such as its contrast, speed and texture. As these quantities are not known exactly, they must be inferred, resulting in a joint probability distribution. Turning this joint distribution over many quantities into a marginal distribution over just the orientation requires integrating out (marginalizing over) all variables except orientation. Marginalization is also critical for probabilistic function approximation, that is, recovering the probability distribution over a function of variables, say f(x,y,z), from p(x,y,z), the joint distribution over x, y and z (Box 1). An example is computing the probability that the sum of two dice is 4. Here the function f(x,y) is simply x + y (x is the number on the first die, y the number on the second) and the quantity of interest is p(f(x,y)) = 4). This probability is obtained by summing the probabilities of all configurations of x and y such that x + y = 4, that is, it is the probability that the first die is 1 and the second is 3 plus the probability that both dice are 2 plus the probability that the first dice is 3 and the second is 1.

The generalized notion of marginalization described here is crucial for performing probabilistic inference in almost all cases, as many operations performed in the nervous system involves computing functions⁴⁶. With probabilistic population code, networks of neurons can compute almost exactly the probability distribution of functions of variables as long as the functions are linear, the noise is Gaussian and the neurons in the circuit use a quadratic nonlinearity with divisive normalization^58,59. The same nonlinearity can be used to perform approximate inference in hard problems, such as computing the probability of each odor in an olfactory scene given the activation of the olfactory receptor neurons⁶⁰. Notably, divisive normalization is found in most neural circuits, from insects to mammals, and might be involved in optimal and approximate marginalization in a variety of settings, including coordinate transformations⁵⁸, object tracking⁵⁸, visual search⁵⁹ and causal reasoning⁵⁸.

A third type of inference is estimation. Given a posterior distribution p(s|r), we are often interested in the value of s corresponding to the peak of this distribution; this is the most probable value of s given the neural activity and is called the maximum a posteriori estimate. Alternatively, we may want to ignore any prior knowledge that we may have and maximize the likelihood. With linear probabilistic population codes, both can be implemented using an attractor network. Such an implementation is consistent with the response of motor neurons such as the ones found in the motor layer of the superior colliculus^61,62.

In addition to inference with probabilistic population codes, neural implementations have also been explored with other types of codes. In codes based on sampling, the neural implementation of marginalization uses a straightforward application of Monte Carlo techniques. For codes in which neuronal activity is proportional to probabilities^33–36, the neural implementation of probabilistic inference is conceptually straightforward, as the required neural operations are identical to the original inferences (see refs. ^63,64 for variations of these ideas). For example, marginalization involves sums of probabilities, and is implemented by adding neural activities. Similarly, evidence integration and cue combination involve products of probability distributions and are implemented by multiplying neural activity. The latter does not appear to be consistent with the kind of evidence integration that is seen in, for example, lateral intraparietal cortex. Moreover, codes in which activity is proportional to probability predict that the width of tuning curves should be wider when the encoded probability distribution is wider, as the two are proportional to one another. This is inconsistent with what is seen in primary visual cortex, where the widths of orientation tuning curves are independent of contrast⁶⁵, even though lower contrast implies higher uncertainty, that is, wider probability distributions (see Table 1). Nonetheless, it would be interesting to design experiments to test further the predictions of this coding scheme.

Table 1.

Neural implementations of probabilistic computations

	Neural implementation
Probabilistic computation	Linear probabilistic population codes	Codes proportional to probabilities	Sampling-based codes
Evidence integration (for example, cue combination, temporal accumulation of evidence for decision-making)	Linear: sums across populations47 or over time56	Nonlinear: products	Nonlinear: products of histograms of samples53
Estimation (for example, maximum likelihood)	Nonlinear: attractor dynamics61,62	Nonlinear: winner take all	Nonlinear: average of samples34,53
Kalman filtering (for example, for motor control, visual object tracking)	Nonlinear: quadratic nonlinearity with divisive normalization58	Nonlinear63,64	Nonlinear: particle filters
Simple marginalization (for example, linear coordinate transforms)	Nonlinear: quadratic nonlinearity with divisive normalization58	Linear63,64	Linear: sums over histogram53
Incorporating prior knowledge	Nonlinear: bias current47	Nonlinear: products	Nonlinear: products of histograms of samples53
Approximate high dimensional inference (for example, olfactory processing)	Nonlinear: for example, divisive normalization60	Nonlinear: products and sums32	Nonlinear: Monte Carlo sampling53

Future challenges

There are a number of proposals for how networks of neurons represent probabilities and perform probabilistic inference. However, there are multiple challenges that have to be overcome before we can develop a comprehensive theory of neural probabilistic inference. Here we discuss three. The first two have to do with learning complex quantities: the distribution over synaptic weights (rather than just a single value) and the structure of a task based on sensory evidence. The third involves the issue of applying the probabilistic approach to complex, real world situations.

Learning a posterior distribution over weights

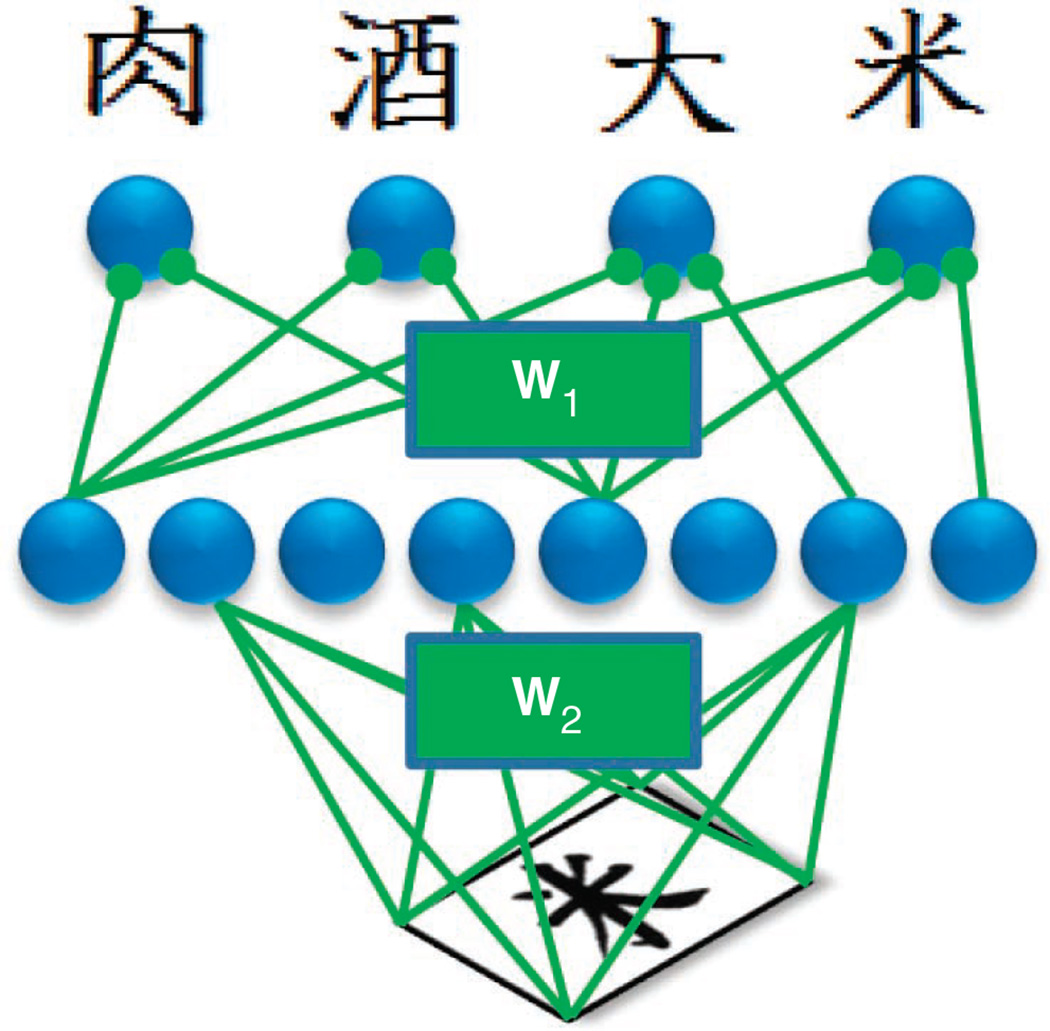
Learning in a neural network is often defined as the problem of finding the best set of weights given a data set and a cost function (see Box 1 for a definition of a cost function). For instance, consider a network that takes as input images of Chinese characters and produces as output a probability distribution over the identity of the characters (Fig. 4). Such a network can be trained using a collection of labeled images to find a set of weights that optimizes performance. As pointed out by MacKay⁶⁶, however, a probabilistic approach to learning would involve computing a posterior distribution over weights, as opposed to a single point estimate. Thus, in this probabilistic perspective, learning is just another form of probabilistic inference. Bayes’ rule, equation (4), still applies, but with a shift in emphasis: the latent variable s is replaced by the weight matrix w and the measurement I is replaced by the data D (in the above example, the set of labeled images):

$$p(\mathbf{w}|\mathbf{D})=\frac{p(\mathbf{D}|\mathbf{w})p(\mathbf{w})}{p(\mathbf{D})}$$ (7)

In most models, the learning rule is designed to infer the best or most likely weights, typically by maximizing the right-hand side of equation (7) via gradient ascent. This approach often yields learning rules that are roughly consistent with those found in biology, such as long-term potentiation and long-term depression⁶⁷, and, in some cases, even an approximation to spike timing–dependent plasticity^68,69. It misses out, though, on what is the main strength of probabilistic approach: a notion of uncertainty. In particular, probabilistic approaches tell us how much the value of a weight can be trusted. That uncertainty can, and should, be taken into account in future computations.

Figure 4.

Neural network for Chinese character identification. The input layer (bottom) corresponds to the image of a particular character. The output layer (top) represents the probability distribution over all possible Chinese characters (only four are shown for clarity). The matrices W₁ and W₂ specify the values of all the weights in the network; these are adjusted to optimize performance. In the probabilistic approach, these weights would be replaced by a probability distribution over weights.

To see how this works, we again consider a network that deciphers Chinese characters, but now we assume that we have learned a probability distribution over weights. As the weights are not known with certainty, the distribution over characters must be computed by averaging over them. This can be done as follows. When a Chinese character is presented, repeatedly pick a particular setting of the weights from the probability distribution over the weights. For each setting, compute the distribution over character identity and then average over those distributions. This is an example of what we earlier called marginalization: we averaged over the values of a nuisance variable that we didn’t care about (the weights) and, in the same way, we averaged over contrast, speed and texture to obtain the orientation of a moving bar.

Averaging over the weights is more robust than simply using a point estimate of the weights^66,70,71, yet this idea has received little attention in neuroscience thus far—possibly because it’s not a simple task for the brain—as it would require a neural mechanism for representing a distribution over weights. The idea that the brain learns and stores a posterior distribution over weights represents a strong departure from the current approaches, which focus on single values, just as the idea that neurons code for distributions rather than values was a departure from classical theories of neural coding. Thinking of population activity as encoding probability distributions has changed our perspective on neural coding and neural computation. Similarly, thinking about probability distributions over weights could, potentially, have a strong effect on our understanding of learning in the brain.

There are several ways the brain could represent distributions over weights. One would be to implement many networks in parallel, with the weights in each network sampled from the posterior distribution. The learning rule would have to involve some form of competition among synapses to prevent them from converging to the same value, although it might be possible to do so by simply adding noise. Alternatively, the synapses themselves could represent a distribution over weights, in the same way that neural activity can represent a distribution over the encoded variable (for example, equation (5)). One possibility, which has recently been explored⁶⁰, would be to use a parameterization such that the log of the posterior distribution over the weights is a linear function of the synaptic weights, exactly analogous to linear probabilistic population codes. It is too early to tell which, if any, of these proposals is used in the brain, as we do not yet know whether the brain even stores a posterior distribution over weights, but we can start to ask whether synaptic learning rules in vivo are consistent with what would be predicted by a learning rule designed to learn a posterior distribution over weights⁶⁰.

Structural learning

In nearly all models in neuroscience, there is an implicit assumption that the learner knows which variables matter and which actions she needs to perform. Consider a perceptual decision-making task in which subjects observe moving dots and have to decide whether the dots are moving to the right or to the left. Neural models of this task almost always consist of a layer of neurons representing the motion in the display, and those neurons project to two units (or populations) that encode the two possible responses. However, when a naive subject faces such a task, there are numerous aspects of the display that could potentially be relevant (the number of dots, their positions, their colors, their speeds); similarly, there are numerous ways to respond (eye movements, pushing a joystick, making a sound). As a result, the subject has to figure out which sensory and motor variables matter for the task⁷². Only after that happens can parameters (such as synaptic weights) be tuned to improve performance. Structural learning—learning the structure of a task given data^73,74— is a difficult problem: it is based on an impoverished feedback signal (typically only a positive reward for correct answers) and the reward does not explicitly specify which sensory variables or which motor actions matter.

One could argue that this problem could be solved by devoting neural circuits to every possible combination of input-output relationships. However, this would require an astronomical number of circuits, and far more neurons and connections than we have in our brains. This problem is already severe when considering a very simple task such as perceptual decision-making, and it becomes intractable when dealing with more complex problems such as learning to drive a car, play chess or understanding which factors control the world economy.

The ability to learn very complex models might very well be what is specific to the mammalian brain, and particularly the human brain. Humans can perform tasks that they could not possibly be prewired for^74,75, such as learning to program a computer or discovering the laws of physics. Thus, understanding structural learning may provide deep insight into human cognition.

To take a specific example, suppose you observe a monkey colony and you would like to infer the hierarchical structure (that is, who dominates whom). From a probabilistic perspective, you should infer a probability distribution over possible structures; after all, with a finite amount of data, there will always be some uncertainty. A natural way to do this is to represent the colony with a graph, with nodes in the graph corresponding to individuals and directed links indicating dominance. The posterior distribution over the structure of this graph (and, in fact, structure in general) is given by Bayes’ theorem

$$p(\text{structure}|\mathbf{D})=\frac{p(\mathbf{D}|\text{structure})p(\text{structure})}{p(\mathbf{D})}$$

where D is data, p(D|structure) is the likelihood and p(structure) is the prior over structures.

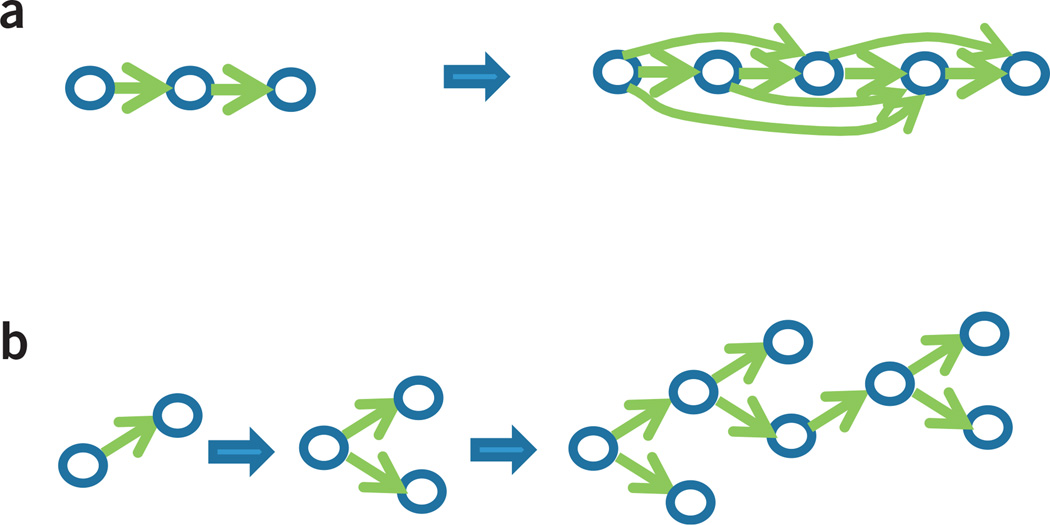
This simple-looking equation hides a great deal of complexity. Consider, for example, the graphs that we would need to describe the monkey colony. The number of such graphs is exponentially large, making it impossible to consider all of them. A natural alternative is to initially consider only simple graphs and let their complexity grow (if needed) as more observations are made. Formally, this is done by assigning higher probability to simple graphs than to complex ones, thereby implementing a form of Occam’s razor. An example based on the dominance in the monkey colony is shown in Figure 5a. Here each graph is the most likely one at any point in the inference process, with graphs to the right resulting from more observations. A slightly more complex example based on animal taxonomy is shown in Figure 5b. In this case, the graph has a tree structure.

Figure 5.

Incremental structural learning. As data is observed, new units and new links are added to capture the structure of the model that best accounts for the data. Shown is the most likely graph at any point during training, and not a distribution over graphs. Indeed, computing the full posterior over graphs is often intractable, in which case one settles for the more likely set of graphs (of which we show only the most likely). (a) Dominance relations in a monkey colony. Each link represents a pair of monkeys in which one actively dominates another. (b) Animal taxonomy, in which case the graph is a tree.

Given the complexity of the issues involved, uncovering the neural basis of structural learning promises to be a formidable challenge for neuroscientists. One obvious issue is that the size of the graph grows with increasing observations. A natural way to handle this growth in a network would be to use a new set of neurons every time a new node appears. However, the vast majority of brain areas cannot create new neurons. Instead, the structural learning process will have to take over pre-existing neurons. A second issue is that the brain does not have the ability to completely rewire itself in a task-dependent manner, as the scaffolding of axons and dendrites is relatively fixed⁷⁶. There is, however, some degree of flexibility, as synaptic boutons can grow and retract, and a large fraction of existing synapses are in fact silent (for example, up to 85% of the parallel fiber synapses are silent⁷⁷).

Despite the difficulty of the problem, there are good reasons to believe that substantial progress can be made in the near future. Some of the computational theories of structural learning are based on the same probabilistic framework that has been used to understand inference and learning in neural circuits, and involve operations such as marginalization^72,74. Thus, there is hope that the type of neural mechanisms that we have discussed above might also be involved in structural learning.

This work might also pave the way to neural theories of how we build complex representations on fast timescales. For instance, every time we hear a sentence, its syntactic structure has to be represented on the fly. Given that we cannot possibly have in our head a representation of all possible sentences, we must build these representations as they are needed. A similar issue arises when dealing with visual scenes, as the precise spatial configuration of visual objects along with their identity cannot be known in advance. These problems are very similar to the problem of structural learning, with the additional complication that the representations have to be created, and erased, extremely quickly. Some authors have argued that this will require a computational architecture very similar to the one found in computers with, in particular, the ability to allocate and de-allocate memory resources on demand via the use of pointers^78,79. How such a mechanism would be implemented in neural circuits remains unclear, although a few solutions have been explored^80–82.

Dealing with intractable real-world problems

Most studies in neuroscience have focused on problems with a small number of variables, all following simple distributions, for which an optimal solution can be easily derived; examples include integration of two conditionally independent cues, visual search with simple, independent stimuli, and temporal integration of sensory evidence for binary decision-making in a stationary environment. For these tasks, humans and animals often exhibit near-optimal behavior, in the sense that they take into account the uncertainty associated with all signals and combine these signals according to their reliability.

Real-life problems, however, are almost always far too complicated to allow for optimal behavior. Optimal behavior requires both full knowledge of the generative model and the ability to perform exact inference, neither of which are possible for most problems of interest. For instance, constructing the generative model for speech is impossible to do exactly because of the wide variations across speakers, the large number of hidden variables that need to be marginalized out and the enormous size of the lexicon. And even if we knew the generative model, computing the true posterior probability distribution over 20,000 words given an audible utterance in a reasonable amount of time is simply not possible.

Given the difficulty of real-world problems, one might imagine that, when confronted with them, the brain no longer relies on a probabilistic approach, but uses instead a set of heuristics or ‘bag of tricks’⁸³. This has, in fact, been proposed for visual processing and domains such as visual tracking⁸⁴. However, it is also possible that the nervous system relies on probabilistic inference, but uses various approximations. This would address one of the most common criticisms of the probabilistic approach, namely, that our behavior is often suboptimal⁸⁵. The probabilistic approach, however, is not about optimality per se⁸⁶, as optimality is often unattainable. Instead, the probabilistic approach is first and foremost about representing knowledge as probability distributions⁸⁷, and second about developing inference and learning algorithms. Recent work has started to investigate the neural implementation of one particular approximation scheme, variational approximations⁶⁰, but the next few years will likely witness a flurry of work in this area, particularly at the behavioral level.

In addition to using approximations, it is common in the probabilistic approach to take advantage of domain-specific prior knowledge. In essence, this approach tames unwieldy likelihood functions by using priors that severely limit the distribution of latent variables. For instance, the ability of human babies to acquire language without much feedback from parents suggests that they are born with a highly structured prior over words and sentences (it should be noted, however, that Chomsky has argued that language acquisition is not a probabilistic process⁸⁸, but this view has been challenged by proponents of probabilistic approaches⁸⁹).

In sum, there are a variety of approximate probabilistic approaches to hard inference problems. However, whether organisms continue to be probabilistic on hard problems or, alternatively, whether organisms abandon the probabilistic approach altogether when the problems become especially difficult can only be answered experimentally.

Discussion

Over the years, neuroscience has divided into a myriad of subfields, such as sensory processing, motor control, decision-making, reinforcement learning, language processing and high-level cognition. However, all neural circuits share similar features and, in neocortex, the detailed circuitry is remarkably well preserved across areas. It is therefore quite possible that these circuits share common computational principles. This is precisely what the probabilistic approach can bring to the table. Most, if not all, of the computations performed by the brain can be formalized as instances of probabilistic inference. Sensory processing, motor control, decision-making, learning and virtually all higher cognitive tasks fall into this class. By treating them as probabilistic inference problems, we may be able to derive general principles that apply to all areas of the brain. Encouragingly, several theories of probabilistic inference have started to emerge, and most, if not all, can be implemented in relatively simple and biologically plausible circuits.

Given that nearly all of the problems faced by the brain can be formulated as probabilistic inference, one might wonder if there is an alternative. It is not immediately clear that there is, as neural representations can always be deemed probabilistic. Indeed, the notion of probabilistic population codes relies only on the assumption that the brain has knowledge of a likelihood function p(r|s) (Box 1) and can use it to compute posteriors (equation (6)). However, we must be careful; the fact that one can compute p(s|r) does not imply that the brain is set up to perform probabilistic inference. This is something we can see very clearly in models. For instance, one could take a standard neural network model of object recognition such as LeNet⁹⁰, present a particular set of stimuli, such as oriented Gabor patches, and compute p(r|s) for those stimuli. The fact that we could determine this distribution might lead us to conclude that LeNet contains a probabilistic representation of orientation. However, this is not what this model was built for: it was built to recognize objects, not perform inference over the orientation of Gabor patches. Thus, the relevant question isn’t whether or not neurons represent probability distributions (as we just pointed out, they always do), but to what extent the brain uses them. If it does, then the only way to understand what the brain is doing is by formalizing neural computation in terms of probabilistic inference. If it doesn’t, then the probabilistic approach will be a relatively useless exercise and one should adopt more mechanistic approaches^90,91.

In summary, there are two fundamental questions on the probabilistic agenda. What is the functional form of the probabilistic representations p(s|r) and to what extent does the rest of the brain make use of those representations? To answer the first question, we need to present stimuli over and over again, measure the neuronal responses, and estimate p(r|s). To answer the second question, we need to a compare behavioral variability to the amount of uncertainty associated with the distribution p(r|s) (after suitably incorporating the prior). The amount of uncertainty in a given area should correspond, at least approximately, to behavioral variability. If this is not the case, then the brain must either be adding noise or making approximations (or both⁹²), and the problem is to determine whether approximations are being used and, if so, what they are. When these approximations are particularly severe, the algorithms used by the brain may no longer be deemed to be probabilistic, although it remains to be seen whether a categorical distinction between probabilistic and non-probabilistic algorithms is justified or useful.

Finally, we should point out that probabilistic inference is not the whole story, as it doesn’t come with a cost function (Box 1). That must be derived or estimated using other methods. The good news, however, is that having probability distributions over variables of interest means that cost functions can be incorporated in a rational manner. Experimentally, this is a potential pitfall of the probabilistic approach: many data sets can be used to support the claim that humans are optimal, as long as one uses the appropriate cost function (or prior distribution)⁸⁵. This problem, however, can be alleviated by using Bayesian model comparison, which automatically controls for the large number of parameters that comes with an overly complex cost function^59,93. Despite its shortcomings, we believe that the probabilistic approach will continue to provide deep insights into how the brain works, not only in mammals, but also in invertebrates.