Automatic structure recovery for additive models

SUMMARY

We propose an automatic structure recovery method for additive models, based on a backfitting algorithm coupled with local polynomial smoothing, in conjunction with a new kernel-based variable selection strategy. Our method produces estimates of the set of noise predictors, the sets of predictors that contribute polynomially at different degrees up to a specified degree M, and the set of predictors that contribute beyond polynomially of degree M. We prove consistency of the proposed method, and describe an extension to partially linear models. Finite-sample performance of the method is illustrated via Monte Carlo studies and a real-data example.

1. Introduction

Because of recent developments in data acquisition and storage, statisticians often encounter datasets with large numbers of observations or predictors. The demand for analysing such data has led to the current heightened interest in variable selection. For parametric models, classical methods include backward, forward and stepwise selection. More recently, many approaches to variable selection have been developed that use regularization via penalty functions. Examples include the lasso (Tibshirani, 1996), smoothly clipped absolute deviation (Fan & Li, 2001), the adaptive lasso (Zou, 2006; Zhang & Lu, 2007), and the L₀ penalty (Shen et al., 2013). Fan & Lv (2010) give a selective overview of variable selection methods.

Variable selection for nonparametric modelling has advanced at a slower pace than for parametric modelling, and has been studied primarily in the context of additive models, which are an important extension of multivariate linear regression. An additive model presupposes that each predictor contributes a possibly nonlinear effect, and that the effects of multiple predictors are additive. Such models were proposed by Friedman & Stuetzle (1981) and serve as surrogates for fully nonparametric models. Most nonparametric variable selection methods studied so far deal with additive models; see Ravikumar et al. (2009), Huang et al. (2010), Fan et al. (2011), and references therein. An exception is Stefanski et al. (2014), which considers variable selection in a fully nonparametric classification model. Additionally, variable selection and structure recovery for the varying coefficient model, a popular extension of the additive model, have been studied: Xia et al. (2004) considered structure recovery towards semi-varying coefficient modelling; Fan et al. (2014) studied a new variable screening method; and for the longitudinal setting Cheng et al. (2014) investigated variable screening and selection, as well as structure recovery.

Partially linear models were proposed by Engle et al. (1986). Combining the advantages of linearity and additivity, these models assume that some covariates have nonlinear additive effects while others contribute linearly. Estimation for a partially linear model requires knowing which covariates have linear effects and which have nonlinear effects, information that is usually not available a priori. Recently, Zhang et al. (2011) and Huang et al. (2012) proposed methods to identify covariates that have linear effects and ones that have nonlinear effects.

We consider an additive model for a scalar response Y and predictors X = (X₁, … , XD)^T,

$$Y=m\left(X\right)+\epsilon =\alpha +\sum _{d=1}^D{m}_d\left(X_d\right)+\epsilon ,E\left(\epsilon \right)=0,\mathrm{var}\left(\epsilon \right)={\sigma }^2,$$ (1)

under the identifiability conditions E{m_d (X_d)} = 0 (d = 1 , … , D). Denote a random sample from model (1) by {(Y_i, Xi): i = 1, … , n}, where X_i =(X_i1, … , X_iD)^T. The goal is to estimate α and m_d (·) (d = 1, … , D).

We a method for estimating m_d(·) that first distinguishes between important predictors and predictors that are unimportant, i.e., those X_d for which m_d(·) = 0. Next, motivated by Zhang et al. (2011) and Huang et al. (2012), the method identifies predictors that have linear effects from the estimated set of important predictors. Then, the method identifies the predictors that have quadratic effects, and so on. This process continues and results in estimates of sets of predictors that have polynomial effects at different degrees, up to some degree M, and the set of predictors for which the corresponding m_d(·) are not polynomial of any degree up to M.

At the core of our structure recovery method is a new nonparametric kernel-based variable selection method derived from the measurement-error model selection likelihood approach of Stefanski et al. (2014). They studied the relationship between lasso estimation and measurement error attenuation in linear models, and used that connection to develop a general approach to variable selection in nonparametric models.

2. Backfitting algorithm

Backfitting coupled with smoothing is commonly used for fitting model (1). Here we use univariate local polynomial smoothing, with ${\mathcal{S}}_{K,h,p}$ denoting the univariate local polynomial smoother with kernel function K (·), bandwidth h and degree p.

Local polynomial smoothing (Fan & Gijbels, 1996) is a well-studied nonparametric smoothing technique. To estimate the regression function g(t) = E(Z…T = t) from an independent and identically distributed random sample {(T_i, Z_i) : i = 1, … , n}, local polynomial regression uses Taylor series approximations and weighted least squares. The local polynomial smoothing estimate $\widehat{g}\left(t_0\right)$ of g(t₀) based on smoother ${\mathcal{S}}_{K,h,p}$ is given by ${\widehat{a}}_0$, the optimizer of

$$\underset{a_0,a_1,\dots ,a_p}{\min }\sum _{i=1}^n{\left\{Z_i-\sum _{j=0}^p{a}_j{(T_i-t_0)}^j\right\}}^{2}K\left(\frac{T_i-t_0}{h}\right).$$

See Fan & Gijbels (1996) for a detailed account of local polynomial modelling.

Using univariate local polynomial smoothing with kernel K(·), bandwidth h_d and degree p_d to estimate m_d(·) in the additive model (1), the backfitting algorithm consists of the following steps.

Step 1

Initialize by setting $\widehat{\alpha }=n^{-1}{\sum }_{i=1}^n{Y}_i$ and ${\widehat{m}}_d(\cdot )\equiv 0$ for d = 1, … , D.

Step 2

For d = 1, … , D:

• (a) apply the local polynomial smoother ${\mathcal{S}}_{K,h_d,p_d}$ to $\left\{\right\{X_{id},Y_i-\widehat{\alpha }-{\sum }_{k\ne d}{\widehat{m}}_k\left(X_{ik}\right)\}:i=1,\dots ,n\}$ and set the estimated function to be the updated estimate ${\widehat{m}}_d(\cdot )$ for m_d (·);

• (b) if necessary, apply centring by updating ${\widehat{m}}_d(\cdot )$ with ${\widehat{m}}_d(\cdot )-n^{-1}{\sum }_{i=1}^n{\widehat{m}}_d\left(X_{id}\right)$.

Step 3

Repeat Step 2 until the changes in all ${\widehat{m}}_d(\cdot )$ (d = 1, … , D) between successive iterations are less than a specified tolerance.

Denote the estimates at convergence by ${\widehat{m}}_d^{\mathrm{BF}}(.;h,p)$ (d = 1, … , D) and ${\widehat{\alpha }}^{\mathrm{BF}}$, where h = (h₁, … , h_D)^T and p = (p₁, … , p_D)^T are the vectors of smoothing bandwidths and local polynomial degrees, respectively. For simplicity we use the same kernel K (·) for each component, and thus K (·) is omitted from the notation ${\widehat{m}}_d^{\mathrm{BF}}(.;h,p)$.

Backfitting works well for problems of moderate dimension D. However, even though backfitting entails only univariate smoothing, its performance deteriorates as D gets larger. Consequently, variable selection is important for the additive model.

3. Variable selection via backfitting local constants

3·1. Variable selection

In Step 2(a) of the backfitting algorithm, any smoothing method can be applied. In this section we consider the local constant smoother, i.e., the local polynomial smoother of degree 0, and propose a nonparametric variable selection method for the additive model (1).

With p_d =0 in Step 2(a) of the backfitting algorithm, we update the estimate ${\widehat{m}}_d\left(x_d\right)$ of m_d (x_d) by the minimizer ${\widehat{a}}_0$ of

$$\underset{a_0}{\min }\sum _{i=1}^n{\left[\left\{Y_i-\widehat{\alpha }-\sum _{k\ne d}{\widehat{m}}_k\left(X_{\mathit{ik}}\right)\right\}-a_0\right]}^{2}K\left(\frac{X_{\mathit{id}}-x_d}{h_d}\right).$$ (2)

Note that K{h_d⁻¹(Xi_d – x_d )} = K(0) for all i when h_d = ∞. In this case, m_d (·) is globally approximated by a₀. The corresponding optimizer of (2) is given by ${\widehat{a}}_0=n^{-1}{\sum }_{i=1}^n\{Y_i-\widehat{\alpha }-{\sum }_{k\ne d}{\widehat{m}}_k(X_{ik}\left)\right\}$, which equals zero because $\widehat{a}=n^{-1}{\sum }_{i=1}^n{Y}_i$ and centring is applied in Step 2(b) of the backfitting algorithm.

Thus, when p_d = 0, the backfitting algorithm leads to the constant zero function ${\widehat{m}}_d^{\mathrm{BF}}(x_d;h,p)$ when h_d = ∞. Consequently, the jth predictor is excluded from the model when h_d = ∞ and is included only when h_d < ∞. The equivalence, h_d < ∞ if and only if the jth predictor is included, is key to the approach described in Stefanski et al. (2014), and we exploit it repeatedly in our method. We assume in this section that the degree of local polynomial smoothing for every function component is 0, i.e., p_d 0 for d = 1, … , D. In this way, the smoothing bandwidth relates directly to the importance of each predictor, with small h_d corresponding to important predictors.

As in Stefanski et al. (2014), we reparameterize h_d as λ_d = 1/h_d, so that large λ_d will correspond to important predictors and λ_d = 0 to unimportant predictors. Predictor smoothing is now determined by the inverse bandwidths λ_d. Stefanski et al. (2014) show that variable selection can be obtained by minimizing a loss function with respect to the λ_d, subject to a bound on the total amount of smoothing as determined by the sum of the λ_d or, equivalently, a bound on the harmonic mean of the bandwidths.

A suitable loss function for backfitting is the sum of squared errors

$$\mathrm{SSE}=\sum _{i=1}^n{\left\{Y_i-{\widehat{\alpha }}^{\mathrm{BF}}-\sum _{d=1}^D{\widehat{m}}_d^{\mathrm{BF}}(X_{\mathit{id}};{\lambda }^{-1},0_D)\right\}}^2,$$

where in the second two arguments of $m_d^{\mathrm{BF}}(.;.,.)$, λ⁻¹ = (1/λ₁, … , 1/λ_D)^T and 0_D denotes the D × 1 zero vector. We shall also write 1_s for the s × 1 vector of ones.

In the absence of constraints, the minimum of sse with respect to λ is 0, and corresponds to overfitted models. As in Stefanski et al. (2014), appropriate regularization is achieved by solving the constrained optimization problem

$$\begin{array}{cc}\hfill & \underset{{\lambda }_1,\dots ,{\lambda }_D}{\min }\frac{1}{n}\sum _{i=1}^n{\left\{Y_i-{\widehat{\alpha }}^{\mathrm{BF}}-\sum _{d=1}^D{\widehat{m}}_d^{\mathrm{BF}}(X_{\mathit{id}};{\lambda }^{-1},0_D)\right\}}^2,\hfill \\ \hfill & \text{subject to}{\lambda }_d\ge 0(d=1,\dots ,D)\text{and}\sum _{d=1}^D{\lambda }_d={\tau }_0.\hfill \end{array}$$ (3)

Solving (3) distinguishes important predictors, ${\widehat{\lambda }}_d>0$, from those that are unimportant, ${\widehat{\lambda }}_d=0$.

3·2. Modified coordinate descent algorithm

The constrained optimization problem (3) is not convex because of the complicated dependence on λ through the backfitting algorithm and the univariate local polynomial smoothing. We have had success using a modified coordinate descent algorithm.

Coordinate descent for high-dimensional lasso regression (Fu, 1998; Daubechies et al., 2004) cycles through variables one at a time, solving simple marginal univariate optimization problems at each step, and thus is computationally efficient. It has been studied extensively, for example by Friedman et al. (2007) and Wu & Lange (2008), among others. However, standard coordinate descent cannot be applied directly to (3).

In our modified coordinate descent algorithm, we initialize with equal smoothing, i.e., we set λ_d = τ₀/D for all d = 1, … , D. We then cycle through all components and make univariate updates. Current solutions are denoted by ${\lambda }_d^{\mathrm{c}}(d=1,\dots ,D)$, where the superscript c means current. Suppose that we are updating the d’th component. Let ${\lambda }_{d^{\prime }}^{\left(1\right)}={(0,\dots ,0,1,0,\dots ,0)}^{\mathrm{T}}$, a vector whose elements are all zero except for the d’th, which is 1, and set ${\lambda }_{-d^{\prime }}^{\mathrm{c}}=({\lambda }_1^{\mathrm{c}},\dots ,{\lambda }_{d^{\prime }-1}^{\mathrm{c}},0,{\lambda }_{d^{\prime }+1}^{\mathrm{c}},\dots ,{\lambda }_D^{\mathrm{c}})∕{\sum }_{d\ne d^{\prime }}{\lambda }_d^{\mathrm{c}}$. The components of ${\lambda }_{d^{\prime }}^{\left(1\right)}$, and ${\lambda }_{-d^{\prime }}^{\mathrm{c}}$ sum to unity. Thus, for any γ ∈ [0, τ₀], the components of $\gamma {\lambda }_{d^{\prime }}^{\left(1\right)}+({\tau }_0-\gamma ){\lambda }_{-d^{\prime }}^{\mathrm{c}}$, sum to τ₀ and satisfy the first constraint in (3). We then update the set of current solutions to the components of the vector $\widehat{\gamma }{\lambda }_{d^{\prime }}^{\left(1\right)}+({\tau }_0-\widehat{\gamma }){\lambda }_{-d^{\prime }}^{\mathrm{c}}$, where $\widehat{\gamma }$ is the optimizer of

$$\underset{\gamma }{\min }\frac{1}{n}\sum _{i=1}^n{\left(Y_i-{\widehat{\alpha }}^{\mathrm{BF}}-\sum _{j=1}^D{\widehat{m}}_j^{\mathrm{BF}}\left[X_{\mathit{ij}};{\{\gamma {\lambda }_{d^{\prime }}^{\left(1\right)}+({\tau }_0-\gamma \left){\lambda }_{-d^{\prime }}^{\mathrm{c}}\right\}}^{-1},0_D\right]\right)}^2$$

subject to 0 ≤ γ ≤ τ₀. Cycling through d’ = 1, … , D completes one iteration of the algorithm. Iterations continue until the change in solutions between successive iterations becomes small enough.

3·3. Tuning

The tuning parameter τ₀ controls the total amount of smoothing, and can be selected by standard methods such as crossvalidation, aic or bic. Denote the optimizer of (3) by $\widehat{\lambda }\left({\tau }_0\right)$. If an independent tuning dataset is available, then τ₀ can be selected by minimizing the sum of squared prediction errors of the estimator $\widehat{m}\{x;\widehat{\lambda }({\tau }_0),0\}={\widehat{\alpha }}^{\mathrm{BF}}+{\sum }_{d=1}^D{\widehat{m}}_d^{\mathrm{BF}}[x_d;{\left\{\widehat{\lambda }\right({\tau }_0\left)\right\}}^{-1},0]$ over the tuning set. For methods such as aic and bic, the degrees of freedom is needed. The local constant smoothing estimator is a linear smoother, and we couple the backfitting algorithm to marginal local constant smoothing. For each function component, the trace of the corresponding smoothing matrix minus 1 can be used as the degrees of freedom. The trace is reduced by 1 to account for the centring applied in Step 2(b) of the backfitting algorithm.

4. Higher-degree local polynomial regression

The approach in § 3 extends readily to higher-degree local polynomial regression. Suppose that we use local degree p* polynomial regression in Step 2(a) of the backfitting algorithm. With p_d = p* in Step 2(a), we update the estimate ${\widehat{m}}_d\left(x_d\right)$ of m_d (x_d) by the minimizer ${\widehat{a}}_0$ of

$$\underset{a_0,\dots ,a_{p^{\ast }}}{\min }\sum _{i=1}^n{\left[\left\{Y_i-\widehat{\alpha }-\sum _{k\ne d}{\widehat{m}}_k\left(X_{\mathit{ik}}\right)\right\}-\sum _{j=0}^{p^{\ast }}{a}_j{(X_{\mathit{id}}-x_d)}^j\right]}^{2}K\left(\frac{X_{\mathit{id}}-x_d}{h_d}\right).$$

As remarked previously, K{h_d⁻¹(X_id – x_d)} = K(0) for all i when h_d = ∞. Consequently, ${\sum }_{j=0}^{p^{\ast }}{a}_j{(X_{id}-x_d)}^j$ is a global approximation of m_d (x_d). For this case, in Step 2(a) of the backfitting algorithm the estimate ${\widehat{m}}_d\left(x_d\right)$ is updated by ${\sum }_{j=0}^{p^{\ast }}{\widehat{c}}_j{x}_d^j$, where ${\widehat{c}}_0,\dots {\widehat{c}}_p$ are the optimizers of ${\min }_{c_p,\dots ,c_p}{\sum }_{i=1}^n{\left[\right\{Y_i-\widehat{\alpha }-{\sum }_{k\ne d}{\widehat{m}}_k\left(X_{ik}\right)\}-{\sum }_{j=0}^{p^{\ast }}{c}_j{X}_{id}^j]}^2$.

Thus, when p_d = p*, the backfitting algorithm yields a polynomial of degree p* as the estimate of m_d(·) when h_d = ∞. The interpretation is that the dth predictor makes a polynomial contribution of degree up to p*. Based on this, we derive a method for detecting predictors that contribute polynomially up to degree p* in the additive model.

Now we use backfitting with univariate local polynomial smoothing of degree p* for every function component, again parameterizing via inverse bandwidths λ_d = 1/h_d. As in the previous section, the general approach of Stefanski et al. (2014) leads to solving

$$\begin{array}{cc}\hfill & \underset{{\lambda }_1,\dots ,{\lambda }_D}{\min }\frac{1}{n}\sum _{i=1}^n{\left\{y_i-{\widehat{\alpha }}^{\mathrm{BF}}-\sum _{d=1}^D{\widehat{m}}_d^{\mathrm{BF}}(X_{\mathit{id}};{\lambda }^{-1},p^{\ast }{1}_D)\right\}}^2,\hfill \\ \hfill & \text{subject to}{\lambda }_d\ge 0(d=1,\dots ,D)\text{and}\sum _{d=1}^D{\lambda }_d={\tau }_{p^{\ast }},\hfill \end{array}$$ (4)

where τ_p* plays the same role as τ₀ in (3), and in the last two arguments of $m_d^{\mathrm{BF}}(.;.,.)$, λ⁻¹ = (1/λ₁, … , 1/λ_D)^T and p*1_D is the product of p* and 1_D. In this case, an optimizer ${\widehat{\lambda }}_d=0$ means that the dth predictor contributes polynomially at a degree no greater than p*.

The modified coordinate descent algorithm and the tuning procedures discussed in § § 3·2 and 3·3 extend naturally to (4).

5. Automatic structure recovery

The procedures in § § 3 and 4 provide the building blocks for the additive model automatic structure recovery method. In combination, they enable estimation of the predictors that are not important, as well as those that contribute at the pth degree polynomially.

We let ${\mathcal{A}}_p$ denote the set of predictors that contribute polynomially at degree p and only at degree p, and we let ${\mathcal{B}}_p$ denote the set of predictors that contribute beyond polynomially degree p, which includes higher-degree polynomials as well as nonpolynomial functions. Thus ${\mathcal{A}}_p$ means at degree p, and ${\mathcal{B}}_p$ indicates beyond degree p. With these naming conventions, a predictor that contributes at degree p = 0 is no more informative than a constant and is therefore unimportant. Specifically, ${\mathcal{A}}_0=\{d:m_d(\cdot )=0\}$, ${\mathcal{A}}_p=\{d:m_d^{\left(p\right)}(\cdot )\ne 0,m_d^{(p+1)}(\cdot )=0\}$ for p = 1,2, … and ${\mathcal{B}}_p=\{d:m_d^{(p+1)}(\cdot )\ne 0\}$ for p = 0, 1, 2, … Here m_d(·) = 0 means that m_d(t) = 0 for any t in its domain of interest, and m_d(·) ≠ 0 means that m_d(t) ≠ 0 for some t. Our automatic structure recovery method proceeds in the following steps.

Step 1

Identify important and unimportant predictors.

With appropriately chosen τ₀, solve (3) to obtain ${\widehat{\lambda }}_0={({\widehat{\lambda }}_{01},\dots ,{\widehat{\lambda }}_{0D})}^{\mathrm{T}}$, and set ${\widehat{\mathcal{A}}}_0=\{d:{\widehat{\lambda }}_{0d}=0\}$ and ${\widehat{\mathcal{B}}}_0={\widehat{\mathcal{A}}}_0^{\mathrm{C}}$, the complement of ${\widehat{\mathcal{A}}}_0$ in the set {1, … D}. Then ${\widehat{\mathcal{A}}}_0$ and ${\widehat{\mathcal{B}}}_0$ are estimates of the sets of unimportant and important predictors, respectively.

Step 2

Identify from ${\widehat{\mathcal{B}}}_0$ the predictors that contribute linearly.

After identifying the set ${\widehat{\mathcal{B}}}_0$ of important predictors, the next step is to identify a subset of ${\widehat{\mathcal{B}}}_0$ consisting of functions that contribute linearly. We remove unimportant predictors X_d with $d\in {\widehat{\mathcal{A}}}_0$ from consideration and apply the method of § 4, namely (4) with p* = 1, to the data $\left\{\right(X_{i{\widehat{\mathcal{B}}}_0},Y_i):i=1,\dots ,n\}$, where $X_{i{\widehat{\mathcal{B}}}_0}$ denotes the subvector of X_i with indices in ${\widehat{\mathcal{B}}}_0$. We define ${\widehat{\alpha }}^{\mathrm{BF}}$ and ${\widehat{m}}_d^{\mathrm{BF}}(x_d;{\lambda }_{{\widehat{\mathcal{B}}}_0}^{-1},1)(d\in {\widehat{\mathcal{B}}}_0)$ to be the backfitting estimates obtained using the data $\left\{\right(X_{i{\widehat{\mathcal{B}}}_0},Y_i):i=1,\dots ,n\}$ with bandwidths ${\lambda }_d^{-1}$ for $d\in {\widehat{\mathcal{B}}}_0$. Let $\#{\widehat{\mathcal{B}}}_0$ denote the cardinality of the set ${\widehat{\mathcal{B}}}_0$. For an appropriately tuned τ₁, we solve the optimization problem

$$\begin{array}{cc}\hfill & \underset{{\lambda }_d:d\in {\widehat{\mathcal{B}}}_0}{\min }\frac{1}{n}\sum _{i=1}^n{\left\{Y_i-{\widehat{\alpha }}^{\mathrm{BF}}-\sum _{d\in {\widehat{\mathcal{B}}}_0}{\widehat{m}}_d^{\mathrm{BF}}(X_{\mathit{id}};{\lambda }_{{\widehat{\mathcal{B}}}_0}^{-1},1_{\#{\widehat{\mathcal{B}}}_0})\right\}}^2,\hfill \\ \hfill & \text{subject to}{\lambda }_d\ge 0(d\in {\widehat{\mathcal{B}}}_0)\text{and}\sum _{d\in {\widehat{\mathcal{B}}}_0}{\lambda }_d={\tau }_1,\hfill \end{array}$$

and denote its optimizer by ${\widehat{\lambda }}_{1d}$, for $d\in {\widehat{\mathcal{B}}}_0$. The set ${\widehat{\mathcal{A}}}_1=\{d\in {\widehat{\mathcal{B}}}_0:{\widehat{\lambda }}_{1d}=0\}$ estimates the set of predictors contributing linearly, and ${\widehat{\mathcal{B}}}_1=\{d\in {\widehat{\mathcal{B}}}_0:{\widehat{\lambda }}_{1d}>0\}$ estimates the set of predictors that contribute beyond linearly.

Step 3

Identify from ${\widehat{\mathcal{B}}}_1$ the predictors that contribute quadratically.

In Step 2 the set ${\widehat{\mathcal{A}}}_1$ of linear predictors was identified. The set ${\widehat{\mathcal{A}}}_1$ is global in principle, and this property can be ensured via profiling (Severini & Wong, 1992). For $d\in {\widehat{\mathcal{A}}}_1$ we denote the global fit coefficient for the linear predictor X_d by β_1d or, in vector form, ${\beta }_{1{\widehat{\mathcal{A}}}_1}$. For a given ${\beta }_{1{\widehat{\mathcal{A}}}_1}$, we Apply the backfitting algorithm of degree p_d = 2 with bandwidth ${\lambda }_d^{-1}(d\in {\widehat{\mathcal{B}}}_1)$ to the data $\left\{\right(X_{i{\widehat{\mathcal{B}}}_1},Y_i-{\sum }_{d\in {\widehat{\mathcal{A}}}_1}{X}_{id}{\beta }_{1d}):i=1,\dots ,n\}$ and denote the corresponding estimates by ${\widehat{\alpha }}^{\mathrm{BF}}\left({\beta }_{1{\widehat{\mathcal{A}}}_1}\right)$ and ${\widehat{m}}_d^{\mathrm{BF}}(x_d;{\lambda }_{{\widehat{\mathcal{B}}}_1}^{-1},2\times 1_{\#{\widehat{\mathcal{B}}}_1},{\beta }_{1{\widehat{A}}_1})(d\in {\widehat{\mathcal{B}}}_1)$; we have given ${\widehat{m}}_d^{\mathrm{BF}}$ a fourth argument to emphasize its dependence on ${\beta }_{1{\widehat{\mathcal{A}}}_1}$. Using profiling, we solve

$$\underset{{\beta }_{1d}:d\in {\widehat{\mathcal{B}}}_1}{\min }\frac{1}{n}\sum _{i=1}^n{\left\{Y_i-\sum _{j\in {\widehat{\mathcal{A}}}_1}{X}_{\mathit{ij}}{\beta }_{1j}-{\widehat{\alpha }}^{\mathrm{BF}}\left({\beta }_{1{\widehat{\mathcal{A}}}_1}\right)-\sum _{d\in {\widehat{\mathcal{B}}}_1}{\widehat{m}}_d^{\mathrm{BF}}(X_{\mathit{id}};{\lambda }_{{\widehat{\mathcal{B}}}_1}^{-1},2\times 1_{\#{\widehat{\mathcal{B}}}_1},{\beta }_{1{\widehat{\mathcal{A}}}_1})\right\}}^2$$

to obtain the best estimate for ${\beta }_{1{\widehat{\mathcal{A}}}_1}$, which we denote by ${\widehat{\beta }}_{1{\widehat{\mathcal{A}}}_1}\left({\lambda }_{{\widehat{\mathcal{B}}}_1}\right)$ to emphasize its dependence on ${\lambda }_{{\widehat{\mathcal{B}}}_1}$. With the above notation and definitions, we solve the optimization problem

$$\begin{array}{cc}\hfill & \underset{{\lambda }_d:d\in {\widehat{\mathcal{B}}}_1}{\min }\frac{1}{n}\sum _{i=1}^n{\left[Y_i-\sum _{j\in {\widehat{\mathcal{A}}}_1}{X}_{\mathit{ij}}{\widehat{\beta }}_{1j}\left({\lambda }_{{\widehat{\mathcal{B}}}_1}\right)-{\widehat{\alpha }}^{\mathrm{BF}}\left\{{{\widehat{\beta }}_1}_{{\widehat{\mathcal{A}}}_1}\right({\lambda }_{{\widehat{\mathcal{B}}}_1}\left)\right\}-\sum _{d\in {\widehat{\mathcal{B}}}_1}{\widehat{m}}_d^{\mathrm{BF}}\{X_{\mathit{id}};{\lambda }_{{\widehat{\mathcal{B}}}_1}^{-1},2\times 1_{{\widehat{\mathcal{B}}}_1},{\widehat{\beta }}_{1{\widehat{\mathcal{A}}}_1}({\lambda }_{{\widehat{\mathcal{B}}}_1}\left)\right\}\right]}^2,\hfill \\ \hfill & \text{subject to}{\lambda }_d\ge 0(d\in {\widehat{\mathcal{B}}}_1)\text{and}\sum _{d\in {\widehat{\mathcal{B}}}_1}{\lambda }_d={\tau }_2\hfill \end{array}$$

for appropriately tuned τ₂, and denote its optimizer by ${\widehat{\lambda }}_{2d}(d\in {\widehat{\mathcal{B}}}_1)$. Then ${\widehat{\mathcal{A}}}_2=\{d\in {\widehat{\mathcal{B}}}_1:{\widehat{\lambda }}_{2d}=0\}$ estimates the set of predictors that contribute quadratically, and ${\widehat{\mathcal{B}}}_2=\{d\in {\widehat{\mathcal{B}}}_1:{\widehat{\lambda }}_{2d}>0\}$ estimates the set of predictors that contribute beyond quadratically.

Steps 4 to M + 1

Identify predictors that have kth-degree polynomial effects by using appropriate τ_k for k 3, 4, ….

After Step 3, we have estimated the set of linear predictors and the set of quadratic predictors. In a straightforward manner Step 3 can be modified to identify the sets of predictors that contribute polynomially at degrees k = 3, k = 4, and so on, up to k = M.

Step M + 2. Fit the final model.

After Step M + 1, we have obtained estimates ${\widehat{\mathcal{A}}}_k$ for k = 0, 1 … , M and ${\widehat{\mathcal{B}}}_M$. The final model is then estimated by combining the profiling technique and the backfitting technique as in Step 3. In this final step, we couple the backfitting algorithm with local linear smoothing, as we want to estimate only the function m_d(·) itself for $d\in {\widehat{\mathcal{B}}}_M$.

6. Theoretical properties

In this section we study the consistency of the proposed structure recovery scheme. We first show that the estimated set of unimportant predictors is consistent.

Proposition 1

Suppose τ₀ → ∞ such that ${\tau }_0^3∕n\to 0$ as n → ∞, and assume that Conditions A1–A5 in the Appendix hold. Then the solution to (3) satisfies ${\widehat{\lambda }}_d\to \infty$ in probability for $d\in {\mathcal{B}}_0$, and ${\widehat{\lambda }}_d\to 0$ in probability for $d\in {\mathcal{A}}_0$. Consequently, $\mathrm{pr}({\widehat{\mathcal{A}}}_0={\mathcal{A}}_0)\to 1$ as n → ∞.

Remark 1

There is a small gap between Proposition 1 and the proposed procedure, which is confounded with the numerical analysis. In our procedure ${\widehat{\mathcal{A}}}_0$ is defined as $\{d:{\widehat{\lambda }}_d=0\}$, but Proposition 1 shows that the solution to (3) satisfies ${\widehat{\lambda }}_d\to 0$ in probability for $d\in {\mathcal{A}}_0$. Thus there would be closer agreement between the proposition and the algorithm if we had defined ${\widehat{\mathcal{A}}}_0$ as $\{d:{\widehat{\lambda }}_d<\delta \}$ for some small δ > 0. However, based on our numerical experience so far, the optimizer is indeed sparse, returning exact zeros. Therefore, we shall keep the definition of ${\widehat{\mathcal{A}}}_0$ as $\{d:{\widehat{\lambda }}_d=0\}$. This remark also applies to Theorem 1.

The consistency in Proposition 1 is readily extended to the estimated set of predictors that contribute polynomially at different degrees, resulting in the following consistency property for the proposed structure recovery scheme.

Theorem 1

Suppose that for k = 0, 1, … , M, τ_k → ∞ and ${\tau }_k^{2k+3}∕n\to 0$ as n → ∞, and assume that Conditions A1–A5 in the Appendix hold. Then the estimators ${\widehat{\mathcal{A}}}_k(k=0,\dots ,M)$ and ${\widehat{\mathcal{B}}}_M$ satisfy $\mathrm{pr}({\widehat{\mathcal{A}}}_k={\mathcal{A}}_k\text{for}k=0,\dots ,M,{\widehat{\mathcal{B}}}_M={\mathcal{B}}_M)\to 1$ as n → ∞.

The proofs of Proposition 1 and Theorem 1 are given in the Appendix.

7. Simulation studies

We use simulation models adapted from Zhang et al. (2011) to study the finite-sample performance of the proposed method. In each model, predictors are generated as X_j = (U_j + ηU)/ (1 + η) for j = 1, … , D, where U₁, … , U_D, U are independent and identically distributed Un[0, 1] variables, with η at levels 0 and 0·5, resulting in pairwise correlations of 0 and 0·2. We compare our method with the smoothing spline analysis-of-variance method (Kimeldorf & Wahba, 1971; Gu, 2002), as well as the linear and nonlinear discovery method of Zhang et al. (2011) and its refitted version, in terms of both integrated squared error and predictor-type identification.

For an estimate $\widehat{f}\left(x\right)$ of the additive model (1), define the integrated squared error $\mathtt{ISE}\left(\widehat{f}\right)=E_X{\left\{f\right(X)-\widehat{f}(X\left)\right\}}^2$, estimated via Monte Carlo using an independent test set of size 1000. The linear and nonlinear discovery methods, original and refitted, are designed to identify predictors having null, linear, nonlinear, or a mixture of linear and nonlinear effects, whereas the goal of the proposed method is to identify predictors that contribute polynomially at different degrees and predictors that contribute beyond polynomially of a specified degree M. In the simulation studies, we fixed M to be 2. We use the Bayesian information criterion for tuning parameter selection in all methods.

Model 1

In the first data-generation model, Y = f₁(X₁)+ f₂(X₂)+ f₃(X₃)+ε with f₁(t)=3t, f₂(t)=2 sin(2πt) and f₃(t)=2(3t – 1)². Here ε ~ N(0, σ²) is independent of the predictors. Two values of the standard deviation, σ = 1 and σ = 2, and two dimensions, D = 10 and D = 20, are considered. For all settings, X₄, … , X_D are unimportant. In terms of the linear and nonlinear discovery classification scheme, X₁ has a purely linear effect, X₂ has a purely nonlinear effect, and X₃ has a mixture of linear and nonlinear effects (Zhang et al., 2011). For our method, X₁ is a linear predictor, X₃ is a quadratic predictor, and X₂ contributes beyond quadratically. Training samples of size n =100 are used. The results from 100 simulated datasets are reported in Tables 1 and 2.

Table 1.

Simulation results for Model 1: average integrated squared errors (×10²) with standard deviations (×10²) in parentheses

D	σ	η	Oracle 1	SSANOVA	LAND	LANDr	PSC	Oracle 2
10	1	0·0	12·5 (5·5)	23·9 (9·0)	11·9 (7·4)	14·9 (6·8)	11·6 (6·2)	9·8 (4·9)
		0·5	13·2 (5·4)	25·5 (8·8)	58·9 (36·8)	17·2 (7·3)	12·3 (5·9)	10·4 (4·4)
	2	0·0	44·0 (22·9)	92·7 (41·6)	82·1 (48·0)	71·2 (42·4)	52·0 (34·7)	37·3 (21·9)
		0·5	50·3 (26·3)	100·4 (35·9)	142·6 (47·9)	88·1 (38·0)	67·4 (34·9)	42·8 (21·7)
20	1	0·0	12·8 (5·4)	45·5 (14·3)	16·4 (12·6)	18·7 (9·7)	14·8 (7·8)	9·9 (4·4)
		0·5	13·4 (5·7)	50·6 (19·6)	64·4 (36·0)	24·4 (11·6)	14·3 (8·9)	11·2 (5·4)
	2	0·0	45·1 (21·0)	187·0 (65·8)	135·8 (70·9)	130·7 (60·1)	69·3 (40·7)	37·8 (18·5)
		0·5	45·7 (18·9)	192·8 (62·8)	169·5 (63·5)	155·3 (63·8)	76·2 (41·7)	40·4 (19·6)

D, dimension; σ, model error standard deviation; η, predictor correlation parameter; SSANOVA, smoothing spline analysis-of-variance method; LAND, linear and nonlinear discovery method; LANDr, linear and nonlinear discovery method, refitted version; PSC, the proposed polynomial structure classification method; Oracle 1, oracle for LAND and LANDr; Oracle 2, oracle for PSC.

Table 2.

Summary of predictor classification performance of the linear and nonlinear discovery method and the proposed method for Model 1

LAND								PSC
D	σ	η	L	NL	L-N	Nil	CC	L	Q	BQ	Nil	CC
10	1	0·0	0·9	0·8	1·0	6·5	54	0·9	1·0	1·0	7·0	91
		0·5	1·0	0·2	0·9	5·9	10	1·0	1·0	1·0	7·0	92
	2	0·0	1·0	0·4	1·0	4·8	5	0·9	1·0	0·9	7·0	74
		0·5	1·0	0·0	0·7	3·8	0	0·6	0·9	0·6	7·0	35
Average SD			0·1	0·4	0·2	1·5		0·3	0·2	0·2	0·0
20	1	0·0	1·0	0·7	1·0	15·6	34	1·0	1·0	1·0	17·0	90
		0·5	1·0	0·2	0·9	14·8	4	1·0	1·0	1·0	17·0	93
	2	0·0	1·0	0·4	1·0	11·0	1	0·9	0·9	0·9	17·0	72
		0·5	0·9	0·1	0·7	10·1	0	0·6	0·9	0·6	17·0	33
Average SD			0·1	0·4	0·2	2·5		0·3	0·3	0·2	0·0

LAND, linear and nonlinear discovery method; PSC, the proposed polynomial structure classification method; D, dimension; σ, model error standard deviation; η, predictor correlation parameter; L, linear; NL, nonlinear; L-N, linear-nonlinear mixture; Nil, noise; CC, proportion (%) of models with fully correct variable classifications; Q, quadratic; BQ, beyond quadratic; Average SD, block-averaged standard deviation.

Table 1 summarizes the performance of the smoothing spline method, the two linear and nonlinear discovery methods, the proposed polynomial structure classification method, and two oracle methods, which are included to assess the utility of the underlying classification schemes irrespective of estimation error. Oracle 1 is the linear and nonlinear discovery oracle that makes use of information on which predictors are noise, purely linear, purely nonlinear, or a mixture of linear and nonlinear. Oracle 2 is the oracle for our method and uses information on which predictors are noise, linear, quadratic, or beyond quadratic. The polynomial structure classification method has the smallest integrated squared error values among all methods for all generating distributions, and oracle 2 dominates oracle 1.

Table 2 summarizes the predictor classification performance of the methods under comparison. For the linear and nonlinear discovery method, the table entries are the average and standard deviation of the numbers of predictors identified as purely linear (X₁), purely nonlinear (X₂), a linear-nonlinear mixture (X₃), and noise (X₄, … , X_D). Similarly, for the proposed method, the table entries are the average and standard deviation of the numbers of predictors identified as linear (X₁), quadratic (X₃), beyond quadratic (X₂), and noise (X₄, … , X_D). Also reported are the percentages of times that all variables were correctly classified according to each method’s underlying classification scheme.

The proposed polynomial structure classification method performs well for all generative models, although both it and the linear and nonlinear discovery method generally perform less well for larger values of D, σ and η. Because the two methods are based on different classification schemes, predictor classification is not directly comparable, except with respect to the noise variables. The proposed method identified all noise variables for all 100 simulated datasets for all generative models, whereas the linear and nonlinear discovery method missed some noise predictors, more in cases where σ, η and especially D were large.

For one simulated dataset with σ = 1, η = 0·5 and D = 10, we plot in Fig. 1 the nonzero optimizers ${\widehat{\lambda }}_j$ of (3) in the first variable selection step as functions of τ₀. The optimizers $\widehat{\lambda }$ corresponding to the important predictors, X₁, X₂ and X₃, change to nonzero values quickly as τ₀ increases and before any unimportant predictors show changes. Only four lines are visible in the graph because the optimizers corresponding to the other six predictors are zero for 0 ≤ τ₀ ≤ 45.

Fig. 1.

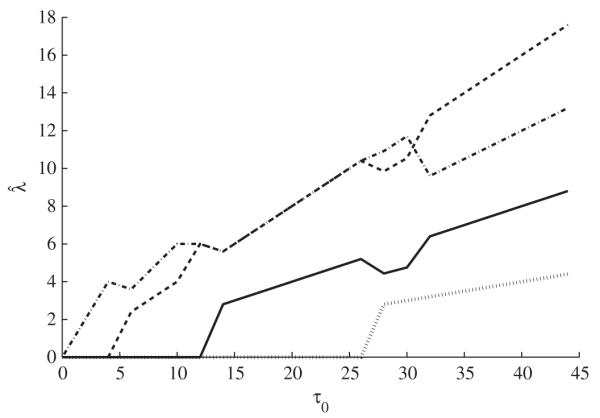
Solution paths to optimization problem (3) for one simulated dataset from Model 1, plotted over 0 < τ₀ ≤ 45. At τ₀ = 40 the paths are, from bottom to top, for variables X₉, X₁, X₃ and X₂.

Model 2

In the second data-generation model, $Y={\sum }_{j=1}^7{f}_j\left(X_j\right)+\epsilon$ with f₁(t)=3t, f₂(t)=−4t, f₃(t)=2t, f₄(t)=2 sin(2πt), f₅(t)=3 sin(2πt)/{2 – sin(2πt)}, f₆(t)=5[0·1 sin(2πt) + 0·2 cos(2πt) + 0·3{sin(2πt)}² + 0·4{cos(2πt)}³ + 0·5{sin(2πt)}³] + 2t and f₇(t)=2(3t – 1)². Here ε ~ N(0, σ²) is independent of the predictors, with σ controlling the noise level; we take σ = 1 or 2. The dimension is D = 20 and so there are 13 noise predictors, X₈, … , X₂₀. For the linear and nonlinear discovery methods, X₁, X₂ and X₃ are linear, X₄ and X₅ are nonlinear, and X₆ and X₇ are mixed linear-nonlinear. For our method, X₁, X₂ and X₃ are linear, X₇ is quadratic, and X₄, X₅ and X₆ are beyond quadratic. Training samples of size n = 250 are used. Tables 3 and 4 present the results from 100 simulated datasets in the same format as for Model 1. Conclusions about the performance of the methods are similar to those for Model 1.

Table 3.

Simulation results for Model 2: average integrated squared errors (×10²) with standard deviations (×10²) in parentheses

σ	η	Oracle 1	SSANOVA	LAND	LANDr	PSC	Oracle 2
1	0·0	15 (4)	25 (6)	16 (5)	17 (5)	14 (4)	14 (4)
	0·5	15 (4)	25 (6)	16 (5)	17 (6)	15 (6)	13 (4)
2	0·0	52 (14)	91 (22)	58 (20)	66 (19)	56 (17)	48 (13)
	0·5	47 (16)	86 (24)	77 (34)	73 (31)	64 (26)	44 (15)

σ, model error standard deviation; η, predictor correlation parameter; SSANOVA, smoothing spline analysis-of-variance method; LAND, linear and nonlinear discovery method; LANDr, linear and nonlinear discovery method, refitted version; PSC, the proposed polynomial structure classification method; Oracle 1, oracle for LAND and LANDr; Oracle 2, oracle for PSC.

Table 4.

Summary of predictor classification performance of the linear and nonlinear discovery method and the proposed method for Model 2

LAND							PSC
σ	η	L	NL	LN	Nil	CC	L	Q	BQ	Nil	CC
1	0·0	3·0	1·6	2·0	12·5	47	3·0	1·0	3·0	13·0	99
	0·5	3·0	1·1	2·0	11·8	16	2·9	1·0	3·0	13·0	89
2	0·0	3·0	1·5	1·9	11·2	14	2·8	1·0	3·0	13·0	74
	0·5	3·0	0·8	1·8	9·7	1	2·2	1·0	2·8	13·0	23
Average SD		0·2	0·6	0·2	2·0		0·3	0·1	0·1	0·1

LAND, linear and nonlinear discovery method; PSC, the proposed polynomial structure classification method; σ, model error standard deviation; η, predictor correlation parameter; L, linear; NL, nonlinear; L-N, linear-nonlinear mixture; Nil, noise; CC, proportion (%) of models with fully correct variable classifications; Q, quadratic; BQ, beyond quadratic; Average SD, block-averaged standard deviation.

8. Extension to partially linear models

The partially linear model is an extension of the additive model where, in addition to predictors X₁, … , X_D, there are predictors Z₁, … , Z_q known to contribute linearly, so that

$$Y=\alpha +\sum _{d=1}^D{f}_d\left(X_d\right)+\sum _{j=1}^q{Z}_j{\gamma }_j+\epsilon .$$ (5)

The Z_j commonly include indicators for categorical variables such as gender, race and location.

We illustrate the extension of our method to the partially linear model (5) via profiling by analysing the diabetes data from Willems et al. (1997). The goal of that study was to understand the prevalence of obesity, diabetes and other cardiovascular risk factors. The data include 18 variables on each of 403 African American subjects from central Virginia, with some missing values. The response variable in our analysis is glycosolated haemoglobin, which is of interest because a value greater than 7·0 is usually regarded as giving a positive diagnosis of diabetes.

We exclude two variables, the second systolic blood pressure and second diastolic blood pressure, as they are missingness-prone replicates of two other included variables, the first systolic and first diastolic blood pressures. Doing so leaves 15 candidate predictors. Twelve of these 15 variables are continuous and are rescaled to the unit interval: X₁ = cholesterol, X₂ = stabilized glucose, X₃ = high density lipoprotein (hdl), X₄ = cholesterol to hdl ratio, X₅ = age, X₆ = height, X₇ = weight, X₈ = first systolic blood pressure, X₉ = first diastolic blood pressure, X₁₀ = waist circumference, X₁₁ = hip circumference, and X₁₂ = postprandial time when samples were drawn. The remaining three variables are categorical variables for location, gender and frame. Location is a factor with two levels, Buckingham and Louisa; we set Z₁ = 0 for Buckingham and Z₁ = 1 otherwise. For gender we set Z₂ =0 for female and Z₂ =1 for male. The frame variable has three levels; we set Z₃ = 0 and Z₄ = 0 for small frames, Z₃ = 1 and Z₄ = 0 for medium frames, and Z₃ = 0 and Z₄ = 1 for large frames.

We fit the partially linear model (5) to study the dependence of glycosolated haemoglobin on the variables X₁, … , X₁₂, Z₁, … , Z₄, using the natural extension of the automatic structure recovery algorithm to discern the effects of X₁, … , X₁₂. We use the Bayesian information criterion to select tuning parameters. Our method identified X₁, X₃, X₆, … , X₁₂ as unimportant predictors; X₅ was selected to have a linear effect, X₄ a quadratic effect, and X₂ a beyond-quadratic effect.

As Fig. 2(a) shows, on the original scale X₄ has one outlier, 19·3, far outside the range of the other observations, which are between 1·5 and 12·2. Upon removing the outlier and reapplying our method, X₁, X₃, X₄, X₆, … , X₁₂ are identified as unimportant, X₅ as having a linear effect, and X₂ as having a beyond-quadratic effect. The nonlinear fit for X₂ is shown in Fig. 2(b).

Fig. 2.

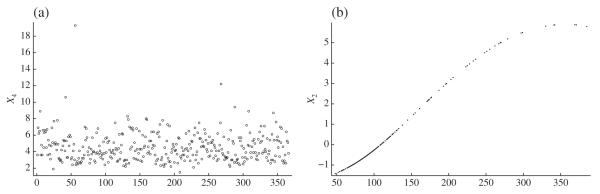
Results of applying our method to the diabetes data: (a) index plot of variable X₄, with an outlier visible in the upper left corner; (b) the beyond-quadratic fit for X₂ (stabilized glucose) after removing the X₄ outlier.

9. Discussion

We have proposed and studied the properties of a new automatic structure recovery and estimation method for the additive model. The method is readily generalizable and can be extended to generalized additive models (Hastie & Tibshirani, 1990) and survival data models (Cheng & Lee, 2009).

Classifying predictors into those that are unimportant and those that contribute through polynomials of specified degree is accomplished by using a nonparametric variable selection method based on the results of Stefanski et al. (2014). Like the nonparametric classification method proposed by Stefanski et al. (2014), each step of our new method uses regularization by bounding a sum of inverse kernel bandwidths. Other choices of penalty, such as ${\sum }_d{\lambda }_d^{\gamma }$ for fixed γ ≥ 0, are possible and worthy of study. Based on our limited experience, γ = 1 gives good overall performance. However, in light of the results in Stefanski et al. (2014), it is expected that γ < 1 would increase sparsity whereas γ > 1 would decrease sparsity but yield regression function estimators that have better mean-squared error properties.

As noted by a referee, modifications to our method and additional development of the theory to accommodate the case of a diverging dimension D would be useful directions to pursue. Alternatively, for data with large D, one could precede the use of our method with application of one of the screening procedures recently developed by Fan et al. (2011) and Cheng et al. (2014).

Appendix

For d = 1, … , D, denote the density of X_d by f_d(·). We assume the following technical conditions from Fan & Jiang (2005), as our method is based on backfitting coupled with local polynomial smoothing.

Condition A1

The kernel function K(·) is bounded and Lipschitz continuous with bounded support.

Condition A2

The densities f_d(·) are Lipschitz continuous and bounded away from zero over their bounded supports.

Condition A3

For all pairs d and d’, the joint density functions of X_d and X_d are Lipschitz continuous on their supports.

Condition A4

For all d = 1, … , D, the (p_d + 1)th derivatives of m_d(·) exist and are bounded and continuous.

Condition A5

The error has finite fourth moment, E(∣ε∣⁴) < ∞.

For the backfitting estimate coupled with local polynomial smoothing as defined in § 3, we have the following asymptotic result.

Lemma A1

Assume that Conditions A1–A5 hold and h_d → 0 such that $n{h}_d^{2p_d+2}\to \infty$ as n n → ∞, for d = 1, … , D. Then

$$\frac{1}{n}\sum _{i=1}^n{\left\{Y_i-{\widehat{\alpha }}^{\mathrm{BF}}-\sum _{d=1}^D{\widehat{m}}_d^{\mathrm{BF}}(X_{\mathit{id}};h,p)\right\}}^2={\sigma }^2+O_{\mathrm{p}}\left(\sum _{d=1}^D{h}_d^{2p_d+2}\right)+O_{\mathrm{p}}\left(\sum _{d=1}^D\frac{1}{{\mathit{nh}}_d}\right).$$ (A1)

Proof

Lemma A1 is a straightforward consequence of the third step in the proof of Theorem 1 in Fan & Jiang (2005). The term on the left-hand side of (A1) is rss₁/n in their notation, which they show converges in probability to σ². Fan & Jiang (2005) did not explicitly state the rate of convergence, but it is readily deduced from their proof. We use their notation in the rest of this proof.

Note that rss₁ = εA_n2ε + B^TB + 2B^T(W_M – I_n)ε and A_n2 = I_n + S^TS – S – S^T + R_n2, according to Fan & Jiang (2005, p. 903). Thus it is enough to track the convergence rates of the different terms. Also, $B=O\left({\sum }_{d=1}^D{h}_d^{p_d+1}\right)+\left({\sum }_{d=1}^D{\stackrel{‒}{m}}_d\right)O\left(1\right)$ almost surely, according to (B.4) in Fan & Jiang (2005), and ${\sum }_{d=1}^D{\stackrel{‒}{m}}_d)=O_p(n^{-1∕2})$ by definition. Consequently, $B^{T}B∕n=O_{\mathrm{p}}\left({\sum }_{d=1}^D{h}_d^{2p_d+2}\right)$. By line 6 from the bottom of the right-hand column of p. 901 in Fan & Jiang (2005), $B^T(W_M-I_n)\epsilon ∕n=O_p(n^{-1}+{\sum }_{d=1}^D{n}^{-1∕2}{h}_d^{p_d+1})$. By (B.11)–(B.24), ${\epsilon }^{\mathrm{T}}{S}^{\mathrm{T}}S∕n-S-S^{\mathrm{T}}\epsilon =O_p\{{\sum }_{d=1}^{D}1∕(n{h}_d\left)\right\}$. As R_n2 = O(1^T1/n) uniformly over its elements, ${\epsilon }^{\mathrm{T}}{R}_{n2}\epsilon ∕n=O_{\mathrm{p}}\{{\sum }_{d=1}^{D}1∕(n{h}_d\left)\right\}$. Combining these terms and noting that $n{h}_d^{2p_d+2}\to \infty$ completes the proof.

For k = 0, 1, … , let π_k be the set of all polynomial functions of degree k. Define $\mathcal{I}=\{d:m_d(\cdot )\in {\pi }_{p_d},d=1,\dots ,D\}$ to be the set of predictors with corresponding additive component functions which are polynomial of degree at most that of the corresponding local polynomial used in the backfitting algorithm. Denote its complement by ${\mathcal{I}}^{\mathrm{C}}=1\{1,\dots ,D\}\backslash \mathcal{I}$.

Proposition A1

Suppose that Conditions A1–A5 hold, that h_d ≥ c₀ > 0 for $d\in \mathcal{I}$ and some constant c > 0, and that h_d’ → 0 and $n{h}_{d^{\prime }}^{2p_d+2}\to \infty$ as n → ∞ for $d^{\prime }\in {\mathcal{I}}^{\mathrm{C}}$. Then

$$\frac{1}{n}\sum _{i=1}^n{\left\{Y_i-{\widehat{\alpha }}^{\mathrm{BF}}-\sum _{d=1}^D{\widehat{m}}_d^{\mathrm{BF}}(X_{\mathit{id}};h,p)\right\}}^2={\sigma }^2+O_{\mathrm{p}}\left(\sum _{d\in {\mathcal{I}}^{\mathrm{c}}}{h}_d^{2p_d+2}\right)+O_{\mathrm{p}}\left(\sum _{d\in {\mathcal{I}}^{\mathrm{c}}}\frac{1}{{\mathit{nh}}_d}\right).$$ (A2)

Proof

Opsomer & Ruppert (1999) studied a backfitting estimator for semiparametric additive models and showed that the estimator of the parametric component is n^1/2-consistent. The condition h_d ≥ c₀ > 0 for $d\in \mathcal{I}$ and some c₀ > 0 implies that the smoothing bandwidth h_d is bounded away from zero for $d\in \mathcal{I}$. As m_d(·) ∈ π_pd for $d\in \mathcal{I}$, there is no approximation bias in using local polynomial smoothing to estimate the corresponding component in the backfitting algorithm. Thus the techniques of Opsomer & Ruppert (1999) can be used to show that the estimator of m_d(·) for $d\in \mathcal{I}$ is n^1/2-consistent as h_d > c₀ > 0. The n^1/2-consistent rate is faster than the consistency rate for smoothing other components.

Proof of Proposition 1

It is easy to show by contradiction that ${\widehat{\lambda }}_d\to \infty$ in probability for $d\in {\mathcal{B}}_0$. If ${\widehat{\lambda }}_{d^{\prime }}$ is bounded for some $d^{\prime }\in {\mathcal{B}}_0$, then the objective function of (3) converges to the sum of σ² plus an additional positive term due to smoothing bias. The additional bias term is caused by bounded ${\widehat{\lambda }}_{d^{\prime }}$, as the corresponding smoothing bandwidth $h_{d^{\prime }}=1∕{\widehat{\lambda }}_{d^{\prime }}$ does not shrink to zero. This is suboptimal, as the smallest limit of the objective is σ². This proves that ${\widehat{\lambda }}_d\to \infty$ in probability for $d\in {\mathcal{B}}_0$.

In (3), local constant smoothing is used for every component function. Thus p_d = 0 for d 1, … , D. The second term on the right-hand side of (A1) or (A2) is due to bias, and the third term is due to variance when using local polynomial smoothing for every component. The condition ${\tau }_0^3∕n\to 0$ as n → ∞ ensures that the variance term is dominated by the bias term. At the same time, note that a bounded and small λ_d for $d\in {\mathcal{A}}_0$ does not introduce any extra term.

If ${\sum }_{d\in {\mathcal{A}}_0}{\widehat{\lambda }}_d\nrightarrow 0$ as n → ∞, consider ${\tilde{\lambda }}_d={\widehat{\lambda }}_d{\tau }_0∕({\tau }_0-{\sum }_{d^{\prime }\in {\mathcal{A}}_0}{\widehat{\lambda }}_{d^{\prime }})$ for $d\in {\mathcal{B}}_0$ and ${\tilde{\lambda }}_d=0$ for $d\in {\mathcal{A}}_0$. In this case, ${\tilde{\lambda }}_d$ diverges to infinity at a faster rate than ${\widehat{\lambda }}_d$ for $d\in {\mathcal{B}}_0$. Consequently, the asymptotic bias term on the right-hand side of (A2) using the ${\tilde{\lambda }}_d$ values is smaller than the bias term on the right-hand side of (A1) using ${\widehat{\lambda }}_d$ values. Here, smaller is in the sense of asymptotic order if ${\sum }_{d\in {\mathcal{A}}_0}{\widehat{\lambda }}_d\to \infty$, and in the sense of the constant multiplying the asymptotic order if ${\sum }_{d\in {\mathcal{A}}_0}{\widehat{\lambda }}_d$ is bounded. Thus the set of ${\widehat{\lambda }}_d$ values with ${\sum }_{d\in {\mathcal{A}}_0}{\widehat{\lambda }}_d\nrightarrow 0$ as n → ∞ is suboptimal, as we are solving a minimization problem (3). This shows that ${\widehat{\lambda }}_d\to 0$ in probability for $d\in {\mathcal{A}}_0$ and therefore completes the proof.

Proof of Theorem 1

From Proposition 1, we have that $\mathrm{pr}({\widehat{\mathcal{A}}}_0={\mathcal{A}}_0)\to 1$ as n → ∞. Conditional on ${\widehat{\mathcal{A}}}_0={\mathcal{A}}_0$, we can prove that $\mathrm{pr}({\widehat{\mathcal{A}}}_1={\mathcal{A}}_1)\to 1$ as n → ∞ using arguments similar to those in the proof of Proposition 1. This process is iterated to complete the proof of the theorem.