Elastic Properties of the Annular Ligament of the Human Stapes—AFM Measurement

Abstract

Elastic properties of the human stapes annular ligament were determined in the physiological range of the ligament deflection using atomic force microscopy and temporal bone specimens. The annular ligament stiffness was determined based on the experimental load-deflection curves. The elastic modulus (Young’s modulus) for a simplified geometry was calculated using the Kirchhoff–Love theory for thin plates. The results obtained in this study showed that the annular ligament is a linear elastic material up to deflections of about 100 nm, with a stiffness of about 120 N/m and a calculated elastic modulus of about 1.1 MPa. These parameters can be used in numerical and physical models of the middle and/or inner ear.

INTRODUCTION

The annular ligament (AL) of the stapes attaches the stapes footplate (SF) to the vestibular window (Brunner 1954, Bolz and Lim 1972). This attachment is known as the stapedio-vestibular joint (SVJ). The SVJ enables the stapes to vibrate (Wolff and Bellucci 1956, Whyte et al. 2002). The movement of the SF causes pressure changes within the fluid, consequently stimulating the cochlea’s sensory hair cells. The bending of the hair cells leads to the conversion of mechanical vibration to action potentials in the auditory nerve fibers. Transmission electron microscopy has shown that the AL of the SVJ is mainly composed of thicker elastic fibers and thinner transverse micro-fibrils (Ohashi et al. 2006). The elastic ligament fibers are regularly arranged in a parallel array and inserted into the cartilaginous matrices. The fibers transversely cross the SVJ between the SF and the vestibular window. The elastic properties of the AL affect the SF displacement amplitude and thus directly affect the middle ear transfer function. It is well known that the vibration amplitude of the SF is dependent on both the frequency and the sound pressure level (SPL) at the tympanic membrane. Several authors have observed linear growth of the SF displacement with the SPL, which indicates that the system is linear (Merchant et al. 1996, Asai et al. 1999). Experiments in healthy human ears have also shown that the SF displacement rises slowly from the low frequencies to near the peak (∼10–20 nm at about 0.8–1.0 kHz for 80 dB SPL) (Asai et al. 1999, Heiland et al. 1999, Hato et al. 2001, Huber et al. 2001, 2003; Stenfelt et al. 2004, Chien et al. 2009) and falls off as frequency increases above the peak.

Knowledge of the mechanical properties of the AL is necessary for modeling sound transmission from the middle ear to the cochlear fluid. Theoretical modeling approaches have been reported for the middle ear mechanics in normal (e.g., Wada et al. 1992, Sun et al. 2002, Gan et al. 2006, Gentil et al. 2011), diseased (e.g. Dai et al. 2007, Gan and Wang 2007, Gan et al. 2009, Zhao et al. 2009) and reconstructed (e.g., Ladak and Funnell 1996, Zahnert et al. 1997, Prendergast et al. 1999, Koike et al. 2000, Ferris and Prendergast 2000, Kelly et al. 2003, Yao et al. 2012) states. However, it is difficult to validate these models. In particular, development of an accurate finite element (FE) model requires assuming a specific value for the stiffness of the AL. Researchers generally estimate the value using a cross-calibration process. However, this has resulted in large differences in the obtained values: for example, Young’s moduli of 0.01 MPa (Sun et al. 2002), 0.065 MPa (Wada et al. 1992, Kelly et al. 2003), 0.2 MPa (Gan et al. 2006), and 5.5 MPa (Gan et al. 2007).

The mechanical properties of the AL have been investigated directly by an electromagnetic probe (Cancura 1979, human temporal bones), the Mössbauer technique (Lynch et al. 1982, living cats), an image analysis system (Gan et al. 2011, fresh human temporal bones), and a laser Doppler vibrometer (Lauxmann et al. 2014, human temporal bone). Although these methods allow the measurement of displacement at the nanometer level, the experiments in temporal bones were conducted for forces above 1 mN. Therefore, the measured displacement of the stapes was significantly larger than the normal displacement induced in healthy ears at, e.g., 100 dB SPL. This means that the AL stiffness obtained from the force-displacement curves may differ from the actual AL stiffness during normal sound transmission.

Thus, there is a need to develop a new technique allowing the measurement of the stiffness of the AL at much smaller displacements. The measurements should be conducted in the physiological range of elongations of the AL elastic fibers, i.e., for SF displacements from 0 to ∼100 nm. Such small displacements are extremely difficult to achieve using a conventional micro-mechanical testing system (e.g., MTS with SMT-1 capacity load cell developed by Interface Inc. or FemtoTools FT–FS100 by Nanoscience Instruments, Inc.).

Atomic force microscopy (AFM) (Binnig et al. 1986) is nowadays commonly used for measuring the mechanical properties of biological samples at the nanoscale (Radmacher 1997, Sugawara et al. 2002, Ikai et al. 2003, Takai 2005, Darling et al. 2006, Murakoshi et al. 2006, Thurner 2009). The AFM technique enables the manipulation of the samples by a precisely controlled piezo-scanner and a micro-cantilever probe. The piezo-scanner can be designed for nanomanipulation with about 50 picometers resolution. The micro-cantilever probe is composed of a soft beam with reflective coating and a tip attached to the end of the beam. In the contact AFM mode, force between the tip and the sample causes the beam to bend. A laser beam is reflected off the beam, small changes in beam deflection are detected by a sensitive photodetector. The analysis of the force-displacement curve recorded by the AFM allows the calculation of the stiffness (Doerner and Nix 1986, Oliver and Pharr 1992). During the analysis, deflection of the cantilever and the tip-sample interaction are treated as two springs in series. So far, the AFM technique has not been used to measure the stiffness of the AL.

The aim of this study is to develop new experimental method for determining the elastic properties of the stapes AL in the physiological range of its deflection. To this end, the AFM technique and fresh human temporal bone specimens were used.

MATERIALS AND METHODS

Measurement System

The measurements were performed in two human temporal bone specimens of the stapes AL. Neither ethics nor IRB approval was required for the use of cadaveric temporal bones under Polish law. In each specimen, we repeated the measurement 30 times. The AFM instrument was used to mechanically load the AL and quantitatively characterize its elastic properties in the physiological range of deformations. In the measurements, the maximum deflection of the AL was limited to 100 nm. The force-displacement curves were recorded by an AFM NT-206 system (Microtestmachines Ltd, Gomel, Belarus). The system consists of a scanning unit, a controller, and software for AFM-data processing, visualization, and analysis.

The scanning unit comprises a base platform and a detachable measuring head. A piezo-mechanism and motors, mounted inside the base platform, provide both approach (loading) and withdrawal (unloading) actions of the sample platform. The range of the vertical motion is 20 mm with steps down to about 200 nm. The measuring head allows high-precision movement (vertical resolution of about 0.3 nm) of the removable cantilever holder. The laser source, the photodiode, and the video camera are integrated with the measuring head. The video camera is focused on the cantilever beam and connected to the controller. The controller allows the control of laser beam placement and positioning on the sample.

The AFM system was equipped with a rectangular cantilever (Fig. 1) made especially for our measurements in the Institute of Micromechanics and Photonics at the Warsaw University of Technology. The cantilever beam was etched out of a thin (60 μm) beryllium copper plate (Alloy Brush 190 CuBe2; Be 1.8 %, Co + Ni 0.3 %, Lamineries Matthey SA, La Neuveville, Switzerland) with a polished reflective upper surface. The nominal spring constant k_{c_nom} of the cantilever was 186 N/m (see Section 2.3). As a tip, a stainless steel bearing ball with a diameter of 0.7 mm was used. The ball was glued with epoxy resin (Epicote 1004, Shell Chemicals, London UK) onto the end of the cantilever beam. The real spring constant (k_c) of the cantilever was measured using the calibration method described by Ekwińska and Rymuza (2009). After the calibration, the cantilever was mounted in the cantilever holder of the measuring head.

FIG. 1.

The cantilever used in our measurement. 1 cantilever beam (length 2.54 mm, width 0.41 mm, thickness 0.061 mm), 2 tip of the cantilever (a steel ball of 0.7-mm diameter).

Data Acquisition

The AFM optical system consists of a digital camera with an attached lens focused on the cantilever. The output of the camera is sent to the computer to allow viewing of the sample during measurement. Using the manual drive, the sample was brought closer to the cantilever until a distance of about 1 mm between the sample and the cantilever was reached. Next, remote-controlled displacements were used to bring the sample into contact with the cantilever. Finally, force-distance (F-d) curves were acquired using the closed-loop force mode with a maximum displacement of ∼100 nm applied at a rate of about 100 nm/s. For each AL specimen, we performed the measurements at different locations on the specimen surface. At the beginning, the tip was placed above the middle of the stapes head (Fig. 2C) and the first curve was recorded. Then, the cantilever was lifted and subsequent measurements were done at 28 other locations in a regular pattern of 5-μm steps within a 15-μm radius around the starting point. The horizontal displacement between measurement points was controlled by the AFM piezo-scanner. Each curve was recorded over 3 s. Finally, the measurement results were calibrated to get the data in nN/nm.

FIG. 2.

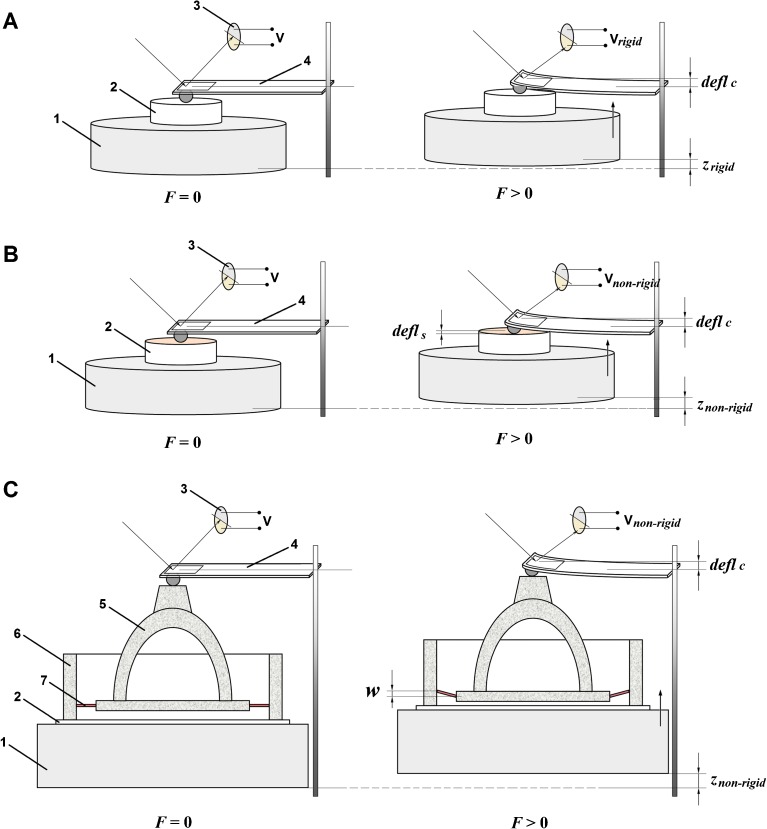
AFM-based nanomechanics measurements. F force acting between the sample and the tip, V voltage of the photodiode, defl _c deflection of the cantilever, defl _s deflection of the sample, w deflection of the AL of the stapes, z displacement of the piezoactuator. A Measurements on a rigid reference sample. The rigid surface acted as an infinitely stiff sample, i.e., a sample that cannot deform and only the cantilever bends. The resulting cantilever deflection is the same as the piezoactuator displacement (defl _c = z _rigid). 1 piezoactuator, 2 sample, 3 photodiode, 4 cantilever. B Measurements on a non-rigid sample. For the non-rigid samples, the measured deflection (defl _c) of the cantilever is not the same as the piezoactuator displacement (z _non-rigid), but defl _c = z _{non ‐ rigid} − defl _s. 1 piezoactuator, 2 sample, 3 photodiode, 4 cantilever. C Measurements on the AL sample. 1 piezoactuator, 2 glass cover slip, 3 photodiode, 4 cantilever, 5 stapes, 6 oval window bone, 7 annular ligament of the stapes.

Sample Preparation

Two fresh cadaveric temporal bones, obtained from donors with ages of 24 and 32 years, were used in this study. The donors had no evidence of otologic disease. The temporal bones were removed from human corpses selected in the Forensic Medicine Institute of Warsaw Medical University no later than on the third day following death. The bodies were stored at 4 °C. The bones were harvested according the standard practice developed by Schuknecht (1968) with the use of a Stryker oscillating saw. During preparation of the specimen, the condition of the AL of the stapes was examined to confirm that otosclerosis in the oval window niche was absent. After being collected, the bones were kept in normal saline at 5 °C until the following day.

The Procedure for Preparation

Temporal bones were dissected under an operating microscope using a standard set of micro-otosurgical equipment and a saw blade mounted on dentist drill tool. First, the temporal bone was washed and wax was removed from the external ear. Then, an anterior tympanotomy was performed and the oval window location was identified relative to the external structures of the temporal bone. The tympanic membrane was carefully removed to expose the ossicles. The incudo-stapedial joint was disarticulated with the use of surgical micro-scissors, and the malleus-incus complex was removed. Subsequently, much of the petrous portion of the temporal bone, including the semicircular canals and the cochlea, was cut off. After size reduction, only the whole stapes and the SVJ with a thin bony rim of the oval window niche were left intact. The bony block also included the beginning of both scala vestibuli and scala tympani as well as the proximal portions of the semicircular canals. The total volume of the specimen was approximately 1 cm³. Finally, the specimens were glued to thin glass coverslips using universal instant adhesive (Loctite 401, Henkel Ltd., UK). The AL specimen is schematically shown in Figure 2C. To prevent drying, the specimens were wrapped in gauze moistened with saline solution. The AFM measurements were performed on the same day.

AFM-Based Nanomechanics Measurements

In AFM measurements (Fig. 2), the cantilever (4) is the element that converts the force (F) acting between sample and tip to the deflection (defl_c) at the tip. For small forces, the relationship between F and the optically measured defl_c is given by Hooke’s law:

$$F=-k_c\cdot def{l}_c$$ 1

where k_c is the spring constant of the cantilever, defl_c is the deflection at the cantilever tip, and F is the force acting between the sample and the tip. The same force (F) causes deflection (defl_s) of the sample depending on the stiffness (k_s) of the sample:

$$def{l}_s=-\frac{F}{k_s}$$ 2

where k_s is the stiffness of the sample, defl_s is the deflection of the sample, and F is the force acting between the sample and the tip.

Calibration and Real Stiffness (Spring Constant) of the Cantilever

Knowledge of the real spring constant k_c of the cantilever is essential for quantitative measurements. Nominal spring constants estimated from the dimensions are not accurate enough since the real value can vary drastically with small variations in the thickness and due to defects in the material. For this reason, it is better to measure rather than calculate this constant. To determine k_c, we conducted a series of calibration tests on two reference samples.

First, we performed the calibration of the sensitivity of the deflection sensor using the AFM NT-206 control software “SurfaceScan”. To that end, the force-displacement curves were recorded on a rigid reference sample (2 in Fig. 2A). This sample was made of a polished silicon wafer. We assumed that the silicon surface acted as an infinitely stiff sample (k_s = ∞), i.e., the sample cannot deform and only the cantilever bends. In that case, the cantilever deflection is equal to the piezoactuator (1) displacement (defl_c = z_rigid). From the curve slope obtained for the region of linear compliance, we determined the deflection sensitivity factor K (in nm/V) as

$$K=\frac{\Delta z_{\mathrm{rigid}}}{\Delta V_{\mathrm{rigid}}}$$ 3

where K is the deflection sensitivity factor (in nm/V), z_rigid is the displacement of the piezoactuator (1, in nm), and V_rigid is the voltage of the photodiode (3, in V) recorded for the rigid reference sample (2).

Subsequently, we performed the calibration of the cantilever stiffness. To that end, the force-displacement curves were recorded on a non-rigid reference sample with known stiffness (k_s-ref) (2 in Fig. 2B). As a reference sample, we used the calibration structure 12Z00010 (Nanoidea Ltd., Warsaw, Poland, http://www.nanoidea.pl) with a stiffness of 35 N/m (traceability certificate attached to the structure). After determining the sensitivity factor K, the deflection (defl_c) of the cantilever can be calculated as

$$def{l}_c=K\cdot \Delta V_{\mathrm{n}\mathrm{o}\mathrm{n}-\mathrm{rigid}}$$ 4

In Eq. 4, the ΔV_non-rigid is equal to the difference between the photodiode output voltage at the first contact point and the voltage at any location in the contact region of the force-distance curve. It should be noted that for the non-rigid samples, the measured deflection (defl_c) of the cantilever is not the same as the piezoactuator (1) displacement (z_non-rigid), but

$$def{l}_c=z_{\mathrm{n}\mathrm{o}\mathrm{n}-\mathrm{rigid}}-def{l}_s$$ 5

Data Analysis and Elastic Modulus Calculation

For the AL sample, the measured deflection (defl_c) of the cantilever depends on both the k_c of the cantilever and the E of the AL. We neglected the indentation of the stapes head caused by the cantilever tip. This is justified because the bone stiffness is much higher than the AL stiffness. In order to calculate the deflection of the AL (w), the deflection of the cantilever (defl_c) should be subtracted from the piezoactuator displacement (z_non-rigid  = z_AL) (Fig. 2C). Using Eqs. 5 and 1, the AL deflection (w) can be calculated as

$$w=def{l}_s=z_{\mathrm{A}\mathrm{L}}-def{l}_c=z_{\mathrm{A}\mathrm{L}}+F/k_c$$ 7

where w is the AL deflection, z_AL is the piezoactuator displacement for the AL sample, defl_c is the measured cantilever deflection (on the AL sample), F is the force applied, and k_c is the cantilever spring constant.

Note that F/k_c corresponds to the deflection of the cantilever on a hard surface at the same force F. Thus, the force-displacement (F-d) curves are converted to the force-deflection (F-w) curves.

Our measurement method requires that the stapes head should not be deformed. To that end, we used a stainless sphere with an extremely large diameter (0.7 mm), as mentioned above. Calculations based on Hertz theory (Young and Budynas 2002, p. 702) showed that the indentation depth (at the maximal force F = 22 μN) is about 1.2 nm. This value corresponds to about 1.2 % of the AL deflection. Therefore, the data analysis based on Eq. 7 is justified.

To estimate a value of E for the AL, we used the Kirchhoff–Love theory for small deformations of thin plates under pure bending (Reddy 2007). For a circular, isotropic, and transversely loaded plate of constant thickness, the governing differential equation in cylindrical coordinates (r, θ, z) can be written in the form

$$\frac{d}{dr}\left[\frac{1}{r}\frac{d}{dr}\left(r\frac{dw}{dr}\right)\right]=-\frac{t\left(r\right)}{B}$$ 8

where w is the plate deflection (in m), t is the shear force (in N/m), $B=\frac{E{h}^3}{12\left(1-{\nu }^2\right)}$ is the bending stiffness of the plate, h is the thickness of the plate, and ν is the Poisson’s ratio.

The AL plate was assumed to be simply supported on the outer periphery and subjected to a uniformly distributed load F around the edge of a central hole (Fig. 3). For this load, the shear force is

$$t\left(r\right)=\frac{F}{2\pi r}$$ 9

FIG. 3.

The AL plate. The AL plate is a circular plate of diameter 2a with a central hole of diameter 2b. The AL plate is composed of n elastic fiber plates separated by amorphous substance. On the outer periphery, the AL plate is simply supported. The AL plate is subjected to a uniformly distributed load F/2πb (in N/m) around the edge of the central hole. 1 central hole (where the SF is placed), 2 annular ligament plate, 3 oval window bone, 4 single elastic fiber plate, 5 amorphous substance.

Substituting Eq. 9 into Eq. 8, the solution for the deflection function w(r) is

$$w\left(r\right)=\frac{F\cdot r^2}{8\pi B}\left(lnr-1\right)-\frac{C_1{r}^2}{4}-C_{2}lnr+C_3$$ 10

The constants C₁, C₂, and C₃ in Eq. 10 can be determined from the boundary conditions at the outer (r = a) and inner (r = b) edges. For analytical simplicity, we assume that the boundary conditions can be written as

$$w\left(r=a\right)=0,M_r\left(r=a\right)=0,M_r\left(r=b\right)=0$$ 11

where $M_r\left(r\right)=B\left(\frac{d^{2}w}{d{r}^2}+\nu \frac{1}{r}\frac{dw}{dr}\right)$ is the radial bending moment.

Using the above boundary conditions (Eq. 11) and the expressions for w(r) and M_r(r), we have calculated the constants C₁, C₂, and C₃ to be

$$\begin{array}{l}{C}_1=\frac{P}{4\pi B}\left(\frac{1-\nu }{1+\nu }-\frac{2b^2}{a^2-b^2}ln\frac{b}{a}\right)\hfill \\ C_2=-\frac{P}{4\pi B}\frac{1+\nu }{1-\nu }\frac{a^2{b}^2}{a^2-b^2}ln\frac{b}{a}\hfill \\ C_3=\frac{P{a}^2}{8\pi B}\left(1+\frac{1}{2}\frac{1-\nu }{1+\nu }-\frac{b^2}{a^2-b^2}ln\frac{b}{a}\right)\hfill \end{array}$$ 12

Substituting the above constants C₁, C₂, and C₃ in Eq. 10 and then simplifying, the AL plate deflection at r = b can be written in the form

$$w=w\left(r=b\right)=\frac{3F\cdot \left(1-{\nu }^2\right)}{4\pi E{h}^3}\cdot \left[\frac{\left(a^2-b^2\right)\cdot \left(3+\nu \right)}{1+\nu }+\frac{4a^2{b}^2\left(1+\nu \right)}{\left(a^2-b^2\right)\cdot \left(1-\nu \right)}{\left(ln\frac{a}{b}\right)}^2\right]=C\cdot \frac{F}{E}$$ 13

where C is a constant, given by

$$C=\frac{3\cdot \left(1-{\nu }^2\right)}{4\pi h^3}\cdot \left[\frac{\left(a^2-b^2\right)\cdot \left(3+\nu \right)}{1+\nu }+\frac{4a^2{b}^2\left(1+\nu \right)}{\left(a^2-b^2\right)\cdot \left(1-\nu \right)}{\left(ln\frac{a}{b}\right)}^2\right]$$ 14

where a, b, and h are the dimensions of the AL plate and ν is the Poisson’s ratio of the AL plate.

Comparing Eq. 13 with Eq. 7, the elastic modulus (E) of the AL can be obtained as

$$E=C\cdot \frac{\frac{F}{z_{\mathrm{A}\mathrm{L}}}\cdot k_c}{k_c+\frac{F}{z_{\mathrm{A}\mathrm{L}}}}=C\cdot \frac{\alpha \cdot k_c}{k_c+\alpha }$$ 15

where $\alpha =\frac{F}{z_{\mathrm{A}\mathrm{L}}}$ is the slope of the force-deflection curve recorded for the AL sample and k_c is the real spring constant of the cantilever.

Measurements of AL Dimensions

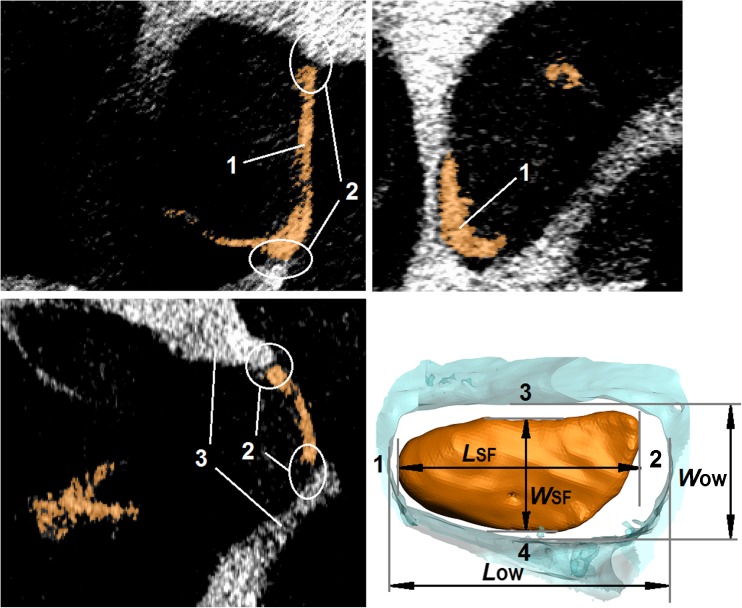
The AL dimensions are needed to calculate the E of the AL based on Eq. 15. Therefore, after the AFM measurements, we scanned the AL samples using a SkyScan 1076 micro-CT System (Bruker–microCT, formerly Skyscan, Kontich, Belgium, www.skyscan.be) according to the methodology described in detail in Kwacz et al. (2012). Briefly, the voxel size was 9 μm and the scans were performed with a source voltage and source current of 100 kV and 100 μA, respectively. An aluminum filter with a thickness of 1 mm was used to reduce the low-energy content of the X-ray energy spectrum, thus reducing beam hardening. The scanning exposure time per frame was 220 ms. The images were acquired at a step angle of 0.7° for a total circular orbit of 360°. In order to improve the quality of the final images, averaging of five frames collected at each angular position was done. The cone beam acquisitions save all of the projection images as 16-bit TIFF files. The SkyScan’s volumetric reconstruction software “NRecon 1.5.1.1” was used to create a set of cross section slices through the object. The output files were saved in 8-bit grayscale BMP format with a size of 2000 × 2000 pixels. The stack of slice images was then used for segmentation and 3D volume reconstruction of the AL using the ScanIP software (Simpleware Ltd, UK, www.simpleware.com). Because the grayscale differences between the AL and the SF were small, the automatic contouring could not be used, and manual segmentation was required. The morphological and smoothing filters, available in the ScanIP software, were used to reduce the noise in the images. After smoothing and segmentation, 3D reconstruction and morphometric measurements of the AL, the SF, and the OW were performed (Fig. 4). The following dimensions were measured: (1) the OW length (L_OW), (2) the OW width (W_OW), (3) the SF length (L_SF), (4) the SF width (W_SF), and (5) the SF thickness at the outer edge. The thickness of the AL was taken to be as the same as the SF thickness on the outer edge (Ohashi et al. 2006).

FIG. 4.

Morphometric measurements of the stapes footplate (SF) and the oval window (OW) based on micro-CT imaging with the use of the Measure Tool in ScanIP software (Simpleware Ltd, UK). 1 stapes footplate (SF), 2 annular ligament (AL), 3 oval window (OW) bone. L _OW length of the OW, W _OW width of the OW, L _SF length of the SF, W _SF width of the SF (dimensions are listed in Table 1).

RESULTS

Dimensions of the AL Plate

The results of the morphometric measurements (Fig. 4) for two temporal bone specimens are listed in Table 1.

TABLE 1.

Dimensions of the AL measured in two human specimens (Specimen 1 and Specimen 2) used in our study. The L _SF, W _SF, L _OW, and W _OW dimensions and the measurement points 1–4 are shown in Figure 4

	Specimen 1	Specimen 2
Length of the SF, L SF (mm)	2.76	2.58
Width of the SF, W SF (mm)	1.22	1.18
Length of the oval window, L OW (mm)	2.95	2.82
Width of the oval window, W OW (mm)	1.41	1.31
Thickness of the AL, h (mm)
At measurement point 1	0.31	0.28
At measurement point 2	0.16	0.15
At measurement point 3	0.23	0.22
At measurement point 4	0.25	0.23

Based on the measured dimensions, we calculated the outer radius (a) and inner radius (b) of the assumed AL circular plate model as a = ¹/₄ (L_OW + W_OW) and b = ¹/₄ (L_SF + W_SF). For Specimen 1 and Specimen 2, respectively, the outer radius is a₁ = 1.09 mm and a₂ = 1.03 mm, and the inner radius is b₁ = 0.99 mm and b₂ = 0.94 mm. The thickness at points 1 to 4 for Specimens 1 and 2 ranged from 0.16 to 0.31 mm and from 0.15 to 0.28 mm, respectively. For use as the constant thickness (h) of the AL circular plate model, we calculated the averages of the measurements at point 1 to 4 for Specimens 1 and 2, giving h₁ = 0.24 mm and h₂ = 0.22 mm, respectively.

Calibration of Deflection Sensor and Cantilever Stiffness

The two reference samples mentioned in Section 2.3 (Calibration and real stiffness (spring constant) of the cantilever) are a rigid sample (Si) and a calibration membrane 12Z00010 (Nanoidea Ltd.). Both Si and membrane were tested 15 times, and the standard deviations of the slopes from the multiple curves were less than 3 % of the average values.

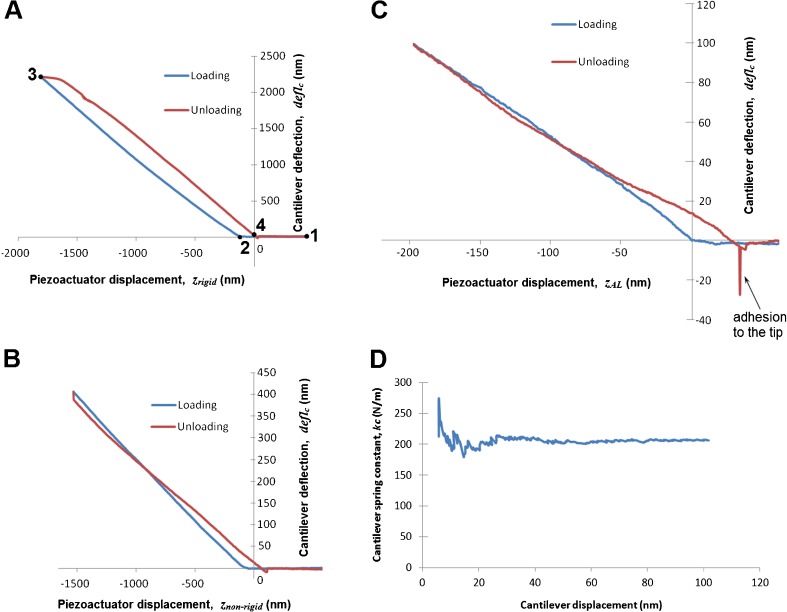
Figure 5A shows the calibration curves recorded on the rigid sample (Si) as described in Section 2.3. At the beginning (point 1), we start the measurement and the cantilever approaches the sample. At point 2, the cantilever comes into contact with the sample and then applies a load to it. The maximum load is at point 3. After that, we reduce the load until the cantilever comes out of contact (point 4). The slope of defl_c/z_rigid is 1 for the range of cantilever displacement up to 1000 nm. Higher displacement than 1 μm might result in nonlinearity of the photodiode. The shift between the unloading and loading curve is caused by the elastic hysteresis of the cantilever beam. Nevertheless, the slope is similar to the one of loading phase. At the end of the measurement, the tip is pulled off from the surface.

FIG. 5.

A Calibration curves (the calibration of the deflection sensor) recorded on the rigid reference sample (silicon wafer). 1 start point, 2 contact point, 3 maximum load, 4 out of contact. B Force-distance curves recorded on the reference sample (calibration structure 12Z00010, Nanoidea Ltd., Piaseczno nearby Warsaw, Poland, http://www.nanoidea.pl). C Measurement curves recorded on the AL sample. D Real spring constant (k _c) of the self-made cantilever determined based on the calibration curves. The cantilever beam (length 2.54 mm, width 0.41 mm) etched out of the 60-μm beryllium copper plate (Alloy Brush 190 CuBe2, Lamineries Matthey SA, La Neuveville, Switzerland).

Figure 5B shows the calibration curves obtained with a calibration structure as described in Section 2.3. The shapes of the curves are actually quite different, exhibiting not just a change of slope due to non-rigidity of the calibration structure, but also force drift during unloading. The force drift causes the cantilever displacement to decrease during the short hold between loading and unloading, which results in a vertical segment. During unloading, the deflected calibration structure interacts with the cantilever, which results a smaller slope of the unloading curve. The slopes of the curves were calculated by the method of least squares. Based on the calibration curves, the real spring constant (k_c) of the self-made cantilever used in our study (Fig. 1) was found to be 200.0 N/m (Fig. 5D). The standard deviation was less than 3 % of the average value. The slope was always calculated after the first 30 nm to avoid the early irregularities and up to 1000 nm or till the end of the measurement.

Spring Constant of the AL of the Human Stapes

Figure 5C shows one set of loading and unloading curves recorded on the AL sample (see Fig. 2C). The curve shape is similar to those of the curves recorded on the calibration samples. This indicates that a similar process occurs during the measurement of the AL sample. Please note that the curves shown in Figure 5C were recorded for piezoactuator displacements less than 200 nm. Therefore, the lower smoothness and departures from straight lines are more obvious than in Figure 5A, B. It can also be seen that the AL sample has a higher adhesion force than the calibration membrane. At the end of unloading on the AL sample, there is a large pull-off force (notation “adhesion to the tip” in Fig. 5C), which is caused by adhesion to the sample. This force is significantly larger than the pull-off force on the calibration samples (Fig. 5A, B). The higher adhesion of the AL sample is caused by the fact that the specimen was kept moist until the measurement, which was necessary to prevent drying and stiffening of the AL. The damp surface had some surface tension effects that were not seen in the dry calibration loads.

Based on the measurement curves (Fig. 5C) and the calibration data, we determined the force-deflection (F-w) curves for the AL (Fig. 6). The colored lines correspond to single measurements, and each black line represents the average slope for that sample. Most of the curves do not pass through the origin because the surface of the stapes head is not flat. For this reason, the value of z_AL in Eq. 7 at F = 0 N is different in each of the measurement points on the stapes head. The slope of the average F-w curve is almost the same for the two specimens. This slope corresponds to the AL stiffness (k_AL). Our measurement results (Table 2) showed that for Specimen 1 and Specimen 2, the k_AL was 115.8 N/m (SD 30.4) and 124.6 N/m (SD 24.5), respectively.

FIG. 6.

The force-deflection (F-w) curves for the two AL specimens. F force acting between the sample and the cantilever, w the AL deflection (where w = z _AL − defl _c according to Eq. 7 and Figure 5C). Colored lines—the curves for single measurements, black lines—the approximated curves.

TABLE 2.

Stiffness (k _AL) and elastic modulus (E) for the two AL specimens (Specimen 1 and Specimen 2) determined in this study

Measurement no.	Specimen 1		Specimen 2
	Stiffness, k AL (N/m)	Elastic modulus, E (MPa)	Stiffness, k AL (N/m)	Elastic modulus, E (MPa)
1	67.5	0.72	115.0	1.16
2	92.5	0.91	102.5	1.08
3	69.0	0.74	106.5	1.10
4	117.0	1.06	117.0	1.17
5	147.5	1.22	167.5	1.45
6	137.5	1.17	137.5	1.29
7	102.5	0.97	177.5	1.49
8	77.0	0.80	137.0	1.29
9	103.0	0.98	102.5	1.08
10	103.0	0.98	98.0	1.04
11	125.0	1.10	97.0	1.04
12	137.0	1.17	125.0	1.22
13	82.5	0.84	167.5	1.45
14	107.0	1.00	83.0	0.93
15	92.0	0.90	150.0	1.36
16	94.0	0.92	168.0	1.45
17	90.0	0.89	155.0	1.39
18	102.5	0.97	134.5	1.28
19	129.0	1.13	114.0	1.15
20	101.0	0.96	104.5	1.09
21	155.0	1.25	142.5	1.32
22	142.5	1.19	129.0	1.25
23	167.5	1.31	101.0	1.07
24	177.5	1.35	114.0	1.15
25	142.5	1.19	114.0	1.15
26	140.0	1.18	197.5	1.58
27	134.5	1.15	105.0	1.09
28	73.0	0.77	114.0	1.15
29	98.0	0.94	122.5	1.21
30	168.0	1.31	110.0	1.13
Mean	115.8	1.05	124.6	1.22
Standard deviation	30.4	0.17	24.5	0.26

Elastic Modulus of the AL

Finally, we determined the elastic modulus (E) of the AL based on Eq. 13 and the measurement data. In Eq. 13, we adopted the dimensions of the AL plate given in Section 3.1, a Poisson’s ratio ν = 0.4, the real spring constant of the cantilever k_c = 200 N/m (see Section 3.2), and the slope of the force-deflection curve α₁ = 115.8 N/m and α₂ = 124.6 N/m. The calculations for Specimen 1 and Specimen 2 gave values for E of 1.05 and 1.22 MPa, respectively.

Additionally, to demonstrate the strong effect of the AL thickness (h) on the AL elastic modulus (E), we calculated E not only for the average values of h but also for values ranging from 0.15 to 0.31 mm. The results of this calculation are shown in Figure 7.

FIG. 7.

The AL elastic modulus (E) calculated for various values of the AL thickness (h from 0.2 to 0.3 mm). The calculations based on Eq. 12. For Specimen 1 and Specimen 2, the following values were adopted: a ₁ = 1.09 mm, b ₁ = 0.99 mm, α ₁ = 115.8 N/m and a ₂ = 1.03 mm, b ₂ = 0.94 mm, α ₁ = 124.6 N/m, respectively. On the graph, the E values for the average h ₁ = 0.24 mm and h ₂ = 0.22 mm are shown.

DISCUSSION

The objective of this study was to develop a new experimental method for determining the elastic properties of the stapes AL in the physiological range of its deflection. To this end, the AFM technique and fresh human temporal bone specimens were used. One of the major applications of AFM is the quantitative measurement of interaction forces between the sample and the probe tip. This technique has been widely employed to examine the mechanical properties of materials in both the micro- and the nanoscale. However, to measure the elastic modulus of the annular ligament of the human stapes, AFM has not been used until now.

Sample Preparation and the Measurement Technique

The measurements were performed in two human cadaveric temporal bone specimens of the stapes AL. Fresh cadaveric temporal bones have been commonly used in experimental measurements of middle- and inner-ear mechanics. It has been experimentally shown that the functioning of the middle ear structures is similar between live and cadaveric ears (Rosowski et al. 1990). In our study, we have used specimens harvested from human cadavers within 48 h after death, protected from drying, and stored without freezing until the measurement. We have performed the AFM measurement in the fourth day after death. The same procedure is widely used by many researchers.

Cantilever Stiffness and Tip Geometry

Proper choice of both cantilever stiffness and tip geometry are necessary to obtain accurate measurement results by AFM. For the measurement of the AL elastic modulus, we have chosen a cantilever with a nominal spring constant of about 200 N/m. However, because the thickness of AFM cantilevers is difficult to control during manufacture, the nominal spring constant for cantilevers from two different batches can vary by almost a factor of two (Cumpson et al. 2003). Therefore, the accurate calibration of the real spring constant of the cantilever is essential for limiting uncertainties and achieving reliable measurement results.

In the literature, a number of different calibration methods have been described. These methods can be divided into three principal classes: dynamic response methods, theoretical methods, and static response methods. Typical accuracies, advantages, and disadvantages of these methods were discussed by Myhra (1998).

Elastic Modulus of the AL of the Human Stapes

Our estimation of the AL elastic modulus was based on a number of simplifying assumptions. In fact, the real FP is not circular, the thickness and width of the AL are not uniform, and the ligament itself does not appear to be either homogeneous or isotropic, having highly oriented fibers and having thicker bands on the medial and lateral sides (Whyte et al. 2002, Ohashi et al. 2006, 2008). Therefore, the resulting Young’s modulus is applicable only if the same simplified model is used.

In our model, the boundary conditions for the AL plate were chosen assuming that the plate is simply supported at the outer periphery (the connection between the AL and OW bone) and the load is axially applied and uniformly distributed at the inner periphery (the connection between the AL and the SF). This allowed us to use plate-bending theory for deriving the load-deflection (F-w) relationship (Eq. 13, Section 2.3). Then, the F-w relationship can be compared with the experimentally obtained force-deflection characteristics (Fig. 6). This comparison allowed us to obtain Eq. 15 for the calculation of the AL elastic modulus.

The boundary conditions (Eq. 11) result from our assumption that the AL fibers act like springs and remain straight when the stapes moves, that is, the AL fibers do not become curved either close to the SF or close to the OW bone. However, there is no literature clearly showing how the AL fibers are deformed during stapes movement. Thus, it is also possible to adopt other boundary conditions, for example, w(a) = 0, M_r(a) = 0, $\frac{dw}{dr}\left(r=b\right)=0$ or w(a) = 0, $\frac{dw}{dr}\left(r=a\right)=0$, $\frac{dw}{dr}\left(r=b\right)=0$. In this work, we did not repeat our modeling for different boundary conditions.

In this study, the deflections were up to only 100 nm, much less than the plate thickness, thus justifying the use of the Kirchhoff–Love theory for thin plates.

The shapes of both the OW niche and the SF are very irregular and vary among individuals (e.g., Hagr et al. 2004; Sim et al. 2013). Numerous authors have treated the AL as an elliptical ring in finite element modeling of the middle ear (Ladak and Funnell 1996; Sun et al. 2002, Gan et al. 2011, Gentil et al. 2011). However, an elliptical shape for the AL plate leads to considerable difficulties in finding an analytical solution for the differential equation describing the plate bending. Therefore, in this study, we have replaced the elliptical shape of the AL rim with a circular shape. Such an approach will certainly affect the calculation of the AL elastic modulus.

It is known that the stapes AL contains a collection of individual elastic fibers that are “regularly arranged in a linear fashion and form a laminated array parallel to the horizontal plane of the SVJ” (Ohashi et al. 2006). Therefore, the AL may display direction-dependent properties caused by structural anisotropy. Due to the radial arrangement of the elastic fibers running from the SF toward the OW, the radial elastic modulus could be smaller than the circumferential elastic modulus. Nevertheless, in this study, we treated the AL as a homogeneous and isotropic structure. The same assumption was made by Lynch et al. (1982) to estimate the AL elastic modulus based on a measured AL compliance. Moreover, AL isotropy has been assumed in most FE models (Sun et al. 2002, Wada et al. 1992, Kelly et al. 2003, Gan et al. 2006, 2007, Kwacz 2013). In this study, we obtained a value for the AL elastic modulus of approximately 1.1 MPa. This value is much higher than the value of 0.01 MPa obtained by Lynch et al. (1982) and lower than the value of 5.5 MPa estimated by Gan et al. (2007). Presumably, the enormous discrepancy between the values given by individual researchers reflects, at least in part, the differences among the models used to make the estimates, which are useful only in the context of their own models.

Spring Constant of the AL of the Human Stapes

Our measurement results indicate that the AL is a linear elastic material, at least up to static deflections of 100 nm. A similar conclusion was reported by Lynch et al. (1982) for stimuli up to 140 dB SPL. Other measurements of stapes motion (Guinan and Peake 1967; Goode et al. 1994) suggest that stapes motions as large as 1 μm are still within the linear regime. The individual lines in Figure 6A, B seem to belong to two different families, one with a slope similar to the average slope and another with a steeper slope. This may be related to the inhomogeneous stiffness distribution of the AL around the SF (Lauxmann et al. 2014), caused by variation in both the AL thickness and the gap width between the SF and the OW. Near point 1 (Fig. 4, Table 1), the elastic fibers of the AL are significantly shorter than those near point 2. Moreover, the AL thickness near point 1 is almost twice as large as the thickness near point 2. This is consistent with the literature (Hagr et al. 2004; Ohashi et al. 2006; Sim et al. 2013). Such an anatomical structure leads to a higher AL stiffness at the SF posterior edge (point 1) than at the anterior edge (point 2). This causes a force applied to the stapes head to induce not only piston-like movement of the SF, but also rotations about its short and long axes (Huber et al. 2008; Sim et al. 2010, Eiber et al. 2012). It may be expected that the SF rotation affects the value of the force recorded by the AFM (Fig. 4). Since the rotation angle depends on the location of the measurement point, the individual F-w curves (Fig. 6) could have different slopes.

We measured a AL spring constant of approximately 120 N/m for SF displacements from 0 to 100 nm, comparable to the range of displacements observed during stapes vibration in normal human ears. Because of measurement difficulties, the AL stiffness in the range below 100 nm has never been reported in the literature.

Cancura (1979) described static measurements of the AL stiffness in nine human temporal bone preparations. He showed that the force-displacement characteristic is linear in the 5–20 mN range with an average stiffness of about 250 N/m. However, the smallest force (5 mN) used by Cancura induces displacements of 20–40 μm (see Cancura 1979, Fig. 5), which is about 200–400 times larger than the largest displacement that we used. This may cause the difference between the AL stiffnesses reported by Cancura and by us.

Lynch et al. (1982) reported dynamic measurements in anesthetized cats with the Mössbauer method. The AL stiffness derived from their data is 430 N/m. This value is about 3.5 times higher than the AL stiffness resulting from our measurement. However, the differences in anatomy between the cat and human ears may explain the difference in the obtained values.

Gan et al. (2011) described measurements in nine fresh human specimens. They applied the load to the stapes head using a 10-N load cell. In their measurement, a preload of 1 mN was used and then the load cell was moved to the maximum displacement of 0.2 mm. They used a constant displacement rate of 2.0 μm/s. Based on the stress–strain relationship (Gan et al. 2011, Fig. 7b, mean value), the AL displacement of 70 μm (recalculated for the shear strain of 1) corresponds to the loading force of 17.5 mN. The AL stiffness derived from this data is 250 N/m, which is about 2 times higher than the value determined in our study. However, both the displacement and the displacement rate are significantly higher than those used in our AFM measurement.

Recently, the AL stiffness in a human temporal bone was reported by Lauxmann et al. (2014). They applied a force from 1 to 50 mN at different points on the SF and measured the induced SF displacement using a laser Doppler vibrometer (LDV). Based on the force-displacement curve (Lauxmann et al. 2014, Fig. 11, green line), the AL stiffness determined from the slope of the curve is 1050 N/m. This value is much higher than the stiffness of 120 N/m obtained in our measurements. A reason for this discrepancy may be differences in measurement procedures. In Lauxmann’s measurement, the force is applied at the center of the SF and an initial force of 1 mN is used at the starting position. In our measurement, the force is applied at the stapes head and it does not exceed the value of 20 μN (Fig. 6). For forces below 20 μN, a lower stiffness may be expected than for forces above 1000 μN. Lauxmann et al. (2014) measured the spatial displacement of the stapes head using a LDV, which required velocities above 0.5 μm/s. The loading velocity in our study (0.1 μm/s) is significantly lower. This may also contribute to the lower value of AL stiffness obtained in our measurement.

The AL spring constant (∼120 N/m) reported here, obtained for small displacements using AFM, is intended to be used in numerical (FE) models of the human middle ear mechanics and to design a suitable membrane for our new chamber stapes prosthesis (Kwacz et al. 2014).

Abbreviations

A, b, h

Dimensions of the annular ligament circular plate (outer radius, inner radius, and thickness, respectively)

AFM

Atomic force microscope

AL

Annular ligament

defl_c

Deflection of the cantilever

E

Elastic (Young’s) modulus of the annular ligament of the human stapes

F

Force acting between the sample and the tip

F-d

Force-distance curve

FE

Finite element

K

Deflection sensitivity factor

k_c

Real spring constant (stiffness) of the cantilever

k_{c_nom}

Nominal spring constant of the cantilever

k_ref

Spring constant of the reference cantilever

L_OW, W_OW

Length and width of the oval window

L_SF, W_SF

Length and width of the stapes footplate

ν

The Poisson’s ratio

SF

Stapes footplate

SPL

Sound pressure level

SVJ

Stapedio-vestibular joint

V

Voltage of the photodiode

V_rigid

Voltage of the photodiode for the rigid sample

w

Deflection of the annular ligament plate

z

Displacement of the piezoactuator

z_AL

Displacement of the piezoactuator on the AL sample

z_rigid

Displacement of the piezoactuator on the rigid sample