COMMUNICATING THE PARAMETER UNCERTAINTY IN THE IQWIG EFFICIENCY FRONTIER TO DECISION-MAKERS

Abstract

The Institute for Quality and Efficiency in Health Care (IQWiG) developed—in a consultation process with an international expert panel—the efficiency frontier (EF) approach to satisfy a range of legal requirements for economic evaluation in Germany's statutory health insurance system. The EF approach is distinctly different from other health economic approaches. Here, we evaluate established tools for assessing and communicating parameter uncertainty in terms of their applicability to the EF approach. Among these are tools that perform the following: (i) graphically display overall uncertainty within the IQWiG EF (scatter plots, confidence bands, and contour plots) and (ii) communicate the uncertainty around the reimbursable price. We found that, within the EF approach, most established plots were not always easy to interpret. Hence, we propose the use of price reimbursement acceptability curves—a modification of the well-known cost-effectiveness acceptability curves. Furthermore, it emerges that the net monetary benefit allows an intuitive interpretation of parameter uncertainty within the EF approach. This research closes a gap for handling uncertainty in the economic evaluation approach of the IQWiG methods when using the EF. However, the precise consequences of uncertainty when determining prices are yet to be defined. © 2014 The Authors. Health Economics published by John Wiley & Sons Ltd.

1. Introduction

Health economic evaluation was explicitly introduced to the German Statutory Health Insurance (SHI) system by the 2007 SHI Competition Reinforcement Act. It required that health economic evaluations should be conducted to set a maximum reimbursable price for pharmaceuticals. Effectively, the SHI—covering ∼90% of the German population—would not have to reimburse an amount greater than the maximum reimbursable price for a new drug. To ensure that the economic evaluation methods conform to a range of legal requirements and constraints—chief among them: no rationing across indication areas—the German Institute for Quality and Efficiency in Health Care (‘Institut für Qualität und Wirtschaftlichkeit im Gesundheitswesen’, IQWiG) developed—in a consultation process with an international expert panel—the efficiency frontier (EF) approach (IQWiG, ²⁰⁰⁹; Caro et al., ²⁰¹⁰). Currently, the EF approach is applied in all ongoing IQWiG health economic reports. Furthermore, a recent act (‘Arzneimittelmarktneuordnungsgesetz’—came into effect in 2011) stipulates that, henceforth, either a manufacturer or the SHI umbrella organization may request the Federal Joint Committee (‘Gemeinsamer Bundesausschuss’)—the highest decision-making body of the joint self-government of physicians, dentists, hospitals, and SHI funds in Germany—to commission IQWiG to undertake a health economic evaluation. Such an evaluation must deliver evidence to establish an appropriate reimbursable price, given a drug's additional benefit or reduced harm.

The EF approach is distinctly different from other health economic approaches (Brouwer and Rutten, 2010). So far, it is unclear how to communicate parameter uncertainty that is inherent to every health economic evaluation within the EF approach to decision-makers. Therefore, the purpose of this report is to evaluate established tools that are used to communicate the results of a probabilistic sensitivity analysis (PSA) in terms of their applicability to the EF approach with the help of a simulation. Among these are tools that perform the following:(i) graphically display overall uncertainty within the IQWiG EF (scatter plots, confidence bands, and contour plots) and (ii) communicate the uncertainty around the reimbursable price. For the latter, we develop a price acceptability curve, which is a modification of the well-known cost-effectiveness acceptability curve (CEAC). Furthermore, it emerges that the net monetary benefit (NMB) allows an intuitive interpretation of parameter uncertainty within the EF approach.

Given the scope of this paper, we do not consider uncertainty with respect to the heterogeneity between (or across) individual patients or structural uncertainty.

2. Background: The Efficiency Frontier Approach

The EF approach (Figure1) aims to provide evidence on an appropriate reimbursable price for treatment strategies in Germany. Appropriate—as defined in the legal framework of Social Code Book V—means as compared with other treatment strategies within the same indication area. To construct an EF, all relevant treatment strategies within one indication are plotted on a plane, with costs on the horizontal and health effects on the vertical axes. All treatment strategies that are not subject to simple or extended dominance are connected in ascending order of effectiveness (IQWiG, ²⁰⁰⁹). The resulting curve consists solely of efficient strategies. For a new treatment strategy under assessment, a reimbursable price must be set such that the associated costs and effect(s) lie on the linearly extrapolated last segment of the EF. The line extrapolated beyond the last segment of an EF uses the same trade-off rate for costs and health effects as for the current most effective technology relative to the second most effective efficient strategy (dashed line in Figure1). Hence, an increase in effectiveness is valued by using an observed indication-specific trade-off between costs and effects.

Figure 1.

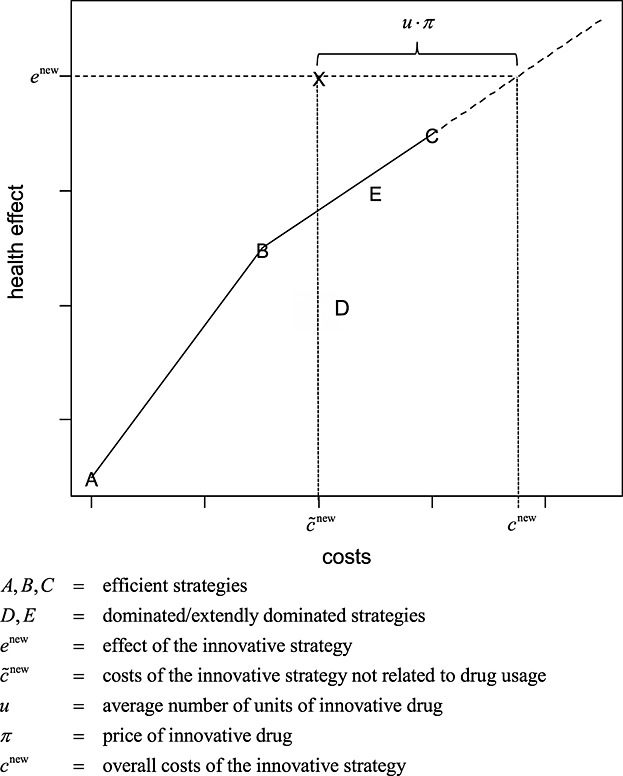
Illustration of the IQWiG efficiency frontier approach. The efficient strategies A, B, and C define the shape of the efficieny frontier. The dashed line is the extension of the last segment of the efficiency frontier (B to C). The horizontal distance between the new innovative strategy and dashed line can be interpreted as the net monetary benefit

When calculating the reimbursable price for a new drug, it is important to distinguish between two cost components: costs that are affected by the drug price and costs not affected by the drug price. Let π be the price of the new drug, and let u be the expected number of drug units needed for treatment. For example, more than one drug application may be needed to cure a patient, and the number of applications may vary across patients; thus, u ⋅ π denotes the average costs defined by the drug price. Let furthermore denote the costs of the new drug not related to the drug price; the overall costs c^new of the new treatment strategy can be calculated as follows:

If e^new denotes the health effect associated with the new treatment strategy and denotes the corresponding cost as indicated by the (extrapolated) EF, the reimbursable price can be calculated as follows:

If the price π differs from π^max, the NMB can be calculated as follows:

Thus, if π = π^max, then NMB = 0.

In essence, the EF approach aids policy makers with two crucial tasks: (i) By determining the trade-off between costs and health effects indicated by the last segment of the EF (Figure1), the policy makers identify the existing implicit threshold within an indication and (ii) estimating a reimbursable price for a new drug by relating this new treatment strategy to already existing treatment strategies.

However, such estimates are subject to parameter uncertainty regarding the input variables, that is, all drug and non-drug costs and health outcomes. This uncertainty should be communicated to decision-makers. Notably, the costs do not necessarily correspond to the drug price of the treatment strategies alone, but they also incorporate use of accompanying services and, depending on the perspective, indirect costs (i.e. costs as a result of productivity loss (Gold et al., ¹⁹⁹⁶)).

To adequately represent uncertainty within the EF approach, two distinctive yet simultaneously occurring aspects of uncertainty must be accounted for in each run of a PSA: First, the new treatment strategy may vary its position on the cost-effectiveness plane, and second, all other treatment strategies may vary their position on the cost-effectiveness plane as well. Because of the latter, the EF varies its shape, and crucially, the trade-off between costs and effects as indicated by the last segment of the EF may vary between each run of the PSA.

3. Simulation Study

To illustrate parameter uncertainty within the EF approach, we performed a Monte Carlo simulation. This simulation corresponds to a PSA in accordance with the approach of Barton et al. (2008); however, we kept the model assumptions to a minimum. Let k denote the number of strategies already available on the market. For our simulation study, we assumed the EF to be based on k = five strategies: three that build the EF, one strictly dominated strategy and one extendedly dominated strategy. However, because of the Monte Carlo simulation process, there has been some random variation, that is, which strategies were dominated and which lay on the EF in each run. A sixth strategy corresponds to the new treatment strategy.

Let e_i, i = 1, …, k, be the health effect of the ith strategy already available on the market, and let c_i be the associated costs. As is common in economic evaluations, the costs and the effects among strategies are correlated; we modelled the joint distribution using the multivariate normal distribution. However, as the costs of the new treatment strategy depend on the price of the new drug, while at the same time this price needs to be determined in that same PSA run, both 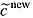and u were modelled in place of c^new.

We define y as the vector of health effects and costs of the comparators, non-drug-price-related costs of the new drug and the number of packages of the new drug (for definitions refer to the preceding texts):

and assume

Regarding μ and Σ, we assume

with corresponding standard errors:

Furthermore, we set the correlation matrix P to

This results in the following covariance matrix:

The values of the correlation matrix P were chosen for the following reasons: First, the health effect across the interventions, in general, is positively correlated. This is because of common causal factors, such as common complementing treatment methods, common background mortality and so on. For simplicity, we chose only one value (i.e. 0.7) that represents the correlation across the health effect of all interventions. Second, costs are, in general, positively associated across interventions, as there is a strong overlap of resource use among strategies. Again, for simplicity, we chose the common value 0.8 for these costs. Third, for a given strategy, the health effects and the costs are, in general, correlated. This correlation may be either positive or negative. A positive correlation would be, for example, because of additional resource consumption in life years gained; a negative correlation would be, for example, because of less resource consumption in cured subjects. We decided to choose a negative value (i.e. −0.7), for reasons of visual clarity when displaying the scatter plot. However, note that this is an arbitrary choice. Finally, the correlation between costs and effects of alternative strategies had to be defined. Because of the already specified correlations described previously, the choice of these values has been limited. For example, as costs across interventions were positively correlated, effects across interventions were also positively correlated, but costs and effects within one intervention were negatively correlated; hence, the correlation between costs and effects of alternative strategies had to be negative as well. Furthermore, the numerical values selected previously restricted the choice of values of the correlation between costs and effects of alternative strategies. Otherwise, the Cholesky decomposition of the covariance matrix would not be defined, which has to be determined within the process of simulating multivariate normally distributed values (Briggs et al., ²⁰⁰⁶; Stollenwerk et al., ²⁰¹⁰). Thus, we chose the value −0.6, which was consistent with the previously chosen values.

The number of runs used for PSA was 1000. For each run of the PSA, the EF approach was applied.

3.1. Displaying uncertainty on the cost-effectiveness plane

The shape of the EF can be highly sensitive to parameter uncertainty. Traditional scatter plots are not suitable to display the uncertainty of the shape of an EF (Figure2, illustration based on the simulation study), as they do not yield information about which dots belong to the common runs of the PSA. This problem can be overcome via confidence bands (Figure3) or contour plots (Figure4). Confidence bands can be constructed pointwise (Appendix). However, these are only defined over the range for which all PSA-based EFs are also defined. Contour plots, instead, are defined over the whole cost-effectiveness plane (refer to Appendix on construction of contour plots). Even though contour plots may appear to display the uncertainty about the shape of the EF reasonably well, neither contour plots nor confidence bands give information about the uncertainty of the reimbursable price, which—as explained above—is the intended output of the EF approach.

Figure 2.

Scatter plot of strategies on the cost-effectiveness plane, based on probabilistic sensitivity analysis

Figure 3.

Pointwise 95% confidence band of efficiency frontier for given costs; the pointwise confidence band is only defined over the range for which all efficiency frontiers are defined

Figure 4.

Contour plot of efficiency frontier; the grid was defined as 10 evenly spaced threshold values ranging from the minimum to the maximum of the simulated values for each axis (refer to Appendix for details)

3.2. Expressing uncertainty around the reimbursable price

Confidence intervals are problematic when applied to incremental cost-effectiveness ratios, as costs and effects can fall into more than one quadrant for the cost-effectiveness plane (Briggs, 2001; Briggs et al., ²⁰⁰⁶). CEACs were developed in response to these problems and provide an elegant solution. These report, for a range of willingness-to-pay threshold values, the probability that the intervention's cost-effectiveness is acceptable. This, however, only relates whether the incremental effects justify the incremental costs in a yes-or-no decision for a given threshold.

We introduce price acceptability curves (PACs). They are analogous to the CEAC; however, the horizontal axis here refers to the price of the new drug. The vertical axis still corresponds to the probability that the innovative strategy is ‘cost effective’. Thus, for each price, it is counted, which percentage of the simulated maximum reimbursable prices is above or on the EF (Figure5).

Figure 5.

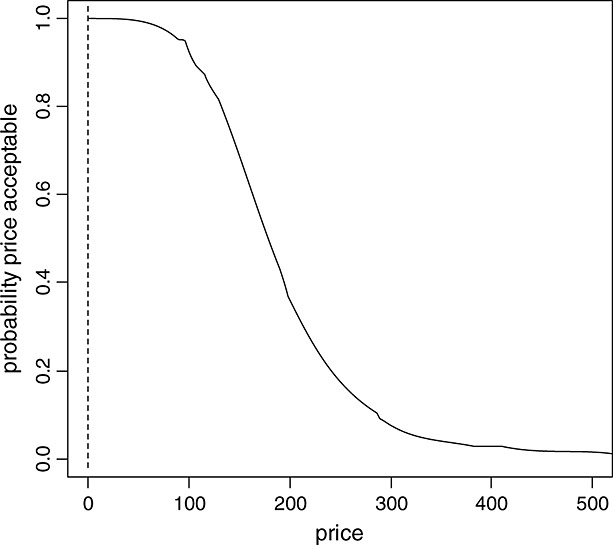
Price acceptability curve based on the IQWiG efficiency frontier approach

Price acceptability curves can be constructed as follows: Within each run of the PSA, the EF approach is applied and the threshold, as determined by the last segment of the EF, is identified. This yields a reimbursable price for each run. Now, for every possible price (x-axis), the PAC illustrates the percentage of the simulation runs where the reimbursable price is equal or below a maximum reimbursable price, that is, the price on the x-axis.

Another way of displaying the uncertainty around the reimbursable price in the context of the EF is using the NMB framework. Within the EF, the NMB has an intuitive graphical interpretation. As can be seen in Figure1, the NMB is the horizontal distance between the new treatment strategy and the last segment of the EF. The distance indicates by how much the price must be increased or lowered to be positioned on the EF. The NMBs for each run of the PSA can be calculated and ordered according to the size of NMB from the highest negative to highest positive values. The NMB can be plotted as a function of the price (Figure6). The vertical axis shows the price π, and the horizontal axis shows, for a given price, the expected NMB over all PSA results. Additionally, the confidence intervals or percentiles of the NMB distribution can be added, yielding a corridor expressing the uncertainty for the decision-maker. Without loss of generality, using the NHB instead of the NMB yields identical conclusions. In this case, the horizontal distance between the new treatment strategy and EF is calculated.

Figure 6.

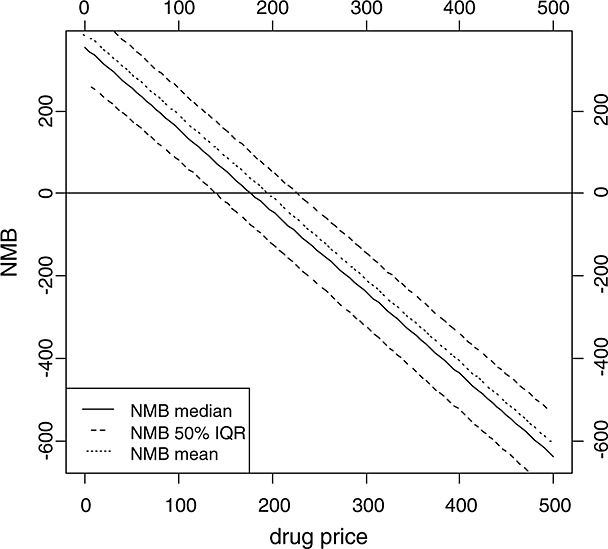
Net monetary benefit based on the IQWiG efficiency frontier approach

4. Discussion

In this paper, we evaluated tools used for the assessment and visual communication of parameter uncertainty in the EF approach. We have discussed scatter plots, confidence bands, and contour plots to display overall parameter uncertainty and developed the PAC, that is, a modification of the CEAC. Furthermore, we presented an approach of displaying the NMB, which has an intuitive interpretation when using the EF approach, as a function of the price.

The dual aim of the EF—(i) establishing the threshold for a given indication and (ii) deriving a recommendation for the reimbursable price of a new treatment strategy—poses a challenge to the traditionally used approaches that build upon a fixed threshold. Therefore, a new aspect of our research question is that the threshold may be regarded as probabilistic and that a probability distribution of a maximum reimbursable price can be derived. This may be relevant also for the non-German context and for approaches where the threshold is estimated based on methods other than the EF approach. For example, in the literature, it has previously been discussed to estimate the threshold as willingness to pay based on population surveys (Hirth et al., ²⁰⁰⁰; Ryan et al., ²⁰⁰⁴). However, also these estimates would be uncertain and should be varied within PSA. Furthermore, given the current debate around value-based pricing, the goal of health economic evaluation might not be a yes-or-no reimbursement decision any longer but rather a price estimate for the new drug. Moreover, uncertainty around such a price estimate needs to be made transparent for decision-makers, that is, to know how wide the corridor of a reliable and valid price estimate could be.

Nevertheless, depicting uncertainty in the aforementioned way entails further open questions: (i) How should the reported uncertainty be interpreted and used to guide decision-making regarding a reimbursable price and (ii) on which percentile would one deliver a reasonable interval or corridor?

(i) One option would be to neglect parameter uncertainty when determining a reimbursable price by sticking to the point estimate of the base case analysis. However, some decision-makers might be tempted to apply uncertainty intervals around the reimbursable price in a similar way as confidence intervals when performing statistical tests. In a simple case, one would assume a symmetric distribution of the price with a two-sided hypothesis. At a 5% ‘significance level’, either the 2.5th or the 97.5th percentile could be applied. A very conservative approach would be to require that the 2.5th percentile would have to be at least on or above the EF. In this scenario, the manufacturer of a new drug would be punished given a high level of uncertainty. Should the decision-maker regard a price as appropriate, if the NHB is not ‘significantly’ below zero, this would be much laxer for the manufacturer. Based on this rationale, the 97.5th percentile of all simulated reimbursable price estimates would serve as the reimbursable price. Thus, manufacturers would, in contrast to the first approach, be rewarded for parameter uncertainty. Given that distributions do not necessarily have to be symmetric, this approach would not be feasible.

(ii) The originally published IQWiG concept did not reflect the depiction of uncertainty when determining a reimbursable price (IQWiG, ²⁰⁰⁹). As the law stipulates that an appropriate price—in relation to other treatment strategies—must be set, one could say that the traditional 95% confidence interval would not serve this purpose. Therefore, IQWiG proposed to additionally display the 25% and 75% percentile, that is, interquartile range, as a reasonable ‘corridor of uncertainty’ and acceptable for both stakeholders, SHI funds and pharmaceutical manufacturers. As the width of the corridor/interval could heavily influence the decision to be taken, it needs to be chosen carefully. At present, we suggest that both questions need to be thoroughly debated by decision-makers and health economic experts in order to identify an answer.

Another conclusion that could be drawn from high uncertainty is that better evidence needs to be generated. However, the PACs report no information regarding to what extent each parameter is responsible for the resulting uncertainty. The contribution of each model parameter to the overall uncertainty could, for example, be detected via analysis of covariance (ANCOVA) (Briggs et al., ²⁰⁰⁶). The ANCOVA approach assumes a linear relationship between the parameter and the target variable (here, the price). Another approach for assessing the value of further data collection is based on estimating the contribution of each parameter to the expected value of perfect information (Claxton, 1999).

While we focused on quantifying and depicting parameter uncertainty when determining a reimbursable price with the IQWiG EF approach, we, the authors, are aware that there is an ongoing debate on the implications of the IQWiG EF approach (Schwarzbach et al., ²⁰⁰⁹; Dintsios and Gerber, ²⁰¹⁰; Greiner et al., ²⁰¹⁰; Sculpher and Claxton, ²⁰¹⁰; Gandjour, ²⁰¹¹). Nevertheless, this was not the subject of this paper and hence has not been addressed.

5. Conclusion

In conclusion, we derived a method of presenting the degree of parameter uncertainty on the reimbursable price within the EF approach. By doing so, we closed a gap within the EF approach. Furthermore, our research may be useful to present the uncertainty of the appropriate reimbursable price, if concepts other than the EF approach are applied to define or estimate the threshold. This may also be helpful outside the German context, as future decisions may more frequently not be simple dichotomous yes-or-no reimbursement decisions but decisions based on a recommended price for a given benefit. However, further research regarding the EF approach and regarding how to determine reimbursable prices is needed.

Appendix

Pointwise confidence bands can be estimated based on the single EFs that result from PSA. For given costs, 95% confidence intervals can be derived by calculating the 2.5% and the 97.5% quantile of the corresponding health effect. For our illustration, we calculated 95% confidence intervals for a sequence of 10 uniquely spaced cost values. Confidence bands were approximated via piecewise linear interpolation.

To calculate contour plots, a grid has to be defined for both costs and the health effects. For each cell within this grid, the runs of the PSA and their crossings by the EF are counted. Each crossing is referred to as a hit. The share of hits is furthermore linked to the middle of one cell, and the general methodology of calculating contour plots is applied (Cleveland, 1993). This is done by creating approximate contours based on interpolating the points over the grid (Cleveland, 1993). In interpreting the contour plots, however, one has to keep in mind that the expected number of hits depends on the widths chosen for the grid: The finer the grid, the lower the expected number of hits. We defined the grid as 10 evenly spaced threshold values ranging from the minimum to the maximum of the simulated values for each axis.

Conflict of Interest

The authors declare that they have no conflict of interest.