Skip to main content
NCBI home page
NIHPA Author Manuscripts logoLink to NIHPA Author Manuscripts
. Author manuscript; available in PMC: 2016 Jan 7.
Published in final edited form as: Phys Med Biol. 2014 Dec 5;60(1):31–48. doi: 10.1088/0031-9155/60/1/31

Anatomy assisted PET image reconstruction incorporating multi-resolution joint entropy

Jing Tang 1, Arman Rahmim 2
PMCID: PMC4489716  NIHMSID: NIHMS647869  PMID: 25479422

Abstract

A promising approach in PET image reconstruction is to incorporate high resolution anatomical information (measured from MR or CT) taking the anato-functional similarity measures such as mutual information or joint entropy (JE) as the prior. These similarity measures only classify voxels based on intensity values, while neglecting structural spatial information. In this work, we developed an anatomy-assisted maximum a posteriori (MAP) reconstruction algorithm wherein the JE measure is supplied by spatial information generated using wavelet multi-resolution analysis. The proposed wavelet-based JE (WJE) MAP algorithm involves calculation of derivatives of the subband JE measures with respect to individual PET image voxel intensities, which we have shown can be computed very similarly to how the inverse wavelet transform is implemented. We performed a simulation study with the BrainWeb phantom creating PET data corresponding to different noise levels. Realistically simulated T1-weighted MR images provided by BrainWeb modeling were applied in the anatomy-assisted reconstruction with the WJE-MAP algorithm and the intensity-only JE-MAP algorithm. Quantitative analysis showed that the WJE-MAP algorithm performed similarly to the JE-MAP algorithm at low noise level in the gray matter (GM) and white matter (WM) regions in terms of noise versus bias tradeoff. When noise increased to medium level in the simulated data, the WJE-MAP algorithm started to surpass the JE-MAP algorithm in the GM region, which is less uniform with smaller isolated structures compared to the WM region. In the high noise level simulation, the WJE-MAP algorithm presented clear improvement over the JE-MAP algorithm in both the GM and WM regions. In addition to the simulation study, we applied the reconstruction algorithms to real patient studies involving DPA-173 PET data and Florbetapir PET data with corresponding T1-MPRAGE MRI images. Compared to the intensity-only JE-MAP algorithm, the WJE-MAP algorithm resulted in comparable regional mean values to those from the maximum likelihood algorithm while reducing noise. Achieving robust performance in various noise-level simulation and patient studies, the WJE-MAP algorithm demonstrates its potential in clinical quantitative PET imaging.

1. Introduction

Positron emission tomography (PET) imaging is one of the most sensitive molecular imaging procedures to quantitatively measure functional processes of human or animal bodies. Having well demonstrated its value in clinical diagnostics and preclinical studies, PET imaging still faces intrinsic challenges. The resolution of PET images is limited by physical degrading factors, which result in undesired cross contamination between adjacent functional regions (Soret et al 2007, Rahmim and Zaidi 2008). Meanwhile, the images are inherently noisy due to limitations imposed by the amount of activity that can be injected and the scan duration. To alleviate the activity spread-out and spill-over in PET images, techniques have been developed to correct for the partial volume effect, through post reconstruction image reconstruction, or during image reconstruction with resolution modeling or incorporation of anatomical priors (Rousset et al 2007, Erlandsson et al 2012, Rahmim et al 2013). It is very difficult for post-reconstruction deconvolution-based techniques to control noise while achieving full resolution recovery, although promising enhancements were noted involving iterative deconvolution with regularization (Kirov et al 2008) and denoising (Boussion et al 2009, Le Pogam et al 2011). Reconstruction-based resolution recovery method (Reader et al 2003) was found to outperform the image-based deconvolution methods (Teo et al 2007, Tohka and Reilhac 2008) in the precision of standardized update value estimation (Hoetjes et al 2010). In addition, techniques incorporating anatomical information in the process of emission image reconstruction (Nuyts et al 2005) have been demonstrated as having enhanced performance relative to postprocessing correction methods (Meltzer et al 1990, Muller-Gartner et al 1992) in terms of image noise versus bias and detection performance.

For anatomy-guided image reconstruction, the higher resolution anatomical information measured from CT or MR images is usually taken as a prior in the maximum a posteriori (MAP) algorithm (Gindi et al 1993, Bowsher et al 1996, Comtat et al 2002, Cheng-Liao and Qi 2011). Earlier studies used segmented anatomical images and encouraged boundaries in the functional image or smoothness within the anatomical regions (Lipinski et al 1997, Baete et al 2004). Recent techniques take the similarity measure between the anatomical and functional images to define the priors, which does not rely on segmentation or labeling of the anatomical images (Nuyts 2007, Tang and Rahmim 2009, Tang et al 2010, Somayajula et al 2011). For the purpose of partial volume correction of PET images, MR images are more favored than CT images as of the excellent soft-tissue contrast (Bai et al 2013). The process using anatomical images to guide functional image formation typically requires registration of the images from different image modalities (Woods et al 1993). The recent advent of integrated PET-MRI systems apparently brings more opportunities for this task and other forms of synergistic analysis by providing simultaneously taken anatomical and functional images, allowing easier spatial alignment with minimal error (Pichler et al 2010, Zaidi et al 2010).

Mutual information (MI) and its joint entropy (JE) term have been taken as the similarity measure to create priors for Bayesian PET image reconstruction techniques. MI measures the dependence of two random variables on each other. Before its adoption in image reconstruction it has been successfully applied to registration of images acquired from different imaging modalities (Pluim et al 2003). Both MI and JE of the image intensities are solely based on global distribution. For the purpose of image registration, methods have been proposed to form a hybrid metric to measure spatial information (SI) from the gradient of images and then combine it with MI (Pluim et al 2000). In image reconstruction with information theoretic priors, SI has been incorporated by adding features that capture the local variation in image intensities of blurred image and its Laplacian (Somayajula et al 2011). Xu and Chen (2007) proposed to apply a multi-resolution scheme to consider SI for image registration. This would involve generating a series of images of different resolutions and then calculating their corresponding gradient images. To avoid the two-step processing, they proposed a wavelet-based multi-resolution strategy so that the two steps are integrated into one.

We developed a closed-form MAP expectation-maximization (EM) PET image reconstruction algorithm incorporating the JE between functional and anatomical image intensities as a prior and demonstrated the superior performance of the JE-MAP algorithm compared to the conventional MAP algorithm with a ‘smoothness prior’ (Tang and Rahmim 2009, Green 1990). Inspired by the wavelet-based multi-resolution application in image registration mentioned above (Xu and Chen 2007), we propose to supply the JE measure with SI generated using wavelet analysis. This approach has the benefit of utilizing theoretical advantages of wavelets, including the ability to decompose an image of certain size into downsampled subbands, allowing concise representation of the image into individual wavelet-derived feature images while preserving original information. Using simulated and clinical brain imaging studies, we quantitatively evaluated the performance of proposed wavelet-based JE (WJE) MAP-EM technique. In particular, the reconstructed images from the proposed algorithm were compared with images from the intensity-only JE-MAP algorithm.

2. Methods

In this study, we propose to incorporate the JE between PET and MR feature images derived from wavelet analysis as the prior within the MAP PET image reconstruction algorithm. We describe the one-step-late (OSL) MAP EM algorithm first, then the generation of feature images through wavelet analysis, followed by the implementation of WJE-MAP algorithm.

2.1. MAP-EM reconstruction algorithm

In previous work (Tang and Rahmim 2009), we developed a one-step-late (OSL) MAP PET image reconstruction algorithm with the JE between anato-functional image intensities as the prior. The MAP estimate of the functional image X from the emission data g is given by

X^=arg maxX≥0P(g|X)P(X)P(g), (1)

where P() indicates the probability of the variable enclosed in parentheses. The prior on the image is assumed to follow a Gibbs distribution

P(X)=1Wexp(−βV(X)), (2)

where W is a normalization factor and βV (X) is the weighted potential function, which has been conventionally used to penalize the inter-voxel intensity variations in the reconstructed image. In the JE-MAP algorithm, the JE H(X, Y) between the PET image X and MR image Y was applied to serve as the potential function. To introduce the WJE-MAP algorithm, let us denote the kth (k = 1, …, K) wavelet analysis generated feature image pair of the PET image and the MR image by {fk(X), fk(Y)}. Instead of the intensity-only JE term, the potential function to apply is the weighted sum of the JE of feature image pairs represented by ∑k=1KβkH(fk(X),fk(Y)), where βk denotes the weighting hyperparameter for a given kth wavelet subband image pair.

For the WJE-MAP algorithm, the image reconstruction process is to seek for the image estimation X^ that maximizes the log-posterior probability

logP(g|X)−∑k=1KβkH(fk(X),fk(Y))+s, (3)

where the constant s represents the contribution of the W term in (2) and the denominator in (1). Modeling Poisson statistics for the first term in (3) and utilizing the OSL EM approach (Green 1990), we arrive at the iterative procedure

xinew=xiold∑jcij+∑k=1Kβk∂H(fk(X),fk(Y))∂xi|xi=xiold∑jcijgj∑icijxiold, (4)

where the new estimate of voxel i in image X is updated from the old estimate. The bin j of emission data g is represented by gj, and cij denotes an element of the system matrix modeling the contribution of voxel i to projection bin j.

2.2. Wavelet-based generation of feature images

We propose to use the subbands generated by wavelet analysis of PET and MR image pairs as feature images from which JEs are calculated. A three-dimension (3D) image can be decomposed into low frequency (L) and high frequency (H) components, via the approximation and detail wavelet filters in a particular direction. This approach can then be repeated along a second dimension, generating LL, LH, HL, HH, and finally performed along the third dimension to generate 8 image subbands (each 1/8 of total sizes, i.e. 1/2 size in each direction), as depicted in figure 1. In this work, we use the nearly symmetric orthogonal wavelet bases in Abdelnour and Selesnick (2001) to decompose the PET and MR image pairs.

Figure 1.

Figure 1

Open in a new tab

Transaxial slices of the 8 wavelet subbands of the phantom PET activity image.

The totality of the 8 subbands for each 3D image will have the same total size as the original image. It is then possible to utilize the entire information provided by some or all of the wavelet subbands for the JE computations. Similar to what was used in Xu and Chen (2007), we first considered the JE of approximation (LLL) and first order detail (HLL, LHL, LLH) wavelet subbands, the former integrating the similarity of image intensity features, and the latter group having features comparable to gradients (depicted in figure 2). After analyzing the results from the 4-subband WJE algorithm, we moved onto using the JE from all the 8 subbands as the potential function.

Figure 2.

Figure 2

Open in a new tab

The joint entropy calculation scheme with 4 wavelet subbands.

2.3. Calculation of JE derivative

Here we note that the proposed MAP-EM algorithm (4) involves calculation of the derivatives of the subband JE terms with respect to intensity of individual voxel in the original full PET image ∂H (fk(X), fk(Y)) /∂xi. We are able to show that this calculation can be performed from the derivatives of the subband JE terms with respect to the corresponding subband voxels similar to how wavelet synthesis is achieved. For simplicity, let us consider wavelet analysis along a particular dimension and denote the wavelet subband image k by X̃k ≜ fk(X), which is given by the convolution-downsampling operation

X˜k=⇓2{X⊗Wk}orx˜jk=∑uxuw2j−uk, (5)

where Wk is the wavelet analysis filter and the downsampling ⇓2 is reflected in the 2j index in the wavelet filter. Then we invoke the chain rule

∂H(X˜k,Y˜k)∂xi=∑l∂H(X˜k,Y˜k)∂x˜lk∂x˜lk∂xi. (6)

The first term on the right hand side, which is the derivate of subband image JE with respect to voxels in the PET subband image, may now be calculated exactly the same way as proposed in Tang and Rahmim (2009). In brief, the joint probability density for JE calculation is approximated by Parzen density estimate through superposition of Gaussian densities (Duda et al 2001).

Let’s refer the derivate to the (subband) PET image voxel from which the (subband) JE is generated as the SDJE (standard derivative of JE). From the definition of x̃j in (5), it follows that

∂H(X˜k,Y˜k)∂xi=∑lSDJEl(X˜k,Y˜k)w2l−ik. (7)

Thus once the SDJE images are calculated, the overall derivative can be derived from a ‘convolution-like’ calculation. Here one may notice an interesting parallel with the wavelet synthesis process: for a synthesis filter W¯k defined such that w¯m≜w−m and using the upsampling operation ⇑2 (inserting zeros between values at odd positions), it can be shown that

∂H(X˜k,Y˜k)∂xi=∑l[⇑2SDJEl(X˜k,Y˜)]lw¯i−lk. (8)

This now looks similar to how wavelet synthesis process is performed (i.e. upsampling each subband, followed by convolution with the synthesis filter). The only difference is that we first perform SDJE calculations on the wavelet-generated MR-PET subband pairs. Figure 3 shows the procedure explained above for calculating the derivatives of the subband JEs with respect to the original PET image voxel intensities.

Figure 3.

Figure 3

Open in a new tab

Diagram for calculating derivative of subband joint entropy (JE) with respect to the full PET image voxel intensities, DWT: discrete wavelet transform.

3. Experiments and Evaluation

3.1. Phantom simulation

We performed simulation study using the BrainWeb phantom (Collins et al 1998). An anatomical model from the BrainWeb database was used to create PET activity and attenuation images. The model consists of a set of ‘fuzzy’ tissue membership classes include gray matter (GM), white matter (WM), cerebrospinal fluid (CSF) and other 8 membership volumes. A voxel value in a volume reflects the proportion of that tissue presented in that voxel. For the anatomical model, the BrainWeb provides simulated T1-weighted MR image for specified SPLASH parameters with (1 mm)3 voxels. The simulator uses first-principles modeling based on the Bloch equations to implement a discrete-event simulation of nuclear MR signal production, and realistically models noise and partial volume effects of image production process.

We created the PET distribution by assigning a clinically realistic activity of 12500 Bq ml−1 in GM, 3250 Bq ml−1 in WM, 0 Bq ml−1 in air, CSF and bone and 1000 Bq ml−1 in all other tissues including skin, muscle, connective tissue, and fat (Vunckx et al 2012). Attenuation coefficients were assigned as 0 cm−1 for air, 0.146 cm−1 for bone and 0.096 cm−1 for other tissues to build the attenuation map. The PET (and MR) image was interpolated to create voxel size of (1.22 mm)3 and image dimension of 256 × 256 × 207 for simulation in the geometry of the high resolution research tomograph (HRRT) (Sossi et al 2005). The simulated PET activity, attenuation and MR images (central transaxial slice) are shown in figure 4. Emission data corresponding to three noise levels were simulated, corresponding to a low-noise (10-min), medium-noise (5-min) and a high-noise (3-min) FDG PET measurement, with decay, normalization and attenuation effects taken into account. The three noise levels are ~1.8 times apart in terms of total counts. Image reconstruction was performed using the maximum likelihood (ML) algorithm (implemented using ordered-subset (OS) EM with 16 subsets in each iteration), the intensity-only JE-MAP algorithm and the WJE-MAP algorithm.

Figure 4.

Figure 4

Open in a new tab

Transaxial slices through the BrainWeb phantom simulating the (a) PET activity (Bq ml−1), (b) PET attenuation (cm−1) and (c) MRI images.

To quantitatively evaluate the images reconstructed from different algorithms, we used the tradeoffs between noise and bias on the GM and WM regions as the metrics. The GM (or WM) region was defined to include the voxels that more than 95 % belong to the GM (or WM) based on the fuzzy tissue class model. For each region of interest (ROI), the normalized mean squared error (NMSE) was calculated to measure bias

NMSE=(X¯−X¯trueX¯true)2, (9)

where X¯=1N∑i=1NXi; Xi denotes the ith voxel reconstructed activity value, and N is the number of voxels in the ROI. Similarly, X̄true is the regional mean value of the phantom activity image. For each ROI, the noise was measured using the normalized standard deviation (NSD) as calculated by

NSD=1N−1∑i=1N(Xi−X¯)X¯, (10)

where Xi and X̄ are defined as those in (9).

3.2. Clinical experiments

We applied the WJE and intensity-only JE MAP techniques to two PET imaging datasets (and corresponding MR images) with tracers for different diagnostic purposes. One set of PET data was acquired using the tracer [11C] DPA-173, which is a radioligand that binds to the translocator protein (TSPO) and serves as a marker of the neuroinflammatory burden (Endres et al 2009). The other tracer was [18F] Florbetapir, which is an FDA approved amyloid-beta imaging agent for clinical evaluation of late-life cognitive impairment in Alzheimer’s disease (Wong et al 2010). PET scans were performed on the second-generation Siemens HRRT (Sossi et al 2005), an LSO-based, 2.5 mm-resolution, dedicated brain PET scanner. The data was first reconstructed using the OS EM algorithm (10 iterations and 16 subsets), with correction for attenuation, normalization, deadtime, scatter and randoms (Rahmim et al 2005). The PET image space consisted of cubic voxels with sizes (1.22 mm)3, spanning dimensions of (31cm)2 transaxially and 25 cm axially. We studied the DPA-173 data with accumulation from 0 to 30 min post-injection while for the Florbetapir data we worked on data with two noise levels. The low noise level has data from 0 to 70 min and the higher noise level has duration time spanning 50–70 min. The structural MR images were created for the corresponding subjects using the T1-weighted MPRAGE sequence. Before MR assisted PET reconstruction was performed, the images were aligned to initially reconstructed PET images using an in-house software implementing rigid mutual-information registration.

To evaluate the performance of the proposed technique and compare it with other methods, we calculated the noise over the ROIs using (10). The ROIs were drawn using an in-house software on the MR image and applied to the registered reconstructed PET images. As the true intensity values of patient experiments are not available, we plotted the regional mean value versus the noise along with iterations on the specified ROIs of the reconstructed PET images.

4. Results

4.1. Simulation Results

As stated in section 2.2, we first applied the JEs of the approximation (LLL) and the first order detail (HLL, LHL, LLH) wavelet subbands in the reconstruction (figure 2). We were able to see improvement in the reconstructed image components made of the subbands involved in the prior formation (Tang and Rahmim 2009b). Therefore we moved on to use all the 8 subbands to form the prior. We show the results from using the all-subband prior here and leave the analysis of results from different combinations of subbands in the Discussion section.

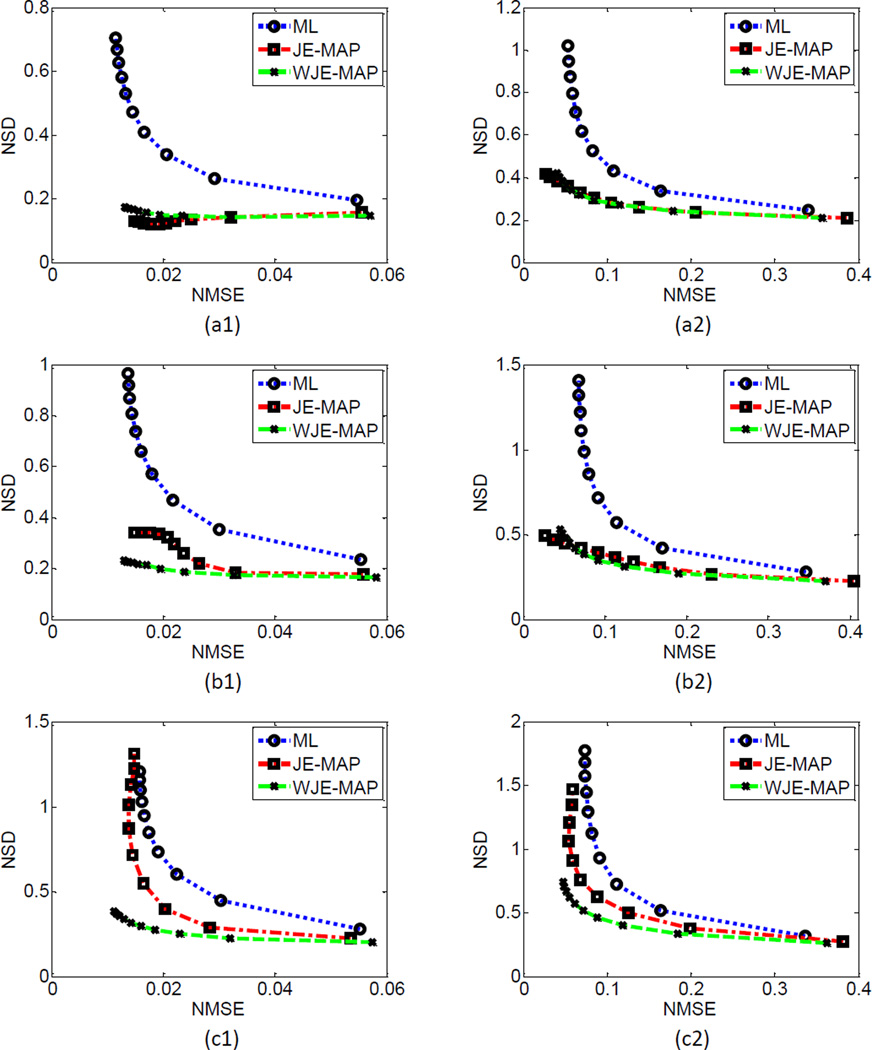
Besides the formation of the prior, the performance of a MAP reconstruction algorithm heavily depends on the weighting factor. We chose the weighting factors that result in similar end-iteration bias before comparing the NSD versus NMSE tradeoff from the MAP algorithms with the ML algorithm. Equal weights were used for the WJE subbands in this study. For the three cases at low-, medium-, and high-noise levels, the NSD versus the NMSE along with iteration number from the ML, JE-MAP, and WJE-MAP algorithms are plotted for GM and WM in figure 5, respectively. For the low-noise level simulation, both the JE-MAP and the WJE-MAP algorithms result in better noise versus bias performance than the ML algorithm, in both the GM (figure 5 (a1)) and the WM (figure 5 (a2)) regions. The results from the two MAP algorithms are close to comparable. In the medium-noise level case, the WJE-MAP algorithm and JE-MAP algorithm perform similarly in the WM region (figure 5 (b2)). The WJE-MAP algorithm demonstrates its advantage over the JE-MAP algorithm in the GM region (figure 5 (b1)) reaching lower noise level with comparable bias. In the high-noise level simulation, the performance of WJE-MAP algorithm clearly surpasses the JE-MAP algorithm in both the GM (figure 5 (c1)) and WM (figure 5 (c2)) regions in terms of noise versus bias tradeoff. The reconstructed images (center transaxial slice, 5th iteration) of the three noise-level simulations from different reconstruction algorithms are plotted in figure 6. The maximum gray level of the reconstructed images is set as twice of the maximum value in the phantom image, so that it is easier to compare the images from different reconstruction algorithms and from different noise levels.

Figure 5.

Figure 5

Open in a new tab

Regional noise (NSD) versus bias (NMSE) plots comparing the proposed WJE-MAP algorithm with the ML and JE-MAP algorithms: (a) 10 min data, (b) 5 min data and (c) 3 min data reconstruction; (1) GM and (2) WM, for the simulation study.

Figure 6.

Figure 6

Open in a new tab

Transaxial slices through the reconstructed images (in Bq ml−1) from (a) 10 min data, (b) 5 min data and (c) 3 min data reconstruction using the (1) ML, (2) JE-MAP and (3) WJE-MAP algorithms, for the simulation study.

4.2. Patient data results

4.2.1. DPA-173 results

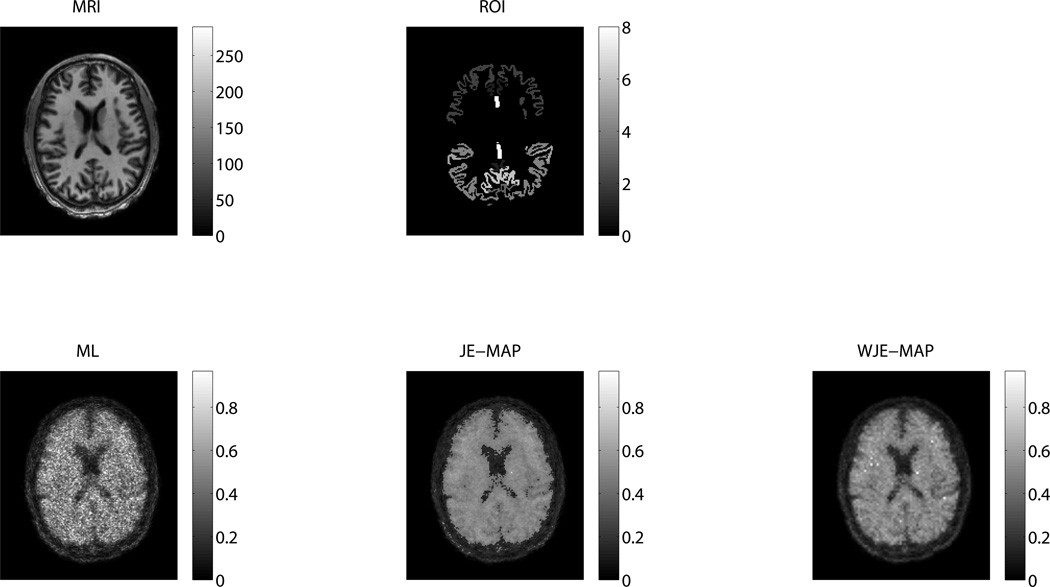
In figure 7, we plot the regional noise versus mean value along with iteration number for different ROIs in the DPA-173 patient images reconstructed from using the ML, JE-MAP, and WJE-MAP algorithms. In most of the regions, the WJE-MAP algorithm suppresses noise while arriving at mean regional values close to what ML algorithm achieves. Its improvement on noise versus bias tradeoff over the ML and also the JE-MAP algorithms is well demonstrated. The relative performance of the reconstruction algorithms in this patient study is similar to that in the high-noise simulation study. For visual comparison, figure 8 shows the transaxial center slice of the reconstructed images (10th iteration) using the different algorithms (together with the MR image used for the MAP reconstructions and the ROIs). The reconstructed images are shown with the same gray level limit for easy comparison.

Figure 7.

Figure 7

Open in a new tab

Regional noise (NSD) versus mean value (in counts) plots comparing the proposed WJE-MAP algorithm with the ML and JE-MAP algorithms, for the DPA-173 patient study.

Figure 8.

Figure 8

Open in a new tab

Transaxial slices through the MR image, the ROIs and the reconstructed PET images (in counts) using the ML, JE-MAP and WJE-MAP algorithms, for the DPA-173 patient study.

4.2.2. Florbetapir results

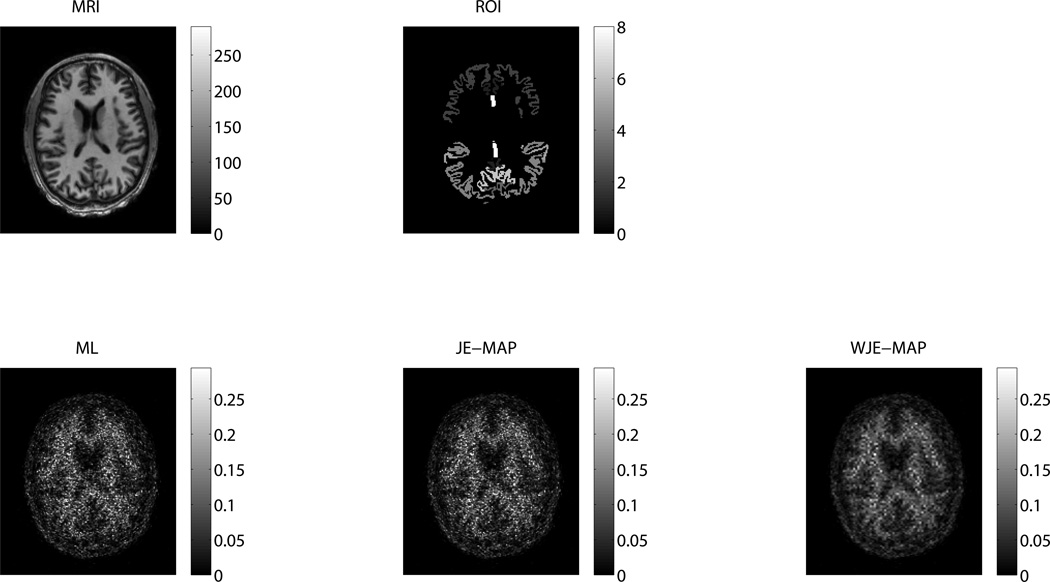
We plot the regional noise versus mean value along with iteration number for different ROIs reconstructed from the 0–70 min Florbetapir data using the ML, JE-MAP and WJE-MAP algorithms in figure 9. This result is comparable to the result from the low-noise simulation case, that is, the performance of the WJE-MAP and the JE-MAP algorithms are comparable (note the scale of the mean value is very small and the difference between the mean values from the two MAP algorithms is about ~ 2%.) The regional noise versus mean value along with iteration number plots for images reconstructed from the 50–70 min data are shown in figure 10. Similar to the results from high-noise simulation case, the WJE-algorithm demonstrates improvement over the ML and the JE-MAP algorithms on the noise versus bias tradeoff in this higher noise Florbetapir patient study. Figures 11 and 12 show the transaxial center slice of the reconstructed images (10th iteration) using the different algorithms (together with the MR image used for the MAP reconstruction and the ROIs). In each figure, the reconstructed images are shown with the same gray level limit for straightforward comparison.

Figure 9.

Figure 9

Open in a new tab

Regional noise (NSD) versus mean value (in counts) plots comparing the proposed WJE-MAP algorithm with the ML and JE-MAP algorithms, for the 0–70 min Florbetapir patient study.

Figure 10.

Figure 10

Open in a new tab

Regional noise (NSD) versus mean value (in counts) plots comparing the proposed WJE-MAP algorithm with the ML and JE-MAP algorithms, for the 50–70 min Florbetapir patient study.

Figure 11.

Figure 11

Open in a new tab

Transaxial slices through the MR image, the ROIs and the reconstructed PET images (in counts) using the ML, JE-MAP and WJE-MAP algorithms, for the 0–70 min Florbetapir patient study.

Figure 12.

Figure 12

Open in a new tab

Transaxial slices through the MR image, the ROIs and the reconstructed PET images (in counts) using the ML, JE-MAP and WJE-MAP algorithms, for the 50–70 min Florbetapir patient study.

5. Discussion

As mentioned in the WJE-MAP algorithm description (subsection 2.2), we first applied the prior with 4 (approximation and the first-order detail) wavelet subbands in the simulation study. This was the initial attempt based on the successful application of spatial information using the specific multi-resolution scheme on image registration (Xu and Chen 2007). Analysis of the reconstructed images demonstrated that the synthesis images composed of the subbands used for prior calculation have noteworthy improvement on noise versus bias tradeoff, compared to the counterpart reconstructed from the ML algorithm (Tang and Rahmim 2009b). To demonstrate the effect of subbands in the WJE-MAP algorithm, we present the NSD versus NMSE results from using the approximation (LLL) subband, from the 4 subbands (approximation and the first order detail), the 7 subbands (approximation, the first-order and the second-order detail), together with all-subband results at the high-noise level simulation in figure 13. Comparing the 4-subband results with that from the LLL subband which carries the low frequency spatial information, we are able to appreciate effect of the higher frequency spatial information added to the algorithm by the first-order detail subbands. Similarly, the effect of the second-order (HHL, LHH and HLH) and the third-order (HHH) detail subbands is demonstrated by comparing the 4-subband results with the 7-subband results and the 7-subband results with the all-subband results, respectively. In short, the effective performance of the WJE-MAP algorithm is contributed from all the wavelet subbands as noise is decomposed and worked on in all of them.

Figure 13.

Figure 13

Open in a new tab

Regional noise (NSD) versus bias (NMSE) plots comparing the proposed WJE-MAP algorithm with LLL subband, 4 subbands (LLL, HLL, LHL and LLH), 7 subbands (all except HHH) and all subbands incorporated in the prior formation, 3 min simulated data reconstruction of (a) GM and (b) WM for the simulation study.

In simulation using the realistic BrainWeb phantom, the WJE-MAP algorithm performs similarly in reconstructing data corresponding to the three noise levels, demonstrating robust improvement on reducing noise while preserving the bias. The intensity-only JE-MAP algorithm performs comparable in the low-noise case with the WJE-MAP algorithm. In the mid-noise case, the WJE-MAP and JE-MAP algorithms perform similarly in the WM region while the benefit of the WJE-MAP algorithm starts to appear in the GM region. It is noted that the WM region has relatively larger areas of voxels belonging to the same tissue class (figure 14 (b)). In contrast, the GM region has smaller isolated structures with varying tissue proportions present in the neighborhood areas (figure 14 (a)). In this case, the WJE-MAP framework can more effectively handle the presence of noise, given its accommodation of the contextual information. For the high-noise situation, the JE-MAP is more affected and misled by noise as it classifies the voxels solely based on intensity values. It may move the intensity values toward wrong peaks in the joint-histogram of the reconstructed PET and MR images (Tang et al 2010). (Further increasing the weighting factor on the prior introduces significant bias in both the GM and the WM regions compared to what are shown in figure 5 (c1) and (c2)). Through the detail comparison, the effect of involving multi-resolution spatial information in the MAP prior creation is clearly demonstrated in less uniform regions and more noisy images. In patient studies with the clinical PET and MR data, the WJE-MAP algorithm shows similar performance to that in the simulation, that is reducing noise and converging to similar values to those from the ML algorithm in both low and high noise situations.

Figure 14.

Figure 14

Open in a new tab

Transaxial slices through the (a) GM and (b) WM classes of the BrainWeb phantom. The color bar shows the proportion of a voxel that belongs to the tissue class.

The improved performance of the WJE-MAP algorithm in high noise data will be especially beneficial in parametric imaging studies where the acquisition time in each frame of the dynamic sequence is rather short. We developed a four-dimensional (4D) direct parametric image reconstruction algorithm and extended the JE-MAP reconstruction methodology within the 4D image reconstruction framework (Tang et al 2010). The potential of the WJE-MAP algorithm will be analyzed in future studies comparing the scheme of applying the anatomical prior to individual frame image reconstruction before the dynamic modeling analysis and that of applying the anatomical information in the direct parametric image reconstruction.

6. Summary

We developed a WJE-MAP algorithm to incorporate local spatial information through multi-resolution subbands in the MR anatomy assisted PET image reconstruction. To implement the idea, we took advantage of the inverse wavelet transform scheme to relate the derivative of subband JEs to the full PET image voxels intensities. Simulation studies with data at different noise levels and patient experiments with different tracers were carried out to evaluate the proposed algorithm and compare it with the intensity-only JE-MAP algorithm. When the simulated noise level was low, the WJE-MAP algorithm performed similarly to the JE-MAP algorithm in terms of noise versus bias tradeoff in both the GM and WM areas. As the noise level increased, the WJE-MAP algorithm showed its advantage over the JE-MAP algorithm in the GM region, which has less uniform activity and smaller isolated structures compared to the WM region. At the high noise level, the WJE-MAP algorithm surpassed the JE-MAP algorithm significantly in both the GM and WM areas. In conclusion, the WJE-MAP algorithm demonstrated robust performance at the various simulated noise levels and also in the patient studies with clinical MR and PET data. Specifically, it resulted in significantly reduced noise while maintaining bias or reconstructed mean values in high noise level data, demonstrating its potential for enhanced quantitative PET imaging.

Acknowledgments

This work was supported by the NSF grant ECCS 1228091 and the NIH grant 1S10RR023623. We wish to thank Dr A Kumar for delineation of ROIs based on co-registered MR images.

References

  1. Abdelnour AF, Selesnick IW. Design of 2-band orthogonal near-symmetric CQF. IEEE Intern. Conf. Acoust., Speech, Signal Processing. 2001;6:3693–3696. [Google Scholar]
  2. Baete K, Nuyts J, Van Paesschen W, Suetens P, Dupont P. Anatomical-based FDG-PET reconstruction for the detection of hypo-metabolic regions in epilepsy. IEEE Trans Med Imaging. 2004;23(4):510–519. doi: 10.1109/TMI.2004.825623. [DOI] [PubMed] [Google Scholar]
  3. Bai B, Li Q, Leahy RM. Magnetic resonance-guided positron emission tomography image reconstruction. Semin Nucl Med. 2013 Jan;43(1):30–44. doi: 10.1053/j.semnuclmed.2012.08.006. [DOI] [PMC free article] [PubMed] [Google Scholar]
  4. Boussion N, Cheze Le Rest C, Hatt M, Visvikis D. Incorporation of wavelet-based denoising in iterative deconvolution for partial volume correction in whole-body PET imaging. Eur J Nucl Med Mol Imaging. 2009;36(7):1064–1075. doi: 10.1007/s00259-009-1065-5. [DOI] [PubMed] [Google Scholar]
  5. Bowsher JE, Johnson VE, Turkington TG, Jaszczak RJ, Floyd CE, Jr, Coleman RE. Bayesian reconstruction and use of anatomical a priori information for emission tomography. IEEE Trans Med Imaging. 1996;15(5):673–686. doi: 10.1109/42.538945. [DOI] [PubMed] [Google Scholar]
  6. Collins DL, Zijdenbos AP, Kollokian V, Sled JE, Kabani NJ, Holmes CJ, Evans AC. Design and construction of a realistic digital brain phantom. IEEE Trans Med Imaging. 1998;17(3):463–468. doi: 10.1109/42.712135. [DOI] [PubMed] [Google Scholar]
  7. Comtat C, Kinahan PE, Fessler JA, Beyer T, Townsend DW, Defrise M, Michel C. Clinically feasible reconstruction of 3D whole-body PET/CT data using blurred anatomical labels. Phys. Med. Biol. 2002;47:1–20. doi: 10.1088/0031-9155/47/1/301. [DOI] [PubMed] [Google Scholar]
  8. Cheng-Liao J, Qi J. PET image reconstruction with anatomical edge guided level set prior. Phys Med Biol. 2011;56(21):6899–6918. doi: 10.1088/0031-9155/56/21/009. [DOI] [PMC free article] [PubMed] [Google Scholar]
  9. Duda RO, Hart PE, Stork DG. Pattern Classification. 2nd edn. New York: Wiley; 2001. [Google Scholar]
  10. Endres CJ, Pomper MG, James M, Uzuner O, Hammoud DA, Watkins CC, Reynolds A, Hilton J, Dannals RF, Kassiou M. Initial Evaluation of (11)C-DPA-713, a Novel TSPO PET Ligand, in Humans. J. Nucl. Med. 2009;50:1276–1282. doi: 10.2967/jnumed.109.062265. [DOI] [PMC free article] [PubMed] [Google Scholar]
  11. Erlandsson K, Buvat I, Pretorius PH, Thomas BA, Hutton BF. A review of partial volume correction techniques for emission tomography and their applications in neurology, cardiology and oncology. Phys. Med. Biol. 2012;57:R119–R159. doi: 10.1088/0031-9155/57/21/R119. [DOI] [PubMed] [Google Scholar]
  12. Gindi G, Lee M, Rangarajan A, Zubal IG. Bayesian reconstruction of functional images using anatomical information as priors. IEEE Trans Med Imaging. 1993;12(4):670–680. doi: 10.1109/42.251117. [DOI] [PubMed] [Google Scholar]
  13. Green PJ. Bayesian reconstructions from emission tomography data using a modified EM algorithm. IEEE Trans Med Imaging. 1990;9(1):84–93. doi: 10.1109/42.52985. [DOI] [PubMed] [Google Scholar]
  14. Hoetjes NJ, van Velden FH, Hoekstra OS, Hoekstra CJ, Krak NC, Lammertsma AA, Boellaard R. Partial volume correction strategies for quantitative FDG PET in oncology. Eur. J. Nucl. Med. Mol. Imaging. 2010;37:1679–1687. doi: 10.1007/s00259-010-1472-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
  15. Kirov AS, Piao JZ, Schmidtlein CR. Partial volume effect correction in PET using regularized iterative deconvolution with variance control based on local topology. Phys Med Biol. 2008;53(10):2577–2591. doi: 10.1088/0031-9155/53/10/009. [DOI] [PubMed] [Google Scholar]
  16. Le Pogam A, Hatt M, Descourt P, Boussion N, Tsoumpas C, Turkheimer FE, Prunier-Aesch C, Baulieu JL, Guilloteau D, Visvikis D. Evaluation of a 3D local multiresolution algorithm for the correction of partial volume effects in positron emission tomography. Med. Phys. 2011;38:4920–4933. doi: 10.1118/1.3608907. [DOI] [PMC free article] [PubMed] [Google Scholar]
  17. Lipinski B, Herzog H, Rota Kops E, Oberschelp W, Muller-Gartner HW. Expectation maximization reconstruction of positron emission tomography images using anatomical magnetic resonance information. IEEE Trans Med Imaging. 1997;16(2):129–136. doi: 10.1109/42.563658. [DOI] [PubMed] [Google Scholar]
  18. Meltzer CC, Leal JP, Mayberg HS, Wagner HN, Jr, Frost JJ. Correction of PET data for partial volume effects in human cerebral cortex by MR imaging. J Comput Assist Tomogr. 1990;14:561–570. doi: 10.1097/00004728-199007000-00011. [DOI] [PubMed] [Google Scholar]
  19. Muller-Gartner HW, Links JM, Prince JL, Bryan RN, McVeigh E, Leal JP, Davatzikos C, Frost JJ. Measurement of radiotracer concentration in brain gray matter using positron emission tomography: MRI-based correction for partial volume effects. J Cereb Blood Flow Metab. 1992;12(2):571–583. doi: 10.1038/jcbfm.1992.81. [DOI] [PubMed] [Google Scholar]
  20. Nuyts J. The use of mutual information and joint entropy for anatomical priors in emission tomography. IEEE NSS/MIC Conf. Record. 2007;6:4149–4154. [Google Scholar]
  21. Nuyts J, Baete L, Beque D, Dupont P. Comparison between MAP and postprocessed ML for image reconstruction in emission tomography when anatomical knowledge is available. IEEE Trans Med Imaging. 2005;24(5):667–675. doi: 10.1109/TMI.2005.846850. [DOI] [PubMed] [Google Scholar]
  22. Pichler BJ, Kolb A, Nagele T, Schlemmer HP. PET/MRI: paving the way for the next generation of clinical multimodality imaging applications. J. Nucl. Med. 2010;51 doi: 10.2967/jnumed.109.061853. 333]6. [DOI] [PubMed] [Google Scholar]
  23. Pluim JP, Maintz JB, Viergever MA. Image registration by maximization of combined mutual information and gradient information. IEEE Trans Med Imaging. 2000;19(8):809–814. doi: 10.1109/42.876307. [DOI] [PubMed] [Google Scholar]
  24. Pluim JP, Maintz JB, Viergever MA. Mutual-information-based registration of medical images: A survey. IEEE Trans Med Imaging. 2003;22(8):986–1004. doi: 10.1109/TMI.2003.815867. [DOI] [PubMed] [Google Scholar]
  25. Rahmim A, Cheng JC, Blinder S, Camborde ML, Sossi V. Statistical dynamic image reconstruction in state-of-the-art high-resolution PET. Phys. Med. Biol. 2005;50:4887–4912. doi: 10.1088/0031-9155/50/20/010. [DOI] [PubMed] [Google Scholar]
  26. Rahmim A, Qi J, Sossi V. Resolution modeling in PET imaging: theory, practice, benefits, and pitfalls. Med. Phys. 2013;40 doi: 10.1118/1.4800806. 064301. [DOI] [PMC free article] [PubMed] [Google Scholar]
  27. Rahmim A, Zaidi H. PET versus SPECT: strengths, limitations and challenges. Nucl Med Commun. 2008;29(3):193–207. doi: 10.1097/MNM.0b013e3282f3a515. [DOI] [PubMed] [Google Scholar]
  28. Reader AJ, Julyan PJ, Williams H, Hastings DL, Zweit J. EM algorithm system modeling by image-space techniques for PET reconstruction. IEEE Trans. Nucl. Sci. 2003;50:13927. [Google Scholar]
  29. Rousset OG, Rahmim A, Alavi A, Zaidi H. Partial volume correction strategies in PET. PET Clin. 2007;2:235–249. doi: 10.1016/j.cpet.2007.10.005. [DOI] [PubMed] [Google Scholar]
  30. Somayajula S, Panagiotou C, Rangarajan A, Li Q, Arridge SR, Leahy RM. PET image reconstruction using information theoretic anatomical priors. IEEE Trans Med Imaging. 2011;30(3):537–549. doi: 10.1109/TMI.2010.2076827. [DOI] [PMC free article] [PubMed] [Google Scholar]
  31. Soret M, Bacharach SL, Buvat I. Partial-volume effect in PET tumor imaging. J. Nucl. Med. 2007;48:932–945. doi: 10.2967/jnumed.106.035774. [DOI] [PubMed] [Google Scholar]
  32. Sossi V, de Jong HWAM, Barker WC, Bloomfield P, Burbar Z, Camborde ML, Comtat C, Eriksson LA, Houle S, Keator D, Knob C, Krais R, Lammertsma AA, Rahmim A, Sibomana M, Teras M, Thompson CJ, Trebossen R, Votaw J, Walker M, Wienhard K, Wong DF. The second generation HRRT - a multi-centre scanner performance investigation 2005. IEEE NSS/MIC Conf. Record. 2005;4:2195–2199. [Google Scholar]
  33. Tang J, Kuwabara H, Wong DF, Rahmim A. Direct 4D reconstruction of parametric images incorporating anato-functional joint entropy. Phys. Med. Biol. 2010;55:4261–4272. doi: 10.1088/0031-9155/55/15/005. [DOI] [PMC free article] [PubMed] [Google Scholar]
  34. Tang J, Rahmim A. Bayesian PET image reconstruction incorporating anato-functional joint entropy. Phys Med Biol. 2009;54(23):7063–7075. doi: 10.1088/0031-9155/54/23/002. [DOI] [PMC free article] [PubMed] [Google Scholar]
  35. Tang J, Rahmim A. Anatomy assisted MAP-EM PET image reconstruction incorporating joint entropies of wavelet subband image pairs; IEEE NSS/MIC Conf. Record; 2009b. pp. 3741–3745. [Google Scholar]
  36. Teo BK, Seo Y, Bacharach SL, Carrasquillo JA, Libutti SK, Shukla H, Hasegawa BH, Hawkins RA, Franc BL. Partial-volume correction in PET: validation of an iterative postreconstruction method with phantom and patient data. J. Nucl. Med. 2007;48:802–810. doi: 10.2967/jnumed.106.035576. [DOI] [PubMed] [Google Scholar]
  37. Tohka J, Reilhac A. Deconvolution-based partial volume correction in Raclopride-PET and Monte Carlo comparison to MR-based method. NeuroImage. 2008;39:1570–1584. doi: 10.1016/j.neuroimage.2007.10.038. [DOI] [PubMed] [Google Scholar]
  38. Vunckx K, Atre A, Baete K, Reilhac A, Deroose CM, Van Laere K, Nuyts J. Evaluation of three MRI-based anatomical priors for quantitative PET brain imaging. IEEE Trans Med Imaging. 2012;31(3):599–612. doi: 10.1109/TMI.2011.2173766. [DOI] [PubMed] [Google Scholar]
  39. Wong DF, Rosenberg PB, Zhou Y, Kumar A, Raymont V, Ravert HT, Dannals RF, Nandi A, Braic JR, Ye W, Hilton J, Lyketsos C, Kung HF, Joshi AD, Skovronsky DM, Pontecorvo MJ. In vivo imaging of amyloid deposition in Alzheimer disease using the radioligand 18F-AV-45 (florbetapir [corrected] F 18). J Nucl Med. 2010 Jun;51(6):913–920. doi: 10.2967/jnumed.109.069088. [DOI] [PMC free article] [PubMed] [Google Scholar]
  40. Woods RP, Mazziotta JC, Cherry SR. MRI-PET registration with automated algorithm. J Comput Assist Tomogr. 1993;17:536–546. doi: 10.1097/00004728-199307000-00004. [DOI] [PubMed] [Google Scholar]
  41. Xu R, Chen Y-W. Wavelet-based multiresolution medical image registration strategy combining mutual information with spatial information. Intern. J. Innov. Comput. Inform. Control. 2007;3:285–296. [Google Scholar]
  42. Zaidi H, Montandon ML, Alavi A. The clinical role of fusion imaging using PET, CT, and MR imaging. Magn. Reson. Imaging Clin. N. Am. 2010;18:133–149. doi: 10.1016/j.mric.2009.09.010. [DOI] [PubMed] [Google Scholar]

RESOURCES