Is Ring Breaking Feasible in Relative Binding Free Energy Calculations?

Abstract

Our interest is relative binding free energy (RBFE) calculations based on molecular simulations. These are promising tools for lead optimization in drug discovery, computing changes in binding free energy due to modifications of a lead compound. However, in the “alchemical” framework for RBFE calculations, some types of mutations have the potential to introduce error into computed binding free energies. Here, we explore the magnitude of this error in several different model binding calculations. We find that some of the calculations which involving ring breaking have significant errors, and this error is especially large in bridged ring systems. Since the error is a function of ligand strain, which is unpredictable in advance, we believe ring breaking should be avoided when possible.

1 Introduction

Here, our interest is in drug lead optimization, where a compound is known which binds the desired target, and we seek to create derivatives of this lead compound which either improve affinity or maintain affinity while improving other properties. Relative binding free energy calculations (RBFE) based on molecular dynamics (MD) simulations can be used to predict binding free energy differences based on chemical changes, in advance of synthesis of the derivative compounds. Thus, they can potentially substantially accelerate the lead optimization process¹ and are of considerable interest for drug discovery applications.

Given a particular model (force field and parameters), alchemical RBFE calculations yield correct relative binding free energies in principle, at least in the limit of adequate sampling, as reviewed elsewhere.^2–4 However, large chemical modifications require substantially more sampling, and hence, with a fixed amount of sampling, increasing the size of the transformation can increase the magnitude of errors due to sampling. Thus, in order to ensure typical modifications are relatively small, we recently designed a program, lead optimization mapper (LOMAP),⁵ for planning efficient RBFE calculations.

LOMAP automatically selects single-topology RBFE calculations spanning a lead series by pairing similar molecules. In LOMAP, we only calculate the RBFE between molecules which have sufficient similarity. Structural similarities are computed on the basis of a similarity score, which relates to the change in the number of atoms during the transformation between the two molecules in question. Specifically, we identify the maximum common substructure shared by two molecules, and identify the change in the number of atoms needed to reach this substructure; we use these changes as the basis for our similarity score. Currently, LOMAP uses two scoring schemes, called “strict” and “loose”, which differ only in how we treat transformations which would break polycyclic ring systems⁶(Fig. 1).

Figure 1.

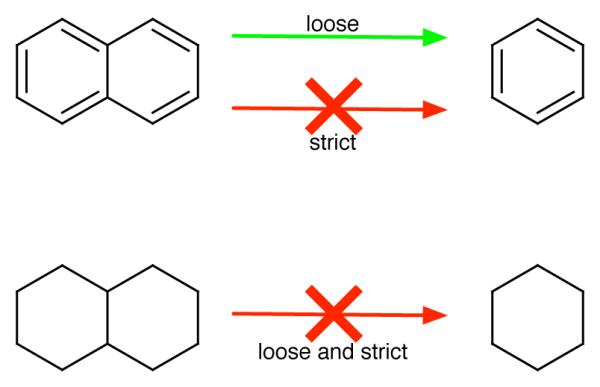
In the strict approach, mutation involving breaking any ring is not allowed (red arrows). Here, “ring breaking” refers to any transformation where atoms remaining in the final system were part of any ring which has been removed. In the loose approach, ring breaking mutations are allowed only when the ring system left behind is rigid (green arrows).

In the strict scoring scheme, we do not allow any ring breaking when we search for the maximum common substructure. For example, in the strict approach, if we consider the pair naphthalene and benzene (Fig. 1), these have no common substructure because a naphthalene to benzene transformation would involve breaking a ring. On the other hand, in the loose scoring scheme, we allow ring breaking happen only when the ring system left behind is relatively rigid or planar (typically aromatic). For example in this case, mutation from naphthalene to benzene is allowed because the remaining ring, benzene, is rigid, while the mutation from decalin to cyclohexane (Fig. 1) is not allowed, because the remaining ring, cyclohexane, is not rigid (indeed, it can undergo significant conformational transitions). LOMAP was designed to use the loose scoring scheme only when absolutely necessary in order to produce RBFE calculations spanning a lead series – for example, if a group of bicyclic molecules could not be connected to single-ring systems via any other means – but it avoids these types of transformations whenever possible. This was done because the effective “deletion” of partial rings in polycyclic (bicyclic, in this example) ring systems can introduce error into the associated themodynamic cycles (Fig. 2).

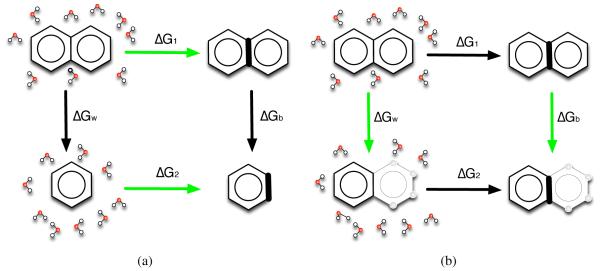
Figure 2.

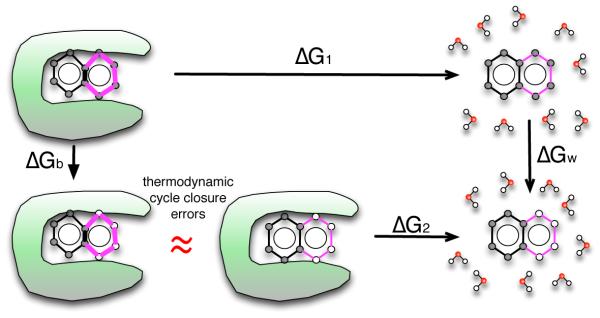
Here, we consider the thermodynamic cycle used for single-topology relative binding free energy calculations, where we compare binding of two ligands 1 and 2 (top and bottom, respectively, where our example shows cartoons of naphthalene and benzene). In this approach, we obtain the difference between the binding free energy of 1, ΔG₁, and the binding free energy of 2, ΔG₂, by perturbing the first ligand into the second in the binding site (ΔG_b) and in water (ΔG_w). These perturbations can involve changing some of the atoms in one or both ligands into dummy atoms (hollow spheres) – atoms which no longer have charge or Lennard-Jones interactions with the remainder of the system, but retain their bonded interactions. In a correct thermodynamic cycle ΔG₁+ΔG_w − ΔG₂ − ΔG_b = 0. However, this is only strictly true when the free energy of the dummy atoms is identical in the binding site and in solution. This criterion is met when the dummy atoms are a set of masses and springs with a conformation which is not affected by that of the remaining “real” atoms. However, if the conformation of the dummy atoms is coupled to the conformation of the remaining portion of the molecule (i.e. when they are members of a ring), these two free energies may in fact differ and the thermodynamic cycle will not close. Here, at bottom left, the binding site is shown to introduce strain into the dummy atom ring (bold bonds), so that the free energy of the left bottom and middle bottom states are no longer equal, causing a cycle closure error (red “approximately equal” sign).

Effectively, the loose scoring scheme means that the thermodynamic cycle our RBFE calculations are based on in these cases no longer formally closes; we potentially have a missing contribution due to a conformational change in the remaining dummy atoms induced by changes in the conformation of the connected interacting atoms, shown by the red “approximately equal” sign in Fig. 2.

More rigorously, we show in the appendix that the dummy atoms can have a nonzero effect on the free energy change whenever there is more than one bond-stretch interaction between the same group of dummy atoms and the remaining interacting atoms (i.e. more than one connection point between the dummy atoms and the rest of the molecule).

In our previous work,⁵ we assumed that any contribution to the free energy change from these dummy atoms would be small in the case where the remaining atoms are in a rigid ring system, and larger when these atoms are in a flexible ring system. Thus, we assumed that, when necessary in order to ensure all compounds in a lead series could be connected, we could break rings in rigid molecules and still introduce only a minimum amount of error in computed binding free energies. However, this was an assumption – the exact magnitude of these contributions is not known. The existence of these errors was well known, but understanding their magnitude is now essential. This has dramatic implications for how we plan free energy calculations. Specifically, can we to allow these types of transformations in special cases? Or do they need to be avoided, or implemented via another route such as absolute free energy calculations? Here we aim to answer these questions. In our initial implementation of LOMAP we assumed that mutations beyond the loose scoring scheme, such as mutation from decalin to cyclohexane, will accumulate substantial errors and in general be unreliable.

Here, we compute the error introduced into single-topology RBFE calculations via both the loose and strict scoring schemes in several model binding calculations, as a function of the amount of strain in the remaining atoms in the ligand. These errors are limited to single-topology approach of the RBFE calculations, other methods like dual-topology approach^7–10 and separated-topology approach¹¹ should not suffer from these errors because they handle these transformations without introducing multiply-connected dummy atoms which interact with remaining atoms. But since the single topology approach is the default method for LOMAP and is widely used in RBFE calculations, these errors are still important.

2 Method

As discussed in the Introduction, we test RBFE calculations in two bicyclic systems: (1) the transformation of naphthalene to benzene (Fig. 3); and (2) the transformation of decalin to cyclohexane (Fig. 4). We also test another case involving a bridged or cage-like ring system, system (3), the transformation of adamantane to bicyclo[3.3.1]nonane (Fig. 5). Here, to avoid the complexity and potential sampling problems introduced by doing these calculations in a receptor binding site, we model “binding” as the transfer of a ligand from water to a “binding site” consisting of the ligand in gas phase with conformational restraints which introduce strain.

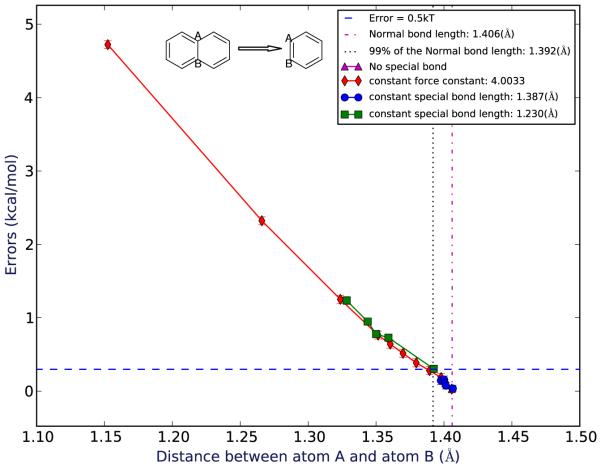
Figure 3.

Errors for mutating naphthalene to benzene as a function of the average distance between the shared atoms observed in the simulations. Spots in different colors represent different force constants/bond length groups of the special bond.

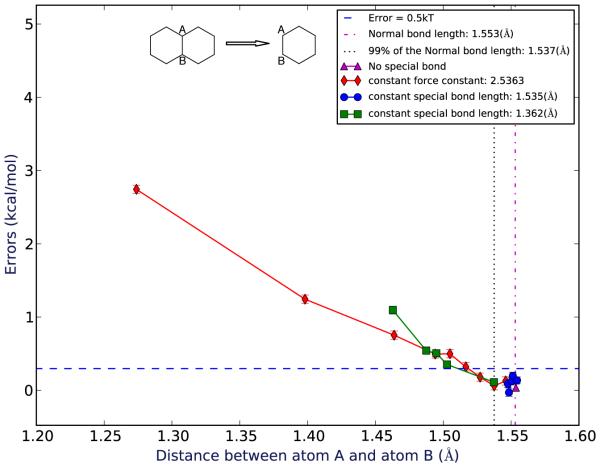
Figure 4.

Errors for mutating decalin to cyclohexane as a function of the average distance between the shared atoms observed in the simulations. Spots in different colors represent different force constants/bond length groups of the special bond.

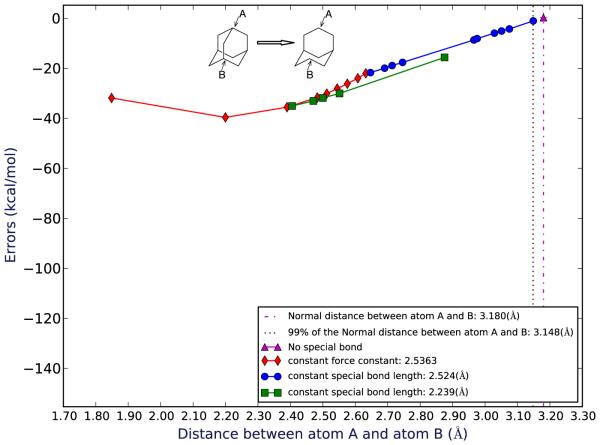
Figure 5.

Errors for mutating adamantane to bicyclo[3.3.1]nonane as a function of the average distance between the shared atoms observed in the simulations. This error is for the system of adamantane-bicyclononane without NDE. The “original” distance is the distance between atom A and atom B in the absolute free energy calculation of bicyclo[3.3.1]nonane without any special bond restraints. Spots in different colors represent different force constants/bond length groups of the special bond.

This is sufficient for our purposes here, as we are solely interested in how introduced strain affects the formal accuracy of RBFE calculations —that is, we seek to determine how much apparent cycle closure error is introduced by ligand strain. Thus, our approach is sufficient, since the error is a function only of the difference in free energy of the dummy atoms when the ligand is under strain (Fig. 6). Since the dummy atoms do not interact with the rest of the system, the error is independent of the environment and dependent only on the degree of ligand distortion or strain.

Figure 6.

The calculations we run are the green arrows. (a) We calculate the absolute “binding” free energy for each molecule, green arrows shown in (a), from water to the hypothetical binding site and then get the difference in absolute binding free energies as ΔΔG_ab = ΔG₁ − ΔG₂. Since in this case ΔG₁ + ΔG_b− ΔG₂ − ΔG_w = 0, then ΔΔG_ab = ΔG_w − ΔG_b. (b) We also calculate the relative “binding” free energy, green arrows shown in (b), by changing atoms to dummy atoms (hollow spheres), and get the relative binding free energy difference as ΔΔG_rl = ΔG_w − ΔG_b. Here the bold bond on the right hand side of both panels represents the bond strained by “binding” to our hypothetical receptor (here represented by introducing restraints).

In order to know how much error is introduced by the approximation in question, we need a way to determine the correct “binding” free energy of the molecules in question. We achieve this by computing the absolute binding free energies for every compound considered (Fig. 6). Here, we compute the free energy to move each molecule from water to the “binding site” —the absolute binding free energy —and then subtract these to obtain the relative binding free energy ΔΔG_ab. Since absolute binding free energy calculations do not involve any ring breaking, they are correct, and provide the gold standard to which we can compare our relative binding free energy results.

Secondly, we calculate the relative binding free energy using a typical thermodynamic circle (Fig. 6) where we calculate the free energy change by transforming molecule 1 to molecule 2 both in water and in the binding site. From this, we obtain the relative binding free energy ΔΔG_rl = ΔG_w − ΔG_b. Since this process includes ring breaking, ΔΔG_rl is our target result.

After doing both of these calculations, we compute the overall error as the difference between the reference result (from absolute calculations) and the target result. This measures the difference between the correct free energy change (as determined by absolute calculations) and the free energy change calculated by the relative calculations, which are in error (due to neglecting the free energy associated with a conformational change in dummy atoms) to some degree.

Here, we are interested in determining how the error changes as a function of ligand strain. Particularly, in the limit of no conformational change within the ligand, the conformation and free energy of the dummy atoms will be identical in both the binding site and solution, and no error will be introduced by deleting¹² part of the ring. However, in the limit of very large strain, the bonds between the dummy atoms will be strained in the binding site but not in solution, introducing substantial error. To examine these effects, we added an additional bond between two atoms (bond type 6 in GROMACS), a spring, which is shown in bold in Fig. 6. By changing the length and force constant for this additional bond, we can then control the bond length for the shared bond for bicyclic systems or the distance between two end atoms in the cage-like system, which controls the strain in bonds between the remaining dummy atoms. The bond length details are shown in Tables 1, 2 and 3.

Table 1.

Errors as a function of bond length (strain) for naphthalene-benzene.

ID	Special bond length (Å)	Force constant(kJmol−1nm−2)	Bond length in simula- tion(Å)	Errors(kcal/mol)
original	none	none	1.4057(8)	0.03 ± 0.04
0	1.387	4.0033	1.3979(6)	0.19 ± 0.06
1	1.370	4.0033	1.3893(7)	0.28 ± 0.06
2	1.350	4.0033	1.3795(7)	0.39 ± 0.05
3	1.330	4.0033	1.3698(7)	0.51 ± 0.05
4	1.310	4.0033	1.3604(6)	0.64 ± 0.05
5	1.290	4.0033	1.3514(8)	0.76 ± 0.05
6	1.230	4.0033	1.3237(6)	1.25 ± 0.05
7	1.110	4.0033	1.2659(6)	2.32 ± 0.05
8	0.870	4.0033	1.1524(5)	4.72 ± 0.05
11	1.387	3.6030	1.3977(6)	0.14 ± 0.05
12	1.387	2.4020	1.4001(8)	0.16 ± 0.05
13	1.387	2.0017	1.4006(6)	0.11 ± 0.05
14	1.387	1.6013	1.4014(6)	0.07 ± 0.05
15	1.387	0.4033	1.4065(7)	0.04 ± 0.04
21	1.230	3.6030	1.3283(6)	1.24 ± 0.05
22	1.230	2.4020	1.3438(6)	0.95 ± 0.05
23	1.230	2.0017	1.3500(6)	0.78 ± 0.05
24	1.230	1.6013	1.3591(6)	0.73 ± 0.04
25	1.230	0.4033	1.3925(8)	0.30 ± 0.04

Table 3.

Errors as a function of bond length (strain) for adamantane-bicyclononane, using distances observed in the absolute simulation of bicyclo[3.3.1]nonane for measuring the bond length. The corresponding error figure for this table is Fig. 5

ID	Special bond length (Å)	Force constant(kJmol−1nm−2)	Distance between atom A and B in simulation(Å)	Errors(kcal/mol)
original	none	none	3.18(7)	0.29 ± 0.03
0	2.524	2.5363	2.63(3)	−21.98 ± 0.10
1	2.494	2.5363	2.61(3)	−23.97 ± 0.10
2	2.456	2.5363	2.58(3)	−26.16 ± 0.10
3	2.421	2.5363	2.54(3)	−28.07 ± 0.10
4	2.383	2.5363	2.51(3)	−30.11 ± 0.10
5	2.347	2.5363	2.48(3)	−31.65 ± 0.10
6	2.239	2.5363	2.39(3)	−35.54 ± 0.10
7	2.019	2.5363	2.20(3)	−39.61 ± 0.10
8	1.585	2.5363	1.85(3)	−31.85 ± 0.10
11	2.524	2.2827	2.65(3)	−21.69 ± 0.08
12	2.524	1.5218	2.69(4)	−19.93 ± 0.05
13	2.524	1.2682	2.71(4)	−18.88 ± 0.05
14	2.524	1.0145	2.75(4)	−17.61 ± 0.04
15	2.524	0.2536	2.97(6)	−8.65 ± 0.03
16	2.524	0.2283	2.98(6)	−8.09 ± 0.03
17	2.524	0.1522	3.03(6)	−5.91 ± 0.03
18	2.524	0.1268	3.05(6)	−5.06 ± 0.03
19	2.524	0.1015	3.08(6)	−4.23 ± 0.03
20	2.524	0.0254	3.15(8)	−1.02 ± 0.03
21	2.239	2.2827	2.41(3)	−35.04 ± 0.08
22	2.239	1.5218	2.47(4)	−33.02 ± 0.05
23	2.239	1.2682	2.50(4)	−31.82 ± 0.05
24	2.239	1.0145	2.55(4)	−30.03 ± 0.04
25	2.239	0.2536	2.88(6)	−15.63 ± 0.03

For each bond length we calculate the cycle closure error as described above. We find that substantial errors are introduced when the bond length change (strain) becomes sufficiently large. To provide perspective in terms of how much strain typically is introduced upon ligand binding, we examined simulations of several different protein-ligand systems and measured how much bond length change is typical on ligand binding.

For all the simulations, we used GROMACS 4.6.¹³

The initial structure files were generated by MarvinSketch 5.11.3 and then converted to mol2 files using the OpenEye OEChem toolkits.¹⁴ The OpenEye OEChem Python toolkit and Omega¹⁵ were used to generate 3D conformations and assign AM1-BCC^16,17 partial charges. Antechamber¹⁸ from AmberTools 13 was used to assign GAFF atom¹⁹ types and then AmberTools’ tleap was used to generate the Amber prmtop and crd files which were converted to GROMACS format using acpype.²⁰ Small molecules were then set up in GROMACS and, for the solute-in-water case, solvated in TIP3P²¹ water in a dodecahedral simulation box with at least 1.2 nm from the solute to the nearest box edge. The number of water molecules was 690 for benzene, 554 for napthalene, 678 for cyclohexane, 552 for decalin, 553 for adamantane and 597 for bicyclo[3.3.1]nonane.

AMBER combination rules (arithmetic average for σ and geometric for ε) were used. Simulations were run using Langevin dynamics, as previously,²² and the simulation timestep was 1 fs. Lennard-Jones interactions were gradually switched off between 0.9 and 1.0 nm, and an analytical correction was applied to the energy and pressure. PME was used for electrostatics, as previously, with a real-space cutoff of 1.2 nm. LINCS was used to constrain bonds to hydrogen. Each system and λ value (where λ is a parameter ranging between 0 and 1, where 0 corresponds to the unmodified system, and 1 corresponds to the end-state of the transformation) was independently minimized for up to 2500 steps of steepest-descents minimization.

Following constant pressure equilibration, box sizes were adjusted at each λ value by an affine transformation to ensure each λ value had the correct volume for the target pressure. After this, we conducted an additional 5 ns of constant pressure production simulation at each λ, discarding the first 100 ps as additional “equilibration”, as previously.²² Here we use Parrinello-Rahman barostat to modulate the pressure.

The parameter λ controls the transformation between end states. In this version of GROMACS, we use three separate λ values, one controlling modification of partial charges (λ_chg, turning solute partial charges to zero), the second controlling modification of the bond inducing strain (λ_bd, introducing this bond) and the third controlling modification of Lennard-Jones interactions (λ_LJ, turning solute LJ interactions to zero). The details of the λ spacing can be found in SI.

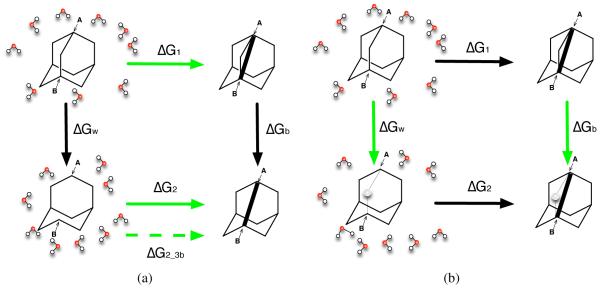
In the case of the bridged ring system, we have to deal with an additional complexity. Because of the absence of a bridging atom in bicyclo[3.3.1]nonane, the internal non-bonded interactions involving atom A and atom B shown in Fig. 5 are different in adamantane compared to those in bicyclo[3.3.1]nonane - that is, the interactions differ not just in strength but in terms of which atoms interact. This is because the bridging atom changes which interactions are excluded and which are 1-4 interactions. Thus, the end state of the simulation which starts from adamantane (ΔG_w (Fig.7)) has the different non-bonded interactions from the starting state of the simulation beginning with bicyclo[3.3.1]nonane (ΔG₂ (Fig. 7)). Unless accounted for, these differences in non-bonded interactions will make the thermodynamic cycle fail to close even the absence of strain/conformational change, since we neglect a contribution due to the free energy of changing the internal non-bonded interactions. We call errors introduced by this change in internal nonbonded interactions “non-bonded discrepancy errors (NDE)”. The NDE is not what we are interested in here, and also is not a necessary feature of binding free energy calculations - particularly, if our simulation package allowed us to change the exclusions and pairs lists with λ so as to remove the effects of the presence (or absence) of the bridging atom on 1-4 and excluded interactions, then we could compute relative binding free energies which were unaffected by NDE. Thus, we are interested in understanding errors aside from NDE. So, to avoid NDE errors in GROMACS, we modify the pairs and exclusions sections in our topology files to create an new reference molecule which has the same internal exclusion and 1-4 interactions as adamantane but the same atoms as bicyclo[3.3.1]nonane. This allows us to maintain the same exclusion and 1-4 interactions while transforming between a molecule which is like bicyclo[3.3.1]nonane into adamantane. With these adjustments, the simulation ΔG₂has the same 1-4 interactions and exclusions as the simulation of ΔG_w; we call this case “adamantane-bicyclononane”. As a comparison, we still run simulations without any adjustments to the topology file (ΔG_{2_3b}). This case - which does include NDE - is called “adamantane-bicyclononane with NDE”. adamantane-bicyclononane with NDE is analyzed using the same simulations as adamantane-bicyclononane (we use the same trajectory file and modify the topology file in order to evaluate the desired free energy using different interactions) as discussed in Fig. 7 (left bottom green/dashed green arrow in Fig. 7).

Figure 7.

The calculations we run for adamantane-bicyclononane and adamantane-bicyclononane with NDE are the green arrows ΔG₁, ΔG_b, ΔG_w with green arrow ΔG₂ for adamantane-bicyclononane and dashed green arrow ΔG_{2_3b} for adamantane-bicyclononane with NDE. The meaning of each simulation is the same as in Fig. 6, with panel (a) showing the absolute "binding" free energy for each molecule and panel (b) showing the relative "binding" free energy. For adamantane-bicyclononane specifically, the bottom absolute simulation ΔG₂ starts from the topology based on the structure of bicyclo[3.3.1]nonane plus topology modifications to maintain the same 1-4 and internal interactions with the end state of the left relative simulation ΔG_w. For adamantane-bicyclononane with NDE, the bottom absolute simulation ΔG_{2_3b} starts from the original topology generated from the structure of bicyclo[3.3.1]nonane.

For all our systems, we use three different sets of special bonds to induce strain in the ligand. These vary in their bond length and force constant, and involve: (1) varying only the length (keeping the same force constant as the original bond, or as a normal carbon-carbon single bond in the case of the cage-like system (which does not initially have a bond between the shared atoms)); (2) varying only the force constant (keeping the same distance between the shared atoms as the original distance; in this case, the initial force constant is that of the original bond or a normal carbon-carbon single bond); (3) varying only the force constant but starting with a reduced distance of 88.7% of the original distance between the shared atoms (this is otherwise the same as case 2). With these combinations, we vary the distance between the shared atoms in the simulations over a wide range. We have 8, 5, and 5 simulations for sets 1, 2 and 3, respectively for the planar ring systems. In the adamantane-bicyclononane case²³ we add additional 5 simulations for set 2 to get a better coverage of the space of the bond length.

3 Results

Here, we examine how ligand strain in our model “binding” system impacts error in computed relative free energy calculations. Strain is controlled by an artificial bond which changes a bond length or distance within the ligand as it binds. In our bicyclic systems, we find that as this shared bond deviates from its original value (i.e., the ligand becomes more strained on binding) the error in the computed binding free energy increases. In the bicyclic systems (Fig. 3, Fig. 4) for the region close to the normal (unrestrained) bond length, the errors for both systems are relatively small and essentially statistically indistinguishable from zero – smaller than 0.5 kT.

On the other hand, for the cage-like system (the bridged ring case), errors are bigger. Unlike the bicyclic ring systems, here there is no bond between atom A and atom B in bicyclo[3.3.1]nonane (Fig. 5), making the distance between atom A and atom B differ substantially from that in adamantane. That is, the distances between atom A and atom B in the simulations of the absolute free energy calculation of bicyclo[3.3.1]nonane (ΔG₂in Fig. 7) and the relative free energy calculation in vacuum (ΔG_b in Fig. 7) are significantly different.

This is not necessarily a problem - it just means that if we want to examine the error as a function of the distance between atom A and atom B, we have two different distances we can use, one which is substantially longer than the other. Thus, we plot the errors vs the distance between atom A and atom B in the simulations based on both of the references – 1, absolute simulations starting from bicyclo[3.3.1]nonane and 2, relative vacuum simulations starting from adamantane. We find that if we use the bond length in the relative calculations from adamantane in vacuum as the “original” bond length, the error is ~ 30 kcal/mol when the bond length is 99% of its original value (Figures showing this result are in SI), while if we use the bond length seen in the absolute calculations from bicyclo[3.3.1]nonane as the "original" bond length, the error is ~ 1 kcal/mol (5). For both of these simulations when the bond length changes by 1%, the errors are significant – larger than 1 kT. For adamantane-bicyclononane with NDE, with numbers which include NDE, compared with adamantane-bicyclononane, the errors are similar when the changes of the bond length are small and larger when the changes of the bond length are large (SI). This was expected because adamantane-bicyclononane with NDE includes additional errors beyond those in adamantane-bicyclononane – in addition to including contributions due to changes in strain/bonded energies, it also includes NDE errors (Fig. 7).

Thus, we find that for the bicyclic systems, large bond length changes do lead to significant errors while small bond length changes (less than 2%) do not result in significant errors in relative binding free energy calculations. But for cage-like systems, even very small changes in internal distance (1%) can lead to very substantial errors (Fig. 5). Here, we assess significance based on the point at which the absolute error in the computed relative binding free energy becomes larger than the statistical uncertainty in our calculations.

For the bicyclic systems, we also examined the amount of strain induced by these bond perturbations in order to provide scale. We calculated the average energy difference between the most strained conformation at which the error is still statistically indistinguishable from zero (the “maximum indistinguishable” or “MI” case) and the original, unstrained case (“original”), both for relative calculations in vacuum. For the naphthalene to benzene system (Table 1), case MI is labeled with ID 1. The average potential energy difference between these two cases is 0.31 kcal/mol. For the decalin to cyclohexane system (Table 2), case MI is labeled with ID 2. The average potential energy difference between these two cases is 1.10 kcal/mol.

Table 2.

Errors as a function of bond length (strain) for decalin-cyclohexane.

ID	Special bond length (Å)	Force constant(kJmol−1nm−2)	Bond length in simula- tion(Å)	Errors(kcal/mol)
original	none	none	1.553(1)	0.04 ± 0.05
0	1.535	2.5363	1.5460(7)	0.13 ± 0.06
1	1.517	2.5363	1.5375(8)	0.06 ± 0.06
2	1.494	2.5363	1.5271(8)	0.18 ± 0.06
3	1.472	2.5363	1.5166(9)	0.32 ± 0.06
4	1.449	2.5363	1.5049(7)	0.50 ± 0.06
5	1.428	2.5363	1.4941(7)	0.50 ± 0.06
6	1.362	2.5363	1.4637(7)	0.75 ± 0.06
7	1.228	2.5363	1.3981(7)	1.24 ± 0.06
8	0.964	2.5363	1.2738(7)	2.74 ± 0.05
11	1.535	2.2827	1.5476(7)	0.09 ± 0.05
12	1.535	1.5218	1.5484(8)	-0.03 ± 0.05
13	1.535	1.2682	1.5503(8)	0.12 ± 0.05
14	1.535	1.0145	1.5512(8)	0.20 ± 0.05
15	1.535	0.2563	1.5544(9)	0.14 ± 0.05
21	1.362	2.2827	1.4628(7)	1.10 ± 0.05
22	1.362	1.5218	1.4874(8)	0.54 ± 0.05
23	1.362	1.2682	1.4949(8)	0.51 ± 0.05
24	1.362	1.0145	1.5027(9)	0.35 ± 0.05
25	1.362	0.2563	1.5373(9)	0.11 ± 0.05

As noted, we originally expected that for the bicyclic system the flexibility or rigidity of the remaining ring system would have a substantial impact on the magnitude of the error, with rigid rings having substantially smaller errors than flexible rings. However, this is not what we find here —both approaches seem to have roughly comparable errors. However, we do find that for the flexible cage-like molecule, errors on ring breaking are much more substantial.

One possible explanation of this phenomenon is that, in the bicyclic system, the remaining ring is rigid enough – and structural changes are small enough – to buffer the effect of bond length changes. However, in the bridged ring system, the geometry dictates that changes in distance between the atoms in question cannot easily be absorbed by small changes in other bond lengths, resulting in significant structural discrepancies between the conformation of the dummy atoms in water and in the binding environment, which, we expected, will lead to larger errors.

We still need some way of determining whether these effects will be significant for real binding free energy calculations, so we examined strain in several real protein-ligand binding systems. Specifically, we examined simulations of several different protein-ligand complexes and the free ligands in solution to determine the magnitude of typical changes in bond length. The simulation trajectories were obtained from our former projects which include six ligands in trypsin, two ligands bound to DNA gyrase²⁴ as provided by Vertex Pharmaceuticals, and ibuprofen in HSA (Human serum albumin). Trajectories and parameter/coordinate files are provided in the supporting material. Our current research efforts do not provide good benchmarks for bond length changes in fused rings systems, but we believe the systems examined here provide some idea of the amount of bond length change which can be expected in general, at least enough so to give a rough idea of the size of the effect.

We found that, in most of these simulations, bond length changes were small. Bond lengths differ in the binding site by less than 1 percent from those in solution. Ibuprofen binding to HSA proved an exception – we saw somewhat larger bond length changes, with two over 1%. (Table 4). Based on work in our model systems, bond length changes of this magnitude would be sufficient to cause errors larger than 0.5 kT, which is small but notable, in the bicyclic system (Fig. 3) and an error as large as 1-30 kcal/mol in the cage-like system depending on how we measure the original bond length (Fig. 5, SI).

Table 4.

Bond length changes in a real protein-ligand complex – ibuprofen binding to HSA.

atom ID 1	atom ID 2	bond length in water(Å)	bond length in complex (Å)	z score	percentage
C1	C3	1.388(1)	1.394(1)	3.4	0.4
C4	C6	1.389(1)	1.399(1)	6.1	0.7
C2	C5	1.388(1)	1.394(1)	4.1	0.5
C11	C5	1.517(2)	1.524(1)	3.3	0.5
C12	C6	1.515(1)	1.528(1)	6.8	0.9
C10	C13	1.535(1)	1.544(1)	4.7	0.6
C7	O1	1.215(1)	1.213(1)	1.6	0.2
C12	C8	1.534(2)	1.546(1)	5.8	0.8
C2	C4	1.388(1)	1.393(1)	2.8	0.3
C7	O2	1.306(1)	1.291(1)	9.4	1.1
C1	C5	1.385(1)	1.394(1)	5.2	0.6
C11	C13	1.535(2)	1.552(1)	6.8	1.1
C3	C6	1.387(1)	1.398(1)	6.9	0.8
C12	C7	1.508(1)	1.521(1)	7.4	0.9
C13	C9	1.536(1)	1.549(1)	6.4	0.8

Data for these systems is provided in the Supporting Information.

4 Conclusions

Fundamentally, the error introduced by ring breaking results from coupling between dummy atoms in multiply-connected groups (such as a ring system which has been turned into dummy atoms) and the conformation of the rest of the system. Specifically, the thermodynamic cycle used for relative free energy calculations assumes that the contribution of the dummy atoms to the free energy of the system is equivalent in the different environments, which is not in general the case. Strain in the ligand or solute induces some degree of conformational change, which affects the free energy of the dummy atoms so that this assumption is no longer met.

In this study, we examined how this error introduced by ring breaking in relative free energy calculations grows as a function of ligand strain in a model binding system. We find that for bicyclic ring systems, errors are relatively small (less than 0.5 kT) and typically not statistically significant if the ligand strain is small – that is, if bond length changes caused by the binding environment are small (less than 2%). However, substantial changes in bond length as large as 1% do seem to occur in some real systems we have examined, suggesting that such perturbations ought to be avoided whenever possible. But we further find that for cage-like or bridged molecules, if we remove the bridge, errors grow much more rapidly as a function of ligand strain. In the system we examined here, even 1% distance changes lead to errors of 1 to many kcal/mol (depending on how the change in bond length is measured). Furthermore, since ligand strain is difficult to predict a priori, there is no way to know in advance how big these errors will be for a specific system of interest. So in all we believe ring breaking should be avoided in relative free energy calculations whenever possible, even for planar rings, though it is especially critical to avoid breaking bridged rings.

If researchers do need to calculate free energy changes for transformations involving ring breaking, we believe dual- or separated-topology^1,11 relative free energy calculations and absolute free energy calculations¹ may be a better options, as these do not suffer from the same limitations.

5 Appendix

In alchemical relative binding free energy calculations, the two molecules before and after mutation usually have different topologies and differing numbers of atoms, and dummy atoms are therefore necessarily introduced in the calculations. To ensure that the effect of the dummy atoms exactly cancels out in the two legs of the simulations, certain rules must be followed regarding which interaction energy terms between the dummy atoms and the physical atoms are kept in the two end points of the relative calculation – specifically, in the states reached at the end point lambda values.

In general, the end point lambda window in alchemical FEP simulations has the following parts: N physical atoms 1, 2, ... N in the mixed molecule, m dummy atoms a, b, c, ... x, and i atoms in the surrounding environment S₁,S₂, ... S_i(the solvent, ion and/or protein). The total interaction energy (bonded and non-bonded) has the following components: the interaction energy between the physical atoms ($U_P^{self}$), the interaction energy between the dummy atoms (U_D), the interaction between dummy atoms and physical atoms (U_PD), the interaction energy between particles in the environment (U_e), and the interaction between the environment and the physical atoms (U_Pe).

$$\begin{array}{cc}\hfill & U(1,2\dots N;a,b,\dots x;S_1,S_2,\dots S_i)=U_p^{self}(1,2,\dots N)+U_D(a,b,\dots x)+U_{PD}(1,2,\dots N;a,b,\dots x)+\hfill \\ \hfill & U_e(S_1,S_2,\dots S_i)+U_{pe}(1,2,\dots N;S_1,S_2,\dots S_i)\hfill \end{array}$$ (1)

Since the dummy atoms do not interact with the surrounding environment, we can define the following effective potential due to the surrounding environment by integrating over these degrees of freedom:

$$U_P^{env}(1,2,\dots N)=kT\ln \int d{S}_{1}d{S}_2\dots d{S}_i\exp (-\beta (U_e+U_{Pe}))$$ (2)

The effective potentials from the environments are different in the two legs of the alchemical FEP simulations. Define

$$U_P=U_P^{self}+U_P^{env}$$ (3)

Then the configurational part of the partition function for the whole system simplifies into:

$$Q=\int d1d2\dots dNdadb\dots dx\exp (-\beta (U_P+U_D+U_{PD}))$$ (4)

It is easy to show that, if there are only one bonded stretch interaction, two bonded angle interactions, and three bonded dihedral angle interactions between the physical atoms and the dummy atoms at the end point then the effect of the dummy atoms exactly cancels out in the two simulations.²⁵ (These interactions could be labeled r_1a, θ_21a, θ_1ab, ϕ_321a, ϕ_21ab andϕ_1abc where the subscripts stand for the atom numbers in Fig. 8; for example θ_1ab refers to the angle between bond 1a and bond ab.) This is also true for fewer retained interactions. The 3m degrees of freedom for the dummy atoms can be decomposed into 3m-6 internal degrees of freedom for the dummy atoms, $x_1^D,x_2^D,\dots x_{3m-6}^D$, and 6 degrees of freedom joining the dummy atoms with the physical atoms $x_1^{PD},x_2^{PD},\dots x_6^{PD}$ (the 6 degrees of freedom listed above). Therefore:

$$\begin{array}{cc}\hfill & Q(1,2,\dots N,a,b,c,\dots x)=\int d1d2\dots dNdadb\dots dx\exp (-\beta (U_P+U_D+U_{PD}))\hfill \\ \hfill & =\int d1d2\dots dN\exp (-\beta U_P)\int d{x}_1^{PD}d{x}_2^{PD}\dots d{x}_6^{PD}\exp (-\beta U_{PD})\int d{x}_1^{D}d{x}_2^D\dots d{x}_{3m-6}^D\exp (-\beta U_D)\hfill \\ \hfill & =Q(1,2,\dots N)Q^D\hfill \end{array}$$ (5)

Now suppose that, in addition to the interactions involving the 6 degrees of freedom mentioned above, one more interaction between the dummy atoms and the physical atoms is retained in the end lambda window, such as the bonded stretch interaction between atoms 2 and d in our example (Fig. 8) of a ring closing mutation involving perturbing a benzene ring to a napthelene ring. If this extra interaction is retained, then

$$\begin{array}{cc}\hfill & Q(1,2,\dots N,a,b,c,\dots x)=\int d1d2\dots dNdadb\dots dx\exp (-\beta (U_P+U_D+U_{PD}))\hfill \\ \hfill & =\int d1d2\dots dN\exp (-\beta U_P)\int d{x}_1^{PD}d{x}_2^{PD}\dots d{x}_6^{PD}\int d{x}_1^{D}d{x}_2^D\dots d{x}_{3m-6}^D\exp (-\beta (U_{PD}^6+U_{r_{2d}}))\exp (-\beta U_D)\hfill \\ \hfill & =\int d1d2\dots dN\exp (-\beta (U_P+U_P^{eff}))\hfill \end{array}$$ (6)

where $U_P^{eff}(1,2,\dots N)=-kT\ln \int d{x}_6^{PD}d{x}_{3m-6}^D\exp (-\beta (U_{PD}^6+U_{r_{2d}}+U_D))$ is the effective potential (restraint) applied on the physical atoms due to the interactions with the dummy atoms. Note that the term U_r2d — the bond stretch potential between atom 2 and d — is introduced because of the restriction of an extra degree of freedom aside from the six rigid-body degrees of freedom. Thus, the final result in Eq. 6 cannot be separated into separate integrals as in Eq. 5 because having only those six degrees of freedom restrained is the prerequisite for ensuring the thermodynamic properties of the dummy atoms and those of the physical atoms are independent.²⁵ Thus, with this extra interaction, the the $U_P^{eff}$ (1,2, ...N) is no longer separable into a part for the dummy atoms and a part for the interaction between physical and dummy atoms. Therefore, the inclusion of additional bonded stretch interactions for the ring opening/closing FEP calculations will introduce a conformational bias for the ligand simulated, and the effect of the dummy atoms does not cancel out in the two legs of the simulations, leading to errors in the calculations.

Figure 8.

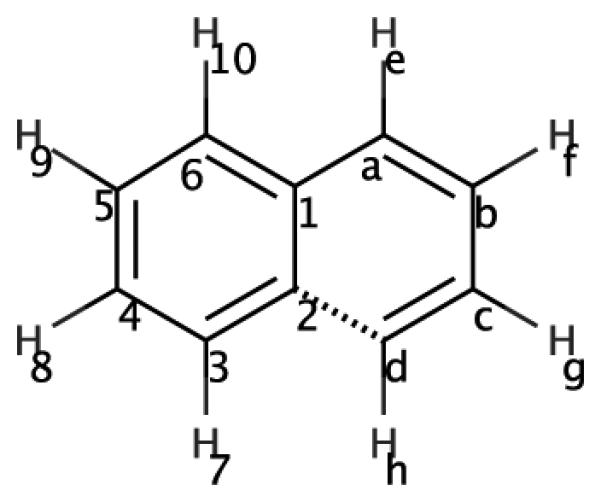
2D structure for naphthalene. Considering a transformation from naphthalene to benzene, the dashed line highlights the fact that the (right-hand) ring which would be transformed to dummy atoms is doubly connected to the remaining ring.