A Weibull multi-state model for the dependence of progression-free survival and overall survival

Abstract

In oncology clinical trials, overall survival (OS), time to progression (TTP) and progression free survival (PFS) are three commonly used endpoints. Empirical correlations among them have been published for different cancers, but statistical models describing the dependence structures are limited. Recently Fleischer et al. proposed a statistical model that is mathematically tractable and shows some flexibility to describe the dependencies in a realistic way, based on the assumption of exponential distributions. This paper aims to extend their model to the more flexible Weibull distribution. We derived theoretical correlations among different survival outcomes, as well as the distribution of overall survival induced by the model. Model parameters were estimated by the maximum likelihood method and the goodness of fit was assessed by plotting estimated vs. observed survival curves for OS. We applied the method to three cancer clinical trials. In the non-small-cell lung cancer trial, both the exponential and the Weibull models provided an adequate fit to the data and the estimated correlations were very similar under both models. In the prostate cancer trial and the laryngeal cancer trial, the Weibull model exhibited advantages over the exponential model and yielded larger estimated correlations. Simulations suggested that the proposed Weibull model is robust for data generated from a range of distributions.

1. Introduction

In the development of anti-cancer therapies the most commonly used endpoints are: overall survival (OS), time to progression (TTP) and progression free survival (PFS). OS is defined as the time from randomization until death from any cause or censoring at the last follow up. TTP is defined as the time from randomization until tumor progression, considering death as censoring. PFS considered both progression and death as events, and is defined as time from randomization to tumor progression or death whichever occurs first. Generally OS is considered as the most reliable clinical endpoint and is preferred by regulatory agencies, because prolonging patients’ lives is the ultimate goal [1]. However, determination of OS may require a prolonged follow-up period and be influenced by subsequent therapies after patients go off a given trial [2]. On the other hand, for the endpoints such as PFS and TTP the events can be observed sooner, and for certain settings these are more direct measures of clinical benefit [3, 4]. PFS and TTP have become more acceptable endpoints, especially in the earlier phases of drug development such as phase II trials [5, 6]. Among these two potential surrogate endpoints for OS, PFS is often preferred over TTP.

To validate PFS or TTP as acceptable surrogates for OS, establishing their correlations is an important aspect. There have been publications of the empirical correlations between these endpoints in different cancers [7, 8, 9, 10], but statistical models describing the dependence structures are very limited. Recently Fleischer et al. proposed a statistical model that is mathematically tractable and shows some flexibility to describe the dependencies in a realistic way [11]. Their model assumed exponential distributions for TTP, survival time before progression, and survival time post progression. They derived the correlations among the survival endpoints (TTP, PFS, and OS) and also the distribution of the OS induced by the model. However, in our attempt to apply their methods to the data from cancer clinical trials, we found cases in which there are discrepancies between the observed OS and their model-based estimated OS. Therefore, we aim to extend their method by generalizing the exponential distribution to the Weibull distribution, which should provide a more flexible model framework and a better fit to real data.

The rest of the article is organized as follows: In §2, we present the general model and the correlations between different endpoints induced by the model. In §3, we describe the method for estimating parameters and assessing overall model fit. In §4, we apply the method to three cancer clinical trials and compare the results with those from the exponential model. In §5 we present simulation results, and we offer concluding comments in §6.

2. The Statistical Model

Following the framework of Fleischer et al. [11], we use OS_orig to represent the hypothetical original OS, which is independent of TTP. Then PFS is given by the minimum of TTP and OS_orig, reflecting the general construction mechanism of the PFS. If death occurs before progression (i.e. PFS ≠ TTP), OS would be the same as PFS. Otherwise if the progression occurred first, we introduced OS’ representing the time to death after progression, and naturally we would expect that the hazard rate for OS’ would be different from the hazard rate for OS_orig, due to the occurrence of progression. In this case OS would be the sum of time to progression (TTP) and the time to death post progression (OS’). Therefore, the general model is:

$$TTP~f_1=\mathit{\text{Weibull}}(\alpha ,{\lambda }_1),O{S}_{\mathit{\text{orig}}}~f_2=\mathit{\text{Weibull}}(\alpha ,{\lambda }_2),PFS=\mathit{\text{min}}(TTP,O{S}_{\mathit{\text{orig}}})$$

$$OS\prime ~f_3=\mathit{\text{Weibull}}(\alpha ,{\lambda }_3),OS\prime ⫫TTP⫫O{S}_{\mathit{\text{orig}}}$$

$$OS=\{\begin{array}{c}PFS,\mathit{\text{if}}PFS\ne TTP\hfill \\ TTP+OS\prime ,\mathit{\text{if}}PFS=TTP;\hfill \end{array}$$

$$\mathit{\text{where}}{\lambda }_1>0,{\lambda }_2>0,{\lambda }_3>0\mathit{\text{and}}\alpha >0.$$ (1)

We assume a Weibull distribution for TTP, OS_orig and OS’, extending the exponential distribution assumption in the earlier work. We allow various rate parameters λ₁, λ₂ and λ₃ but assume a same shape parameter α, for the purpose of mathematical convenience (will be shown in the subsequent proofs). In practice often times the shape of the hazard function for progression and death are similar, e.g. if the hazard of progression increases over time, then the hazard of death increases over time as well; therefore the assumption of the same shape parameter α seems plausible. Note that in our parametrization, a variable T follows Weibull(α, λ) means f (t) = λαt^α−1exp(−λt^α).

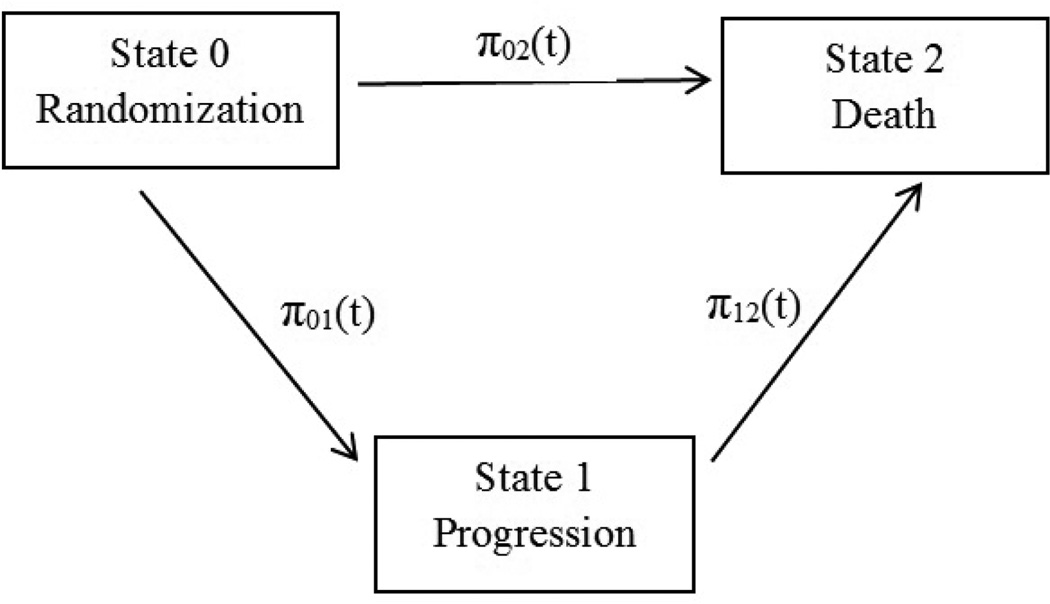
The model could also be represented as a multi-state model as illustrated in Figure 1. At randomization (or the study entry in a single-arm trial) the state is 0, progression of disease is state 1 and death is state 2. A patient could reach the absorbing state 2 (death) directly or through the transient state 1 (progression). The transition intensities (or hazards) from the state i to the state j at time t are denoted as π_ij(t). The exponential model [11] assumed that the transition intensities are constant over time, i.e., π₀₁(t) = λ₁, π₀₂(t) = λ₂, and π₁₂(t) = λ₃. Our extended Weibull model allows the transition intensities to change over time, i.e., π₀₁(t) = λ₁αt^α−1, π₀₂(t) = λ₂αt^α−1, and π₁₂(t) = λ₃αt^α−1.

Figure 1.

The multi-state Weibull model.

Then similar to Fleischer et al. [11], we can derive the five theorems:

Theorem 1

Under the general model (1), the distribution of PFS is:

$$PFS~\mathit{\text{weibull}}(\alpha ,{\lambda }_1+{\lambda }_2);$$

The probability that progression occurs first is:

$$p_0=\mathit{\text{Prob}}(PFS=TTP)=\mathit{\text{Prob}}(TTP<OS)=\frac{{\lambda }_1}{{\lambda }_1+{\lambda }_2}.$$

Theorem 2

Under the general model (1), the correlation between PFS and OS is:

$$\mathit{\text{Corr}}(PFS,OS)=\sqrt{\frac{\mathrm{\Gamma }(1+\frac{2}{\alpha })-{\mathrm{\Gamma }}^2(1+\frac{1}{\alpha })}{\mathrm{\Gamma }(1+\frac{2}{\alpha })-{\mathrm{\Gamma }}^2(1+\frac{1}{\alpha })+\frac{{\lambda }_1^2[\mathrm{\Gamma }(1+\frac{2}{\alpha })-{\mathrm{\Gamma }}^2(1+\frac{1}{\alpha })]+{\lambda }_1{\lambda }_2\mathrm{\Gamma }(1+\frac{2}{\alpha })}{{({\lambda }_1+{\lambda }_2)}^{(2-2/\alpha ){\lambda }_3^{2/\alpha }}}}}.$$

Theorem 3

Under the general model (1), the correlation between TTP and OS is:

$$\mathit{\text{Corr}}(TTP,OS)=\frac{\mathit{\text{Cov}}(TTP,OS)}{\sqrt{\frac{\mathrm{\Gamma }(1+\frac{2}{\alpha })-{\mathrm{\Gamma }}^2(1+\frac{1}{\alpha })}{{\lambda }_1^{\frac{2}{\alpha }}}·(\frac{\mathrm{\Gamma }(1+\frac{2}{\alpha })-{\mathrm{\Gamma }}^2(1+\frac{1}{\alpha })}{{({\lambda }_1+{\lambda }_2)}^{\frac{2}{\alpha }}}+\frac{{\lambda }_1^2[\mathrm{\Gamma }(1+\frac{2}{\alpha })-{\mathrm{\Gamma }}^2(1+\frac{1}{\alpha })]+{\lambda }_1{\lambda }_2\mathrm{\Gamma }(1+\frac{2}{\alpha })}{{({\lambda }_1+{\lambda }_2)}^2{\lambda }_3^{\frac{2}{\alpha }}})}};$$

$$\mathit{\text{Cov}}(TTP,OS)=\frac{{\lambda }_1}{{\lambda }_1+{\lambda }_2}[\frac{\mathrm{\Gamma }(1+\frac{2}{\alpha })}{{({\lambda }_1+{\lambda }_2)}^{\frac{2}{\alpha }}}+\frac{{\mathrm{\Gamma }}^2(1+\frac{1}{\alpha })}{{({\lambda }_1+{\lambda }_2)}^{\frac{1}{\alpha }}{\lambda }_3^{\frac{1}{\alpha }}}]+\frac{{\lambda }_2\alpha }{{\lambda }_1^{\frac{1}{\alpha }}}{\int }_0^{\infty }{x}^{\alpha }\text{exp}(-{\lambda }_2{x}^{\alpha })UIG(1+\frac{1}{\alpha },{\lambda }_1{x}^{\alpha })dx-\frac{{\mathrm{\Gamma }}^2(1+\frac{1}{\alpha })}{{\lambda }_1^{\frac{1}{\alpha }}}[\frac{1}{{({\lambda }_1+{\lambda }_2)}^{\frac{1}{\alpha }}}+\frac{{\lambda }_1}{({\lambda }_1+{\lambda }_2){\lambda }_3^{\frac{1}{\alpha }}}],$$

where UIG is the Upper Incomplete Gamma function UIG $(a,t)={\int }_t^{\infty }{u}^{a-1}{e}^{-u}du$.

Theorem 4

Under the general model (1), the conditional correlation between TTP and OS is:

$$\mathit{\text{Corr}}(TTP,OS|TTP<OS)=\frac{{\lambda }_3^{\frac{1}{\alpha }}}{\sqrt{{\lambda }_3^{\frac{2}{\alpha }}+{({\lambda }_1+{\lambda }_2)}^{\frac{2}{\alpha }}}}.$$

Theorem 5

Under the general model (1), the survival function for OS at any time point × is:

$$S_{OS}(x)=\text{exp}[-({\lambda }_1+{\lambda }_2)x^{\alpha }]+{\lambda }_1\alpha {\int }_0^x{y}^{\alpha -1}\text{exp}[-({\lambda }_1+{\lambda }_2)y^{\alpha }-{\lambda }_3{(x-y)}^{\alpha }]dy$$

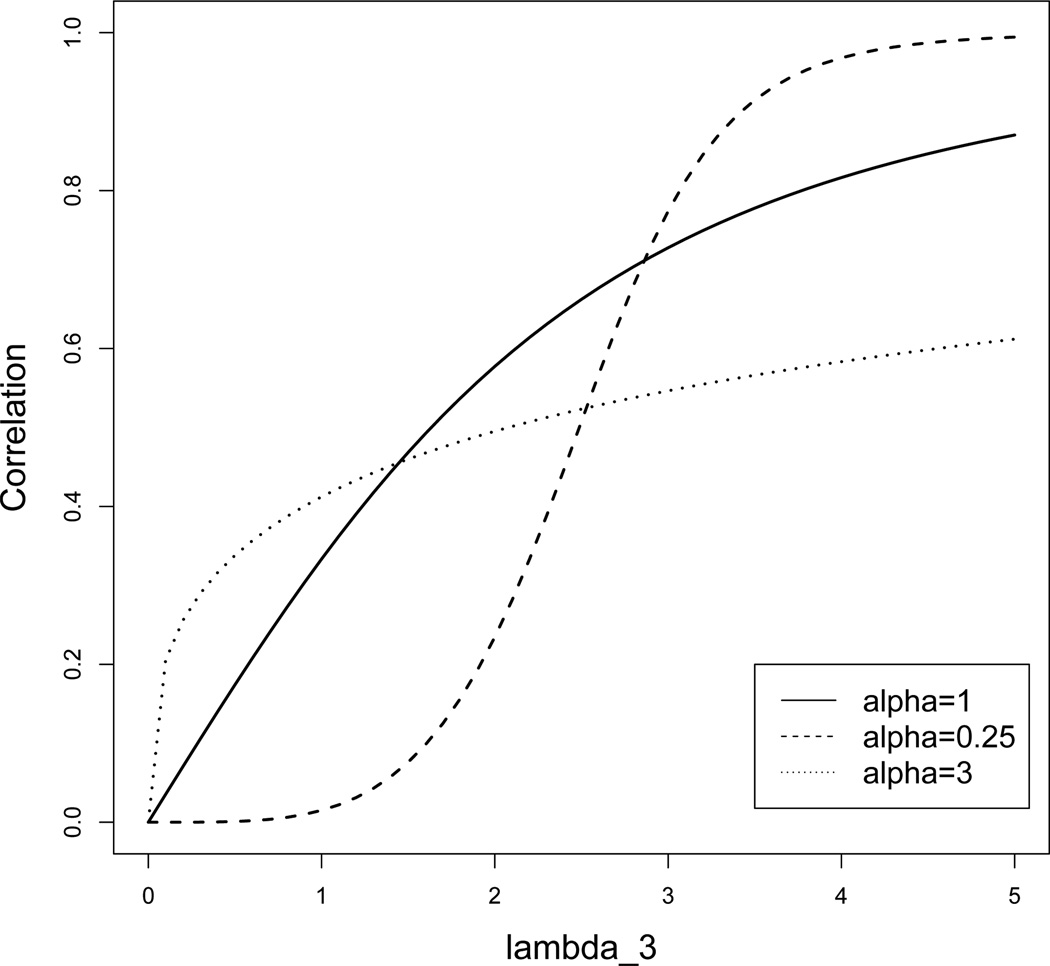
Proofs of the above theorems are provided in the Appendix. Figure 2 illustrates the correlation between PFS and OS based on Theorem 2. In this example, the parameters λ₁ and λ₂ are fixed as λ₁ = 2 and λ₂ = 1. We show three scenarios of α and various scales of λ₃. Obviously for a fixed value of α, the correlation becomes larger when λ₃ increases, and the value of α influences how the correlation changes with λ₃.

Figure 2.

Correlation of PFS and OS for λ₁ = 2, λ₂ = 1, variable λ₃ and α.

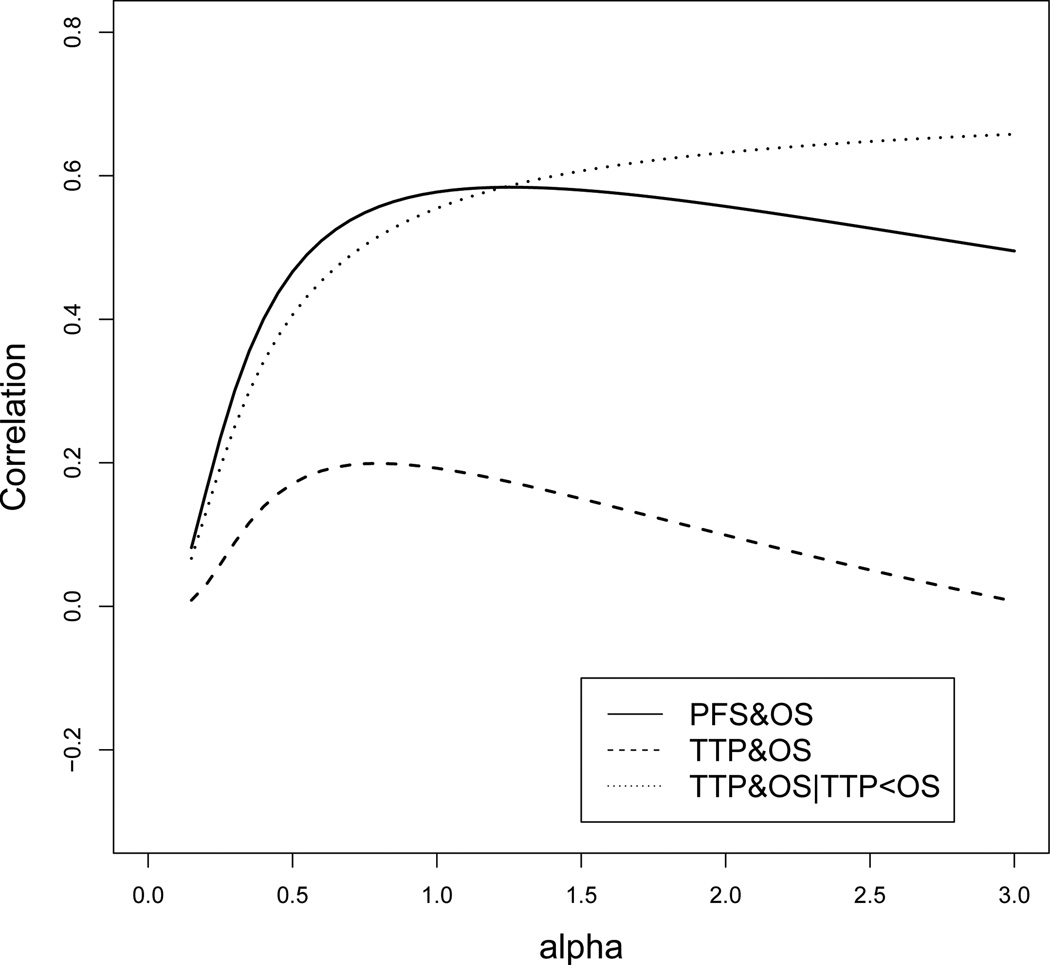
To calculate the correlation between TTP and OS based on Theorem 3, we need numerical integration to obtain the integral in the formula of Cov(TTP,OS). For any values of (λ₁, λ₂, λ₃, α), the three correlations could be calculated using Theorems 2–4. Figure 3 illustrates the correlations for λ₁ = 2, λ₂ = 1, λ₃ = 2 and variable α. We note that the correlation Corr(PFS,OS) and the conditional correlation Corr(TTP,OS|TTP<OS) are always greater than zero, but the correlation Corr(TTP,OS) could be less than zero. When λ₁, λ₂, and λ₃ are fixed, the shape parameter α has a relatively greater influence on Corr(PFS,OS) and Corr(TTP,OS|TTP<OS), and a lesser influence on Corr(TTP,OS).

Figure 3.

Correlations of Corr(PFS,OS), Corr(TTP,OS) and Corr(TTP,OS|TTP<OS), for λ₁ = 2, λ₂ = 1, λ₃ = 2 and variable α.

Moreover using Theorem 5, we can obtain the overall survival probability at any time. We again use numerical integration to calculate the integral in the formula. We also note that when α = 1, all of the above theorems (1–5) lead to the same results as shown in Fleischer et al. [11].

3. Model Estimation

We denote θ = (α, λ₁, λ₂, λ₃) as the vector of parameters to be estimated, and θ̂ = (α̂, λ̂₁, λ̂₂, λ̂₃) as the corresponding maximum likelihood estimates (MLEs). Typically the observed data contain four types of patients: 1. patients who progress and then censor without death; 2. patients who progress and then die; 3. patients who die before progression; 4. patients who censor without progression or death. We used δ_i as the indicator for patient type i (i = 1, 2, …, n); δ_i = k means patient i is of type k. For a patient of type 1 or 2, we observe two times: t_i1 representing the time to progression and t_i2 representing the time after progression to death or censoring. For a patient of type 3 or 4, we only observe one time: t_i1 representing the time to death or censoring and t_i2 is missing. We can then calculate the likelihood $L_i^{(k)}(\theta )$ (k = 1, 2, 3, 4), for each type of patient:

• If δ_i = 1 then

  $$L_i^{(1)}(\theta )=P(TTP=t_{i1})P(O{S}_{\mathit{\text{orig}}}>t_{i1})P(OS\prime >t_{i2})=f_1(t_{i1})S_2(t_{i1})S_3(t_{i2})$$
• If δ_i = 2 then

  $$L_i^{(2)}(\theta )=P(TTP=t_{i1})P(O{S}_{\mathit{\text{orig}}}>t_{i1})P(OS\prime =t_{i2})=f_1(t_{i1})S_2(t_{i1})f_3(t_{i2})$$
• If δ_i = 3 then

  $$L_i^{(3)}(\theta )=P(TTP>t_{i1})P(O{S}_{\mathit{\text{orig}}}=t_{i1})=S_1(t_{i1})f_2(t_{i1})$$
• If δ_i = 4 then

  $$L_i^{(4)}(\theta )=P(TTP>t_{i1})P(O{S}_{\mathit{\text{orig}}}>t_{i1})=S_1(t_{i1})S_2(t_{i1})$$

Recall that f₁(·) and S₁(·) are the density and survival functions for TTP which follow Weibull(α, λ₁), f₂(·) and S₂(·) are the density and survival functions for OS_orig which follow Weibull(α, λ₂), and f₃(·) and S₃(·) are the density and survival functions for OS’ which follow Weibull(α, λ₃). Summing the log likelihood across all subjects gives the overall log likelihood:

$$\text{log}L(\theta )=\sum _{i=1}^n\sum _{k=1}^4\text{log}{L}_i^{(k)}(\theta ){\mathrm{I}}_{({\delta }_i=k)}$$

Applying an optimization algorithm to the likelihood we can obtain the MLEs. In our analyses, we use the optim() function in R with the BFGS (Broyden Fletcher Goldfarb Shanno) optimization method [12]. We reparameterize all parameters (log transformation) to avoid boundary constraints in the optimization procedures. Simulations suggest that the MLE estimates behave well, with mean estimates very close to the true values.

After obtaining the MLEs, we can substitute the values of (α̂, λ̂₁, λ̂₂, λ̂₃) into Theorems 2–4 to calculate the estimated correlations. Similarly, we can estimate the survival function for OS at any time point × according to Theorem 5. Plotting this OS against time × we have the estimated OS curve based on the model, which can be compared to the Kaplan-Meier (KM) curve of the OS from the observed data. A good agreement between two curves suggests a good overall fit.

Because our model assumes a common α for TTP, OS_orig, and OS’, it would be useful to formally test this assumption. To do so we could fit another Weibull model with three different shape parameters, by simply changing the S and f in the formulas of $L_i^{(k)}$. Then we can compare the two models using the likelihood ratio (LR) test. A significant p value would suggest that the assumption of a common α is violated.

All analyses are conducted in R. Sample R codes are provided in the supplement and full codes are available from the authors.

4. Application

We applied our methods to three examples of cancer clinical trials from the Radiation Therapy Oncology Group (RTOG). In all three examples, PFS was the primary endpoint and OS was one of the secondary endpoints. The first study was a phase III trial to compare prophylactic cranial irradiation versus observation in patients with locally advanced non-small-cell lung cancer (RTOG 0214) [13, 14]. The failure event of PFS was defined as the earliest event of death due to any cause, local progression, regional metastasis, distant metastasis, or second primary tumor. The second study was a phase III trial to compare whole-pelvic versus prostate-only radiotherapy and neoadjuvant versus adjuvant combined androgen suppression (RTOG 9413) [15]. The failure event of PFS was defined as the first occurrence of local progression, regional nodal failure, distant failure, biochemical (PSA) failure or death due to any cause. The third study was a randomized trial to compare three treatments for patients with locally advanced cancer of the larynx (RTOG 9111) [16]. The failure event of PFS was defined as laryngectomy or death due to any cause. In RTOG 0214 and RTOG 9111 neither OS or PFS was significantly different between treatment arms; therefore, all treatment arms were pooled in our analyses. In RTOG 9413, although OS was similar across treatment arms, PFS was significantly higher in the patients treated with whole-pelvic radiotherapy (WPRT) than those treated with prostate-only radiotherapy (PORT), so the two treatment groups were analyzed separately.

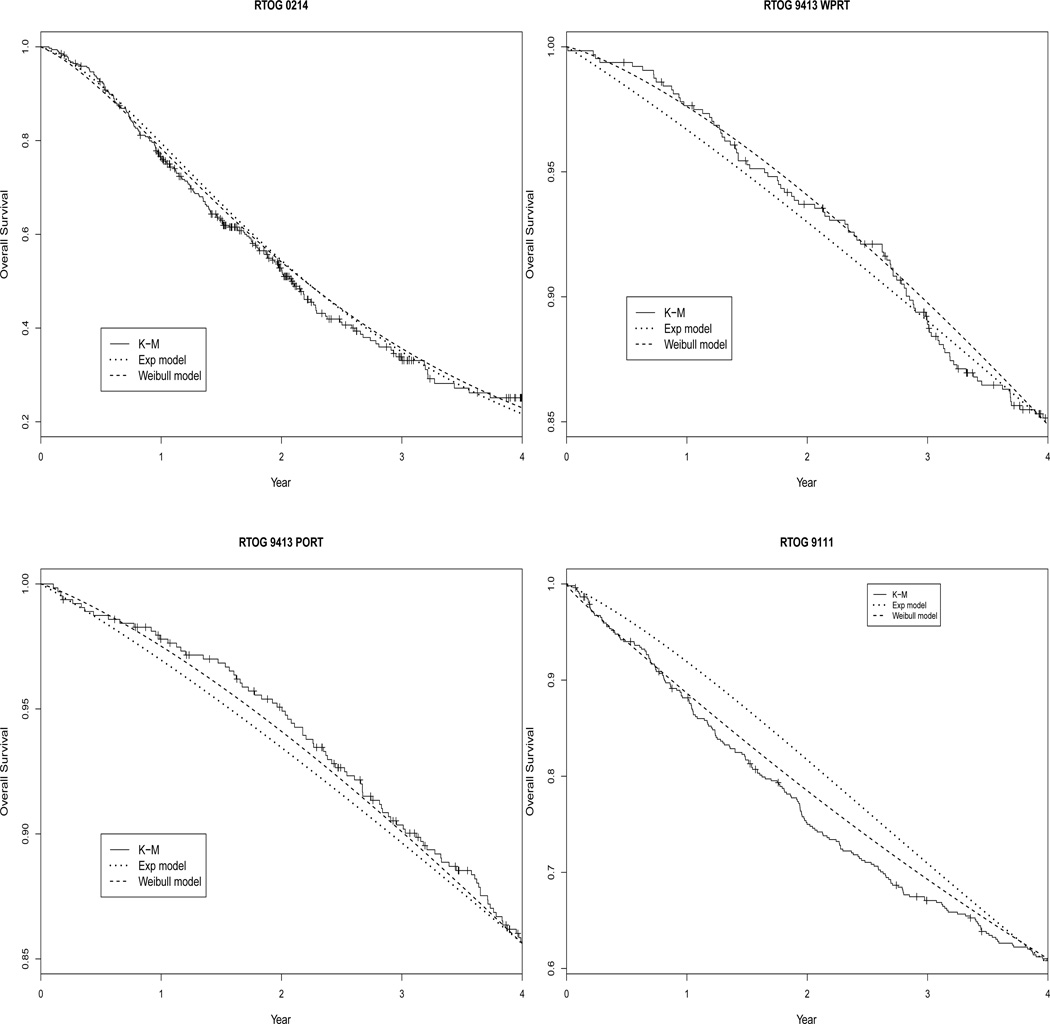
Table 1 presents the estimated parameters from the exponential model and the Weibull model, Table 2 presents the estimated correlations from the two models by substituting MLEs into Theorems 2–4, and Figure 4 shows the estimated KM curve for OS together with the estimated curves for OS based on Theorem 5. In the first trial RTOG 0214, the estimated log(α) in the Weibull model is very close to 0, so that the Weibull model essentially reduces to the exponential model. Therefore the estimated log(λ)s under the two models are almost identical (Table 1), the estimated correlations under two models are almost the same as well (Table 2), and the estimated OS survival curves from both models are almost overlapping with the observed KM curve (Figure 4). Interestingly, comparing our Weibull model with the same shape parameter to the Weibull model with different shape parameters, the LR test gives a p value of 0.0183 suggesting a violation of the common α assumption. In the model with different shape parameters, the estimated αs are 0.93, 1.35 and 0.88. Therefore, when forcing a common α as in our proposed Weibull model, the estimated α is close to 1 reflecting an average of the three αs. This trial example suggests that our Weibull model could fit the data well even if the assumption of common shape parameter is questionable, and the exponential model and Weibull model fit the data similarly well when the shape parameter α is close to 1.

Table 1.

Parameter estimates from exponential and Weibull models.

	exponential			Weibull
	log(λ1)	log(λ2)	log(λ3)	log(α)	log(λ1)	log(λ2)	log(λ3)
RTOG 0214	−0.846	−2.418	0.037	−0.057	−0.817	−2.382	0.043
RTOG 9413 WPRT	−2.066	−3.481	−2.527	0.219	−2.361	−3.778	−2.710
RTOG 9413 PORT	−2.011	−3.586	−2.535	0.138	−2.187	−3.763	−2.649
RTOG 9111	−1.710	−2.768	−1.086	−0.260	−1.463	−2.524	−0.907

Table 2.

Estimated correlations from exponential and Weibull models.

	exponential			Weibull
	PFS&OS	TTP&OS	Conditional TTP&OS	PFS&OS	TTP&OS	Conditional TTP&OS
RTOG 0214	0.897	0.679	0.895	0.901	0.682	0.897
RTOG 9413 WPRT	0.460	0.228	0.453	0.527	0.269	0.536
RTOG 9413 PORT	0.446	0.240	0.440	0.491	0.269	0.494
RTOG 9111	0.820	0.496	0.812	0.835	0.511	0.814

Figure 4.

Observed KM curve and model-estimated curves for OS based on Theorem 5.

In the second trial RTOG 9413, the LR test for the common α gives a p value of 0.6065 for both WPRT and PORT treatment arms, supporting the use of the proposed model. Also for both treatment arms, the estimated log(α) in the Weibull model is greater than 0 so the estimated log(λ)s under the two models are somewhat different and the correlations estimated from the Weibull model are greater than those from the exponential model. Figure 4 suggests that for both treatment arms the Weibull model fit better to the observed data than the exponential model. Comparing the parameter estimates for the two treatment arms, we observe a greater difference in log(λ₁) than in log(λ₂) or log(λ₃). This suggests that the treatment has some influence on the hazard of TTP but not on the hazard of death – either before or after progression. This is consistent with the original study findings that PFS is significantly different between treatment arms while OS is not.

In the third trial RTOG 9111, the p value for the the LR test of the common α is 0.3679. The estimated log(α) in the Weibull model is less than 0, leading to different estimates of log(λ)s and correlations under the two models. In Figure 4, although both estimated curves show some departure from the observed KM curve, the estimated curve from the Weibull model is closer to the KM curve suggesting a better fit with the Weibull model.

5. Simulation

We have conducted simulations to evaluate the fit of the two models (exponential model and Weibull model), using data sets generated from various distributions. In all simulations, we considered a moderate sample size of 500 subjects. For each subject, we generated TTP, OS_orig, OS’ from the assumed distributions and applied a fixed censoring time. One data set was generated for each scenario.

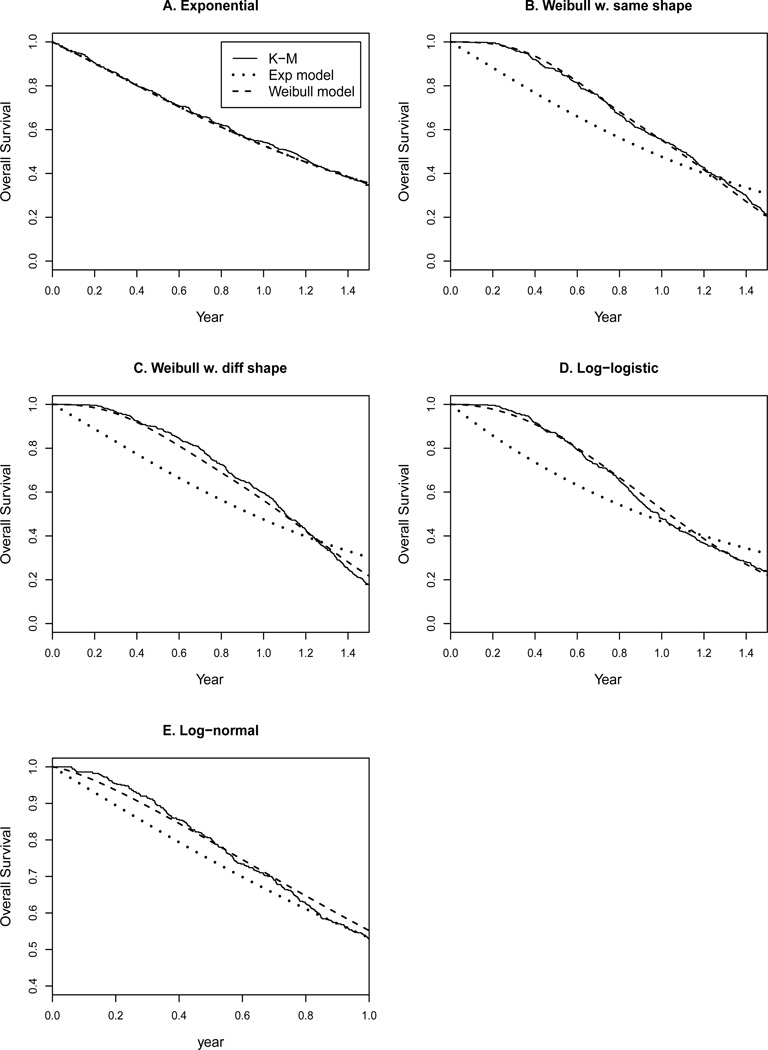
In the first scenario, the event times were generated from exponential distributions. More specifically, TTP was generated from exponential(λ₁ = 1), OS_orig was generated from exponential(λ₂ = 0.5), and OS’ was generated from exponential(λ₃ = 1). This led to a mean TTP of 1 year, a mean OS_orig of 2 years, a mean OS’ of 1 year, and a mean OS of 0.99 years. We then applied a fixed censoring time at 1.5 years. In the data set we generated, 119 subjects progressed and were then censored without death, 190 subjects progressed and then died, 137 subjects died before progression, and 54 patients were censored without progression or death. We fitted the exponential model and the Weibull model separately to the data set and estimated MLEs. We estimated model-based correlations according to Theorems 2–4 and summarized these in Table 3. We also estimated model-based survival functions for OS according to Theorem 5, and Figure 5 (Figure 5A for this scenario) shows the observed KM curve for OS and the estimated curves from the two models. As expected, because the data were generated from exponential distributions, correlations under the two models were similar and both models fit the observed data perfectly.

Table 3.

Estimated correlations from the exponential and Weibull models, in simulated data sets from various distributions.

	exponential			Weibull
Data distribution	PFS&OS	TTP&OS	Conditional TTP&OS	PFS&OS	TTP&OS	Conditional TTP&OS
Exponential	0.574	0.214	0.555	0.573	0.215	0.553
Weibull w. same shape	0.560	0.159	0.534	0486	0.022	0.648
Weibull w. diff shape	0.504	0.175	0.488	0.474	0.046	0.593
Log-logistic	0.000	−0.062	0.000	0.204	−0.137	0.041
Log-normal	0.479	0.112	0.457	0.504	0.094	0.515

Figure 5.

Fit of two models to data sets simulated from various distributions.

In the second scenario, the event times were generated from Weibull distributions with the same shape parameter. More specifically, TTP was generated from Weibull(α = 3, λ₁ = 2), OS_orig was generated from Weibull(α = 3, λ₂ = 1), and OS’ was generated from Weibull(α = 3, λ₃ = 2). This led to a mean TTP of 0.71 years, a mean OS_orig of 0.89 years, and a mean OS’ of 0.71 years, with a fixed censoring time at 1.5 years. The final OS had a mean of 1.03 years. Figure 5B suggests that the Weibull model fit the data perfectly but the exponential model fit poorly, because the data violated the exponential distribution assumption. Table 3 suggests that the exponential model overestimated correlations between PFS and OS and between TTP and OS, but underestimated the conditional correlation between TTP and OS.

Because our Weibull model assumed the same shape parameter in distributions of the three endpoints, in the third scenario we generated the event times from Weibull distributions with different shape parameters. More specifically, TTP was generated from Weibull(α = 2, λ₁ = 2), OS_orig was generated from Weibull(α = 3, λ₂ = 1), and OS’ was generated from Weibull(α = 4, λ₃ = 2). So TTP had a mean of of 0.63 years, OS_orig had a mean of 0.89 years, OS’ had a mean of 0.76 years, and finally OS had a mean of 1.05 years. The LR test of the common α assumption gave a p value of < 0.0001, as expected. However, even though the data violated the assumption of the same shape parameter, our Weibull model could still fit satisfactorily. As shown in Figure 5C, there was an adequate fit with the Weibull model but a lack of fit with the exponential model. Table 3 shows that correlations under the two models differed by −0.13 to 0.11. The correlations under the Weibull model should be more accurate given that the Weibull model fit the data better.

Moreover because the Weibull distribution assumed a monotone hazard function, we generated event times from log-logistic distributions to allow hazards with non-monotone shapes. With our notation, time T follows log-logistic (α, λ) means that the hazard function is (αt^α−1λ)/(1 + λt^α). In this example, TTP was generated from log-logistic(α = 3, λ₁ = 2), OS_orig was generated from log-logistic(α = 3, λ₂ = 1), and OS’ was generated from log-logistic(α = 3, λ₃ = 2). So the hazard functions of all three event times first increased and then decreased. The data then had a mean TTP of 0.96 years, a mean OS_orig of 1.21 years, a mean OS’ of 0.96 years, and a mean OS of 1.00 years. Figure 5D shows that the curve based on the Weibull model was much closer to the KM curve, compared to the curve based on the exponential model. This indicated that the Weibull model provided better fit than the exponential model even if the underlying distribution was not Weibull. Table 3 shows that correlations under the two models differed by −0.08 to 0.20.

Lastly, we generated event times from log-normal distributions. TTP was generated from log-normal(μ = −0.5, σ = 1), OS_orig was generated from log-normal(μ = 0.1, σ = 1), and OS’ was generated from log-normal(μ = −0.2, σ = 1). The final OS had a mean of 1.01 years. Figure 5E shows that the Weibull model fit the data somewhat better than the exponential model. Table 3 shows that correlations under the two models differed by −0.02 to 0.06.

We also used one simulation example to explore the implications of our model on power calculations. We assumed that the data consisted of two groups with a fixed follow up of 1.5 years. We assumed the data of the treatment group were from our model with TTP~Weibull(α = 3, λ₁ = 2), OS_orig ~Weibull(α = 3, λ₂ = 1), and OS’~Weibull(α = 3, λ₃ = 2), and the data of the control group were from our model with TTP~Weibull(α = 3, λ₁ = 2.7), OS_orig ~Weibull(α = 3, λ₂ = 1.7), and OS’~Weibull(α = 3, λ₃ = 2.7). This meant that the one-year survival for OS was 45% in the control group and 57% in the treatment group. Using the standard method assuming OS is exponentially distributed and neglecting any correlation between OS and PFS, the one-year survival for OS translated to a hazard rate of 0.56 and 0.80 for the two groups, respectively. Thus, we would need a total of 396 subjects (i.e., 256 events in 1.5 year follow up period) to detect such a difference with 80% power. In contrast, by generating 4000 data sets with a sample size of 396 subjects (198 per group) from the assumed Weibull model and conducting log-rank test on each data set, 94.8% of them gave a significant p value. Therefore, the power is much higher using our proposed model compared to using the standard exponential model.

6. Discussion

We have proposed a Weibull statistical model to describe the dependence between PFS and OS, which is a direct extension of the earlier work of Fleischer et al [11]. Under the model framework we derived analytical correlations among TTP, PFS and OS, and presented five theorems that are similar in structure to Fleischer et al. When generalizing from exponential to Weibull distributions, the results of the theorems become complex and not straightforward. Nevertheless, the extended model is more robust and realistic for data we often observe in various studies, as shown in our clinical trial examples.

As illustrated by Figure 1, our proposed model actually falls under the umbrella of general illness-death models. The transition intensities under this three-state model are simply the hazard rates for TTP, OS_orig and OS’. So the distribution function of OS in Theorem 5 can also be derived using the techniques for multi-state models and calculating the transition probabilities from one state to another. In addition to the usual focus of multi-state models on estimating transition probabilities, our paper had another goal of estimating correlations among different survival endpoints.

The correlations among TTP, PFS and OS can be estimated using the presented Theorems 2–4. In the three clinical trials, we observed small differences in the the estimated correlations under the Weibull model and the exponential model, presumably because the estimated α was close to 1, so that the advantage of the Weibull over the exponential model was modest. In the simulation examples, the differences of the estimated correlations under the two models were moderate, in the range of −0.13 to 0.20. Theoretically, as illustrated in Figure 2 and 3, the correlations from the two models could be substantially different under some parameter values. In applications of the methods to real data, one cannot predict the magnitude of the difference before fitting the Weibull model and estimating the shape parameter α. Since the Weibull model in general is more flexible and fits data better than the exponential model, the correlations under the Weibull model should be more accurate. Naively applying an exponential model could potentially over- or under- estimate the true correlations.

In our Weibull model, we assume that the three event times share the same shape parameter α, which makes the analytical derivations of the correlations feasible. As shown in our appendix, the derivations are already complex under the current assumption, and would become untraceable if we generalized to Weibull distributions with different shape parameters. In analysis of real data, one can always fit the Weibull model with different shape parameters and conduct the LR test for common α, as we demonstrate in §4. A non-significant LR test would justify the use of our proposed Weibull model with a common α. Even in the cases that the common α assumption is violated, our Weibull model could still fit data adequately, as shown in RTOG 0214 and in the simulation example. Nevertheless, one could choose the model with three shape parameters if the common α assumption is a concern, but should keep in mind that under this model the correlations among the survival endpoints and the distribution of OS cannot be derived analytically.

Although the Weibull model provides more flexibility than the exponential model, it is possible that the Weibull model still misspecifies the underlying distribution, especially if the data are actually from a distribution with a non-monotone hazard function. However in our two simulation examples with data from log-logistic distributions and log-normal distributions, our Weibull model seems to provide an adequate fit.

The majority of the paper focuses on one-group scenarios but we explore a two-group scenario through one real trial example and one simulation example. In RTOG 9413, we fit the proposed model to the two treatment groups separately and the group-specific estimates reveal how the treatment influences the hazards of progression and death. Moreover under our proposed model although the distributions for TTP, OS_orig and OS’ are Weibull which implies proportional hazard between groups, the induced OS will not have proportional hazards. So our model would be useful when the data exhibit non-proportionality features. Lastly by considering the dependence structure between PFS and OS, our Weibull model would be more powerful than the standard method assuming a simple exponential distribution for OS. This is demonstrated by the last simulation example and a thorough investigation of this issue will be our future research.

Appendix

We first note that for a Weibull distribution with parameters (λ, α),

$$E(T)={\lambda }^{-\frac{1}{\alpha }}\mathrm{\Gamma }(1+\frac{1}{\alpha }),E(T^2)={\lambda }^{-\frac{2}{\alpha }}\mathrm{\Gamma }(1+\frac{2}{\alpha })$$

$$\mathit{\text{Var}}(T)={\lambda }^{-\frac{2}{\alpha }}\mathrm{\Gamma }(1+\frac{2}{\alpha })-{\lambda }^{-\frac{2}{\alpha }}{[\mathrm{\Gamma }(1+\frac{1}{\alpha })]}^2$$

Proof of Theorem 1

$$P(PFS\ge t)=P(\mathit{\text{min}}(TTP,O{S}_{\mathit{\text{orig}}})\ge t)=P(TTP\ge t)P(O{S}_{\mathit{\text{orig}}}\ge t)=\text{exp}[-({\lambda }_1+{\lambda }_2)t^{\alpha }]$$

That is, PFS follows Weibull (α, λ₁ + λ₂).

$$p_0=\mathit{\text{Prob}}(PFS=TTP)=P(TTP<O{S}_{\mathit{\text{orig}}})={\int }_{y<x}{\lambda }_1\alpha y^{\alpha -1}\text{exp}(-{\lambda }_1{y}^{\alpha })\dot{\lambda }\alpha x^{\alpha -1}\text{exp}(-{\lambda }_2{x}^{\alpha })dxdy={\int }_0^{\infty }{\lambda }_1\alpha y^{\alpha -1}\text{exp}(-{\lambda }_1{y}^{\alpha })[{\int }_y^{\infty }{\lambda }_2\alpha x^{\alpha -1}\text{exp}(-{\lambda }_2{x}^{\alpha })dx]dy={\int }_0^{\infty }{\lambda }_1\alpha y^{\alpha -1}\text{exp}(-{\lambda }_1{y}^{\alpha })\text{exp}({\lambda }_2{y}^{\alpha })dy=\frac{{\lambda }_1}{{\lambda }_1+{\lambda }_2}{\int }_0^{\infty }({\lambda }_1+{\lambda }_2)\alpha y^{\alpha -1}\text{exp}[-({\lambda }_1+{\lambda }_2)y^{\alpha }]dy=\frac{{\lambda }_1}{{\lambda }_1+{\lambda }_2}.$$

Proof of Theorem 2

$$E(PFS·OS)=E(PFS·OS|PFS<OS)\mathit{\text{Prob}}(PFS<OS)+E(PFS·OS|PFS=OS)\mathit{\text{Prob}}(PFS=OS)=E(PFS·(PFS+OS\prime ))\mathit{\text{Prob}}(PFS=TTP)+E(PFS·PFS)\mathit{\text{Prob}}(PFS\ne TTP)=E(PF{S}^2+PFS·OS\prime )p_0+E(PF{S}^2)(1-p_0)=E(PF{S}^2)+E(PFS)·E(OS\prime )p_0={({\lambda }_1+{\lambda }_2)}^{-\frac{2}{\alpha }}\mathrm{\Gamma }(1+\frac{2}{\alpha })+{({\lambda }_1+{\lambda }_2)}^{-\frac{1}{\alpha }}\mathrm{\Gamma }(1+\frac{1}{\alpha })·{\lambda }_3^{-\frac{1}{\alpha }}\mathrm{\Gamma }(1+\frac{1}{\alpha })·\frac{{\lambda }_1}{{\lambda }_1+{\lambda }_2}=\frac{1}{{({\lambda }_1+{\lambda }_2)}^{\frac{2}{\alpha }}}\mathrm{\Gamma }(1+\frac{2}{\alpha })+\frac{{\lambda }_1}{{({\lambda }_1+{\lambda }_2)}^{(1+\frac{1}{\alpha })}{\lambda }_3^{\frac{1}{\alpha }}}{\mathrm{\Gamma }}^2(1+\frac{1}{\alpha })$$ (2)

$$E(PFS)=\frac{1}{{({\lambda }_1+{\lambda }_2)}^{\frac{1}{\alpha }}}\mathrm{\Gamma }(1+\frac{1}{\alpha }),(\text{use Theorem}1)$$ (3)

$$E(OS)=E(OS|PFS<OS)\mathit{\text{Prob}}(PFS<OS)+E(OS|PFS=OS)\mathit{\text{Prob}}(PFS=OS)=E(PFS+OS\prime )\mathit{\text{Prob}}(PFS=TTP)+E(PFS)\mathit{\text{Prob}}(PFS\ne TTP)=E(PFS+OS\prime )p_0+E(PFS)(1-p_0)=E(PFS)+E(OS\prime )p_0={({\lambda }_1+{\lambda }_2)}^{-\frac{1}{\alpha }}\mathrm{\Gamma }(1+\frac{1}{\alpha })+{\lambda }_3^{-\frac{1}{\alpha }}\mathrm{\Gamma }(1+\frac{1}{\alpha })·\frac{{\lambda }_1}{{\lambda }_1+{\lambda }_2}=\mathrm{\Gamma }(1+\frac{1}{\alpha })[\frac{1}{{({\lambda }_1+{\lambda }_2)}^{\frac{1}{\alpha }}}+\frac{{\lambda }_1}{({\lambda }_1+{\lambda }_2){\lambda }_3^{\frac{1}{\alpha }}}]$$ (4)

$$\mathit{\text{Cov}}(PFS,OS)=E(PFS·OS)-E(PFS)E(OS),(\text{use}(2),(3)\text{and}(4))=\frac{1}{{({\lambda }_1+{\lambda }_2)}^{\frac{2}{\alpha }}}\mathrm{\Gamma }(1+\frac{2}{\alpha })+\frac{{\lambda }_1}{{({\lambda }_1+{\lambda }_2)}^{(1+\frac{1}{\alpha })}{\lambda }_3^{\frac{1}{\alpha }}}{\mathrm{\Gamma }}^2(1+\frac{1}{\alpha })-\frac{1}{{({\lambda }_1+{\lambda }_2)}^{\frac{1}{\alpha }}}\mathrm{\Gamma }(1+\frac{1}{\alpha })·\mathrm{\Gamma }(1+\frac{1}{\alpha })[\frac{1}{{({\lambda }_1+{\lambda }_2)}^{\frac{1}{\alpha }}}+\frac{{\lambda }_1}{({\lambda }_1+{\lambda }_2){\lambda }_3^{\frac{1}{\alpha }}}]=\frac{\mathrm{\Gamma }(1+\frac{2}{\alpha })-{\mathrm{\Gamma }}^2(1+\frac{1}{\alpha })}{{({\lambda }_1+{\lambda }_2)}^{\frac{2}{\alpha }}}$$ (5)

$$\mathit{\text{Var}}(PFS)=\frac{1}{{({\lambda }_1+{\lambda }_2)}^{\frac{2}{\alpha }}}[\mathrm{\Gamma }(1+\frac{2}{\alpha })-{\mathrm{\Gamma }}^2(1+\frac{1}{\alpha })],(\text{use Theorem}1)$$ (6)

$$E(O{S}^2)=E(O{S}^2|PFS<OS)\mathit{\text{Prob}}(PFS<OS)+E(O{S}^2|PFS=OS)\mathit{\text{Prob}}(PFS=OS)=E({(PFS+OS\prime )}^2)\mathit{\text{Prob}}(PFS=TTP)+E(PF{S}^2)\mathit{\text{Prob}}(PFS\ne TTP)=E(PF{S}^2+O{S}^{\prime 2}+2PFS·OS\prime )p_0+E(PF{S}^2)(1-p_0)=E(PF{S}^2)+E(O{S}^{\prime 2})p_0+2E(PFS)E(OS\prime )p_0,(\text{use Theorem}1\text{and Weibull distribution properties})={({\lambda }_1+{\lambda }_2)}^{-\frac{2}{\alpha }}\mathrm{\Gamma }(1+\frac{2}{\alpha })+{\lambda }_3^{-\frac{2}{\alpha }}\mathrm{\Gamma }(1+\frac{2}{\alpha })·\frac{{\lambda }_1}{{\lambda }_1+{\lambda }_2}+2{({\lambda }_1+{\lambda }_2)}^{-\frac{1}{\alpha }}\mathrm{\Gamma }(1+\frac{1}{\alpha })·{\lambda }_3^{-\frac{1}{\alpha }}\mathrm{\Gamma }(1+\frac{1}{\alpha })·\frac{{\lambda }_1}{{\lambda }_1+{\lambda }_2}=\mathrm{\Gamma }(1+\frac{2}{\alpha })[\frac{1}{{({\lambda }_1+{\lambda }_2)}^{\frac{2}{\alpha }}}+\frac{{\lambda }_1}{({\lambda }_1+{\lambda }_2){\lambda }_3^{\frac{2}{\alpha }}}]+2{\mathrm{\Gamma }}^2(1+\frac{1}{\alpha })\frac{{\lambda }_1}{{({\lambda }_1+{\lambda }_2)}^{(1+\frac{1}{\alpha })}{\lambda }_3^{\frac{1}{\alpha }}}$$ (7)

$$\mathit{\text{Var}}(OS)=E(O{S}^2)-E^2(OS),(\text{use}(7)\text{and}(4))=\mathrm{\Gamma }(1+\frac{2}{\alpha })[\frac{1}{{({\lambda }_1+{\lambda }_2)}^{\frac{2}{\alpha }}}+\frac{{\lambda }_1}{({\lambda }_1+{\lambda }_2){\lambda }_3^{\frac{2}{\alpha }}}]+2{\mathrm{\Gamma }}^2(1+\frac{1}{\alpha })\frac{{\lambda }_1}{{({\lambda }_1+{\lambda }_2)}^{(1+\frac{1}{\alpha })}{\lambda }_3^{\frac{1}{\alpha }}}-{(\mathrm{\Gamma }(1+\frac{1}{\alpha })[\frac{1}{{({\lambda }_1+{\lambda }_2)}^{\frac{2}{\alpha }}}+\frac{{\lambda }_1}{({\lambda }_1+{\lambda }_2){\lambda }_3^{\frac{1}{\alpha }}}])}^2=\frac{\mathrm{\Gamma }(1+\frac{2}{\alpha })-{\mathrm{\Gamma }}^2(1+\frac{1}{\alpha })}{{({\lambda }_1+{\lambda }_2)}^{\frac{2}{\alpha }}}+\frac{{\lambda }_1^2[\mathrm{\Gamma }(1+\frac{2}{\alpha })-{\mathrm{\Gamma }}^2(1+\frac{1}{\alpha })]+{\lambda }_1{\lambda }_2\mathrm{\Gamma }(1+\frac{2}{\alpha })}{{({\lambda }_1+{\lambda }_2)}^2{\lambda }_3^{\frac{2}{\alpha }}}$$ (8)

Equations 5, 6 and 8 give

$$\mathit{\text{Corr}}(PFS,OS)=\sqrt{\frac{\mathrm{\Gamma }(1+\frac{2}{\alpha })-{\mathrm{\Gamma }}^2(1+\frac{1}{\alpha })}{\mathrm{\Gamma }(1+\frac{2}{\alpha })-{\mathrm{\Gamma }}^2(1+\frac{1}{\alpha })+\frac{{\lambda }_1^2[\mathrm{\Gamma }(1+\frac{2}{\alpha })-{\mathrm{\Gamma }}^2(1+\frac{1}{\alpha })]+{\lambda }_1{\lambda }_2\mathrm{\Gamma }(1+\frac{2}{\alpha })}{{({\lambda }_1+{\lambda }_2)}^{(2-2/\alpha )}{\lambda }_3^{2/\alpha }}}}.$$ (9)

Proof of Theorem 3

$$\mathit{\text{Var}}(TTP)=\frac{\mathrm{\Gamma }(1+\frac{2}{\alpha })-{\mathrm{\Gamma }}^2(1+\frac{1}{\alpha })}{{\lambda }_1^{\frac{2}{\alpha }}},(\text{use Weibull properties});$$ (10)

$$E(TTP·OS,PFS=OS)=E(TTP·PFS,PFS<TTP)=E(TTP·O{S}_{\mathit{\text{orig}}},O{S}_{\mathit{\text{orig}}}<TTP)={\int }_{x<y}xy{\lambda }_2\alpha x^{\alpha -1}\text{exp}(-{\lambda }_2{x}^{\alpha }){\lambda }_1\alpha y^{\alpha -1}\text{exp}(-{\lambda }_1{y}^{\alpha })dxdy={\int }_0^{\infty }x{\lambda }_2\alpha x^{\alpha -1}\text{exp}(-{\lambda }_2{x}^{\alpha })dx{\int }_x^{\infty }y{\lambda }_1\alpha y^{\alpha -1}\text{exp}(-{\lambda }_1{y}^{\alpha })dy={\int }_0^{\infty }{\lambda }_2\alpha x^{\alpha }\text{exp}(-{\lambda }_2{x}^{\alpha })dx\frac{1}{{\lambda }_1^{\frac{1}{\alpha }}}{\int }_{{\lambda }_1{x}^{\alpha }}^{\infty }{t}^{\frac{1}{\alpha }}\text{exp}(-t)dt=\frac{{\lambda }_2\alpha }{{\lambda }_1^{\frac{1}{\alpha }}}{\int }_0^{\infty }{x}^{\alpha }\text{exp}(-{\lambda }_2{x}^{\alpha })UIG(1+\frac{1}{\alpha },{\lambda }_1{x}^{\alpha })dx$$ (11)

$$E(TTP·OS)=E(TTP·OS|PFS<OS)\mathit{\text{Prob}}(PFS<OS)+E(TTP·OS,PFS=OS)=p_{0}E(PFS(PFS+OS\prime ))+E(TTP·OS,PFS=OS)=p_0[E(PF{S}^2)+E(PFS)E(OS\prime )]+E(TTP·OS,PFS=OS),(\text{use Theorem}1,\text{Weibull properties and}(11))=\frac{{\lambda }_1}{{\lambda }_1+{\lambda }_2}·[{({\lambda }_1+{\lambda }_2)}^{-\frac{2}{\alpha }}\mathrm{\Gamma }(1+\frac{2}{\alpha })+{({\lambda }_1+{\lambda }_2)}^{-\frac{1}{\alpha }}\mathrm{\Gamma }(1+\frac{1}{\alpha })·{\lambda }_3^{-\frac{1}{\alpha }}\mathrm{\Gamma }(1+\frac{1}{\alpha })]+\frac{{\lambda }_2\alpha }{{\lambda }_1^{\frac{1}{\alpha }}}{\int }_0^{\infty }{x}^{\alpha }\text{exp}(-{\lambda }_2{x}^{\alpha })UIG(1+\frac{1}{\alpha },{\lambda }_1{x}^{\alpha })dx=\frac{{\lambda }_1}{{\lambda }_1+{\lambda }_2}[\frac{\mathrm{\Gamma }(1+\frac{2}{\alpha })}{{({\lambda }_1+{\lambda }_2)}^{\frac{2}{\alpha }}}+\frac{{\mathrm{\Gamma }}^2(1+\frac{1}{\alpha })}{{({\lambda }_1+{\lambda }_2)}^{\frac{1}{\alpha }}{\lambda }_3^{\frac{1}{\alpha }}}]+\frac{{\lambda }_2\alpha }{{\lambda }_1^{\frac{1}{\alpha }}}{\int }_0^{\infty }{x}^{\alpha }\text{exp}(-{\lambda }_2{x}^{\alpha })UIG(1+\frac{1}{\alpha },{\lambda }_1{x}^{\alpha })dx$$ (12)

$$\mathit{\text{Cov}}(TTP,OS)=E(TTP·OS)-E(TTP)E(OS),(\text{use Weibull property and}(4))=E(TTP·OS)-\frac{1}{{\lambda }_1^{\frac{1}{\alpha }}}\mathrm{\Gamma }(1+\frac{1}{\alpha })·\mathrm{\Gamma }(1+\frac{1}{\alpha })[\frac{1}{{({\lambda }_1+{\lambda }_2)}^{\frac{2}{\alpha }}}+\frac{{\lambda }_1}{({\lambda }_1+{\lambda }_2){\lambda }_3^{\frac{1}{\alpha }}}]=E(TTP·OS)-\frac{{\mathrm{\Gamma }}^2(1+\frac{1}{\alpha })}{{\lambda }_1^{\frac{1}{\alpha }}}[\frac{1}{{({\lambda }_1+{\lambda }_2)}^{\frac{1}{\alpha }}}+\frac{{\lambda }_1}{({\lambda }_1+{\lambda }_2){\lambda }_3^{\frac{1}{\alpha }}}]=\frac{{\lambda }_1}{{\lambda }_1+{\lambda }_2}[\frac{\mathrm{\Gamma }(1+\frac{2}{\alpha })}{{({\lambda }_1+{\lambda }_2)}^{\frac{2}{\alpha }}}+\frac{{\mathrm{\Gamma }}^2(1+\frac{1}{\alpha })}{{({\lambda }_1+{\lambda }_2)}^{\frac{1}{\alpha }}{\lambda }_3^{\frac{1}{\alpha }}}]+\frac{{\lambda }_2\alpha }{{\lambda }_1^{\frac{1}{\alpha }}}{\int }_0^{\infty }{x}^{\alpha }\text{exp}(-{\lambda }_2{x}^{\alpha })UIG(1+\frac{1}{\alpha },{\lambda }_1{x}^{\alpha })dx-\frac{{\mathrm{\Gamma }}^2(1+\frac{1}{\alpha })}{{\lambda }_1^{\frac{1}{\alpha }}}[\frac{1}{{({\lambda }_1+{\lambda }_2)}^{\frac{1}{\alpha }}}+\frac{{\lambda }_1}{({\lambda }_1+{\lambda }_2){\lambda }_3^{\frac{1}{\alpha }}}];$$ (13)

$$\mathit{\text{Corr}}(TTP,OS)=\frac{\mathit{\text{Cov}}(TTP,OS)}{\sqrt{\mathit{\text{Var}}(TTP)\mathit{\text{Var}}(OS)}},(\text{use equations}(8)\text{and}(10)=\frac{\mathit{\text{Cov}}(TTP,OS)}{\sqrt{\frac{\mathrm{\Gamma }(1+\frac{2}{\alpha })-{\mathrm{\Gamma }}^2(1+\frac{1}{\alpha })}{{\lambda }_1^{\frac{2}{\alpha }}}·(\frac{\mathrm{\Gamma }(1+\frac{2}{\alpha })-{\mathrm{\Gamma }}^2(1+\frac{1}{\alpha })}{{({\lambda }_1+{\lambda }_2)}^{\frac{2}{\alpha }}}+\frac{{\lambda }_1^2[\mathrm{\Gamma }(1+\frac{2}{\alpha })-{\mathrm{\Gamma }}^2(1+\frac{1}{\alpha })]+{\lambda }_1{\lambda }_2\mathrm{\Gamma }(1+\frac{2}{\alpha })}{{({\lambda }_1+{\lambda }_2)}^2{\lambda }_3^{\frac{2}{\alpha }}})}}.$$

Proof of Theorem 4

$$E(TTP·OS|TTP<OS)=E(TTP·OS|PFS=TTP)=E(PFS·(PFS+OS\prime ))=E(PF{S}^2)+E(PFS)E(OS\prime ),(\text{use Weibull properties})={({\lambda }_1+{\lambda }_2)}^{-\frac{2}{\alpha }}\mathrm{\Gamma }(1+\frac{2}{\alpha })+{({\lambda }_1+{\lambda }_2)}^{-\frac{1}{\alpha }}\mathrm{\Gamma }(1+\frac{1}{\alpha })·{\lambda }_3^{-\frac{1}{\alpha }}\mathrm{\Gamma }(1+\frac{1}{\alpha })=\frac{\mathrm{\Gamma }(1+\frac{2}{\alpha })}{{({\lambda }_1+{\lambda }_2)}^{\frac{2}{\alpha }}}+\frac{{\mathrm{\Gamma }}^2(1+\frac{1}{\alpha })}{{({\lambda }_1+{\lambda }_2)}^{\frac{1}{\alpha }}{\lambda }_3^{\frac{1}{\alpha }}};$$ (14)

$$E(TTP|TTP<OS)=E(TTP|PFS=TTP)=E(PFS)=\frac{\mathrm{\Gamma }(1+\frac{1}{\alpha })}{{({\lambda }_1+{\lambda }_2)}^{\frac{1}{\alpha }}};$$ (15)

$$E(OS|TTP<OS)=E(OS|PFS=TTP)=E(PFS+OS\prime )=E(PFS)+E(OS\prime ),(\text{use Weibull properties})={({\lambda }_1+{\lambda }_2)}^{-\frac{1}{\alpha }}\mathrm{\Gamma }(1+\frac{1}{\alpha })+{\lambda }_3^{-\frac{1}{\alpha }}\mathrm{\Gamma }(1+\frac{1}{\alpha })=\mathrm{\Gamma }(1+\frac{1}{\alpha })[\frac{1}{{({\lambda }_1+{\lambda }_2)}^{\frac{1}{\alpha }}}+\frac{1}{{\lambda }_3^{\frac{1}{\alpha }}}];$$ (16)

$$\mathit{\text{Cov}}(TTP,OS|TTP<OS)=\mathit{\text{Cov}}(TTP,OS|PFS=TTP)=E(TTP·OS|PFS=TTP)-E(TTP|PFS=TTP)E(OS|PFS=TTP),(\text{use}(14),(15),(16))=\frac{\mathrm{\Gamma }(1+\frac{2}{\alpha })}{{({\lambda }_1+{\lambda }_2)}^{\frac{2}{\alpha }}}+\frac{{\mathrm{\Gamma }}^2(1+\frac{1}{\alpha })}{{({\lambda }_1+{\lambda }_2)}^{\frac{1}{\alpha }}{\lambda }_3^{\frac{1}{\alpha }}}-\frac{\mathrm{\Gamma }(1+\frac{1}{\alpha })}{{({\lambda }_1+{\lambda }_2)}^{\frac{1}{\alpha }}}·\mathrm{\Gamma }(1+\frac{1}{\alpha })[\frac{1}{{({\lambda }_1+{\lambda }_2)}^{\frac{1}{\alpha }}}+\frac{1}{{\lambda }_3^{\frac{1}{\alpha }}}]=\frac{\mathrm{\Gamma }(1+\frac{2}{\alpha })-{\mathrm{\Gamma }}^2(1+\frac{1}{\alpha })}{{({\lambda }_1+{\lambda }_2)}^{\frac{2}{\alpha }}};$$ (17)

$$\mathit{\text{Var}}(TTP|TTP<OS)=\mathit{\text{Var}}(TTP|PFS=TTP)=\mathit{\text{Var}}(PFS),(\text{use Weibull properties})=\frac{\mathrm{\Gamma }(1+\frac{2}{\alpha })-{\mathrm{\Gamma }}^2(1+\frac{1}{\alpha })}{{({\lambda }_1+{\lambda }_2)}^{\frac{2}{\alpha }}};$$ (18)

$$\mathit{\text{Var}}(OS|TTP<OS)=\mathit{\text{Var}}(OS|PFS=TTP)=E(O{S}^2|PFS=TTP)-E^2(OS|PFS=TTP)=E{(PFS+OS\prime )}^2-E^2(PFS+OS\prime )=E(PF{S}^2)+2E(PFS)E(OS\prime )+E(O{S}^{\prime 2})-{[E(PFS)+E(OS\prime )]}^2,(\text{use Weibull properties})={({\lambda }_1+{\lambda }_2)}^{-\frac{2}{\alpha }}\mathrm{\Gamma }(1+\frac{2}{\alpha })+2{({\lambda }_1+{\lambda }_2)}^{-\frac{1}{\alpha }}\mathrm{\Gamma }(1+\frac{1}{\alpha })·{\lambda }_3^{-\frac{1}{\alpha }}\mathrm{\Gamma }(1+\frac{1}{\alpha })+{\lambda }_3^{-\frac{2}{\alpha }}\mathrm{\Gamma }(1+\frac{2}{\alpha })-{[{({\lambda }_1+{\lambda }_2)}^{-\frac{1}{\alpha }}\mathrm{\Gamma }(1+\frac{1}{\alpha })+{\lambda }_3^{-\frac{1}{\alpha }}\mathrm{\Gamma }(1+\frac{1}{\alpha })]}^2=[\mathrm{\Gamma }(1+\frac{2}{\alpha })-{\mathrm{\Gamma }}^2(1+\frac{1}{\alpha })][\frac{1}{{({\lambda }_1+{\lambda }_2)}^{\frac{2}{\alpha }}}+\frac{1}{{\lambda }_3^{\frac{2}{\alpha }}}];$$ (19)

$$\mathit{\text{Corr}}(TTP,OS|TTP<OS)=\frac{\mathit{\text{Cov}}(TTP,OS|TTP<OS)}{\sqrt{\mathit{\text{Var}}(TTP|TTP<OS)\mathit{\text{Var}}(OS|TTP<OS)}},(\text{use}(17),(18),(19))=\frac{\frac{\mathrm{\Gamma }(1+\frac{2}{\alpha })-{\mathrm{\Gamma }}^2(1+\frac{1}{\alpha })}{{({\lambda }_1+{\lambda }_2)}^{\frac{2}{\alpha }}}}{\sqrt{\frac{\mathrm{\Gamma }(1+\frac{2}{\alpha })-{\mathrm{\Gamma }}^2(1+\frac{1}{\alpha })}{{({\lambda }_1+{\lambda }_2)}^{\frac{2}{\alpha }}}·[\mathrm{\Gamma }(1+\frac{2}{\alpha })-{\mathrm{\Gamma }}^2(1+\frac{1}{\alpha })][\frac{1}{{({\lambda }_1+{\lambda }_2)}^{\frac{2}{\alpha }}}+\frac{1}{{\lambda }_3^{\frac{2}{\alpha }}}]}}=\frac{{\lambda }_3^{\frac{1}{\alpha }}}{\sqrt{{\lambda }_3^{\frac{2}{\alpha }}+{({\lambda }_1+{\lambda }_2)}^{\frac{2}{\alpha }}}}.$$ (20)

Proof of Theorem 5

Given OS≠PFS, then OS=PFS+OS’, so that

$$P(OS<x|OS\ne PFS)=P(PFS+OS\prime <x)={\int }_{y+z<x}({\lambda }_1+{\lambda }_2)\alpha y^{\alpha -1}\text{exp}[-({\lambda }_1+{\lambda }_2)y^{\alpha }]{\lambda }_3\alpha z^{\alpha -1}\text{exp}(-{\lambda }_3{z}^{\alpha })dydz={\int }_0^x({\lambda }_1+{\lambda }_2)\alpha y^{\alpha -1}\text{exp}[-({\lambda }_1+{\lambda }_2)y^{\alpha }]{\int }_0^{x-y}{\lambda }_3\alpha z^{\alpha -1}\text{exp}(-{\lambda }_3{z}^{\alpha })dzdy={\int }_0^x({\lambda }_1+{\lambda }_2)\alpha y^{\alpha -1}\text{exp}[-({\lambda }_1+{\lambda }_2)y^{\alpha }][1-\text{exp}(-{\lambda }_3{(x-y)}^{\alpha })]dy={\int }_0^x({\lambda }_1+{\lambda }_2)\alpha y^{\alpha -1}\text{exp}[-({\lambda }_1+{\lambda }_2)y^{\alpha }]dy-{\int }_0^x({\lambda }_1+{\lambda }_2)\alpha y^{\alpha -1}\text{exp}[-({\lambda }_1+{\lambda }_2)y^{\alpha }-{\lambda }_3{(x-y)}^{\alpha }]dy=1-\text{exp}[-({\lambda }_1+{\lambda }_2)x^{\alpha }]-({\lambda }_1+{\lambda }_2)\alpha {\int }_0^x{y}^{\alpha -1}\text{exp}[-({\lambda }_1+{\lambda }_2)y^{\alpha }-{\lambda }_3{(x-y)}^{\alpha }]dy;$$ (21)

Given OS=PFS, then OS follows Weibull(α, λ₁ + λ₂), so that

$$P(OS<x|OS=PFS)=1-\text{exp}[-({\lambda }_1+{\lambda }_2)x^{\alpha }];$$ (22)

$$P(OS<x)=P(OS<x|OS=PFS)P(OS=PFS)+P(OS<x|OS\ne PFS)P(OS\ne PFS)=P(OS<x|OS=PFS)(1-p_0)+P(OS<x|OS\ne PFS)p_0,(\text{use}(22)\text{and}(21))=(1-\text{exp}[-({\lambda }_1+{\lambda }_2)x^{\alpha }])(1-p_0)+\left(1-\text{exp}[-({\lambda }_1+{\lambda }_2)x^{\alpha }]-({\lambda }_1+{\lambda }_2)\alpha {\int }_0^x{y}^{\alpha -1}\text{exp}[-({\lambda }_1+{\lambda }_2)y^{\alpha }-{\lambda }_3{(x-y)}^{\alpha }]dy\right)p_0=1-\text{exp}[-({\lambda }_1+{\lambda }_2)x^{\alpha }]-p_0({\lambda }_1+{\lambda }_2)\alpha {\int }_0^x{y}^{\alpha -1}\text{exp}[-({\lambda }_1+{\lambda }_2)y^{\alpha }-{\lambda }_3{(x-y)}^{\alpha }]dy,(\text{use Theorem}1)=1-\text{exp}[-({\lambda }_1+{\lambda }_2)x^{\alpha }]-{\lambda }_1\alpha {\int }_0^x{y}^{\alpha -1}\text{exp}[-({\lambda }_1+{\lambda }_2)y^{\alpha }-{\lambda }_3{(x-y)}^{\alpha }]dy;$$ (23)

Therefore, the survival function for OS is:

$$S_{OS}(x)=\text{exp}[-({\lambda }_1+{\lambda }_2)x^{\alpha }]+{\lambda }_1\alpha {\int }_0^x{y}^{\alpha -1}\text{exp}[-({\lambda }_1+{\lambda }_2)y^{\alpha }-{\lambda }_3{(x-y)}^{\alpha }]dy.$$