Effect of glucose on the biomechanical function of arterial elastin

Abstract

Elastin is essential to provide elastic support for blood vessels. As a remarkably long-lived protein, elastin can suffer from cumulative effects of exposure to biochemical damages, which can greatly compromise its biomechanical properties. Non-enzymatic glycation is one of the main mechanisms of aging and its effect is magnified in diabetic patients. The purpose of this study is to investigate the effects of glucose on mechanical properties of isolated porcine aortic elastin. Elastin samples were incubated in 2 M glucose solution and were allowed to equilibrate for 4, 7, 14, 21 or 28 days at 37°C. Equibiaxial tensile tests were performed to study the changes of elastic properties of elastin due to glycation. Significant decreases in tissue dimension were observed after 7 days glucose incubation. Elastin samples treated for 14, 21 or 28 days demonstrate a significant increase in hysteresis in the stress-stretch curves, indicating a greater energy loss due to glucose treatment. Both the longitudinal and the circumferential directions show significant increases in tangent modulus with glucose treatment, however only significant increases are observed after 7 days for the circumferential direction. An eight-chain statistical mechanics based microstructural model was used to study the hyperelastic and orthotropic behavior of the glucose-treated elastin and the material parameters were estimated using a nonlinear least squares method. Material parameters in the model were related to elastin density and fiber orientation, and, hence, the possible microstructural changes in glucose-treated elastin. Estimated material parameters show a general increasing trend in elastin density per unit volume with glucose incubation. The simulation results also indicate that more elastic fibers are aligned in the longitudinal and circumferential directions, rather than in the radial direction.

Introduction

Elastic fibers, one of the major structural components of the extracellular matrix (ECM), are essential to provide elasticity to the aortic wall and to accommodate intermittent deformations encountered during cardiac cycles. These resilient networks are made primarily of a protein called elastin. Elastic fibers consist of an inner crosslinked elastin core surrounded by a mantle of fibrillin-rich microfibrils (Mecham 2008). In elastic arteries, such as the aorta, elastic fibers form thick concentric fenestrated layers of elastic laminae, with inter-laminar connecting fibers distributed radially through the vessel wall (O’Connell et al. 2008). Each elastic lamina alternates with a layer of smooth muscle cells (SMCs), and together, organize into a laminar unit which is considered as the functional unit of the vessel wall (Brooke et al. 2003; Wolinsky and Glagov 1967; Davis, 1993).

Pathogenesis of vascular diseases, including hypertension, atherosclerosis, stenosis and aneurysms has been associated with elastin disorders in structure and function and its altered interaction with other arterial constituents (Campa et al. 1987; Menashi et al. 1987; Kobs et al. 2005; Arribas et al. 2006; Krettek et al. 2003). From a biomechanical viewpoint, abnormalities in elastin can alter mechanical homeostasis and promote SMC proliferation, migration and synthesis of ECM and eventually contribute to the development of disease (Ito et al. 1997; Ito et al. 1998; Li et al. 1998; Karnik et al. 2003; Ailawadi et al. 2009; Yamamoto et al. 1993). Therefore, it is important to have a better understanding of the mechanical properties of elastin and its alteration in disease, as well as the mechanisms by which elastin is degraded/damaged, influencing the arterial remodeling. To understand the mechanical function of elastin in the arterial wall, purified elastin was obtained and mechanically tested using both uniaxial stretching (Lillie and Gosline 2002; Watton et al. 2009; Stephen et al. 2013) and biaxial tensile testing methods (Gundiah et al. 2007; Zou and Zhang 2009; Zou and Zhang 2012). It has been shown that the elastin network in the thoracic aorta possesses anisotropic mechanical behavior, and it becomes increasingly anisotropic with distance from the heart (Zou and Zhang 2009; Watton et al. 2009).

Elastin is a long-lived ECM protein and it can suffer from cumulative effects of biochemical damages. Non-enzymatic glycation of elastin has been shown to increase with aging (Konova et al. 2004). Stiffening of the arterial wall among diabetic patients has been attributed to glycation crosslinks of elastin and collagen (Sims et al. 1996). In vitro studies have also shown that glucose treatments stiffens arterial elastin (Winlove et al., 1996, Zou and Zhang, 2012), increases the storage and loss modulus (Lillie and Gosline 1996), and also changes the viscoelastic stress relaxation behavior of elastin (Zou and Zhang 2012). We have previously studied the mechanical behavior of elastin using a biaxial tensile testing method and demonstrated that short-term glucose treatment (48 hours) induces changes in both the elastic and viscoelastic properties of elastin (Zou and Zhang 2012). The present study aims to fully understand the mechanical properties of elastin with longer period of glucose treatment. To this end, the changes in the mechanical properties of elastin were studied with 4, 7, 14, 21 or 28 days of glucose treatment. Histology studies and Transmission Electron Microscopy (TEM) were performed to examine the elastin samples and to identify possible ultrastructure changes due to glucose treatment. A statistical mechanics based constitutive model was implemented to describe the orthotropic hyperelastic behavior of elastin with glucose effects.

Materials and Methods

Sample preparation

Porcine thoracic aortas were harvested from a local abattoir and transported to laboratory on ice. Aortas were cleaned of adherent tissues and fat and rinsed in distilled water. Squared samples of about 20mm × 20mm were cut from the cleaned aortas. All samples were taken from the similar longitudinal region of aortas to minimize the changes of mechanical properties with longitudinal position (Zou and Zhang 2009). Purified elastin was obtained using cyanogen bromide (CNBr) treatment while cells, collagen and other ECM components were removed (Zou and Zhang 2009). Briefly, aortic samples were treated with 50 mg/ml CNBr in 70% formic acid solution for 19h at room temperature with gentle stirring. Tissue samples were then gently stirred for 1h at 60°C and followed by 5 min of boiling to inactivate CNBr. Elastin tissue samples were kept in 1× phosphate buffered saline (PBS) solution before further experiment.

Glucose treatment

Before glucose treatment, the side lengths and thickness of each elastin sample were carefully measured using a digital caliper. Thickness was determined by averaging the measurements taken at 8 positions over the sample. Tissue samples (n=7) were then incubated in 2 M glucose solution and were allowed to equilibrate at 37°C for 4, 7, 14, 21 or 28 days. The dimensions of the tissue samples were re-measured after glucose treatment.

Histology studies

Aorta and elastin samples were fixed in 10% formaldehyde (Fisher Scientific) for histological studies. A cross-section of about 6 μm in thickness was cut along the longitudinal direction and stained with Movat’s pentachrome, which stains collagen fibers yellow, nuclei/elastic fibers purple to black, SMCs red and ground substance blue (Taylor et al. 1999; Arbustini 2002; Chow et al. 2013).

Transmission electron microscopy (TEM)

Aorta and purified elastin samples were fixed in 3% glutaraldehyde in 0.1 M sodium cacodylate buffer (pH 7.4). The samples were then washed in buffer, and sequentially treated with 1% osmium tetroxide in buffer, 2% tannic acid in buffer and 2% uranyl acetate in water as previously described (Davis 1993). The samples were dehydrated through a graded series of methanol to propylene oxide, inflitrated with propylene oxide:Epon mixtures and embedded in pure Epon. The blocks were polymerized at 60°C for 3 days. Thin sections (60 nm) were counterstained with methanolic uranyl acetate and lead citrate and viewed using a Tecnai 12 transmission electron microscope at 120 kV. Images were digitally captured.

Mechanical Testing

Biaxial tensile tests were performed before and after glucose treatment to study the effects of glucose on the mechanical function of elastin (n=7). After glucose treatment, samples were maintained in glucose solution during mechanical testing to keep chemical balance. Control experiments were performed in 1× PBS before glucose treatment. Although not shown in this study, our experimental results showed minimal alterations in the mechanical properties of elastin samples incubated in PBS for up to 28 days. Sandpaper tabs were glued at the sides of tissue samples with sutures looping around. The sutures were connected to the linear positioners of the biaxial tensile tester. Load cells mounted in both circumferential and longitudinal sample directions were used to measure and record the load applied to the sample. Samples were preconditioned for 10 cycles with 10 s of half cycle time by applying an equibiaxial tension of 40 N/m. After preconditioning, 10 cycles of equibiaxial tension of 100 N/m was applied to each sample to allow the sample to exhibit repeatable loading and unloading responses. Before each cycle, a small preload of 5 ± 0.05 N/m was applied in order to ensure tautness of the sutures. Four carbon dot markers were placed at the center of the sample, and a CCD camera was used to track the displacement of markers from which the stretches in both directions were determined (Chow et al. 2013). Cauchy stress and stretch were calculated and used to describe the mechanical behaviors of elastin.

Statistical Analysis

Sample dimensions and tangent modulus of elastin samples before and after glucose treatment were averaged over the number of samples. The averaged results are expressed in the form of mean ± SD. Statistical analysis was performed by JMP Pro (version 10.0.2, SAS Institute Inc.) using one-way analysis of variance (ANOVA) followed by Dunnett’s post hoc comparisons. Differences are considered to be significant when p < 0.05.

Constitutive Modeling

Based on the analogy between the entangled long molecular chains and the structural protein framework seen in the elastin network, a statistical mechanics based orthotropic hyperelastic microstructural model was implemented to study the effects of glucose treatment on the mechanical behavior of elastin. The model assumes that the fiber network consists of eight-chain orthotropic unit elements where every single chain is modeled as a freely jointed chain (Bischoff et al. 2002). This model has been adapted by Zou and Zhang (2009) to study the orthotropic hyperelastic behavior of the elastin network, to which interested readers are referred for more details. Briefly, the unit element is characterized by a, b and c in three orthogonal principal material directions a, b and c, with eight chains situated along the diagonals of the element and linked together at the center of the element. Different dimensions of the basic unit element in the three principal material directions induce the orthotropic response. The normalized chain vector P⁽ⁱ⁾ (i = 1, 2, …, 8 denotes the chain number) is expressed in terms of a, b and c as:

$$\begin{array}{l}{\mathbf{P}}^{(1)}=-{\mathbf{P}}^{(5)}=\frac{a}{2}\mathbf{a}+\frac{b}{2}\mathbf{b}+\frac{c}{2}\mathbf{c}\\ {\mathbf{P}}^{(2)}=-{\mathbf{P}}^{(6)}=\frac{a}{2}\mathbf{a}+\frac{b}{2}\mathbf{b}-\frac{c}{2}\mathbf{c}\\ {\mathbf{P}}^{(3)}=-{\mathbf{P}}^{(7)}=\frac{a}{2}\mathbf{a}+\frac{b}{2}\mathbf{b}-\frac{c}{2}\mathbf{c}\\ {\mathbf{P}}^{(4)}=-{\mathbf{P}}^{(8)}=\frac{a}{2}\mathbf{a}-\frac{b}{2}\mathbf{b}-\frac{c}{2}\mathbf{c}\end{array}$$ (1)

The final form of the homogenized strain energy function is given as:

$$W=W_0+\frac{nk\mathrm{\Theta }}{4}\left[N\sum _{i=1}^4\left(\frac{{\rho }^{(i)}}{N}{\beta }_{\rho }^{(i)}+ln\frac{{\beta }_{\rho }^{(i)}}{sinh{\beta }_{\rho }^{(i)}}\right)-\frac{{\beta }_P}{\sqrt{N}}ln\left({\lambda }_a^{a^2}{\lambda }_b^{b^2}{\lambda }_c^{c^2}\right)\right]+B[cosh(J-1)-1]$$ (2)

where W is the overall energy, W₀ is a constant, B is a parameter that controls the bulk compressibility, and J is the determinant of deformation gradient tensor related to mechanical stretch. Parameters λ_a, λ_b, and λ_c are stretches along these directions. N = (a² + b² + c²)/4 is the number of rigid links within each individual freely-jointed chain. ρ⁽ⁱ⁾ are the normalized deformed lengths of the constituent chains in the unit element. ${\beta }_{\rho }^{(i)}={ℒ}^{-1}({\rho }^{(i)}/N)$ is the inverse Langevin function. $P=\sqrt{a^2+b^2+c^2}/2$ is the initial normalized length of each chain. Parameter n is the chain density per unit volume, k = 1.38×10⁻²³ J/K is Boltzmann’s constant, and Θ = 298K is absolute temperature.

The second Piola-Kirchhoff stress tensor can be calculated from strain energy function in Eq. (2) as $\mathbf{S}=2\frac{\partial W}{\partial \mathbf{C}}$, where C is the right Cauchy-Green strain. The Cauchy stress can then be calculated by applying a push forward operation as $\mathit{\sigma }=\frac{1}{J}{\mathbf{FSF}}^T$ (Holzapfel 2000). The tensor form of the Cauchy stress is

$$\mathit{\sigma }=\frac{nk\mathrm{\Theta }}{4J}\{\sum _{i=1}^4\frac{\left(\mathbf{F}{\mathbf{P}}^{(i)}\right){\left(\mathbf{F}{\mathbf{P}}^{(i)}\right)}^T}{{\rho }^{(i)}}{\beta }_{\rho }^{(i)}-\frac{{\beta }_P}{\sqrt{N}}[\frac{a^2}{{\lambda }_a^2}(\mathbf{Fa}){(\mathbf{Fa})}^T+\frac{b^2}{{\lambda }_b^2}(\mathbf{Fb}){(\mathbf{Fb})}^T+\frac{c^2}{{\lambda }_c^2}(\mathbf{Fc}){(\mathbf{Fc})}^T\left]\right\}+Bsinh(J-1)\mathbf{I}$$ (3)

where P⁽ⁱ⁾ can be obtained from Eq. (1), and F is the deformation gradient.

Parameter Estimation

Four independent material parameters a, b, c and n were estimated by using a direct search method (fminsearch function) in Matlab (version R2011a, MathWorks Inc). At each stretch recorded in the experiment, Cauchy stress is calculated according to Eq. (3). The summation of the squared differences between the estimated and experimental Cauchy stress is minimized (Zeinali-Davarani et al. 2013, 2015), and the corresponding material parameters a, b, c and n are obtained. A root-mean-square (RMS) measure of the goodness of fit is calculated as (Zeinali-Davarani et al. 2013, 2015):

$$\text{RMS}=\sqrt{\frac{1}{\mathit{num}}\sum _1^{\mathit{num}}{\left({\sigma }_L^{\mathit{est}}-{\sigma }_L^{\mathit{exp}}\right)}^2}+\sqrt{\frac{1}{\mathit{num}}\sum _1^{\mathit{num}}{\left({\sigma }_C^{\mathit{est}}-{\sigma }_C^{\mathit{exp}}\right)}^2}$$ (1)

Results

Histology images in Figure 1 show the removal of collagen, cells and other ECM components in the purified elastin sample. The Movat’s pentachrome stain of the intact aorta sample shows the presence of elastic fibers, collagen fibers and SMCs, whereas the purified elastin sample is devoid of collagen fibers and SMCs.

Figure 1.

Histology images of cross-sections of (a) intact porcine thoracic aorta and (b) purified elastin with Movat’s pentachrome stain. Collagen fibers yellow, nuclei/elastic fibers purple to black, smooth muscle cells red, and ground substance blue. Scale bars represent 20 μm.

Figure 2 shows the normalized size changes of elastin samples after glucose treatment, obtained by dividing the sizes of elastin samples measured after glucose treatment by dimensions before glucose treatment (n=7). After glucose treatment, there is a significant decrease of tissue dimensions in both the side lengths and thickness (p<0.05), except for the thickness after 4 days of glucose treatment (p=0.1602).

Figure 2.

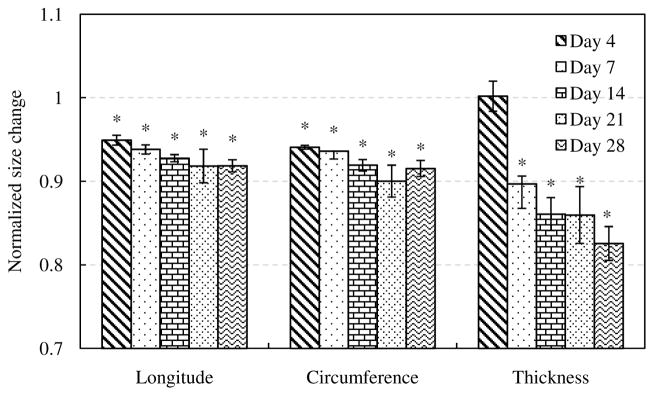
Size changes of elastin with glucose treatment for 4, 7, 14, 21 and 28 days (n=7). The size after glucose treatment were normalized to the size of elastin samples before treatment. (^*p<0.05)

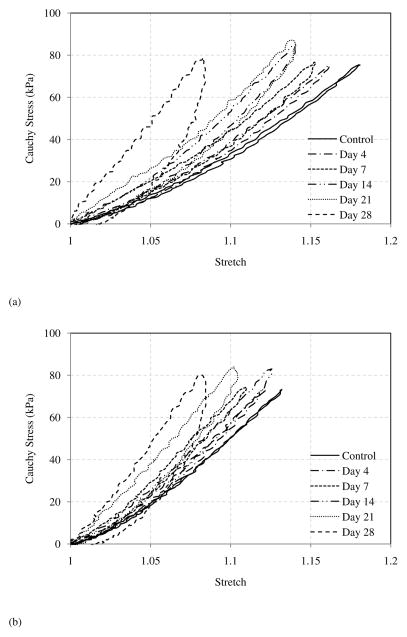
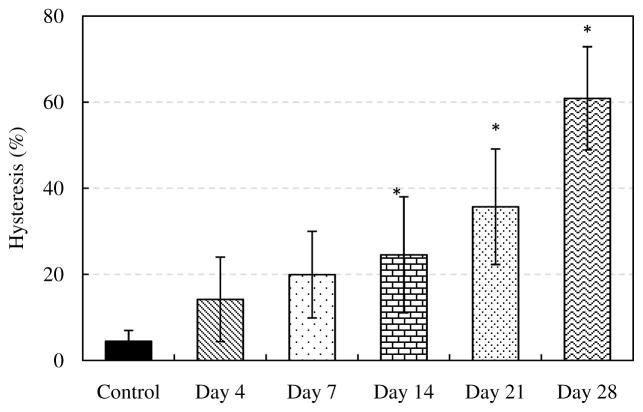
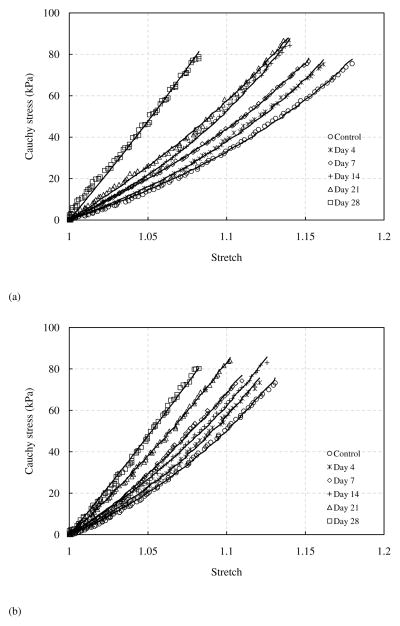
Representative comparison of Cauchy stress versus stretch curves in both the longitudinal and circumferential directions is shown in Figure 3. There are several interesting changes observed from the stress-stretch curves. For elastin samples without glucose treatment, the loading and unloading stress-stretch curves almost overlap, i.e., the hysteresis is very small. However, an increasing trend in hysteresis with incubation time was observed. Figure 4 shows hysteresis, calculated as the total area between the loading and unloading curves divided by the area under the loading curve (McClure et al. 2009), of elastin samples before and after glucose treatment (n=7). The hysteresis increases gradually from less than 10% in untreated elastin to nearly 60% after 28 days of glucose treatment.

Figure 3.

Representative Cauchy stress - stretch relationship of elastin sample before and after glucose treatment in the (a) longitudinal and (b) circumferential directions.

Figure 4.

Hysteresis percent values for control and glucose treated elastin (n=7) for 4, 7, 14, 21 and 28 days. (^*p<0.05)

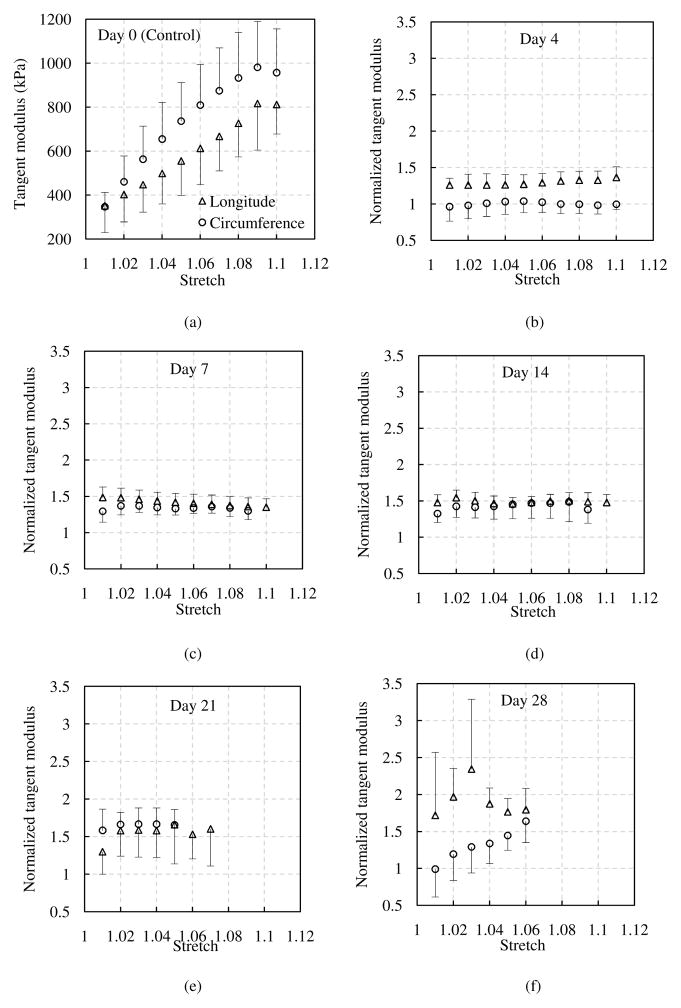
It also appears that the elastin gradually stiffens in both the longitudinal and circumferential directions with glucose treatment (Fig. 3). To better compare the elastic behavior of elastin before and after glucose treatment, tangent modulus was obtained by differentiating the experimental Cauchy stress-stretch curves. Figure 5a presents the averaged tangent modulus at the control condition. Figures 5b–f shows the normalized tangent modulus, obtained by dividing the tangent modulus after glucose treatment at each treatment time by the modulus at the control condition of the corresponding sample. The tangent modulus shows a significant increase in both the longitudinal and circumferential directions after glucose treatment compared with the control group, except the tangent modulus of 4 days treatment in the circumferential direction, which remains similar to that of the control group (p=0.9690).

Figure 5.

(a) Averaged tangent modulus of elastin at control condition. Normalized tangent modulus of elastin with glucose treatment for (b) 4 days, (c) 7 days, (d) 14 days, (e) 21 days and (f) 28 days (n=7). The tangent modulus after glucose treatment was normalized to the control elastin samples.

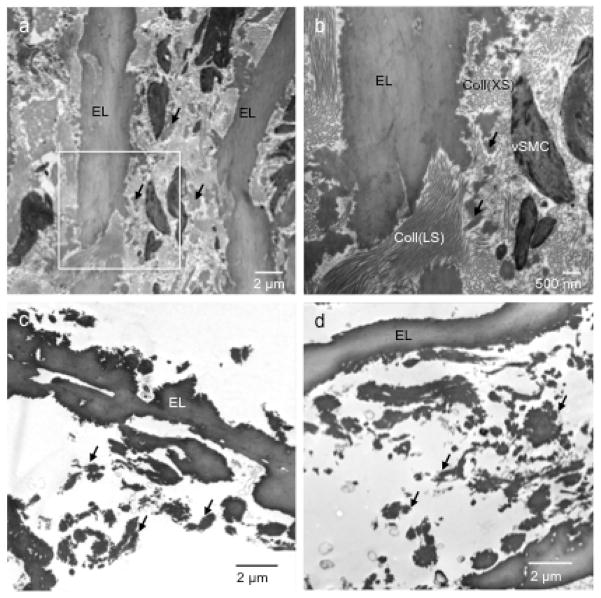
TEM images of the intact pig aorta show elastic laminae, SMCs and collagen fibers arranged in an orderly manner with circumferential SMC layers alternating with interposing elastic laminae (Fig. 6a). Intertwining collagen fiber bundles are evident and appear to be oriented in both the longitudinal and circumferential directions of the arterial wall (Fig. 6b). Elastin deposits, possibly representing the inter-laminar connecting fibers, can also be seen. Figures 6c and 6d verify that the purified elastin maintains its structural integrity despite the removal of SMCs, collagen and other ECM components. Overall, the TEM images show no obvious ultrastructure changes in the elastin due to glucose treatment. It is interesting that the smaller elastin deposits present between the continuous elastic laminae, which are seen in the intact aorta (Fig. 6b), remain intact in the purified elastin. These smaller deposits appear to have interconnections with the continuous elastic laminae and may therefore be important for maintaining the interspacing and structural integrity of the tissue.

Figure 6.

Transmission electron microscopy (TEM) images of (a, b) intact porcine thoracic aorta at two magnifications with the intersect square image zoomed in, (c) purified elastin without glucose treatment, and (d) purified elastin after 28 days of glucose treatment. EL - elastic laminae; vSMC - smooth muscle cells; Coll (LS) - collagen fibers in longitudinal section; Coll (XS) - collagen fibers in cross-section. Arrows indicate inter-laminar elastin deposits.

Figure 7 shows the representative modeling results of equibiaxial tests of the elastin network with glucose treatment. Considering the hysteresis, especially with long-term glucose treatment, only the loading part of Cauchy stress versus stretch was modeled. The estimated material parameters and RMS are summarized in Table 1.

Figure 7.

Representative modeling results (lines) of Cauchy stress versus stretch of elastin before and after glucose treatment in the (a) longitudinal, and (b) circumferential directions. Experimental results were also shown in symbols for comparison.

Table 1.

Summary of material parameters of elastin samples (n=7) with glucose treatment.

Sample number	Treatment time (days)	n (1/m3)	a	b	c	N	RMS
1	0	1.13 × 1025	1.4935	1.7739	0.8946	1.5444	1.1907
	4	1.18 × 1025	1.3989	1.6967	1.0003	1.4591	1.5184
	7	6.48 × 1024	1.4421	1.5418	0.7652	1.2606	1.4578
	14	1.79 × 1025	1.5580	1.8290	0.8837	1.6385	1.3817
	21	2.60 × 1025	1.4222	1.7968	1.0974	1.6138	1.7416
	28	7.59 × 1025	1.7254	1.8712	0.8990	1.8217	3.8791
2	0	1.24 × 1025	1.5884	1.7043	1.0046	1.6092	1.0822
	4	1.32 × 1025	1.5695	1.7024	0.9901	1.5854	1.7506
	7	1.69 × 1025	1.5908	1.7313	1.0027	1.6334	1.6604
	14	1.95 × 1025	1.5596	1.6306	1.1341	1.5944	1.5732
	21	2.37 × 1025	1.6568	1.8057	1.0337	1.7685	1.8025
	28	4.79 × 1025	2.1527	2.2802	0.8101	2.6224	3.3212
3	0	1.02 × 1025	1.4399	1.5710	1.2299	1.5135	1.1636
	4	1.16 × 1025	1.3654	1.4825	1.2794	1.4248	1.1841
	7	1.39 × 1025	1.7389	1.9039	0.8844	1.8577	1.0634
	14	1.21 × 1025	1.6127	1.6447	1.0454	1.5997	1.3552
	21	2.19 × 1025	1.8901	2.0661	0.8366	2.1353	1.2410
	28	5.34 × 1025	2.9967	2.9788	0.2534	4.4794	2.4627
4	0	1.45 × 1025	1.5593	1.5707	1.0598	1.5054	1.0845
	4	2.08 × 1025	1.7229	1.7014	0.9895	1.7106	1.0247
	7	1.70 × 1025	1.7523	1.6579	0.8312	1.6275	1.4329
	14	3.33 × 1025	2.0868	1.9728	0.4754	2.1181	2.5507
	21	6.10 × 1025	2.5250	2.3262	0.4060	2.9879	3.3298
5	0	1.04 × 1025	1.4263	1.5144	1.1155	1.3931	1.2294
	4	2.34 × 1025	1.6974	1.7415	0.9229	1.6915	2.2253
	7	2.56 × 1025	1.7846	1.7350	0.9011	1.7517	2.2975
	14	4.25 × 1025	1.9158	2.0374	0.8889	2.1529	3.4350
	21	6.94 × 1025	2.4514	2.7168	0.9097	3.5545	2.3225
	28	7.59 × 1025	2.1249	2.3669	0.4593	2.5820	5.9968
6	0	8.84 × 1024	1.5330	1.4271	1.0644	1.3799	1.3091
	4	2.52 × 1025	1.9619	1.7038	0.7204	1.8178	2.5445
	7	1.38 × 1025	1.7360	1.4897	0.8164	1.4748	2.3302
	14	2.46 × 1025	1.8911	1.6587	0.7196	1.7114	3.0014
	21	5.50 × 1025	2.6637	2.2116	0.2765	3.0158	3.2733
	28	5.64 × 1025	2.0398	1.7480	0.6239	1.9014	9.4000
7	0	9.69 × 1024	1.2229	1.3002	1.2230	1.1704	1.7976
	4	8.56 × 1024	1.4205	1.3793	1.0556	1.2586	2.0850
	7	1.05 × 1025	1.5447	1.5634	0.9043	1.4120	1.8857
	14	7.12 × 1024	1.4615	1.4573	0.8827	1.2597	2.7882
	21	9.82 × 1024	1.4917	1.4813	0.9294	1.3209	2.5402
	28	8.89 × 1024	1.5011	1.4923	0.8677	1.3083	2.8187

Discussion

The mechanical properties of glucose treated aortic elastin were studied using biaxial tensile testing and constitutive modeling. The interaction between glucose and elastin, so called glycation, induces several interesting and important changes in elastin. Mechanical testing results show that the stiffness of elastin increases gradually with glucose treatment. In addition, glucose treated elastin exhibits a large hysteresis upon loading and unloading compared to the control. Moreover, the amount of hysteresis also increases with treatment times. Hysteresis, as one of the characteristic behaviors of viscoelasticity (Humphrey 2003), exhibited a significant increase, which indicated that the viscoelastic properties of elastin were affected by glucose treatment. Hysteresis is proportional to the energy dissipated within a loading cycle and, along with relaxation and creep responses, are known as the main features of the viscoelastic properties of many biological materials. It is important to study the viscoelastic properties of elastin since it provides arteries with elasticity and the ability to recover from pulsatile deformation (McClure et al. 2009). Several mechanisms are likely playing a role in viscoelastic behavior of materials. The time dependent mechanical characteristics of interstitial fluid flow passing through the ECM may be a factor determining the multiphasic biological materials viscoelastic response. The time dependent nature of the conformational changes in macromolecules in response to external loads may be another factor in tissues (Knauss and Emri 1981). Here, we showed that glucose treatment significantly increases the hysteresis behavior of elastin. The glycation process has been shown to have a deswelling\dehydrating effect on elastin, reducing the free space available for the configurational changes in elastin chain molecules upon loading and, hence, increasing the relaxation time (Lillie and Gosline 1996) and inducing more relaxation (Zou and Zhang 2012). Together, these findings suggest that viscoelastic properties of elastin are strengthened partly due to the dehydrating effects of glycation.

The macroscopic reduction in tissue size observed in our experiments suggests that the process of glucose treatment is accompanied by water redistribution as well as ultrastructural changes to the protein. It has been shown that glycation of elastin does occur although elastin has relatively low content of lysine residues (Stephen et al. 2013). The redistribution of water may, in part, be expected to modify the time dependent mechanical characteristic of interstitial fluid flow in the elastin matrix and/or structural characteristics of the protein that provide its elastomeric characteristics. The viscoelastic properties of elastin are closely related to the water content of the fibers. At the physiological state elastin is at a hydrated state of about 40–50% of hydration. Glucose has been used as an osmotic desweller to dehydrate the elastin network (Lillie and Gosline, 1996). Samouillan et al. (2004) studied the effect of hydration on the viscoelastic properties of elastin through the analysis of the glass transition temperature. Their study demonstrated that the glass transition temperature falls drastically with hydration, and the protein/water hydrogen bonds plays a crucial role in increasing the mobility of elastin in the relaxed state.

Water is known to act as a plasticizer in the functionality of elastin, i.e., elastin is elastic only when it is hydrated (Gosline 1978a; Gosline 1978b; Andrady and Mark 1980; Winlove and Parker 1990). Water plays an essential role in the molecular dynamics of elastin by facilitating the motions of the polypeptide chains (Debelle and Tamburro 1999; Villani and Tamburro 1995; Villani et al. 2000). The elastin network contains intrafibrillar, extrafibrillar and bulk water (Lillie et al. 1996). Hydration water, which refers to the intra- and extrafibrillar water, has been shown to contribute to the elasticity of elastin from both experiments (Gosline and French 1979) and simulations (Li et al. 2001). A study by Gosline and French (1979) showed that removing only 10% of the hydration water of elastin can greatly influence elasticity. Molecular dynamics simulations by Li et al. (2001) further supports the important role of hydration water in the mechanism of elasticity. Debelle and Alix (1999) proposed that the bulk water may also contribute to elastin elasticity through interactions with the hydration water of the molecule. The hydrogen bonds formed between bulk solvent water and hydration water molecules loose the hydrogen bonds between the hydration water molecules and the polypeptide chains, which allows higher chain mobility.

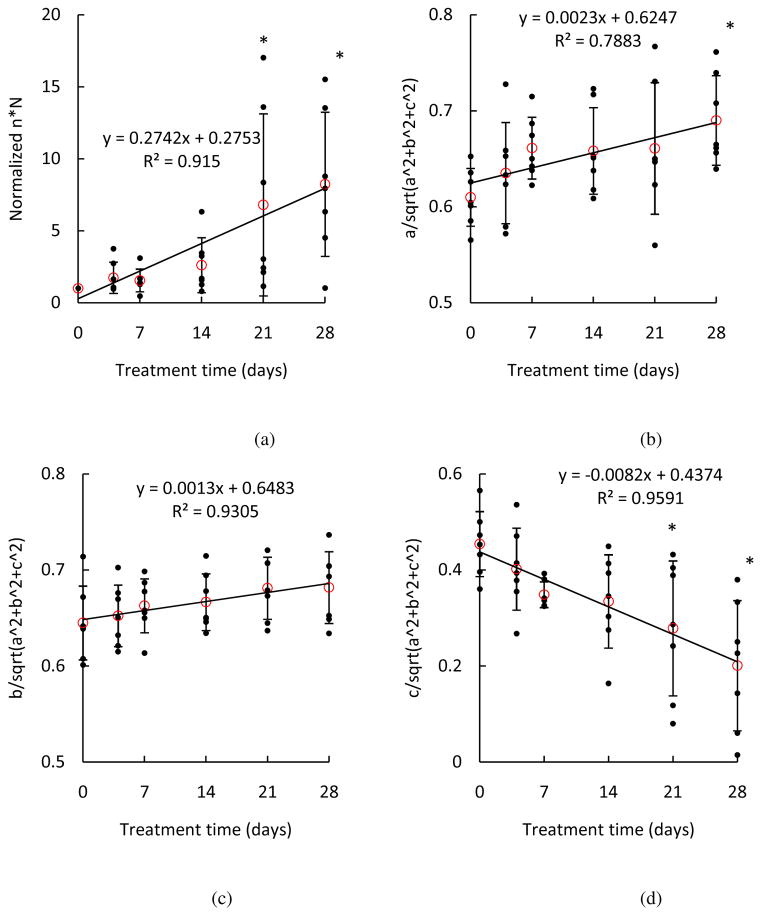
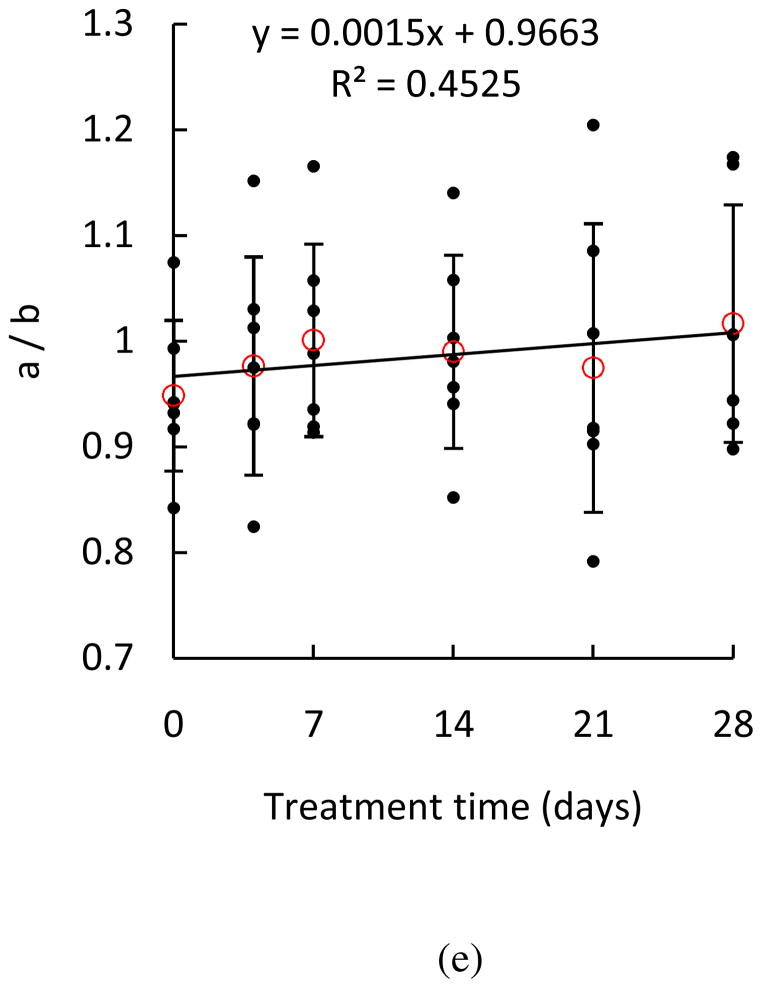
In this study, we evaluated the alteration in biaxial mechanical properties of aortic elastin when treated with glucose using a microstructural-based constitutive model with the goal of relating the changes of mechanical behavior with alterations in the microstructure of elastin network with glucose treatment. To study the changes of material properties and possible links with microstructure, the changes in material parameters with glucose treatment were studied in Fig. 8. Parameter n × N, number of rigid links per unit volume, was calculated to provide information on elastin density. In Figure 8a, the normalized n × N shows an increasing trend (p = 0.0005), indicating an increase of elastin density with glucose treatment, which coincides with the decrease in sample dimensions shown in Fig. 2. The values of $a/\sqrt{a^2+b^2+c^2},\mathrm{b}/\sqrt{a^2+b^2+c^2}$ and $\mathrm{c}/\sqrt{a^2+b^2+c^2}$ provide information on the spatial fiber distribution. As shown in Figures 8b–d, the increasing trend of $a/\sqrt{a^2+b^2+c^2}(p=0.0144)$ and $\mathrm{b}/\sqrt{a^2+b^2+c^2}(p=0.1624)$ indicates that elastic fibers are more aligned in the longitudinal and circumferential directions with glucose treatment, while the decreasing trend of $\mathrm{c}/\sqrt{a^2+b^2+c^2}(p=0.0002)$ indicates that elastic fibers are less oriented in the radial direction. The ratio a/b in Fig. 8e suggests the degree of anisotropy by comparing the material parameters in the longitudinal and circumferential directions, with the ratio of a/b = 1 being isotropic. In most cases, b is greater than a suggesting that elastin fibers have a preferential distribution in the circumferential direction, and therefore the elastin network is stiffer in the circumferential direction. Although the changes are not significant (p = 0.6112), there is a trend that the samples after glucose treatment become more isotropic, as can also be observed from the representative stress-stretch curves in Fig 3. The increase of elastin density as well as changes of spatial distribution of elastic fibers shown in Fig. 8 indicate realignment of the elastic fibers, which result in an increase in stiffness of the longitudinal and circumferential directions. It is possible that the elastic fibers are more packed with a decrease in spacing due to the osmotic deswelling effect from the glucose treatment. The removal of water accompanied by shrinkage of the tissue will cause an increase in the density of the elastin fibers while the quantity of total elastin fibers remains the same throughout the glucose treatment process.

Figure 8.

Estimated material parameters (a) n×N, (b) $a/\sqrt{a^2+b^2+c^2}$, (c) $\mathrm{b}/\sqrt{a^2+b^2+c^2}$, (d) $\mathrm{c}/\sqrt{a^2+b^2+c^2}$, and (e) a/b of elastin samples treated with glucose for 4, 7, 14, 21 and 28 days (n = 7). The material parameters n and N of each elastin sample were normalized to the parameters before glucose treatment. (^*p<0.05)

No obvious ultrastructure changes were identified from the TEM studies; however, molecular level structural modifications due to the interactions between elastin and glucose are possible. We would like to point out that in the present study we focused our effort on elucidating the alteration of the biomechanical function of elastin with glucose treatment. However blood vessels are complex biological materials with hierarchical ultrastructures. Elastin and collagen, the two major ECM components that are essential to accommodate deformations encountered during physiological functions, have complex mechanical and biological interactions in modifying the dynamic behavior of blood vessels (Chow et al. 2013, 2014). The effect of glucose on arterial function in vivo is much more complicated and involves interactions not only between glucose and elastin, but also between glucose and other structural components, such as collagen. Nevertheless, elucidating the changes in elastin is an important first step towards understanding the effect of glucose on arterial mechanics.

Conclusions

Biomechanical studies reveal several interesting and important changes associated with non-enzymatic elastin glycation. Specifically, the stiffness of elastin samples increases significantly with glucose treatment. In addition, glucose treated elastin exhibits a large hysteresis in the stress-stretch curves. Redistribution of water in the elastin network associated with glycation may play an important role in controlling the mechanical function of elastin. Future studies are needed to understand the biochemical structural and dynamical modifications in glucose-treated elastin. The statistical mechanics based constitutive model simulates the mechanical response at the macro-level reasonably well with microstructural material parameters suggesting a denser elastin network with preferential fiber distribution in the circumferential and longitudinal directions as a result glucose treatment.