Advances in Computationally Modeling Human Oral Bioavailability

Abstract

Although significant progress has been made in experimental high throughput screening (HTS) of ADME (absorption, distribution, metabolism, excretion) and pharmacokinetic properties, the ADME and Toxicity (ADME-Tox) in silico modeling is still indispensable in drug discovery as it can guide us to wisely select drug candidates prior to expensive ADME screenings and clinical trials. Compared to other ADME-Tox properties, human oral bioavailability (HOBA) is particularly important but extremely difficult to predict. In this paper, the advances in human oral bioavailability modeling will be reviewed. Moreover, our deep insight on how to construct more accurate and reliable HOBA QSAR and classification models will also discussed.

1. Introduction

It is estimated that the entire chemical space exceeds 10⁶⁰ molecules, and it is impossible to synthesize all of them given the fact that the total weight of earth is only about 6.0 ×10²⁷ grams. As a matter of fact, there are only 27 million compounds have been registered.¹ Even though the synthesized compounds only occupy a tiny fraction of the entire chemical space, it is much larger than the biological chemical space due to the fact that there are a few thousands of small molecules within our own bodies. As the biological chemical space only represent an amazingly small fraction of the entire chemical space, it is understandable that to discover small molecules that efficiently interact with protein targets is a very difficult task. Although numerous new technologies, such as combinatorial chemistry, high throughput screening and computer-aided drug design have been applied to facilitate the discovery of new drugs, the number of new molecular entities approved annually by FDA (U.S. Food and Drug Administration) has not changed significantly in the last two decades. What are the major reasons that cause the attrition of drug candidates during clinical trials? The lack of efficiency and poor ADME-Tox (absorption, distribution, metabolism, excretion, and toxicity) and pharmacokinetics are responsible for most of the drug attrition.²

Among the many ADME-Tox/PK properties, bioavailability is particularly important for the orally administered drugs. Today, high throughput screenings of human oral bioavailability (HOBA) are routinely conducted in pharmaceutical companies. However, the in vitro and in vivo assays are much time consuming and costly. Only a tiny fraction of synthesized and screened compounds are selected to do the analysis. In silico HOBA modeling, on the other hand, is much more efficient and can deal with large screening libraries. Moreover, in silico HOBA models can serve as drug likeness filters to prioritize screening libraries. Those filters typically have better discriminative power than the conventionally used drug likeness filters, like Lipinski’s ‘Rule of Five’.³ It is a trend that in silico ADME-tox models, particularly HOBA, are incorporated into the paradigm of drug lead identification and optimization procedures.^4–16

1.1 ADME-Tox

As one of the hot fields in computer-aided drug design (CADD), numerous reviews have been published recently on the progress of ADME-Tox modeling,^17–21 here in this paper we only focus on the latest advances of in silico modeling of human oral bioavailability. ADME-Tox properties which can be broadly classified into two categories, namely, the “physicochemical” and “physiological”. The physicochemical properties, including aqueous solubility, logarithm of octanol – water partition coefficient (logP), logarithm of octanol – water distribution coefficient (logD) and pKa, etc., are governed by simple physicochemical laws. The physiological ADME-Tox properties can be further grouped into in vitro ADME-Tox properties (such as Caco-2 permeability and MDCK permeability, liver microsomes, etc.) and in vivo pharmacokinetic properties (such as oral bioavailability, human intestinal absorption – HIA, plasma protein binding – PPB, urinary excretion, area under the plasma concentration – time curve (AUC), total body clearance (Cl), volume of distribution, elimination half time (t1/2), etc.). As physiological ADME-Tox properties, particularly oral bioavailability, are governed by many factors, it is a very challenging task to adequately model and accurately predict the physiological ADME-Tox properties.

1.2 human oral bioavailability

Oral bioavailability (OBA) is one of the most important pharmacokinetic properties in drug discovery. As the oral form is the most convenient way to administrate a drug, it is not a surprise that about 80% of the dosage forms in the worldwide market are administrated orally.²² OBA represents the percentage of an oral dose that is available to produce pharmacological actions. In practice, OBA is defined as the fraction of the oral does that reaches the system circulation in an active form and measured by the ratio of the dose-corrected AUC (area under curve) of the oral route to that of the intravenous route. For an oral drug, the amount of the active form that reaches the system circulation is reduced due to incomplete absorption in gastrointestinal track and the first-pass metabolism. Therefore, oral bioavailability is ranged from 0 to 100%.

It is a very challenging task to adequately model and accurately predict the oral bioavailability of a drug because this physiological property is a complex function of many biological and physicochemical properties, which include the aqueous solubility of the drug in the gastrointestinal tract, the intestinal membrane permeability, and the extend of the first-pass metabolism occurred in liver, gut and intestine, and even the dosage form of the drug. Moreover, the measurement of oral bioavailability of a drug is affected by other factors like whether the drug is taken with or without food, whether other drugs are taken concurrently, as well as the disease states, etc. Those factors may alter the drug absorption, the liver metabolism. For example, the oral bioavailability of patients with liver disease may be increased due to the reduced liver metabolism. The above factors may vary from patient to patient and from time to time for the same patient. This complicate picture explains why the measurement errors of oral bioavailability are very large. According to the survey of 367 drugs conducted by Wang et al.,²³, the average unsigned error and root-mean square error of the experimental measurements are 12.1 and 14.5%, respectively.

In order to develop an oral drug with high bioavailability, medicinal chemists apply a simple rule to select drug candidates: those having high aqueous solubility and high membrane permeability tend to have high OBA; those having low aqueous solubility and low permeability tend to have poor OBA; and the others might need careful formulation to improve their dissolution or absorption rate. This simple rule is based on the fact that drug dissolution and permeability control the rate and extent of drug absorption in GI track. Certainly, a drug with high oral bioavailability should also be largely free from fast-pass metabolism.

1.3 In silico models of HOBA prediction

Attempts have been made to predict HOBA back to Year 2000 by Andrews, Bennett and Xu,²⁴ and Yoshida and Topliss.^25,26 Later on, numerous models were published^25,27,28 and reviewed by ourselves,²⁹ and others.³⁰ The following is a brief summary of HOBA models developed prior to 2008: most models were developed using relatively small data sets (n < 600) and they merely make reliable prediction for the compounds in the screening libraries. For the classification models developed before 2008, the rates of the correct assignment are usually lower than 70%; for the QSAR models, the RMSE are ranged from 24 to 30%. In the following, we will present reviews on the latest HOBA models.

2. Recent Advances in HOBA Modeling

In 2008, a classifier was developed by Ma et al. with GA (genetic algorithm)–CG (conjugated gradient)–SVM (support vector machine) method for 866 compounds that have human oral bioavailability data.³¹ GA was applied to select descriptors that were calculated using Cerius 2 software package (http://www.accelyrs.com), while SVM was used to construct classification model and CG was applied to optimize the parameters of kernel functions of SVM. The predict accuracy, 80% for the training set (690 compounds) and 86% for the test set (76 compounds) is encouraging. However, the classifier has poor performance for the “negative” class: the prediction accuracy is only 44% and the false positive (FP) is even larger than true negative (TN). This phenomenon can be explained by that fact that a very small cutoff of 20% was applied to assign ‘positive’ and ‘negative’ classes. Even the prediction accuracy is good, it cannot be used to further discriminate the compounds belong to the “positive” class.

In 2009, a set of predictive models for human bioavailability were developed by Imawaka et al. using the human oral administration data and animal pharmacokinetic data as descriptors.³²

$$OBA=\frac{AU{C}_{po}/{\mathit{\text{Dose}}}_{po}}{AU{C}_{iv}/{\mathit{\text{Does}}}_{iv}}=\frac{C{L}_{\mathit{\text{tot}}}}{C{L}_{po}}=\frac{\beta \times V{d}_{\beta }}{C{L}_{po}}$$ (1)

Where AUC_po and AUC_iv are the areas under the plasma concentration-time curves for the oral administration and intravenous administration, respectively; Dose_po and Dose_iv are the doses of the two types of administrations accordingly; Vd_β and β are the distribution volume of the terminal phase and the elimination rate constant, respectively. Vd_β is estimated with the animal data using Eq. (2).

$$V{d}_{\beta }\approx V{d}_{ss}=V_B\times R_B+f_P\times V_E+(1-f_P)\times R_{E/I}\times V_B\times (1-H_C)+V_T\times f_P/f_T$$ (2)

Where f_P and f_T are the free fraction of drug in plasma and tissue; V_B and V_E, the volumes of blood and the extracellular fluid, are assumed to be 80 ml/kg and 260 ml/kg, respectively; R_b, the blood to plasma concentration ratio is assumed to be 0.945 if not available; V_T represents the volume the tissue into which the drug is distributed; R_E/I, which is set to 1.4, is the ratio of the amounts of binding protein in the extracellular fluid to that in plasma; H_c, the hematocrit value, is set to 0.42; After taking the above assumed constants into Eq. 2, Eq. 2 becomes Eq. 3.

$$V{d}_{\beta }=f_P\left[\frac{V_T}{f_T}\right]+80R_B+195f_P+65$$ (3)

The authors proposed three methods to estimate [V_T/f_T] using the animal values of Vd_β, R_B and f_P. In Method 1a, the [V_T/f_T] of human is assumed equal to that of animal; in Method 1b, Eq. 4 is used to calculate the [V_T/f_T] of human:

$${\left[\frac{V_T}{f_T}\right]}_{\mathit{\text{human}}}=0.6628{\left[\frac{V_T}{f_T}\right]}_{\mathit{\text{rat}}}^{1.096}$$ (4)

Method 2 is similar to Method 1a except that the [V_T/f_T]_animal values come from not only rat but also other animals. Once [V_T/f_T]_human is obtained, then human Vd_β can be calculated with Eq. 3 using human [V_T/f_T], f_P and R_B.

The performance of the three calculation protocols was summarized in Table 1. The AUE and RMSE of Protocol 3 (using Method 2 to calculate [V_T/f_T]_human) is 10.7 and 15.4%, respectively. Unfortunately, the statistic parameters (AUE and RMSE) were calculated using a small set of data and the reliability may be questionable. The RMSE of the Protocol 1 (using Method 1a to calculate [V_T/f_T]_human) and Protocol 2 (using Method 1b to calculate [V_T/f_T]_human) are 20.9 and 23.2, respectively.

Table 1.

Summary of the latest computational models for predicting human oral bioavailability

#	Authors	Model Type	Descriptors	Modeling Tools	Performance
1	Ma et al.	Classification	Cerius 2 descriptors	GA-GC-SVM	Ntrain = 690, Ntest = 76, for the test set: TP = 58, FN = 2, TN=7, FP =9, Rsuc = 86%
2	Imawaka et al.	Direct calculation	Animal pharmacokinetic data	Direct calculation, Vbβ estimated using Method 1a	N=61, AUE=15.0, RMSE=20.9
3	Imawaka et al.	Direct calculation	Animal pharmacokinetic data	Direct calculation, Vbβ estimated using Method 1b	N=61, AUE=17.0, RMSE=23.2
4	Imawaka et al.	Direct calculation	Animal pharmacokinetic data	Direct calculation, Vbβ estimated using Method 2	N=28, AUE=10.7, RMSE=15.4
5	Tian et al.	QSAR	Basic molecular properties and structural fingerprint	Genetic function approximation and multiple liner regression	N=996, R=0.79, qLOO=0.72, RMSE=22.3%, Rtest=0.71 RMSEtest=23.6%
6	Paixão, et al.	QSAR	In vitro Papp and Clint, etc.	Regression	N=49, RMSE=16%
7	Paixão, et al.	QSAR	In silico Papp, in vitro Clint, etc.	Regression	N=25, RMSE=19.8%
8	Paixão, et al.	QSAR	In vitro Papp, in silico Clint, etc.	Regression	N=22, RMSE=31.9%
9	Paixão, et al.	QSAR	In silico Papp and Clint, etc.	Regression	N=68, RMSE=34.6%
10	Ahmed, et al.	Classification	physiochemical and structural properties	logistic classifier	Ntrain = 969, Rsuc = 71%
11	Xu et al.	QSAR	Dragon descriptors	SVM-regression	Ntrain = 156, Ntest = 36, R2 = 0.8, Q2 = 0.72, RMSE = 31%, RMSEtest = 22%
12	Xu et al.	QSAR	Dragon descriptors	SVM-regression	Ntrain = 122, Ntest = 27, R2 = 0.75, Q2 = 0.63, RMSE = 28%, RMSEtest = 77%
13	Xu et al.	QSAR	Dragon descriptors	SVM-regression	Ntrain = 180, Ntest = 44, R2 = 0.78, Q2 = 0.80, RMSE = 36%, RMSEtest = 36%
14	Xu et al.	QSAR	Dragon descriptors	SVM-regression	Ntrain = 197, Ntest = 43, R2 = 0.69, Q2 = 0.68, RMSE = 42%, RMSEtest = 46%
15	Olivares-Morales et al.	Classification	Rat oral bioavailability	Receiver operating characteristics	N=123, Rsuc=69 %
16	Olivares-Morales et al.	Classification	Dog oral bioavailability	Receiver operating characteristics (ROC)	N=126, Rsuc=75 %
17	Olivares-Morales et al.	Classification	NHP oral bioavailability	Receiver operating characteristics (ROC)	N=40, Rsuc=90 %

In 2011, we have performed a systematic study on understanding how various molecular descriptors correlate to HOBA and developed a set of classification and QSAR models to predict HOBA using a large database of 1014 compounds.³³ We could not find any property-based rule which has sufficient discriminative power to serve as a predictor for HOBA. We then constructed a set of multiple linear regression models using genetic function approximation. The best model has achieved a very encouraging performance in modeling HOBA: R = 0.79, Q_LOO = 0.72, RMSE = 22.3 % for the training set; R_test = 0.71 and RMSE_test = 23.6% for the test set.

In 2012, a set of HOBA models were developed by Paixão, et al.³⁴ using a set of in vitro and in silico physiological properties as descriptors, including absorption and solubility at the gastrointestinal pH range 1.5–7.5, apparent permeability - P_app, and intrinsic clearance - Cl_int.³⁴ The authors divided the whole data set into four sets according to the availability of in vitro data of P_app and Cl_int. For the 49 drugs for which both in vitro P_app and Cl_int are available, a computer model with an excellent predictive ability was constructed: RMSE=16.0%, 84% of data within ±20% and 96% within ±35% error margins. Unfortunately, when only in silico data of P_app and Cl_int were applied, the performance of the computer model is much worse: RMSE=34.6.0%, 53% of data within ±20% and 74% within ±35% error margins. As suggested in Table 1, apparent permeability is a more important descriptor than intrinsic clearance for modeling HOBA.

Recently, Xu et al.³⁵ constructed a set of QSAR models using our HOBA database.³⁶ The descriptors of those models, which include constitutional and topological descriptors, walk and path counts, connectivity indices, etc., were calculated using Dragon.³⁷ The best-performed model, which was constructed by SVM-regression has R²_test and RMSE_test of 0.80 and 31%, respectively. Apparently, the predictability of this model is not strong. Other linear models constructed by multiple linear regression and partial-least-square fitting perform even worse.

In 2012, a set of classifiers were developed by Ahmed and Ramakrishnan for a large dataset of HOBA.³⁸ To get the optimal descriptors, the authors first constructed classifiers for both HIA and Caco-2 permeability using both the physiochemical and structural properties as descriptors. The underlying descriptors that are effective in discriminating between distinct classes were then identified by partial least squares discriminant analysis. 47 descriptors which are common for both HIA and Caco-2 were used to construct classifiers for HOBA. The best performed classifier, the logistic classifier, achieves a classification accuracy of 71%. However, the authors didn’t further evaluate the classifier using external test set.

In 2014, Olivares-Morales et al. developed a set of classification models for HOBA using animal oral bioavailability data.³⁹ The HOBA data were classified into two groups (high and low) using a cutoff of 50%. Optimal OBA_animal thresholds were identified for mouse (67%), rat (22%), dog (58%) and non-human primates (35%) through ROC (receiver operating characteristics) analysis. The performance of the classification models are summarized in Table 2. It is not a surprise that the model based on the oral bioavailability of non-human primate has a very high predictability.

Table 2.

The performance of classification models predicting HOBA from animal data.^*

Species	Threshold	TP	FP	TN	FN	Sensitivity	Specificity	Successful Rate
Rat	22%	54	17	31	21	0.72	0.65	69%
Dog	58%	51	20	44	11	0.82	0.69	75%
NHP	35%	20	4	16	0	1.00	0.80	90%

^*TP: true positive, FP: false positive, TN: true negative, FN: false negative, sensitivity: TP/(TP+FN), specificity: TN/(TN+FP) and successful rates: (TP+TN)/(TP+TN+FP+FN) were calculated according to Table SII of Ref. The performance of the classification

In summary, there is some progress on the in silico modeling of human oral bioavailability in recent years: (1) the database has been expanded from ~600 to about ~1000, more high quality data make it possible to develop more reliable models; (2) more experimental pharmacokinetic data, either from human or animals were used to construct models for HOBA; (3) for QSAR models using descriptors purely based on molecular structures, the best QSAR model could predict HOBA for the external dataset with an RMSE of 23–24%, marginally better than models developed before 2008; (4) as to the classification models using common molecular structure-based descriptors, the best successful rate is about 70%, not much difference from the models constructed before 2008. The representative HOBA QSAR models and classifiers were summarized in Table 1.

3. Discussion

In the last section, several representative HOBA models developed in last six years were reviewed. It is obvious that more effort is needed to develop more accurate and predicative models for this important ADME/PK property. What are the strategies to achieve the goal of developing high quality HOBA models?

3.1 Database construction

First of all, more high quality human oral bioavailability data is needed. It is not an easy task to collect a large number of HOBA database since one needs AUC for both the oral and intravenous administrations to measure HOBA (Eq. 1). However, the intravenous does is not always available due to safety and solubility reason. This situation becomes even severer by the fact that the HOBA data which are owned by the pharmaceutical companies industry, usually do not exist in public domain.

A big advantage of in-house database owned by pharmaceutical companies is that the data are consistent and have less variation. The following are some publications on HOBA using in-house data sets: an analysis of bioavailability performed by Veber et al. in with a dataset containing over 1100 compounds owned by GSK;⁴⁰ a study of oral bioavailability for 591 structures from the GlaxoWellcome’s internal database by Andrew et al.²⁴ Unfortunately, these in-house data are usually not available for the public scientific community. On the other hand, the HOBA data in the public domain may lack of self-consistency as the HOBA data usually come from more than one source and significant variability might exist between different sources.

To successfully model HOBA, it is critical to collect a large amount of reliable and consistent experimental data. We have put a lot of effort to construct the HOBA database. In 2006, we collected HOBA data for 577 drugs from Goodman and Gilman’s the Pharmacological Basis of Therapeutics, both the 9^th and 10^th editions. In 2007, the database was expanded to 805 and some experimental data were updated using the latest literatures.³⁶ Now the third version of the HOBA database has collected human oral bioavailability for more than 1000 drugs. The latest database is accessible from http://cadd.suda.edu.cn/admet/. To achieve high reliability and consistency of the database, a great effort was put to verify the newly collected data. Suspicious data were recognized when there are large root-mean-square deviations of the HOBA data for the same drugs. We also pay extra attention to entries that have large prediction errors by our HOBA models. This strategy was successfully used by ourselves to verify the aqueous solubility data in the Beilstein dataset.¹⁵

3.2. Descriptors

To successfully model human oral bioavailability, another key factor is to select suitable molecular descriptors. There are thousands of descriptors available, not only for 1D, but also for 2D and 3D. Lots of descriptors are redundant and should be eliminated using covariance analysis. The widely used molecular descriptors include Abraham,⁴¹ Volsurf,⁴² Molsurf,⁴³ Adriana.Code,⁴⁴ FAF-Drugs2,^45,46 Dragon,³⁷ Mold,⁴⁷ Cerius 2 (www.accelrys.com), Molconn-Z (www.tripos.com), and so on. To wisely select proper molecular descriptors to model a property, one needs know some basic knowlege on that property. As to HOBA, it is a function of f_a, the fraction of drug does that is absorbed in the gastrointestinal tract and F_G, the fraction of drug dose that escape first pass metabolism in the gastrointestinal tract and F_H, the fraction of drug does that escape first pass metabolism in the liver.

$$OBA=f_a\times F_G\times F_H$$ (5)

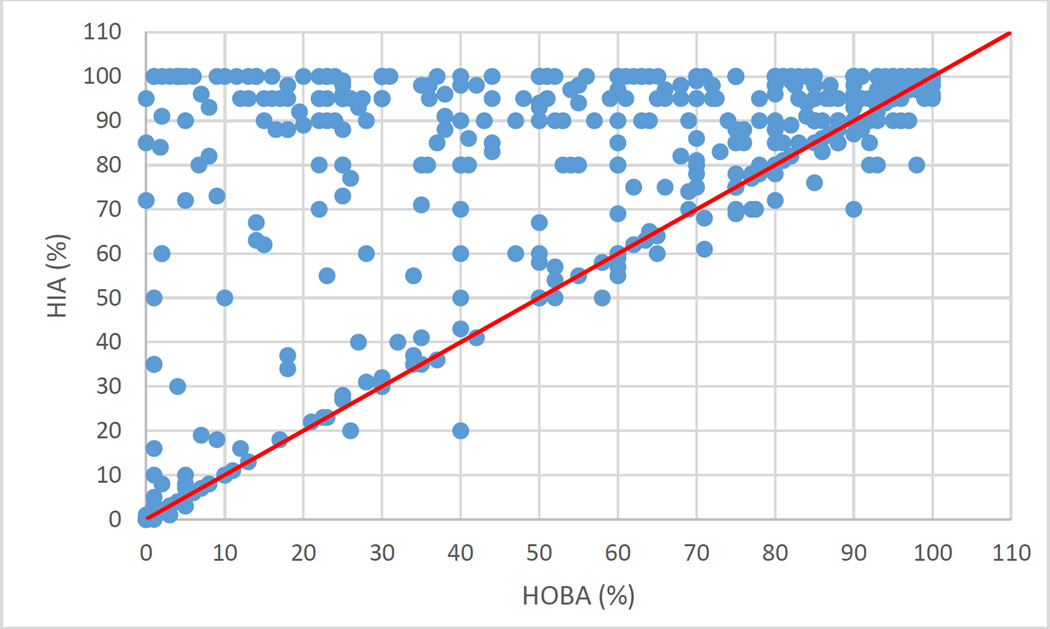
We recently studied the relationship between HOBA and HIA (human intestinal absorption) for 510 compounds that have both values measured. The correlation coefficient between HOBA and HIA is 0.63. In these 510 compounds, 182 show a significant difference between HOBA and HIA (HIA – HOBA ≥20). Those compounds are considered to have a significant first-pass metabolism rate while the others do not. The relationship between HOBA and HIA is shown in Fig. 1. It is obvious that most compounds have HIA larger than or equal to HOBA (on or above the red line). Similar result was found in our previous publication.³³ Given the fact that HIA is highly correlated to HOBA and it defines the upper limit of HOBA, HIA data from in vitro/in vivo analysis can be a good descriptor for HOBA. Molecular descriptors that well describe HIA, such as logP and logD which are measures of lipophilicity, aqueous solubility, should also be good descriptors for HOBA.

Figure 1.

Relationship between human oral bioavailability and human intestinal absorption for 510 drugs. The red line is the diagonal line where the X-axis and Y-axis values are equal, the correlation coefficient R is 0.63.

As HOBA is also a function of F_G and F_H, the molecular descriptors that describe the substructures directly participating the metabolism reactions should be good descriptors for modeling HOBA. Indeed, many of the best-performed models were constructed using counts of molecular fragments, molecular fingerprints as descriptors.^23,33 Moda et al. found that the use of all atoms, bonds, connections and chirality to define molecular fragments led to a set of encouraging models in their study.²⁸ Although not been used, we expect that pharmacophore fingerprints, such as those produced by the Tuplets model of Sybyl,⁴⁸ could be good descriptors for HOBA.

Other experimental data of pharmacokinetic properties, such as bioavailability of animals, volume of distribution, AUC concentration – time curve, C_max, t_1/2, clearance, plasma protein binding, etc. can be valuable descriptors for HOBA. The only problem of this type of descriptors is that they are available only for a very limited set of molecules.

3.3. Model construction

In the next step, QSAR or classification models are constructed using the calculated descriptors. In order to develop statistically significant and robust models, the whole dataset is divided into a training set, a cross-validating set and a test set. The predictability of a model is objectively evaluated by the test set. In our work of modeling aqueous solubility,¹⁵ we performed 85/15 cross-validation test (85% of data randomly selected into training set and 15% into test set) 10,000 times and we found out that Q², AUE and RMSE had Gaussian distributions. For example, the mean, maximum and minimum of Q² were 0.832, 0.884 and 0.762, respectively for the ASM-ATC-LOGP model. As to RMSE, the mean, maximum and minimum were 0.841, 0.959 and 0.732, respectively for the ASM-ATC-LOGP model. It is obvious that the Q² and RMSE_test depends on how a test set is formed. Obrezanova et al. suggested to split a dataset into training, test and cross-validation sets through classification analysis of the 2D path-based fingerprints of molecular structures.⁴⁹ First of all, the cluster centroids and singletons automatically enter the training set; the others were sorted by the Y-values and assigned to the raining set, cross-validation set and test set randomly with the userdefined probabilities.

As listed in Table 1, a variety of statistical tools have been applied to construct QSAR models for HOBA. The following are the most commonly-used tools: multiple linear regressions (MLR), partial least square fitting (PLS), genetic algorithms (GA), artificial neural network (ANN), support vector machines-regression (SVMR), Gaussian processes (GP), etc. When a great number of descriptors are applied to model HOBA, hybrid methods, such as GA/MLR or GA/PLS or GA/SVMR are recommended since the hybrid methods can effectively avoid the over-fitting problem by selecting a subset of descriptors to construct QSAR models. In the fitness functions of GA, not only the performance of the model (R², Q², RMSE_train, RMSE_test) matter, but also the number of descriptors selected. The more descriptors selected, the larger the penalty. Gaussian processes,^49,50 which is able to model non-linear relationships and select important descriptors from a large pool, could have a great application on HOBA modeling. More importantly, GP is inherently to avoid overtraining and provide a way to objectively estimating the uncertainty of prediction.

As to classification models of HOBA, support vector machine, recursive partitioning, k-nearest neighbors, etc. are the commonly used methods. The performance of a classifier strongly depends on how to define ‘+’ and ‘−’ or multiple classes. There is still no consensus on which cutoffs should be used to form the classes. The following cutoffs have ever been used to construct two-class classifiers: 20% by Ma et al. (if HOBA>=20%, then the molecule belongs to the ‘+’ class, otherwise, it is in ‘−‘ class),³¹ 30% by ourselves,³⁶ and 50% by Olivares-Morales et al.³⁹ Few classifiers were published for more than two classes.²⁶ To construct a successful classifier, the number of data in each classes should be balanced, otherwise, one may have good sensitivity but poor specificity or vice versa. Classification sensitivity and specificity are described by numbers of true positives (TP), true negatives (TN), false positives (FP) and false negatives (FN) using the following equations: sensitivity = TP/(TP+FN), specificity = TN/(TN+FP).

How can we improve the prediction accuracy of HOBA for a new compound outside of the training set? The first approach is based on the concept of ‘the domain of applicability’ proposed by Konovalov et al.⁵¹ and Weaver et al.⁵² In this approach, the entries that have the similar descriptor profile to that of the compound to be predicted are selected and put into the training set. The models constructed using this specific training set are then used to predict the HOBA of the compound. Certainly, this approach may not be suitable in database screening if the model construction procedure takes a long time.

The second possible approach to improve prediction accuracy of HOBA is to develop consensus models by combining two or more models together. We constructed a set of consensus models to model bioavailability (30 models), plasma protein bonding (20 models) and urinary excretion (30 models).⁵³ All those models were constructed by MLR using GA to select descriptors, the count of molecular fragments. More reliable prediction was achieved with the consensus models for all the three ADME-Tox properties. The concept of “consensus modeling” was also applied by other researchers in ADME prediction. For example, Abshear et al. evaluated the performance of four QSAR models in KnowItAll (http://www.bio-rad.com) on predicting the intrinsic solubility of 113 diverse organic compounds.⁵⁴ The absolute average errors (AAE) of the four models are 0.314, 0.422, 0.327 and 0.324 log units, respectively. However, the prediction error is reduced to 0.257 log unit by using a consensus model combined with the four individual models. With more and more HOBA models published, it is possible to achieve more reliable prediction utilizing the strategy of consensus modeling.

3.4. Other Development

Besides human oral bioavailability, a set of models were constructed for predicting bioavailability administrated through other routes. For example, a spreadsheet-based model to estimate bioavailability of chemicals from dermal exposure was constructed by Dancik et al. recently.⁵⁵

Some models were developed to predict animal bioavailability: Nomoto et al. constructed a computational model for rate bioavailability using in vitro intestinal parameters as descriptors.⁵⁶ De Buck et al. developed computer models for predicting a set of physiological properties including bioavailability for 50 structurally diverse compounds in rat.⁵⁷ Grabowski and Jaroszewski developed models to predict bioavailability of veterinary drugs.⁵⁸

Computer models for modeling HOBA of specific types of drugs were also reported recently. Artemenko et al. constructed PLS models for a set of 362 antiviral drugs. The performance of the model with R²_test > 0.6 is satisfactory.⁵⁹ QSPR models were developed for modeling and predicting both MEK inhibitory activity and oral bioavailability of novel isothiazole-4-carboxamidines.⁶⁰

4. Conclusions

In this paper, the latest progress on the in silico modeling of human oral bioavailability is reviewed. Due to the complexity of this physiological property and the lack of the high quality and self-consistent experimental data, there is still a long way to go to reliably predict human oral bioavailability for arbitrary compounds in the screening libraries.

Abbreviations

ADME-Tox

Absorption, Distribution, Metabolism, Excretion, and Toxicity

HOBA

Human oral bioavailability

HIA

Human intestinal absorption

QSAR

Quantitative structure – activity relationship

MLR

Multiple linear regressions

GA

Genetic algorithm

LOO

Leave-one-out

R²

Regression coefficient

Q²

Cross-validation regression coefficient

AUE

Average unsigned error

RMSE

Root-mean-square error

AUE_test

Average unsigned error of the test set

RMSE_test

Root-mean-square error of the test set

N

Number of data points

N_test

Number of data points in a test set

LogP

Logarithm of octanol – water partition coefficient

LogD

Logarithm of water distribution coefficient