Subgroup identification in personalized treatment of alcohol dependence

Abstract

Background

Identification of patient subgroups to enhance treatment effects is an important topic in personalized (or tailored) alcohol treatment. Recently, several recursive partitioning methods have been proposed to identify subgroups benefitting from treatment. These novel data mining methods help to address the limitations of traditional regression-based methods that focus on interactions.

Methods

We propose an exploratory approach, using recursive partitioning methods, e.g., interaction tree and virtual twins, to flexibly identify subgroups in which the treatment effect is likely to be large. We apply these tree-based methods to a pharmacogenetic trial of ondansetron.

Results

Our methods identified several subgroups based on patients’ genetic and other prognostic covariates. Among the 251 subjects with complete genotype information, the interaction tree method identified 118 with specific genetic and other prognostic factors, resulting in a 17.2% decrease in the percentage of heavy drinking days (PHDD). The virtual twins method identified 88 subjects with a 21.8% decrease in PHDD. Overall, the Virtual Twins subgroup achieved a good balance between the treatment effect and the group size.

Conclusions

A data mining approach is proposed as a valid exploratory method to identify a sufficiently large subgroup of subjects that is likely to receive benefit from treatment in an alcohol dependence pharmacotherapy trial. Our results provide new insights into the heterogeneous nature of alcohol dependence, and could help clinicians to tailor treatment to the biological profile of individual patients, thereby achieving better treatment outcomes.

Introduction

Alcohol use disorders (AUDs) constitute a major public health problem worldwide that accounts for significant morbidity and mortality. Three medications have been approved in the United States to treat AUD: disulfiram, acamprosate, and naltrexone. However, many patients have limited or no response to these medications (e.g., Anton et al. 2006), which leads to a reluctance on the part of physicians to prescribe medications, representing an important barrier to the dissemination of pharmacological treatments (Oliva et al. 2011; Weber 2010). Developing new and more effective medications to treat AUDs is a high priority for researchers (Willenbring 2007).

Medications to treat AUD have been identified and evaluated using the whole sample, a “one-size fits all” approach that leaves little room for individual treatment. However, considerable heterogeneity exists among people with AUDs, suggesting a need for personalized treatment approaches based on individual features, e.g., genetic variation (Heilig et al. 2011). The goal of personalized medicine is “to develop new therapies and optimize prescribing by steering patients to the right drug at the right dose at the right time” (Hamburg and Collins 2010). Ongoing research has informed studies that match alcohol medications to patients based on genotype (Kranzler and McKay 2012). In one of the first such studies, we discovered that alcoholics with two specific variations of a gene related to the neurotransmitter serotonin were capable of reducing their drinking significantly using the medication ondansetron (Johnson et al. 2011). These findings can help clinicians to prescribe ondansetron to patients who are likely to benefit from this drug, replacing the current trial-and-error process. It may also inform the development of new therapeutic agents that can improve the treatment and prevention of AUD.

In the above pharmacogenetic study, we were interested in the moderating effect of genetic variations on treatment, i.e., the interaction between treatment and genotypes (Gail and Simon 1985). A common approach to evaluate moderators is to use regression methods to test the significance of the interaction terms. However, such an analytical strategy suffers from the large number of potential interaction terms, arbitrary definition of covariate cutoffs to form actual subgroups, and other common problems associated with subjective post hoc analysis. For example, in an ondansetron study (Johnson et al. 2013), a total of 21 genetic variations (polymorphisms) were examined for their associations with drinking outcomes. Each common polymorphism (minor allele frequency >5%) has three genotype levels (e.g., LL/LS/SS in the promoter region polymorphism 5-HTTLPR of the SLC6A4 gene), resulting in a total of 3²¹ possible genotype combinations! Traditional regression models are limited to analyzing no higher than three-way interaction terms (e.g., polymorphism-1 by polymorphism-2 by treatment), which make these methods impractical to assess higher order interactions. Thus, new techniques are needed to tackle such high dimensional data.

Several statistical approaches developed within the machine learning and data mining communities have been proposed recently to identify subgroups of patients for which there are differential effects of specific treatments. Most of these methods rely on tree-based search methods, e.g., the classification and regression tree (CART) methodology (Breiman et al. 1984; Zhang and Singer 2010). Trees form subgroups by bisecting the covariate space so that the heterogeneity in the effects of the treatment on the response variable is maximized between the resultant “child” nodes (e.g., a highly significant treatment effect in one partition and a non-significant treatment effect in the other). Once a rule is selected, the same logic is applied to split either child node, stopping when there is no additional benefit from splitting any further.

Some notable developments include interaction trees (IT: Negassa et al. 2005 and Su et al. 2009), virtual twins (VT: Foster et al. 2011), and relative effectiveness (Zhang et al. 2010). Unlike traditional methods of subgroup (or subset) analysis in clinical trials that rely on multiple comparison procedures applied to a small number of pre-specified subgroups, nonparametric methods based on recursive partitioning appear flexible and efficient in that they allow the generation of subgroups within a very broad “model space” and can handle higher-order complex treatment-by-covariates interactions in high-dimensional data.

However, most of these up-to-date methods have not yet been applied in alcohol pharmacogenetic studies. In this paper, we aim to fill a crucial gap in the development of new pharmacogenetic analytic tools and their applications in alcohol treatment trials. These methods were tested in a recently completed alcohol dependence pharmacogenetic trial of ondansetron (Johnson et al. 2011).

Methods

Data

Johnson et al. (2011) conducted a double-blind, placebo-controlled trial of ondansetron, a serotonin-3 (5-HT3) receptor antagonist, to reduce drinking severity in 283 alcohol-dependent subjects (aged 20 to 78 years), who were enrolled in the 11-week randomized trial after a 1-week single-blind placebo lead-in. All subjects received weekly, standardized cognitive behavioral therapy as their psychosocial treatment in addition to either ondansetron (4 µg/kg twice daily) or placebo.

At enrollment, genotyping was performed on all samples for Long (L) and Short (S) alleles of the functional insertion-deletion polymorphism (5′-HTTLPR) in the promoter region of SLC6A4 gene. Subjects were randomly assigned to receive either ondansetron or placebo from weeks 2 through 12, stratified by 5-HTTLPR genotype (LL/ vs. LS/SS). Their daily drinking level during the treatment period was recalled and recorded using the timeline follow-back method (TLFB, Sobell and Sobell 1992). Samples were also retrospectively genotyped for a functional single-nucleotide polymorphism (SNP), rs1042173 (T/G), in the 3′-untranslated region of the same gene. Subsequently, Johnson et al. (2013) examined an additional 19 SNPs in HTR3A and HTR3B genes, which encode the 5-HT3A and 5-HT3B subunits of the 5-HT3 receptor, to determine whether these variants moderated ondansetron treatment outcome. This resulted in a total of 21 genetic polymorphisms to be considered as predictors of ondansetron response.

Statistical Analysis

We took the reduction from baseline PHDD to the average PHDD during treatment period as our primary outcome, rather than the original longitudinal daily heavy drinking index. It is of note that we did not perform any imputation on missing values for this outcome. The covariates included PHDD_base (PHDD at baseline), age, onage (age of onset of alcohol dependence), race (Hispanic vs. others), gender, and the 21 genetic polymorphisms. We removed subjects with any missing genotypes, leaving 251 subjects in the analysis. Using linear regression, ondansetron patients had 0.7% lower PHDD than placebo patients (p=0.422), showing no significant difference between treatment and placebo in the overall sample.

We tried two data mining methods, i.e., interaction tree and virtual twins, to identify genetic and other prognostic moderators of ondansetron. We compared the results of these analyses to identify new pharmacogenetic findings.

Interaction Tree (IT)

Interaction tree is a tree-based exploratory procedure for subgroup analysis (Su et al. 2009, 2011). It divides the data into subgroups of contrasted treatment effects by partitioning the data recursively, i.e., covariates are recursively evaluated at each data partitioning step in growing a tree. Thus, subjects in the terminal nodes with top treatment effects are those who are the most responsive to treatment. Following a CART convention (Breiman et al., 1984), interaction tree analysis consists of three major steps: growing, pruning, and validation.

In the growing step, the split is restricted to a binary question on a predictor X_j. If X_j is continuous, the question takes the form of X_j ≤ c for some real value c. Otherwise, if X_j is nominal with categories C = {c₁, …, c_r}, then the question takes the form of X_j ∈ A, A ⊂ C. The aim is to find a split among all valid candidates that bisects the data into two subsets with the greatest heterogeneity in treatment. In other words, the best split would show the greatest interaction with treatment.

A linear regression model for the continuous response Y is used to assess the interaction effect:

$$Y~{\beta }_0+{\beta }_{1}trt+{\beta }_{2}s+{\beta }_{3}trt\times s,$$ (1)

where s is the indicator associated with a split. The split is evaluated via the Wald test statistic for hypothesis H₀: β₃ = 0 vs. H_a: β₃ ≠ 0, i.e., G(s) = {β̂₃/se(β̂₃)}².

The best split s* is the one that yields the maximum G(s) among all candidates. The same procedure is applied to split either child node recursively until some lenient stopping rules are satisfied, resulting in a large initial tree, denoted by 𝒯₀.

The final tree model is one of the subtrees of 𝒯₀. To select the best subtree, a pruning procedure is first applied to narrow down the subtree choices. This leads to a sequence of nested subtrees of decreasing size. Then a cross-validation method is applied to assess the performance of each subtree in the sequence. IT adopts the pruning method and a bootstrap based validation procedure proposed by LeBlanc and Crowley (1993), where a detailed description can be found.

Virtual Twins

The Virtual Twins method (Foster et al. 2011) involves predicting the response to treatment and control ‘twins’ for each subject. Based on the prediction, an optimal subset can be found with an enhanced treatment effect.

The Virtual Twins method has two steps: estimation of the paired outcome and a subsequent search for the optimal subset. In step 1, a random forest is used to learn the outcome ‘twins’ of the ith subject, E(Y_i|trt_i = 0, X_i) and E(Y_i|trt_i = 1, X_i), where E(Y|trt = 0, X) is the expected outcome for a subject in the placebo group with covariate value X. The response of input is Y while the covariate includes X_i, trt_i, and their interaction X_i × I(trt_i = 0), X_i × I(trt_i = 1). The inclusion of both X_i × I(trt_i = 0) and X_i × I(trt_i = 1) is not essential, but their inclusion improves the property of the method. The estimates for E(Y_i|trt_i = 0, X_i) and E(Y_i|trt_i = 1, X_i) are denoted as Ê_0i and Ê_1i respectively. The treatment effect of subject i is thus evaluated as Z_i = Ê_1i − Ê_0i.

In step 2, a regression tree is built to find a parsimonious number of Xs that are strongly associated with Z and hence can define the desired subset, using the rpart package in R with minimal terminal node size at 5. Following the standard procedure in CART, a complexity parameter for pruning is chosen by cross-validation.

Traditional Regression Methods

For comparison, we also included the results obtained using traditional regression methods, where the interaction terms of genotype and treatment were examined. Due to the extremely large number (3²¹) of genotype combinations, only the two-way interaction of each SNP and treatment was considered. Along the lines of Johnson et al. (2013), subjects were identified if there existed >10% PHDD difference between the two arms, at a significance level of p<0.05. Analogous to the minimal split restriction in tree methods, we excluded rare genotypes with an occurrence ≤ 5.

Results

All the results shown below were based on 251 subjects with complete genotype information in our analyses.

Interaction Tree

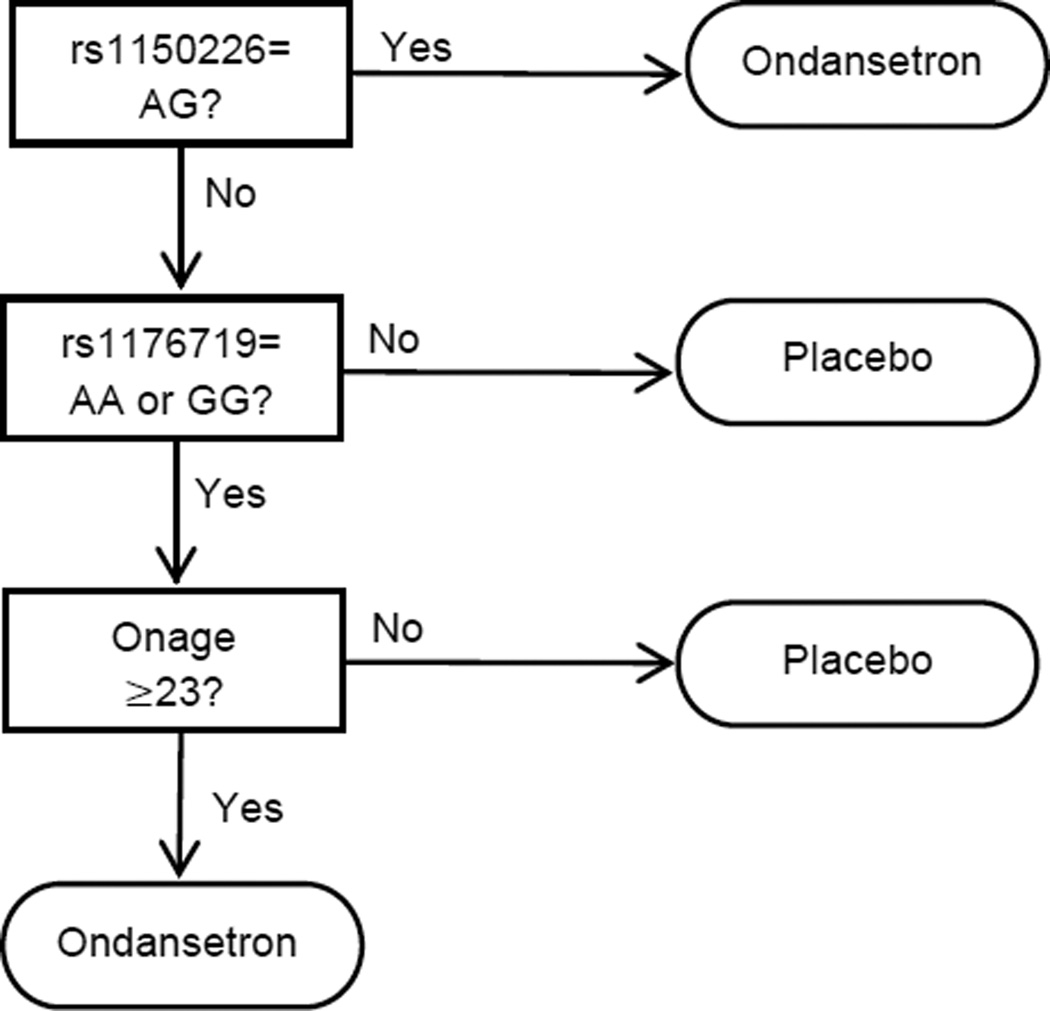
We built our interaction tree using the default setup. In the pruning process, we adopted BIC as the selection criterion. Figure 1 shows the structure of the selected interaction tree. The tree depth is 4, implying treatment-by-covariates interactions of possibly up to the fifth-order. Terminal nodes with a significant marginal treatment effect at p≤0.05 were selected to be the optimal subgroup, i.e.: (1) rs1150226 is {AG}; (2) otherwise, rs1176719 is in {AA or GG} and Onset age>=23. A total of 118 subjects (47%) of the 251 subjects with non-missing values were selected. The sample mean difference of PHDD in the selected subgroup was 17.2%. Compared to the overall sample mean difference of 0.7% in PHDD, the subjects in the target groups showed a much greater reduction in PHDD in the ondansetron arm than the placebo arm.

Figure 1.

Subgroup identified by interaction tree.

Virtual Twins

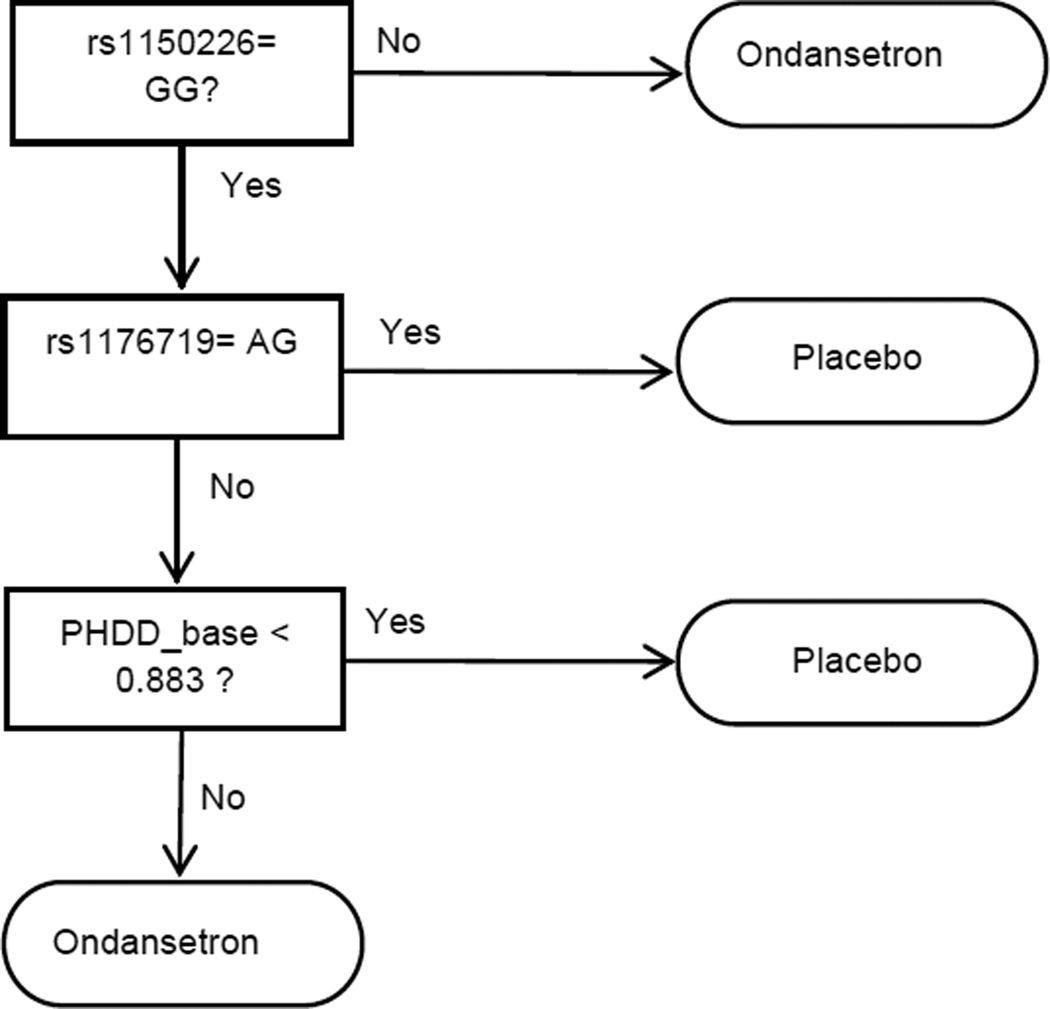
We ran Step 1 in the R randomForest package with all options in default, but the number of trees was set at 1000. We obtained an estimate for the global average treatment effect Z of 0.03. In the recursive partition process, we set the complexity parameter to be 0.05 according to the cross-validation provided in the rpart package. As shown in Figure 2, the final VT tree is also of depth 4. The two terminal nodes with greater group average (suggested threshold in Foster et al. (2011): global average of Z + 0.05) were selected as the proposed subgroup. We gave ondansetron to subjects with: (1) rs1150226 is not {GG}; (2) otherwise, PHDD_base>0.883 and rs1176719 is not {AG}.

Figure 2.

Subgroup identified by Virtual Twins.

The selected subgroup has 88 subjects (35%) with a treatment effect of 21.8% in the 251 subjects with non-missing genotypes.

Traditional Regression Method (TRM)

Using the TRM to examine the interaction terms of genotype and treatment, we identified a combination of 4 genotypes: rs1150226:AG, rs17614942:AC, rs1062613:CC, rs2276302:GG (TRM, N=57 among 251 subjects). Having at least one of these genotypes was predictive of an ondansetron treatment response. The estimated mean difference of PHDD between treatment and placebo was 26.3% in the TRM subgroup (p=0.001).

Comparison of Results

The Interaction Tree method identified two genotypes: rs1150226:AG and rs1176719:AA or GG in addition to the background attribute age of onset. The Virtual Twins method identified two genotypes: rs1176719:AA or GG and rs1150226:AA or AG. Four genotypes were identified in TRM: rs1150226:AG, rs17614942:AC, rs1062613:CC, and rs2276302:GG. We noted that all subgroups include rs1150226, though the Virtual Twins method included either AA or AG, while the TRM and Interaction Tree only identified AG. Furthermore, we found that rs1176719:AA or GG was shared by the IT and VT methods.

Comparison of the efficacy was also done using a dichotomous responder vs. non-responder endpoint efficacy variable, percentage of subjects with no heavy drinking days (PSNHDD), which has been endorsed by the U.S. Food and Drug Administration as an important outcome measure for phase III trials (Falk et al. 2010). To increase power, subjects having at most 1 heavy drinking day (PS1HDD) during the final 4 weeks of the treatment period were considered to be “responders”. By doing so, the number of “responders” increased from 48 (PSNHDD) to 64 (PS1HDD). Because many subjects dropped out early, we imputed their missing drinking outcomes as heavy drinking days as defined in Falk et al. (2010), making the sample size consistent with our analysis of PHDD. The odds ratios (ORs) for TRM, and the subgroup identified by other tree-based methods were shown in Table 1. The p values given in the table were computed using Fisher’s exact test.

Table 1.

Subgroup Comparison: Odds Ratio for PS1HDD (percentage of subjects with at most heavy drinking days) in month 3 of follow up.

Method	Number	OR	P-Value
TRM*	57	5.0	0.015
Virtual Twins	88	3.8	0.017
Interaction Tree	118	2.1	0.059

^*TRM: traditional regression method.

Generally, smaller subgroups had larger ORs and more significant p values. Notably, the OR for ondansetron vs. placebo in both the TRM and the Virtual Twins subgroups were comparable (5.0 vs. 3.8), though the latter subgroup had 54% more subjects than the former. Such subjects can be defined as “super-responders.” The subgroup identified by the Interaction Tree had an OR of 2.1, with more than double the number of subjects in the TRM subgroup. Overall, the Virtual Twins subgroup achieved a good balance of the treatment effect (OR=3.8) and the group size (88 of 251, or 35%). A Phase III trial specifically targeting this subgroup could be conducted to confirm this personalized medicine hypothesis.

Similarity in selected subjects

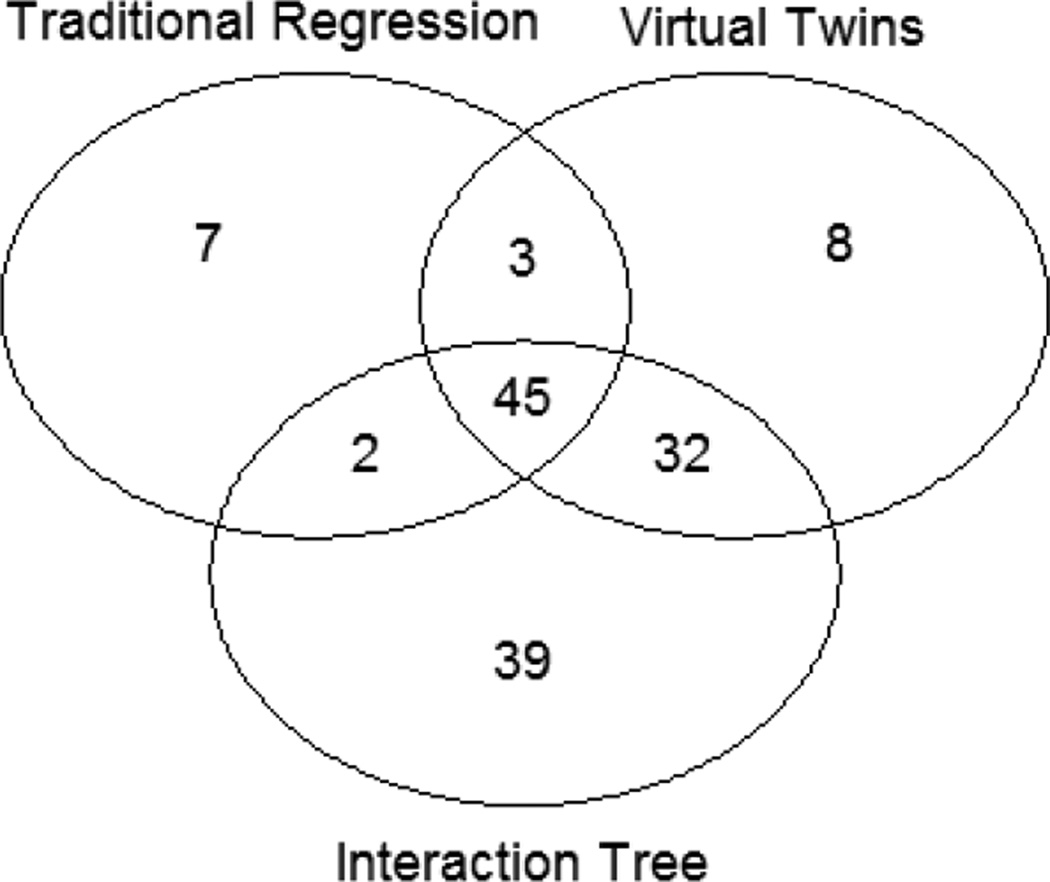
Note that while the subgroup identification criteria generated by different methods may appear different as defined by different covariates, the actual subsets of subjects targeted by these signatures may be quite similar. Therefore, we compared the identified subsets of subjects to see how different they actually were. Table 2 showed the overlap between subgroups S1 and S2 using Jaccard similarity coefficients, defined as |S1∩S2|/|S1∪S2|, where |S| denotes the size (e.g., number of subjects) of set S, and ∩ and ∪ denote the union and intersection set operation, respectively. We also used a Venn diagram in Figure 3 to illustrate the relation of these sets graphically.

Table 2.

Jaccard’s Similarity Coefficients (|S1∩S2|/|S1∪S2|) among Subgroups Identified by Different Methods

Subgroup	Size	Treatment		Similarity = intersection size / union group size * 100%
		Effect	P-value	Full	TRM	VT	IT
Full	251	0.007	0.422	100	22.71	35.06	47.01
TRM	57	0.263	0.001	22.71	100	49.48	36.72
VT	88	0.218	0.001	35.06	49.48	100	59.69
IT	118	0.172	0.001	47.01	36.72	59.69	100
Union	136	0.150	0.002	54.18	41.91	64.71	86.76

Figure 3.

Venn Diagram of the Results from Different Methods

The numbers in the Venn diagram are numbers of subjects who were responsive to ondansetron. A total of 115 subjects were not identified by any of the three methods.

A total of 136 (54%) subjects, were selected by at least one of the identification methods, with a treatment effect of 0.15 on PHDD. As shown in Table 2 and Figure 3, subjects identified by these methods tended to overlap. IT was the most comprehensive method, containing more than 80% of the subjects selected by the VT and TRM (Figure 3).

Discussion

In this paper, we applied two up-to-date data mining tree-based methods to identify the subgroups that were most responsive to ondansetron in an alcohol pharmacogenetic trial. Conventionally, subgroups are preplanned; otherwise post-hoc subgroup analysis arouses controversy due to a lack of validation. Multiplicity involved in the examination of many subgroups greatly inflates the type I error rate. Moreover, traditional statistical methods to identify subgroups are restricted to univariate exploration: namely, covariates are assessed one-by-one. The models for assessing treatment-by-covariate interaction are also limited to cross-product terms up to second-order. In addition, it is difficult to determine the final number of subgroups. The tree-based methods essentially overcome these limitations. Tree methods are known to deal effectively with higher-order complex interactions through their hierarchical structure. For the purpose of conducting subgroup analysis, tree methods optimally bisect data into groups that show maximum heterogeneity in treatment effects. The built-in validation process helps to avoid false positive subgroups and automatically determines the number of subgroups. The splitting rules leading to each subgroup are amenable to interpretation.

On the other hand, tree methods for subgroup analysis also have limitations. These and many other data mining methods are not intended to conform with a statistical significance testing framework. Owing to their adaptive nature, the p-values reported for resultant subgroups can be overly optimistic and should not be interpreted without being recomputed using an independent data set obtained in a subsequent study. Also, if a continuous covariate interacts with the treatment in a truly linear form (i.e., with a cross-product term), a cumbersome tree structure may be required to fully represent the heterogeneity structure of treatment effects, compared to TRM. Nevertheless, most covariates (including all the genetic variables in this ondansetron trial) are categorical, for which trees are more efficient.

We compared the results to those using traditional regression methods. All methods successfully identified a subgroup within which the treatment effect on PHDD was highly significant (p-value = ~ 0.001). We also note that these methods yielded similar subgroups via slightly different paths (e.g., rs1150226, rs1176719, PHDD_base).

Our study attempted to identify a subgroup with a large enough effect size to be clinically meaningful. Specifically, we expect that the selected subgroup will contain at least 1/3 of the population. It should be noted that there is a trade-off between the effect size and the sample size. Although a smaller sample size, as identified by the traditional regression method, tended to have a large effect size, it may not be practical to develop medication for a very small patient population. In contrast, the tree-based methods, e.g., the Virtual Twins method, yielded a larger subgroup (i.e., about 35% of the total population), with an adequate effect size of 0.22 on PHDD.

The statistical associations of PHDD with ondansetron treatment and the rs1150226 and rs1176719 genotypes may have a biological basis. The polymorphism rs1150226 is located in the promoter region of the HTR3A gene, and rs1176719 is located in the intron 4 region (NM 000869.5) of the HTR3B gene, close to an intron-exon boundary. HTR3A encodes the primary target molecule of ondansetron (the 5-HT3A subunit), and the product of the HTR3B gene (the 5-HT3B subunit) is necessary to stabilize the 5-HT3A receptor subunit at the cell surface. The exact molecular mechanisms by which these two polymorphisms moderate ondansetron response remain to be determined. Yet, given the location of these two variants within the genes, it is possible that ondansetron may modulate HTR3A and HTR3B gene expression levels in an allele-based manner leading to differences in receptor subunit expression at the cell surface.

These methods can be extended in several directions. First, in many alcohol treatment trials, daily drinking records are repeatedly measured using the TLFB method over a period of time. It would be of interest to explore the aforementioned subgroup identification methods in such intensive longitudinal data, through the method of Su et al. (2011), to improve the power for repeated measures data. Second, in most of the current work, efficacy, e.g., reduction in PHDD, has been used as the primary focus in subgroup identification. However, safety measures, such as adverse events, should be taken into account simultaneously in pharmacogenetic studies. It would be of interest to develop new data mining/machine learning methods that take efficacy and safety into account concurrently as outcomes. Finally, what we have considered so far is within the framework of tree-based approaches. Other data mining tools, e.g., support vector machine (SVM) (Cortes and Vapnik 1995) or least absolute shrinkage and selection operator (“lasso”) (Tibshirani 1996), can also be adopted in the estimation procedure.

Missing data are a major problem in longitudinal alcohol clinical studies. Different methods should be used to accommodate different missing mechanisms (Little and Rubin 2002), e.g.: missing completely at random (MCAR; dropout independent of response), missing at random (MAR; dropout dependent only on observed response), and missing not at random (MNAR; informative dropout - dropout dependent on unobserved response). For example, imputation has been used in several studies, e.g., Johnson et al. (2007) and Falk et al. (2010) to provide a complete dataset. In our current study, we did not perform any imputation for the PHDD outcome, but did a worst case imputation (e.g., imputed all missing values to heavy drinking) in the PS1HDD study instead (This way the two analyses had the same sample size for comparison). Subgroup identification methods introduced heretofore can then be applied to the imputed heavy drinking outcome. However, the performance of these methods on imputed data has not been not extensively investigated, either empirically or theoretically. An alternative approach to tackling missing data is to use a sensitivity analysis of the informative dropout , e.g., with a joint model of longitudinal drinking level and time to dropout (e.g., Johnson et al. 2011). The application of tree-based methods to this joint model is an interesting topic for future research.