Perceptual evaluation of voice source models

Abstract

Models of the voice source differ in their fits to natural voices, but it is unclear which differences in fit are perceptually salient. This study examined the relationship between the fit of five voice source models to 40 natural voices, and the degree of perceptual match among stimuli synthesized with each of the modeled sources. Listeners completed a visual sort-and-rate task to compare versions of each voice created with the different source models, and the results were analyzed using multidimensional scaling. Neither fits to pulse shapes nor fits to landmark points on the pulses predicted observed differences in quality. Further, the source models fit the opening phase of the glottal pulses better than they fit the closing phase, but at the same time similarity in quality was better predicted by the timing and amplitude of the negative peak of the flow derivative (part of the closing phase) than by the timing and/or amplitude of peak glottal opening. Results indicate that simply knowing how (or how well) a particular source model fits or does not fit a target source pulse in the time domain provides little insight into what aspects of the voice source are important to listeners.

I. INTRODUCTION

Mathematical models of the voice source have been designed to provide high quality voicing for synthetic speech while minimizing the bandwidth for its transmission, and to model perceptually important aspects of the voice source. In this study we assessed the fit of five such models of the voice source—the Rosenberg model (Rosenberg, 1971), Liljencrants-Fant (LF) model (Fant et al., 1985), Fujisaki-Ljungqvist model (Fujisaki and Ljungqvist, 1986), and two models proposed by Alwan and colleagues (Shue and Alwan, 2010; Chen et al., 2012)—to the shape of the glottal flow derivative and to glottal source spectra, and then examined the ability of the models to match the target voice qualities.

The purpose of this exercise was to determine the relationship between listeners' judgments of voice quality and theoretically important landmark points or model segments. As presently implemented, most models of the voice source describe time-domain features of vocal fold vibration or of glottal flow, including peak glottal opening/peak flow and the negative peak of the flow derivative, which is associated with the instant of maximum excitation (Fant, 1993). Models are typically evaluated in terms of their fit to empirical pulse shapes (e.g., Fujisaki and Ljungqvist, 1986; Gobl and Ní Chasaide, 2010; Shue and Alwan, 2010). For example, the LF model captures changes in the glottal flow derivative using sinusoidal and exponential functions (Fant et al., 1985), and Fant attributed its widespread use to its ability to capture “essentials” of a variety of glottal wave shapes (Fant, 1995, p. 119). The primary limitation to this approach is that modeling and fit assessment focus largely on the shape of the pulses, with minimal consideration of the perceptual importance of the features on which fit is based—the functional significance of the events being measured (Westbury, 1991). From a functional point of view, source models that do not capture aspects of the voice that are important to listeners, or models that include features that are not perceptible, are neither adequate nor theoretically correct.

Although models differ in the features they fit and in the equations used (as described below), the importance of these differences has not been determined, so we cannot identify the “best” model in this functional sense. Developing such an understanding is problematic, however, because voice production occurs as changes in glottal configuration and the air pressure waveform shape over time, but perception is better modeled in the spectral domain (Plomp, 1964; Doval et al., 1997; Kreiman and Gerratt, 2005). For example, we do not hear the negative peak of the differentiated glottal waveform; we hear its spectral consequences. Thus, perceptual evaluation of time-domain source models requires interpretation of the spectral consequences of time-domain events, a difficult problem that has resisted solution to date (but see van Dinther et al., 2004, 2005, who describe the relationship between LF model parameter R_g and a voice quality continuum from breathy to pressed).

One possibility for bridging the gap between the time and spectral domains is to convert temporal parameters into spectral ones (Ananthapadmanabha, 1984; Fant and Lin, 1988; Doval et al., 1997; Doval et al., 2006; Kane et al., 2010). However, the correspondence between time- and spectral-domain parameters is usually not straightforward (Fant and Lin, 1988; Gobl and Ní Chasaide, 2010), and pulse shape changes have effects throughout the spectrum, rather than altering one specific spectral component (Doval and d'Alessandro, 1997; Henrich et al., 2001). For example, Henrich et al. (2001) found that H1*-H2*,¹ which is a perceptually meaningful component of the voice spectrum (Esposito, 2010), could be modeled only by using a combination of time-domain parameters, rather than by a single parameter (cf. Chen et al., 2011; Chen et al., 2013b). Moreover, for any given source model, a particular value of H1*-H2* could be obtained from several combinations of the same parameters, so that no one-to-one correspondence between time-domain events and spectral consequences was observed.

Another problem with converting time-domain parameters to spectral ones is the lack of perceptual validation. That is, expressing a time-domain parameter in terms of spectral characteristics does not establish the perceptibility of the proposed time-domain model parameters. This is a problem not just for spectral parameters derived from time-domain models, but for any model of the voice source: If perceptual validity has not been systematically assessed, it remains unclear whether (and which) deviations in fit between the models and the data are functionally important to the listener. We address this issue by relating physical matches among models to perceived matches among sounds. Doing so enables us to determine (a) which deviations between the modeled source and natural source are perceptually meaningful; (b) whether differences in the time domain matter perceptually to a greater or lesser extent than those in the spectral domain; and (c) what is required to make a valid model of the voice source.

A. The source models

This paper assesses the relationship between model fit and perceptual accuracy by studying five time-domain source models (three of which are related)—the Rosenberg model (Rosenberg, 1971), the Fujisaki-Ljungqvist model (Fujisaki and Ljungqvist, 1986), the Liljencrants-Fant (LF) model (Fant et al., 1985), and two models proposed by Alwan and colleagues (Shue and Alwan, 2010; Chen et al., 2012)—and one model that describes the voice source in the spectral domain (Table I; Kreiman et al., 2014; see also Cummings and Clements, 1995). The Rosenberg model (Rosenberg, 1971), in contrast to the other models, describes the opening and closing phases of the glottal flow volume velocity with separate trigonometric functions that incorporate two timing parameters and one amplitude parameter. In comparison, the six-parameter Fujisaki-Ljungqvist model and the four-parameter LF model represent the first derivative of the glottal volume velocity pulse, which incorporates lip radiation effects (Gobl and Ní Chasaide, 2010). The LF model (Fant et al., 1985) combines an exponentially increasing sinusoidal function and an exponential function with one amplitude parameter (E_e) and three time points; the Fujisaki-Ljungqvist model (Fujisaki and Ljungqvist, 1986) uses polynomials to model the shape and duration of different segments of the flow derivative waveform. Recent studies (Shue and Alwan, 2010; Chen et al., 2012) have proposed models of the glottal area waveform (as derived from high-speed endoscopic recordings of the laryngeal vibrations) rather than the flow pulse or its derivative. With four parameters, the first of these (Shue and Alwan, 2010) uses a combination of sinusoidal and exponential functions similar to the LF model, but with the ability to adjust the slopes of the opening and closing phases separately. The model of Chen et al. (2012) modified the Shue-Alwan model by redefining parameters (speed of opening and speed of closing) to allow for lower computational complexity, faster waveform generation, and more accurate pulse shape manipulation.

TABLE I.

The source models.

Model	Description	Parameters
Rosenberg	Models flow volume velocity with trigonometric functions	Time from onset of pulse to peak Time from peak to offset Maximum amplitude
LF	Models flow derivative with an exponentially increasing sinusoidal function from first point to negative peak and an exponential function from negative peak to final point	Negative peak Time of max flow Time of max discontinuity Return time constant
Fujisaki-Ljungqvist	Models flow derivative with polynomial functions	Open phase duration Pulse skew Time from closure to maximum negative flow Slope at glottal opening Slope prior to closure Slope following closure
Shue-Alwan, Chen et al.	Model flow volume velocity; functions similar to LF	OQ Asymmetry coefficient Speed of opening phase Speed of closing phase

The time-domain models differ in the number of parameters they use and in the functions used to model changes in glottal flow pulse shape over time, but also share a number of parameters, giving the impression that these are important determinants of voice quality and aspects of production. For example, glottal open time of the source pulse is explicitly represented in the Rosenberg and Fujisaki-Ljungqvist models, and occurs as part of the open quotient (OQ) parameter in the models of Shue and Alwan and Chen et al. (see Table I). Similarly, pulse skew is represented in the models of Rosenberg, Fujisaki and Ljungqvist, Shue and Alwan, and Chen et al.

In summary, understanding the perceptual importance of differences among source models offers a source of insight into the relationship between voice production and the resultant perceived voice quality. Given that source models differ in how they fit the pulses, our plan was to determine which aspects of pulse shape are perceptually important by examining the perceptual consequences of differences among models in their fits to the same target source pulses. We began by measuring physical fit of the models to the target pulses, and then used these fits to predict which models should provide the best perceptual accuracy. Finally, we created stimuli that varied only in voice source, and measured perceptual matches of stimuli synthesized with each source model to the target stimuli, to determine the usefulness of time domain features of the voice sources for modeling voice quality.

II. MODELING GLOTTAL PULSES

A. Voice samples

To widely sample the range of possible voice qualities, stimuli were based on 40 1-s samples (20 M, 20 F) of the vowel /a/, excerpted from sustained phonations produced by normal speakers and by speakers with vocal pathology. Samples were selected at random from a library of recordings gathered under identical conditions, and ranged from normal to severely pathological. Samples were directly digitized at 20 kHz using a Brüel and Kjær 1/2 in. microphone (model 4193) placed 10 cm from the speaker's lips at a 45° angle, with 16 bit resolution and a linear-phase sigma-delta analog-to-digital converter to avoid aliasing.

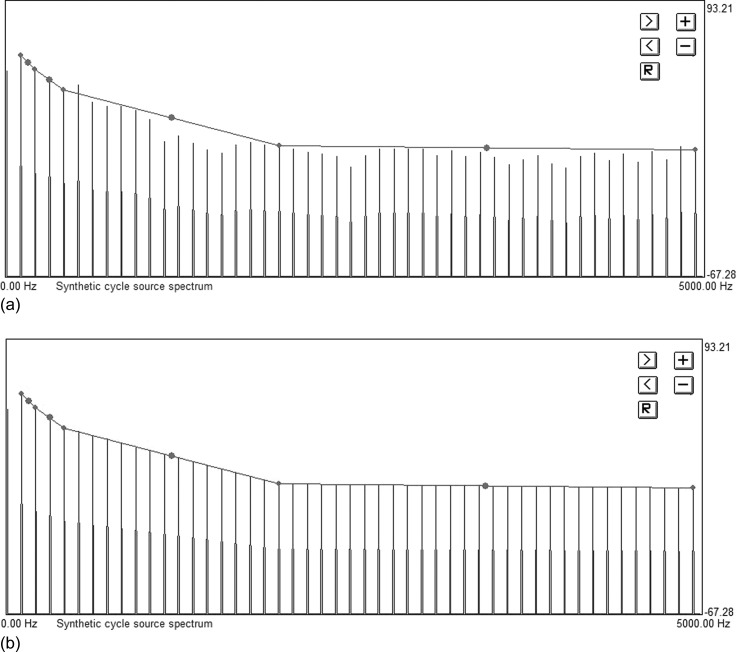
Evaluation of the accuracy and validity of source models requires that investigators extract an accurate estimate of the voice source from the natural voice signal, to provide a target to which the different source models can be fitted and compared. To accomplish this, the recordings were first downsampled to 10 kHz. Estimates of the sources of these voice samples were then derived via inverse filtering using the method described by Javkin et al. (1987). Because inverse filtering is imprecise at best (e.g., Alku, 2011), these estimates were corrected using analysis-by-synthesis (AbS) to create synthetic voice samples that precisely matched the quality of the original natural voice samples (Kreiman et al., 2010), as follows. The spectrum of a single representative source pulse extracted via inverse filtering was calculated and used to model the harmonic part of the voice source. Spectra were divided into four segments (H1–H2, H2–H4, H4 to the harmonic nearest 2 kHz [H4–2 kHz], and the harmonic nearest 2 kHz to the harmonic nearest 5 kHz [2–5 kHz]), and harmonic amplitudes within each range were adjusted so that slope decreased smoothly within that range (Fig. 1). The spectral characteristics of the inharmonic part of the source (the noise excitation) were estimated using cepstral-domain analysis similar to that described by de Krom (1993). Spectrally shaped noise was synthesized by passing white noise through a 100-tap finite impulse response filter fitted to that noise spectrum. To model frequency and amplitude contours, F0 was tracked pulse by pulse on the time domain waveform by an automatic algorithm. The time-domain representation of the harmonic source was derived from the spectral representation via inverse fast Fourier transform (FFT), and a train of source pulses with the appropriate periods and amplitudes was added to the noise time series to create a complete glottal source waveform. Formant frequencies and bandwidths were estimated using autocorrelation linear predictive coding analysis with a window of 25.6 ms (or 51.2 ms if F0 was near or below 100 Hz). The complete synthesized source was then filtered through the vocal tract model to generate a synthetic version of the voice (the AbS token), and all parameters were manipulated until the synthetic token adequately matched the natural target voice sample. Note that all changes to the harmonic part of the voice source were made by altering the slope and/or amplitude of the spectral segments defined above, and not in the time domain. The experiment described in Sec. II B below demonstrated that listeners were unable to reliably distinguish these synthetic copies from the original natural tokens (d′ = 0.78).

FIG. 1.

(Color online) The spectral-domain source model. (a) A source spectrum before adjustment of individual harmonic amplitudes. (b) The same spectrum after harmonic amplitude adjustment.

Each AbS-derived source function was next fitted with the five time-domain source models (Rosenberg, LF, Fujisaki and Ljungqvist, Shue and Alwan, and Chen et al.). Models were fitted in two ways in order to create variation in fits to the opening versus closing phases of the cycle. In the first, one cycle of the flow derivative signal (derived from the source spectrum via inverse FFT) for each speaker was normalized to a maximum amplitude of 1 prior to model fitting. In the second, we fit each model to the target pulses after normalizing the amplitude of the negative peak to −1. Normalization emphasized the peaks of the glottal pulse, because those points have traditionally been associated with differences in voice quality (Fant, 1993). Because the models of Rosenberg, Shue and Alwan, and Chen et al. describe the glottal flow pulse, and not the flow derivative, first-derivative representations were calculated mathematically in these cases, so that all models were fitted in the flow derivative domain. Each derivative-domain source model was then fitted to these pulses using a mean square error (MSE) criterion, for which each point of the waveform was weighted equally.

Eleven synthetic versions of each target voice were created by filtering the target AbS source or one of the corresponding model-fitted sources (five sources per voice, one from each of the five different models, times two normalization methods) through the vocal tract model created for the voice during the AbS process. Vocal tract models, F0 and amplitude contours, the noise-to-harmonics ratio, and all other synthesizer parameters were held constant across versions, so that only source characteristics differed across the eleven stimuli within a given voice “family.”

B. Experiment 1: Validating the synthesis

To verify that the AbS tokens were in fact indiscriminable from the natural voice samples (and thus could fairly be used as the standard of perceptual evaluation for the other source models), and to quantify the discriminability of the other stimuli from the AbS token, the following experiment was undertaken.

1. Method

Only stimuli for which source amplitude was normalized to the positive peak of the flow derivative waveform were used in this experiment, because we had no theoretical reason to expect an effect of normalization method on the discriminability of voices created with the different source models. Stimuli consisted of the 6 synthetic versions of each of the 40 voices, along with the original, natural voice sample. Each stimulus was 1 s in duration. Stimuli were normalized for peak amplitudes and multiplied by 25 ms onset and offset ramps prior to presentation.

All procedures were approved by the UCLA IRB. Twenty-two listeners (UCLA students and staff) participated in the experiment. They ranged in age from 18 to 61 years (M = 27.3 years; sd = 11.84 years). All reported normal hearing. Following the methods used in Kreiman et al. (2007b), listeners heard pairs of voices in which either the natural voice sample (40 trials) or a synthetic token created with a model-fitted source (200 trials) was paired with the corresponding AbS-derived tokens. In an additional 56 trials, both voices in a pair were identical, for a total of 296 trials. The inter-stimulus interval was 250 ms.

Stimuli were presented in a double-walled sound suite over Etymotic ER-1 insert earphones (Etymotic Research, Inc., Elk Grove Village, IL) in random order at a comfortable constant listening level. Listeners could hear the pairs of stimuli twice (in the AB and BA orders) before responding. They judged whether the stimuli within a pair were the same or different, and then rated their confidence in their choice on a five-point scale ranging from 1 (“wild guess”) to 5 (“positive”). Testing time averaged about 40 min.

2. Results

Responses were pooled across listeners to estimate overall discriminability. Rates of correct and incorrect “different” responses (hits and false alarms) were calculated for each voice. Across voices, hit rates ranged from 0% to 59.1%, with an average of 28.53% (SD = 14.71%). False alarm rates ranged from 0% to 11.8%, with an average of 1.96% (SD = 2.67%).

Same and different responses were combined with confidence ratings to create a ten-point scale ranging from “positive voices are the same” (=1), through “wild guess voices are the same/different” (=5 or 6, respectively), and ending with “positive voices are different” (=10). d′ was calculated for each voice from these recoded ratings using SPSS software (Version 20.0; SPSS, Inc.). Averages are given for each source model in Table II. Results indicate that on average the model-fitted tokens were easy to distinguish from the target AbS token, but that the AbS token was not reliably distinguishable from the original natural voice sample. Significant differences among models were observed [one-way analysis of variance (ANOVA); F(5, 234) = 33.43, p < 0.01, r²= 0.42]. Tukey post hoc tests showed that the natural voice was harder to distinguish from the AbS token, and the Rosenberg model easier to distinguish from the AbS sample, than were any other tokens (p < 0.01). The other models did not differ from one another in discriminability from the target AbS token (p > 0.01).

TABLE II.

Discriminability of token synthesized with each model-fitted token from the target AbS token. Standard deviations are given parenthetically.

Model	Average d′
Natural token	0.78 (0.41)
Rosenberg	3.28 (0.87)
LF	2.30 (0.87)
Fujisaki-Ljungqvist	2.62 (1.46)
Shue-Alwan	2.49 (0.76)
Chen et al.	2.49 (0.74)

III. EVALUATING MODEL FIT TO TIME-DOMAIN PULSE SHAPES AND SOURCE SPECTRA

A. Model fit in the time domain

The physical fit of the five source models to the source pulses derived via AbS (henceforth the “targets”) was evaluated in three ways. First, we measured the distance between the target and each modeled pulse with respect to two time-domain landmarks on the differentiated and undifferentiated source pulses: the moment of peak opening (t_p in the LF model, identified as the zero crossing in the flow derivative domain), and the negative peak of the flow derivative [point (t_e, E_e) in the LF model], which corresponds in theory to the time of maximum excitation. These landmarks were selected because they represent hypothetically important physical events in the glottal cycle, because they are parameters used to calculate the source models, and because they can be marked reliably. Prior to fit estimation, for each voice “family” (the target AbS token and the five different modeled versions of that token), amplitudes were scaled such that the peak-to-peak amplitude of the tallest pulse in the family equaled 100 and the differences among family members in amplitudes relative to the tallest member were preserved. All pulses were also normalized to a duration of 100. (Because all pulses within a family had the same duration, relative length was not an issue.) After normalization, time and amplitude coordinates were recorded for the two points on each pulse, and the differences between time and amplitude coordinates of each point on the target and modeled pulses were calculated, along with the total Euclidean distance between points, as the first indices of the fit between the models and the data.

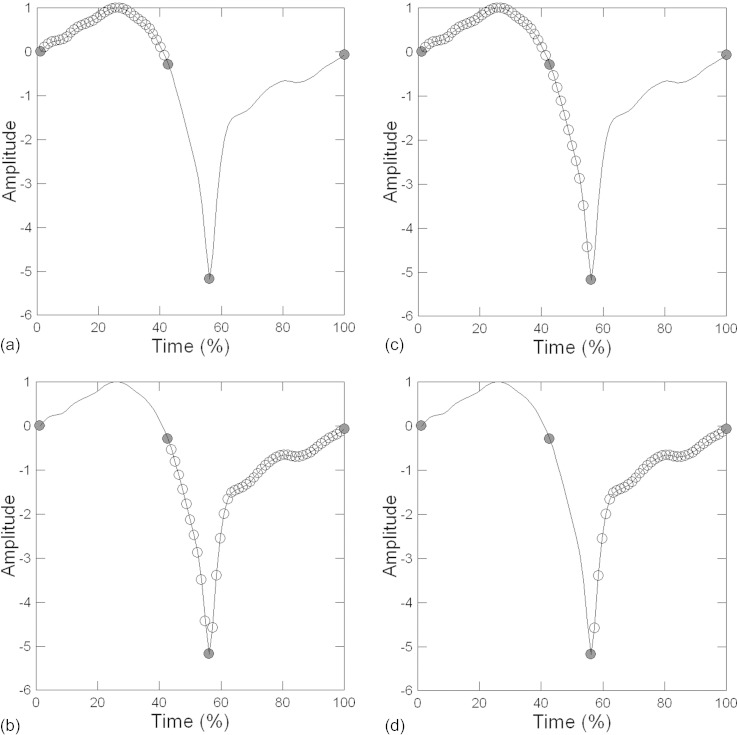
Second, fit was evaluated by measuring MSE fits between the target and modeled pulses (cf. Chen et al., 2013a). MSE fits were calculated for the complete pulses, and also for four different pulse segments: from the first point to the moment of peak opening (the opening phase); from the peak opening to the last point of the pulse (the closing phase); from the first point to the time of maximum excitation (the first segment of the LF model); and from the time of maximum excitation to the last point of the pulse (the second segment of the LF model). Landmark points and glottal pulse segments are shown in Fig. 2.

FIG. 2.

The landmark points and model segments used to measure fit of the different source models to the target pulses. (a) The opening phase of the glottal cycle. (b) The closing phase. (c) The first segment of the LF model. (d) The second segment of the LF model.

1. Results

Values of p throughout this section were adjusted for multiple comparisons because of the interrelationships among segments, landmarks, and spectral-domain features of the source pulses.

Figure 3 shows the fit of each source model to the same target source pulse, and mean MSE fits across voices and normalization methods are given in Table III. For both peak opening and the negative peak of the flow derivative, points were significantly better matched in timing (x dimension) than in amplitude [y dimension; peak opening: matched sample t (399) = −6.31, p < 0.01; negative peak: matched sample t (399) = −6.11, p < 0.01]. Differences between source models in matches to landmark points were statistically reliable but minimal [F(4, 1595) = 6.92, p < 0.01; r²= 0.01]: Points were better matched overall for the LF, Shue and Alwan, and Chen et al. models than they were for the Rosenberg model, but only with respect to timing of the negative peak of the flow derivative waveform (Tukey post hoc tests; p < 0.01).

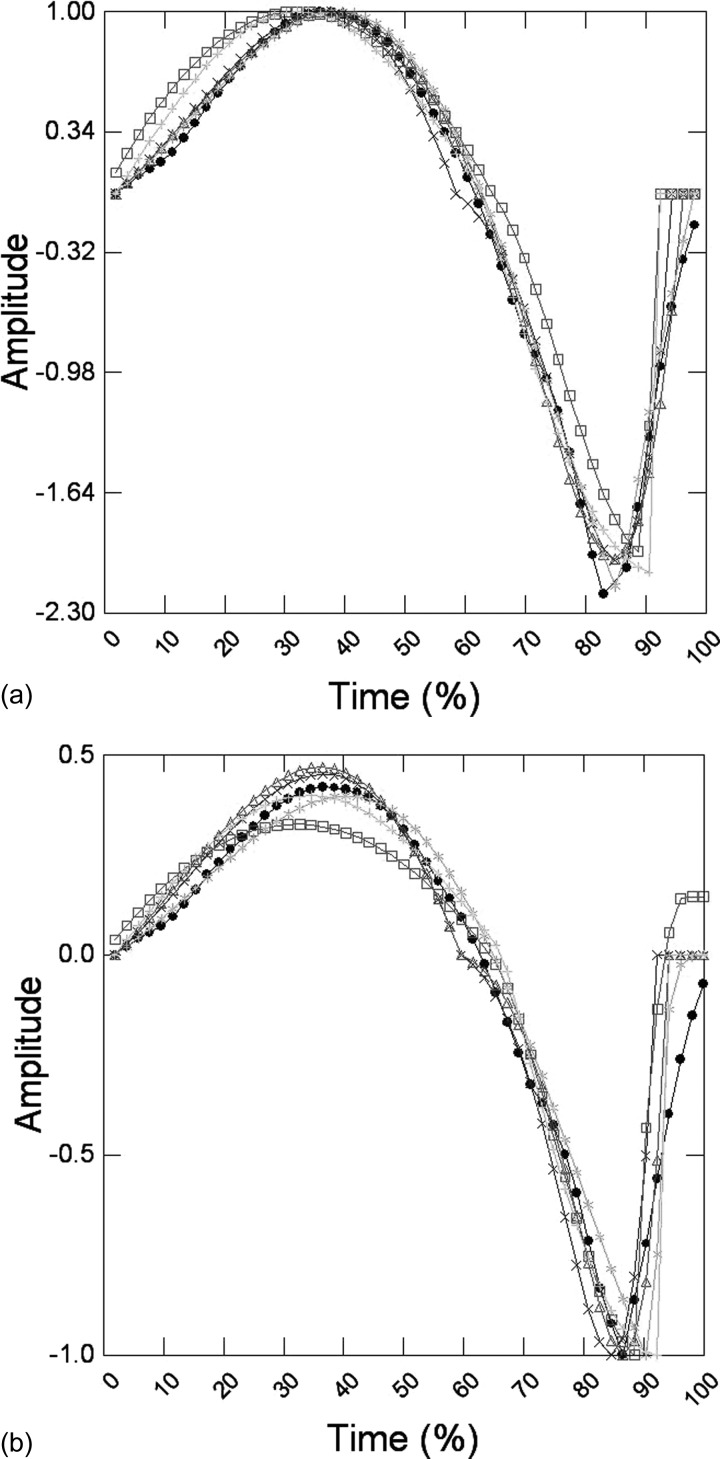
FIG. 3.

(Color online) The fits of Rosenberg (+), LF (*), Fujisaki and Ljungqvist (□), Shue and Alwan (×), and Chen et al. (△) models to a single source pulse (•). (a) Pulses normalized to the positive peak of the flow derivative. (b) Pulses normalized to the negative peak of the flow derivative.

TABLE III.

Average MSE fit of the five source models to the target AbS pulses.

Model
MSE fit	Rosenberg	LF	Fujisaki/Ljungqvist	Shue/Alwan	Chen et al.
Mean	0.095	0.053	0.138	0.084	0.071
SD	0.15	0.10	0.23	0.21	0.16
Range	0.007–0.94	0.002–0.74	0.008–1.29	0.005–1.22	0.004–0.98

No significant differences were observed among models in their overall MSE fit to the target pulses [F(4, 395) = 2.70, p > 0.01]. A two-way ANOVA comparing MSE fits for the opening versus closing phases of the pulses showed significantly better fits for the opening phase than for the closing phase [F(1, 790) = 40.31, p < 0.01], but no differences between models and no interaction between models and segments. A parallel ANOVA comparing fits for the first and second segments of the LF model produced the same result [F(1, 790) = 17.54, p < 0.01], reflecting the correlation between fits to the opening phase and the first LF segment (r = 0.74) and between the closing phase and the second LF model segment (r = 0.79).

B. Model fit in the spectral domain

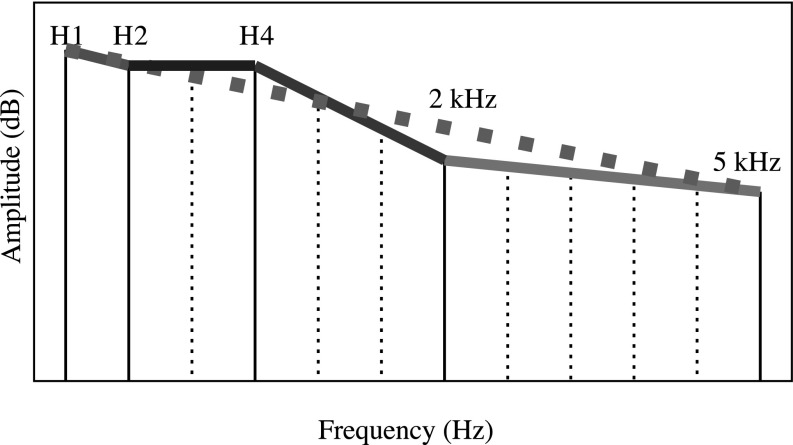
Finally, we compared the spectra of the modeled pulses to those of the targets with respect to spectral slope in five ranges: H1–H2, H2–H4, H4 to the harmonic nearest 2 kHz in frequency (H4–2 kHz), the harmonic nearest 2 kHz to the highest harmonic (nearest 5 kHz, 2–5 kHz), and to the overall spectral slope from the first harmonic to the highest harmonic (H1–Hn) (Kreiman et al., 2007a; shown schematically in Fig. 4). Source spectra were generated automatically by the AbS software, which computes a pitch-synchronous Fourier transform of the flow derivative of the glottal source pulse. The AbS software provides the amplitudes of any selected harmonic and computes the spectral slope for any selected frequency range. Fits between the spectral components of the target AbS versus model-fitted sources were calculated by first subtracting the component slope value of the target source from the model-fitted source, to obtain the raw difference (in dB) in slope. The absolute (unsigned) difference in spectral slope was then normalized across models by dividing the absolute difference by the largest difference in spectral slope (across all models) for a given voice. Normalization allows for comparisons across models for a specific voice as well as differences across voices.

FIG. 4.

(Color online) Schematic of the spectral slope parameters measured (frequencies are not to scale). Harmonics that do not form endpoints of components appear as small dotted lines. The large dotted line refers to H1 − Hn (the difference in slope between the first and final harmonics).

1. Results

A two-way ANOVA (model by spectral segment) assessed the fit of the different source models to the target pulses in the spectral domain. It revealed significant main effects of model [F(4, 1975) = 55.71, p < 0.01], spectral segment [F(4, 1975) = 10.44, p < 0.01], and a small but significant interaction between model and spectral segment [F(16, 1975) = 6.71, p < 0.01; because of the small size of this effect, it will not be interpreted further]. Tukey post hoc tests indicated that spectral fits were best for the Shue and Alwan, Chen et al., and LF models (which did not differ significantly); the fit for the Rosenberg model was significantly worse than for all other models, and the fit for the Fujisaki-Ljungqvist model was better than that for the Rosenberg model, but worse than that for the first three models (all p < 0.01). Further Tukey tests indicated that fit to the highest part of the spectrum (2–5 kHz) was significantly worse than fit to the three lower frequency segments (H1–H2, H2–H4, H4–2 kHz), which did not differ.

C. Discussion

The analyses in this section explored various aspects of the physical fit between five source models and a large set of target source pulses. In the time domain, models did not differ from one another in MSE fits to overall flow derivative pulse shapes, nor did they differ meaningfully in how well they matched landmark points on the target source pulses. All models consistently fit the opening phase better than the closing phase of the source pulses, and fit was better to landmark points in timing than in amplitude. In the spectral domain, the Rosenberg and Fujisaki-Ljungqvist models provided significantly worse fit to the target spectra than did the LF, Shue and Alwan, and Chen et al. models, which did not differ. Spectral matches were significantly worse in the frequencies above 2 kHz than in frequencies below 2 kHz.

These findings are not in and of themselves informative about the importance of the differences observed. As noted in the Introduction, models of the voice source have two primary functions: to describe phonatory behavior at the glottis, or to capture perceptually important aspects of the voice source, for example, for use in high-quality speech synthesis (e.g., Fujisaki and Ljungqvist, 1986). Although validating models with respect to glottal vibratory patterns requires data about physical vocal fold movements (for example, from high-speed imaging), the present data do make predictions about which models should provide the best perceptual fit, and what aspects of the pulses should be perceptually important. They can thus be used to guide assessments of the perceptual validity of the different source models. First, differences among the models in how well they perceptually match the target voices should not be predictable from either overall MSE fits or matches to individual landmark points, because the models did not differ in how well they matched these features. Second, stimuli synthesized with the Fujisaki-Ljungqvist and Rosenberg models should provide the worst perceptual match to the targets, because they provided the worst matches to source parameters in the spectral domain that are associated with differences in voice quality (Klatt and Klatt, 1990; Gordon and Ladefoged, 2001). Stimuli synthesized with the LF, Shue and Alwan, and Chen et al. models should provide good perceptual matches to the target voices, because of the good spectral matches provided by these models. We test these predictions in the following experiment, which probes perceptual similarity among tokens in detail.

IV. PREDICTING SIMILARITY IN QUALITY FROM DIFFERENCES IN SOURCE MODEL FIT

Because similarity and discriminability are not coterminous—voices can be very similar and still be easy to distinguish—the following experiment examined the similarity between versions of the stimulus voices, as a supplement to the measures of discriminability already described.

A. The sort-and-rate task

1. Participants

Forty-eight listeners (UCLA staff and students) participated in this experiment.² They ranged in age from 18 to 62 years of age (M = 26.7 years; sd = 9.14 years). All reported normal hearing.

2. Stimuli and task

All procedures were approved by the UCLA IRB. Subjects were assigned at random to one of two groups (both n = 24). The first group heard stimuli created with glottal pulses normalized to the positive peak of the flow derivative, and the second heard stimuli created with pulses normalized to the negative peak. In both cases, stimuli were blocked according to voice “families,” each consisting of an original voice sample, the AbS synthesized voice, and the five synthetic tokens created with the model-fitted sources. Listeners assessed the similarity of the different family members in a visual sort-and-rate task (Granqvist, 2003; Esposito, 2010; Chen et al., 2013a; Zhang et al., 2013). In this task, each family was presented in a separate trial; each listener completed 10 trials, such that across trials and subjects each family was judged by 12 listeners. Stimuli were presented in random order in a double-walled sound suite over Etymotic ER-1 earphones, as before.

At the beginning of a trial, stimuli were represented at the top of a computer screen by randomly ordered icons with different colors and shapes. Listeners played the voices by clicking the icons, and then dragged each icon onto an unlabeled line, so that perceptually similar sounds were placed close to one another and perceptually dissimilar sounds were placed farther away from one another. Listeners were instructed to base their sort on whatever criteria seemed appropriate to them; no instructions were provided about the nature of any underlying perceptual dimension(s). They were also instructed that they could use as little or as much of the line as they chose. Participants were able to listen to the stimuli as many times as necessary, in any order, and were able to reorder the stimuli until they were satisfied with their sorting, after which testing advanced to the next trial. Listeners had no difficulty understanding or completing the task, which lasted about 45 min.

3. Results

For each listener and trial, we first calculated the distance between the icons representing the AbS token and those for each of the other voice samples in that family. To normalize for differences in scale use across listeners and trials, these distance data were assembled into dissimilarity matrices (12 matrices/voice/normalization method, one from each listener who heard that voice in the sort and rate task) and analyzed via non-metric individual differences multidimensional scaling (MDS; 40 voices times 2 normalization methods, or 80 total analyses).

Solutions were found in 1 dimension for all except three analyses, for which two-dimensional solutions were selected. R² and stress values are given in Table IV. Matched sample t-tests indicated that scaling results accounted for significantly more variance for source pulses normalized to the negative peak vs the positive peak (R²: t(39) = 3.06, p < 0.01; stress: t(39) = −2.84, p < 0.01). Perceptual distances between voice tokens were calculated from stimulus coordinates in the resulting configuration for use in subsequent analyses.³

TABLE IV.

R² and stress values for the multidimensional scaling analyses.

	Normalization method
	Positive peaks		Negative peaks
	R2	Stress	R2	Stress
Mean	0.77	0.22	0.83	0.2
SD	0.1	0.05	0.1	0.06
Range	0.5–0.94	0.12–0.33	0.5–0.96	0.1–0.33

As might be expected, similarity and discriminability are significantly, but only moderately, correlated (r = 0.47, p < 0.01). One-way ANOVA revealed significant differences among models in goodness of perceptual match to the AbS target voice [F(4, 395) = 48.54, p < 0.01, R²= 0.33]. Post hoc Tukey tests (p < 0.01) indicated that the Rosenberg model provided a significantly worse match to the target than any other model. Significant differences were also observed between the Fujisaki-Ljungqvist model and the LF, Shue and Alwan, and Chen et al. models, consistent with the predictions discussed previously.

B. Relating model fit to perceptual fit

Using stepwise multiple regression (p to enter/remove= 0.05), we next assessed the extent to which different aspects of model match to the targets predicted perceptual similarity. The dependent variable in these analyses was the MDS-derived perceptual distance between each modeled token and the AbS target token. Three sets of predictor variables were examined: (1) total MSE fit and fit to the opening and closing phases; (2) distances in time, amplitude, and total distance between landmark points; and (3) differences in spectral slopes. None of the MSE fit variables, and no combination of variables, was significantly associated with perceived similarity between AbS and modeled tokens across models and voices (p > 0.05). With respect to landmark points, the extent of perceptual match between the target and model-based tokens was best predicted by match to the negative peak of the flow derivative in both time and amplitude [F(2, 397) = 79.60, p < 0.01; R²= 0.29]. Similarity in quality was better predicted by spectral match in the ranges H1–H2, H2–H4, H4–2 kHz, and H1–Hn [F(4, 395) = 71.33, p < 0.01; R²= 0.42].

V. GENERAL DISCUSSION AND CONCLUSIONS

To recapitulate, in the time domain the LF, Shue and Alwan, and Chen et al. source models provided the best perceptual matches to the target AbS stimuli, although stimuli created with all these models were easy to distinguish from the targets (Table II). Consistent with predictions, the perceptual match provided by the Fujisaki-Ljungqvist model was worse, and that for the Rosenberg model was worse still. Thus, a larger number of model parameters does not imply a better perceptual match; e.g., the six-parameter Fujisaki-Ljungqvist model provided a worse perceptual match than the four-parameter LF model. Also consistent with predictions, neither MSE fits to pulse shapes nor fits to landmark points predicted these patterns of difference in quality. Finally, the source models fit the opening phase of the glottal pulses better than they fit the closing phase, but at the same time similarity in quality was better predicted by the timing and amplitude of the negative peak of the flow derivative (part of the closing phase) than by the timing and/or amplitude of peak glottal opening. Reminiscent of the admonition of Westbury (1991) that analyses relying on “identifying ‘magic’ moments in time and places in space” (p. 1870) ignore the functional significance of the events being measured, we conclude that simply knowing how (or how well) a particular source model fits or does not fit a target source pulse in the time domain tells us very little about what is important to listeners.

These results show that we do not know what events in the time domain are responsible for what listeners hear. This lack of perceptual validity is a serious deficiency that reveals a limitation to traditional approaches to source modeling, which begin with attempts to copy pulse shapes and then seek to explain perception in terms of timing of glottal events. For example, the LF model (Fant et al., 1985) was developed to describe the time course of glottal flow. Subsequent research focused on relating the timing of events to their spectral consequences (Ananthapadmanabha, 1984; Fant and Lin, 1988; Fant, 1995; Doval et al., 1997, 2006; Kane et al., 2010). However, as discussed in Sec. I, the correspondence between timing events and spectral configuration is hardly straightforward (Fant and Lin, 1988; Doval and d'Alessandro, 1997; Henrich et al., 2001; Gobl and Ní Chasaide, 2010).

The present results suggest an alternative approach: determining the spectral features of sounds that predict what listeners hear, and then seeking (and modeling) the time-domain causes of those specific spectral changes. This alternative has received little attention (but see Kreiman et al., 2014). Traditionally, spectral-domain modeling of the voice source was discouraged because it was time-consuming, yielded artifacts, and still required some temporal information, such as period length. Moreover, the relevant spectral parameters had yet to be identified, and were less closely tied to physiology than were time-domain parameters (Ananthapadmanabha, 1984, p. 10). However, these concerns have become largely irrelevant. Computational constraints and artifacts are no longer common (Doval et al., 1997; Kreiman et al., 2010), and much progress has been made in determining spectral parameters that vary across voices and to which listeners are sensitive (Kreiman et al., 2007a; Kreiman et al., 2014). Both approaches (modeling in the time domain vs in the spectral domain) share the goal of mapping between voice production and perception; but in the second case the functional significance of the magic moments or places is established a priori, ensuring that results will be perceptually meaningful, however complex the associations between physical and psychoacoustic events prove to be.

Two limitations of the present study must be noted. First, although spectral slope parameters predicted voice quality much better than did glottal pulse shapes, spectral slope still accounted for only 42% of the variance in our perceptual data. Because of the large number of voices and source models studied here, no one listener heard more than 12.5% of the stimuli (10 voice families out of 80), so that data used in the MDS analyses were cumulated across subjects, which presumably added variability to the data. Examination of subject weights for the MDS analyses revealed no systematic differences among listeners, consistent with this interpretation. Second, with the normalizations applied during model fitting, more weight was assigned to peaks in the glottal pulse. This may have led to suboptimal matches in terms of overall MSE in the time domain model fitting. This experimental design is a compromise between achieving the best model fitting in terms of MSE and prioritizing the points which been traditionally considered to be perceptually important. However, because normalization may have limited the extent of model fit to the pulses, results cannot be interpreted as a definitive test of how valid each model is. In any event, our data indicate that substantially more variance is accounted for by spectral parameters than by time-domain features of the source pulses, so that prediction of quality is much more straightforward in the spectral domain.