Self-consistent description of electrokinetic phenomena in particle-based simulations

Abstract

A new computational method is presented for study suspensions of charged particles undergoing fluctuating hydrodynamic and electrostatic interactions. The proposed model is appropriate for polymers, proteins, and porous particles embedded in a continuum electrolyte. A self-consistent Langevin description of the particles is adopted in which hydrodynamic and electrostatic interactions are included through a Green’s function formalism. An Ewald-like split is adopted in order to satisfy arbitrary boundary conditions for the Stokeslet and Poisson Green functions, thereby providing a formalism that is applicable to any geometry and that can be extended to deformable objects. The convection-diffusion equation for the continuum ions is solved simultaneously considering Nernst-Planck diffusion. The method can be applied to systems at equilibrium and far from equilibrium. Its applicability is demonstrated in the context of electrokinetic motion, where it is shown that the ionic clouds associated with individual particles can be severely altered by the flow and concentration, leading to intriguing cooperative effects.

I. INTRODUCTION

There is considerable interest in understanding the structure and dynamics of suspensions of charged particles over multiple length scales, both at equilibrium and far from equilibrium. Examples include DNA or protein flow in microfluidic devices, in cellular environments, or colloidal self-assembly in external fields. Beyond any direct interaction (van der Waals or electrostatic) between particles, the motion of a particle in solution induces important hydrodynamic and electrostatic interactions that some times compete against each other, leading to electro-osmotic or electro-kinetic phenomena that remain poorly understood.

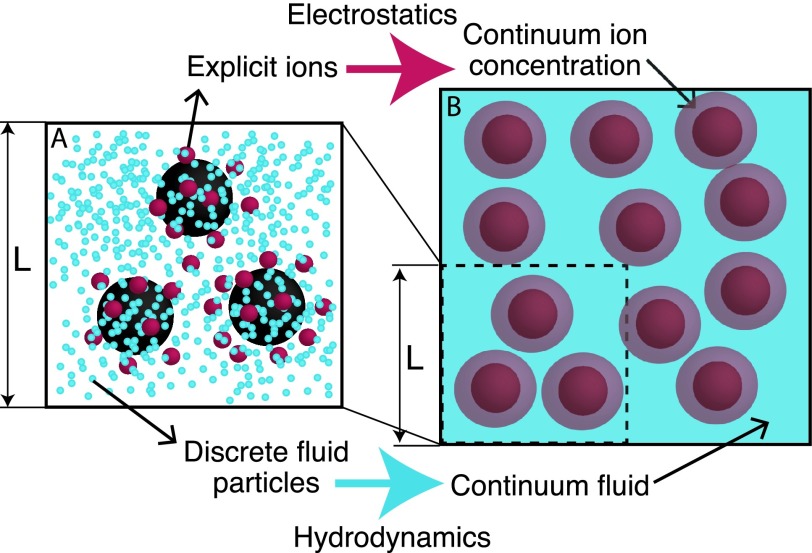
Resolving the dynamics of solvents or charged species over short and long length scales remains a significant challenge. The central question is how to evolve these systems, while preserving molecular resolution of discrete macromolecules or colloids, adopting continuum descriptions for solvent and ions (see Figure 1). Past attempts have primarily relied on Lattice Boltzmann (LB),^1–12 Stochastic Rotational Dynamics (SRD),^13–24 Stokesian Dynamics (SD),^25–32 Ewald sums,³³ and the General geometry Ewald-like method (GgEm)^34–40 for the hydrodynamic evolution, i.e., the momentum equations. On the other hand, solution of charges have been treated by Ewald-based methods⁴¹ or Poisson-Boltzmann (PB) solutions.^42–50 A notable exception, where both interactions are solved simultaneously, is the Smoothed Profile Method (SPM).^51–57 In SPM, discrete particles are included into the continuum formalism through smoothing functions (see the review of particle-based methods by Yamaguchi et al.⁵⁸). LB and SRD methods rely on collision operators to evolve fluid dynamics, thus imposing theoretical limits at zero inertia or strict incompressibility (Ma = Re = 0). In addition, they present limitations regarding the size of the systems that can be studied. A salient limitation of SPM and LB is the mesh dependency that naturally develops at finite concentrations of the discrete entities. The method that we propose in this work, provides a way of resolving these problems.

FIG. 1.

Discrete charged soft particles embedded in an electrolyte solvent. (a) A level of description that requires to treat soft particles, ions and fluid as discrete entities. (b) The proposed method provides resolution for the interesting discrete entities whereas a continuum description for the electrolyte solvent.

II. MATHEMATICAL MODEL

We are presenting a novel theoretical method that resolves the dynamical coupling between discrete charged soft particles and continuum electrolyte solvents. It is presented as a generalization of the GgEm approach, which can be used for bulk and confined systems, both at equilibrium and far from equilibrium. The dynamics of the soft particles follows a Fokker-Planck equation for the probability density, resulting in a stochastic evolution equation. The solvent and the continuum ions, on the other hand, are evolved according to momentum and mass balances, including Nernst-Planck diffusion mechanisms (see Fig. 1).

We consider a collection of N_P soft particles, with charge ez_ν and hydrodynamic radius a, suspended in a solvent that includes N_I charged species (continuum ions). The same model has been used successfully to describe polymeric materials, including DNA,^{35,36,39,59–62} but past work did not consider electrostatic interactions. Soft particles and continuum ions contribute to a charge density, defined as

$${\displaystyle \rho \left(\mathbf{x}\right)=F\sum _{j=1}^{N_I}{z}_j{C}_j\left(\mathbf{x}\right)+\sum _{\nu =1}^{N_P}{z}_{\nu }e\delta (\mathbf{x}-{\mathbf{x}}_{\nu }),}$$ (1)

where F = eN_A is Faraday’s constant (N_A is Avogadro’s number), z_j is the valence of the continuum ions (j = 1, …, N_I), C_j is the concentration of the continuum species, z_ν is the soft particle’s valence (ν = 1, …, N_P), and e is the elementary charge. The soft particles, at this point, are considered point-charges. If electroneutrality is not satisfied at a local level, the charge density will drive an electrostatic potential given by the solution of Poisson’s equation,

$${\displaystyle {\nabla }^2\varphi \left(\mathbf{x}\right)=-\frac{\rho \left(\mathbf{x}\right)}{{ϵ}_0ϵ},}$$ (2)

where ϵ₀ is the vacuum permittivity and ϵ is the solvent relative permittivity. The electric field (E(x) = − ∇ϕ(x)) drives an electric force on the ions. Electric forces on the continuum ions and the total forces on the soft particles define a force density given by

$${\displaystyle \mathit{\rho }\left(\mathbf{x}\right)=F\sum _{j=1}^{N_I}{z}_j{C}_j\left(\mathbf{x}\right)\mathbf{E}\left(\mathbf{x}\right)+\sum _{\nu =1}^{N_p}{\mathbf{f}}_{\nu }\delta (\mathbf{x}-{\mathbf{x}}_{\nu }),}$$ (3)

where f_ν represents the total non-Brownian and non-hydrodynamic force acting on particle ν. Neglecting inertia (Re = 0), the solvent velocity can be written as v(x) = v₀(x) + u(x), (where v₀(x) is the unperturbed velocity and u(x) is the velocity perturbation), and it is given by the solution of a Stokes system of equations. The velocity perturbation is driven by the force density, i.e.,

$${\displaystyle \begin{array}{rl}\hfill -\nabla p\left(\mathbf{x}\right)+\eta {\nabla }^2\mathbf{u}\left(\mathbf{x}\right)& =-\mathit{\rho }\left(\mathbf{x}\right),\hfill \\ \hfill \nabla \cdot \mathbf{u}\left(\mathbf{x}\right)& =0,\hfill \end{array}}$$ (4)

where η is the solvent viscosity.

The evolution of the ions within the solvent follows a species balance with the total flux defined as a sum of convection and diffusion fluxes. The latter are given by the Nernst-Planck diffusion, resulting in

$${\displaystyle \frac{\partial C_j}{\partial t}=-\mathbf{v}\cdot \nabla C_j+D_j{\nabla }^2{C}_j+D_j{z}_j(e/k_{B}T)\left[C_j{\nabla }^2\varphi +\nabla C_j\cdot \nabla \varphi \right],}$$ (5)

where D_j is the diffusion coefficient of ion j, k_B is Boltzmann’s constant, and T is the absolute temperature.

Each of the N_P discrete ions behaves, for the moment, as a point-force and a point-charge. The discrete ions have a hydrodynamic radius, a, and interact via a repulsive excluded volume potential. Neglecting inertia (Reynolds, Re = 0), for each discrete ion, ν = 1, …, N_P, the force balance requires

$${\displaystyle {\mathbf{f}}_{\nu }^H+{\mathbf{f}}_{\nu }^S+{\mathbf{f}}_{\nu }^E+{\mathbf{f}}_{\nu }^V+{\mathbf{f}}_{\nu }^B=0,}$$ (6)

where, for bead ν, ${\mathbf{f}}_{\nu }^H$ is the hydrodynamic force, ${\mathbf{f}}_{\nu }^V$ is the particle-particle excluded volume force, ${\mathbf{f}}_{\nu }^E$ is the electrostatic force, ${\mathbf{f}}_{\nu }^B$ is the Brownian force, and ${\mathbf{f}}_{\nu }^S$ are any other potential forces that may arise in the system.^35,39 The dynamics of the discrete ions in the solvent is described by the probability density in configuration space. The diffusion equation for the configurational distribution function has the form of a Fokker-Planck equation, which corresponds to the following system of stochastic differential equations of motion for the discrete ion positions:

$${\displaystyle \mathit{d}\mathbf{R}=\left[{\mathbf{V}}_0+\frac{1}{k_{B}T}\mathbf{D}\cdot \mathbf{F}+\frac{\partial }{\partial \mathbf{R}}\cdot \mathbf{D}\right]\mathit{dt}+\sqrt{2}\mathbf{B}\cdot \mathit{d}\mathbf{W}.}$$ (7)

Here, R is a vector containing the 3N_P coordinates of the soft particles, and where R_ν = x_ν denotes the Cartesian coordinates of particle ν. The vector V₀, of length 3N_P, represents the unperturbed velocity field, with V_0,ν = v₀(x_ν). The vector F has length 3N_P, with F_ν = f_ν being the total non-Brownian, non-hydrodynamic force acting on bead ν. Finally, the independent components of dW are obtained from a real-valued Gaussian distribution function with zero mean and variance dt. The diffusion tensor D (or mobility tensor) is a 3N_P × 3N_P tensor. It may be separated into the Stokes drag and the hydrodynamic interaction tensor, Ω_νμ,

$${\displaystyle {\mathbf{D}}_{\nu \mu }=k_{B}T\left[\frac{\mathit{\delta }}{\zeta }{\delta }_{\nu \mu }+(1-{\delta }_{\nu \mu }){\mathbf{\Omega }}_{\nu \mu }\right],}$$ (8)

where δ is a 3 × 3 identity matrix and δ_νμ is the Kronecker delta. The Brownian perturbation, dW, is coupled to the hydrodynamic interactions through the fluctuation-dissipation theorem: D = B ⋅ B^T.

The characteristic variables for the system are set by the soft particle: hydrodynamic radius, a, for length, particle diffusion time, ζa²/k_BT, for time (where ζ = 6πηa is the drag coefficient), e/4πϵ₀ϵa for the electrostatic potential, and the elementary charge e for the charge. There are two scales for velocity: one for the unperturbed velocity field v₀ and one for the velocity fluctuations u_c = k_BT/ζa. The uniform concentration for one of the species, C₀, is used as the characteristic concentration of ions within the solvent. Therefore, P_e,j = v₀a/D_j defines a Peclet number for species j based on the imposed flow field v₀, and β_j = ζD_j/k_BT is the ratio between particle and continuum-ion diffusion coefficients. The ratio between electrostatic forces and thermal forces defines the so-called Bjerrum length, λ_B = e²/4πϵ₀ϵk_BT, and the ionic strength, $I=\frac{1}{2}\sum _j^{N_I}{C}_j{z}_j^2$, defines the so-called Debye length, ${\mathrm{\lambda }}_D^{-2}=2N_A{e}^{2}I/{ϵ}_0ϵk_{B}T$.

III. NERNST-PLANCK-GgEm

The key feature of GgEm-like methods is to decompose the charge-density and force-density expressions into a local (free-space) contribution and a global (bounded) contribution, in analogy to Ewald-like methods. The “local” densities are defined by

$${\displaystyle \begin{array}{rl}\hfill {\rho }_l\left(\mathbf{x}\right)& =\sum _{\nu =1}^{N_P}{z}_{\nu }\left[\delta (\mathbf{x}-{\mathbf{x}}_{\nu })-g_E(\mathbf{x}-{\mathbf{x}}_{\nu })\right],\hfill \\ \hfill {\mathit{\rho }}_l\left(\mathbf{x}\right)& =\sum _{\nu =1}^{N_P}{\mathbf{f}}_{\nu }\left[\delta (\mathbf{x}-{\mathbf{x}}_{\nu })-g_H(\mathbf{x}-{\mathbf{x}}_{\nu })\right],\hfill \end{array}}$$ (9)

which produce a local contribution to the electrostatic potential ϕ_l(x) and the velocity perturbation u_l(x). The “global” densities are given by

$${\displaystyle \begin{array}{rl}\hfill {\rho }_g\left(\mathbf{x}\right)& =\sum _{j=1}^{N_I}{z}_j{\beta }_j{C}_j+\sum _{\nu =1}^{N_P}{z}_{\nu }\left[g_E(\mathbf{x}-{\mathbf{x}}_{\nu })\right],\hfill \\ \hfill {\mathit{\rho }}_g\left(\mathbf{x}\right)& ={\mathrm{\lambda }}_b\sum _{j=1}^{N_I}{z}_j{\beta }_j{C}_j\mathbf{E}+\sum _{\nu =1}^{N_P}{\mathbf{f}}_{\nu }\left[g_H(\mathbf{x}-{\mathbf{x}}_{\nu })\right]\hfill \end{array}}$$ (10)

and are responsible for the global contribution of the potential ϕ_g(x) and velocity perturbation u_g(x). The linearity of the Poisson and Stokes equations implies that

$${\displaystyle \varphi \left(\mathbf{x}\right)={\varphi }_l\left(\mathbf{x}\right)+{\varphi }_g\left(\mathbf{x}\right)}$$ (11)

and

$${\displaystyle \mathbf{u}\left(\mathbf{x}\right)={\mathbf{u}}_l\left(\mathbf{x}\right)+{\mathbf{u}}_g\left(\mathbf{x}\right).}$$ (12)

The screening functions, g_E,H(x), satisfy ∫_{all space}g_E,H(x) dx = 1. The local contributions, ϕ_l(x) and u_l(x), are calculated analytically assuming an unbounded domain, only considering neighbor particles. For Poisson’s equation, the screening function is a Gaussian,

$${\displaystyle g_E\left(r\right)=\left(\frac{{\alpha }^3}{{\pi }^{3/2}}\right)e^{(-{\alpha }^2{r}^2)},}$$ (13)

while for the Stokes equations, it is a modified Gaussian,³⁴

$${\displaystyle g_H\left(r\right)=\left(\frac{{\alpha }^3}{{\pi }^{3/2}}\right)e^{(-{\alpha }^2{r}^2)}\left[\frac{5}{2}-{\alpha }^2{r}^2\right].}$$ (14)

The global contributions are found numerically, requiring that ϕ_l + ϕ_g and u_l + u_g satisfy appropriate boundary conditions. For example, homogeneous Dirichlet boundary conditions require ϕ_g(x) = − ϕ_l(x) and u_g(x) = − u_l(x). For problems with periodic boundary conditions, Fourier techniques are used to guarantee the periodicity of the global contributions. The periodicity for local contributions is obtained through a minimum image convention.

The point-source regularization (i.e., soft particle) is implemented with the same screening functions from GgEm introducing two additional length scales ${\xi }_E^{-1}$ and ${\xi }_H^{-1}$. These length scales are related to the hydrodynamic radius a. For the point-force (hydrodynamics), this is achieved by limiting the maximum velocity on the fluid driven by the regularized-force, which at Re = 0 is given by Stokes’ law. The regularization for the point-charge is achieved by distributing the total charge throughout the particle, thereby “confining” the charge to the particle volume. The regularization parameters are ${\xi }_E^R=3/a$ and ${\xi }_H^R=\sqrt{\pi }/3a$.

IV. APPLICABILITY

In what follows, several general remarks are presented regarding the applicability of the method. Three aspects must be considered: the discrete elements, the continuum solvent, and the time discretization. GgEm-based methods offer advantages when treating point-sources, e.g., point-charges or point-forces. At its core, this is a methodology that efficiently calculates Green’s functions in any geometry (resulting in the correct regimes, including Re = Ma = 0 restrictions). Therefore, any particle description that may be achieved by singular solutions can be considered. In this work, for instance, we illustrate NP-GgEm in the context of soft-beads, a model that is important for coarse-grain descriptions of polymers. However, rigid or deformable non-penetrating particle representations can be included with singular distributions over a surface (immersed-boundary,^63,64 accelerated boundary⁶⁵), or by the multipole expansion (Stokesian-dynamic approaches⁶⁶).

The charged ions within the solvent are represented by continuum concentration distributions that obey the natural restrictions involved in the continuum approximation. Quantities such as the diffusion coefficient or the valence enter the formalism through such distributions. Note, however, that some caution must be exercized when the Debye length approaches zero. This requires that an extremely fine global mesh be used, thereby increasing computational demands. In this limit, the usefulness of the method is limited given that local electroneutrality is hardly broken.

The most salient difference between NP-GgEm and other approaches is the transient solution for the continuum ions, in that one need not adopt a Poisson-Boltzmann solution surrounding any discrete charge. This offers advantages far from equilibrium, because the characteristic time scales associated with externally applied forces (electrostatic or hydrodynamic fields) can be orders of magnitude longer than the characteristic ionic diffusion time, and simply deform and disrupt the corresponding ionic clouds.

The discrete and numerical evolution of the model has the same restrictions of any numerical continuum solver. In particular, charge and field ranges, ion and particle concentrations, and external forces determine the level of spatial and temporal discretization required for a stable and convergent solution. The restrictions at this level therefore depend on the computational efficiency of the method and not so much on the physical model. For example, NP-GgEm provides accurate solutions for large charges and fields and requires smaller time stepping with finer meshes (see Appendix C for a numerical implementation in periodic domains using fast Fourier transform (FFT)).

V. RESULTS

The method is validated by comparing its results to available approximate analytical solutions for soft particles. Most of these solutions correspond to equilibrium conditions and result from a linearized Poisson-Boltzmann approximation (i.e., low potentials). More specifically, we calculate the electrostatic potential surrounding a single charged soft-particle at equilibrium and the interaction potential energy between two particles.

For ion-penetrable particles, Ohshima and co-workers have obtained a set of solutions for multiple problems,^67–72 including the electrostatic potential for one and two particles, the interaction energy between two particles, and the electrophoretic mobility of a single particle. Validating NP-GgEm with these equilibrium conditions provides a basis to determine whether ions diffuse properly and whether the ion-clouds surrounding the soft particles are consistent with available models.

A soft particle, of radius a, in a one-one electrolyte (at low potential) will generate an electrostatic potential given by^69–72

$${\displaystyle \varphi \left(r\right)={\varphi }_0\frac{a}{r}exp[-\kappa (r-a)],}$$ (15)

where κ⁻¹ = λ_D and ϕ₀ is the surface potential defined as follows:

$${\displaystyle {\varphi }_0=\left(z_{\nu }e\right)\frac{exp(-\kappa a)}{{ϵ}_0ϵ\kappa a}{\int }_0^{a}r{g}_E^R\left(r\right)sinh\left(\kappa r\right)dr.}$$ (16)

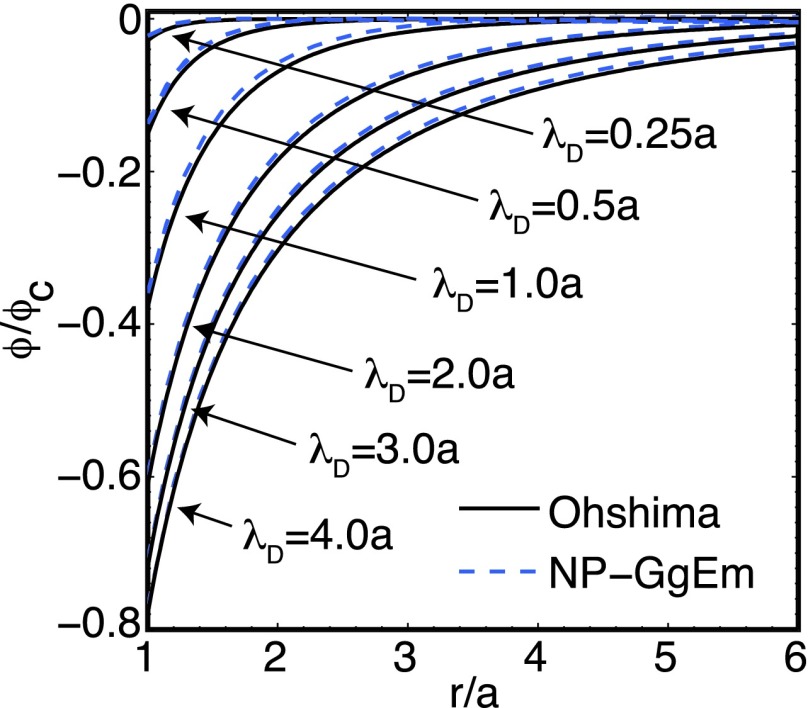
Figure 2 shows a comparison between Eq. (15) from Ohshima’s work (solid lines) and the NP-GgEm solution (dotted lines) for different ionic strengths.

FIG. 2.

Electrostatic potential induced by a soft particle with charge density $g_E^R$ as a function of the distance from the particle for different ionic strengths or Debye lengths. The characteristic electrostatic potential ϕ_c = e/4πϵ₀ϵa.

By superimposing the solution for single particles, the potential and the electrostatic energy, Φ(r), can be obtained from the solution in Eq. (15). Ohshima^72–75 obtained an approximate expression for two soft particles with uniform charge density at low potential (full analytical expressions can also be obtained using infinite reflections^67,76). The electrostatic interaction energy at a distance r is obtained from the free energy (F) induced by the electrostatic potential. For soft particles with a non-uniform charge density, the electrostatic energy is given by

$${\displaystyle \mathrm{\Phi }\left(r\right)=F\left(r\right)-F\left(\infty \right)=4\pi {ϵ}_0ϵa_1{a}_2{\varphi }_{0,1}{\varphi }_{0,2}\frac{exp[-\kappa (r-a_1-a_2)]}{R},}$$ (17)

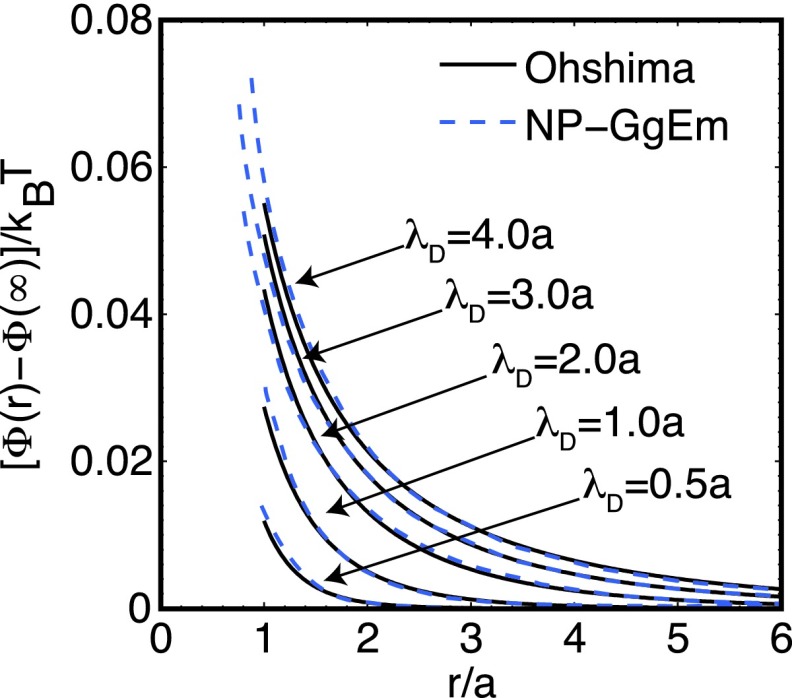
where a₁ and a₂ are the radii of the soft particles. In the case of soft particles defined by the Gaussian charge density $g_E^R$, the surface potentials are given by Eq. (16). Figure 3 shows the electrostatic energy between the particles as a function of the distance between them for different ionic strengths. Similar to the induced electrostatic potential, at low potentials and equilibrium, the results given by the NP-GgEm follow closely the behavior predicted by Ohshima.

FIG. 3.

Electrostatic interaction energy between two soft particles as a function of the distance for different solvent concentrations (Debye length). Continuum lines are the approximate solution by Ohshima using a linearized Poisson-Boltzmann approximation, while dotted lines are the predictions by the NP-GgEm. The characteristic energy is k_BT.

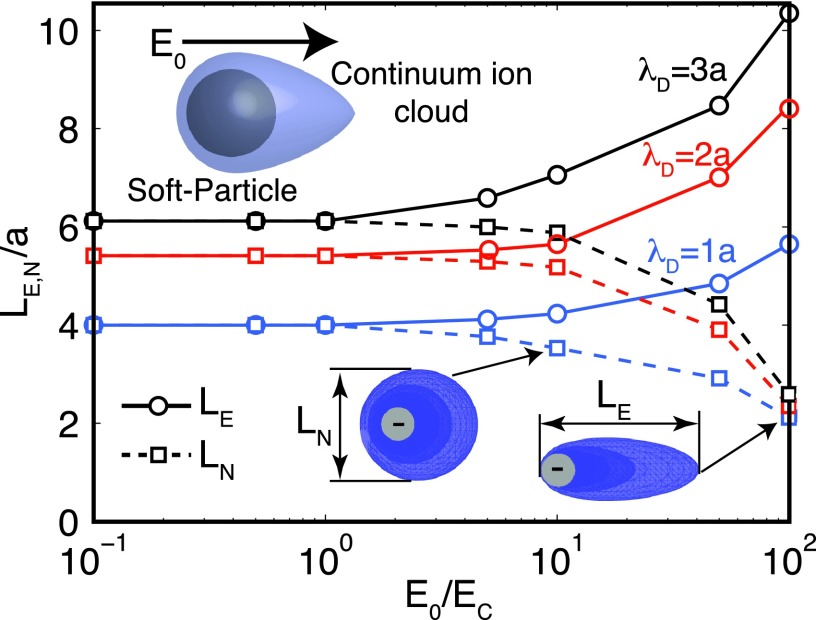
Imposing an electric field on a charged particle deforms the ion clouds that surround the particle, leading to a change of the particle’s electrophoretic mobility, as described in the Appendix D. Figure 4 illustrates how ionic clouds that surround the soft particles are deformed when an external electric field is applied, as a function of the salt concentration. As the electric field increases, the ion cloud elongates along the field direction, L_E, whereas shrinks in the neutral directions L_N.

FIG. 4.

Ionic cloud dimensions, in the neutral (L_N) and applied field direction (L_E), as a function of the applied field for different Debye lengths (salt concentration). The soft particles are embedded in a charged solvent and the applied field deforms the continuum ionic cloud. Blue iso-concentration surfaces depict the counter-ions surrounding the negatively charged soft particles.

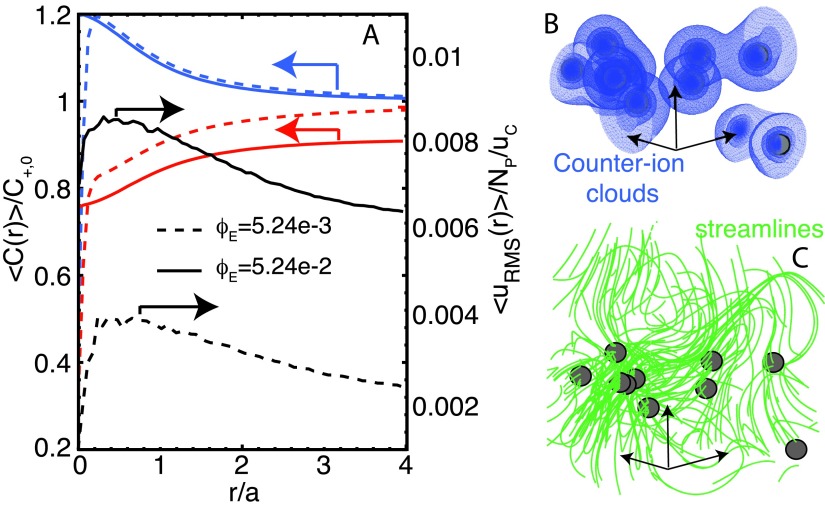
Non-equilibrium, finite concentrations, interacting ionic clouds and fluctuating hydrodynamic interactions, are built in the NP-GgEm. To illustrate the behavior of these types of systems, Brownian soft particles are simulated in a solvent at different λ_D s (salt concentrations). Diffusing soft particles of charge z_ν = − 1 and z_ν = − 2 are simulated in a periodic box of size L = 20a. Note that global electroneutrality is enforced through the continuum ions. Soft particle concentration is defined in terms of an effective volume fraction: ϕ_E = 4N_pπa³/3L³. Figure 5 provides representative results for NP-GgEm. In the figure, average counter- and co-ion concentration and RMS velocity profiles are shown as a function of distance from the soft particle, for λ_D = 2a. At equilibrium, the 2D concentration profiles suggest that they follow PB-like behavior. However, instantaneous concentration iso-surfaces (ion clouds) demonstrate how, even at low concentrations, the ion clouds merge and interact with each other, being deformed by the Brownian motion of the particles. The figure also includes the RMS velocity perturbation (normalized by the number of particles) as a function of the distance from the soft particle at different concentrations. The flow streamlines (green) are also plotted. The RMS velocity exhibits a slow decaying tail, accounting for the long-range behavior of HI, and it increases non-linearly with concentration.

FIG. 5.

(a) Average concentration and velocity fluctuations as a function of the distance from the soft particle, r/a. Red and blue lines are for co- and counter-ion concentration profiles, respectively; black lines depict RMS velocity profiles. (b) Instantaneous counter-ion clouds (blue) and (c) velocity streamlines (green). The soft particles have negative changed and they are embedded in a solvent with λ_D = 2a at an effective volume fraction ϕ_e = 5.24 × 10⁻³ (N = 10).

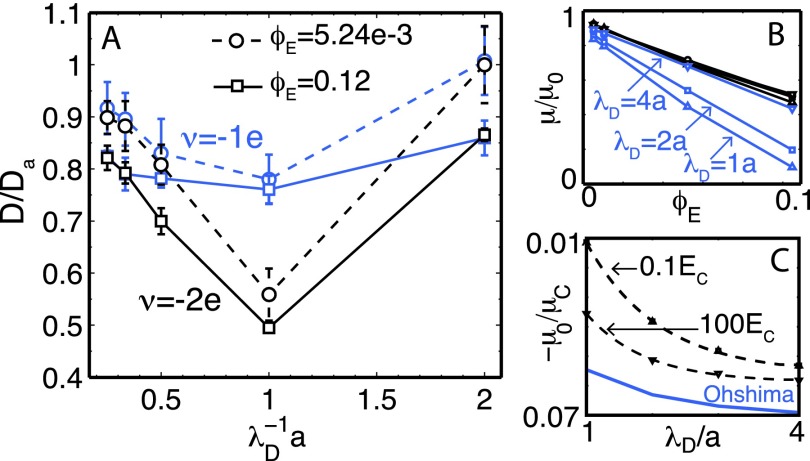
One key property of interest in charged colloidal systems is the diffusion coefficient, and its dependence on the concentration, charge, and salt. To illustrate the behavior of this property, and the usefulness of the approach proposed here, in Fig. 6, we show the soft particle diffusion coefficient as a function of the Debye length for two different concentrations and charges. The simulations were evolved from 200 to 1000 characteristic particle-diffusion times, thereby providing sufficient statistics. In general, the diffusion coefficient decreases by increasing soft particle concentration and charge. For high salt (low λ_D), the diffusion coefficient approaches the infinite dilute and non-charge system. As the salt concentration increases, electrolyte drag and collective motion drive a non-monotonic behavior, decreasing mobility at first and then increasing it. This behavior of diffusing charge particles in a charge solvent was also been observed in other systems.^77–79 In the figure, the electrophoretic mobility, μ = u/E₀, for soft particles of charge ν = − 1 is also shown. The figure includes two applied electric fields: a weak E₀ = 0.1E_C and a strong E₀ = 100E_C (where the characteristic field is E_C = e/4πϵ₀ϵa²). We recall that fluid can penetrate the soft particles, causing the electrophoretic mobility to change with the applied electric field. The electrophoretic mobility at zero concentration, μ₀, and an approximate solution for non-fluid-penetrated soft particles⁶⁷ as a function of the Debye length for the two applied fields are both included in the figure. For weak fields, there is a stronger dependence on Debye length, and the electrophoretic mobility approaches to zero, meaning that the fluctuating hydrodynamic interactions (driven by Brownian motion) affect particle trajectories, averaging down the electrophoretic induced motion. On the other hand, for strong fields, the normalized mobility collapses into a single curve, maintaining the dominance of the electrokinetic forces. Ohshima’s solution is obtained from the linearized PB; other authors had suggested different solutions that result in similar approximations for these electrokinetic properties, which are restricted to zero concentrations and weak potentials. The approach we proposed here avoids the approximation of electrokinetic properties and relationships. It provides a platform for other colloidal and polymeric systems, including deformable objects, rigid suspensions, and cells, where lubrication forces and slip conditions are important.

FIG. 6.

(a) Diffusion coefficient as a function of the salt concentration (Debye length, λ_D), soft particles charge, ν, and effective volume fraction, ϕ_E. The diffusion coefficient is normalized with the particle diffusion coefficient D_a = k_BT/6πηa. (b) Electrophoretic mobility, μ, as a function of the effective volume fraction and salt concentration for a weak (blue lines) and a strong (black lines) imposed fields, E₀. (c) Electrophoretic mobility at zeroth concentration, μ₀, as a function of the Debye length for the two applied fields in (b). The blue line represent Ohshima’s approximate solution for non-fluid-penetrated soft particles.⁶⁷

VI. CONCLUSIONS

With the method described here, it is possible to perform efficient simulations of discrete charged elements embedded in charged solvents at non-equilibrium conditions. It should find applications in a wide variety of situations involving the physics of polymeric and colloidal systems including micro- and nano-scale systems.

APPENDIX A: GgEm CONTRIBUTIONS

Local contributions to the electrostatic potential, ϕ_l(x), and the velocity perturbation, u_l(x), are calculated assuming an unbounded domain, considering the N_P discrete ions only, i.e.,

$${\displaystyle \begin{array}{rl}\hfill {\varphi }_l\left(\mathbf{x}\right)& =\sum _{\nu =1}^{N_P}{G}_l(\mathbf{x}-{\mathbf{x}}_{\nu })z_{\nu },\hfill \\ \hfill {\mathbf{u}}_l\left(\mathbf{x}\right)& =\sum _{\nu =1}^{N_P}{\mathbf{G}}_l(\mathbf{x}-{\mathbf{x}}_{\nu })\cdot {\mathbf{f}}_{\nu },\hfill \end{array}}$$ (A1)

where G_l(x) and G_l(x) are the “smoothed” free-space Green’s functions for the Laplace and Stokes equations, respectively. These functions are obtained taking the corresponding free-space Green’s function and subtracting the smoothed function from the solution with a forcing term given by g_E or g_H.

For the Poisson’s equation, a Gaussian defined by

$${\displaystyle g_E\left(r\right)=\left(\frac{{\alpha }^3}{{\pi }^{3/2}}\right)e^{(-{\alpha }^2{r}^2)}}$$ (A2)

yields a simple expression for G_l(x),

$${\displaystyle G_l\left(\mathbf{x}\right)=\frac{\text{erfc}\left(\alpha r\right)}{r},}$$ (A3)

where r = |x|. For the Stokes equations, we found that a modified Gaussian³⁴ defined by

$${\displaystyle g_H\left(r\right)=\left(\frac{{\alpha }^3}{{\pi }^{3/2}}\right)e^{(-{\alpha }^2{r}^2)}\left[\frac{5}{2}-{\alpha }^2{r}^2\right]}$$ (A4)

yields the following expression for G_l(x):

$${\displaystyle {\mathbf{G}}_l\left(\mathbf{x}\right)=\frac{3}{4}\left[\mathit{\delta }+\frac{\mathbf{xx}}{r^2}\right]\frac{\text{erfc}\left(\alpha r\right)}{r}-\frac{3}{4}\left[\mathit{\delta }-\frac{\mathbf{xx}}{r^2}\right]\frac{2\alpha }{{\pi }^{1/2}}{e}^{(-{\alpha }^2{r}^2)}.}$$ (A5)

The global contributions are found numerically, requiring that ϕ_l(x) + ϕ_g(x) and u_l(x) + u_g(x) satisfy appropriate boundary conditions. For instance, homogeneous Dirichlet boundary condition for the electrostatic potential (a conducting surface) would require ϕ_g(x) = − ϕ_l(x). For no-slip velocity, we require that u_g(x) = − u_l(x). For problems with periodic boundary conditions, Fourier techniques can be used to guarantee the periodicity of the global contributions. The periodicity on the local contributions is obtained using the minimum image convention for the discrete ions.

The global contribution is obtained on a set of M_g discrete points on a mesh; any technique (finite differences, finite elements, spectral methods) may be used to find it. After global contributions are resolved, interpolation is used to get the value of the global contributions at the location x_ν of each discrete ion.^80,81

Note that the parameter α⁻¹ in Eqs. (A2) and (A4) provides a length scale for the exponentially decaying local contribution. It also indicates the resolution required in the global calculation. In regular GgEm, α is selected to minimize the computational cost between local and global contributions; α is independent of the number of discrete particles: α≁N_p in GgEm.³⁴ However, the nature of the local contribution results in an infinite resolution for the short scale particle-particle interactions, while dictating the required mesh resolution for the global one. On the other hand in NP-GgEm, the mesh resolution is given by the fluid characteristic length scales. As a consequence, α provides the resolution for the local contribution while stating the independence on the discrete ions, i.e., for fix fluid conditions, like constant Debye length or ionic strength, NP-GgEm is O(N_p).

APPENDIX B: NUMERICAL SCHEME AND APPROXIMATIONS

For a system of interest, the valences z_j and z_ν, the imposed electric and velocity fields E₀ and v₀, the physical properties ϵ, η, D_j, a, and T, and the continuum concentrations C_j,0, are all given. All characteristic variables can then be calculated, including ionic strength I and Debye length λ_D = κ⁻¹. These are particularly important because the system must be globally neutral, i.e.,

$${\displaystyle \left(F\sum _{j=1}^{N_I}{C}_{j,0}{z}_j\right)V=\sum _{\nu =1}^{N_P}{z}_{\nu }e{V}_{\nu },}$$ (B1)

where V and V_ν = 4/3πa³ are the system and particle ν volume, respectively. In a confined system, Eq. (B1) must include all charges on walls, if any.

At time t = t_k, the continuum ions’ concentrations [C_j(x)]^k and soft particles positions R^k (${\mathbf{R}}_{\nu }^k={\mathbf{x}}_{\nu }^k$) are defined. Concentration fields and particle positions define the charge density at time t_k: [ρ(x)]^k. NP-GgEm is then used to calculate the electrostatic potential from Poisson’s equation,

$${\displaystyle {\left[{\nabla }^2\varphi \right]}^k=-4\pi {\left[\rho \right]}^k.}$$ (B2)

The same scheme used to approximate gradients and interpolate the solution in the global solution ([ϕ_g]^k) may be used to compute the electrostatic field and force, [E]^k = − [∇ϕ]^k and ${\left[{\mathbf{f}}_{\nu }^E\right]}^k={\hat{\mathrm{\lambda }}}_B{z}_{\nu }{\left[\mathbf{E}\right]}^k$.

The electrostatic force at the soft particles plus any other non-hydrodynamic-non-Brownian forces is used to find the force density: [ρ]^k. NP-GgEm is used for the second time to calculate the velocity perturbation from Stokes equations,

$${\displaystyle -\nabla p^k+\frac{1}{6\pi }{\nabla }^2{\mathbf{u}}^k=-{\mathit{\rho }}^k,\nabla \cdot {\mathbf{u}}^k=0.}$$ (B3)

At this moment, both systems, continuum ions and soft particles, are ready to be evolved in time. For the species balance, any desirable integration scheme can be used. However, a second order semi-implicit Euler scheme provides a perfect balance between numerical stability and computational efficiency.⁸¹ The concentrations at time t = t_k + Δt = t_k+1 are given by

$${\displaystyle {\left[C_j-\frac{\mathrm{\Delta }t}{2}{\psi }_j{\nabla }^2{C}_j\right]}^{k+1}=\left[C_j+\frac{\mathrm{\Delta }t}{2}{\psi }_j{\nabla }^2{C}_j-\left({\psi }_j{P}_{e,j}{\mathbf{v}}_0+\mathbf{u}\right)\cdot \nabla C_j\right.{\left.+{\mathrm{\lambda }}_B{\psi }_j{z}_j\left(C_j{\nabla }^2\varphi +\nabla C_j\cdot \nabla \varphi \right)\right]}^k.}$$ (B4)

The soft particle new positions are obtained from an Îto first order integration^82–84 and a mid-point algorithm, proposed by Fixman,^85–87 to keep the O(N_p) character of the NP-GgEm scheme,

$${\displaystyle \begin{array}{rcl}\hfill {\mathbf{R}}^{\ast }& \hfill =\hfill & \mathbf{R}\left(t_k\right)+\frac{1}{2}\left[{\mathbf{V}}_0\left(\mathbf{R}\right)+\mathbf{D}\left(\mathbf{R}\right)\cdot \mathbf{F}\left(\mathbf{R}\right)\right]\mathrm{\Delta }t\hfill \\ \hfill & \hfill \hfill & +\frac{1}{2}\sqrt{2}\mathbf{D}\left(\mathbf{R}\right){\mathbf{B}}^{-1}\left(\mathbf{R}\right)\cdot \mathrm{\Delta }\mathbf{W}\left(t_k\right),\hfill \\ \hfill \mathbf{R}(t_k+\mathrm{\Delta }t)& \hfill =\hfill & \mathbf{R}\left(t_k\right)+\left[{\mathbf{V}}_0\left({\mathbf{R}}^{\ast }\right)+\mathbf{D}\left({\mathbf{R}}^{\ast }\right)\cdot \mathbf{F}\left({\mathbf{R}}^{\ast }\right)\right]\mathrm{\Delta }t\hfill \\ \hfill & \hfill \hfill & +\sqrt{2}\mathbf{D}\left({\mathbf{R}}^{\ast }\right){\mathbf{B}}^{-1}\left(\mathbf{R}\right)\cdot \mathrm{\Delta }\mathbf{W}\left(t_k\right).\hfill \end{array}}$$ (B5)

NP-GgEm yields $\left[\mathbf{D}\cdot \mathbf{F}\right]$ without explicit construction of D, and it is desirable to time-integrate the stochastic differential equation without requiring this product in a “matrix-free” formulation. The integration in Eq. (B5) includes a scheme that performs the time-integration without needing to evaluate ∂/∂R ⋅ D.^87,88 The final remaining step is to evaluate B⁻¹ ⋅ dW in a matrix-free way. As noted by Fixman,⁸⁶ this can be done by a Chebyshev polynomial approximation method that requires only matrix-vector products, not the matrix itself. This approach has already been implemented in unbounded and periodic domains.^{32,34,35,37,39,40,59,89,90}

It is important to remember that proper selection of the time step Δt is required. There are three different characteristic time scales that must be followed in order to obtain an accurate and stable solution: soft particle diffusion time (a²ζ/k_BT), continuum ions’ diffusion time (${\mathrm{\lambda }}_D^2/min\left(D_j\right)$), and convection time (a/max(u)). We found that a dynamical selection of the time step, keeping a desired resolution of the smallest time, is the best way to ensure a stable solution.

APPENDIX C: NUMERICAL IMPLEMENTATION FOR A PERIODIC DOMAIN: FFT

For a three dimensional periodic domain, NP-GgEm uses spectral element solutions based on FFT. In this numerical implementation, all functions, global fields, and concentrations are expressed in Fourier space as

$${\displaystyle {\varphi }_g\left(\mathbf{x}\right)=\sum _{\mathbf{k}}{\tilde{\varphi }}_g\left(\mathbf{k}\right)exp(i\mathbf{k}\cdot \mathbf{x}),}$$ (C1)

$${\displaystyle {\mathbf{u}}_g\left(\mathbf{x}\right)=\sum _{\mathbf{k}}{\tilde{\mathbf{u}}}_g\left(\mathbf{k}\right)exp(i\mathbf{k}\cdot \mathbf{x}),}$$ (C2)

$${\displaystyle p_g\left(\mathbf{x}\right)=\sum _{\mathbf{k}}{\tilde{p}}_g\left(\mathbf{k}\right)exp(i\mathbf{k}\cdot \mathbf{x}),}$$ (C3)

$${\displaystyle C_j\left(\mathbf{x}\right)=\sum _{\mathbf{k}}{\tilde{C}}_j\left(\mathbf{k}\right)exp(i\mathbf{k}\cdot \mathbf{x}),}$$ (C4)

where k = {k₁, k₂, k₃} are the Fourier modes in the x₁-, x₂-, and x₃-direction, respectively. Forcing terms, i.e., global charge- and force-densities, are also transformed into Fourier space,

$${\displaystyle {\rho }_g\left(\mathbf{x}\right)=\sum _{\mathbf{k}}{\tilde{\rho }}_g\left(\mathbf{k}\right)exp(i\mathbf{k}\cdot \mathbf{x}),}$$ (C5)

$${\displaystyle {\mathit{\rho }}_g\left(\mathbf{x}\right)=\sum _{\mathbf{k}}{\tilde{\mathit{\rho }}}_g\left(\mathbf{k}\right)exp(i\mathbf{k}\cdot \mathbf{x}).}$$ (C6)

The inner product of the orthonormal basis provides the Fourier modes for the velocity global contribution from Stokes equations,

$${\displaystyle \begin{array}{rl}\hfill {\tilde{p}}_g\left(\mathbf{k}\right)& =-\frac{i}{k^2}\mathbf{k}\cdot {\tilde{\mathit{\rho }}}_g\left(\mathbf{k}\right),\hfill \\ \hfill {\tilde{\mathbf{u}}}_g\left(\mathbf{k}\right)& =6\pi \frac{{\tilde{\mathit{\rho }}}_g\left(\mathbf{k}\right)}{k^2}-6\pi \frac{\mathbf{k}{\tilde{p}}_g\left(\mathbf{k}\right)}{k^2},\hfill \end{array}}$$ (C7)

where ${\tilde{p}}_g\left(\mathbf{k}\right)$ is the global contribution to the pressure field and to

$${\displaystyle {\tilde{\varphi }}_g\left(\mathbf{k}\right)=4\pi \frac{{\tilde{\rho }}_g\left(\mathbf{k}\right)}{k^2},}$$ (C8)

as the global contribution to the electrostatic potential from Poisson’s equation.

Once a function and its Fourier coefficients are known, the gradients and laplacian are calculated directly from the FFT scheme,

$${\displaystyle f\left(\mathbf{x}\right)={\sum }_{\mathbf{k}}\tilde{f}\left(\mathbf{k}\right)exp(i\mathbf{k}\cdot \mathbf{x}),}$$ (C9)

$${\displaystyle \frac{\partial f}{\partial x_i}\left(\mathbf{x}\right)={\sum }_{\mathbf{k}}\left(i{k}_i\right)\tilde{f}\left(\mathbf{k}\right)exp(i\mathbf{k}\cdot \mathbf{x}),}$$ (C10)

$${\displaystyle {\nabla }^{2}f\left(\mathbf{x}\right)=-{\sum }_{\mathbf{k}}\left(k^2\right)\tilde{f}\left(\mathbf{k}\right)exp(i\mathbf{k}\cdot \mathbf{x}).}$$ (C11)

Therefore, the evolution equation for the concentrations may be written as follows:

$${\displaystyle {\left[C_j-\frac{\mathrm{\Delta }t}{2}{\psi }_j{\nabla }^2{C}_j\right]}^{k+1}={\left[b_j\right]}^k,}$$ (C12)

where

$${\displaystyle {\left[b_j\right]}^k=\left[C_j+\frac{\mathrm{\Delta }t}{2}{\psi }_j{\nabla }^2{C}_j-\left({\psi }_j{P}_{e,j}{\mathbf{v}}_0+\mathbf{u}\right)\cdot \nabla C_j\right.{\left.+{\mathrm{\lambda }}_B{\psi }_j{z}_j\left(C_j{\nabla }^2\varphi +\nabla C_j\cdot \nabla \varphi \right)\right]}^k,}$$ (C13)

which consists of known functions, gradients, and laplacians.

With the Fourier transform for the concentration, the Fourier coefficients for each concentration can be obtained from Eq. (C12) and the corresponding dot product with the orthonormal Fourier basis,

$${\displaystyle {\tilde{C}}_j\left(\mathbf{k}\right)=\frac{{\tilde{b}}_j\left(\mathbf{k}\right)}{1+(\mathrm{\Delta }t/2){\psi }_j{k}^2},}$$ (C14)

where ${\tilde{b}}_j\left(\mathbf{k}\right)$ is the Fourier transform of [b_j(x)]^k.

APPENDIX D: ANALYTICAL APPROXIMATE SOLUTIONS FOR THE ELECTROPHORETIC MOBILITY

Ohshima provided an expression for the electrophoretic mobility of soft particle when the fluid is not able to pass through them.^{70–72,91–93} This type of soft particle is useful when representing cells, but not when representing “beads” in polymer, proteins, or other molecules. NP-GgEm can also be generalized for colloids and non-penetrating fluid particles. For a non-fluid penetrated particle with uniform charge density ρ_U, the electrophoretic mobility, μ = U/E, is given by

$${\displaystyle \mu =\frac{{\rho }_U}{\eta {\mathrm{\lambda }}^2}\left[1+\frac{1}{3}{\left(\frac{\mathrm{\lambda }}{\kappa }\right)}^2\left(1+e^{-2\kappa a}-\frac{1-e^{-2\kappa a}}{\kappa a}\right)\right.+\frac{1}{3}{\left(\frac{\mathrm{\lambda }}{\kappa }\right)}^2\frac{1+1/\kappa a}{{\left(\mathrm{\lambda }/\kappa \right)}^2-1}\times \left\{\left(\frac{\mathrm{\lambda }}{\kappa }\right)\frac{1+e^{-2\kappa a}-\left(1-e^{-2\kappa a}\right)/\kappa a}{\left(1+e^{-2\mathrm{\lambda }a}\right)/\left(1-e^{-2\mathrm{\lambda }a}\right)-1/\mathrm{\lambda }a}\right.\left.\left.-\left(1-e^{-2\kappa a}\right)\right\}\right],}$$ (D1)

where λ = ζ/V_p is a drag coefficient density and ρ_U = z_νe/V_P.

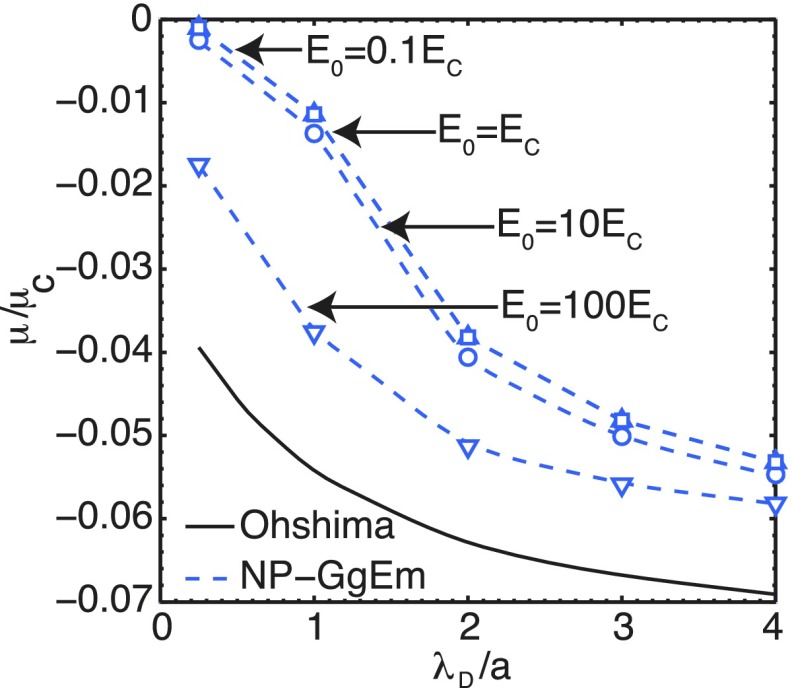
As mentioned above, the soft particle model adopted here provides a good representation of macromolecules, such as DNA, in complex flows. As an external field is applied, ion clouds are deformed, and when the particle moves, perturbs the fluid, affecting the total velocity v₀ + u, which in turn affects the diffusion of the ion clouds. Due to the fact that fluid flow can pass through the particles, it is expected that the electrophoretic mobility will be lower than when the fluid cannot penetrate (i.e., non-slip boundary conditions at the particles). In addition, there is also a dependence of the electrophoretic mobility on the applied field, contrary to the non-penetrating case. Figure 7 shows the electrophoretic mobility as a function of the Debye length for different applied fields E₀. There are several features to highlight. First, the shape of the curve approaches Ohshima’s solution at high electric fields. Second, at low Debye lengths (high ion concentrations) and low fields, the electrophoretic mobility is very small. This is due to the fact that for small Debye lengths, ions fully penetrate the soft particle, creating a pseudo-neutral particle, where the effects of low fields are almost negligible.

FIG. 7.

Electrophoretic mobility of non-penetrating fluid soft particles given by Ohshima’s solution and the fluid-penetrating soft particles by NP-GgEm. The characteristic electric field E_c = e/4πϵ₀ϵa² and the characteristic velocity u_c = k_BT/ζa.