Risk Analysis of Prostate Cancer in PRACTICAL, a Multinational Consortium, Using 25 Known Prostate Cancer Susceptibility Loci

Abstract

Background

Genome-wide association studies have identified multiple genetic variants associated with prostate cancer (PrCa) risk which explain a substantial proportion of familial relative risk. These variants can be used to stratify individuals by their risk of PrCa.

Methods

We genotyped 25 PrCa susceptibility loci in 40,414 individuals and derived a polygenic risk score (PRS). We estimated empirical Odds Ratios for PrCa associated with different risk strata defined by PRS and derived age-specific absolute risks of developing PrCa by PRS stratum and family history.

Results

The PrCa risk for men in the top 1% of the PRS distribution was 30.6 (95% CI 16.4–57.3) fold compared with men in the bottom 1%, and 4.2 (95% CI 3.2–5.5) fold compared with the median risk. The absolute risk of PrCa by age 85 was 65.8% for a man with family history in the top 1% of the PRS distribution, compared with 3.7% for a man in the bottom 1%. The PRS was only weakly correlated with serum PSA level (correlation=0.09).

Conclusions

Risk profiling can identify men at substantially increased or reduced risk of PrCa. The effect size, measured by OR per unit PRS, was higher in men at younger ages and in men with family history of PrCa. Incorporating additional newly identified loci into a PRS should improve the predictive value of risk profiles.

Impact

We demonstrate that the risk profiling based on SNPs can identify men at substantially increased or reduced risk that could have useful implications for targeted prevention and screening programs.

Introduction

Genome-wide association studies (GWAS) have identified multiple common genetic variants associated with prostate cancer (PrCa) risk. The risks associated with such variants are generally modest, but in combination their effects may be substantial, and may provide the basis of targeted prevention (1). However, since the risks associated with these variants are modest, large studies are required to estimate their risks precisely. To facilitate this estimation, we genotyped 25 PrCa susceptibility SNPs in studies from the PRACTICAL consortium. PRACTICAL is an international PrCa consortium that includes more than 78 studies, including men of European, Asian or African ancestry, and has a combined dataset of over 130,000 samples (http://practical.ccge.medschl.cam.ac.uk/). In the current analysis, we utilised data from 31,833 cases and controls from 24 studies in PRACTICAL and 8,581 samples from replication stage of a GWAS (“GWAS stage 3”). Sixteen out of the twenty five SNPs that we used in this study were identified through studies that included PRACTICAL (2–4) and nine SNPs were identified by other GWAS (5–10).

Materials and Methods

Samples

The current analysis was restricted to individuals of European ancestry, based on self-reported ethnicity, and thus we excluded samples with non-European ancestry. Data were contributed from 25 studies in PRACTICAL and GWAS stage 3. Twenty five SNPs were genotyped specifically for this analysis in 31,833 cases and controls in PRACTICAL phase III, unless the genotype data were already available. We also included four studies from the GWAS stage 3 conducted in the United Kingdom and Australia, comprising a further 8,581 cases and controls (11). In this replication stage 1,536 SNPs were genotyped, including the 25 susceptibility SNPs analysed here. These two datasets were combined to give a total of 40,414 samples (20,288 cases and 20,126 controls). Three studies (MCCS, PFCS and UKGPCS) that were included in the GWAS stage 3 also contributed genotyping of additional samples for PRACTICAL phase III (Table 1, Supplementary Table 1 and Supplementary Notes). Studies provided a minimum core dataset that included disease status, age at diagnosis/observation and ethnicity. Twenty two studies provided data on family history and eighteen studies provided data on Gleason score.

Table 1.

Total numbers of cases and controls used in the analyses

Study	Controlsa	Casesa	Totala
GWAS Stage 3	4,076	4,505	8,581
PRACTICAL	16,050	15,783	31,833
Total	20,126	20,288	40,414
Totalb	18,343	16,643	34,986

^aAnalyses were restricted to men of European ancestry (see text).

^bTotal after excluding 5 studies that oversampled cases with family history.

Where studied included more than one individual from the same family, only the index case was included, so that the analyses were based on unrelated men. For analyses of the polygenic risk score (PRS) we also excluded 5 studies (MAYO, PCFS, TASPRAC, ULM and UTAH) that oversampled cases with family history of PrCa. This reduced the total number of samples to 34,986 (16,643 cases and 18,343 controls). All studies were approved by the relevant ethics committees.

Eighty Nine percent (31,150) of the samples had information on age at diagnosis (interview/blood draw for controls). The mean age at diagnosis for the cases was 64 years, slightly higher than the mean age at interview/blood draw for the controls (58 years; Supplementary Table 2a). Family history information was available for 21,209 (60.6%) samples and among samples with family history information, 10.7% of controls and 18.2% of cases had a family history of PrCa. Before excluding studies with oversampled familial cases, these percentages were 12.9% and 22.6% respectively (Supplementary Table 2a and b).

Genotyping

Genotyping was performed in two experiments; these were subject to separate QC procedures appropriate to the platforms used, before the data were combined for statistical analysis. In PRACTICAL phase III, genotyping of samples from 2 studies was performed by Sequenom, while 22 study sites performed the 5’exonuclease assay (Taqman™) using the ABI Prism 7900HT sequence detection system according to the manufacturer’s instructions. Primers and probes were supplied directly by Applied Biosystems as Assays-By-Design™. Assays at all sites included at least four negative controls and 2–5% duplicates on each 384-well plate. Quality control guidelines were followed by all the participating groups as previously described (4). In addition, all sites also genotyped 16 CEPH samples. We excluded individuals that were not typed for at least 80% of the SNPs attempted. Data on a given SNP for a given site were also excluded if they failed any of the following QC criteria: SNP call rate >95%, no deviation from Hardy-Weinberg equilibrium in controls at P<.00001; <2% discordance between genotypes in duplicate samples and in the CEPH control samples. Cluster plots for SNPs that were close to failing any of the QC criteria were re-examined centrally.

GWAS Stage 3 genotypes were generated using an Illumina Golden Gate Assay. All SNPs for this analysis passed the QC filters used for this experiment: call rate>95%, a minor allele frequency in controls of >1%, or genotype frequency in controls consistent with Hardy-Weinberg equilibrium at p<0.00001. Duplicate concordance was 99.99% (11).

Statistical methods

We used combined data across all studies for the analysis. We assessed the association between each SNP and PrCa using a 1-degree-of-freedom Cochran-Armitage trend test, stratified by studies. Odds ratios (OR) and 95% confidence intervals (95% CI) associated with each genotype and cancer risk, and genotypes for pairs of SNPs, were estimated using unconditional logistic regression, stratified by study as a covariate. Both per-allele ORs, and genotype-specific ORs, were estimated. Heterogeneity in the OR estimates among studies was evaluated using a likelihood ratio test, by comparing with a model in which separate ORs were estimated for each study.

Modification of the ORs by disease aggressiveness and family history was assessed by using both family history (Yes vs. No) and Gleason score (<8 vs. ≥8) as binary variables. A test for association between SNP genotype at a locus and Gleason score as an ordinal variable was also performed, using polytomous regression. Modification of the ORs by age was assessed using a case-only analysis, assessing the association between age and SNP genotype in the cases using polytomous regression. The associations between SNP genotypes and PSA level were assessed using linear regression, after log-transformation of PSA level to correct for skewness.

Contribution to Familial Risk

The contribution of the known SNPs to the familial risk of PrCa, under a multiplicative model, was computed using the formula:

$$\raisebox{1ex}{$\sum _k(\text{log}{\lambda }_k)$}\!\left/ \!\raisebox{-1ex}{$(\text{log}{\lambda }_0)$}\right.$$

where λ₀ is the observed familial risk to first degree relatives of PrCa cases, assumed to be 2 (12), and λ_k is the familial relative risk due to locus k, given by:

$${\lambda }_k=\frac{p_k{r}_k^2+q_k}{{(p_k{r}_k+q_k)}^2}$$

where P_k is the frequency of the risk allele for locus k, q_k = 1 − P_k and r_k is the estimated per-allele odds ratio (13).

To evaluate evidence for interactions between pairs of SNPs, we used a likelihood ratio test and evaluated the evidence for departures from a multiplicative model, by comparing models with and a model without the interaction term for each pair of SNPs. The interaction term was the product of the allele doses for the two SNPs, hence leading to a 1 degree of freedom test for an interaction. Based on the assumption of a log-additive model, we constructed a PRS from the summed genotypes weighted by the estimated per-allele log-odds ratios for each SNP, as estimated by logistic regression as above. Thus for each individual j we derived:

$${\mathit{\text{Score}}}_j=\sum _{i=1}^N{\beta }_i{g}_{ij}$$

Where:

• N : Number of SNPs (25)

• g_ij : Allele dose at SNP i (0, 1, 2) for individual j

• β _i : Per-allele log-odds ratio of SNP i

The missing genotypes for an individual were replaced with the mean genotype of each SNP separately for cases and controls. A sensitivity analysis, in which analyses were based on samples with complete genotype data, gave very similar results (data not shown). We then standardised the PRS by dividing by the overall standard deviation of PRS in the controls.

The risk of PrCa was estimated for the percentiles of the distribution of the PRS; <1%, 1–10%, 10–25%, 25–75% (defined here as “median risk”), 75–90%, 90–99%, >99%; and per standard deviation when fitted as a continuous covariate. We evaluated the fit of the combined risk score to a log-linear model by comparing the model with the PRS fit as a continuous covariate with a model in which separate parameters were estimated for percentiles of risk adjusted for age at diagnosis and family history, using a likelihood ratio test.

We used a likelihood ratio test to evaluate the evidence for interaction between PRS and age at diagnosis/observation, PRS and family history and also family history and age at diagnosis/observation by comparing models with and a model without an interaction term. Effect sizes by family history were compared using a case-only analysis. Analyses were performed using Stata 13.

The relative risk estimates were used to obtain estimates of the absolute risk of PrCa by PRS category and family history. Since we observed evidence for an interaction between PRS and age, we used both models with and without PRS × age interaction term. Absolute risks were constrained such that the age-specific incidences, averaged over all categories of PRS and family history, were consistent with the age-specific incidences of PrCa for the UK population for 2012 (http://ci5.iarc.fr/CI5plus) (14). The model was adjusted for age at diagnosis (age <55, 55–59, 60–64, 65–70 and 70+). The procedure for deriving the age-specific incidences for each SNP profile category has been performed following the procedure explained by Antoniou et al. (15, 16), but adjusted to allow for competing causes of death.

For this purpose, we categorised PRS into seven risk groups (k=risk group 1 to 7), based on the percentile in the controls: <1%, 1–10%, 10–25%, 25–75%, 75–90%, 90–99% and >99%. We could not find any evidence for an interaction between PRS and family history of PrCa (P-value=0.49) and assumed that family history and PRS are independently predictive of PrCa risk. Under this model, the PrCa incidence ${\lambda }_k^h(t)$ at age t for an individual in risk group k and family history group h (h=1 with family history, h=0 no family history) was assumed to follow a model of the form: ${\lambda }_k^h(t)\mathrm{=}{\lambda }_0(t)\text{exp}({\beta }_k^h)$ where λ₀ (t) is the baseline PrCa incidence and $\text{exp}({\beta }_k^h)$ is the risk ratio in the risk group k and family history group h, relative to the baseline category (h=0, k=1), approximated by the odds ratio estimates from the logistic regression analysis. To obtain the baseline incidence, λ₀ (t), we constrained the PrCa incidence averaged all risk groups to agree with the population age-specific PrCa incidences μ(t) (the incidence of PrCa at age t per 100,000 individuals in the UK (14)). The baseline incidence can be obtained for each age by:

$${\lambda }_0(t)=\mu (t)\frac{p_0\sum _1^k{f}_k{S}_k^0(t-1)+p_1\sum _1^k{f}_k{S}_k^1(t-1)}{p_0\sum _1^k{f}_k{S}_k^0(t-1)\text{exp}({\beta }_k^0)+p_1\sum _1^k{f}_k{S}_k^1(t-1)\text{exp}({\beta }_k^1)}$$

Here P₀ is the probability of having no family history in the population (89.26% in the controls in this dataset) and p₁ = 1 − p₀ is the probability of having family history in the population (10.74% in the controls in this dataset). f_k is frequency of the SNP profile risk group k (f₁=0.01, (f₂=0.09, (f₃=0.15, (f₄=0.5, (f₅=0.15, (f₆=0.09, (f₇=0.01) and $S_k^h(t)$ is the probability of surviving PrCa by age (t) in the risk group k for samples in the family history group h, which can be derived from incidence rates ${\lambda }_k^h(t)$ for ages <t using the formula $S_k^h(t)=\text{exp}(-\sum _0^t{\lambda }_k^h(t-1))$. Since definition $S_k^h(0)=1$ for all k and h, it was possible to solve the above equation recursively, starting at age t=0, to obtain the baseline incidences and hence the age-specific PrCa incidences at age (t), ${\lambda }_k^h(t)$, for each group. We then computed the absolute risk by age t, adjusting for mortality from other causes, for each risk group, using the formula: $\sum _0^t{S}_k^h(t)\times {\lambda }_k^h(t)\times S_c(t)$

Where $S_c(t)=\exp (-\sum _0^t{\mu }_c(t-1))$ is the probability of not dying from another cause of death by age t, based on the age-specific mortality rates μ_c(t). The age-specific mortality rates, μ_c(t), was estimated by using all causes incidences of death per 100,000 individuals for England and Wales (http://www.ons.gov.uk/ons/index.html) and the PrCa death incidence per 100,000 individuals in UK in year 2012 (14).

Results

All 25 SNPs showed evidence of association with PrCa (P=0.02 to P=1.4×10⁻⁴⁶), with effect sizes that were consistent with previous reports. The largest per-allele OR estimate was 1.56 (95% CI 1.44–1.68) for rs16901979 on 8q24 (Table 2). For each of the 24 autosomal SNPs, the effect size was larger for rare homozygotes than for heterozygotes, and the estimates were consistent with a multiplicative (log-additive) model. There was no evidence for heterogeneity among studies (Table 2).

Table 2.

Summary results of 25 SNPs using PRACTICAL and GWAS Stage 3 datasets in European.

Markera Chr/Nearby Gene	Allelesb Positionc	MAFd	Per allelee OR (95%CI)	Het OR e,f 95%CI)	Hom ORe,g (95%CI)	P-valueh	P-valuei
rs721048 2 / EHBP1	C/T 63131731	0.18	1.11 (1.07–1.16)	1.09 (1.04–1.15)	1.32 (1.17–1.48)	9.8×10−8	0.13
rs1465618 2 / THADA	G/A 43553949	0.2150	1.07 (1.03–1.11)	1.08 (1.03–1.13)	1.14 (1.03–1.26)	1.9×10−4	0.39
rs12621278 2 / ITGA6	A/G 173311553	0.06	.75 (.70–.80)	.76 (.71–82)	.38 (.24–.58)	4.9×10−17	0.57
rs2660753 3 / Unknown	G/A 87110674	0.10	1.12 (1.06–1.18)	1.12 (1.06–1.19)	1.32 (1.09–1.61)	1.2×10−5	0.73
rs17021918 4 / PDLIM5	G/A 95562877	0.35	.88 (.85–.91)	.86 (.83–90)	.80 (.74–.85)	6.7×10−15	0.39
rs12500426 4 / PDLIM5	G/T 95514609	0.46	1.10 (1.06–1.13)	1.11 (1.06–1.18)	1.20 (1.12–1.28)	4.8×10−8	0.54
rs7679673 4 / TET2	C/A 106061534	0.40	.88 (.85–.90)	.87 (.83–.91)	.77 (.72–.82)	1.0×10−16	0.08
rs9364554 6 / SLC22A3	C/T 160833664	0.29	1.10 (1.06–1.14)	1.12 (1.07–1.18)	1.18 (1.09–1.27)	4.8×10−8	0.85
rs10486567 7 / JAZF1	G/A 27976563	0.23	.85 (.82–.89)	.86 (.81–.91)	.72 (.63–.81)	4.5×10−12	0.21
rs6465657 7 / LMTK2	A/G 97816327	0.46	1.10 (1.06–1.13)	1.09 (1.04–1.15)	1.21 (1.13–1.28)	3.4×10−9	0.32
rs1447295 8 / Unknown	G/T 128485038	0.11	1.41 (1.35–1.48)	1.41 (1.34–1.49)	2.01 (1.69–2.41)	1.4×10−46	0.50
rs6983267 8 / Unknown	C/A 128413305	0.49	.82 (.79–85)	.80 (.76–85)	.67 (.63–.72)	2.3×10−35	0.61
rs16901979 8 / Unknown	G/T 128124916	0.03	1.56 (1.44–1.68)	1.55 (1.43–1.69)	2.39 (1.47–3.86)	3.8×10−28	0.29
rs2928679 8 / SLC25A37	C/T 23438975	0.48	1.04 (1.01–1.07)	1.03 (.97–1.09)	1.08 (1.01–1.16)	.02	0.10
rs1512268 8 / NKX3.1	G/A 23526463	0.43	1.13 (1.10–1.17)	1.13 (1.08–1.19)	1.29 (1.21–1.37)	2.6×10−16	0.19
rs4962416 10 / CTBP2	A/G 126696872	0.28	1.04 (1.01–1.08)	1.03 (.98–1.08)	1.11 (1.02–1.21)	.02	0.68
rs10993994 10 / MSMB	G/A 51549496	0.39	1.24 (1.20–1.28)	1.21 (1.15–1.27)	1.56 (1.46–1.66)	7.9×10−41	0.36
rs7931342 11 / Unknown	C/A 68994497	0.50	.84 (.81–86)	.86 (.82–91)	.70 (.65–74)	4.8×10−27	0.86
rs7127900 11 / Unknown	G/A 2233574	0.19	1.23 (1.18–1.28)	1.24 (1.18–1.30)	1.47 (1.32–1.65)	6.3×10−26	0.63
rs4430796 17 / HNF1B	A/G 36098040	0.48	.81 (.79–84)	.81 (.77–85)	.66 (.62–71)	2.7×10−38	0.79
rs11649743 17 / HNF1B	G/A 36074979	0.19	.88 (.85–92)	.88 (.83–92)	.79 (.70–90)	5.6×10−10	0.25
rs1859962 17 / Unknown	T/G 69108753	0.48	1.17 (1.14–1.21)	1.22 (1.15–1.28)	1.38 (1.30–1.47)	3.7×10−24	0.19
rs2735839 19 / KLK2/KLK3	G/A 51364623	0.15	.81 (.77–85)	.82 (.78–86)	.62 (.53–73)	1.1×10−19	0.06
rs5759167 22 / BIL/TTLL1	G/T 43500212	0.50	.84 (.82–87)	.83 (.79–87)	.71 (.67–76)	3.4×10−28	0.87
rs5945619 X / NUDT11	T/C 51241672	0.36	1.13 (1.10–1.16)	-	1.28 (1.22–1.35)	1.9×10−20	0.10

^adbSNP rs number,

^bMajor/minor allele, based on the frequencies in controls in PRACTICAL III data,

^cBuild 37 position,

^dMAF in controls in combined European dataset.

^eOR = odds ratio (minor allele) from a logistic regression using all European samples stratified by studies with no adjustment,

^fOR in heterozygotes, relative to major allele homozygotes,

^gOR in minor allele homozygotes, relative to major allele homozygotes,

^hCochran-Armitage test for trend.

ⁱHeterogeneity P-value among studies

Gleason score was available for 15,107 (74.5%) of the cases used in the analyses; of these, 2,139 had a score of 8+ and 12,968 had a score less than 8. One SNP, rs1447295, on chromosome 8, showed a larger effect size with increasing grade (P=0.001), while four SNPs (rs17021918, rs1512268, rs7127900 and rs2735839) showed a larger effect sizes with decreasing grade (P<0.02; Supplementary Table 3).

Thirteen of the SNPs (rs1465618, rs7679673, rs10486567, rs1447295, rs6983267, rs16901979, rs10993994, rs7931342, rs7127900, rs4430796, rs11649743, rs1859962 and rs5759167) showed a higher per-allele OR for cases with a PrCa family history than those without (P<0.05), while no SNPs showed an effect in the opposite direction consistent with the predictions under a polygenic model (17) (Supplementary Table 3).

Data on serum PSA level were available for 3,922 controls from 6 studies. Six SNPs (rs1447295, rs6983267, rs1512268, rs10993994, rs7127900 and rs2735839) showed association with PSA concentration levels significant at P-value < 0.03. rs1447295 showed an association with PSA in the opposite direction of the PrCa risk association but the rest of five SNPs showed an association with PSA in the same direction of the PrCa risk association (Supplementary Table 4).

Seven SNPs (rs1465618, rs12621278, rs10993994, rs7127900, rs1859962, rs2735839 and rs5945619) showed an evidence for a trend in the per-allele ORs with age; in each case the effect size was larger for cases diagnosed at younger ages (Supplementary Table 5).

The combined effect of all pairs of SNPs was evaluated through a logistic regression model that included each pair of SNPs and an interaction term. The interaction term was significant at P-value <0.05 level for 29 pairs (out of 300 possible pairs) compared with 15 expected by chance, and significant at the P-value <0.01 level for 12 pairs compared with 3 expected by chance. However, no pair was significant at the P-value <0.05 level after a bonferroni correction for the number of tests (nominal significance P-value=1.6×10⁻⁴, Supplementary Table 6).

Under the assumption that these 25 SNPs combined approximately multiplicatively to alter the risk of PrCa, we constructed a PRS for 16,643 cases and 18,343 controls based on the estimated per-allele ORs of 25 SNPs, standardised by the standard deviation in controls. The standardised PRS had a mean=0.651 (range −3.81–5.36; SD=0.98) in cases and mean=0.104 (range −4.05–4.15; SD=1) in controls. The standardised PRS was strongly associated with disease risk (OR per unit PRS =1.74, 95%CI 1.70–1.78). The OR per unit increase of the standardised PRS declined with age from 1.76 (95% CI 1.62–1.92) in cases diagnosed at age less than 55 to 1.48 (95% CI 1.37–1.60) in cases diagnosed at age 70+ (P-value= 2.6×10⁻⁴, Supplementary Table 5).

The OR per unit increase of PRS was larger for men with PrCa family history (1.79 Vs 1.70; P-value= 1.8×10⁻⁴, Supplementary Table 3). We found no evidence of an interaction between PRS and family history (P-value=0.49) or between age at diagnosis and family history (P-value=0.11) but there was some evidence for an interaction between PRS and age at diagnosis (P-value=0.003).

There was no evidence of a difference in the OR per unit PRS according to Gleason Score (OR=1.75, GS<8 Vs OR=1.65, GS 8+) after adjusting for age at diagnosis and family history (P=0.37; Supplementary Table 3). The correlation between PSA and the PRS was weak, both in controls (correlation=0.09) and in cases (correlation =0.02).

When PRS was categorised by percentile, the top 1% of the population had an estimated OR of 30.6 (16.4–57.3) compared with the bottom 1% of the population, and an OR of 4.2 (95%CI 3.2–5.5) compared with the median population risk (defined as the 25–75% risk group). The bottom 1% of the population had an estimated OR of 0.14 (95% CI 0.08–0.24) compared with the median risk (Table 3). After allowing for an interaction between PRS and age, the OR for the top 1% of the population, relative to the median risk group, decreased from 5.6, for men below age <55 years, to 3.8 for men aged 70+ years (Supplementary Table 7 & 8).There was no difference between fit of the model with a continuous covariate for PRS and the model with separate parameters for percentiles of the PRS (P=0.24). In particular, the predicted ORs for the top 1% and the bottom 1% of the population, based on a log-linear model, did not differ from that observed.

Table 3.

Odds ratios for PrCa by percentile of the PRS and family history.

Percentiles		ORa,b	ORa,c
PRS Group	< 1%	1 (baseline)	0.14 (0.08–0.24)
	1–10%	2.98 (1.66–5.35)	0.41 (0.36–0.47)
	10–25%	4.59 (2.58–8.17)	0.63 (0.57–0.70)
	25–75%	7.23 (4.08–12.80)	1 (baseline)
	75–90%	12.13 (6.83–21.54)	1.68 (1.54–1.83)
	90–99%	16.70 (9.38–29.72)	2.31 (2.09–2.56)
	>= 99%	30.63 (16.36–57.34)	4.24 (3.24–5.53)
Family History		2.52 (2.29–2.78)	2.52 (2.29–2.78)

^aORsobtained by fitting PRS group, family history and age at diagnosis jointly.

^bORs compared to men in the 1st percentile as baseline.

^cORs compared to men in the 25^th–75^th percentile as baseline.

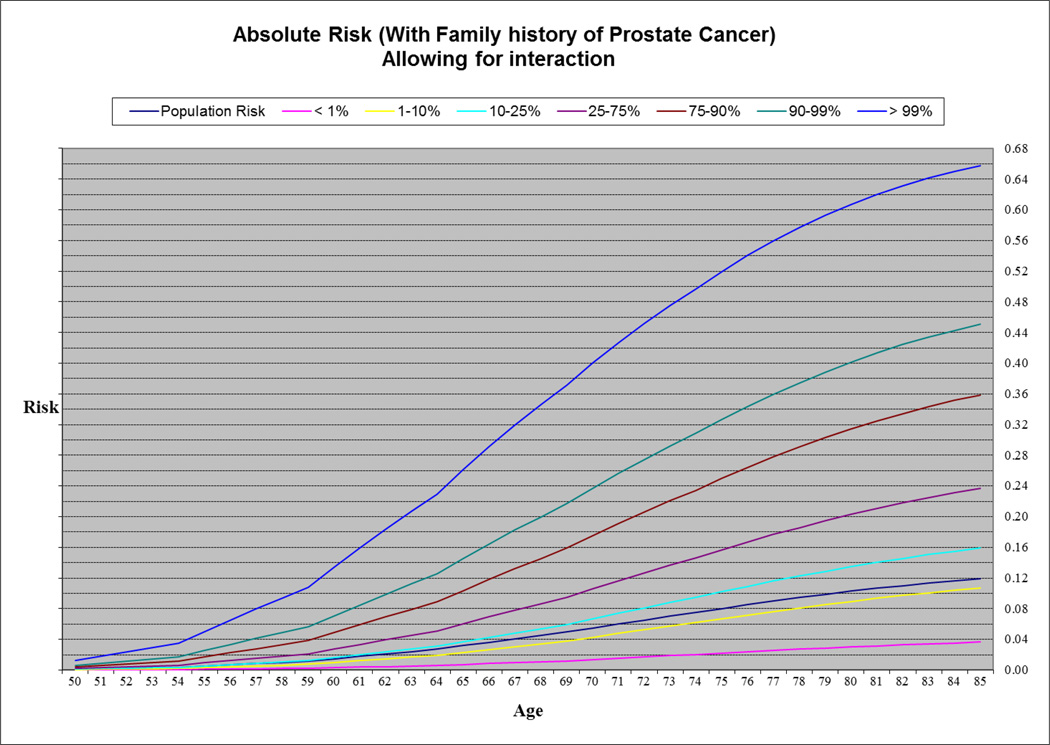
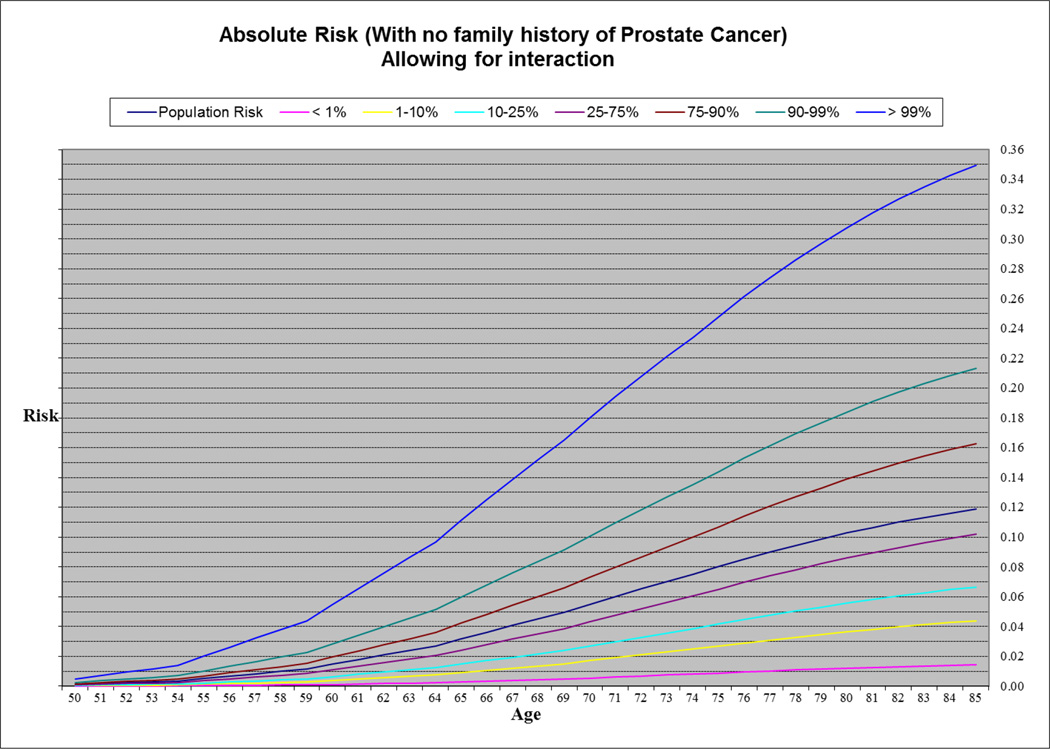
To estimate the absolute risk of PrCa for different risk groups defined by the combined genotypes at the 25 PrCa susceptibility loci, we fitted a logistic regression model that It included parameters for PRS (in 7 categories) together with family history of PrCa once with (Supplementary Table 7) and once without a PRS × age at diagnosis interaction term (Table 3). We used both models (adjusted for age at diagnosis and family history) in order to estimate effect sizes for PRS. Then we used the UK age-specific incidences of PrCa (0 to 85+ years) (14) to estimate age-specific absolute risks of PrCa in the general population after considering competing causes of death for fourteen risk groups defined by PRS and family history (seven PRS risk groups and two family history, see methods). Based on this analysis, the absolute risk of PrCa by age 85 for a man in the top 1% of the risk distribution with family history of PrCa was 65.8% (67.1% in a model not allowing for interaction) and for a man in the lowest 1% was 3.65% (3.67% in a model not allowing for interaction). The absolute risk for a man in the top 1% of the risk distribution with no family history of PrCa was 35.0% (36.1% in a model not allowing for interaction) and 1.46% (1.47% in a model not allowing for interaction) for someone in the lowest 1%. By comparison, the estimated absolute risk for a man in the 25–75% category was 10.2% in the absence of a family history of PrCa, and 23.7% for a man with family history (Figure 1 & 2, Supplementary Figure 1 & 2).

Figure 1.

Absolute risk of PrCa by age in men with family history.

Figure 2.

Absolute risk of PrCa by age in men with no family history.

Discussion

These results demonstrate that risk profiling based on SNPs can identify men at substantially increased or reduced risk of PrCa. We derived a PRS based on a sum of SNP genotypes, weighted by their per-allele log ORs. The estimated ORs for the highest and lowest 1% of the population (4.2 and 0.14, respectively) were consistent with those predicted under a simple polygenic model in which the log OR increases linearly with the PRS. We also showed that the effect size, measured by OR per unit PRS, was higher at younger ages. As expected, the majority of loci, and the PRS, showed a stronger effect for familial cases. In a logistic regression model, both PRS and family history were independently associated with PrCa risk. The OR due to family history was attenuated after adjustment for the PRS (from 2.63 to 2.50), as expected given that family history is, at least in part, a reflection of genetic susceptibility. However, the degree of attenuation (5% on a log-scale) was markedly less than 18%, the estimated contribution of these 25 loci to the familial risk of PrCa estimated based on their ORs and allele frequencies in this study (see methods). The reason for this difference is unclear but might reflect interactions between the known susceptibility loci summarised in the PRS and other factors influencing family history.

In order to investigate the added value of PRS, once we estimated the absolute risk for individuals with family history without fitting their PRS information and then repeated the same procedure after adding their PRS information. The absolute risk of PrCa for a man at age 85 with family history was estimated to be 26.5% when PRS information was ignored. When we incorporated PRS information, a man at age 85,depend on his PRS risk group, could have an absolute risk ranging from 3.67% (if a man is in the bottom 1% of the risk distribution) to 67.1% (if a man is in the top 1% of the risk distribution, Supplementary Figure 1 and 3). These observations indicate that family history and the PRS independently influence risk and can be combined to provide stronger discrimination.

Chatterjee et al. derived theoretical estimates for the predictive performance of polygenic models for ten complex traits or common diseases, including PrCa, using published estimates for individual SNPs (18). They estimated that ~7% of the population will be at two-fold risk or greater for PrCa. We estimated, empirically, that the (average) risk to men in the 90–99% category of the PRS was 2.41 fold, relative to the population median, or approximately 2 fold relative to the population mean. However, this is an average risk over the 90–99% category, so that the percentile of the PRS at which the risk exceeds 2 fold will be >90%. Based on the estimated log(OR) per standardised PRS, approximately 6% of men will have a risk of greater than twofold, very close to the estimate of Chatterjee et al (18).

These results show that genetic risk profiling using SNPs could be useful in defining men at high risk for the disease for targeted prevention and screening programs. The benefits of screening, relative to the costs, will be most favourable among men at higher risk. If, for example, the benefit-cost ratio is favourable for screening men at a greater than two-fold risk, the PRS provides an effective method for identifying such men.

While these analyses demonstrate the value of SNPs for risk prediction, a risk model could be improved in various ways. The analyses presented here are based on the 25 loci first identified to be associated with PrCa. Recently, however, additional loci have been identified (13, 19) and more than 100 common susceptibility loci are now known. In total, these loci increase the estimated proportion of the familial risk to 33% (19). Incorporating all known loci into a PRS should improve the predictive value of risk profiles.

Additionally, the analyses presented here consider family history as a binary (yes/no) covariate. It is known that the risk of PrCa is dependent on both the number of affected relatives and their ages. MacInnis et al. (12, 20) have shown using segregation analysis that the familial aggregation of PrCa can be modelled as the combined effect of a recessive allele and a polygenic component, and that the polygenic component can be further partitioned into a component due to measured SNPs and an unmeasured component. This approach should provide more powerful prediction, particularly in families with multiple cases of the disease. Finally, it is known that serum or urine PSA level is associated with PrCa risk, with the association persisting for several decades. Although some of the risks SNPs are also related to PSA level in the expected direction, the PSA level is only weakly correlated with PRS, indicating that incorporating PSA level and potentially other markers such as MSMB (21) into a risk algorithm should further improve the discrimination (22).

The absence of clear differences in the relative risk associated with SNPs by disease aggressiveness, even in this very large study, is striking. We did not find any convincing evidence for differences in the predictive values of the PRS by disease aggressiveness. The effect size was higher for less aggressive disease, but the difference was still small (1.75 vs. 1.65). This result is in contrast to the clear differences in SNP associations by disease pathology seen in other diseases, for example in breast and ovarian cancer, and indicates that aggressive and non-aggressive disease, at least as measured by Gleason score, share these genetic risk factors as a common aetiology.

Analysis of pairwise combinations of SNPs did not identify any clear examples of departure from a multiplicative model, after adjusting for multiple testing. We did, however, find an excess of interactions at the P<0.01 level over the number that would be expected by chance. This suggests that interactions on this scale likely to exist, but their effect sizes are small and that very large sample sizes, exemplified by this collaborative study, will be required to identify and characterise them. If such interactions could be identified reliably, they may improve the predictive value of the risk profiling, and also provide insights into the biological interactions between the underlying risk variants.