Targeted Estimation of Binary Variable Importance Measures with Interval-Censored Outcomes

Abstract

In most experimental and observational studies, participants are not followed in continuous time. Instead, data is collected about participants only at certain monitoring times. These monitoring times are random and often participant specific. As a result, outcomes are only known up to random time intervals, resulting in interval-censored data. In contrast, when estimating variable importance measures on interval-censored outcomes, practitioners often ignore the presence of interval censoring, and instead treat the data as continuous or right-censored, applying ad hoc approaches to mask the true interval censoring. In this article, we describe targeted minimum loss–based estimation (TMLE) methods tailored for estimation of binary variable importance measures with interval-censored outcomes. We demonstrate the performance of the interval-censored TMLE procedure through simulation studies and apply the method to analyze the effects of a variety of variables on spontaneous hepatitis C virus clearance among injecton drug users, using data from the “International Collaboration of Incident HIV and HCV in Injecting Cohorts” project.

1 Introduction

Determining the effect importance of a large collection of biomarkers on an outcome is a frequent goal in applications involving epidemiology. For example, epidemiologists often wish to determine the effects of a variety of behavioral and biological factors on health outcomes. In practice, epidemiological data is not collected in continuous time. Rather, information on study outcomes is typically limited to observation intervals, resulting in interval-censored outcomes.

Practitioners often ignore interval censoring when conducting their analysis. One common approach involves using a misspecified parametric model and forward imputing the outcome to the final time of interest. For example, in analyzing factors associated with the interval-censored outcome of spontaneous hepatitis C virus clearance within 2 years of incident infection, Grebely et al. [1] used a logistic regression approach. Their analysis both assumed a logistic relationship between variables and outcome and ignored interval censoring of clearance by forward imputing the clearance outcome to the 2-year endpoint.

Pooled logistic regression model is also a common approach. Pooled logistic regression applies logistic regression to an expanded dataset, obtained by creating new observations for participants at each time they are monitored. This method also assumes a logistic relationship between time-dependent covariates and outcome, as well as assuming the relationship stays the same over time.

Another approach ignoring interval censoring involves obtaining estimates using targeted learning methodology, but forward imputing the outcome to the final time of interest. This approach is more principled in the sense that the estimates obtained would be valid in the absence of interval censoring, but nonetheless fails to account for interval censoring. For example, Bembom et al. [2] estimated the effects of a variety of biomarkers on viral load outcome under HIV treatment change using targeted minimum loss–based estimation (TMLE) of variable importance measures, but ignored interval censoring of the viral load outcome and instead effectively used forward imputation.

To account for interval censoring, nonparametric maximum likelihood estimators (NPMLE) for the marginal distribution of an interval-censored event time have been studied for various types of interval-censored data. For example, Groeneboom and Wellner [3] study the NPMLE for “case 1” data, and Geskus and Groeneboom [4] study the NPMLE for “case 2” data. “Case 1”, or current status, data is obtained when participants are only observed once, at a fixed monitoring time. At this monitoring time, we observe an indicator of whether or not the event has occurred. “Case 2” data involves monitoring participants at least twice, observing an indicator of whether or not the event has occurred at each monitoring time and obtaining the final data by using the two monitoring times bounding the interval of outcome occurrence. However, these NPMLE approaches only estimate the marginal event time distribution and thus do not provide estimates of covariate effects on the outcome event.

Semiparametric regression models for interval-censored data have been proposed to analyze the effects of various covariates on the outcome event. Proportional hazards models have been studied by, for example, Cai and Betensky [5], Huang and Wellner [6], and Finkelstein [7]. Proportional odds models have been studied by, for example, Rabinowitz et al. [8], Rossini and Tsiatis [9], and Huang and Wellner [6]. Accelerated failure time models have been studied by, for example, Tian and Cai [10], Huang and Wellner [6], and Rabinowitz et al. [11]. In these models, effect estimates are given by the estimated regression coefficient, and hence still suffer from model misspecification.

In this article, we propose making less restrictive modeling assumptions and clearly defining the target parameter of interest when analyzing the effects of a variety of variables on an interval-censored outcome. In particular, we define variable importance measures (VIM) as functions of the true data-generating distribution, instead of as coefficients in possibly misspecified models. We use a nonparametric statistical model, which makes no statistical assumptions about the form of the underlying true data-generating distribution, and only make non-testable assumptions about the causal model generating the data.

We develop TMLE methods to estimate VIM in the presence of interval-censored outcomes. Our interval-censored TMLE procedure (IC-TMLE) provides consistent estimates, valid inference, and a variety of other desirable properties under regularity conditions. We show that ignoring interval censoring leads to incorrect VIM estimates and inference and demonstrate the superior performance of IC-TMLE. We apply IC-TMLE to estimate VIM of spontaneous hepatitis C virus (HCV) clearance among injection drug users, using data from the “International Collaboration of Incident HIV and HCV in Injecting Cohorts” (InC3) project.

The remainder of our article is organized as follows. We formalize the observed data structure in Section 2. The target VIM parameter, including two formulation possibilities, is presented in Section 3. We discuss estimation of VIM and the IC-TMLE algorithm in Section 4. Simulation study results appear in Section 5. We use IC-TMLE to analyze data from the InC3 project in Section 6. Finally, we conclude in Section 7.

2 Data structure

2.1 Observed data

We consider the following observed data structure. Observations, consisting of time-varying covariates L(t) and time-to-event outcome process Y(t), are collected from each participant i = 1, …, n at different discrete monitoring times t. The outcome process Y(t) indicates whether the event has been observed by time t. Monitoring process Δ(t) indicates whether monitoring occurs at time t. Each participant is observed at time t = 0: we measure baseline covariates W = L(0), and assign or observe binary “treatment” A for which we want to estimate a VIM. Note that the definitions of A and W depend upon the VIM being analyzed. Since our outcome of interest is a time-to-event, we assume the event has not yet occurred at baseline, and the outcome process Y(t) only jumps once.

Although, for simplicity, this article only discusses the case of a single treatment at time 0, the approach described in this article can be easily extended to treatments at multiple time points. Note that A does not need to be an actual treatment: it may be a behavioral or biological marker observed at baseline. We label subsequent monitoring times as t = 1, 2, …, τ, where τ is the monitoring time at which we aim to measure the final outcome. The monitoring time τ is often specified after data has been collected and is often an earlier monitoring time than the final monitoring time available. Note that the t numerical labels can be determined by bucketing the true monitoring times into τ intervals or by simply numbering the visits. Since not every participant is observed at every monitoring time, we encode the measurements at every monitoring time t as the tuple (Δ(t), Δ(t)L(t), Δ(t)Y(t)) = (Δ(t), L^*(t), Y^*(t)), so that the covariates and outcome process are defined at every t. If we do observe data at time t, the true L(t) and Y(t) values are used, since Δ(t) = 1. Otherwise, monitoring does not occur at time t, so Δ(t) = 0, and we use degenerate values for L(t) and Y(t). This observed data structure can be represented, ordered in the assumed collection order, as the random variable $O=(W,A,{\{\mathrm{\Delta }(t),L^{\ast }(t),Y^{\ast }(t)\}}_{t=1}^{\tau })$.

Since our interest is in observing the value of Y(τ), the missing indicator of primary interest is Δ(τ). We view the intermediate Δ(t) indicators and associated measurements as simply intermediate data, rather than missing indicators to intervene upon. To clarify this distinction, we use the notation $L^{\prime }={\{\mathrm{\Delta }(t),L^{\ast }(t),Y^{\ast }(t)\}}_{t=1}^{\tau -1}$ as a single variable indicating all intermediate data, Y = Y^*(τ) as the final outcome of interest, and Δ = Δ(τ) as the indicator of monitoring at that final time. Using this notation, we represent the observed data structure as O = (W, A, L′, Δ, Y).

2.2 Statistical and causal model

We assume the following nonparametric structural causal model (NPSCM), as in Pearl [12], which encodes the non-testable causal assumptions about the time ordering of the observed data.

$$\begin{array}{cc}W=& f_W(U_W)\\ A=& f_A(W,U_A)\\ L^{\prime }=& f_{L^{\prime }}(W,A,U_{L^{\prime }})\\ \mathrm{\Delta }=& f_{\mathrm{\Delta }}(W,A,L^{\prime },U_{\mathrm{\Delta }})\\ Y=& f_Y(W,A,L^{\prime },\mathrm{\Delta },U_Y)\end{array}\}$$ (1)

In eq. (1), U = (U_W, U_A, U_L′, U_Δ, U_Y) are unobserved exogenous random variables, while the functions f are deterministic and not restricted to any functional form. Each endogenous variable W, A, L′, Δ, Y is only a function of its parents (variables preceding it in the assumed time ordering), and its corresponding U random variable, which captures additional randomness in each endogenous variable not accounted for by the parents alone.

Our statistical model is indexed by the functions f and the random variable U. We put no restrictions on their statistical distributions. We will make randomization assumptions in the next section, which are non-testable causal assumptions. However, our statistical model remains semiparametric because we make no distributional form assumptions. Hence, the observed data O is a random variable with data-generating distribution P, which is an element of semiparametric statistical model 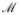, i.e., O ~ P ∈ .

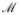3 Target parameter

3.1 Formulation possibilities

In this section, we consider two possible formulations of the target VIM parameter. To clarify our exposition, we focus on the risk difference parameter as our example.

3.1.1 Static intervention formulation

The first possible target parameter formulation is given by:

$$\begin{array}{l}{\psi }_{\text{static}}^F=E[Y^{A=1,\mathrm{\Delta }=1}-Y^{A=0,\mathrm{\Delta }=1}]\\ =E[Y^{1,1}]-E[Y^{0,1}]\end{array}$$ (2)

The following static intervention on the NPSCM yields the counterfactual outcome Y^a,1:

$$d_{(a,1)}:\{\begin{array}{c}A=a\\ \mathrm{\Delta }=1\end{array}$$ (3)

The above intervention is straightforward to understand: we set the treatment at baseline to the desired value and ensure that monitoring occurs at the final time τ, so that we can check whether the event of interest has occurred. Using the NPSCM, counterfactual data following the intervention (3) can be generated as follows. First, draw U. Then, generate W = f_W(U_W). Next, generate L′^,a = f_L′ (W, a, U_L′). Finally, generate Y^a,1 = f_Y (W, a, L′, 1).

3.1.2 Stochastic intervention formulation

To reflect the fact that our parameter of interest is whether the event of interest has occurred by time τ, and hence does not necessarily depend on being monitored at exactly time τ, we introduce the following redefinition of the data. At time t = 0, define Y^#(0) = Y^*(0), Δ^#(0) = Δ(0), and L^#(0) = L^*(0). At times t > 0:

$$\begin{array}{l}{Y}^{\#}(t)=Y^{\#}(t-1)\text{if}I(Y^{\#}(t-1)=1)\\ {\mathrm{\Delta }}^{\#}(t)={\mathrm{\Delta }}^{\#}(t-1)\text{if}I(Y^{\#}(t-1)=1)\\ L^{\#}(t)=L^{\#}(t-1)\text{if}I(Y^{\#}(t-1)=1)\end{array}$$ (4)

The above redefinition sets all values of the data deterministically after observing that the event of interest has occurred. Note that Y^#(t) = 1 implies that Δ^#(t) = 1. Also, note that Y^#(t) and Δ^#(t) will equal Y^*(t) and Δ(t), unless Δ(t) = 0 and Y^*(t) = 0, respectively. This is due to the fact that the data redefinition only changes the values of Y^*(t) and Δ(t) if they are not already equal to one. Using these observations, we can express the data redefinition (4) equivalently as:

$$\begin{array}{cc}{Y}^{\#}(t)=& Y^{\ast }(t)+(1-Y^{\ast }(t))Y^{\#}(t-1)\\ {\mathrm{\Delta }}^{\#}(t)=& \mathrm{\Delta }(t)+(1-\mathrm{\Delta }(t)){\mathrm{\Delta }}^{\#}(t-1)Y^{\#}(t-1)\\ L^{\#}(t)=& L^{\#}(t-1)Y^{\#}(t-1)+L^{\ast }(t)(1-Y^{\#}(t-1))\end{array}$$ (5)

Using redefinition (5), our observed data structure is now O^# = (W, A, L′^#, Δ^#, Y^#), where Δ^# = Δ^#(τ) and Y^# = Y^#(τ).

With this redefinition in hand, we now define a second possible target parameter:

$$\begin{array}{l}{\psi }_{\text{stochastic}}^F=E[Y^{\#,A=1,\mathrm{\Delta }=\delta }-Y^{\#,A=0,\mathrm{\Delta }=\delta }]\\ =E[Y^{\#,1,\delta }]-E[Y^{\#,0,\delta }]\end{array}$$ (6)

The following stochastic intervention on the NPSCM (involving a static intervention on baseline treatment A, and stochastic intervention on the monitoring mechanism Δ^#) yields the counterfactual outcome Y^#,a,δ:

$$d_{(a,\delta )}:\{\begin{array}{c}A=a\\ {\mathrm{\Delta }}^{\#}=\delta =\{\begin{array}{ccc}1& \text{if}& Y^{\#}(\tau -1)=0\\ {\mathrm{\Delta }}^{\#}(\tau -1)& \text{if}& Y^{\#}(\tau -1)=1\end{array}\end{array}$$ (7)

The stochastic intervention on the monitoring process Δ^# ensures that we enforce monitoring at time τ if we have not yet observed the event of interest and do not intervene on the monitoring process if the event of interest has already been observed (in that case, Δ^# = Δ^#(τ − 1) already, by the redefinition of the data).

As in the static intervention case, we can use the NPSCM to generate counterfactual data following the intervention (7). We begin by drawing U. Then, we generate W = f_W(U_W). Next, we generate L′ = f_L′ (W, a, U_L′). Finally, we compute the value δ from L′ and generate Y = f_Y (W, a, L′, δ).

3.1.3 Equivalence of proposed intervention formulations

While the stochastic intervention formulation might seem more desirable, since it does not require intervention when the event of interest is already known to have occurred, both formulations result in the same statistical parameter. For a proof, see Section “Proof of equivalence of intervention formulations” in the Appendix. In the remainder of this article, we use the simpler static intervention representation of the parameter. Hence, we our target VIM parameter is:

$$\begin{array}{l}\psi =E_W[E_{L^{\prime }}[E[Y\mid W,A=1,L^{\prime },\mathrm{\Delta }=1]]]-E_W[E_{L^{\prime }}[E[Y\mid W,A=0,L^{\prime },\mathrm{\Delta }=1]]]\\ ={\psi }_1-{\psi }_0\end{array}$$ (8)

In principle, the two formulations possibilities would require two sets of identifiability assumptions, as discussed in Sections “Identifiability of static intervention parameter” and “Identifiability of stochastic intervention parameter” in the Appendix. However, we show in Section “Proof of equivalence of intervention formulations” in the Appendix that the identifiability assumptions are equivalent.

The causal assumptions needed for eq. (8) to be identifiable from the distribution of the observed data are consistency, randomization, and positivity. The consistency assumption requires that intervening on treatment to set A = a and intervening on monitoring to set Δ = 1 in the NPSCM yields the observed outcome Y if the observed treatment and monitoring values equal a and 1, respectively. The randomization assumption requires that, given the observed past, treatment and monitoring are independent of counter-factual outcomes. The positivity assumption requires that, given the observed past, the conditional probability of treatment A = a, and monitoring Δ = 1, are positive.

Note that even in the case that the causal assumptions fail to hold, the parameter (8) still remains an interesting variable importance measure of the effect of A on the outcome Y. In that case, eq. (8) represents the effect of A on Y, controlling for the measured confounders W, and ensuring that monitoring occurs at the final time of interest.

3.2 Representation as function of iterated conditional means

Observe that the VIM ψ is a function of the density P(O), since, if P(O) were known, we could calculate (8) exactly: first compute conditional distributions from the full joint distribution, then perform integrations.

Although ψ depends on P, we do not need to know all of P in order to calculate ψ. This can be seen by factorizing P(O) as follows:

$$\begin{array}{l}P(O)=P_W(W)P_A(A\mid W)P_{L^{\prime }}(L^{\prime }\mid A,W)P_{\mathrm{\Delta }}(\mathrm{\Delta }\mid W,A,L^{\prime })P_Y(Y\mid W,A,L^{\prime },\mathrm{\Delta })\\ =Q_W{g}_A{Q}_{L^{\prime }}{g}_{\mathrm{\Delta }}{Q}_Y\end{array}$$ (9)

Now, observe that our VIM parameter (8) only depends on the distribution P through its Q factors in eq. (9), and hence may be represented as ψ(Q). Furthermore, observe that ψ(Q) may be represented as an iterative conditional expectation: first conditioning on {L′,W}, then on only {W}. This can be seen as follows. We first introduce some additional notation:

$$\begin{array}{cc}{\overline{Q}}_Y^{a,1}=& E[Y\mid W,A=a,L^{\prime },\mathrm{\Delta }=1]\\ {\overline{Q}}_{L^{\prime }}^{a,1}=& E_{L^{\prime }}[{\overline{Q}}_Y^{a,1}\mid W,A=a]\\ {\overline{Q}}_W^{a,1}=& E_W[{\overline{Q}}_{L^{\prime }}^{a,1}]\end{array}\}$$ (10)

Using the conditional mean notation (10), we can re-express the components of our target parameter as follows:

$$\begin{array}{l}{\psi }_a=E_W[E_{L^{\prime }}[E[Y\mid W,A=a,L^{\prime },\mathrm{\Delta }=1]]]\\ =E_W[E_{L^{\prime }}[{\overline{Q}}_Y^{a,1}]]\\ =E_W[{\overline{Q}}_{L^{\prime }}^{a,1}]\\ ={\overline{Q}}_W^{a,1}\end{array}$$ (11)

4 Estimation

4.1 TMLE overview

TMLE is a general framework for constructing estimators of a statistical parameter ψ under a semiparametric model. The procedure consists of two steps. The first step involves obtaining an initial estimate Q̂ of the portion Q of the data-generating distribution P that is needed to calculate ψ. The second step obtains an update Q̂^* of Q̂ through a fluctuation that is targeted toward optimizing the bias-variance trade-off for ψ. Finally, the TMLE estimate of ψ is given by the substitution (plug-in) estimate ψ̂ = ψ(Q̂^*).

We recommend using Super Learning to obtain the initial estimate of Q. Super Learning is a machine learning algorithm which involves proposing a library of candidates estimators, and using cross-validation to data-adaptively select the weighted combination of the candidates that minimizes the cross-validated risk. Through this process, Super Learning does not make any parametric assumptions about the form of density estimated. We refer to van der Laan et al. [13] and van der Laan and Rose [14] for additional discussion.

Since Super Learning (and any other density estimation procedure) is tailored for the estimation of Q, its bias-variance trade-off is not optimal for ψ. This explains the need for the updating step in TMLE. In the updating step, we use the initial estimate as a fixed offset and fluctuate it by performing parametric regression with a so-called clever covariate, implied by the efficient influence curve, that is constructed for optimal bias-variance trade-off with respect to ψ. For additional details, we refer the reader to van der Laan and Rubin [15] and van der Laan and Rose [14].

Under regularity conditions, the resulting TMLE estimator ψ̂ has the property that

$$\widehat{\psi }-{\psi }_0\approx \frac{1}{n}\sum _{i=1}^n{D}^{\ast }(O_i)$$ (12)

where ψ₀ is the true parameter value, and D^* is the efficient influence curve. Satisfying (12) results in many desirable properties. In particular, such an estimator is asymptotically linear, consistent, and efficient. Asymptotic linearity refers to the empirical mean representation, which allows us to make use of the Central Limit Theorem and obtain valid inference. Consistency means our estimate is asymptotically unbiasedness, in the sense that ψ̂ approaches the true value ψ₀ as sample size increases. Efficiency means that ψ̂ has the minimum asymptotic variance (implied by the efficient influence curve) among all asymptotically linear unbiased estimators. Furthermore, a TMLE estimator is well-defined, in the sense that it does not suffer from multiple solutions. It is a substitution estimator and thus respects global constrains. For example, if ψ is a probability, the TMLE procedure will result in an estimate between 0 and 1. The TMLE procedure is also double robust, meaning that ψ is consistent as long as either Q or g is estimated consistently, and has good performance for finite samples. Finally, estimated confidence intervals for TMLE are conservative as long as g is estimated consistently, even if Q is not estimated consistently. For a additional details, we refer the reader to van der Laan and Rubin [15] and van der Laan and Rose [14].

4.2 Efficient influence curve

In order to proceed with the TMLE procedure, we need to determine the efficient influence curve (also known as the canonical gradient) of ψ, which will allow us to construct the clever covariate needed for the updating step of TMLE, as described in Section 4.1.

As shown in Section 3.2, our VIM parameter of interest, ψ, only depends on P through Q. As a result, we may derive the canonical gradient for ψ by first finding any gradient D in a model in which g is known, and then projecting that gradient into the tangent space of Q to obtain the canonical gradient.

Furthermore, from Section 3.2, ψ may be represented as an iterative conditional expectation. As a result, van der Laan and Gruber [16] show that the efficient influence curve for ψ is: $D^{\ast }=D_Y^{\ast }+D_{L^{\prime }}^{\ast }+D_W^{\ast }$. We use the notation $D_Z^{\ast }=\mathrm{\Pi }(D\mid T_Z)$ to represent the projection of D onto the tangent space T_Z of Q_Z, for an arbitrary random variable Z. The D^* components are given by:

$$\begin{array}{cc}{D}_Y^{\ast }=& \frac{I(A=a,\mathrm{\Delta }=1)}{g_A(a\mid W)g_{\mathrm{\Delta }}(1\mid W,a,L^{\prime })}(Y-{\overline{Q}}_Y^{a,1})\\ D_{L^{\prime }}^{\ast }=& \frac{I(A=a)}{g_A(a\mid W)}({\overline{Q}}_Y^{a,1}-{\overline{Q}}_{L^{\prime }}^{a,1})\\ D_W^{\ast }=& {\overline{Q}}_{L^{\prime }}^{a,1}-\psi ({\overline{Q}}_W^{a,1})\end{array}\}$$ (13)

4.3 Interval-censored TMLE of variable importance measures

Following the general interval-censored TMLE development of Carone et al. [17] and the TMLE of an intervention-specific mean outcome described in van der Laan and Gruber [16], we estimate variable importance measures in the presence of interval-censored outcomes using the following IC-TMLE algorithm. Note that, although the parametric fluctuation could take different forms, the logistic regression model used below ensures that the fluctuations respect the characteristics of the observed data. For further discussion, see Gruber and van der Laan [18].

We begin by obtaining an initial estimate ${\overline{Q}}_{Y,n}^{a,1}$ of the first conditional mean outcome ${\overline{Q}}_Y^{a,1}=E[Y\mid W,A=a,L^{\prime },\mathrm{\Delta }=1]$ by regressing Y onto {W, A = a, L′, Δ = 1}. This initial estimate can be obtained using, for example, parametric logistic regression or data-adaptive Super Learning. Second, we fluctuate this initial estimate to obtain an updated estimate ${\overline{Q}}_{Y,n}^{a,1,\ast }$. To do the update, we use the initial estimate as a fixed offset and perform a univariate regression of Y onto the clever covariate $\frac{I(A=a,\mathrm{\Delta }=1)}{g_A{g}_{\mathrm{\Delta }}}$.

Next, we obtain an initial estimate ${\overline{Q}}_{L^{\prime },n}^{a,1}$ of the second conditional mean outcome ${\overline{Q}}_{L^{\prime }}^{a,1}=E[{\overline{Q}}_Y^{a,1}\mid W,A=a]$ by regressing the TMLE ${\overline{Q}}_{Y,n}^{a,1,\ast }$ from the previous step onto {W, A = a}. As before, this initial estimate is then fluctuated to obtain an updated estimate ${\overline{Q}}_{L^{\prime },n}^{a,1,\ast }$. The update is obtained by using the initial estimate as a fixed offset in a univariate regression of the TMLE ${\overline{Q}}_{Y,n}^{a,1,\ast }$ onto the clever covariate $\frac{I(A=a)}{g_A}$.

Finally, we estimate ${\overline{Q}}_W^{a,1}=E[{\overline{Q}}_{L^{\prime }}^{a,1}]$ as the empirical mean of the TMLE from the previous step: ${\overline{Q}}_{W,n}^{a,1,\ast }=\frac{1}{n}{\sum }_{i=1}^n{\overline{Q}}_{L^{\prime },n}^{a,1,\ast }(W_i)$. This same estimate also gives the TMLE of ψ, since $\psi ({\overline{Q}}^{a,1})={\overline{Q}}_W^{a,1}$. Hence, the TMLE of ψ is ${\psi }^{\ast }=\frac{1}{n}{\sum }_{i=1}^n{\overline{Q}}_{L^{\prime },n}^{a,1,\ast }(W_i)$.

The IC-TMLE algorithm is summarized as follows:

1. Obtain initial estimators g_A,n(a|w) of g_A(a|w) and g_Δ,n(1|w, a, l′) of g_Δ(1|w, a, l′) using Super Learning.

2. Obtain initial estimator ${\overline{Q}}_{Y,n}^{a,1}$ of ${\overline{Q}}_Y^{a,1}$ by using Super Learning to perform logistic regression of Y onto W and L′ among the observations with A = a and Δ = 1.

3. Fit a parametric logistic regression, among observations with A = a and Δ = 1, of Y onto clever covariate $\frac{I(A=a)I(\mathrm{\Delta }=1)}{g_{A,n}(a)g_{\mathrm{\Delta },n}(1)}$, offset by the fitted values from ${\overline{Q}}_{Y,n}^{a,1}$ (making sure to set these fitted values equal to 1 for any observations with Y_t = 1 for some Y_t ∈ L′). Obtain ${\overline{Q}}_{Y,n}^{a,1,\ast }$.

4. Obtain initial estimator ${\overline{Q}}_{L^{\prime },n}^{a,1}$ of ${\overline{Q}}_{L^{\prime }}^{a,1}$ by using Super Learning to perform logistic regression of ${\overline{Q}}_{Y,n}^{a,1,\ast }$ onto W, among the observations with A = a. Note that we calculate the clever covariate of ${\overline{Q}}_{Y,n}^{a,1,\ast }$ as $\frac{I(A=a)[I(\mathrm{\Delta }=1)=1]}{g_{A,n}(a)g_{\mathrm{\Delta },n}(1)}$, i.e., we calculate the clever covariate setting A = a and Δ = 1 for all observations with A = a. Similarly, we calculate the offset of ${\overline{Q}}_{Y,n}^{a,1,\ast }$ using predictions from ${\overline{Q}}_{Y,n}^{a,1}$ for all observations with A = a. Furthermore, if a built-in method to obtain predictions from a glm object with offset is not available (e.g., R), ${\overline{Q}}_{Y,n}^{a,1,\ast }$ must be calculated manually.

5. Fit a parametric logistic regression, among observations with A = a, of ${\overline{Q}}_{Y,n}^{a,1,\ast }$ (calculated as described in the previous step) onto clever covariate $\frac{I(A=a)}{g_{A,n}(a)}$, offset by the fitted values from ${\overline{Q}}_{L^{\prime },n}^{a,1}$ (note that we do not need to set any of these fitted values equal to 1, since Y₀ = 0 for all observations). Obtain ${\overline{Q}}_{L^{\prime },n}^{a,1,\ast }$.

6. Estimate ${\overline{Q}}_W^{a,1}$ with the empirical mean ${\overline{Q}}_{W,n}^{a,1}=\frac{1}{n}{\sum }_{i=1}^n{\overline{Q}}_{L^{\prime },n}^{a,1,\ast }(W_i)$. This is also the TMLE ${\overline{Q}}_{W,n}^{a,1,\ast }$, as well as the TMLE of $\psi ({\overline{Q}}_n^{a,1,\ast })$, since ${\overline{Q}}_{W,n}^{a,1,\ast }=\psi ({\overline{Q}}_n^{a,1,\ast })$. Note that we calculate ${\overline{Q}}_{L^{\prime },n}^{a,1,\ast }$ among all observations, and the procedure is analogous to the procedure for calculating ${\overline{Q}}_{Y,n}^{a,1,\ast }$ described above. To be explicit, we obtain the offset using the predictions from ${\overline{Q}}_{L^{\prime },n}^{a,1}$ for all observations, set the clever covariate to the case that A = a for all observations, and calculate the predictions from a glm object with offset (manually, if needed).

Note that unlike conventional regression models, we define the parameter of interest nonparametrically, as the mean outcome under an intervention. We thus define our parameter to be a parameter we are interested in estimating. In contrast, a regression coefficient is not the actual parameter of interest, even if the model is correctly specified, and thus lacks a causal interpretation.

Furthermore, we avoid estimating conditional distributions by using the sequential regression representation of our target parameter ψ, presented in Section 3.2. This shows that we do not need to estimate the entire conditional distributions. Instead, we only need to estimate conditional means, for each of the conditional distributions. As a result, IC-TMLE iteratively fits a series of regressions.

5 Simulation studies

In this section, we present simulations comparing our IC-TMLE procedure to several alternative methods: a TMLE ignoring interval censoring by using forward imputation (F-TMLE), a TMLE ignoring interval censoring by using only complete case data (CC-TMLE), a mean outcome within treatment groups using forward imputation (F-Mean), and a mean outcome within treatment groups using only complete case data (CC-Mean). We performed all computations in R and used the tmle package of [26] and SuperLearner package of [27].

In each of our simulated datasets, A ~ Bern(0.5), and hence, mean outcomes within-treatment groups using only complete case data would be unbiased if censoring was uninformative. Also, note that both alternative TMLE procedures estimate well-defined effect measures for the data structure they analyze (forward imputed data, or complete case data), but nonetheless fail to take interval censoring into account.

5.1 Simulated data structure

Our simulated data structure is as follows. We observe a binary treatment A at baseline, two covariates (L_t,1, L_t,2) collected at baseline and over time, and a binary outcome Y_t collected at baseline and over time t. The outcome at baseline is zero for all observations: Y₀ = 0. The covariates and outcome are collected at baseline t = 0, and at each of two subsequent follow-up times t = 1, 2. There is no censoring at baseline, so Δ₀ = 1, but each subsequent follow-up time is subject to censoring. The outcome of interest is the outcome value at the final follow-up time τ = 2.

5.2 Motivating example: inadequacy of parametric models

To motivate our IC-TMLE approach, we begin by presenting a simulation demonstrating the failure of common logistic modeling approaches in the presence of interval-censored data. Logistic regression is an example of a parametric statistical model and hence makes the assumption that the data-generating probability distribution is known up to a finite number of parameters. However, the underlying data-generating distribution is generally always unknown in any experimental or observational study. Additionally, estimated odds ratios obtained via logistic regression are conditional on the remaining covariates in the model being held fixed. As a result, unless the logistic regression model is forced to not include interactions (which is not justifiable), the resulting odds ratios are functions of these remaining covariates, and hence are not well-defined effect measures.

Furthermore, logistic modeling approaches commonly used by practitioners often ignore the interval-censored structure of the data. Instead, ad hoc strategies such as complete case analysis or forward imputation are typically employed in an attempt to mask the interval censoring. While methods for fitting regression models that take interval censoring into account have been proposed (for example, Bacchetti and Quale [19], Goetghebeur and Ryan [20], Sparling et al. [21]), such models still suffer from the problems discussed in the previous paragraph. In this article, we use logistic regression as our motivating example, because this was the method used in the previous analysis [1] of the same InC3 dataset which we analyze in Section 6.

Our simulated data is generated as follows:

$$\begin{array}{ccc}{W}_1& ~& N(0,1)\\ W_2& ~& U(-0.5,0.5)\\ A& ~& \mathit{Bern}(0.5)\\ Y_0& =& 0\\ {\mathrm{\Delta }}_1& ~& \mathit{Bern}(\text{expit}(2-0.2W_1-0.2W_2+0.4W_{1}A+0.4W_{2}A))\\ L_1& =& W_1+N(0.2,1)\\ L_2& =& W_2+U(-1,0.5)\\ Y_1& =& max(Y_0,\mathit{Bern}(\text{expit}(-2-W_1-W_2)))\\ {\mathrm{\Delta }}_2& =& max(\mathit{Bern}(0.3),\mathit{Bern}(\text{expit}(-2+2.5L_1-5.5{AL}_1)))\\ Y_2& =& max(Y_1,\mathit{Bern}(\text{expit}(3L_1)))\end{array}\}$$ (14)

In the simulated data structure (14), the Y_t process is a time-to-event outcome since it begins at zero and only jumps (at most) once to one. In the case of Y₁, this can be seen by observing that Y₀ = 0, and the Bernoulli term is either 0 or 1. For Y₂, the Bernoulli term is again either 0 or 1, and by taking the maximum with Y₁, we ensure that if Y₁ already jumped to one, Y₂ equals one.

Observe that A only affects the monitoring variables Δ₁ and Δ₂. As a result, in truth, A has no effect on the outcome Y₂, since Y₂ is not a function of either Δ₁ or Δ₂. Hence, a successful logistic regression would estimate the coefficient of A to be zero.

We generated a sample of size 1,000 from eq. (14), and fitted two types of logistic regression models to estimate the effect of A on Y₂. In the first, we employ forward imputation to fill in the value of Y₂ if Δ₂ = 0, and regress Y₂ onto A, W₁, W₂. In the second, we use complete case analysis, and regress Y₂ onto A, W₁, W₂, but only among the observations with Δ₂ = 1.

In the forward imputation approach, we obtain a coefficient estimate for A of −0.18, with a p-value of < 0.001, and a 95% confidence interval of (−0.24, −0.12). In the complete case analysis approach, we obtain a coefficient estimate for A of −0.18, with a p-value of < 0.001, and a 95% confidence interval of (−0.26, −0.09). Hence, both logistic regression approaches claim that A has a highly significant effect on Y₂, when in reality no such effect exists.

5.3 Simulation 1: no effect of A on Y

In this simulation, we generated data from eq. (14), as in Section 5.2. As described in the previous section, variable A has no effect on Y. The true values of ψ₁ and ψ₀ are both 0.64, and the true risk difference is ψ = ψ₁ − ψ₀ = 0. We performed 1,000 simulations on each of sample sizes n = 200, 500, 1, 000. Results are presented in Table 1.

Table 1.

Simulation 1 results

		IC-TMLE	F-TMLE	CC-TMLE	F-MEAN	CC-mean
n = 200
	BIAS
	ψ	−0.0670	−0.1661	−0.1475	−0.0001	−0.2216
	ψ1	−0.0402	−0.3337	−0.0705	−0.3338	−0.1090
	ψ0	0.0267	−0.1676	0.0770	−0.3337	0.1127
	MSE
	ψ	0.0160	0.0323	0.0321	0.0321	0.0588
	ψ1	0.0070	0.1136	0.0105	0.1136	0.0176
	ψ0	0.0062	0.0307	0.0109	0.0308	0.0164
	COVER
	ψ	0.856	0.305	0.647	0.309	0.364
n = 500
	BIAS
	ψ	−0.0164	−0.1673	−0.1553	−0.0001	−0.2260
	ψ1	−0.0114	−0.3344	−0.0729	−0.3345	−0.1106
	ψ0	0.0051	−0.1671	0.0823	−0.3344	0.1153
	MSE
	ψ	0.0039	0.0300	0.0279	0.0299	0.0546
	ψ1	0.0018	0.1127	0.0074	0.1128	0.0143
	ψ0	0.0018	0.0289	0.0086	0.0290	0.0148
	COVER
	ψ	0.959	0.029	0.265	0.029	0.038
n = 1, 000
	BIAS
	ψ	0.0055	−0.1688	−0.1549	−0.0001	−0.2272
	ψ1	0.0001	−0.3354	−0.0727	−0.3354	−0.1117
	ψ0	−0.0046	−0.1666	0.0822	−0.3353	0.1157
	MSE
	ψ	0.0018	0.0295	0.0258	0.0295	0.0533
	ψ1	0.0008	0.1129	0.0063	0.1129	0.0134
	ψ0	0.0008	0.0282	0.0076	0.0282	0.0140
	COVER
	ψ	0.979	0.000	0.046	0.000	0.000

Note: The best performing method in each row is in bold.

The IC-TMLE method shows strong performance. It has the lowest bias and MSE for ψ₁ and ψ₀ across all sample sizes. As sample size increases, bias and MSE decrease for all parameters. Coverage rate is high across all sample sizes and improves with sample size.

Each of the other methods exhibits undesirable behavior. Bias for all parameters tends to stay constant with increasing sample size, and coverage rates decrease as sample size increases. Since the true value of ψ is zero, the low coverage rates mean that the competing methods tend to claim a significant effect, when in fact no such effect exists. At sample size 1,000, each competing method has coverage rate under 5%, meaning that each competing method claims a false significant effect over 95% of the time.

Although F-MEAN has low bias for ψ, this is only due to the lucky fact that the large biases in ψ₁ and ψ₀ cancel out in the risk difference. Alternative parameters, e.g., relative risk, would not have bias cancellation. Even though F-MEAN’s bias for ψ is low, coverage for ψ is poor. At sample size 200, F-MEAN has a coverage rate of roughly 31%, and by sample size 1,000, the coverage rate has dropped to 0%.

5.4 Simulation 2: A affects Y

In this simulation, we generated data according to the laws below. Here, the variable A has a positive effect on Y. The true value of ψ₁ is 0.80, the true value of ψ₀ is 0.72, and the true risk difference is ψ = ψ₁ − ψ₀ = 0.08.

$$\begin{array}{ccc}{W}_1& ~& N(0,1)\\ W_2& ~& U(-0.5,0.5)\\ A& ~& \mathit{Bern}(0.5)\\ Y_0& =& 0\\ {\mathrm{\Delta }}_1& ~& \mathit{Bern}(\text{expit}(-3W_{1}A+8W_{2}A+2W_1(1-A)-2(1-A)W_2))\\ L_1& =& W_1+0.1A+N(0.2,1)\\ L_2& =& W_2+0.1A+U(-1,0.5)\\ Y_1& =& max(Y_0,\mathit{Bern}(\text{expit}(W_1-W_2+0.05A)))\\ {\mathrm{\Delta }}_2& =& max(\mathit{Bern}(0.3),\mathit{Bern}(\text{expit}(-2+10L_{1}A-10L_{2}A-15L_1(1-A)+15L_2(1-A)-0.2A)))\\ Y_2& =& max(Y_1,\mathit{Bern}(\text{expit}(-2L_1+2L_2+0.1A)))\end{array}\}$$ (15)

As in the previous simulation, we performed 1,000 simulations from eq. (15) on each of sample sizes n = 200, 500, 1,000. Results appear in Table 2.

Table 2.

Simulation 2 results

		IC-TMLE	F-TMLE	CC-TMLE	F-MEAN	CC-mean
n = 200
	BIAS
	ψ	−0.0309	−0.1561	−0.0883	−0.0795	−0.0836
	ψ1	−0.0190	−0.3824	−0.0624	−0.3822	−0.0605
	ψ0	0.0118	−0.2263	0.0259	−0.3028	0.0231
	MSE
	ψ	0.0105	0.0296	0.0174	0.0298	0.0164
	ψ1	0.0039	0.1488	0.0082	0.1487	0.0079
	ψ0	0.0057	0.0537	0.0056	0.0536	0.0054
	COVER
	ψ	0.924	0.387	0.810	0.396	0.836
	ψ, ∅	0.095	0.001	0.021	0.002	0.023
	ψ̸, ∅	0.012	0.229	0.043	0.217	0.031
n = 500
	BIAS
	ψ	−0.0176	−0.1582	−0.0914	−0.0795	−0.0879
	ψ1	−0.0128	−0.3838	−0.0651	−0.3837	−0.0639
	ψ0	0.0048	−0.2256	0.0263	−0.3042	0.0239
	MSE
	ψ	0.0039	0.0270	0.0119	0.0271	0.0113
	ψ1	0.0014	0.1483	0.0059	0.1482	0.0057
	ψ0	0.0021	0.0518	0.0027	0.0518	0.0025
	COVER
	ψ	0.943	0.047	0.647	0.064	0.687
	ψ, ∅	0.155	0.000	0.017	0.000	0.017
	ψ̸, ∅	0.002	0.439	0.046	0.430	0.044
n = 1, 000
	BIAS
	ψ	−0.0118	−0.1591	−0.0935	−0.0795	−0.0899
	ψ1	−0.0082	−0.3841	−0.0647	−0.3840	−0.0636
	ψ0	0.0036	−0.2249	0.0288	−0.3045	0.0263
	MSE
	ψ	0.0017	0.0262	0.0105	0.0262	0.0098
	ψ1	0.0006	0.1480	0.0050	0.1479	0.0049
	ψ0	0.0010	0.0511	0.0018	0.0511	0.0017
	COVER
	ψ	0.961	0.000	0.396	0.000	0.431
	ψ, ∅	0.303	0.000	0.008	0.000	0.013
	ψ̸, ∅	0.000	0.723	0.047	0.718	0.039

Notes: The rows ψ, ∅ and ψ̸, ∅ indicate the fraction of 95% confidence intervals for ψ claiming a significant result with the correct (positive) sign and incorrect (negative) sign, respectively. The best performing method in each row is in bold.

IC-TMLE has the lowest bias and highest coverage across all sample sizes. Bias and MSE decrease as sample increases, coverage and correctly signed confidence interval rates increase with sample size, and incorrectly signed confidence interval rate decreases as sample size increases.

Other methods show relatively constant bias with increasing sample size, lower coverage rate and fewer correctly signed confidence intervals with increasing sample size, and more incorrectly signed confidence intervals as sample size increases. A bias comparison for ψ₁ is particularly informative: across all sample sizes, each of the competing methods retains high bias, while IC-TMLE starts out with the lowest bias and also steadily reduces bias at each increase in sample size. The competing methods are also particularly poor in terms of coverage: coverage rates are low, incorrect significant effects are often claimed, and correct significant effects are rarely found.

6 Data analysis

6.1 InC3 data

The “International Collaboration of Incident HIV and HCV in Injecting Cohorts” (InC3) is a merged international multi-cohort project of pooled observational longitudinal data, both biological and behavioral, from 9 prospective cohorts of injection drug users (IDU). Hepatitis C virus (HCV) is a particularly common infection among injection drug users, and spontaneous viral clearance of HCV is often observed. However, the determinants of spontaneous viral clearance of HCV infection among injection drug users have not been extensively studied. Understanding the factors that play a role in driving HCV clearance is of significant interest, as doing so would aid in the identification of risk factors for chronic infection, as well as suggest possible directions for pharmaceutical development.

Merge 1 data from the InC3 project consists of baseline and longitudinal data collected on 522 HCV-infected injection drug users across the 9 study cohorts. Data about IDU from different cohorts are similar in several ways. For example, each cohort aimed to schedule regularly spaced visits for follow-up (although a scheduled visit is not the same as an actual visit!), and collected similar behavioral and biological measurements for each IDU. However, data about IDU from different cohorts also differs in several ways. For example, each cohort used different follow-up intervals and may not have collected all desired behavioral or biological measurements. As a result, the data is interval censored and consists of missing observations. Some IDU also received drug therapy to treat their HCV infection, resulting in right-censoring of the spontaneous clearance outcome. We refer to Grebely et al. [22] and the InC3 website [23] for additional details about the InC3 cohort.

6.2 Previous work

Grebely et al. [1] used logistic regression to model the binary outcome of HCV clearance within 2 years of estimated incident infection as a function of variables of interest to analyze factors associated with spontaneous clearance. As demonstrated in Section 5.2, this type of forward imputation logistic regression modeling does not account for interval censoring and often results in incorrect estimates and inference.

6.3 Analysis

We apply IC-TMLE to estimate variable importance measures for the effects of age, ethnicity, gender, infecting genotype, and IL28B gene on the interval-censored outcome of spontaneous HCV clearance among injection drug users in the InC3 data. Following Grebely et al. [1], we defined clearance as two consecutive HCV RNA negative tests and analyzed clearance within 2 years of incident infection. If clearance was observed for an IDU, all subsequent clearance outcomes were also set to clearance being true. As a result, the outcome at each monitoring time was defined as the indicator of whether or not the IDU had cleared their HCV infection at or before that monitoring time.

Since the focus of this article is the interval-censored nature of the clearance outcome, we handled interval censoring of the initial infection date and right-censoring of the outcome as follows. The first time infection was observed and was used as the incident infection time t = 0. We used Inverse Probability of Censoring Weighting (IPCW) prior to applying the IC-TMLE procedure to account for the right-censoring of spontaneous clearance for IDU who received drug therapy to treat their HCV infection. Using IPCW to weight the original observed data structure before applying a TMLE is not fully efficient, but still retains many desirable efficiency and robustness properties. For additional details, we refer to van der Laan and Rose [14]. A fully efficient estimator would require developing a TMLE for the estimation problem that also incorporates right-censoring of the outcome. Such an estimator would be significantly more complex and would be an interesting area for future research. The number of IDU not receiving HCV drug therapy is n₁ + n₀ = 429.

Given our assumed Structural Causal Model, variables included in W are different depending for each variable A we analyze. In particular, variables included in W cannot be affected by A. To account for this, we grouped available baseline variables into several categories (personal, date, location, gene, base-behavior, and age) describing their general type. Personal baseline variables included unchanging characteristics of study participants, such as gender, origin, and ethnicity. Date baseline variables included all year or date variables, such as birth date and cohort entry date. Location baseline variables included location-specific information, such as site and center. Gene baseline variables included values of all measured genes. Base-behavior variables included baseline information about injection and prison prior to HCV infection. Age baseline variables included the ages of the IDU at various life events, such as age at cohort entrance. Note that all of these variables are required to have occurred prior to HCV infection. If such information was not available (e.g., the participant was already infected with HCV upon entrance to a cohort), the variables were treated as missing.

When A represented IL28B or age, W included personal, date, location, gene, and age baseline variables. When A represented ethnicity or gender, W included personal, date, location, and gene baseline variables. When A represented infecting genotype, W included personal, date, location, gene, age, and base-behavior variables.

We analyzed factors A which had at least 15 IDU with A = 1. We did not analyze, for example, Asian ethnicity, since the number of Asian IDU was below 15. For this reason, the numbers within each variable analyzed do not necessarily sum to the total number of IDU within the dataset.

L′ consisted of all baseline variables not included in W (and therefore is also different depending on A), as well as the time-dependent variables collected at the last monitoring time prior to 1 year after incident infection date. Δ was an indicator of being monitored between 1 year and 2 years after incident infection date. Y was an indicator of whether clearance was observed between 1 year and 2 years after incident infection date. Note that, due to our definition of clearance, if clearance was observed prior to 1 year, and Δ = 1, then Y = 1, as well. On the other hand, if clearance was observed prior to 1 year, but Δ = 0, recall from Section 3.1.3 that we still effectively know that clearance has occurred, and our estimates will not be changed.

We selected the monitoring interval of between 1 and 2 years from incident infection date for several reasons. First, we are able to analyze all clearance prior to 2 years, as in Grebely et al. [1]. Second, clearance of acute HCV infection typically occurs within 1 year of infection, as discussed in Page et al. [24] and Grebely et al. [25]. Third, using smaller intervals resulted in many fewer IDU being observed within the interval, resulting in poorer estimates. Together, this rationale was an attempt to balance the trade-off between, on the one hand, obtaining precise estimates through having a large enough number of IDU with Δ = 1, and, on the other hand, obtaining results with strong interpretation by using a small window to examine the time-to-event outcome of clearance at a specific time.

6.4 Results

The results of our analysis are presented in Table 3. Female gender, IL28B CC, and several middle age ranges showed a significantly positive effect on HCV clearance. Unknown gender, all other IL28B analyzed, unknown and indigenous ethnicity, infecting genotype 2 and 3, and several younger and older age ranges showed a significantly negative effect on HCV clearance.

Table 3.

InC3 analysis results

	95% Sig	ψ̂	95% CI	min(n0, n1)
Age
Age < 20	✓	−0.235	(−0.291, −0.178)	25
Age < 25	✓	−0.154	(−0.232, −0.075)	179
Age < 30		0.011	(−0.071, 0.094)	120
Age < 35	✓	0.147	(0.082, 0.213)	63
Age < 40	✓	0.218	(0.160, 0.277)	34
Age 20–40	✓	0.184	(0.129, 0.239)	69
Age 20–35	✓	0.088	(0.024, 0.152)	98
Age 25–35		−0.040	(−0.152, 0.072)	187
Age 25–40	✓	0.093	(0.012, 0.174)	213
Gender
Male		−0.081	(−0.196, 0.035)	260
Female	✓	0.125	(0.016, 0.233)	154
Unknown	✓	−0.262	(−0.316, −0.208)	15
Genotype
1		−0.029	(−0.136, 0.077)	157
2	✓	−0.275	(−0.360, −0.190)	21
3	✓	−0.125	(−0.214, −0.035)	97
Not done		0.036	(−0.072, 0.145)	127
IL28B
CC	✓	0.194	(0.098, 0.291)	190
CT	✓	−0.165	(−0.260, −0.070)	146
TT	✓	−0.181	(−0.288, −0.075)	46
Missing	✓	−0.183	(−0.270, −0.097)	38
Ethnicity
White		0.037	(−0.062, 0.135)	104
Indigenous	✓	−0.251	(−0.340, −0.163)	31
Other		0.168	(−0.159, 0.495)	16
Unknown	✓	−0.254	(−0.306, −0.202)	29

Notes: Check marks in the “95% Sig” column indicate that the analyzed variable had a significant effect on clearance, at the 95% level, and n₁ and n₀ are the number of IDU with A = 1 and A = 0, respectively.

Since the InC3 study is observational, we are likely to have violations to our causal assumptions. In particular, it is unlikely that the randomization assumption holds, because there are almost certainly unmeasured variables affecting both monitoring times and outcomes. As a result, we do not recommend interpreting our estimated effects as causal. However, as mentioned in Section 3.1.3, our estimated effects are still interesting variable importance measure of the effect of A on the outcome.

Variables that show a significantly positive or negative effect on HCV clearance should be studied further. Those that show a significantly negative effect on HCV clearance are potential risk factors for chronic infection. On the other hand, those that show a significantly positive effect on HCV clearance should be analyzed more closely for underlying biological explanations that may suggest directions for pharmaceutical development.

It is important to note that estimates may be poor and confidence intervals may be overly optimistic (i.e., too small) when min(n₀, n₁)is small, where n₁ and n₀ are the number of IDU with A = 1 and A = 0, respectively. For example, when min(n₀, n₁) is small, our estimate of variance may not be able to detect whether the true variance of ψ is large. This is due to the fact that, in our case, the term g_A in the denominator of two of the influence curve components in eq. (13) is the conditional probability that A = a given covariates W. We might expect g_A to be small, and hence, the variance to be large. However, for factors with small min(n₀, n₁), we may not observe participants where g_A is small, resulting in variance estimates and confidence intervals that are artificially small.

6.5 Considerations for future analyses

While this article’s focus was on the interval-censored nature of the HCV clearance outcome in the InC3 data, several other considerations would be fruitful for further analysis.

Future analysis should note that if the factor of interest A has a very small number of people (e.g., 21 participants with infecting genotype 2 in the Merge 1 InC3 dataset), the VIM of A may be excessively determined by the specific individuals within that small group. As a result, factors where min(n₀, n₁)was very small should be investigated further for a dataset with larger min(n₀, n₁)to establish whether or not the effect remains. Furthermore, improved variance estimation methods for sparse data of this nature are needed.

Additional choices of the Δ monitoring interval should also be studied. We attempted to balance the trade-off between precise and interpretable estimates, but additional analysis should be done to analyze the sensitivity of conclusions presented here to alternative choices of Δ.

Finally, interval censoring of the initial infection date should be studied. Since this article focused on the interval censoring of the clearance outcome, we treated the first time infection was observed as the incident infection time. However, the incident infection time is in truth also subject to interval censoring and should be studied in future work.

7 Discussion

While most experimental and observational data, particularly in genetics and epidemiology, is interval-censored, practitioners consistently fail to account for interval-censored outcomes in their analyses of variable importance measures. In this article, we presented a TMLE algorithm tailored for estimating VIM in the presence of interval-censored outcomes, IC-TMLE. We discussed the desirable statistical properties of IC-TMLE, showed its superior performance compared to other methods through a series of simulation studies, and used it to estimate VIM of spontaneous HCV clearance using the InC3 data.

The IC-TMLE procedure provides VIM estimates that can be used to determine the effects of a large collection of variables on an outcome subject to interval censoring. The ubiquity of interval-censored outcomes and the importance of obtaining valid variable importance measures indicate the wide-ranging applicability of our novel IC-TMLE approach to estimating VIM in the presence of interval-censored outcomes.

Appendix

Identifiability of static intervention parameter

In an ideal (impossible) experiment, we would observe the static intervention (3) on all participants for both a values, and the causal effect of A on Y could be estimated by using the counterfactual outcomes to directly compute the empirical average ${\widehat{\psi }}_{\mathit{static}}^F=\frac{1}{n}{\sum }_{i=1}^n(Y_i^{1,1}-Y_i^{0,1})$. Of course, in reality, we can never conduct the ideal experiment described by eq. (3) (which explains why the data is called counterfactual). Instead, for eq. (2) to be identifiable from the observed data, we need the following causal assumptions:

• (C1)Y^a,1 = Y^A,1 | A = a

  Consistency 1: Intervening on the NPSCM to set treatment to A = a yields the observed data if the actual observed treatment is A = a.

• (C2)Y^A,1 = Y^A,Δ | Δ = 1

  Consistency 2: Intervening on the NPSCM to set monitoring to Δ = 1 yields the observed data if the actual observed monitoring is Δ = 1.

• (R1)Y^a,1⊥⊥A | W

  Randomization 1: No unmeasured confounders associated with both treatment A and counterfactual outcome Y^a,1.

• (R2)Y^a,1⊥⊥Δ | W,A = a,L′

  Randomization 2: No unmeasured confounders associated with both monitoring Δ and counterfactual outcome Y^a,1.

• (P1)P(A = a | W) > 0

  Positivity 1: Conditional probability of treatment, for both a = 1 and a = 0, is positive for all covariate possibilities W.

• (P2)P(Δ = 1 | W,A = a,L′) > 0

  Positivity 2: Conditional probability of monitoring at time τ is positive for all covariate possibilities W, A, L′.

Under the above assumptions, we may express the components of ${\psi }_{\text{static}}^F$ as follows. Note that we use the shorthand notation E_L′ to indicate the expectation with respect to the conditional distribution of L′ | W, A = a. The abbreviation TR stands for the Tower Rule.

$$\begin{array}{l}E[Y^{a,1}]\stackrel{(\text{TR})}{=}{E}_W[E[Y^{a,1}\mid W]]\\ \stackrel{(\mathrm{R}1),(\mathrm{P}1)}{=}{E}_W[E[Y^{a,1}\mid W,A=a]]\\ \stackrel{(\mathrm{C}1)}{=}{E}_W[E[Y^{A,1}\mid W,A=a]]\\ \stackrel{(\text{TR})}{=}{E}_W[E_{L^{\prime }}[E[Y^{A,1}\mid W,A=a,L^{\prime }]]]\\ \stackrel{(\mathrm{R}2),(\mathrm{P}2)}{=}{E}_W[E_{L^{\prime }}[E[Y^{A,1}\mid W,A=a,L^{\prime },\mathrm{\Delta }=1]]]\\ \stackrel{(\mathrm{C}2)}{=}{E}_W[E_{L^{\prime }}[E[Y^{A,\mathrm{\Delta }}\mid W,A=a,L^{\prime },\mathrm{\Delta }=1]]]\end{array}$$ (16)

Eq. (16) is a function of the distribution of the observed data, allowing us to identify eq. (2) from the observed data.

Identifiability of stochastic intervention parameter

Ideally, we would observe the stochastic intervention (7) on all participants for both a values, and the causal effect of A on Y could be estimated by using the counterfactual outcomes to directly compute the empirical average ${\widehat{\psi }}_{\text{stochastic}}^F=\frac{1}{n}{\sum }_{i=1}^n(Y_i^{\#,1,\delta }-Y_i^{\#,0,\delta })$. Since the ideal experiment described by eq. (7) is not possible, for eq. (6) to be identifiable from the observed data, we need the following causal assumptions:

• (C1)Y^#,a,δ = Y^#,A,δ | A = a
• (C2)Y^#,A,δ = Y^#,A,Δ# | Δ^# = δ
• (R1)Y^#,a,δ⊥⊥A | W
• (R2)Y^#,a,δ⊥⊥Δ^# | W,A = a,L′^#
• (P1)P(A = a | W) > 0
• (P2)P(Δ^# = δ | W,A = a,L′^#) > 0

Under the above assumptions, we may express the components of ${\psi }_{\text{stochastic}}^F$ as follows:

$$\begin{array}{l}E[Y^{\#,a,\delta }]\stackrel{(\text{TR})}{=}{E}_W[E[Y^{\#,a,\delta }\mid W]]\\ \stackrel{(\mathrm{R}1),(\mathrm{P}1)}{=}{E}_W[E[Y^{\#,a,\delta }\mid W,A=a]]\\ \stackrel{(\mathrm{C}1)}{=}{E}_W[E[Y^{\#,\delta }\mid W,A=a]]\\ \stackrel{(\text{TR})}{=}{E}_W\left[E_{L^{\prime \#}}\left[E\left[Y^{\#,\delta }\mid W,A=a,L^{\prime \#}\right]\right]\right]\\ \stackrel{(\mathrm{R}2),(\mathrm{P}2)}{=}{E}_W\left[E_{L^{\prime \#}}\left[E\left[Y^{\#,\delta }\mid W,A=a,L^{\prime \#},{\mathrm{\Delta }}^{\#}=\delta \right]\right]\right]\\ \stackrel{(\mathrm{C}2)}{=}{E}_W\left[E_{L^{\prime \#}}\left[E\left[Y^{\#}\mid W,A=a,L^{\prime \#},{\mathrm{\Delta }}^{\#}=\delta \right]\right]\right]\end{array}$$ (17)

As before, the last equation above is a function of the distribution of the observed data, allowing us to identify eq. (6) from the observed data.

Proof of equivalence of intervention formulations

Under the stochastic intervention, from eq. (17), we have that

$$\begin{array}{l}E[Y^{\#,a,\delta }]=E_W\left[E_{L^{\prime \#}}\left[E\left[Y^{\#}\mid W,A=a,L^{\prime \#},{\mathrm{\Delta }}^{\#}=\delta \right]\right]\right]\\ =E_W\left[E_{L^{\prime \#}}\left[E\left[Y^{\#}(\tau -1)+(1-Y^{\#}(\tau -1))Y^{\ast }(\tau )\mid W,A=a,L^{\prime \#},{\mathrm{\Delta }}^{\#}=\delta \right]\right]\right]\\ =E_W\left[E_{L^{\prime \#}}\left[Y^{\#}(\tau -1)+(1-Y^{\#}(\tau -1))E\left[Y^{\ast }(\tau )\mid W,A=a,L^{\prime \#},{\mathrm{\Delta }}^{\#}=\delta \right]\right]\right]\end{array}$$ (18)

Now, since Y^#(τ − 1) ∈ L′^# and Y^#(τ − 1) is binary, we can simplify

$$E\left[Y^{\ast }(\tau )\mid W,A=a,L^{\prime \#},{\mathrm{\Delta }}^{\#}=\delta \right]$$ (19)

by considering the value of Y^#(τ − 1) and the definition of δ:

$$\begin{array}{l}(19)=E\left[Y^{\ast }(\tau )\mid W,A=a,L^{\prime \#},{\mathrm{\Delta }}^{\#}=(1-Y^{\#}(\tau -1))+Y^{\#}(\tau -1){\mathrm{\Delta }}^{\#}(\tau -1)\right]\\ =E\left[Y^{\ast }(\tau )\mid W,A=a,L^{\prime \#},{\mathrm{\Delta }}^{\#}=1\right]Y^{\#}(\tau -1)+E\left[Y^{\ast }(\tau )\mid W,A=a,L^{\prime \#},{\mathrm{\Delta }}^{\#}=1\right](1-Y^{\#}\tau -1))\\ =E\left[Y^{\ast }(\tau )\mid W,A=a,L^{\prime \#},{\mathrm{\Delta }}^{\#}=1\right]\end{array}$$ (20)

The above calculations hold because, no matter the value of Y^#(τ − 1), the stochastic intervention results in Δ^# = 1. This can be seen by noting that if Y^#(τ − 1) = 1, then Δ^#(τ − 1) = 1, resulting in Δ^#(τ) = 1. On the other hand, if Y^#(τ − 1) = 0, the stochastic intervention also tells us to set Δ^#(τ) = 1. Now, using the equality of eqs (19) and (20), we can simplify eq. (18) as:

$$(18)=E_W\left[E_{L^{\prime \#}}\left[Y^{\#}(\tau -1)+(1-Y^{\#}(\tau -1))E\left[Y^{\ast }(\tau )\mid W,A=a,L^{\prime \#},{\mathrm{\Delta }}^{\#}=1\right]\right]\right]$$ (21)

Under the static intervention, from eq. (16), we have:

$$\begin{array}{l}E[Y^{a,1}]=E_W[E_{L^{\prime }}[E[Y^{\ast }(\tau )\mid W,A=a,L^{\prime },\mathrm{\Delta }=1]]]\\ =E_W[E_{L^{\prime }}[E[Y^{\ast }(\tau )\mid W,A=a,L^{\prime },\mathrm{\Delta }=1,Y^{\#}(\tau -1)=1]Y^{\#}(\tau -1)+E[Y^{\ast }(\tau )\mid W,A=a,L^{\prime },\mathrm{\Delta }=1,Y^{\#}(\tau -1)=0](1-Y^{\#}(\tau -1))]]\\ =E_W[E_{L^{\prime }}[Y^{\#}(\tau -1)+(1-Y^{\#}(\tau -1))E[Y^{\ast }(\tau )\mid W,A=a,L^{\prime },\mathrm{\Delta }=1]]]\end{array}$$ (22)

To see the equivalence of eqs (21) and (22), observe that the only difference lies in the use of L′ versus L′^#. However, L′ and L′^# contain equivalent information: L′^# was constructed from L′, which shows that any information contained in L′^# is also contained in L′, and on the other hand, the data redefinition equations can easily be used to derive L′ from L′^#. Finally, since both versions of the data contain identical information, the causal assumptions needed for identifiability are also interchangeable.