A Comparison of a Maximum Exertion Method and a Model-Based, Sub-Maximum Exertion Method for Normalizing Trunk EMG

Abstract

The problem with normalizing EMG data from patients with painful symptoms (e.g. low back pain) is that such patients may be unwilling or unable to perform maximum exertions. Furthermore, the normalization to a reference signal, obtained from a maximal or sub-maximal task, tends to mask differences that might exist as a result of pathology. Therefore, we presented a novel method (GAIN method) for normalizing trunk EMG data that overcomes both problems. The GAIN method does not require maximal exertions (MVC) and tends to preserve distinct features in the muscle recruitment patterns for various tasks. Ten healthy subjects performed various isometric trunk exertions, while EMG data from 10 muscles were recorded and later normalized using the GAIN and MVC methods. The MVC method resulted in smaller variation between subjects when tasks were executed at the three relative force levels (10%, 20%, and 30% MVC), while the GAIN method resulted in smaller variation between subjects when the tasks were executed at the three absolute force levels (50 N, 100 N, and 145 N). This outcome implies that the MVC method provides a relative measure of muscle effort, while the GAIN-normalized EMG data gives an estimate of the absolute muscle force. Therefore, the GAIN-normalized EMG data tends to preserve the EMG differences between subjects in the way they recruit their muscles to execute various tasks, while the MVC-normalized data will tend to suppress such differences. The appropriate choice of the EMG normalization method will depend on the specific question that an experimenter is attempting to answer.

1. Introduction

The magnitudes of raw EMG signals are fraught with variability from sources that are independent of force produced by muscle contraction. Subcutaneous fat thickness, skin impedance, and electrode placement are the most evident sources of such variability (De Luca, 1997; Soderberg and Knutson, 2000; Staudenmann et al., 2010; Turker, 1993). Therefore, to be able to compare EMG data between different subjects, days, muscles, or studies, some type of signal normalization procedure is necessary to eliminate such effects (Bolgla and Uhl, 2007; Dankaerts et al., 2004; Jackson et al., 2009; Knutson et al., 1994; Lehman and McGill, 1999; Yang and Winter, 1983; Yang and Winter, 1984). Most commonly, the raw EMG signal (after appropriate processing) is expressed as a percentage of the maximum EMG value obtained from the isometric maximum voluntary contraction (MVC), elicited from a given muscle group (Lehman and McGill, 1999; Ng et al., 2002; Vera-Garcia et al., 2010). An additional advantage of the MVC method is that the normalized EMG data has a physiological interpretation of a level of muscle activation in relation to its maximum.

Several studies questioned the reliability of EMG data obtained from MVCs. They demonstrated better reliability when sub-maximal exertions in the standardized reference tasks were used for the normalization purposes (Dankaerts et al., 2004; Yang and Winter, 1983). Another problem with the MVC method is that it is not always possible to elicit maximum effort from populations such as the elderly or patients with painful symptoms. For example, the maximum trunk force exertions of patients with low back pain (LBP) are lower than those of healthy controls (Hakkinen et al., 2003; McNeill et al., 1980) and this diminished effort is significantly related to fear-avoidance behavior (Hirsch et al., 1991; Thomas et al., 2008). Therefore, in situations where MVC is not feasible, researchers have used sub-maximal task contractions (Mientjes et al., 1999) or ratios of EMG signals from different muscles (Lariviere and Arsenault, 2008; van Dieën et al., 2003a) to directly compare two groups of subjects. An alternative method of extrapolating MVC, based on sub-maximal exertions, has been also proposed for that purpose (Marras and Davis, 2001; Marras et al., 2001). This method uses subjects’ anthropometry to predict maximum trunk moments, and a set of sub-maximal exertions to extrapolate maximum EMG values. However, all normalization methods based on some reference signals (maximal or sub-maximal) might mask the true differences between the subjects.

De Luca (1997) warned that the EMG amplitude normalization is designed to reduce variability between subjects and “tends to suppress distinctions in the data that would be associated with abnormal or pathological cases.” For example, in a test task a subject activates lumbar muscles on one side to a lesser extent (let’s say 50 μV) than on the other side (e.g. 100 μV) due to inhibition from pain or other sources. This recruitment pattern will likely persist during an attempted MVC or sub-maximal reference exertion (e.g. 500 μV vs. 1000 μV). Consequently, in contrast to the raw EMG (5 μV vs. 10 μV), normalized EMG amplitude will not show any side-to-side difference (10% MVC vs. 10% MVC). A similar example was illustrated very clearly by Lehman and McGill (1999), although the authors were making a case for the superiority of the MVC normalization process in the interpretation of EMG. In that case study, the EMG data from the upper and lower portions of the rectus abdominis were presented for one subject. The raw EMG demonstrated a large difference in muscle activity between the two portions of the muscle. In contrast, as in our hypothetical example, MVC-normalized EMG suggested that both parts of the rectus abdominis were equally active. The authors concluded that the interpretation based on raw EMG data was incorrect, even though the neuromuscular independence between upper and lower rectus abdominis is a possibility (Moreside et al., 2008). But what if the Lehman and McGill’s example were a case of pathology, in which one portion of the rectus abdominis muscle was severely inhibited? If this were indeed an abnormality exhibited by the subject, then the interpretation of muscle activity based on the MVC-normalized EMG data was incorrect. Thus, it will never be known if this difference in raw EMG magnitude was real or stemmed from different factors such as electrode placement and skin impedance. Unfortunately, this problem cannot be resolved using raw EMG, MVC normalization, or sub-MVC normalization. These methods are inadequate when the research objectives are to identify certain differences in muscle activation between various population samples or between individual subjects.

The purpose of the present study was to describe a novel EMG normalization method designed to overcome the problems described above. It is based on a biomechanical model and uses a set of sub-maximal ramp contractions, thus not requiring maximum exertions. This method, which we will refer to as the GAIN method, has been used in our previous study on trunk muscle recruitment patterns in patients with LBP (van Dieën et al., 2003a). In the current paper, we describe the GAIN method in more detail and characterize its performance by comparing it to the MVC method. Theoretically, the MVC-normalized EMG data provides a relative measure of muscle effort, while the GAIN-normalized EMG data gives an estimate of the absolute muscle force (van Dieën et al., 2003a). Therefore, the following hypothesis was formulated. If we study a task performed at the same relative effort level (e.g. 50% maximum moment), then the MVC-normalized EMG data will have less between-subjects variability than the GAIN-normalized EMG data. On the other hand, if the task is executed at the same absolute load level (e.g. 50 Nm), then the GAIN-normalized EMG data will have less between-subjects variability than the MVC-normalized EMG data.

2. Methods

Subjects performed isometric ramp exertions in trunk flexion, extension, and left and right lateral bending. MVCs were executed to elicit maximum activation (EMG_max) from 10 major trunk muscle groups. Subsequently, EMG values corresponding to various force levels of isometric ramp exertions were normalized using either the MVC method or a new GAIN method, which is based on a biomechanical model and optimization of sub-maximal ramp exertions.

2.1. Subjects

Ten subjects (6 males and 4 females) volunteered for this study. Their characteristics are listed in Table 1. Subjects were not included in the study if they had spinal surgery or disabling LBP. They all read and signed an informed consent form approved by the university’s IRB in accordance with the Declaration of Helsinki.

Table 1.

The subject characteristics and the isometric force exertion levels expressed as the moments about the L4-L5 intervertebral joints. Values are means and the standard deviations are in parentheses.

		Males [n=6]	Females [n=4]
Age		38.0 (7.9)	35.8 (9.2)
Height [m]		1.75 (0.07)	1.67 (0.03)
Weight [kg]		83.5 (13.8)	74.4 (6.4)
Maximum moments attained during the maximum ramp exertions [Nm]	Extension	332.0 (79.2)	205.5 (40.7)
	Flexion	181.9 (50.1)	96.1 (10.5)
	Lateral bending	194.2 (52.1)	135.8 (12.6)
Moments reached during the sub-maximum ramp exertions used for EMG normalization [Nm]	Extension	83.2 (11.4)	60.1 (5.1)
	Flexion	84.1 (11.5)	62.8 (4.7)
	Lateral bending	83.7 (12.1)	61.3 (3.8)
Moments corresponding to the absolute force levels [Nm]	50N	18.7 (2.0)	17.8 (1.0)
	100N	37.5 (4.0)	35.6 (1.8)
	145N	54.4 (5.8)	51.1 (3.2)

2.2. EMG recording

After appropriate skin preparation with rubbing alcohol, Ag–AgCl, disposable surface EMG electrodes were placed over the following 10 muscles on both sides of the body: rectus abdominis (RA, 3 cm lateral to the umbilicus), external oblique (EO, medial to the mid auxiliary line at the level of the umbilicus), internal oblique (IO, halfway between anterior superior iliac spine and symphysis pubis), thoracic erector spinae (TE, 5 cm lateral to T9 spinous process), and lumbar erector spinae (LE, 3 cm lateral to L4 spinous process). Each pair of electrodes was spaced 3 cm center-to-center along the direction of the muscle fibers. A reference electrode was placed laterally over the 10th rib on the right side. The EMG signals were band-pass filtered between 20 and 420 Hz, differentially amplified, and digitized at a sampling rate of 1600 Hz. After removing the offset (DC bias), all EMG data were digitally rectified and low-pass filtered at a cut-off frequency of 0.5 Hz (dual pass, 4^th order Butterworth filter). This cut-off frequency was adequate in the context of slow, isometric ramp exertions.

2.3. Procedures

After verifying the quality of EMG signals on an oscilloscope, the subjects performed three maximal and four sub-maximal, isometric ramp exertions in trunk flexion, extension, and left and right lateral bending. A special frame was used to immobilize the pelvis and lower limbs in a semi-seated posture (Fig. 1). The subjects pulled against a cable attached to a chest harness on one end and to a strain-gauged assembly on the other end to measure the force. The maximal exertions were used to establish force levels expressed as a percentage of the maximum force for the experimental trials. The sub-maximal, ramp exertion trials lasted 10 seconds. In 2 of the trials, the subjects exerted gradually larger force up to the maximum of 200N for males and 160N for females. The different force levels reflected gender differences in their maximum strength capabilities (McNeill et al., 1980). Depending on the direction of exertion, these values represented between 25% and 46% for males, and between 29% and 65% for females of their maximum trunk moments (Table 1). The data obtained from these sub-maximal ramp trials were used in the GAIN method for EMG normalization, described in the next section. The remaining 2 ramp trials were executed up to 50% of the maximum force. These were the experimental trials used for the comparison between the two EMG normalization methods.

Figure 1.

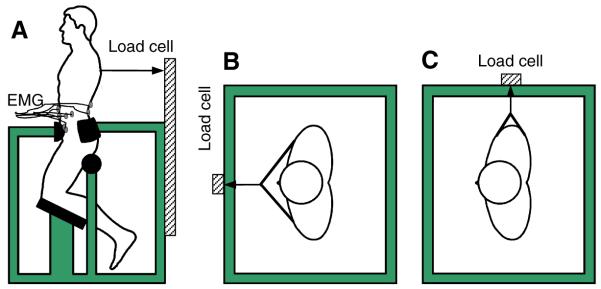
The apparatus for exerting isometric moments in trunk flexion (A), extension (B) and lateral bending (C).

Subjects also performed a single trial of MVC by exerting trunk flexion, extension, and lateral bending moments on an examination table against the resistance provided manually by one of the investigators. If a subject or an investigator felt that a maximum effort was not achieved, the trial was repeated after a short rest period. These tasks were designed to elicit maximum voluntary activation of trunk muscles. The maximum EMG (EMG_max) values obtained during these test contractions served as normalization factors in the MVC method.

2.4. Obtaining normalization gains from sub-maximum ramp contractions

This EMG normalization method was first described and implemented by (van Dieën et al., 2003b). A detailed EMG-driven biomechanical model of the lumbar spine and an optimization algorithm were used to obtain the EMG-to-muscle force gains for each electrode site. The EMG data acquired during all ramp exertions, along with the external forces were entered into the biomechanical model, which first calculated the 3D external moments (about x, y, and z axes, corresponding to lateral bending, axial torsion, and flexion/extension) acting on each intervertebral joint. A least mean square optimization algorithm was then used to find a set of 10 muscle gains (for 10 EMG recording sites) that would result in the best possible match between the external and model-predicted moments about the x, y, and z axes at 6 lumbar joints (T12-S1).

The biomechanical model was described previously in detail (Cholewicki and McGill, 1996). It consisted of a rigid pelvis and sacrum, 5 lumbar vertebrae separated by a lumped parameter, nonlinear disc and ligament equivalent for rotational joint stiffness about the 3 axes, rigid ribcage, and 90 muscle fascicles. Three axes of rotation (x, y, and z) were assigned to each intervertebral joint between T12 and S1, for a total of 18 degrees-of-freedom (6 joints × 3 axes). Normally, the moments necessary to balance the external load and upper body weight (M_External) are partitioned between all 90 muscle fascicles (M_Muscle) with the assistance of EMG:

$${\mathbf{M}}_{External}={\mathbf{M}}_{Muscle}=\sum _{i=1}^{90}({\mathbf{r}}_i\times {\widehat{f}}_i)\cdot F_i$$ (1)

where r_i is a muscle moment arm and f_i is the unit force vector (i.e. line of action). F_i is the muscle force, which is a function of EMG, physiological cross-sectional area (PCSA) and a gain (g).

$$F_i=g_i\cdot EM{G}_i\cdot PCS{A}_i$$ (2)

Combining (1) and (2) yields

$${\mathbf{M}}_{External}={\mathbf{M}}_{Muscle}=\sum _{i=1}^{90}({\mathbf{r}}_i\times {\widehat{f}}_i)\cdot g_i\cdot EM{G}_i\cdot PCS{A}_i$$ (3)

In this study, internal unit moments were grouped by summing moments generated by all the muscle fascicles (n muscle fascicles) driven by each of the 10 EMG electrodes:

$${\mathbf{M}}_{External}={\mathbf{M}}_{Muscle}=\sum _{i=1}^{10}{g}_i\cdot EM{G}_i\cdot \sum _{j=1}^n({\mathbf{r}}_i\times {\widehat{f}}_i)\cdot PCS{A}_j$$ (4)

The gains for each EMG electrode site were estimated using constrained optimization and data from the ramp contractions in all directions. The cost function was the sum of squared differences between the external joint moments in 3 axes and the corresponding muscle moment estimated by the model. This fit was optimized for all eight ramp exertions simultaneously (2 trials × 4 directions). The constraints were based on the assumption that the ratio of left and right gains had to be within 75 to 125% of the ratio of left and right EMG averaged across all ramps. In addition, the gains had to be positive.

The gains represented the maximum muscle stress (σ_max) divided by the maximum EMG amplitude (EMG_max) and were derived as follows. In the EMG-driven spine model, muscle force (F in Eq. 1) is calculated knowing the level of muscle activation, expressed as a fraction of the maximum voluntary activation, and measured with MVC-normalized EMG signal ($\frac{EMG}{EM{G}_{\text{max}}}$):

$$F=\frac{EMG}{EM{G}_{\text{max}}}\cdot {\sigma }_{\text{max}}\cdot PCSA$$ (5)

Since F = g · EMG · PCSA from Eq. 2, it follows that

$$g=\frac{{\sigma }_{\text{max}}}{EM{G}_{\text{max}}}$$ (6)

Consequently, by rearranging Eq. (2), EMG signals normalized with the gain method (EMG multiplied by the corresponding gains) give us an estimate of muscle force per unit cross-sectional area.

$$EMG\cdot g=\frac{F}{PCSA}$$ (7)

It should be pointed out that PCSA of 90 muscles is already determined a priori in our biomechanical model (Cholewicki and McGill, 1996). However, both F and PCSA in Eq. (7) represent 10 single equivalent muscles corresponding to 10 EMG electrode sites. Each single equivalent muscle is biomechanically representative of all muscle fascicles driven by the EMG signal recorded from a given electrode site.

It should be also noted that the gain represents the ratio of maximum muscle tension and maximum EMG amplitude (Eq. 6). While the former term is expected to vary little within subjects, the latter may vary widely between muscles. For example, skin impedance, sub-cutaneous fat thickness, and/or the electrode placement in relation to the muscle belly will differ between the recording sites. The different gains reflect these differences and represent optimal EMG-to-force scaling factors for each recording site.

2.5. Data analysis

For the purpose of comparing between the two methods, we selected two kinds of isometric force exertion levels from the experimental ramp trials: absolute and relative force levels. The absolute force levels were 50N, 100N, and 145N, and the relative force levels were 10%, 20%, and 30% of the maximum isometric force. On average, the absolute and relative force ranges were similar (Table 1). The corresponding EMG signals were normalized with both methods.

For statistical comparisons of normalized EMG data, between-subject variances were computed using a minimum norm quadratic unbiased estimator (MINQUE) model (PASW Statistics 18, SPSS Inc., Chicago, IL, USA) for each EMG normalization method and type of force exertion separately. The force level (50N, 100N, and 145N for the absolute force levels, or 10%, 20%, and 30% of the maximum force for the relative force levels), direction (extension, flexion, and left and right lateral bending), and muscles were fixed factors and subjects were a random factor. The EMG data, normalized with both methods, had different units. To make the comparison of variances meaningful, these data had to be further normalized to have the same means. Therefore, each normalized EMG data point was divided by the group mean obtained within each method and force type condition prior to the analysis of variance. The ratio of between-subjects variances in the EMG data normalized with the two methods was calculated and the resultant F-values were examined for statistical significance. For visual comparisons, coefficients of variation (CV) in the normalized EMG data (between the subjects) were computed for each muscle, direction, method, and force level. Only the muscles acting as agonists in each direction were included in this calculation.

The reproducibility of the GAIN method was tested by deriving the EMG gains from ramp trials 1 and 2 separately. The intra-class correlation coefficients (ICC) were then computed to see how reproducible the gains were between the two trials. The validity of the GAIN method was determined by examining the resultant maximum muscle stress. Since we recorded EMG_max for each subject in our study, we could obtain σ_max by rearranging Eq. (6):

$${\sigma }_{\text{max}}=gEM{G}_{\text{max}}$$ (8)

The assumption here was that these stresses should fall between 20 and 100 N/cm² to indicate some level of construct validity of our model and the gain method. This assumption was based on a number of studies indicating that the maximum physiological muscle tension per unit cross-sectional area falls within this range (Ikai and Fukunaga, 1968; Klein et al., 2001; Maughan et al., 1983; Reid and Costigan, 1987).

3. Results

The maximum isometric moment generated about the L4-L5 lumbar level was 332.0 (SD=79.2) Nm in trunk extension, 181.9 (50.1) Nm in flexion, and 194.2 (52.1) Nm in lateral bending for the males. The females produced 205.5 (40.7) Nm in extension, 96.1 (10.5) Nm in flexion, and 135.8 (12.6) Nm in lateral bending. All of the optimization routines converged and reached a stable solution. Overall, these solutions resulted in a very good match between the external intervertebral moments and the model-estimated, counteracting muscle moments. The root mean square difference, averaged across all the intervertebral joints, axes, exertion directions, and subjects was 9.6 (1.5) Nm. The correlation coefficients between the external and model-estimated lateral bending and flexion/extension moments at L4-L5 were 0.95 (0.01) averaged across all subjects (Fig. 2).

Figure 2.

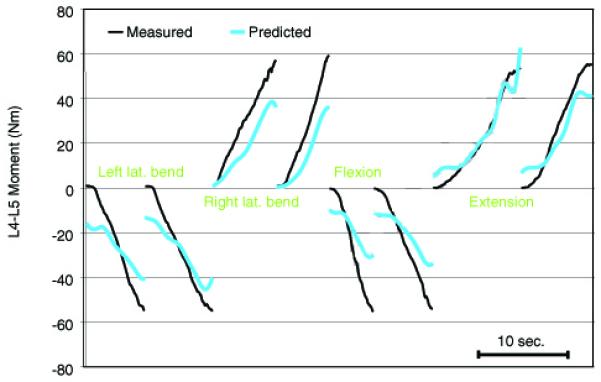
An example of externally measured and model-estimated moments at L4-L5 for one subject.

3.1. Comparison between two methods

Both EMG normalization methods produced expected between-subjects variances that depended on the type of force exertion. For the relative force levels, variance was lower in the EMG signals normalized with the MVC method than with the GAIN method (F_{(9, 9)} = 4.76, p < 0.05) (Table 3, Fig. 3). For the absolute force levels, the trend was reversed. The variance was greater in the EMG signals normalized with the MVC method than with the GAIN method (F_{(9, 9)} = 4.82, p < 0.05) (Table 3, Fig. 4). An example of data comparing the activities of the left lumbar erector spinae muscles of one male and one female during isometric trunk extension efforts are presented in Table 4.

Table 3.

Between-subject variances in the normalized EMG data computed separately for each normalization method and exertion type. The critical value of F_{(9, 9)} was 3.18 at alpha = 0.05.

Method[GRH]Exertion Type	Relative Force	Absolute Force
GAIN method	0.081	0.011
MVC method	0.017	0.053
Ratio [F(9,9)]	4.76	4.82

Figure 3.

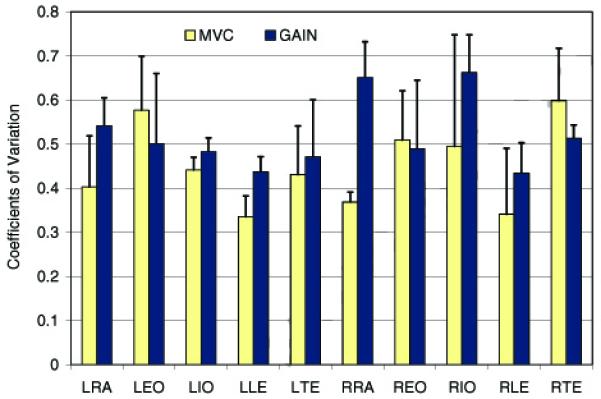
Coefficients of variation in the normalized EMG data recorded from 10 muscles when all subjects performed isometric trunk exertions at the same relative force levels. The EMG data were normalized with the MVC and GAIN methods. The coefficients were averaged across exertion levels and directions. L, R – Left, Right; RE – Rectus Abdominis; EO – External Oblique; IO – Internal Oblique; LE – Lumbar Erector Spinae; TE – Thoracic Erector Spinae.

Figure 4.

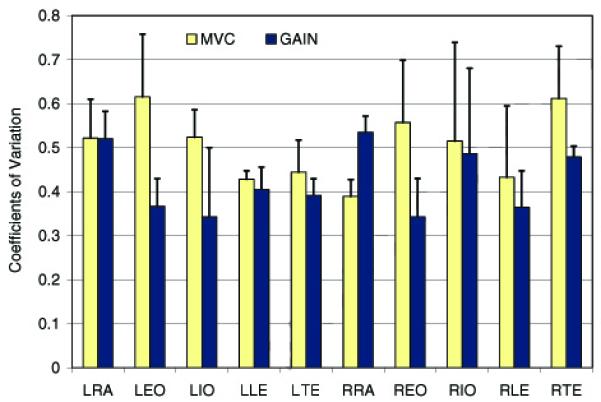
Coefficients of variation in the normalized EMG data recorded from 10 muscles when all subjects performed isometric trunk exertions at the same absolute force levels. The EMG data were normalized with the MVC and GAIN methods. The coefficients were averaged across exertion levels and directions. L, R – Left, Right; RE – Rectus Abdominis; EO – External Oblique; IO – Internal Oblique; LE – Lumbar Erector Spinae; TE – Thoracic Erector Spinae.

Table 4.

An example of data comparing the activities of the left lumbar erector spinae muscles of one male (age 50 years, height 1.68m, weight 81.6kg) and one female (age 32 years, height 1.68m, weight 72.1kg) during isometric trunk extension efforts at relative (50% of maximum) and absolute (200N) force targets.

	Relative Force [50% of max.]		Absolute Force [200N]
	Male	Female	Male	Female
Raw EMG [mV]	900	160	800	200
MVC method [%MVC]	33	36	30	43
GAIN method [N/cm2]	17	6	16	14

3.2. Validity of the GAIN method

The reproducibility of gains obtained from two separate ramp trials was excellent. The ICC coefficients ranged from 0.78 to 1.00 depending on the muscle (Table 2). The average estimate of the maximum muscle stress (σ_max in Eq. (8)) was 59 (SD=51) N/cm² (Table 2). Fifteen percent of these estimates fell below 20 N/cm² and 16% were above 100 N/cm², which we assumed to be a physiological range.

Table 2.

The average EMG gains (g) obtained from the sub-maximal ramp exertion trials and the corresponding maximum muscle stress. The intra-class correlation coefficients (ICC) between the gains obtained from 2 separate ramp trials are also presented. The standard deviations are in parentheses.

	RRA	REO	RIO	RTE	RLE	LRA	LEO	LIO	LTE	LLE
Gains “g”	81(50)	161(126)	77(51)	67(50)	40(15)	67(42)	175(182)	88(59)	61(32)	42(17)
Muscle stress “σmax” [N/cm2]	38(47)	109(71)	62(40)	46(35)	44(27)	36(43)	114(81)	47(32)	41(25)	51(28)
ICC(2,1) between two trials	0.78	1.00	0.87	0.97	0.98	0.89	0.99	0.93	0.80	0.89

4. Discussion

The problem with obtaining meaningful EMG data from patients with painful symptoms (e.g. LBP) lies in the normalization process. Such patients are often unwilling or unable to perform true MVC exertions (Hakkinen et al., 2003; Hirsch et al., 1991; McNeill et al., 1980; Thomas et al., 2008) and the normalization to a reference signal, obtained from a standardized task, will tend to suppress differences that might exist as a result of pathology (De Luca, 1997). Therefore, we presented a novel method (GAIN method) for normalizing trunk EMG data that overcomes both problems. It does not rely on any specific reference contraction (maximal or sub-maximal). Instead, an optimum EMG-to-force gain is computed for each muscle by concurrently fitting predicted and measured spine moments from the entire, multidirectional exertion data set. Because of this optimization of the gains, the GAIN method tends to preserve distinct EMG features in the muscles recruitment pattern for various tasks. Currently, there is no gold standard, which such a method can be validated against. Therefore, we compared the performance of the GAIN method with the MVC method to demonstrate its advantages and disadvantages.

Our data supported the hypothesized performance of the two methods for normalizing EMG. The MVC method resulted in smaller variation between subjects when tasks were executed at the relative force levels, while the GAIN method resulted in smaller variation between subjects when the tasks were executed at the absolute force levels. This outcome implies that the MVC normalization method results in a relative measure of muscle effort, while the GAIN method provides an estimate of the absolute muscle force. The difference between these two methods was illustrated in Table 4 with a sample of EMG data recorded from one male and one female subject. Clearly, the raw EMG is not suitable for interpretation as it would suggest that the left lumbar erector spinae muscle of a male was nearly 6 times more active than the female when the exertion task was performed at the same relative force level and 4 times more active at the same absolute force level. The MVC-normalized data showed similar level of EMG for the male (33% MVC) and the female (36% MVC) at the same relative force level (50% of maximum force). In contrast, the GAIN method showed nearly three times greater muscle activity for the male (17 N/cm²) than the female (6 N/cm²), reflecting the higher muscle force for the male at the same relative force level. At the absolute force exertion of 200N, the MVC-normalized EMG was higher for the female (43% MVC) than the male (30% MVC), because this exertion force represented more effort for the female. However, the GAIN method resulted in nearly identical EMG values (16 and 14 N/cm²), because both the male and the female generated the similar amount of muscle force to produce 200N of trunk extension force. Therefore, as an absolute measure, the GAIN-normalized EMG data will tend to preserve the EMG differences between subjects in the way they recruit their muscles to execute various tasks, while the MVC-normalized data will tend to suppress such differences.

Because the two normalization methods extract different information encoded in the EMG signals, their appropriate applications will depend on the purpose of EMG normalization. For example, when a research question concerns the differences between individuals or study populations, the GAIN method would be preferable over the MVC or other reference contraction-type methods. The gain method will tend to preserve true EMG distinctions in muscle activation patterns, even if these distinctions are also present during the sub-maximal ramp exertions. In contrast, the MVC or other reference contraction-type methods will tend to mask abnormal or pathological features in the normalized EMG data, if such features are also present during the reference exertions. On the other hand, if the research question deals with the general pattern of muscle recruitment in a given task, or the EMG measures before and after some experimental treatment (e.g. fatigue), then the MVC or other reference contraction-type methods are preferable, because they will reduce variability between the subjects (De Luca, 1997; Lehman and McGill, 1999) and increase the power of the study. The experimenter must weigh the advantages and disadvantages of each method and select the most appropriate one in relation to the questions that he or she is attempting to answer.

The advantage of the GAIN method is that the EMG_max data are not needed and are included in the estimates of gains obtained with an optimization algorithm. On the other hand, the drawbacks of the GAIN method lie in the necessity of using a biomechanical model. Apart from increasing the level of analytical difficulty, biomechanical models carry several limitations. The most critical limitation is the inaccuracy in representing real anatomy. As long as two individuals or populations that are being compared, do not differ anatomically (i.e. height, weight, muscles cross-sectional areas, moment arms, etc.), the GAIN method will not introduce any systematic bias. However, when the populations are anatomically distinct, then scaleable and/or individualized models are required to assure that differences in the GAIN-normalized EMG data did not arise from the different anatomies.

Care must be also taken to record EMG from a number of uncorrelated ramp exertions (trunk moments) that is equal to or greater than the number of estimated gains in order to converge on a stable solution. For example, all moment-EMG data recorded during a ramp exertion in a single direction are approximately linearly dependent. Therefore, the input data from other exertion directions are also needed. In the current study, we used the moment-EMG input data from exertions in 4 directions (flexion, extension, left, and right lateral bending) measured at 6 intervertebral joints about 3 rotational axes for a total of 72 linearly independent data sets. The combined moment exertions about more than one axis could be also used and should be explored in future studies.

The reliability and accuracy of the GAIN method was very good as indicated by ICC coefficients greater than 0.78 and small differences between external and model-predicted spine moments (less than 10 Nm, on the average). This suggests that the biomechanical model has internal or construct validity. However, any valid spine model can be used in the GAIN method. For example, simpler models with 10 muscles, would give a one-to-one correspondence between a muscle and the EMG electrode site (Granata and Marras, 1993; Schultz and Andersson, 1981; Schultz et al., 1982).

There are several ways in which the accuracy and reliability of the GAIN method can be improved. As mentioned earlier, individualized and anatomically more accurate biomechanical models would produce more accurate muscle moments and, in turn, more accurate EMG gains. For example, improvements in modeling of the abdominal musculature are needed in our model to better predict trunk flexion moments (Fig. 2) and a more physiological maximum stress in the external oblique muscles (Table 2). Nevertheless, these modeling inaccuracies are the same for all subjects and do not produce any comparison bias, as long as the two populations are anthropometrically similar. In addition, the inclusion of axial rotation, combined (multidirectional) moment exertions (Talebian et al., 2010), and/or varying external moment arms (Kingma et al., 2007) should theoretically help the optimization algorithm to find gains that will more accurately represent the actual way in which an individual recruits his or her trunk muscles. Future studies should establish the minimum necessary set of ramp exertions and their magnitude to optimize estimates of the gains. Between-days reliability also needs to be established.

Biography

Dr. Jacek Cholewicki is a Walter F. Patenge Professor and the Ingham Foundation Research Fellow in spinal biomechanics. He co-directs the Michigan State Center for Orthopedic Research (MSUCOR). Dr. Cholewicki received his Ph.D. degree in Kinesiology from the University of Waterloo in Canada in 1994. From 1993 to 2007, Dr. Cholewicki worked in the Biomechanics Research Laboratory at Yale University School of Medicine, before being recruited to Michigan State University College of Osteopathic Medicine. His research interests lie in the areas of lumbar and cervical spine function, spine injury mechanisms, tissue loading, and biomechanical modeling using EMG. His current projects include motor control of spine stability in the context of low back pain, and optimal rehabilitation strategies. Dr. Cholewicki is the recipient of the Bioengineering Research Prize Award for 2005 from the International Society for the Study of the Lumbar Spine (ISSLS) and the Rose Excellence in Research Award for the best research article of 2007 in the area of Orthopaedic Physical Therapy.

Jaap H. van Dieën, Faculty of Human Movement Sciences, VU University Amsterdam, vanderBoechorststraat 9, NL-1081 BT Amsterdam, the Netherlands, 31-205988501

j.vandieen@fbw.vu.nl, www.ifkb.nl, www.move.vu.nl, www.move-age.eu

Jaap van Dieën worked as a researcher in physical ergonomics at the Institute for Agricultural Engineering in Wageningen, the Netherlands from 1986 till 1996. He obtained a PhD from the Faculty of Human Movement Sciences at the VU University Amsterdam the Netherlands in 1993 and has been affiliated to this faculty since 1996. In 2002, he was appointed as full professor. Jaap van Dieën is the director of MOVE-AGE a joint doctorate program of three European universities on ageing and mobility. In addition, he leads a research group focusing on mechanical aspects of ageing and musculoskeletal disorders. His main research interest regards the effects of task demands, fatigue, ageing, and disorders on joint load and stability. Jaap van Dieën has (co-) authored over 180 papers in international scientific journals. He was an editor of the European Journal of Applied Physiology, and currently is section editor of Human Movement Sciences and serves on the editorial advisory board of the Journal of Electromyography and Kinesiology and the editorial boards of Clinical Biomechanics, Manual Therapy, IIE Transactions on Occupational Ergonomics and Human Factors and the Journal of Back and Musculoskeletal Rehabilitation. Jaap van Dieën has been the treasurer of ISEK since 2006.

Angela Lee is a Research Assistant at MSU Center for Orthopedic Research. She received her B.Sc. in Kinesiology with a minor in Mathematics from Simon Fraser University, in Canada, in 2005. Currently, she is a Masters candidate in Public Health at Michigan State University. Her research interests lie in identifying risk factors predisposing individuals to low-back pain.

Dr. N. Peter Reeves is an Assistant Professor in the College of Osteopathic Medicine at Michigan State University. In 2007, he obtained a Doctorate in Biomedical Engineering from Yale University. His research focuses on dynamic spine stability, and in particular, understanding how the spine is controlled to accomplish daily activities while avoiding injury. Prior to returning to graduate school, he worked for a number of years as an ergonomic/work reintegration consultant developing musculoskeletal injury prevention and management programs. He is the recipient of the 2005 International Society for the Study of the Lumbar Spine (ISSLS) Basic Research Award, and the 2008 Rose Excellence in Research Award for Orthopaedic Physical Therapy Research.