Successional dynamics in Neotropical forests are as uncertain as they are predictable

Significance

Although forest succession has been approached as a predictable process, successional trajectories vary widely, even among nearby stands with similar environmental conditions and disturbance histories. We quantified predictability and uncertainty during tropical forest succession using dynamical models describing the interactions among stem density, basal area, and species density over time. We showed that the trajectories of these forest attributes were poorly predicted by stand age and varied significantly within and among sites. Our models reproduced the general successional trends observed, but high levels of noise were needed to increase model predictability. These levels of uncertainty call into question the premise that successional processes are consistent over space and time, and challenge the way ecologists view tropical forest regeneration.

Abstract

Although forest succession has traditionally been approached as a deterministic process, successional trajectories of vegetation change vary widely, even among nearby stands with similar environmental conditions and disturbance histories. Here, we provide the first attempt, to our knowledge, to quantify predictability and uncertainty during succession based on the most extensive long-term datasets ever assembled for Neotropical forests. We develop a novel approach that integrates deterministic and stochastic components into different candidate models describing the dynamical interactions among three widely used and interrelated forest attributes—stem density, basal area, and species density. Within each of the seven study sites, successional trajectories were highly idiosyncratic, even when controlling for prior land use, environment, and initial conditions in these attributes. Plot factors were far more important than stand age in explaining successional trajectories. For each site, the best-fit model was able to capture the complete set of time series in certain attributes only when both the deterministic and stochastic components were set to similar magnitudes. Surprisingly, predictability of stem density, basal area, and species density did not show consistent trends across attributes, study sites, or land use history, and was independent of plot size and time series length. The model developed here represents the best approach, to date, for characterizing autogenic successional dynamics and demonstrates the low predictability of successional trajectories. These high levels of uncertainty suggest that the impacts of allogenic factors on rates of change during tropical forest succession are far more pervasive than previously thought, challenging the way ecologists view and investigate forest regeneration.

Unexplained variation (uncertainty) is ubiquitous in ecology, and often constrains our ability to elucidate the mechanisms that drive variation in forest structure and dynamics. This issue is reflected in the long-standing controversy over the relative importance of determinism and stochasticity in shaping community assembly (1–4). Although it has been widely demonstrated that both deterministic and stochastic processes drive community assembly in mature forests (5, 6), their relative importance in explaining forest succession has not been rigorously evaluated (7). More than one-half of the tropical biome is in some stage of recovery from past human disturbance (8), yet no previous study has quantitatively assessed the extent to which regenerating forests follow predictable trajectories.

Since the early days of community ecology, succession has been viewed either as a deterministic (1) or a stochastic (2) process. Forest succession, however, has been traditionally approached as a predictable process, mostly driven by autogenic factors intrinsic to the forest site (9, 10). Deviations from this expectation are usually attributed to allogenic factors, such as prior land use or priority effects (11, 12). As a result, most of our knowledge on forest succession is based on chronosequences (13), a space-for-time substitution approach that assumes that succession follows a single, largely deterministic trajectory over time. Recent studies, however, have shown that successional pathways vary widely, even among neighboring stands with similar environmental conditions and disturbance history (14–18). In the case of posthurricane succession in Nicaragua, such variation has been attributed to stochastic processes associated with nonequilibrium community dynamics (18). As long-term successional studies in the tropics are rare, assessing predictability of successional trajectories in species-rich communities has not been possible across a broader range of geographical and historical settings.

Successional dynamics has been typically studied through the lens of three widely used forest attributes—stem density, basal area, and species density, whose dynamics are often evaluated independently of one another (12). These metrics, however, are likely to change interdependently during succession. In particular, successional changes in stem density are associated with changes in basal area, and vice versa (9, 17). Yet, other possible interrelations between these attributes have not been previously explored in a successional scenario. For instance, although rates of change in species density are expected to depend upon changes in stem density (19, 20), it is not clear whether changes in basal area affect rates of species gain or loss. Also, the causal relationship between species density and rates of change in stem density and basal area is poorly understood. To our knowledge, a clear synthesis addressing the simultaneous interdependence of the rates of change of these three forest attributes is currently lacking. A promising approach to address this issue is to view regenerating tropical forests as complex adaptive systems, which integrate many of the features characterizing reassembling plant communities, namely self-organization, memory, nonlinearity, and uncertainty (21, 22). Through such a holistic perspective, we can gain a mechanistic understanding of how the interacting components influencing succession produce a system dynamics that cannot be easily predicted from their individual behavior (23).

Here, we develop a novel modeling approach that addresses these dynamic interdependencies and that quantifies predictability and uncertainty in successional pathways by integrating both deterministic and stochastic components. We apply these models to an unparalleled dataset from seven lowland tropical secondary forests spanning four Neotropical countries (Brazil, Costa Rica, Mexico, and Nicaragua). Each study site includes 4–15 plots that document long-term successional forest dynamics (Table S1). Within each site, plots were established in close proximity and share similar land use history, climate, and soil conditions. These data comprise most of the studies on secondary forest dynamics in the Neotropics and encompass different land use histories and climate regimes, providing an unprecedented opportunity to investigate the generality of the successional dynamics observed.

Table S1.

Description of each site

Site	No. of plots	Plot area, ha	Stand age at first census, y	Measurement period	Total no. of tree species recorded	Previous land use	Minimum dbh, cm
Brazil 1 (31, 39)	15	0.0125–0.06	2–19	1999–2010	398	None	3
Brazil 2 (31, 39)	13	0.01–0.06	2–11	1999–2010	246	Pasture	3
Costa Rica 1 (14)	6	1	12–35	1997–2012	366	Pasture	5
Costa Rica 2 (14)	4	0.33–1.16	1–25	1987–2011	360	None	10
Mexico wet (17)	10	0.05	2–17	2000–2010	206	Fallow cornfields	5
Mexico dry (16)	12	0.04	3–60	2003–2012	75	Fallow cornfields	5
Nicaragua (18)	12	0.1	2	1990–2007	328	None	5

Characteristics of the study plots for each of the seven sites. Literature references are in parentheses next to the site.

To quantify predictability and uncertainty during succession, we first illustrate among-plot variability in the successional trajectories of stem density, basal area, and species density, and evaluate the effect of stand age on these forest attributes. Then, we quantify the predictability of successional trajectories within each site by modeling succession as the realization of a dynamical, strictly deterministic process resulting from the initial conditions in stem density, basal area, and species density, and the simultaneous interaction among these state variables over successive time steps (Fig. 1). Finally, we assess the degree of uncertainty underlying the predictability of the deterministic model by incorporating a stochastic component governed by a parameter that defines the relative magnitude of the deterministic and the stochastic components (Fig. 1). This approach allows us to address the following questions: (i) How much of the variation in successional trajectories within each site is explained by stand age? (ii) Can a single dynamical model describe the simultaneous interaction among rates of change in stem density, basal area, and species density? (iii) What is the relative importance of predictability and uncertainty in successional trajectories within each site? (iv) Is any of the forest attributes more predictable than the others? (v) Is the degree of uncertainty in successional trajectories related to previous land use?

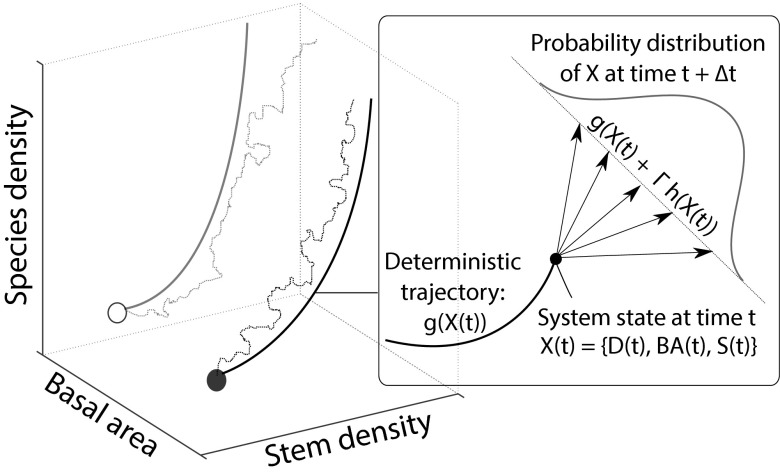
Fig. 1.

Illustration of the model as the realization of the process X(t) starting at two different initial conditions. The model integrates predictability and uncertainty as described by a system of stochastic differential equations, where X denotes the state of the system at a given time. The system is characterized by three state variables: stem density, basal area, and species density. The thick lines represent two trajectories, expressed by the deterministic component of the model only, in a phase space defined by normalized stem density, basal area, and species density, and starting at two different initial conditions. The thin, dotted lines represent two trajectories, as expressed by the stochastic model. As the zoom shows, the stochastic trajectory is the result of a random walk starting at the initial condition. The stochastic model drives the system from time $t$ to time $t+\mathrm{\Delta }t$, and the possible outcomes follow a Gaussian probability distribution.

Results

Variability in Successional Trajectories and Effect of Stand Age.

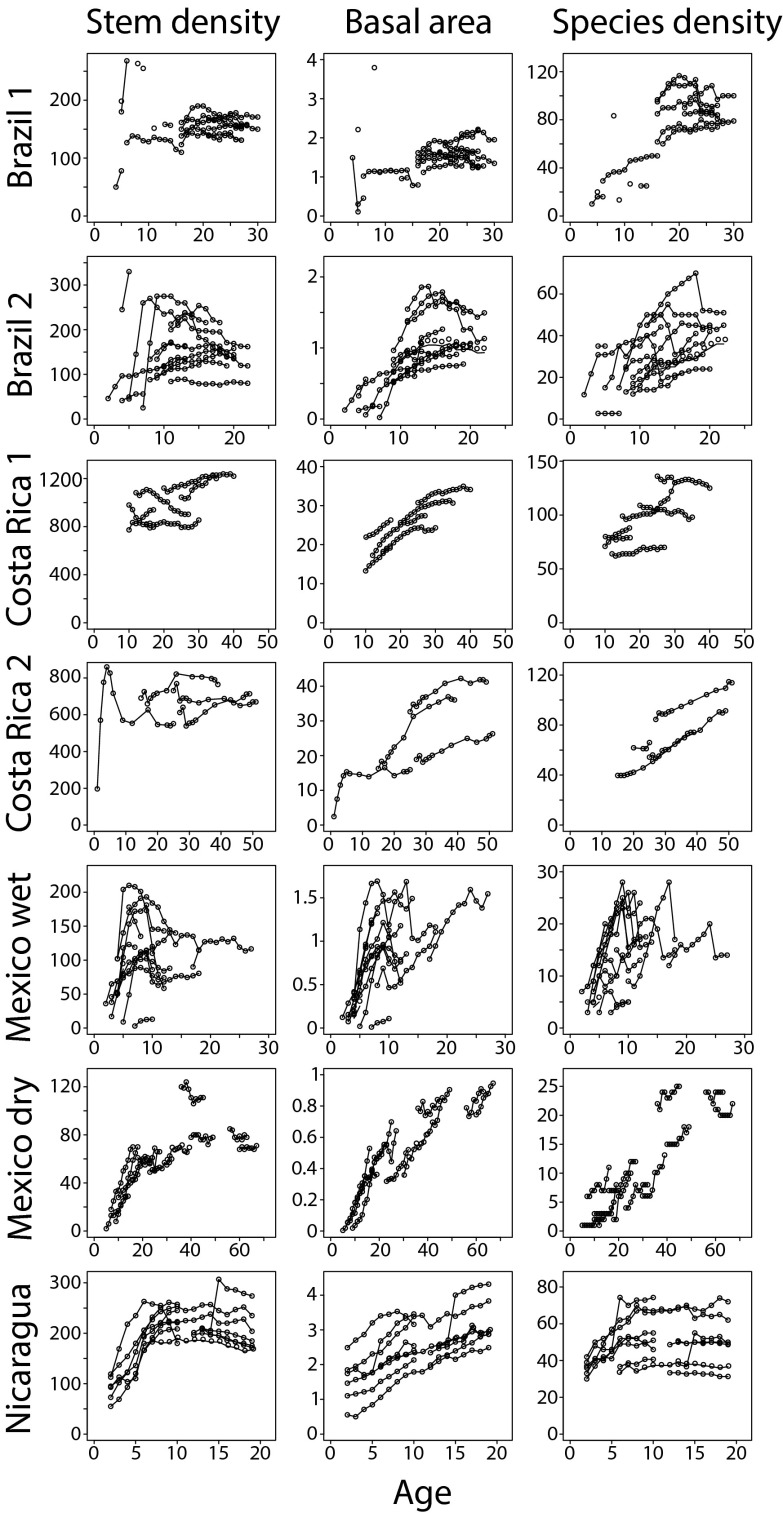
Successional trajectories of stem density, basal area, and species density varied widely within and among sites (Fig. 2). Within each site, plot identity (random effect) was more important than stand age since abandonment (fixed effect) in explaining variation in forest attributes, accounting for over 60% of the total variance in most cases (Table S2). For instance, in Brazil 1, plot identity explained over 80% of the variance in all three attributes, and stand age did not significantly predict basal area or species density. Sites without previous land use (Costa Rica 2 and Nicaragua) showed similar patterns to sites used previously as pastures (Brazil 2 and Costa Rica 1), with plot identity explaining over 90% of the variance in certain cases. Strikingly, the contribution of age and its interaction with plot identity was low in comparison with that of plot identity alone, explaining less than 20% of the total variance within sites (Table S2).

Fig. 2.

Observed successional trajectories of stem density, basal area, and species density. For each plot within each site, temporal changes in stem density, basal area (in square meters), and species density are plotted against age since pasture or clearcut abandonment (lines connecting same symbols). Each of these attributes was standardized by plot size, depending upon the site (Methods).

Table S2.

Relative effects of plot and stand age on the forest structure attributes

Forest attribute	Term	Brazil 1	Brazil 2	Costa Rica 1	Costa Rica 2	Mexico wet	Mexico dry	Nicaragua
Stem density	Plot	87.6	69.8	86.8	29.6	60.1	87.2	26.3
	Age	0.3*	0.8**	0.3**	1.0ns	1.7**	4.1***	30.2***
	Plot × Age	7.1***	10.7***	11.1***	7.5ns	15.4**	7.8***	18.0***
Basal area	Plot	87.6	78.8	86.2	77.7	53.6	86.6	60.1
	Age	10−3 ns	4.7***	10.8***	14.5***	17.0***	10.1***	31.7***
	Plot × Age	7.8***	11.9***	1.6***	4.4***	11.3***	2.1***	3.8***
Species density	Plot	93.9	73.4	95.1	68.1	45.3	95.1	66.6
	Age	10−3 ns	7.8***	0.4***	30.6***	16.3***	2.6***	14.1***
	Plot × Age	2.5***	5.9***	3.5***	0.8***	11.5***	1.2***	8.4***

Results from one-way repeated-measures ANOVA testing, for each site, the effect of plot identity (random effect) and stand age (fixed effect) on stem density, basal area, and species density. Reported are the percentage of variance explained by age, plot factors, and their interaction. Plot factors were not tested for significance because they were treated as random effects (***P < 0.001; **P < 0.01; ns, nonsignificant).

Predictability in Successional Trajectories.

To quantify predictability of successional trajectories within each site, we modeled succession as the realization of a dynamical process resulting from initial conditions in stem density, basal area, and species density, and their simultaneous interaction, over successive time steps. We evaluated the fit of three candidate dynamical models (Methods). The nonlinear dynamical model performed markedly better than the linear model or the linear model with interactions, both of which performed poorly (Table S3).

Table S3.

Predictive power of the candidate deterministic models

Site	Linear model (9) (Eq. 2a)		Lineal model with interactions (9) (Eq. 2b)		Nonlinear model (18) (Eq. 2c)
	NSE	AIC	NSE	AIC	NSE	AIC
Brazil 1	0.96	−669.2	0.96	−740.2	0.98	−983.2
Brazil 2	0.77	−555.5	−9,066,779	−673.7	0.92	−919.5
Costa Rica 1	−28.2	+1,107.7	−43,311,385	+4,497.4	0.95	−602.1
Costa Rica 2	−18.7	+524.2	0.81	−290.6	0.92	−264.6
Mexico wet	−0.62	−563.7	−29,741,865	+5,776.9	0.89	−626.8
Mexico dry	−10.4	−1,253.0	−2,600,253	+5,534.9	0.98	−1,233.6
Nicaragua	−3.1	+890.5	−11,087,299	+6,302.8	0.93	−1,020.3

Linear model (Eq. 2a), linear model with interactions (Eq. 2b), and nonlinear model (Eq. 2c). For each candidate model, we report the Nash–Sutcliffe efficiency coefficient (NSE) and the Akaike information criterion (AIC), which accounts for the number of parameters of each model (in parentheses). Values in bold indicate the best-fit model for each site.

As the nonlinear model included nine terms and 18 parameters (Methods), we attempted to reduce the number of parameters through backward elimination of terms that were not supported by available data (9). More specifically, rates of change in stem density or in basal area are not likely to be causally related with species density, and the relationship between rates of change in species density and basal area has not been explored yet in a successional scenario. We tested the seven possible combinations that had eight, seven, or six terms (16, 14, and 12 parameters, respectively) instead of the nine terms (18 parameters) included in the full nonlinear model. The model that best fitted the observed data differed among sites (Table S4), indicating that the processes driving successional dynamics were neither consistent nor uniform across a broad range of secondary forests.

Table S4.

Backward elimination of the terms that were the most unlikely to influence rates of change in the three forest structure attributes evaluated

Model	No. of parameters	Metric	Brazil 1	Brazil 2	Costa Rica 1	Costa Rica 2	Mexico wet	Mexico dry	Nicaragua
$\{\begin{array}{c}\frac{dD}{dt}=f\left(D,BA,S\right)\\ \frac{dBA}{dt}=f\left(D,BA,S\right)\\ \frac{dS}{dt}=f\left(D,BA,S\right)\end{array}$	18	AIC	−983.2	−919.5	−602.1	−264.6	−626.8	−1,233.6	−1,020.3
		NSE	0.98	0.92	0.95	0.92	0.89	0.98	0.93
$\{\begin{array}{c}\frac{dD}{dt}=f\left(D,BA,\mathit{S}\right)\\ \frac{dBA}{dt}=f\left(D,BA,S\right)\\ \frac{dS}{dt}=f\left(D,BA,S\right)\end{array}$	16	AIC	−1,077.7	−1,004. 2	−615.7	−288.5	−608.7	−1,154.1	−964.4
		NSE	0.98	0.93	0.93	0.94	0.88	0.97	0.94
$\{\begin{array}{c}\frac{dD}{dt}=f\left(D,BA,S\right)\\ \frac{dBA}{dt}=f\left(D,BA,\mathit{S}\right)\\ \frac{dS}{dt}=f\left(D,BA,S\right)\end{array}$	16	AIC	−1,038.7	−963.4	−627.3	−299.7	−569.4	−1,260.8	−852.8
		NSE	0.98	0.93	0.93	0.94	0.88	0.98	0.94
$\{\begin{array}{c}\frac{dD}{dt}=f\left(D,BA,S\right)\\ \frac{dBA}{dt}=f\left(D,BA,S\right)\\ \frac{dS}{dt}=f\left(D,\mathit{B}\mathit{A},S\right)\end{array}$	16	AIC	−1,037.8	−1,008.2	−570.6	−266.1	−614.2	−1,208.5	−848.1
		NSE	0.98	0.94	0.95	0.95	0.88	0.98	0.90
$\{\begin{array}{c}\frac{dD}{dt}=f\left(D,BA,\mathit{S}\right)\\ \frac{dBA}{dt}=f\left(D,BA,\mathit{S}\right)\\ \frac{dS}{dt}=f\left(D,BA,S\right)\end{array}$	14	AIC	−1,001.8	−978.8	−594.8	−286.7	−627.5	−1,384.9	−964.7
		NSE	0.98	0.94	0.95	0.96	0.89	0.98	0.94
$\{\begin{array}{c}\frac{dD}{dt}=f\left(D,BA,\mathit{S}\right)\\ \frac{dBA}{dt}=f\left(D,BA,S\right)\\ \frac{dS}{dt}=f\left(D,\mathit{B}\mathit{A},S\right)\end{array}$	14	AIC	−1,050.5	−1,118.9	−576.6	−294.9	−640.3	−1,332.8	−1,096.8
		NSE	0.98	0.94	0.95	0.96	0.88	0.98	0.94
$\{\begin{array}{c}\frac{dD}{dt}=f\left(D,BA,S\right)\\ \frac{dBA}{dt}=f\left(D,BA,\mathit{S}\right)\\ \frac{dS}{dt}=f\left(D,\mathit{B}\mathit{A},S\right)\end{array}$	14	AIC	−1,108.1	−853.7	−646.3	−305.3	−604.1	−1,421.9	−861.8
		NSE	0.98	0.92	0.95	0.94	0.89	0.98	0.89
$\{\begin{array}{c}\frac{dD}{dt}=f\left(D,BA,\mathit{S}\right)\\ \frac{dBA}{dt}=f\left(D,BA,\mathit{S}\right)\\ \frac{dS}{dt}=f\left(D,\mathit{B}\mathit{A},S\right)\end{array}$	12	AIC	−1,007.4	−926.1	−686.9	−310.4	−621.1	−1,389.1	−820.8
		NSE	0.98	0.94	0.95	0.95	0.89	0.97	0.93

These were (i) the effect of species density (S) on the rates of change in stem density (D), (ii) the effect of species density (S) on the rates of change in basal area (BA), and (iii) the effect of basal area (BA) on the rates of change in species density (S). Eliminated terms are in bold in the equations. We compared the original nonlinear model with seven models resulting from the elimination of each of these three terms separately, and all its possible combinations. For each candidate model, we report its number of parameters, the Nash–Sutcliffe efficiency coefficient (NSE), and the approximate Akaike information criterion (AIC). Values in bold indicate the best-fit model for each site.

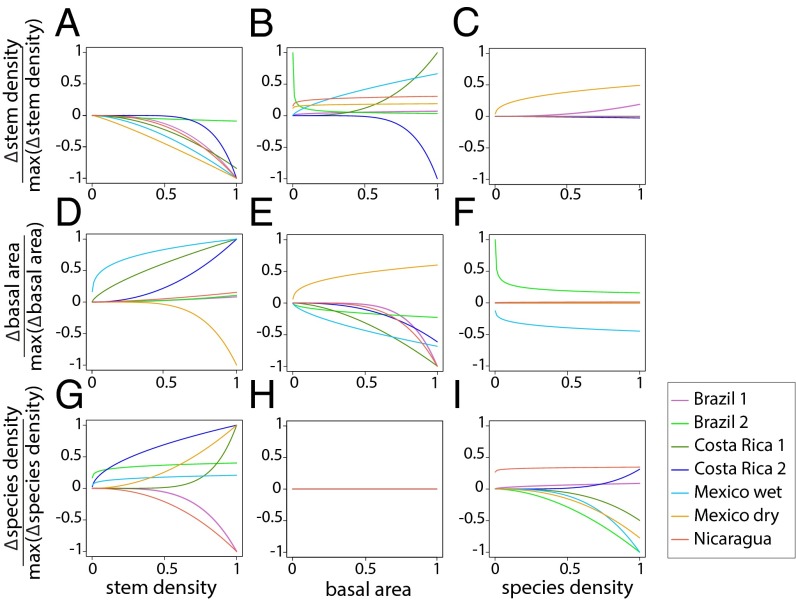
Fig. 3 shows how the derivatives (rates of change) of stem density, basal area, and species density varied as a function of each attribute alone, based upon the fitted parameters of the best-fit nonlinear model for each site. Some bivariate patterns were consistent among sites, suggesting generality in successional processes across study sites. In most sites, increasing stem density led to decreasing rates of change in stem density, but to positive and increasing rates of change in basal area (Fig. 3 A and D). These results suggest high tree mortality in dense early successional stands, whereas the remaining trees rapidly accumulate basal area. Similarly, stands with high basal area showed positive and increasing rates of change in stem density in most sites, but negative and decreasing rates of change in basal area (Fig. 3 B and E). These findings indicate that, when stands reach a saturation point in terms of basal area, regulation occurs through the death of large trees, rather than through recruitment limitation. Also, in most sites, rates of change in species density increased as stem density increased (Fig. 3G), but decreased as species density increased (Fig. 3I). These results reflect species colonization through tree recruitment early in succession, whereas, as succession unfolds, rates of species gain reach a saturation point determined by the number of species that can establish in the community (20). Notably, rates of change in stem density, basal area, and species density showed wide variation among sites, even in cases when the direction of these trends was consistent among sites (Fig. 3 and Table S5).

Fig. 3.

Among-site variation in the values of the fitted parameters of the deterministic model. Derivatives of stem density (A–C), basal area (D–F), and species density (G–I) as a function of each of these properties alone, obtained from the fitted parameters of the nonlinear dynamical model in Eq. 2c. The derivative of each forest attribute is divided by its observed maximum to evaluate the contribution of each attribute to each derivative on a unitless scale. Note that stand age is not explicitly addressed in the plot axes.

Table S5.

Parameter estimates of the best-fit model based on the genetic algorithm optimization method

Parameter estimate	Brazil 1	Brazil 2	Costa Rica 1	Costa Rica 2	Mexico wet	Mexico dry	Nicaragua
a11	−1.42 (−0.89 ± 0.03)	−0.19 (−0.86 ± 0.02)	−0.23 (−0.82 ± 0.02)	+0.02 (−0.71 ± 0.02)	−1.38 (−0.72 ± 0.02)	−0.08 (−0.87 ± 0.02)	−0.74 (−0.76)
a12	+0.10 (+0.06 ± 0.03)	+0.07 (+0.29 ± 0.01)	+0.28 (+0.39 ± 0.02)	−0.16 (+0.20 ± 0.02)	+0.92 (+0.32 ± 0.02)	+0.02 (+0.24 ± 0.02)	+0.23 (+0.40 ± 0.02)
a13	+0.27 (+0.01 ± 0.02)	0	0	0	0	+0.04 (+0.22 ± 0.02)	0
a21	+0.03 (+0.09 ± 0.02)	+0.04 (+0.24 ± 0.02)	+0.13 (+0.38 ± 0.02)	+0.27 (+0.46 ± 0.02)	+1.04 (+0.26 ± 0.02)	−0.06 (+0.30 ± 0.02)	+0.21 (+0.17 ± 0.02)
a22	−0.34 (−0.63 ± 0.02)	−0.09 (−0.83 ± 0.02)	−0.13 (−0.59 ± 0.02)	−0.16 (−0.59 ± 0.02)	−0.71 (−0.80 ± 0.02)	+0.04 (−0.41 ± 0.02)	−1.38 (−0.76 ± 0.02)
a23	0	+0.06 (+0.34 ± 0.02)	0	0	−0.47 (+0.28 ± 0.02)	0	+0.02 (+0.26 ± 0.01)
a31	+0.47 (+0.25 ± 0.03)	+0.04 (+0.32 ± 0.02)	+0.07 (+0.19 ± 0.02)	+0.05 (+0.30 ± 0.01)	+0.18 (+0.38 ± 0.01)	+0.21 (+0.30 ± 0.01)	−0.47 (+0.34 ± 0.01)
a32	0	0	0	0	0	0	0
a33	+0.04 (−0.46 ± 0.02)	−0.09 (−0.56 ± 0.02)	−0.03 (−0.46 ± 0.02)	+0.02 (−0.53 ± 0.02)	−0.88 (−0.64 ± 0.02)	−0.16 (−0.48 ± 0.02)	+0.16 (−0.70 ± 0.02)
b11	+ 2.95 (+0.73 ± 0.03)	+0.69 (+1.19 ± 0.02)	+1.90 (+1.32 ± 0.03)	+0.16 (+1.32 ± 0.03)	+1.64 (+1.19 ± 0.02)	+1.16 (+1.19 ± 0.02)	+2.57 (+1.32 ± 0.02)
b12	+0.35 (+0.81 ± 0.03)	−0.48 (+0.78 ± 0.02)	+3.05 (+1.29 ± 0.03)	+6.24 (+1.28 ± 0.03)	+0.67 (+0.75 ± 0.02)	+0.07 (+1.08 ± 0.02)	+0.10 (+0.71 ± 0.02)
b13	+2.29 (+0.78 ± 0.03)	0	0	0	0	+0.36 (+1.01 ± 0.02)	0
b21	+1.62 (+0.85 ± 0.03)	−2.11 (−1.0 ± 0.02)	+0.70 (+1.13 ± 0.03)	+2.14 (+1.29 ± 0.03)	+0.26 (+1.04 ± 0.02)	+4.72 (+1.15 ± 0.02)	+1.54 (+1.07 ± 0.01)
b22	+5.47 (+0.86 ± 0.03)	+0.48 (+1.07 ± 0.02)	+1.67 (−1.31 ± 0.03)	+2.58 (+1.55 ± 0.03)	+0.66 (+1.16 ± 0.02)	+0.33 +1.24 ± 0.02)	+4.11 (+0.92 ± 0.02)
b23	0	−0.27 (+0.91 ± 0.02)	0	0	+0.18 (+0.91 ± 0.02)	0	+0.29 (+0.91 ± 0.02)
b31	+4.10 (+0.69 ± 0.03)	+0.13 (+1.02 ± 0.02)	+6.3 (+1.24 ± 0.03)	+0.53 (+1.14 ± 0.03)	+0.22 (+0.88 ± 0.02)	+1.96 (+1.28 ± 0.02)	+2.24 (+0.89 ± 0.01)
b32	0	0	0	0	0	0	0
b33	+0.48 (+0.81 ± 0.04)	+1.81 (+1.25 ± 0.02)	+3.11 (−1.24 ± 0.04)	+4.49 (+1.86 ± 0.04)	+3.24 (+1.22 ± 0.03)	+2.33 (+1.23 ± 0.03)	+0.04 (+1.29 ± 0.01)

The genetic algorithm is the best optimization method for estimating nonlinear dynamic operators, for which an analytic optimization is not possible. Because this method does not provide confidence intervals for the parameter estimates, also reported are the mean and the SE of the parameter values of the 100 (5%) best runs.

The dynamical models also revealed several interactions among state variables that have not been demonstrated in previous studies. In Brazil 1 and Mexico dry, increased species density was associated with positive and increasing rates of change in stem density (Fig. 3C). In Brazil 2 and Mexico wet, rates of change in basal area decreased dramatically at low levels of species density, and then stabilized (Fig. 3F). Although these patterns may not reflect causal relationships, they might mirror the resultant patterns of underlying processes specific to some sites. For instance, during the first years of succession in Mexico wet, the low diversity assemblage of pioneer species experienced an acute mortality episode that was accompanied by a sudden reduction in basal area (17).

Relative Importance of Predictability and Uncertainty in Successional Trajectories.

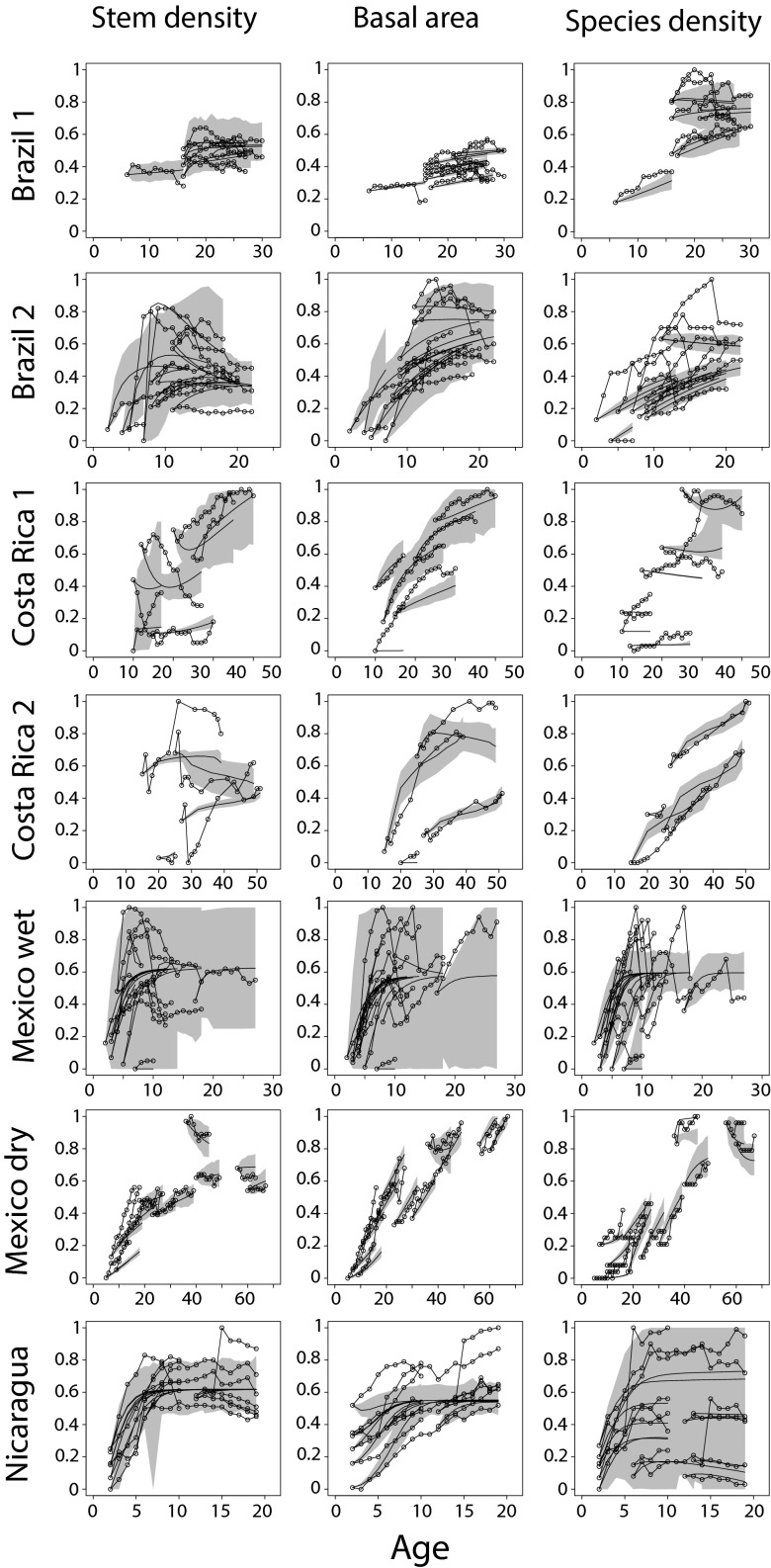
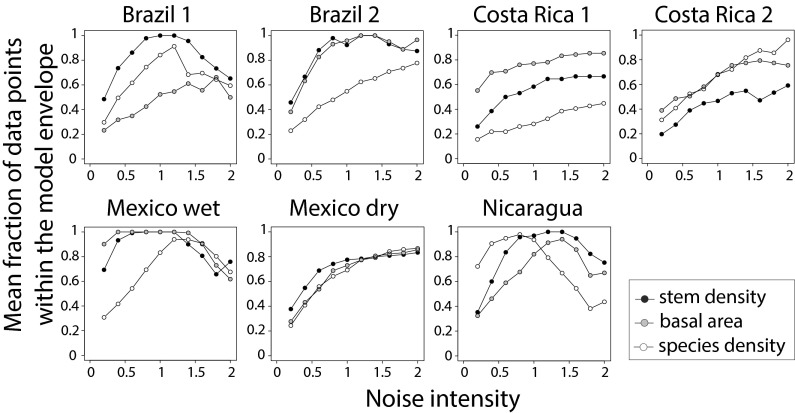
Despite the overall good fit of the nonlinear deterministic models (Fig. S1), the correlation between observed and predicted temporal trajectories of the three state variables for each plot within each site was not significantly positive in many cases (143/201; Table S6). To assess the degree of uncertainty underlying the predictability of the deterministic model, we incorporated a stochastic component to the nonlinear models by generating 1,000 trajectories given the observed initial conditions and a parameter $\alpha$, which modulates the amount of noise integrated to the model. The model envelopes defined by the stochastic trajectories included the greatest part of the observed trajectories only when the relative magnitude of the stochastic and deterministic components was set to be similar ($0.8<\alpha <1.2$; Fig. 4), and only in one or two of the three attributes. The sole site for which the model was able to predict the entire set of time series for all three attributes was Mexico wet, and this needed an important contribution of the stochastic component ($\alpha >1$). Although the predictability of the model (the fraction of data points within the model envelope) increased as the relative magnitude of the stochastic component increased, it never reached the maximum value (one) for many forest attributes in certain sites (e.g., Costa Rica 1 and Mexico dry). Indeed, in some cases, the predictability of the stochastic model decreased as $\alpha$ increased (e.g., species density in Nicaragua) because the addition of noise to the nonlinear deterministic model launched the trajectory of the system into a region of phase space with negative values in the state variables, resulting in a mathematical artifact (Methods).

Fig. S1.

Modeled successional pathways of community attributes. For each plot within each site, temporal changes in the standardized values in stem density, basal area, and species density are plotted against age since abandonment (thin lines connecting blank dots). Continuous thick curves show the fitted deterministic model (Eq. 2c). The gray envelopes are defined by the 1,000 trajectories generated by the stochastic model for $\alpha =0.5$.

Table S6.

Relationship between the observed and predicted values of stem density, basal area, and species density within each site

Site	Forest structure attribute	Range in the slopes	Significantly positive	Significantly negative	Nonsignificant
Brazil 1 (8)	Stem density	−0.16 to +0.44	0	0	8
	Basal area	−0.47 to +0.61	0	0	8
	Species density	−0.21 to +0.82	3	0	5
Brazil 2 (12)	Stem density	−2.40 to +4.33	11	1	0
	Basal area	+0.03 to +11.78	6	0	6
	Species density	−0.02 to +1.10	3	2	7
Costa Rica 1 (6)	Stem density	0 to +0.67	1	0	5
	Basal area	+0.01 to +0.99	3	0	3
	Species density	−0.10 to +0.07	0	0	6
Costa Rica 2 (4)	Stem density	+0.07 to +0.22	1	0	3
	Basal area	+0.02 to +0.81	2	0	2
	Species density	+0.32 to +0.98	1	0	3
Mexico wet (13)	Stem density	−0.35 to +1.81	3	2	8
	Basal area	0 to +0.97	6	0	7
	Species density	−0.87 to +1.69	1	0	12
Mexico dry (12)	Stem density	−0.44 to +1.24	2	1	9
	Basal area	+0.07 to +1.01	5	0	7
	Species density	−0.01 to +1.28	5	0	7
Nicaragua (12)	Stem density	−0.33 to +0.74	0	0	12
	Basal area	0 to +1.43	5	0	7
	Species density	−0.04 to +0.76	0	0	12
Total no. of cases			58	6	137

The results summarize a linear ANCOVA model relating the predicted to the observed values in stem density, basal area and species density in each site, based on the best-fit nonlinear model (Eq. 2c), and including plot as a covariate. Reported are the range in the estimated slopes relating observed to predicted values for each plot, the number of slopes that were significantly positive, significantly negative, and nonsignificantly different from zero. The numbers in parentheses refer to the number of plots included in this analysis for each site.

Fig. 4.

Predictability of the stochastic model as a function of noise intensity. Mean fraction of the observed data points describing the successional trajectories in stem density, basal area, and species density that lie within the envelope generated by the stochastic model at different levels of noise intensity.

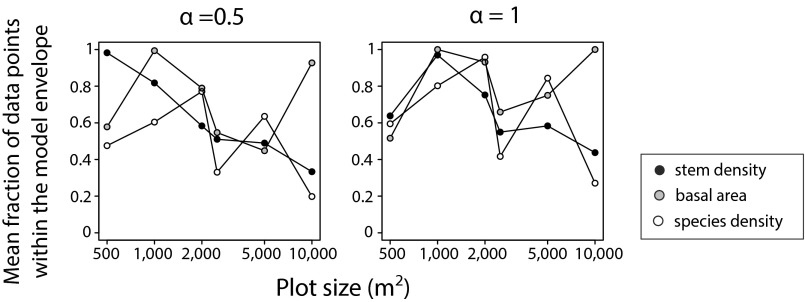
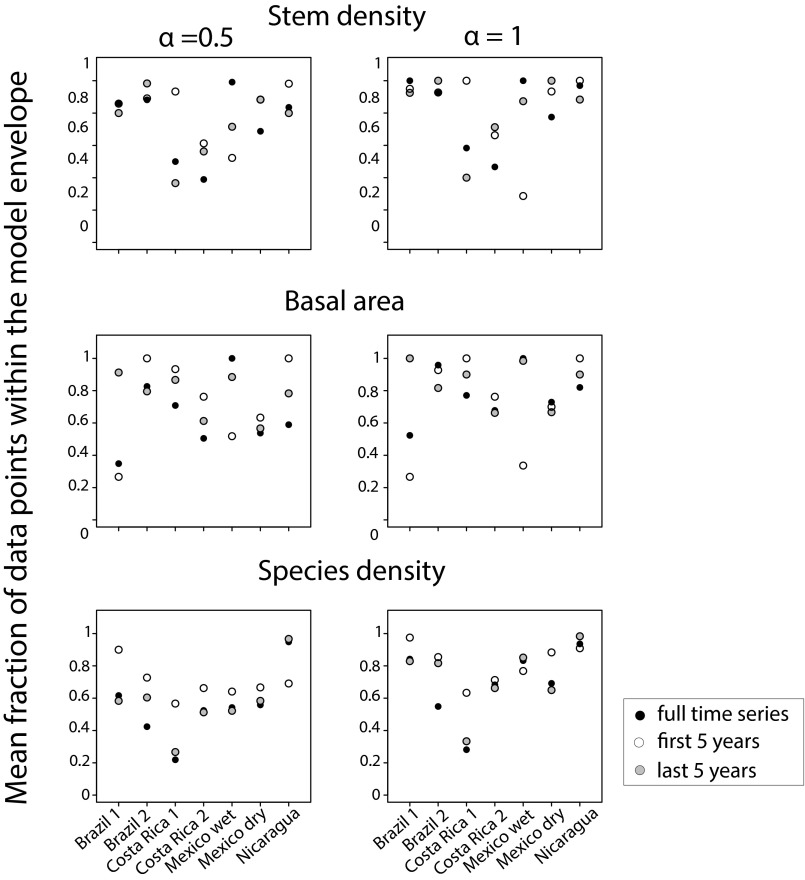
Overall, the observed patterns were highly idiosyncratic, and the predictability of forest attributes did not show consistent trends across attributes, sites, or land use history. None of the forests attributes showed higher predictability than the others (Fig. 4), and sites without any previous land use (Brazil 1, Costa Rica 2, and Nicaragua) showed similar patterns to those used for pastures (Brazil 2 and Costa Rica 1) or agriculture (Mexico wet and Mexico dry). Furthermore, the magnitude of noise intensity required to increase model predictability was independent of plot size and of time series length (Figs. S2 and S3). Indeed, the larger Costa Rican plots (>1 ha) showed similar idiosyncratic patterns to those observed in other sites.

Fig. S2.

Effect of plot size on stochastic model performance. Mean fraction of the observed data points describing the successional trajectories of stem density, basal area, and species density that are within the model envelopes generated by the stochastic model, depending upon plot size, for $\alpha =0.5$ and $\alpha =1$. Plot sizes represent a subsampling of the 1-ha plots from Costa Rica 1. Plot size does not have a systematic effect on the predictability (fraction of data points within the model envelope) of any of the forest attributes evaluated.

Fig. S3.

Effect of time series length on stochastic model performance. For each site, mean fraction of the observed data points describing the successional trajectories of stem density, basal area, and species density that are within the model envelopes generated by the stochastic model, depending upon time series length, for $\alpha =0.5$ and $\alpha =1$. If time series length had an effect on model performance, shorter times series would have been expected to show lower predictability, that is, a smaller fraction of observed data points would occur within the model envelopes. Time series length does not have a systematic effect on the predictability (fraction of data points within the model envelope) of any of the forest attributes evaluated, at any of the sites.

Discussion

Our multisite, long-term study sheds new light on the nature of successional dynamics. Our model was able to reproduce many of the general successional trends observed for these trajectories, yet the spatiotemporal trajectories in these forest attributes revealed high levels of uncertainty. Even when accounting for previous land use and variation in initial conditions at the first census, the deterministic and stochastic components of the model had to be similar in magnitude to predict successional trajectories accurately. Although variation in successional pathways has been widely acknowledged (14, 15, 18), quantifying the magnitude of this variability has remained an elusive goal. To our knowledge, our results provide the first quantitatively robust, multisite assessment of the extent of uncertainty during tropical forest succession using long-term datasets.

Previous attempts to model secondary forest dynamics have focused on mechanistic approximations based on species-specific equations to predict changes in species performance and composition in temperate stands (24, 25). This level of accuracy is impractical in tropical forests, where hundreds of tree species coexist. Here, we intended to represent nature through models focusing on the autogenic forces that drive succession. We acknowledge that our approach was not strictly mechanistic, yet parameters estimated by the deterministic component of our model reinforced our understanding of stand dynamics at different stages of succession. We detected different processes occurring early in succession, such as density-dependent thinning and basal area accumulation as a consequence of increasing tree recruitment (9). Likewise, the competitive pressure leading to a decrease in species colonization rates was also observed in most sites (20). Although these results have already been reported in the literature, they validate our model and demonstrate that the fitted parameters do reveal many of the ecological processes driving successional dynamics. Our model further reveals previously unexplored patterns, such as the relationship between species density and rates of change in stem density and basal area. As these associations were only observed in a few sites, further work may help to disentangle the mechanisms through which species diversity affects biomass dynamics and thereby ecosystem function (26). Overall, the strength of these processes differed widely among sites, which may reflect site-specific characteristics related to species composition, stand age distribution, and environmental and landscape factors.

Most of our understanding in tropical successional ecology is embedded in a deterministic framework where successional pathways are primarily driven by autogenic factors, and prior disturbances due to anthropogenic land use are typically the only allogenic, external forces considered (11, 12). Our results showed that successional pathways were highly idiosyncratic among nearby plots of the same age since abandonment with similar disturbance history, and therefore we strongly advise caution in making inferences about rates of vegetation change based on single-time censuses (27). Interestingly, the strength of such idiosyncrasy was not linked to the nature or intensity of prior land use. The sites where secondary forests were regenerating after pasture (Brazil 2 and Costa Rica 1) or shifting cultivation (Mexico wet and Mexico dry) did not show any notable difference in terms of predictability of successional trajectories compared with sites with forests regenerating after clear-cutting with no subsequent land use (Brazil 1 and Costa Rica 2). Even the forest plots in Nicaragua, where monitoring in all plots started simultaneously soon after the passage of Hurricane Joan, showed high among-plot variability in their successional trajectories.

The complexity of site factors and their interaction with land use is widely acknowledged and challenges our ability to predict successional pathways at local or regional spatial scales (7). Topographic variation in soil quality and drainage, distance to other forest patches, continuous changes in the surrounding landscape, initial species and functional composition, fire frequency, and neighborhood effects all influence rates of vegetation change in successional pathways (27). Moreover, a myriad of local factors including priority effects, invasive species, weed control, last crop planted, nutrient treatments, pathogen and herbivore loads, and persistent edge effects can alter successional processes and push community trajectories in unpredictable directions (18). Although the nonlinear model developed here does not explicitly include local and landscape factors, a key feature of our approach is its high sensitivity to initial conditions in stem density, basal area, and species density, which may account for some of these historical contingencies. Our results underscore the need for future cross-site, long-term successional studies that consider local, previously unmeasured factors, and ongoing changes in the surrounding landscape.

By emphasizing the emergent properties of communities, we believe that the model developed here represents, to date, the best approach for characterizing tropical forest successional dynamics. Despite the high levels of uncertainty detected, we might be able to elucidate the underlying processes behind the patterns observed, and to anticipate ecosystem change through the further development of high-dimensional models (28). Other metrics, such as species and functional dominance could also provide critical insights about the dynamic relation between functional traits and biomass accumulation (26). A challenging goal remains to model multidimensional variables such as species or functional composition. Although more complex, successional pathways based on these metrics may be more predictable, as species and functional composition are likely to be determined by niche-based processes (29, 30).

A potential limitation of our results is that they portray the first decades of succession, which reflect the predominant age classes of regenerating forests in the Neotropics (12). Only one site, Mexico dry, comprises secondary stands over 60 y old, and Nicaragua is the sole site that shows rates of change in forest structure since the beginning of the successional process (18). Despite representing the most extensive monitoring of forest succession in the tropics, 10–15 y of census data are insufficient to capture the entire range over which rates of vegetation change are the most dynamic (20). Longer time series would allow to evaluate the extent of convergence in successional trajectories within the next decades (31). Also, they would give essential information about how secondary forests respond to unpredictable climatic events, thereby elucidating forest resilience and identifying potential tipping points (32). As abrupt changes are unlikely to be predicted by deterministic models, our approach would provide insights about the extent of uncertainty in these atypical cases.

Because all natural systems interact with their surroundings and are subject to historical contingencies, it is highly impractical to measure all of the factors affecting forest succession. This complexity constrains our capacity to distinguish ecological signals from noise in the successional process. When patterns do not follow deterministic predictions, ecologists often invoke stochasticity (3). Such a dual perception of ecological processes hampers a synthetic understanding of community reassembly in regenerating forests (6). Indeed, in complex adaptive systems, erratic patterns can arise from either stochastic processes that emerge from seemingly random fluctuations, or from unexplained but causal variability emerging from “unknown unknowns” (33). Thus, despite the high levels of ecological noise observed here, what we typically view as stochasticity may ultimately be explained by deterministic factors that have not been measured or incorporated. Our study calls for a better evaluation of the historical contingencies and landscape variables affecting succession. As regenerating forests have a great potential to become important biodiversity reservoirs and deliver environmental cobenefits in an economically viable manner (34), we urgently need a better interpretation of research findings related with successional ecology. If secondary succession is highly context dependent—as supported by this study—evaluating the extent of uncertainty in successional trajectories in relation to local, landscape, and regional variables will allow a better understanding of the sources of variation in stand dynamics in human-modified landscapes. New, integrated approaches that model communities as complex systems will enable prediction of response envelopes to guide the research agenda and the effective management of regenerating forests, which currently encompass more than one-half of all tropical forests globally (8).

Methods

Study Sites and Data.

We used multitemporal (repeated-measures) forest dynamics data from multiple lowland Neotropical terra firme forests located in Brazil, Costa Rica, Mexico, and Nicaragua (more details in SI Methods and Table S1). Within each site, 4–15 permanent plots were established in secondary stands of different ages but with similar disturbance histories and environmental conditions, and were monitored annually for at least 8 y, except for a few plots that were accidentally burnt.

Dynamical Modeling.

We quantified predictability and uncertainty during succession in each of the seven sites by using dynamic, stochastic models to fit the observed rates of change in stem density, basal area, and species density simultaneously (Fig. 1). We excluded from this analysis six plots in Brazil 1, one in Brazil 2, and two in Mexico wet as they were monitored for less than 4 consecutive years because of burnings. Stochastic models integrate predictability (deterministic drivers) and uncertainty (stochasticity), as described by a system of stochastic differential equations of the Langevin form (35):

$$\frac{d}{dt}\mathit{X}\left(t\right)=\mathit{g}\left(\mathit{X}\left(t\right),t\right)+\mathit{h}\left(\mathit{X}\left(t\right),t\right)\cdot \mathrm{\Gamma }\left(t\right),$$ [1]

where X denotes the state of the system at a given time, characterized by three state variables: stem density, basal area, and species density. The right side of Eq. 1 describes the magnitude of the derivative of each component X over time as the sum of a deterministic function $\mathit{g}\left(\mathit{X}\left(t\right),t\right)$, and a stochastic function $\mathit{h}\left(\mathit{X}\left(t\right),t\right)\cdot \mathrm{\Gamma }\left(t\right)$, where $\mathrm{\Gamma }\left(t\right)$ stands for terms of Gaussian white noise (Fig. 1).

Deterministic component of the model.

We first defined the deterministic component of Eq. 1, $\mathit{g}\left(\mathit{X}\left(t\right),t\right)$, through a system of first-order differential equations, where the change in each state variable at time $t+\tau$ depends only on its state at time $t$. For each site, this system of equations simultaneously models all of the observed trajectories of stem density, basal area, and species density over time, starting at the first census value for each plot. It must be noted that initial conditions for each plot denote the first observation available for each trajectory and are not modeled as the beginning of the successional process at $t_0$ after land abandonment. Thus, our results are not biased by among-plot variability in stand age at first census, or by temporal changes in the rates of change in forest structure attributes as succession unfolds.

Because forest structure attributes varied over widely different ranges, we normalized these state variables by scaling them between 0 and 1, so that $X=\left(x-x_{min}\right)/\left(x_{max}-x_{min}\right)$. This standardization allowed values to be adjusted for different levels of magnitude, without changing the shape of the distribution. The common z standardization was not applied to keep the state variables positive. Otherwise, this would cause mathematical artifacts in one of our candidate models (Eq. 2c), as the system of equations cannot be solved in the domain of the real numbers because a negative number cannot be raised to a fractional power.

For each of the seven sites, we tested three candidate models. Linear functions are the most commonly used approximation to investigate the relationships between quantitative variables, and provide an accurate picture for assessing local stability points in the study of dynamical systems. Thus, our first model described a linear relationship between the rates of change in stem density (D), basal area (BA), and species density (S) as follows:

$$\{\begin{array}{c}\frac{dD}{dt}=a_{11}D+a_{12}BA+a_{13}S\\ \frac{dBA}{dt}=a_{21}D+a_{22}BA+a_{23}S\\ \frac{dS}{dt}=a_{31}D+a_{32}BA+a_{33}S\end{array}.$$ [2a]

Because this model ignores possible interactions among the state variables, which are frequent in ecological systems, we formulated a second, alternative model, which included interactions among the state variables as follows:

$$\{\begin{array}{c}\frac{dD}{dt}=a_{11}D+a_{12}D\times BA+a_{13}D\times S\\ \frac{dBA}{dt}=a_{21}BA+a_{22}BA\times D+a_{23}BA\times S\\ \frac{dS}{dt}=a_{31}S+a_{32}S\times D+a_{33}S\times BA\end{array}.$$ [2b]

However, most systems are inherently nonlinear in nature. Indeed, rates of community change during succession are characterized by saturating curves (20). Also, as successional trajectories are highly sensitive to initial conditions, small differences may be amplified and lead to divergent trajectories, thereby resulting in nonlinearities (23). For these reasons, the third model included nonlinearities in the system as follows:

$$\{\begin{array}{c}\frac{dD}{dt}=a_{11}{D}^{b_{11}}+a_{12}B{A}^{b_{12}}+a_{13}{S}^{b_{13}}\\ \frac{dBA}{dt}=a_{21}{D}^{b_{21}}+a_{22}B{A}^{b_{22}}+a_{23}{S}^{b_{23}}\\ \frac{dS}{dt}=a_{31}{D}^{b_{31}}+a_{32}B{A}^{b_{32}}+a_{33}{S}^{b_{33}}\end{array}.$$ [2c]

The best-fit model was found using a genetic algorithm, a heuristic method in which a randomly created population of parameters is optimized by means of crossover and mutation operators in a process that mimics natural selection (36). By these means, new solutions to the system of equations are created, different from the parent solutions, thereby avoiding local minima. The algorithm was run 2,000 times until reaching the minimum objective function, i.e., the minimum root-mean-square error of the observations and model estimates, as follows:

$$\min \left(\delta \right)={\displaystyle \sum }_{i=1}^n\left(\frac{\left|D_{obs}-D_{sim}\right|}{\text{max}\left(D_{obs}\right)}+\frac{\left|B{A}_{obs}-B{A}_{sim}\right|}{\text{max}\left(B{A}_{obs}\right)}+\frac{\left|S_{obs}-S_{sim}\right|}{\text{max}\left(S_{obs}\right)}\right),$$ [3]

where D, BA, and S are the normalized, temporal trajectories in stem density, basal area, and species density, respectively, $\delta$ refers to the objective function, and n, the number of plots within a site. This method implements a numerical solution for these first-order differential equations by defining a ∆t = 0.1 y. This time step is small enough to assume that the instantaneous rate of change modeled can be assimilated to the rate of change at each time step.

We assessed the predictive power of the three candidate models using the Nash–Sutcliffe model efficiency (NSE) coefficient (37), defined as follows:

$$NSE=1-\frac{{{\displaystyle \sum }}_{i=1}^n{\left(Y_i^{obs}-Y_i^{sim}\right)}^2}{{{\displaystyle \sum }}_{i=1}^n{\left(Y_i^{obs}-\overline{Y_{obs}}\right)}^2},$$ [4]

where $Y_i^{obs}$ is the ith observed value, $Y_i^{sim}$ is the ith simulated value, ${\overline{Y}}_{obs}$ is the mean of observed data, and n is the total number of observations for each site. The NSE coefficient is a normalized statistic that determines the relative magnitude of the residual variance compared with the measured data variance. This metric indicates how well the plot of observed versus modeled data fits the 1:1 line. NSE ranges between $-\infty$ and 1, with NSE = 1 being the optimal value. Values between 0 and 1 are generally viewed as acceptable levels of performance, whereas values <0 indicates that the mean observed value is a better predictor than the simulated one, which indicates unacceptable model performance (37).

To account for the number of parameters as a criterion for model selection and avoid overfitting, we calculated an approximate Akaike information criterion (AIC) for each model, as follows:

$$AIC=-2\hspace{0.17em}\hspace{0.17em}\times \hspace{0.17em}loglik+\left(2\hspace{0.17em}\times \hspace{0.17em}npar\right),$$ [5]

where loglik is the log-likelihood of the regression relating observed and fitted values and npar is the number of parameters of each candidate model. This approximate AIC balances the goodness of fit (as measured by the log-likelihood of the regression relating observed and fitted values) and the number of parameters of the models (38).

Because the nonlinear model (Eq. 2c) performed better than the linear model (Eq. 2a) or the linear model with interactions (Eq. 2b), we did a backward elimination of the terms for which no previous information on their effects on the rates of change in stem density, basal area, or species density was available. These were (i) the effect of species density on the rates of change in stem density, (ii) the effect of species density on the rates of change in basal area, and (iii) the effect of basal area on the rates of change in species density. Overall, we compared the seven models resulting from the elimination of these three terms separately and all its possible combinations (Table S4). For each site and each attribute, the best-fit model was selected using the NSE and AIC, as described above.

Stochastic component of the model.

In a second step, we incorporated the stochastic component of Eq. 1 as Gaussian white noise added to each of the coefficients estimated from Eq. 2c. We generated a set of infinite trajectories of the process constrained within an envelope, given the set of initial conditions observed in each site (Fig. 1). The width of the envelope depends on the magnitude of the stochastic component in Eq. 1, so that

$$h\left(\mathit{X}\left(\mathit{t}\right)\right)=\alpha \cdot g\left(\mathit{X}\left(\mathit{t}\right)\right),$$ [6]

where $\alpha$ is the modulating factor determining noise intensity. When $\alpha =0$, the magnitude of the stochastic component of the model is null. If $\alpha =1$, the deterministic and stochastic components of the model are equivalent. If $\alpha >1$, the magnitude of the stochastic component of the model is greater than that of the deterministic model. In the stochastic model, each component of X is treated as a random process. If we set $X\left(t_i\right)=x +\hspace{0.17em}\mathrm{\Delta }x$, then the distribution of the predicted values of $x$ at the next step of the trajectory $X\left(t_i+\tau \right)$ is given by a Gaussian function with mean $x\hspace{0.17em}+\hspace{0.17em}g\left(x\right)\tau$ and SD $h\left(x\right)\sqrt{\tau }$ (35) (Fig. 1). The codes for running the stochastic model were written in Matlab 7.2.

SI Methods

Study Sites and Data.

In Brazil, study plots were located about 80 km north of Manaus, Amazonas (2°24′S, 54°54′W). Forests regenerating after clear-cut with little or no burning were dominated by species of the genus Cecropia, whereas areas following pasture were typically dominated by species of the genus Vismia (31, 39). Because of these differences in land use, we grouped plots into two sites called Brazil 1 (Cecropia-dominated) and Brazil 2 (Vismia-dominated), and analyzed them separately. In Costa Rica, study plots were located in the Sarapiquí region, Heredia (10°25′N, 84°00′W). As in Brazil, secondary forest plots were analyzed separately according to their land use, so that two different sites were defined. Plots established on abandoned pastures were classified as Costa Rica 1, and those that were clear-cut without subsequent use were classified as Costa Rica 2 (14). In Mexico, study plots were located in two different regions: one site, adjacent to Montes Azules Biosphere Reserve, Chiapas (16°01′N, 90°55′W), is dominated by wet forests (Mexico wet) (17); the second site, on the Pacific slope of the Isthmus of Tehuantepec, Oaxaca (16°39′N, 95°00′W), is dominated by deciduous dry forests (Mexico dry) (16). All Mexican plots were established on abandoned cornfields. In Nicaragua, study plots were located in regenerating primary wet forests of the Caribbean coast (12°3′N, 83°56′W), established after the landfall of Hurricane Joan of October 1988 (18). The plots comprised by each site share similar climate, soil type, land use history, and vegetation composition.

Multiple stemmed individuals were tallied as a single individual. We standardized stem density, basal area, and species richness by plot size, depending upon the site (0.04 ha for Mexico dry, 0.05 ha for Brazil and Mexico wet, 0.1 ha for Nicaragua, and 1 ha for Costa Rica 1 and 1.16 ha for Costa Rica 2). We measured species richness within each plot as species density because the modeling procedure already takes into account temporal changes in stem density, and other commonly used metrics of diversity such as rarefied richness, which controls for differences in stem density, would have been redundant. Although we acknowledge that the species–area relationship is not linear, this standardization was only performed in Brazil 1 and Brazil 2, which had variable plot sizes. In these two sites, as the plots were very small (0.01–0.06 ha), the relationship between species richness and area was linear (39). We chose the smallest plot size to perform the standardization to avoid improper extrapolation of species counts from smaller to larger areas. In Costa Rica 2, all plots were 1.16 ha, except for one, which increased from 0.33 to 1.16 ha in the third census period. For this site, we omitted species density values in the first two censuses for the smallest plot.

Effects of Stand Age and Plot Factors.

For each site, we used one-way random-effects ANOVA for repeated measures to test for the effect of stand age since abandonment (fixed effect) and plot identity (random effect) on stem density, basal area, and species density in each site. These analyses were performed using the R statistical package (40).

Importance of Plot Size and of Time Series Length.

We assessed the effect of plot size and of time series length in the level of noise needed to increase model predictability. To assess the effect of plot size, we subsampled the plots from Costa Rica 1, one of the sites with the biggest plots, and ran the stochastic model in subplots of 500, 1,000, 2,000, 5,000, and 10,000 m². We then evaluated whether the fraction of data points describing the trajectories in stem density, basal area, and species density that were within the envelope generated by the stochastic model for $\alpha =0.5$ and $\alpha =1$ varied depending upon sample size.

We assessed the effect of time series length by subsampling either the first or the last 5 y of data for each plot within each site. We then compared the outcome of the stochastic model based on these two data subsets and the one using the original data for $\alpha =0.5$ and $\alpha =1$.