Score As You Lift (SAYL): A Statistical Relational Learning Approach to Uplift Modeling

Abstract

We introduce Score As You Lift (SAYL), a novel Statistical Relational Learning (SRL) algorithm, and apply it to an important task in the diagnosis of breast cancer. SAYL combines SRL with the marketing concept of uplift modeling, uses the area under the uplift curve to direct clause construction and final theory evaluation, integrates rule learning and probability assignment, and conditions the addition of each new theory rule to existing ones.

Breast cancer, the most common type of cancer among women, is categorized into two subtypes: an earlier in situ stage where cancer cells are still confined, and a subsequent invasive stage. Currently older women with in situ cancer are treated to prevent cancer progression, regardless of the fact that treatment may generate undesirable side-effects, and the woman may die of other causes. Younger women tend to have more aggressive cancers, while older women tend to have more indolent tumors. Therefore older women whose in situ tumors show significant dissimilarity with in situ cancer in younger women are less likely to progress, and can thus be considered for watchful waiting.

Motivated by this important problem, this work makes two main contributions. First, we present the first multi-relational uplift modeling system, and introduce, implement and evaluate a novel method to guide search in an SRL framework. Second, we compare our algorithm to previous approaches, and demonstrate that the system can indeed obtain differential rules of interest to an expert on real data, while significantly improving the data uplift.

1 Introduction

Breast cancer is the most common type of cancer among women, with a 12% incidence in a lifetime [2]. Breast cancer has two basic categories: an earlier in situ stage where cancer cells are still confined to where they developed, and a subsequent invasive stage where cancer cells infiltrate surrounding tissue. Since nearly all in situ cases can be cured [1], current practice is to treat in situ occurrences in order to avoid progression into invasive tumors [2]. Nevertheless, the time required for an in situ tumor to reach invasive stage may be sufficiently long for an older woman to die of other causes, raising the possibility that treatment may not have been necessary.

Cancer occurrence and stage are determined through biopsy, a costly, invasive, and potentially painful procedure. Treatment is also costly and may generate undesirable side-effects. Hence there is a need for pre-biopsy methods that can accurately identify patient subgroups that would benefit most from treatment, and especially, those who do not need treatment. For the latter, the risk of progression would be low enough to employ watchful waiting (mammographic evaluation at short term intervals) rather than biopsy [26].

Fortunately, the literature confirms that the pre-biopsy mammographic appearance as described by radiologists can predict breast cancer stage [28, 29]. Furthermore, based on age, different pre-biopsy mammographic features can be used to classify cancer stage [18]. A set of mammography features is differentially-predictive if it is significantly more predictive of cancer in one age group as compared to another. We may be able to use such differentially-predictive features to recommend watchful waiting for older in situ patients accurately enough to safely avoid additional tests and treatment.

In fact, younger women tend to have more aggressive cancers that rapidly proliferate, while older women tend to have more indolent cancers [8, 13]. We assume that younger in situ patients should always be treated, due to the longer potential time-span for cancer progression. We also assume that older in situ patients whose mammography features are similar to in situ in younger patients should also be treated, because the more aggressive nature of cancer in younger patients may be conditioned on those features. On the other hand, older in situ patients whose mammography features are significantly different from features observed in younger in situ patients are less likely to experience rapid proliferation, and can thus be recommended for watchful waiting.

The general task of identifying differentially predictive features occurs naturally in diverse fields. Psychologists initially assessed for differential prediction using linear regression, defining it as the case where a common regression equation results in systematic nonzero errors of prediction for given subgroups [6]. The absence of differential prediction over different groups of examinees was an indicator of the fairness of a cognitive or educational test [31].

Psychologists aim to decrease differential prediction on their tests. This is not the case in the closely related concept of uplift modeling, a modeling and classification method used in marketing to determine the incremental impact of an advertising campaign on a given population. Uplift modeling is effectively a differential prediction approach aimed at maximizing uplift [11, 16, 23]. Uplift is defined as the difference in a model or intervention M’s lift scores over the subject and control sets:

$${\mathit{\text{Uplift}}}_M={\mathit{\text{Lift}}}_M(\mathit{\text{subject}})-{\mathit{\text{Lift}}}_M(\mathit{\text{control}}).$$ (1)

Given a fraction ρ such that 0 ≤ ρ ≤ 1, a model M’s lift is defined as the number of positive examples amongst the model’s ρ-highest ranking examples. Uplift thus captures the additional number of positive examples obtained due to the intervention. We generate an uplift curve by ranging ρ from 0 to 1 and plotting Uplif t_M. The higher the uplift curve, the more profitable a marketing model/intervention is.

The motivating problem at hand can readily be cast as an uplift modeling problem (see Table 1). Even though we are not actively altering the cancer stage as a marketing intervention would alter the subject population behavior, one may argue that time is altering the cancer stage. Our subject and control sets are respectively older and younger patients with confirmed breast cancer —where time, as an intervention, has altered the cancer stage— and we want to predict in situ versus invasive cancer based on mammography features. By maximizing the in situ cases’ uplift, which is the difference between a model’s in situ lift on the older and younger patients, we are identifying the older in situ cases that are most different from younger in situ cases, and thus are the best candidates for watchful waiting. Exactly like a marketing campaign would want to target consumers who are the most prone to respond, we want to target the ones that differ the most from the control group.

Table 1.

Casting mammography problem in uplift modeling terms

Intervention	Subject Group	Control Group	Positive Class	Negative Class
Time	Older cohort	Younger cohort	In Situ	Invasive

In recent work, Nassif et al. inferred older-specific differentially-predictive in situ mammography rules [20]. They used Inductive Logic Programming (ILP) [14], but defined a differential-prediction-sensitive clause evaluation function that compares performance over age-subgroups during search-space exploration and rule construction. To assess the resulting theory (final set of rules), they constructed a TAN classifier [9] using the learned rules and assigned a probability to each example. They finally used the generated probabilities to construct the uplift curve to assess the validity of their model.

The ILP-based differential prediction model [20] had several shortcomings. First, this algorithm used a differential scoring function based on m-estimates during clause construction, and then evaluated the resulting theory using the area under the uplift curve. This may result in sub-optimal performance, since rules with a high differential m-estimate score may not generate high uplift curves. Second, it decoupled clause construction and probability estimation: after rules are learned, a TAN model is built to compute example probabilities. Coupling these two processes together may generate a different theory with a lower ILP-score, but with a more accurate probability assignment. Finally, rules were added to the theory independently of each other, resulting in redundancies. Having the addition of newer rules be conditioned on the prior theory rules is likely to improve the quality and coverage of the theory.

In this work, we present a novel relational uplift modeling Statistical Relational Learning (SRL) algorithm that addresses all the above shortcomings. Our method, Score As You Lift (SAYL), uses the area under the uplift curve score during clause construction and final theory evaluation, integrates rule learning and probability assignment, and conditions the addition of new theory rules to existing ones. This work makes two main contributions. First, we present the first multi-relational uplift modeling system, and introduce, implement and evaluate a novel method to guide search in an SRL framework. Second, we compare our algorithm to previous approaches, and demonstrate that the system can indeed obtain differential rules of interest to an expert on real data, while significantly improving the data uplift.

2 Background: The SAYU Algorithm

Score As You Use (SAYU) [7] is a Statistical Relational Learner [10] that integrates search for relational rules and classification. It starts from the well known observation that a clause or rule r can be mapped to a binary attribute b, by having b(e) = 1 for an example e if the rule r explains e, and b(e) = 0 otherwise.

This makes it possible to construct classifiers by using rules as attributes, an approach known as propositionalization [32]. One limitation, though, is that often the propositional learner has to consider a very large number of possible rules. Moreover, these rules tend to be very correlated, making it particularly hard to select a subset of rules that can be used to construct a good classifier.

SAYU addresses this problem by evaluating the contribution of rules to a classifier as soon as the rule is generated. Thus, SAYU generates rules using a traditional ILP algorithm, such as Aleph [27], but instead of scoring the rules individually, as Aleph does, every rule SAYU generates is immediately used to construct a statistical classifier. If this new classifier improves performance over the current set of rules, the rule is added as an extra attribute.

Algorithm 1.

SAYU

Rs ← {}; M0 ← InitClassifier(Rs)

while DoSearch() do

e+ ← RandomSeed();

⊥e+ ← saturate(e);

while c ← reduce(⊥e+) do

M ← LearnClassifier(Rs ∪ {c});

if Better(M, M0) then

Rs ← Rs ∪ {c}; M0 ← M;

break

end if

end while

end while

Algorithm 1 shows SAYU in more detail. SAYU maintains a current set of clauses, Rs, and a current reference classifier, M₀. SAYU extends the Aleph [27] implementation of Progol’s MDIE algorithm [17]. Thus, it starts search by randomly selecting a positive example as seed, e⁺, generating the corresponding bottom clause, ⊥_e⁺, and then generating clauses that subsume ⊥_e⁺. For every new such clause c, it constructs a classifier M and compares M with the current M₀. If better, it accepts c by adding it to Rs and making M the default classifier. SAYU can terminate search when all examples have been tried without adding new clauses. In practice, termination is often controlled by a time limit.

Quite often, most execution time will be spent learning classifiers. Therefore, it is important that the classifier can be learned in a reasonable time. Further, the classifier should cope well with many related attributes. We use the TAN classifier, a Bayesian network that extends naive Bayes with at most one other edge per attribute [9]. TAN has quadratic learning time, which is acceptable for SAYU, and compensates well for highly dependent attributes.

Second, comparing two classifiers is not trivial. SAYU reserves a tuning set for this task: if the classifier M has a better score on both the initial training and tuning sets, the new rule is accepted. The scoring function depends on the problem at hand. Most often SAYU has been used in skewed domains, where the area under the precision-recall curve is regarded as a good measure [5], but the algorithm allows for any metric.

The original SAYU algorithm accepts a logical clause as soon as it improves the network. It may be the case that a later clause would be even better. Unfortunately, SAYU will switch seeds after selecting a clause, so the better clause may be ignored. One solution is to make SAYU less greedy by exploring the search space for each seed, up to some limit on the number of clauses, before accepting a clause. We call this version of SAYU exploration SAYU: we will refer to it as e-SAYU, and to the original algorithm as greedy SAYU, or g-SAYU.

Algorithm 2.

e-SAYU

Rs ← {}; M0 ← InitClassifier(Rs)

while DoSearch() do

e+ ← RandomSeed();

⊥e+ ← saturate(e+);

ce+ ← ⊤; Me+ ← M0;

while c ← reduce(⊥e+) do

M ← LearnClassifier(Rs ∪ {c});

if Better(M, Me) then

ce+ ← c; Me+ ← M;

end if

end while

if ce+ ≠ ⊤ then

Rs ← Rs ∪ {ce+}; M0 ← Me+;

end if

end while

Algorithm 2 details e-SAYU. It differs from g-SAYU in that it keeps track, for each seed, of the current best classifier M_e⁺ and best clause c_e⁺. At the end, if a clause c_e⁺ was found, we commit to that clause and update the classifier.

3 Background: Uplift Modeling

Next we discuss uplift in more detail and compare it to related measures.

3.1 Uplift

Let P be the number of positive examples and N the number of negative examples in a given dataset D. Lift represents the number of true positives detected by model m amongst the top-ranked fraction ρ. Varying ρ ∈ [0, 1] produces a lift curve. The area under the lift curve AUL for a given model and data becomes:

$$AUL=\int \mathit{\text{Lift}}(D,\rho )d\rho \approx \frac{1}{2}\sum _{k=1}^{P+N}({\rho }_{k+1}-{\rho }_k)(\mathit{\text{Lift}}(D,{\rho }_{k+1})+\mathit{\text{Lift}}(D,{\rho }_k))$$ (2)

Uplift compares the difference between the model M over two groups, subjects s and controls c. It is obtained by:

$$\mathit{\text{Uplift}}(M_s,M_c,\rho )={\mathit{\text{Lift}}}_{M_s}(S,\rho )-{\mathit{\text{Lift}}}_{M_c}(C,\rho ).$$ (3)

Since uplift is a function of a single value for ρ, the area under the uplift curve is the difference between the areas under the lift curves of the two models, Δ(AUL).

It is interesting to note the correspondence of the uplift model to the differential prediction framework [20]. The subjects and controls groups are disjoint subsets, and thus form a 2-strata dataset. Lift_M is a differential predictive concept, since maximizing Uplift(M_s, M_c, ρ) requires Lift_Ms (S, ρ) ≫ Lift_Mc (C, ρ). Finally, Uplift is a differential-prediction-sensitive scoring function, since it is positively correlated with Lift_Ms (S, ρ) and negatively correlated with Lift_Mc (C, ρ).

3.2 Lift AUC and ROC AUC

In order to obtain more insight into this measure it is interesting to compare uplift and lift curves with receiver operating characteristic (ROC) curves. We define AUL as the area under the lift curve, and AUR as the area under the ROC curve. There is a strong connection between the lift curve and the ROC curve: Let $\pi =\frac{P}{P+N}$ be the prior probability for the positive class or skew, then:

$$AUL=P*(\frac{\pi }{2}+(1-\pi )AUR)[30,p.549].$$ (4)

In uplift modeling we aim to optimize for uplift over two sets, that is we aim at obtaining new classifiers such that Δ(AUL*) > Δ(AUL), where Δ(AUL) = AUL_s − AUL_c, subscripts s and c referring to the subject and control groups, respectively. The equation Δ(AUL*) > Δ(AUL) can be expanded into:

$$AU{L}_s^{*}-AU{L}_c^{*}>AU{L}_s-AU{L}_c.$$ (5)

Further expanding and simplifying we have:

$$P_s(\frac{{\pi }_s}{2}+(1-{\pi }_s)AU{R}_s^{*})-P_c(\frac{{\pi }_c}{2}-(1-{\pi }_c)AU{R}_c^{*})>P_s(\frac{{\pi }_s}{2}+(1-{\pi }_s)AU{R}_s)-P_c(\frac{{\pi }_c}{2}-(1-{\pi }_c)AU{R}_c)$$

$$P_s(1-{\pi }_s)AU{R}_s^{*}-P_c(1-{\pi }_c)AU{R}_c^{*}>P_s(1-{\pi }_s)AU{R}_s-P_c(1-{\pi }_c)AU{R}_c{P}_s(1-{\pi }_s)(AU{R}_s^{*}-AU{R}_s)>P_s(1-{\pi }_s)(AU{R}_c^{*}-AU{R}_c)$$

and finally

$$\frac{AU{R}_s^{*}-AU{R}_s}{AU{R}_c^{*}-AU{R}_c}>\frac{P_{c}1-{\pi }_c}{P_{s}1-{\pi }_s}.$$ (6)

In a balanced dataset, we have ${\pi }_c={\pi }_s=\frac{1}{2}$ and P_c = P_s, so we have that $\frac{1-{\pi }_c}{1-{\pi }_s}=1$. In fact, if the subject and control datasets have the same skew we can conclude that Δ(AUL*) > Δ(AUL) implies Δ(AUR*) > Δ(AUR).

In the mammography dataset, the skews are P_s = 132, ${\pi }_s=\frac{132}{132+401}(\text{older})$ and ${\pi }_c=\frac{110}{110+264}(\text{younger})$ Thus equation 6 becomes:

$$\frac{AU{R}_s^{*}-AU{R}_s}{AU{R}_c^{*}-AU{R}_c}>0.86.$$ (7)

Therefore we cannot guarantee that Δ(AUL*) > Δ(AUL) implies Δ(AUR*) > Δ(AUR) on this data, as we can increase uplift with rules that have similar accuracy but cover more cases in the older cohort, and there are more cases to cover in the older cohort. On the other hand, breast cancer is more prevalent in older women [1], so uplift is measuring the true impact of the model.

In general, we can conclude that the two tests are related, but that uplift is sensitive to variations of dataset size and skew. In other words, uplift is more sensitive to variations in coverage when the two groups have different size. In our motivating domain, this is particularly important in that it allows capturing information related to the larger prevalence of breast cancer in older populations.

4 SAYL: Integrating SAYU and Uplift Modeling

SAYL is a Statistical Relational Learner based on SAYU that integrates search for relational rules and uplift modeling. Similar to SAYU, every valid rule generated is used for classifier construction via propositionalization, but instead of constructing a single classifier, SAYL constructs two classifiers; one for each of the subject and control groups. Both classifiers use the same set of attributes, but are trained only on examples from their respective groups. If a rule improves the area under the uplift curve (uplift AUC) by threshold θ, the rule is added to the attribute set. Otherwise, SAYL continues the search.

Algorithm 3.

SAYL

Rs ← {}; $M_0^s,M_0^c$ ← InitClassifiers(Rs)

while DoSearch() do

$e_s^{+}$ ← RandomSeed();

${\perp }_{e_s^{+}}$ ← saturate(e);

while c ← reduce(${\perp }_{e_s^{+}}$) do

Ms, Mc ← LearnClassifiers(Rs ∪ {c});

if Better(Ms, Mc, $M_0^s,M_0^c$) then

Rs ← Rs ∪ {c}; $M_0^s,M_0^c$ Ms, Mc;

break

end if

end while

end while

The SAYL algorithm is shown as Algorithm 3. Like SAYU, SAYL maintains separate training and tuning example sets, accepting rules only when the classifiers produce a better score on both sets. This requirement is often extended with a specified threshold of improvement θ, or a minimal rule coverage requirement minpos. Additionally, SAYL also has a greedy (g-SAYL) and exploratory (e-SAYL) versions that operate in the same fashion as they do for SAYU.

The key difference between SAYL and SAYU, then, is that SAYL maintains a distinction between the groups of interest by using two separate classifiers. This is what allows SAYL to demonstrate differential performance as opposed to standard metrics, such as the area under a precision-recall curve. To compute uplift AUC, SAYL simply computes the area under the lift curve for each of the groups using the two classifiers and returns the difference.

SAYL and SAYU also differ in selecting a seed example to saturate. Instead of selecting from the entire set of positive examples, SAYL only selects seed examples from the positive examples in the subject group. This is not necessary, but makes intuitive sense as clauses produced from examples in the subject set are more likely to produce greater lift on the subject set in the first place.

5 Experimental Results

Our motivating application is to detect differential older-specific in situ breast cancer by maximizing the area under the uplift curve (uplift AUC). We apply SAYL to the breast cancer data used in Nassif et al. [20]. The data consists of two cohorts: patients younger than 50 years form the younger cohort, while patients aged 65 and above form the older cohort. The older cohort has 132 in situ and 401 invasive cases, while the younger one has 110 in situ and 264 invasive.

The data is organized in 20 extensional relations that describe the mammogram, and 35 intensional relations that connect a mammogram with related mammograms, discovered at the same or in prior visits. Some of the extensional features have been mined from free text [19]. The background knowledge also maintains information on prior surgeries. The data is fully described in [18].

We use 10-fold cross-validation, making sure all records pertaining to the same patient are in the same fold. We run SAYL with a time limit of one hour per fold. We run folds in parallel. On top of the ILP memory requirements, SAYL requires an extra 0.5 gigabyte of memory for the Java Virtual Machine. For each cross-validated run, we use 4 training, 5 tuning and 1 testing folds. For each fold, we used the best combination of parameters according to a 9-fold internal cross-validation using 4 training, 4 tuning and 1 testing folds. We try both e-SAYL and g-SAYL search modes, vary the minimum number minpos of positive examples that a rule is required to cover between 7 and 13 (respectively 5% and 10% of older in situ examples), and set the threshold θ to add a clause to the theory if its addition improves the uplift AUC to 1%, 5% and 10%. We concatenate the results of each testing set to generate the final uplift curve.

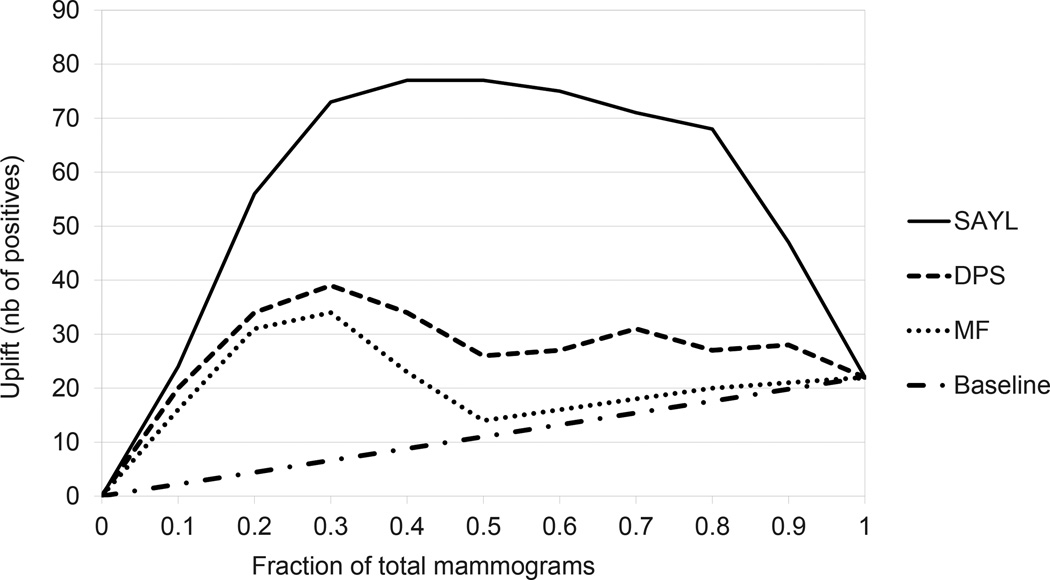
Table 2 compares SAYL with the Differential Prediction Search (DPS) and Model Filtering (MF) ILP methods [20], both of which had minpos = 13 (10% of older in situ). A baseline random classifier achieves an uplift AUC of 11. We use the Mann-Whitney test at the 95% confidence level to compare two sets of experiments. We show the p-value of the 10-fold uplift AUC paired Mann-Whitney of each method as compared to DPS, DPS being the state-of-the-art in relational differential prediction. We also plot the uplift curves in Figure 1.

Table 2.

10-fold cross-validated SAYL performance. AUC is Area Under the Curve. Rule number averaged over the 10 folds of theories. For comparison, we include results of Differential Prediction Search (DPS) and Model Filtering (MF) methods [20].

Algorithm	Uplift AUC	Lift(older) AUC	Lift(younger) AUC	Rules Avg #	DPS p-value
SAYL	58.10	97.24	39.15	9.3	0.002	*
DPS	27.83	101.01	73.17	37.1	-
MF	20.90	100.89	80.99	19.9	0.0039	*
Baseline	11.00	66.00	55.00	-	0.0020	*

We compute the p-value comparing each method to DPS, * indicating significance.

Fig. 1.

Uplift curves for the ILP-based methods (Differential Prediction Search (DPS) and Model Filtering (MF), both with minpos = 13 [20]), a baseline random classifier, and SAYL with cross-validated paramters. Uplift curves start at 0 and end at 22, the difference between older (132) and younger (110) total in situ cases. The higher the curve, the better the uplift.

SAYL 10-fold cross-validation chose g-SAYL in 9 folds and e-SAYL in 1, while minpos was 13 (10% of older in situ) in 5 folds, and 7 (5%) in the remaining 5 folds. θ was selected to be 1% in 4 folds, 5% in 3 folds, and 10% in the remaining 3 folds. Table 3 shows how sensitive SAYL is to those different parameters.

Table 3.

10-fold cross-validated SAYL performance under various parameters. Minpos is the minimum number of positive examples that a rule is required to cover. θ is the up-lift AUC improvement threshold for adding a rule to the theory. We also include results of SAYL using cross-validated parameters and Differential Prediction Search (DPS).

minpos	θ (%)	search mode	Uplift AUC	Lift(older) AUC	Lift(younger) AUC	Rules Avg #	DPS p-value
13	1	g-SAYL	63.29	96.79	33.50	16.4	0.002	*
13	1	e-SAYL	43.51	83.82	40.31	2.0	0.049	*
13	5	g-SAYL	58.06	96.14	38.07	5.9	0.002	*
13	5	e-SAYL	53.37	85.66	32.29	1.8	0.027	*
13	10	g-SAYL	61.68	96.26	34.58	3.6	0.002	*
13	10	e-SAYL	65.36	90.50	25.14	1.1	0.002	*
7	1	g-SAYL	65.48	98.82	33.34	18.3	0.002	*
7	1	e-SAYL	25.50	74.39	48.90	3.0	0.695
7	5	g-SAYL	58.91	96.67	37.76	5.8	0.002	*
7	5	e-SAYL	32.71	79.52	46.81	2.5	0.557
7	10	g-SAYL	61.98	96.87	34.89	3.6	0.002	*
7	10	e-SAYL	52.35	83.64	31.29	1.6	0.002	*
-	-	SAYL	58.10	97.24	39.15	9.3	0.002	*
13	-	DPS	27.83	101.01	73.17	37.1	-

We compute the p-value comparing each method to DPS, * indicating significance.

6 Discussion

6.1 Model Performance

SAYL significantly outperforms DPS (Table 2, Figure 1), while ILP-based runs have the highest older and younger lift AUC (Tables 2, 3). This is because ILP methods use different metrics during clause construction and theory evaluation, and decouple clause construction from probability estimation. SAYL builds models that are slightly less predictive of in situ vs. invasive over the younger subset, as measured by the slightly lower older lift AUC, but on the other hand it effectively maximizes uplift. In fact, increasing lift on one subset will most often increase lift on the other subset, since both sets share similar properties. SAYL avoids this pitfall by selecting rules that generate a high differential lift, ignoring rules with good subject lift that are equally good on the controls. These results confirm the limitations of a pure ILP approach, demonstrating significantly higher uplift using SAYL.

e-SAYL explores a larger search space for a given seed before selecting a rule to add to the theory. This results in smaller theories than greedy g-SAYL. Increasing θ, the uplift AUC improvement threshold for adding a rule to the theory, also results in smaller theories, as expected. Ranging minpos between 7 and 13 doesn’t seem to have a sizable effect on rule number.

g-SAYL’s performance remains constant across all parameters, its uplift AUC varying between 58.06 and 65.48. At the same time, its theory size ranges from 3.6 to 18.3. This indicates that the number of rules is not correlated with uplift AUC. Another indication comes from e-SAYL, whose theory size changes little (1.1 – 3.0), while its performance tends to increase with increasing minpos and θ. Its uplift AUC jumps from the lowest score of 25.50, where it is significantly worse than g-SAYL, to nearly the highest score of 65.36. In fact, g-SAYL outperforms e-SAYL on all runs except minpos = 13 and θ = 10%.

e-SAYL is more prone to over fitting, since it explores a larger search space and is thus more likely to find rules tailored to the training set with a poor generalization. By increasing minpos and θ, we are restricting potential candidate rules to the more robust ones, which decreases the chances of converging to a local minima and overfitting. This explains why e-SAYL had the worst performances with lowest minpos and θ values, and why it achieved the second highest score of all runs at the highest minpos and θ values. These limited results seem to suggest using e-SAYL with minpos and θ equal to 10%.

6.2 Model Interpretation

SAYL returns two TAN Bayes-net models, one for the older and one for the younger, with first-order logic rules as the nodes. Each model includes the classifier node, presented top-most, and the same rules. All rules depend directly on the classifier and have at least one other parent. Although both models have the same rules as nodes, TAN learns the structure of each model on its corresponding data subset separately, resulting in different networks. SAYL identifies the features that best differentiate amongst subject and control positive examples, while TAN uses these features to create the best classifier over each set.

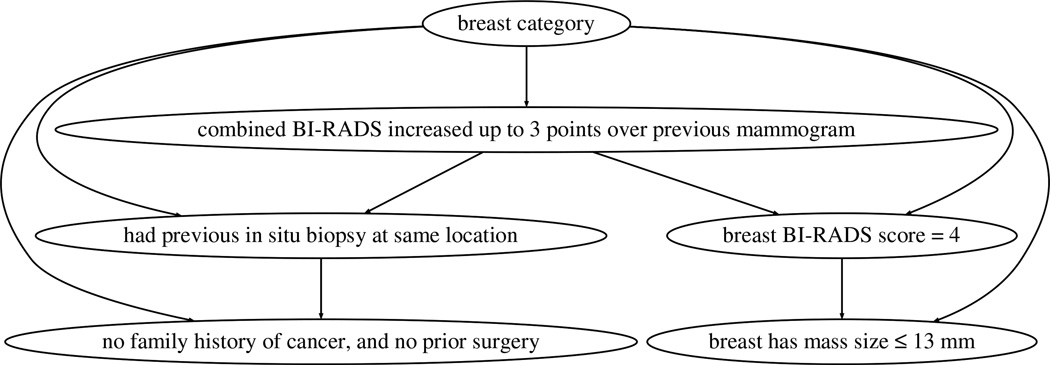
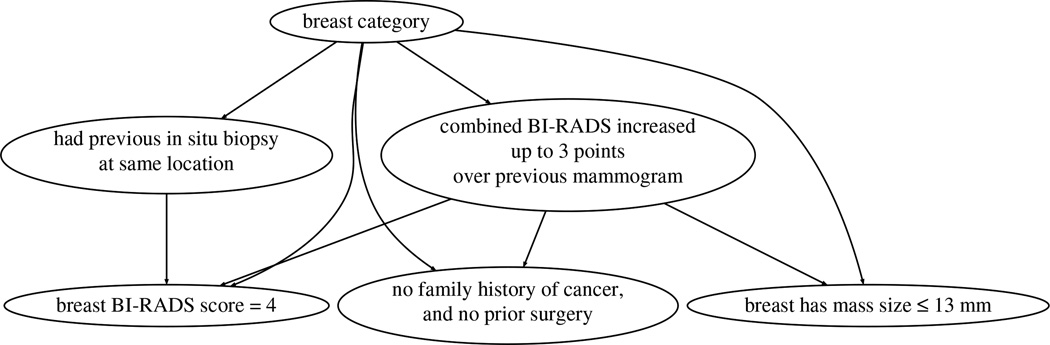
To generate the final model and inspect the resulting rules, we run SAYL with 5 folds for training and 5 for tuning. As an example, Figures 2 and 3 respectively show the older and younger cases TAN models of g-SAYL with minpos = 13 and θ = 5%. The older cohort graph shows that the increase in the combined BI-RADS score is a key differential attribute. The BI-RADS score is a number that summarizes the examining radiologist’s opinion and findings concerning the mammogram [3]. We then can see two sub-graphs: the left-hand side sub-graph focuses on the patient’s history (prior biopsy, surgery and family history), whereas the right-hand side sub-graph focuses on the examined breast (BI-RADS score, mass size). In contrast, the younger cohort graph is very different: the graph has a shorter depth, and the combined BI-RADS increase node is linked to different nodes…

Fig. 2.

TAN model constructed by SAYL over the older cases: the topmost node is the classifier node, and the other nodes represent rules inserted as attributes to the classifier. Edges represent the main dependencies inferred by the model.

Fig. 3.

TAN model constructed by SAYL over the younger cases. Notice that is has the same nodes but with a different structure than its older counterpart.

As the number of rules increases, it becomes harder for humans to interpret the cohort models, let alone their uplift interaction. In ILP-based differential prediction methods [20], theory rules are independent and each rule is an older in situ differential rule. In SAYL, theory rules are dependent on each other, whereas a rule can be modulating another rule in the TAN graph. This is advantageous because such modulated rule combinations can not be expressed in ILP-theory, and therefore might not be learnable. On the other hand, SAYL individual rules are not required to be older in situ specific. A SAYL rule can predict invasive, or be younger specific, as long as the resulting model is uplifting older in situ. Which decreases clinical rule interpretability.

The average number of rules returned by SAYL is lower than ILP-based methods (Table 2), SAYL effectively removes redundant rules by conditioning the addition of a new rule on previous ones. We also note that SAYL, like SAYU, tends to like short rules [7]. DPS found five themes amongst its older in situ rules with a significantly better precision and recall: calcification, prior in situ biopsy, BI-RADS score increase, screening visit, and low breast density [20].

For SAYL runs returning small theories, the resulting rules tend to be differential and fall within these 5 themes. For example, g-SAYL with minpos = 13 and θ = 10% returns 3 rules:

1. Current study combined BI-RADS increased up to 3 points over previous mammogram.

   Had previous in situ biopsy at same location.

   Breast BI-RADS score = 4.

These rules cover two of the 5 DPS themes, namely prior in situ biopsy and BI-RADS score increase.

As the number of SAYL returned rules increases, rule interactions become more complex, individual rules tend not to remain older in situ differential, and rules are no longer confined to the above themes. In the Figures 2 and 3 example, we recover the prior in situ biopsy and BI-RADS score increase themes, but we also have non-thematic rules like “no family history of cancer, and no prior surgery”. In the two runs returning the largest theories, g-SAYL with θ = 1% and minpos = 7 and 13, we recover 4 of the themes, only missing calcification. Note that, as the graph size increases, medical interpretation of the rules becomes more difficult, as well as identifying novel differential themes, since rules are conditioned on each other.

Although the SAYL rules may not be differential when viewed individually, the SAYL final model is differential, significantly outperforming DPS in uplift AUC. DPS, on the other hand, is optimized for mining differential rules, but performs poorly as a differential classifier. SAYL returns a TAN Bayes net whose nodes are logical rules, a model that is human interpretable and that offers insight into the underlying differential process. Greedy g-SAYL’s performance depended little on the parameters, while exploratory e-SAYL’s performance increased when requiring more robust rules.

7 Related Work

Differential prediction was first used in psychology to assess the fairness of cognitive and educational tests, where it is defined as the case where consistent nonzero errors of prediction are made for members of a given subgroup [6]. In this context, differential prediction is usually detected by either fitting a common regression equation and checking for systematic prediction discrepancies for given subgroups, or by building regression models for each subgroup and testing for differences between the resulting models [15, 31]. If the predictive models differ in terms of slope or intercept, it implies that bias exists because systematic errors of prediction would be made on the basis of group membership. An example is assessing how college admission test scores predict first year cumulative grades for males and females. For each gender group, we fit a regression model. We then compare the slope, intercept and/or standard errors for both models. If they differ, the test exhibits differential prediction and may be considered unfair.

In contrast to most studies of differential prediction in psychology, marketing’s uplift modeling assumes an active agent. Uplift modeling is used to understand the best targets for an advertising campaign. Seminal work includes Radcliffe and Surry’s true response modeling [23], Lo’s true lift model [16], and Hansotia and Rukstales’ incremental value modeling [11]. As an example, Hansotia and Rukstales construct a regression and a decision tree, or CHART, model to identify customers for whom direct marketing has sufficiently large impact. The splitting criterion is obtained by computing the difference between the estimated probability increase for the attribute on the subject set and the estimated probability increase on the control set.

In some applications, especially medical decision support systems, gaining insight into the underlying classification logic can be as important as system performance. Insight into the classification logic in medical problems can be an important method to discover disease patterns that may not be known or easily otherwise gleaned from the data. Recent developments include tree-based approaches to uplift modeling [24, 25], although ease-of-interpretation was not an objective in their motivating applications. Wanting to maximize rule interpretability, Nassif et al. [20] opted for ILP-based rule learning instead of decisiontrees because the latter is a special case of the former [4].

To the best of our knowledge, the first application of uplift modeling in medical domains is due to Jaśkowski and Jaroszewicz [12], who adapt standard classifiers by using a simple class variable transformation. Their transformation avoids using two models by assuming that both sets have the same size and combining the examples into a single set. They also propose an approach where two classifiers are learned separately but they help each other by labeling extra examples. Instead, SAYL directly optimizes an uplift measure.

Finally, we observe that the task of discriminating between two dataset strata is closely related to the problem of Relational Subgroup Discovery (RSD), that is, “given a population of individuals with some properties, find subgroups that are statistically interesting” [32]. In the context of multi-relational learning systems, RSD applies a first propositionalization step and then applies a weighted covering algorithm to search for rules that can be considered to define a sub-group in the data. Although the weighting function is defined to focus on unexplored data by decreasing the weight of covered examples, RSD does not explicitly aim at discovering the differences between given partitions.

8 Future Work

A key contribution of this work is constructing a relational classifier that maximizes uplift. SAYL effectively identifies older in situ patients with mammography features that are significantly different from those observed in the younger in situ cases. But one may argue that, for a model to be clinically relevant, we should take into account all mammography features when staging an uplift comparison. We can start the SAYL TAN model with the initial set of attributes, and then learn additional rules, composed of relational features or a combinations of attributes, to maximize uplift [21]. This could potentially increase the achievable lift on both the subject and control groups, making the uplift task harder.

Given the demonstrated theoretical similarity between lift and ROC curves (Section 3.2), and the fact that ROC curves are more widely used especially in the medical literature, it is interesting to compare our approach with a SAYL version that optimizes for ROC AUC.

Finally, we are in the process of applying SAYL to different problems. For example, working on uncovering adverse drug effects, SAYL can be used to construct a model identifying patient subgroups that have a differential prediction before and after drug administration [22].

9 Conclusion

In this work, we present Score As You Lift (SAYL), a novel Statistical Relational Learning algorithm and the first multi-relational uplift modeling system. Our algorithm maximizes the area under the uplift curve, uses this measure during clause construction and final theory evaluation, integrates rule learning and probability assignment, and conditions the addition of new theory rules to existing ones. SAYL significantly outperforms previous approaches on a mammography application (p = 0.002 with similar parameters), while still producing human interpretable models. We plan on further investigating the clinical relevance of our model, and to apply SAYL to additional differential problems.