Support Vector Machines for Differential Prediction

Abstract

Machine learning is continually being applied to a growing set of fields, including the social sciences, business, and medicine. Some fields present problems that are not easily addressed using standard machine learning approaches and, in particular, there is growing interest in differential prediction. In this type of task we are interested in producing a classifier that specifically characterizes a subgroup of interest by maximizing the difference in predictive performance for some outcome between subgroups in a population. We discuss adapting maximum margin classifiers for differential prediction. We first introduce multiple approaches that do not affect the key properties of maximum margin classifiers, but which also do not directly attempt to optimize a standard measure of differential prediction. We next propose a model that directly optimizes a standard measure in this field, the uplift measure. We evaluate our models on real data from two medical applications and show excellent results.

1 Introduction

Recent years have seen increased interest in machine learning, with novel applications in a growing set of fields, such as social sciences, business, and medicine. Often, these applications reduce to familiar tasks, such as classification or regression. However, there are important problems that challenge the state-of-the-art.

One such task, differential prediction, is motivated by studies where one submits two different subgroups from some population to stimuli. The goal is then to gain insight on the different reactions by producing, or simply identifying, a classifier that demonstrates significantly better predictive performance on one subgroup (often called the target subgroup) over another (the control subgroup). Examples include:

• – Seminal work in sociology and psychology used regression to study the factors accounting for differences in the academic performance of students from different backgrounds [5, 15, 26].

• – Uplift modeling is a popular technique in marketing studies. It measures the impact of a campaign by comparing the purchases made by a subgroup that was targeted by some marketing activity versus a control subgroup [16, 9, 20].

• – Medical studies often evaluate the effect of a drug by comparing patients who have taken the drug against patients who have not [7, 4].

• – Also within the medical domain, breast cancer is a major disease that often develops slower in older patients. Insight on the differences between older and younger patients is thus crucial in determining whether treatment is immediately necessary [19, 18].

Differential prediction has broad and important applications across a range of domains and, as specific motivating applications, we will consider two medical tasks. One is a task in which we want to specifically identify older patients with breast cancer who are good candidates for “watchful waiting” as opposed to treatment. The other is a task in which we want to specifically identify patients who are most susceptible to adverse effects of COX-2 inhibitors, and thus not prescribe such drugs for these patients.

The adverse drug event task alone is of major worldwide significance, and the significance of the breast cancer task cannot be overstated. Finding a model that is predictive of an adverse event for people on a drug versus not could help in isolating the key causal relationship of the drug to the event, and using machine learning to uncover causal relationships from observational data is a big topic in current research. Similarly, finding a model that can identify patients with breast cancer that may not be threatening enough in their lifetime to require treatment could greatly reduce overtreatment and costs in healthcare as a whole.

Progress in differential prediction requires the ability to measure differences in classifier performance between two subgroups. The standard measure of differential prediction is the uplift curve [23, 22], which is defined as the difference between the lift curves for the two subgroups. Several classification and regression algorithms have been proposed and evaluated according to this measure [22, 23, 19, 10]. These models were designed to improve uplift, but do not directly optimize it. We show that indeed it is possible to directly optimize uplift and we propose and implement the SVM^upl model, which does so. This model is constructed by showing that optimizing uplift can be reduced to optimizing a linear combination of a weighted combination of features, thus allowing us to apply Joachims' work on the optimization of multivariate measures [13]. We evaluate all models on our motivating applications and SVM^upl shows the best performance in differential prediction in most cases.

The paper is organized as follows. Section 2 presents our motivating applications in greater detail. In Section 3 we introduce uplift modeling and the uplift measure that we will use to evaluate our models. We also present results on a synthetic dataset in this section to give further insight in the task. We discuss multiple possible approaches to differential prediction that do not directly optimize uplift in Section 4. Section 5 discusses previous work on SVMs that optimize for multi-variate measures, and Section 6 presents how to extend this work to optimize uplift directly. We discuss methodology in Section 7 and evaluate all of the proposed models on our motivating applications in Section 8. Finally, Section 9 presents conclusions and future work.

2 Medical Applications

To illustrate the value of differential prediction in our motivating applications we first discuss both in further detail.

Breast cancer is the most common cancer among women [2] and has two basic stages: an earlier in situ stage where cancer cells are still localized, and a subsequent invasive stage where cancer cells infiltrate surrounding tissue. Nearly all in situ cases can be cured [1], thus current practice is to treat in situ occurrences in order to avoid progression into invasive tumors [2]. Treatment, however, is costly and may produce undesirable side-effects. Moreover, an in situ tumor may never progress to invasive stage in the patient's lifetime, increasing the possibility that treatment may not have been necessary. In fact, younger women tend to have more aggressive cancers that rapidly proliferate, whereas older women tend to have more indolent cancers [8, 11]. Because of this, younger women with in situ cancer should be treated due to a greater potential time-span for progression. Likewise, it makes sense to treat older women who have in situ cancer that is similar in characteristics to in situ cancer in younger women since the more aggressive nature of cancer in younger patients may be related to those features. However, older women with in situ cancer that is significantly different from that of younger women may be less likely to experience rapid proliferation, making them good candidates for “watchful waiting” instead of treatment. For this particular problem, predicting in situ cancer that is specific to older patients is the appropriate task.

COX-2 inhibitors are a family of non-steroidal anti-inflammatory drugs (NSAIDs) used to treat inflammation and pain by directly targeting the COX-2 enzyme. This is a desirable property as it significantly reduces the occurrence of various adverse gastrointestinal effects common to other NSAIDs. As such, some early COX-2 inhibitors enjoyed rapid and widespread acceptance in the medical community. Unfortunately, clinical trial data later showed that the use of COX-2 inhibitors also came with a significant increase in the rate of myocardial infarction (MI), or “heart attack” [14]. As a result, physicians must be much more careful when prescribing these drugs. In particular, physicians want to avoid prescribing COX-2 inhibitors to patients who may be more susceptible to the adverse effects that they entail. For this problem, predicting MI that is specific to patients who have taken COX-2 inhibitors, versus those who did not, is the appropriate task to identify the at-risk patients.

3 Uplift Modeling

The fundamental property of differential prediction is the ability to quantify the difference between the classification of subgroups in a population, and much of the reference work in this area originates from the marketing domain. Therefore, we first give a brief overview of differential prediction as it relates to marketing. In marketing, customers can be broken into four categories [21]:

Persuadables Customers who respond positively (e.g. buy a product) when targeted by marketing activity.

Sure Things Customers who respond positively regardless of being targeted.

Lost Causes Customers who do not respond (e.g. not buy a product) regardless of being targeted or not.

Sleeping Dogs Customers who do not respond as a result of being targeted.

Thus, targeting Persuadables increases the value produced by the marketing activity, targeting Sleeping Dogs decreases it, and targeting customers in either of the other groups has no effect, but is a waste of money. Ideally then, a marketing team would only target the Persuadables and avoid targeting Sleeping Dogs whenever possible. Unfortunately, the group to which a particular individual belongs is unknown and is not readily observable. An individual cannot be both targeted and not targeted to determine their response to marketing activity directly. Only the customer response and whether they were in the target or control group can be observed experimentally (see Table 1).

Table 1.

Customer groups and their expected responses based on targeting. Only the shaded region can be observed experimentally.

Target		Control
Response	No Response	Response	No Response
Persuadables, Sure Things	Sleeping Dogs, Lost Causes	Sleeping Dogs, Sure Things	Persuadables, Lost Causes

In this scenario, since we cannot observe customer groups beforehand, standard classifiers appear less than ideal. For example, training a standard classifier to predict response, ignoring that the target and control subgroups exist, is likely to result in a classifier that identifies Persuadables, Sure Things, and Sleeping Dogs as they represent the responders when the target and control subgroups are combined. Recall, however, that targeting Sure Things is a waste of money, and targeting Sleeping Dogs is harmful. Even training on just the target subgroup is likely to produce a classifier that identifies both Persuadables and Sure Things. The point of differential prediction in this domain is then to quantify the difference between the target and control subgroups. While it may be simple and intuitive to simply learn two separate models and subtract the output of the control model from the target model, recent work suggests that this is less effective than modeling the difference directly [22]. Thus, the goal is to produce a single classifier that maximizes predictive performance on the target subgroup over the control subgroup. The idea is that such a classifier characterizes properties that are specific to the target subgroup, thereby making it effective at identifying Persuadables. That is, such a classifier will produce a larger output for customers who are more likely to respond positively as a direct result of targeting, and a smaller output for those who are unaffected or are more likely to respond negatively. The classifier could then be used in subsequent marketing campaigns to select who should be targeted and who should not.

There are many possible measures that could be used to quantify the difference in predictive performance between the target and control subgroups. In marketing, the uplift measure is often used to quantify this difference as well as to evaluate the performance of classifiers designed for differential prediction. Thus, this task is often referred to as uplift modeling.

3.1 Uplift

In this work, we will consider two subgroups, which we will refer to as A and B, representing target and control subgroups respectively, and where subgroup A is the subgroup of most interest.

The lift curve [24] reports the total percentage examples that a classifier must label as positive (x-axis) in order to obtain a certain recall (y-axis), expressed as a count of true positives instead of a rate. As usual, we can compute the corresponding area under the lift curve (AUL). Note that the definition of the lift curve is very similar to that of an ROC curve.

Uplift is the difference in lift produced by a classifier between subgroups A and B, at a particular threshold percentage of all examples. We can compute the area under the uplift curve (AUU) by subtracting their respective AULs:

$$\mathit{\text{AUU}}={\mathit{\text{AUL}}}_A-{\mathit{\text{AUL}}}_B$$ (1)

Notice that, because uplift is simply a difference in lift at a particular threshold, uplift curves always start at zero and end at the difference in the total number of positive examples between subgroups. Higher AUU indicates an overall stronger differentiation of subgroup A from B, and an uplift curve that is skewed more to the left suggests a more pronounced ranking of positives from subgroup A ahead of those from subgroup B.

3.2 Simulated Customer Experiments

To demonstrate that uplift modeling does help to produce classifiers that can specifically identify Persuadables, we generated a synthetic population of customers and simulated marketing activity to produce a dataset for which we knew the ground truth customer groups. We present results on this synthetic dataset, but save algorithmic details for later sections.

To generate a customer population, we first generated a random Bayesian network with 20 nodes and 30 edges. We then randomly selected one node with four possible values to be the customer group feature. Next, we drew 10,000 samples from this network. This left us with a population of customers for which one feature defined the group they belonged to and the rest represented observable features.

We then subjected this population to a simulated marketing activity. We randomly selected roughly 50% of the entire population to be part of the target subgroup. Next, we produced a response for each customer based on their customer group and whether or not they were chosen to be targeted. For this demonstration, we determined each response based on the strongest stereotypical interpretation of each customer group. That is, Persuadables always responded when targeted and never responded when not. Sleeping Dogs never responded when targeted and always responded when not. Sure Things and Lost Causes always and never responded respectively.

We removed the customer group feature from the training set and trained three different classifiers to demonstrate performance. First, we trained a standard SVM classifier on the entire dataset with a positive response as the positive class. Next, we trained a standard SVM on just the target subgroup. Finally, we trained an SVM designed to maximize uplift, about which we will go into greater detail later.

We evaluated the results using 10-fold cross-validation and used internal cross-validation to select parameters in the same way that we will show later on our medical datasets.

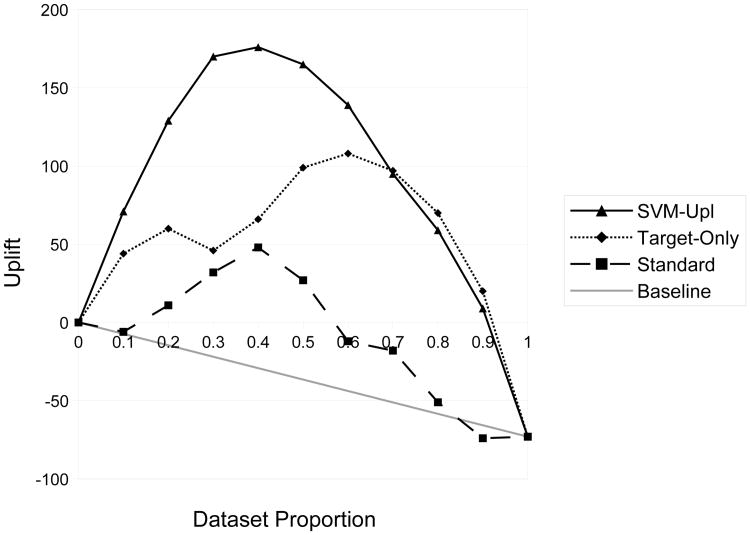
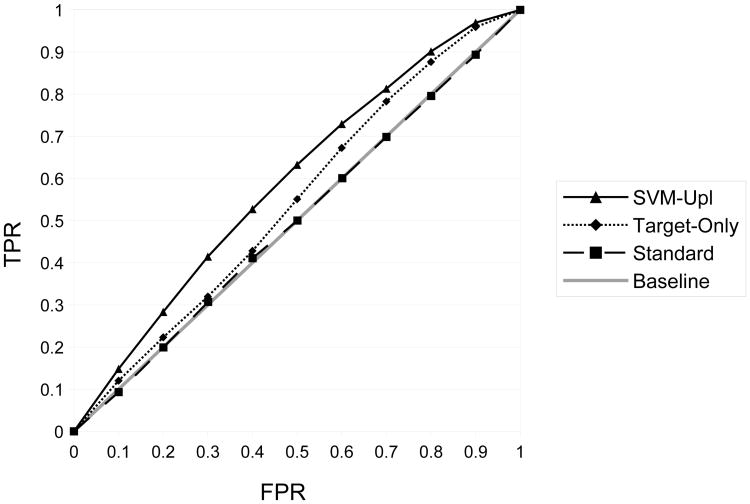
Figure 1 shows the uplift curves on the synthetic customer dataset. As expected, the SVM designed to maximize uplift produces the highest uplift curve, while the standard SVM trained on the entire dataset produces the lowest. Figure 2 shows ROC curves on the synthetic customer dataset when the Persuadable customers are considered to be the positive class. Recall that this feature was unobserved at training time, but identifying Persuadables is the real goal in the marketing domain. As hoped, the SVM that maximizes uplift has the highest ROC curve whereas the standard SVM trained on the entire dataset hovers around the diagonal.

Fig. 1.

Uplift curves (higher is better) for three different classifiers on the simulated customer dataset.

Fig. 2.

ROC curves (higher is better) for three different classifiers on the simulated customer dataset when the Persuadable customer group is treated as the positive class.

3.3 Applying Uplift Modeling to Medical Tasks

In this work, we propose that the task addressed in the marketing domain can be mapped to our motivating medical tasks, suggesting that the uplift measure is a reasonable measure for evaluation of our models.

In the COX-2 inhibitor task, variability in response to the drug suggests that there will be some people at increased risk of MI as a result of taking the drug, some who are at increased risk of MI regardless of treatment, some who are at decreased risk regardless, and perhaps even some who are at decreased risk as a result of taking the drug. Just like in the marketing task, which group an individual belongs to cannot be directly observed. An individual cannot both take the drug and not take the drug to determine its effect. Only the MI outcome and whether or not the individual took the drug can be observed experimentally. We propose that training a classifier to identify individuals for which taking a COX-2 inhibitor increases their risk of MI is analogous to identifying Persuadables.

In the breast cancer task, the analogy is not as obvious, but we know that younger patients often have aggressive cancers while older patients have both aggressive and indolent cancers. Again, which type of cancer a patient has is not directly observable and it is unreasonable to not treat patients in an attempt to determine which have less aggressive varieties. We propose that training a classifier to identify less aggressive varieties of cancer (seen in older patients) is also analogous to identifying Persuadables.

4 Uplift-Agnostic Models

There are many different possible approaches to learning a classifier that is differentially predictive and we have reviewed how this task is approached and evaluated in the marketing domain. We first introduce a number of possibilities in this section that do not directly optimize the uplift measure at training time.

4.1 Standard SVM

To better understand the problem, we start from the standard maximum margin classifier [25]. This classifier minimizes:

$$\frac{1}{2}{\Vert \mathbf{w}\Vert }^2+C\sum _{i=1}^N{\xi }_i$$ (2)

subject to ξ_i ≥ 1 − y_i 〈x_i, w〉, ξ_i ≥ 0, and where is (x, y) feature vector and label pair notation representing examples. The formulation tries to minimize the norm of the weight vector, w, and hence maximize the margin, while softly allowing a number of errors ξ_i whose cost depends on the parameter C.

For the sake of comparison, we evaluate the ability of a standard linear SVM model to produce uplift in our applications of interest. In this case we simply ignore the fact that the examples fall into two subgroups.

4.2 Subgroup-Only SVM

Another intuitive possible approach to achieving differential prediction, without modifying the original optimization, is to only train on the subgroup of most interest. In this way, the classifier should perform well on the subgroup used to train it, whereas it should not perform as well on the other subgroup. In our applications, that would mean only training on the data for the older subgroup of breast cancer patients, or the subgroup of MI patients who have been prescribed COX-2 inhibitors.

4.3 Flipped-Label SVM

Jaskowski and Jaroszewicz [10] propose a general method for adapting standard models to be differentially predictive. This is accomplished by flipping the classification labels in the secondary subgroup during training. In this way, the classifier is trained to correctly predict the positive class on the subgroup of interest, subgroup A, whereas it is trained to predict the negative class in the secondary subgroup, subgroup B. The resulting classifier should then, ideally, perform much better on subgroup A than subgroup B.

4.4 Two-Cost SVM

Another possibility is to simply treat the errors on the different subgroups differently. In the case of the SVM optimization, we would clearly like the cost to be different for the two subgroups. Specifically, we would like to maximize the cost difference between the two, but that problem is ill-defined, suggesting the following adaptation of the standard minimization problem:

$$\frac{1}{2}{\Vert \mathbf{w}\Vert }^2+C_A\sum _{i=1}^{|A|}{\xi }_i+C_B\sum _{j=1}^{|B|}{\xi }_j$$ (3)

subject to ξ_i ≥ 1 – y_i 〈x_i, w〉, ξ_j ≥ 1 – y_j 〈x_j, w〉, ξ_i ≥ 0, ξ_j ≥ 0. As a first step, we assume C_A ≥ 0 and C_B ≥ 0, so we continue penalizing errors on subgroup B. We call this method the two-cost model, and although this problem is similar to addressing class weight, there is an important difference. When addressing class skew, the ratio between C⁺ and C⁻ can be estimated from the class skew in the data. On the other hand, a natural ratio between C_A and C_B may not be known beforehand: if C_A ≈ C_B, there will be little differential classification, but if C_A ≫ C_B the errors may be captured by set B only, leading to over-fitting.

5 Multivariate Performance Measures

Our goal is to find the parameters w that are optimal for a specific measure of uplift performance, such as AUU. Similar to AUC [13, 28, 17], AUL depends on the rankings between pairs of examples. We next, we focus on the SVM^perf approach [13]. This approach hypothesizes that we want to find the h that minimizes the area of a generic loss function Δ over an unseen set of examples S′:

$$R^{\Delta }(h)=\int \Delta ((h({\mathbf{x}}_1^{\prime }),\dots ,h({\mathbf{x}}_{n^{\prime }}^{\prime })),(y_1^{\prime },\dots ,y_{n^{\prime }}^{\prime }))d\mathit{Pr}(S^{\prime })$$ (4)

Note that we use a (x, y) feature vector and label pair notation to represent examples throughout. Also, in practice we cannot use equation (4), we can only use the training data:

$${\widehat{R}}^{\Delta }(h)=\Delta ((h({\mathbf{x}}_1),\dots ,h({\mathbf{x}}_n)),(y_1,\dots ,y_n))$$ (5)

Let tuples ȳ = (y₁,…,y_n) and ȳ′ be assignments over the n examples, 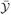is the set of all possible assignments. Ψ(x, y) is a measure-specific combination of features of inputs and outputs in our problem, such that one wants to maximize w^TΨ:

$$\underset{{\overline{y}}^{\prime }\in \overline{\mathcal{Y}}}{argmax}\{{\mathbf{w}}^T\Psi (\overline{\mathbf{x}},{\overline{y}}^{\prime })\}$$ (6)

Then the problem reduces to:

$$\underset{\mathbf{w},\xi \ge 0}{min}\frac{1}{2}{\Vert \mathbf{w}\Vert }^2+C\xi$$ (7)

given the constraints:

$$\forall {\overline{y}}^{\prime }\in \overline{\mathcal{Y}}\backslash \overline{y}:{\mathbf{w}}^T[\Psi (\overline{\mathbf{x}},\overline{y})-\Psi (\overline{\mathbf{x}},{\overline{y}}^{\prime })]\ge \Delta ({\overline{y}}^{\prime },\overline{y})-\xi$$ (8)

which is a quadratic optimization problem and can be solved by a cutting plane solver [12], even if it involves many constraints (one per element in 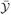\ȳ).

The formulation applies to the AUC by defining it as $1-\frac{\text{BadPairs}}{N\times P}$, where N is the number of negative examples, P is the number of positive examples, and BadPairs is the number of pairs (i, j) such that y_i = 1, y_j = −1, and $y_i^{\prime }>y_j^{\prime }$. Joachims thus addresses the optimization problem in terms of pairs $y_{ij}^{\prime }$, where $y_{ij}^{\prime }$ is 1 if $y_i^{\prime }>y_j^{\prime }$, and −1 otherwise. The loss is the number of swapped pairs:

$${\Delta }_{\mathit{\text{AUC}}}({\overline{y}}^{\prime },\overline{y})=\sum _{i=1}^P\sum _{j=1}^N\frac{1}{2}(1-y_{ij}^{\prime })$$ (9)

The combination of features Ψ should be symmetric to the loss, giving:

$${\mathbf{w}}^T\Psi (\overline{\mathbf{x}},{\overline{y}}^{\prime })=\frac{1}{2}\sum _{i=1}^P\sum _{j=1}^N{y}_{ij}^{\prime }({\mathbf{w}}^T{\mathbf{x}}_i-{\mathbf{w}}^T{\mathbf{x}}_j)={\mathbf{w}}^T\frac{1}{2}\sum _{i=1}^P\sum _{j=1}^N{y}_{ij}^{\prime }({\mathbf{x}}_i-{\mathbf{x}}_j)$$ (10)

The optimization algorithm [12] finds the most violated constraint in equation (8). This corresponds to finding the $y_{ij}^{\ast }$ that minimize w^T[Ψ(x̄, ȳ) – Ψ(x̄, ȳ′)] – Δ_AUC(ȳ′, ȳ), or, given that Ψ(x̄, ȳ) is fixed, that maximize:

$${\mathbf{w}}^T\Psi (\overline{\mathbf{x}},{\overline{y}}^{\prime })+{\Delta }_{\mathit{\text{AUC}}}({\overline{y}}^{\prime },\overline{y})$$

Expanding this sum resumes into independently finding the $y_{ij}^{\ast }$ such that:

$$y_{ij}^{\ast }=\underset{y_{ij}^{\prime }\in \{1,-1\}}{argmax}{y}_{ij}^{\prime }(({\mathbf{w}}^T{\mathbf{x}}_i-\frac{1}{2})-({\mathbf{w}}^T{\mathbf{x}}_j+\frac{1}{2}))$$ (11)

Joachims' algorithm then sorts the ${\mathbf{w}}^T{\mathbf{x}}_i-\frac{1}{2}$ and ${\mathbf{w}}^T{\mathbf{x}}_j+\frac{1}{2}$, and generates labels from this total order.

6 Maximizing Uplift

Recall from Section 3.1 the similarity between lift and ROC. The two are actually closely related. As shown in Tufféry [24], and assuming that we are given the skew $\pi =\frac{P}{P+N}$, the AUL is related to the AUC by:

$$\mathit{\text{AUL}}=P(\frac{\pi }{2}+(1-\pi )\mathit{\text{AUC}})$$ (12)

Expanding equation (1) with equation (12):

$$\mathit{\text{AUU}}=P_A(\frac{{\pi }_A}{2}+(1-{\pi }_A){\mathit{\text{AUC}}}_A)-P_B(\frac{{\pi }_B}{2}+(1-{\pi }_B){\mathit{\text{AUC}}}_B)$$ (13)

P_A, P_B, π_A, and π_B are properties of the two subgroups, and thus independent of the classifier. Removing constant terms we see that maximizing uplift is equivalent to:

$$\mathit{max}(\mathit{\text{AUU}})\equiv \mathit{max}(P_A(1-{\pi }_A){\mathit{\text{AUC}}}_A-P_B(1-{\pi }_B){\mathit{\text{AUC}}}_B)\propto \mathit{max}({\mathit{\text{AUC}}}_A-\frac{P_B(1-{\pi }_B)}{P_A(1-{\pi }_A)}{\mathit{\text{AUC}}}_B)$$ (14)

Defining $\lambda =\frac{P_B(1-{\pi }_B)}{P_A(1-{\pi }_A)}$ we have:

$$\mathit{max}(\mathit{\text{AUU}})\equiv \mathit{max}({\mathit{\text{AUC}}}_A-\lambda {\mathit{\text{AUC}}}_B)$$ (15)

Therefore, maximizing AUU is equivalent to maximizing a weighted difference between two AUCs.

Equation (15) suggests that we can use the AUC formulation to optimize AUU. First, we make it a double maximization problem by switching labels in subgroup B:

$$\mathit{max}(\mathit{\text{AUU}})\equiv \mathit{max}({\mathit{\text{AUC}}}_A-\lambda (1-{\mathit{\text{AUC}}}_B^{-}))\equiv \mathit{max}({\mathit{\text{AUC}}}_A+\lambda {\mathit{\text{AUC}}}_B^{-})$$ (16)

The new formulation reverses positives with negatives making it a sum of separate sets.

At this point, we can encode our problem using Joachims' formulation of the AUC. In this case, we have two AUCs. One, as before, is obtained from the y_ij where the i, j pairs range over A. The second corresponds to pairs y_kl where the k, l pairs range over B. On switching the labels, we must consider y_lk where k ranges over the positives in B, and l over the negatives in B.

After switching labels, we can expand equation (9) to obtain our new loss Δ_AUU as the weighted sum of two losses:

$${\Delta }_{\mathit{\text{AUU}}}({\overline{y}}^{\prime },\overline{y})=\sum _{i=1}^{P_A}\sum _{j=1}^{N_A}\frac{1}{2}(1-y_{ij}^{\prime })+\sum _{k=1}^{P_B}\sum _{j=1}^{N_B}\frac{1}{2}(1-y_{ik}^{\prime })$$ (17)

From equation (10) we construct a corresponding weighted sum as the new Ψ:

$$\Psi (\overline{\mathbf{x}},{\overline{y}}^{\prime })=\frac{1}{2}\sum _{i=1}^{P_A}\sum _{j=1}^{N_A}{y}_{ij}^{\prime }({\mathbf{x}}_i-{\mathbf{x}}_j)+\lambda \frac{1}{2}\sum _{k=1}^{P_B}\sum _{l=1}^{N_B}{y}_{lk}^{\prime }({\mathbf{x}}_l-{\mathbf{x}}_k)$$ (18)

The two sets are separate, so optimizing the y_ij does not change from equation (11), as their maximization does not depend on the y_lk. Optimizing the y_lk follows similar reasoning to the y_ij and gives:

$$y_{lk}^{\ast }=\underset{y_{lk}^{\prime }\in \{1,-1\}}{argmax}{y}_{lk}^{\prime }(({\mathbf{w}}^T{\mathbf{x}}_l-\frac{1}{2})-({\mathbf{w}}^T{\mathbf{x}}_k+\frac{1}{2}))$$ (19)

Thus, we now have two independent rankings: one between the labels for the examples in A, and the other between the labels for the examples in B. We can sort them together or separately, but we simply have to label the sets independently to obtain the ȳ* of the most violated constraint. Note that the computation of the ȳ* in this setting is independent of λ, but λ still affects the solutions found by the cutting-plane solver through Δ and Ψ.

7 Experiments

We implemented our SVM^Upl method using the SVM^perf codebase, version 3.00¹. We implemented the two-cost model using the LIBSVM codebase [3], version 3.17². All other uplift-agnostic approaches were run using LIBSVM, but required no changes to the code.

Recall that our motivating applications are to produce a differential older-specific classifier for in situ breast cancer, and produce a differential COX-2 specific classifier for myocardial infarction (MI). We apply all of the proposed approaches to the breast cancer data used in Nassif et al. [19] and the MI data used in Davis et al. [6]. Their composition is shown in Table 2.

Table 2.

Composition of the breast cancer and MI datasets for our motivating applications. In the breast cancer dataset the older subgroup is the target subgroup, and in situ breast cancer is the positive class. In the MI dataset the COX-2 inhibitor subgroup is the target subgroup, and MI is the positive class.

Older		Younger		COX-2 Inhibitors		No COX-2 Inhibitors
In Situ	Invasive	In Situ	Invasive	MI	No MI	MI	No MI
132	401	110	264	184	1,776	184	1,776

The breast cancer data consists of two cohorts: patients younger than 50 years old form the younger cohort, while patients aged 65 and above form the older cohort. The older cohort has 132 in situ and 401 invasive cases, while the younger one has 110 in situ and 264 invasive.

The MI data consists of patients separated into two equally-sized subgroups: patients who have been prescribed COX-2 inhibitors and those who have not. The group prescribed COX-2 inhibitors has 184 patients who had MI, and 1776 who did not. The subgroup not prescribed COX-2 inhibitors has the same number of patients for each outcome.

We use 10-fold cross-validation for evaluation. Final results were produced by concatenating the output test results for each fold. Cost parameters were selected for each fold using 9-fold internal cross-validation. For all approaches, the cost parameter was selected from {10.0, 1.0, 0.1, 0.01, 0.001, 0.0001, 0.00001}. For the two-cost model, C_A and C_B were selected from all combinations of values from the set such that C_A > C_B. We plot the final uplift curves for each approach along with the uplift for a baseline random classifier in Figures 3 and 4.

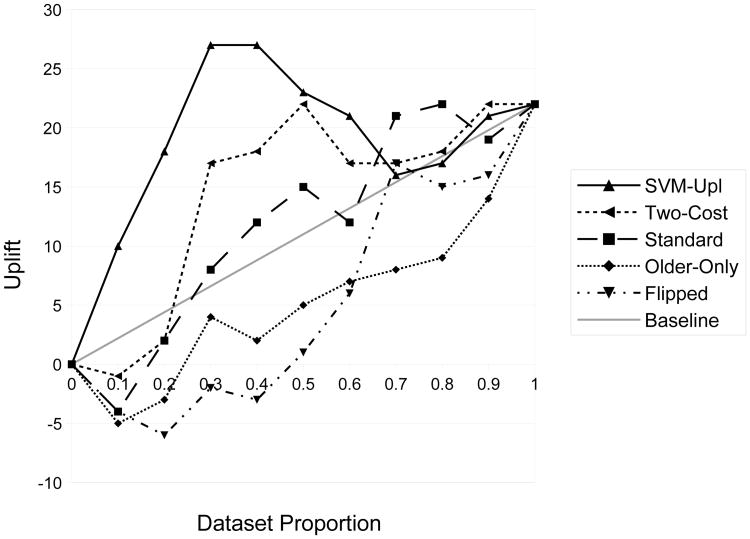
Fig. 3.

Uplift curves (higher is better) for all approaches on the breast cancer dataset.

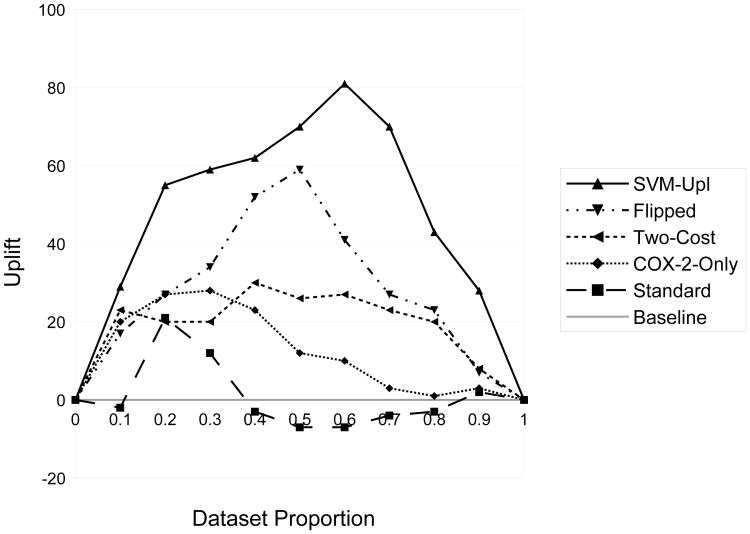
Fig. 4.

Uplift curves (higher is better) for all approaches on the MI dataset. Note that the baseline uplift lies on the x-axis due to the equal number of patients with MI in each subgroup.

Tables 3 and 4 compare SVM^Upl with every other approach proposed as well as a fixed baseline random classifier. We use the Mann-Whitney test at the 95% confidence level to compare approaches based on per-fold AUU. We show the per-fold mean, standard deviation, and p-value of the 10-fold AUU paired Mann-Whitney of each method as compared to SVM^Upl (* indicates significance).

Table 3.

10-fold cross-validated performance for all proposed approaches on the breast cancer dataset (* indicates significance).

Model	Older	Younger	AUU	Per-fold	Per-fold	SVMUpl
	AUL	AUL		AUU μ	AUU σ	p-value
SVMUpl	64.26	45.05	19.21	1.93	0.78	-
Two-Cost	74.30	60.76	13.54	1.45	1.18	0.432
Older-Only	67.70	61.85	5.85	1.03	1.15	0.037 *
Standard	75.35	64.34	11.01	1.26	0.38	0.049 *
Flipped	53.90	49.08	4.82	0.77	0.58	0.020 *
Baseline	66.00	55.00	11.00	1.10	0.21	0.004 *

Table 4.

10-fold cross-validated performance for all proposed approaches on the MI dataset (* indicates significance).

Model	COX-2	No COX-2	AUU	Per-fold	Per-fold	SVMUpl
	AUL	AUL		AUU μ	AUU σ	p-value
SVMUpl	123.38	72.70	50.68	5.07	2.04	-
Two-Cost	126.23	106.25	19.99	2.43	1.54	0.004 *
COX-2-Only	151.50	137.70	13.80	1.18	1.52	0.002 *
Standard	147.69	146.49	1.20	-0.16	1.25	0.002 *
Flipped	102.15	73.63	28.52	2.97	1.35	0.037 *
Baseline	0.00	0.00	0.00	0.00	0.00	0.002 *

8 Evaluation

The results on the breast cancer dataset in Table 3 show that SVM^Upl produces significantly greater uplift than all proposed approaches, except for the two-cost model. This exception may be a result of the higher variance of the model on this particular dataset. The results on the MI dataset in Table 4 show that SVM^Upl produces the greatest uplift in all cases.

Figure 3 shows SVM^Upl with an uplift curve that dominates the rest of the approaches until around the 0.7 threshold on the breast cancer dataset. Most other approaches produce curves that sit around or below the baseline.

Figure 4 tells a similar story, with SVM^Upl dominating all other methods across the entire space on the MI dataset. In this dataset, however, only the standard SVM approach consistently performs below the baseline, whereas all other methods appear to produce at least modest uplift.

9 Conclusions and Future Work

We introduced a support vector model directed toward differential prediction. The SVM^Upl approach optimizes uplift by relying on the relationship between AUL and AUC, and on the linearity of the multivariate function used in prior work to optimize AUC. The results suggest that SVM^Upl does indeed achieve better uplift in unseen data than the other approaches.

Differential prediction has many important applications, particularly in the human sciences and medicine, raising the need for future work. For example, in some applications, it may be important to ensure some minimal performance over subgroup B, even at the cost of uplift. It may also be important to be able to interpret the learned model and understand what features improve uplift most. SVMs do not lend themselves as easily to this task as some models, but feature coefficients could be used to identify which are the most or least important. Finally, there is some very recent additional work on SVMs for uplift modeling [27] that does not directly optimize uplift, the main focus of this paper, but it will be important to compare results as such new methods are developed.