Cortical Folding of the Primate Brain: An Interdisciplinary Examination of the Genetic Architecture, Modularity, and Evolvability of a Significant Neurological Trait in Pedigreed Baboons (Genus Papio)

Abstract

Folding of the primate brain cortex allows for improved neural processing power by increasing cortical surface area for the allocation of neurons. The arrangement of folds (sulci) and ridges (gyri) across the cerebral cortex is thought to reflect the underlying neural network. Gyrification, an adaptive trait with a unique evolutionary history, is affected by genetic factors different from those affecting brain volume. Using a large pedigreed population of ∼1000 Papio baboons, we address critical questions about the genetic architecture of primate brain folding, the interplay between genetics, brain anatomy, development, patterns of cortical–cortical connectivity, and gyrification’s potential for future evolution. Through Mantel testing and cluster analyses, we find that the baboon cortex is quite evolvable, with high integration between the genotype and phenotype. We further find significantly similar partitioning of variation between cortical development, anatomy, and connectivity, supporting the predictions of tension-based models for sulcal development. We identify a significant, moderate degree of genetic control over variation in sulcal length, with gyrus-shape features being more susceptible to environmental effects. Finally, through QTL mapping, we identify novel chromosomal regions affecting variation in brain folding. The most significant QTL contain compelling candidate genes, including gene clusters associated with Williams and Down syndromes. The QTL distribution suggests a complex genetic architecture for gyrification with both polygeny and pleiotropy. Our results provide a solid preliminary characterization of the genetic basis of primate brain folding, a unique and biomedically relevant phenotype with significant implications in primate brain evolution.

THE extent of folding of the cerebral cortex, known as “cortical gyrification,” has dramatically increased during primate evolution, in parallel with increasing brain volumes. The cortex of Old World monkeys is significantly more folded (gyrified) than that of New World monkeys (Zilles et al. 1989; Martin 1990), and the great apes have the highest degree of gyrification in nonhuman primates (Preuss et al. 2004). Humans are outliers even within the primate clade, with our brain being almost 30% more folded than that of chimps (Rogers et al. 2010). Powerful physical constraints on the upper limit of human neonatal brain volume drive selection toward the most compact brain possible (Rosenberg and Trevathan 2002), while humankind’s ecological niche demands high cognitive potential. Since the cell bodies of neurons–the functional units of information processing in the brain–are located in the outermost layer of the laminar brain system, folding the cerebral cortex is an effective method of increasing surface area in which to allocate neurons with minimal overall brain volume expansion.

Selection for a larger brain volume does not automatically create one that is more folded. In fact, in baboons, genetic changes associated with increased brain size have been shown to result in a cortex with fewer folds (Rogers et al. 2010). Human congenital abnormalities also demonstrate the separation of these two phenotypes: conditions of abnormal brain volumes typically present with normal gyrification and vice versa (Stevenson 2006). These findings suggest that gyrification has a separate genetic basis from brain size, so the trend of increased folding in the primate lineage involves selective forces that have been working separately but in tandem with those increasing gross brain volume. While there has been extensive work examining changes in brain size among primates, cortical gyrification has a unique evolutionary history that has not yet been broadly explored.

Previous studies using magnetic resonance (MR) imaging provide preliminary evidence for a heritable genetic component to cortical variation in the baboon population studied here, generally estimating the heritability of cortical morphological features as between 20 and 40% (Mahaney et al. 1993; Rogers et al. 2007; Kochunov et al. 2010). As only ∼150 MR scans were previously available, however, precise genetic mapping was impossible. By expanding the sample to glean information from ∼1000 skull computed tomography (CT) scans collected in this pedigreed population, we were able to thoroughly assess variation and conduct QTL mapping to isolate defined chromosome regions affecting cortical gyrification phenotypes. QTL techniques are useful in that they provide an unbiased way to discover novel genomic regions associated with traits of interest in addition to implicating known genes in performing unanticipated novel functions. Additionally, conditions of dominance and epistatic interactions can be assessed and the power and strength of a genetic association to the phenotype quantified. The pedigree of the baboon population with which we are working includes six generations, resulting in a genomic linkage map (Rogers et al. 2000; Cox et al. 2006) that is quite well saturated with molecular markers thanks to the many resultant recombination events. This allowed us to isolate relatively narrow regions of interest containing small numbers of candidate genes. The advantage of pedigree-based linkage analyses lies in the fact that variants can be examined directly using identity-by-descent information rather than relying on variant state as a proxy. Furthermore, the effect size attributable to the implicated chromosomal regions can be reasonably estimated and situations of polygeny and/or pleiotropy detected.

Gyrification is extremely interesting from an evolutionary perspective for its neurobiological implications. Not only is increased gyrification useful for fitting more neurons within the skull, but patterns of sulci and gyri have direct implications with regard to the neural network (Ventura-Antunes et al. 2013). As would be expected from a trait that is at least partially controlled by genetic variation, sulci are not randomly distributed across the cortex; consistent folds appear within species and the degree and pattern of cortical folding shows phylogenetic trends in primates (Zilles et al. 1989, 2013; Krubitzer 2009; Chen et al. 2013). There are a number of hypotheses explaining the mechanisms behind the development of cortical gyrification and why sulci appear where they do, many involving mechanical tension on axonal tracts, the neuronal connections that allow communication between brain regions. The original tension-based hypothesis proposed by Van Essen (1997) posits that these white-matter tracts place tension on the laminar cortical surface layers, pulling regions together more strongly if more axons pass between them. The presence of mechanical tension on connectivity tracts between brain cells has been demonstrated empirically both in vitro (Heidemann and Buxbaum 1990, 1994; Herculano-Houzel et al. 2010) and in vivo (Xu et al. 2009, 2010) in addition to fitting with computational models of gyrification (Hilgetag and Barbas 2006; Mota and Herculano-Houzel 2012). Therefore, extending the hypothesis to an evolutionary viewpoint, if there is pressure for increased folding, the path of least physical resistance would be for sulci to form that separate the regions of lowest mechanical tension, i.e., those with low connectivity. Functional connectivity would therefore parallel anatomical propinquity (Van Essen 1997; Hilgetag and Barbas 2006; Toro et al. 2008; Herculano-Houzel et al. 2010; Mota and Herculano-Houzel 2012; Zilles et al. 2013), meaning that the gyrification pattern is a direct external proxy for the underlying neural network.

Ultimately, the final adult gyrification pattern depends on the genetic and developmental processes underlying these traits. Modularity is ubiquitous in biological systems, including brain networks (Zhou et al. 2006; Chen et al. 2008; Meunier et al. 2009, 2010). It has been proposed that modularity would lead to the minimum possible distances between interacting regions of the cortex as an adaptive scheme for efficient neural processing (Sporns et al. 2004; Meunier et al. 2010). Indeed, it has been shown that anatomical proximity is associated with a higher number of connecting axons (Markov et al. 2011, 2014). Elucidating the exact structure of modularity and the location of module borders over the cortex, as is done in this study, exposes both the historical pattern of selection on brain features and the potential constraints imposed on future evolutionary alteration of the cerebrum. For example, if traits are within the same genetic module—i.e., they are controlled by the same gene or set of genes—it is difficult to modify them independently of one another because a mutation will have a corresponding effect on both traits. Traits that have a history of close interaction should group into the same cluster while those experiencing different selective pressures should theoretically fall into separate modules. Thus, defining and comparing the borders of cortical-folding modules across biological domains (genetic, anatomical, developmental, connectivity) has significant implications for the ease of future adaptive alteration of the cortex by elucidating potential constraints on the full breadth of phenotypic space that can be explored.

If traits function together during life or develop together, the principle of morphological integration predicts that they will also be inherited together due to the pleiotropic effects of common genes (Cheverud 1996; Wagner 1996; Barton 2006; Wagner et al. 2007; Klingenberg 2008). Similarly, if sulcal formation is indeed guided by axonal tension related to the number of tracts uniting regions during development, then one should suspect that a similar pattern of variation will occur in sulcal anatomy, developmental programs, and the pattern of intrahemispheric connectivity. Here, we statistically test these predictions of a tension-based model for sulcal development and assess the degree of morphological integration of the baboon’s cortex across the biological domains of phenotype, genotype, anatomy, connectivity, and development. Specifically, a similar partitioning of variation between anatomy (location of individual sulci in the context of a hemisphere), connectivity (number of axonal tracts connecting specific regions), and development (embryonic day of appearance of the sulcus) would support an interrelationship predicted by such a model.

This study sheds light on the genetic architecture underlying cortical gyrification in baboons. Specifically, we examine the structure of modularity over gyrification across biological domains and the interplay between domains (relevant to the ease of altering the shape of gyrification in response to particular evolutionary selective pressures), estimate the quantitative genetic effect on variation in cortical folding, and identify novel DNA regions associated with gyrification in this primate species. Such characterization provides a solid framework for future studies that seek to delve into the sequence evolution and function of candidate genes affecting brain topology and provides a more thorough understanding of the genetics underlying the evolution of brain folding and its consequences for function. Our results have medical implications for the many congenital disorders associated with abnormal cortical gyrification.

Materials and Methods

Study population and pedigree details

The study population consists of olive baboons, Papio hamadryas anubis, and yellow baboons, P. h. cynocephalus, and their hybrids living in the Southwest National Primate Research Center (SNPRC) in San Antonio, Texas. Although there has been considerable debate over the classification of olive and yellow baboons as either separate species or subspecies of P. hamadryas, we are here considering them as subspecies, as they are found to freely and successfully interbreed in the wild, in captivity, and in our study population (Alberts and Altmann 2001; Groves 2001; Jolly 2001; Charpentier et al. 2012). There are currently ∼1600 animals living at the facility that are part of a managed breeding endeavor that has produced a full six-generation pedigree. The colony is divided into group cages of 10–30 adult females and their young offspring with one male, which results in the least amount of aggression between animals and assists in determining paternity of offspring. The population is maintained with an adult female:male ratio of ∼3:1 due to the harem-style housing conditions at the SNPRC.

The ancestral kinship relationships have been documented for at least six generations (>30 years), allowing for use of all possible pair-wise relatedness coefficients in quantitative genetic analysis. A total of 2426 individuals are included and grouped into one unbroken extended pedigree. Of these, 2044 have been genotyped for ∼300 short tandem repeat (STR) (microsatellite) loci (Rogers et al. 2000; Cox et al. 2006). Full sibships range in size from 2 to 12 individuals with a median of 5. Full information on the current state of the colony can be found on the SNPRC website: http://txbiomed.org/primate-research-center.

Skulls were collected at necropsy from 985 pedigreed baboons (see below). As the samples underwent a freezing process for their transfer to Washington University, destroying brain cells, we were unable to directly dissect their brains. However, CT scans were obtained, and 100 of these individuals had additionally been MR-scanned while alive (Kochunov et al. 2010; Rogers et al. 2010). We developed a method for virtual processing of CT images to create a well-textured virtual brain upon which biologically meaningful measurements could be reliably taken. Although we only used the CT measurements in analyses for the sake of consistency, we compared our CT endocast-based measurements with those taken on the overlapping MR scans to ensure accuracy and repeatability of data.

Endocast creation and landmark measurement

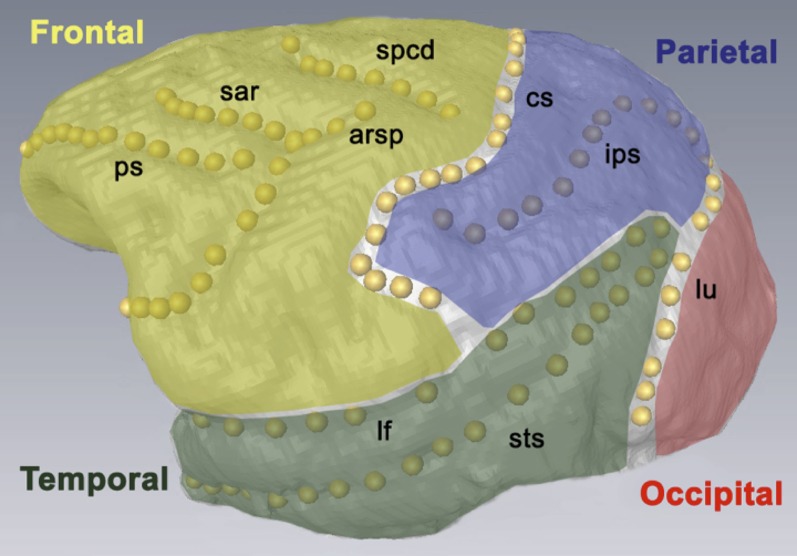
Over a period of 15 years, the heads of 985 animals were collected at necropsy and scanned at 0.6 or 0.7 mm with a 64-slice General Electric 3D CT scanner at the Mallinckrodt Institute of Radiology at Washington University. Virtual endocasts displaying brain topology were generated from the cranial CT scans by 3D image segmentation using the freeware program ITK-SNAP (Yushkevich et al. 2006). Images were processed with a standardized upper image threshold to minimize resolution differences, and seeds were arranged to maximize endocranial coverage. Three-dimensional landmark coordinates were collected on processed endocasts by manually placing points along specific brain sulci on the segmentation mesh using the Amira 5 program (Stalling et al. 2005). The total length along the 3D brain surface was captured for metric traits. The lengths of the following 10 sulci were collected on both the left and right hemispheres of the endocasts: arcuate rectus spur (arsp), central sulcus (cs), inferior arcuate rectus (iar), intraparietal sulcus (ips), lateral fissure (lf), lunate sulcus (lu), principal sulcus (ps), superior arcuate rectus (sar), superior precentral dimple (spcd), and superior temporal sulcus (sts) (Table 1; Supporting Information, Table S1; Figure 1). The quantitative genetic results presented here are of the average standardized length across hemispheres for each sulcus to reduce unnecessary complexity. Three additional non-metric traits were collected on both hemispheres. These were whether the inferior tips of the cs were forked or unforked and the presence or absence (p/a) of the (left, L, and right, R) spcd and arsp (Table 1 and Table S2). The location of the two p/a sulci can be seen in Figure 1, as can an example of a cs with a forked inferior tip . All endocasts were double-measured for all identifiable sulci to ensure accuracy and quantify measurement error. Landmarks were collected on both hemispheres separately and double measurements were made at least 1 day apart to remove any potential measuring bias. An extremely conservative approach was taken in data collection such that when the sulcus was not clearly defined, the trait was logged as missing and omitted from analysis. This resulted in a considerable—but typical for endocast-based studies of brain topology (Cheverud et al. 1990)—amount of missing data. Analyses were thus done in a pair-wise fashion. Differences in sample sizes between traits can be seen in Table 2.

Table 1. Anatomical descriptions of landmark sulci.

Trait code	Trait full name	Anatomical description of sulcus
arsp	Arcuate rectus spur	Possible posterior spur off of junction of arcuate rectus inferior and superior projections.
cs	Central sulcus	Major fold extending interiorly from midline of brain separating frontal and parietal brain lobes and curling rostrally or branching before reaching the lateral sulcus.
iar	Inferior arcuate rectus	Inferior branch of the arcuate rectus spanning from junction with arsp and/or sar to inferio-rostral edge of frontal lobe.
ips	Intraparietal sulcus	On lateral surface of parietal lobe spanning from inferio-frontal portion to intersection with lu just inferior to midline.
lf	Lateral fissure	Separates frontal and parietal lobes from temporal lobe and spans superior-posteriorly from superior-frontal edge of temporal lobe to approximate intersection with sts.
lu	Lunate sulcus	Separates parietal and temporal lobes from occipital lobe and spans inferiorly from intersection with ips just inferior to midline.
ps	Principal sulcus	Runs posterior-laterally from frontal edge of frontal lobe, ending just before intersection with iar.
sar	Superior arcuate rectus	Frontal portion of arcuate rectus running fronto-laterally from intersection with iar and/or arsp.
sts	Superior temporal sulcus	Runs superior-posteriorly from inferio-frontal edge of temporal lobe to approximate intersection with lf.
spcd	Superior precentral dimple	Possible short lateral fold in frontal lobe superior to arcuate rectus.
Larsp_yn		Non-metric: presence/absence of left hemisphere arsp.
Rarsp_yn		Non-metric: presence/absence of right hemisphere arsp.
Lcs_forked		Non-metric: indicates whether the inferior tip of the left cs is forked or unforked.
Rcs_forked		Non-metric: indicates whether the inferior tip of the right cs is forked or unforked.
Lspcd_yn		Non-metric: presence/absence of left hemisphere spcd.
Rspcd_yn		Non-metric: presence/absence of right hemisphere spcd.

Anatomical characterization of the position on the hemisphere, proximal, and terminal ends of the 10 metric and 6 non-metric cortical-folding traits examined on each brain hemisphere. Left and right hemispheres were collected separately on different days. Non-metric traits are in boldface type.

Figure 1.

Brain-fold traits examined by brain area. Fully annotated left hemisphere of a representative CT-based virtual endocast showing placement of all 10 metric sulci and their partitioning into anatomical lobe regions. Landmark points used in data collection are seen as dots along the sulcus curvature. Anatomical lobe region assignment is designated by placement of sulcus and name.

Table 2. Trait heritability results.

Sulcus	h2	h2 SE	h2 P-value	n	Significant covariates	Average length	Vp	Va
arsp*	0.354	0.081	<0.001	675	Age2, CC	15.9	5.911	2.092
cs*	0.281	0.076	<0.001	621	Sex, CC	95.84	8.497	2.388
iar	0.053	0.072	0.178	670	Age, age-by-sex, age2, CC	60.2	25.418	1.347
ips*	0.133	0.075	0.002	491	Age, age-by-sex, CC	75.72	12.936	1.721
lf*	0.235	0.103	<0.001	429	Sex, CC	99.34	18.579	4.366
lu*	0.197	0.121	0.01	360	Sex, CC	75.73	10.836	2.135
ps*	0.512	0.113	<0.001	541	Age, sex, age-by-sex, CC	59.49	5.385	2.757
sar	0.053	0.048	0.077	574		27.504	18.635	0.988
spcd	0.01	0.045	0.406	507		35.793	17.301	0.173
sts*	0.114	0.09	0.036	359	Sex, age, age-by-sex, age2, CC	115.86	15.184	1.731
Larsp_ yn	—		0.5	627		0.812
Lcs_forked*	0.134	0.097	0.021	606		0.606
Lspcd _yn	—		0.5	663		0.905
Rarsp _yn*	0.129	0.070	0.003	737		0.826
Rcs_forked	0.065	0.060	0.076	669		0.590
Rspcd_ yn*	0.15		0.019	747		0.876

Heritability (h²) estimates, heritability standard errors (SE), and significance (P) calculated for each of the 10 metric sulcal length measures (boldface) and 6 nonmetric traits (roman). Significant results are indicated with asterisks by the trait name. Covariates that emerged as significant for that trait during screening and the trait sample size are listed. Age-by-sex is the interaction between age and sex; CC is cranial capacity. Sulcus average lengths are in millimeters. “Average length” reports for nonmetric traits are the frequency of occurrence of the presence of that trait for arsp and spcd phenotypes and the frequency of forked cs. Vp is the phenotypic variation for traits; Va is the additive genetic variation for traits.

Covariate screening

Prior to quantitative genetic testing, pertinent covariates were screened for an effect on each phenotype, and the mean effect of significant covariates (P < 0.05) was regressed out. All quantitative genetic analyses were conducted on the resultant residuals. This removes concerns about confounding genetic results with correlated variation in other traits while preserving the natural variation in our phenotypes. Covariates that were not significant for traits were not included in the genetic analysis. Covariates screened for were age, sex, the interaction of age and sex (age × sex), age², and cranial capacity (CC), as has been done in previous studies on this population (Kochunov et al. 2010; Rogers et al. 2010). Table 2 documents which covariates were significant for each of the traits. An extended description and rationale for each covariate is provided in the Supporting Information.

Quantitative genetics and creation of correlation matrices

Heritability (h²) estimates and genetic correlations were calculated using the Sequential Oligogenic Linkage Analysis Routines (SOLAR) software package (Almasy and Blangero 1998). SOLAR, which is thoroughly described elsewhere (Almasy and Blangero 1998), implements a maximum-likelihood-based algorithm and uses variance component methods to determine heritability and pair-wise genetic correlations assuming a Gaussian distribution. Non-metric traits were analyzed using an algorithm tailored to discrete phenotypes (Duggirala et al. 1997; Williams et al. 1999). This involves a liability threshold model for dichotomous traits. Variance component methods are useful for large, complex pedigrees. SOLAR takes into account all relatedness coefficients between individuals to determine an identity by descent matrix that can then be used to map traits. The covariance matrix, Ω, for an extended pedigree is Ω = 2Φσ²_g + Iσ²_e, where the kinship matrix, Φ, gives all pair-wise kinship coefficients; σ²_g is the genetic variance due to additive genetic effects; σ²_e is variance from individual-specific environmental effects; and I is an identity matrix. The genetic matrix created for this study can be found in Table S3.

The matrix of phenotypic variation (Table S4) was created from the covariate-corrected data using the R statistical package (R Core Team 2012). Prior to cross-domain matrix comparison, sulci were screened on the two hemispheres separately in case they exhibited different modular structures (Cheverud et al. 1990; Hutchison and Cheverud 1992; Sun et al. 2005; Im et al. 2010), but both left and right sides displayed the same patterns. The two were thus centered and averaged to add to the sample size, reduce unnecessary noise, and maintain compatible dimensionality of all matrices for comparison.

An anatomic similarity matrix was created based on sulcus locations on the cerebral cortex (Table S5). Lobes were partitioned at their traditionally defined borders (Figure 1). The following rubric was followed to assign values in the matrix: if the two sulci in question intersect, a value 0.9 was assigned; if sulci are adjacent, 0.6; in adjacent lobes but have other folds between them, 0.3; and in nonadjacent lobes, 0.1. The only sulcus that has a different number value assigned from the ones listed is spcd compared to other frontal sulci. Since these folds are in the same lobe but are not adjacent, a value of 0.5 was assigned.

Markov et al. (2014) quantify the degree of connectivity between 97 brain regions in Macaca fascicularis, another member of the tribe Papionini, by counting the number of axons physically connecting different brain regions. We used these data to create a connectivity similarity matrix for landmark sulci, with connectivity amount between pairs of sulci ranging from 0 (no axons connecting regions) to 1 (self) (Table S6). As the raw matrix was not symmetric due to differences between numbers of axons projecting from source to target vs. from target to source, a compromise matrix of the average between these two measures was used. Some regions were characterized only as an axon source and not a target, in which case this measure alone was used in downstream analyses.

A developmental matrix was created from data published by Sawada et al. (2012) illustrating the ontogeny of cortical development in M. fascicularis (Sawada et al. 2012) (Table S7). We created a distance matrix between sulci based on their relative times of developmental emergence in days from conception. Sulci emerge between embryonic days 70 and 135. This distance matrix was then converted into a similarity matrix by taking the reciprocal of the data for the sake of comparison with other matrices in analyses. In designing this project, we chose baboon sulci that are orthologous to those present in the macaque specifically for comparison with literature-based data. Macaques are the most closely related primate to baboons that have been extremely well described in terms of brain development and functional connectivity. It is reasonable to suspect that sulcal embryonic timing and connectivity would be similar between these two species due to their similar brain structures and evolutionary and genetic relatedness. Our Mantel comparisons represent a theoretical proof-of-concept test, so slight differences in patterns between these Papionini species will not seriously impact interpretation.

Since genetic and phenotypic correlations are estimates of the true values and thus have error incorporated into them, it is necessary to assess the degree of repeatability within the correlations to determine the true significance of the patterns of matrix similarity detected. In general, a matrix’s repeatability (t) is the proportion of the variance observed in measurements that is due to true population variation as opposed to error variation. Since there will always be some error incorporated into estimates, if two population matrices are perfectly correlated, the largest correlation value that can be observed between them will be a function of both of their repeatabilities. Thus, our Mantel matrix correlations could seem low when considered independently, but could actually be approaching the maximum possible value that can be attained, given the degree of error in estimates. For this reason, both the Monte-Carlo matrix correlation value, its P-value, the maximum t value attainable, and the ratio of the observed r over the maximum t (how close to perfectly the matrices actually are correlated, with error) are provided here. Repeatability was calculated for both estimated matrices as previously described (Cheverud 1996). As we cannot calculate t for the theoretical matrices (developmental, connectivity, anatomical lobe), their maximum possible Mantel correlation value was conservatively assumed to be 1.

Modularity and cluster analysis

We used Mantel’s test to identify the degree of structural similarity between phenotypic, genetic, connectivity, and developmental matrices. Mantel tests assess the similarity of the pattern of variation present in compared matrices and provide an estimate of the probability that the observed structural similarity could be observed under a null hypothesis of no similarity. Mantel tests were done using the ade4 package of R (Dray and Dufour 2007). In all Mantel tests, 9999 randomizations were performed. Mantel tests were quite robust to slight variations in the construction of literature-based matrices. Each comparison of matrix pairs conducted here addressed a distinct biological hypothesis. For example, the genotype–phenotype Mantel comparison tested the hypothesis that there is genetic control over trait variation patterns, while anatomy–development tested the hypothesis that a fold’s position on the endocast could be used to predict how early in embryonic development the sulcus would appear. Since these comparisons address different hypotheses and we are interested in each hypothesis separately, our Mantel comparisons do not represent a situation where there is need to control for multiple testing as they do not constitute a set of tests of the same hypothesis.

Hierarchical cluster analysis was performed on the phenotypic and genetic matrices to visualize the structure of variation using an agglomerative approach (Hartigan 1975, 1985). These correlation matrices were converted into a distance matrix format for these purposes. A variety of methods (average, Ward, complete linkage) were used to determine the most robust cluster arrangement, which generally was represented by the average linkage method. For this reason, only average linkage clustering results are reported in this article.

k-Means testing was conducted using the two traditional algorithms (Hartigan and Wong 1979; Lloyd 1982) to independently determine the correct number of clusters and assign sulci to clusters based on their phenotypic and genetic relationships. k-Means is a heuristic criterion rather than a statistical approach, so there is no discrete cutoff point for clustering. Rather, it can be used to inform and corroborate results of the hierarchical clustering. The “elbow” in the k-means results was identified by examining the improvement of explanation of variation with each additional cluster. The greatest improvement to the ratio of the between-cluster sum-of-squares to the total sum-of-squares after which there was minimal improvement was determined to be the preferred value for k. Both algorithms agreed on the number of clusters for both matrices.

QTL mapping

QTL mapping was used to pinpoint chromosomal regions affecting variation in all metric cortical phenotypes. QTL analysis has a very low rate of type I error, but is limited in its ability to identify genes of small effect. We do not presume that we can identify all the loci affecting cerebral gyrification in this study. However, implicating any genomic regions as affecting gyrification is a substantial step forward in this incipient research field. QTL analysis was conducted using SOLAR, which minimizes the false-positive rate of QTL peaks by limiting results to true relatedness as opposed to simply sharing an allelic state. SOLAR was also used to calculate LOD scores across the baboon genome. A LOD score indicates the ratio of the likelihood of obtaining a signature of linkage if the marker and locus are indeed linked vs. the likelihood of obtaining the observed result by chance. The SNPRC has created an extensive whole-genome microsatellite-based linkage map for this population based on genotypes from 284 marker loci that are 2354 cM long (Rogers et al. 2000; Cox et al. 2006). Markers were selected to be as evenly spaced throughout the genome as possible, with an average intermarker distance of 8.9 cM and average heterozygosity of the microsatellite loci of 0.74.

LOD score thresholds were calculated on both chromosome-wise and genome-wide scales in SOLAR using a modification of the approach suggested by Feingold et al. (1993), controlling for the overall false-positive rate, given the finite marker locus density in the baboon genome map and pedigree complexity. This modification improves the accuracy of results for continuously varying quantitative traits in complex pedigrees with multiple relative classes. QTL power calculations for a pedigree of this constitution were conducted during linkage map creation. In simulations with 1000 replicates at each QTL-specific effect size, there was determined to be 80% power to detect a significant QTL responsible for as small as 5.5% of the total phenotypic variance (Lander and Kruglyak 1995; Almasy and Blangero 1998). For this, simqtl procedures were implemented, modeling a quantitative trait that is influenced by a single, bi-allelic QTL with a residual additive genetic effect due to polygenes. To control for genome-wide false-positive QTL hits, the expected LOD scores estimated for a QTL with a specific effect size between 0.01 and 0.05 were calculated. These values were used to determine the thresholds for genome-wide significance at LOD = 2.75 and for suggestive evidence of linkage at LOD = 1.53 at α = 0.05 with this pedigree configuration. Such a significance threshold corresponds to the expected type I error rate of once per 20 whole-genome linkage screens. Power tests were based on the 840 baboons that were part of the pedigree at that point in time. All 840 animals are phenotyped and genotyped in this study. These power calculations thus represent a minimum estimate of the true power for QTL detection of our current, expanded data set.

Results

Endocast validation

Due to a very close ontogenetic relationship between brain shape and the bones of the skull, sulci are visible as ridges on the endocranial surface in Old World Monkeys, making endocasts useful for analysis of cortical features (Moss and Young 1960; Falk 1986, 1987; Enlow 1990; Bruner 2003; Holloway et al. 2005). The utility of CT-based virtual endocasts for studies of primate brain evolution, including in examination of cortical-folding features, has been validated in both anthropology and paleoneurobiology (Zollikofer et al. 1998; Bruner 2003, 2004, 2007, 2008; Zollikofer and de León 2005; Carlson et al. 2011; Balzeau et al. 2012; Falk 2014; Kobayashi et al. 2014). Our measurements taken on these CT scan-based virtual endocasts showed extremely high repeatability (average = 93%), implying reliable and consistent data collection. Furthermore, we found an exceptionally tight correlation between the sulcal length measurements taken on CT endocasts compared with those from 100 magnetic resonance imaging scans of the same individuals (average = 95%). This verifies the biological meaningfulness of endocast cortical measurements; these CT-based virtual endocasts consistently and reliably capture the sulcal shape variation of the true cortex. See Supporting Information for details on repeatability calculations.

Heritability

There is a moderate genetic basis to variation in both the metric and non-metric cortical sulcal traits measured in this population. The average of sulcal length heritability (h²) for all metric traits with a sample size great enough to reach significance was 0.26, which is within the normal range for morphological traits (Visscher et al. 2008). The lengths of 7 of the 10 landmark sulci were significantly heritable—all but iar, sar, and spcd. Of the covariates included in the analyses, cranial capacity was typically significant, with age, sex, and their interactions occasionally being so. Table 2 shows the h² results for all traits, their individual significance levels, significant covariates, and sample sizes.

Three of the non-metric traits had significant h² estimates: Lcs_forked, Rarsp_yn, and Rspcd_yn. The average significant h² calculated for non-metric traits was 0.14. Non-metric traits were controlled for the same covariates as metric to ensure that h² corresponded only to genetic variation of the phenotype in question. These h² estimates are likely underestimates, as any error in the data would detract from the true value; here, ∼5–10% of trait variation was due to measurement error. The difficulty in assessing heritability of sulcal pattern has been noted in previous studies (Winterer and Goldman 2003).

Mantel testing and cluster analysis

Matrix repeatabilities (t) were calculated for the two matrices created from our data: phenotypic and genetic. The t-value was 0.34 for the genetic matrix and 0.98 for the phenotypic. All permutations between distance matrices created from correlation matrices were compared to test different biological hypotheses about cortical modularity, development, and connectivity. Four of these comparisons indicated statistically significant similarity between matrix pairs (Table 3). The four statistically similar matrix comparisons, listed with their Monte-Carlo observed matrix correlations and P-values, were genetic–phenotypic (r = 0.39, P = 0.003), anatomic–developmental (r = 0.29, P = 0.048), connectivity–anatomic (r = 0.51, P = <0.001), and connectivity–developmental (r = 0.29, P = 0.040). Taking into account the fact that 0.563 is the maximum matrix correlation that could be observed using our data set between the phenotypic and genetic matrices in light of the matrix repeatabilities, the corrected genetic–phenotypic matrix correlation is 0.693.

Table 3. Mantel testing results.

Comparison	Monte-Carlo correlation	P-value	Maximum t	Ratio
Genetic–phenotypic*	0.390	0.003	0.563	0.693
Phenotypic–development	0.066	0.254	0.948	0.069
Phenotypic–connectivity	−0.046	0.616	0.948	−0.049
Phenotypic–anatomy	0.202	0.094	0.948	0.213
Genetic–development	−0.096	0.728	0.335	−0.286
Genetic–connectivity	−0.121	0.755	0.335	−0.361
Genetic–anatomy	−0.078	0.700	0.335	−0.234
Anatomy–development*	0.289	0.048	1.000	0.289
Connectivity–development*	0.288	0.040	1.000	0.288
Anatomy–connectivity*	0.511	<0.001	1.000	0.511

Monte-Carlo matrix correlation, the P-value of the test, the maximum possible t value attainable with error, and the ratio of the estimated matrix correlation to the maximum t are shown for all domains compared. The ratio indicates the corrected matrix correlation value. The four significant comparisons are indicated by asterisks.

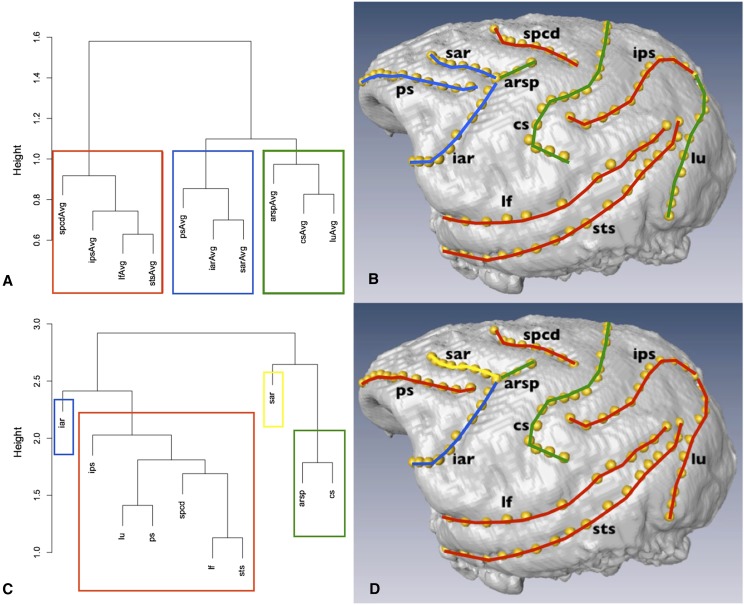
Hierarchical clustering and k-means methods were used to determine the appropriate module breakdown of the phenotypic and genetic relationships. Agglomerative hierarchical clustering links individual traits to one another iteratively to create a network. k-Means testing provides an estimate of the quality of fit in grouping n traits into k clusters. Table 4 contains the results for k-means examination of phenotypic and genetic data in tests from k = 2 to k = 7. Clustering analyses of the phenotypic correlations suggested three clusters of approximately equivalent size (ps, iar, sar; cs, lu, arsp; and spc, ips, lf, sts) (Figure 2, A and B). Although there was not an obvious elbow for the phenotypic data, the amount of improvement drops most dramatically after three clusters (Table 4). For this reason, combined with the fact that partitioning phenotypic variation into three modules additionally is the most biologically realistic outcome, k = 3 was determined to be the correct cluster number for the data. All clustering methods agreed on both cluster number and assignment of traits into groups at k = 3.

Table 4. Cluster number determination from k-means testing.

k	Phenotypic	Genetic
2	44.8	36.7
3	61.5*	47.6
4	71.8	61.9*
5	76.0	69.3
6	83.4	79.2
7	85.2	83.3

Results for k-means testing of phenotypic and genetic correlation matrices using the average of the Lloyd (1982) and Hartigan and Wong (1979) algorithms. Hypothesized cluster number is the k-value input into the heuristic. Numbers reported for the phenotypic and genetic matrices are the average of the two algorithms’ results for the ratio of the between-groups sum-of-squares to the total sum-of-squares. The point at which the curve was determined to have its “elbow” is indicated with an asterisk.

Figure 2.

Sulcus module assignments for phenotype (A and B) and genotype (C and D). Hierarchical clustering dendrograms (left) were created using the average linkage method. Colored boxes illustrate the module borders determined by k-means testing using the Hartigan–Wong algorithm. Annotated endocasts (right) visualize sulcus module assignment. Module color is retained between phenotype and genotype.

The clustering results for k-means and hierarchical clustering were both most compatible with there being four genetic modules (Table 4 and Figure 2, C and D). k-Means testing and hierarchical cluster analysis did not perfectly agree on the precise assignment of sulci into clusters due to the larger standard errors in genetic data, but the most consistent results across all algorithms are presented here. These clustering results are shown as produced by the average linkage criterion for hierarchical clustering and the Hartigan–Wong method for k-means testing. For consistency, phenotypic results are plotted using these methods as well.

QTL mapping and genetic architecture

One QTL passed the stringent genome-wide threshold, while 11 additional peaks passed the suggestive LOD threshold. All peaks passing either threshold are documented in Table 5. Peaks prioritized for follow-up were selected based on the criteria of LOD score, peak width, and the presence of compelling positional candidate genes. To control for the unlikely event that a false peak managed to break the lower threshold, only the highest peaks were selected for further examination (Figure 3; Table 6).

Table 5. QTL mapping results.

Baboon chromosome	Trait	LOD score	Human ortholog	Locus (cM)	Proximal CI (Mbp)	Distal CI (Mbp)
3	arsp	1.806	7_21	120	41	125
3	lu	3.187	7_21	39	14.2	33.4
4	arsp	1.688	6	65	87.6	128.5
5	iar	1.699	4	133	154.5	180
6	arsp	1.649	5	85	9	14.6
6	cs	2.472	5	39	9	76.7
8	arsp	1.631	8	50	10	40
9	ps	2.378	10	40	26	69
11	lu	1.680	12	56	44	100
12	ips	1.565	2q	145	132	140
12	lu	2.162	2q	127	226.5	233

Locations and widths of all QTL peaks passing suggestive (LOD = 1.53) or stringent (LOD = 2.75) thresholds using the full population. QTL width confidence interval (CI) boundaries were determined by the one-LOD drop point on either side of the peak marker. Linkage map locus positions are in centimorgans. CI basepair positions are in million basepairs.

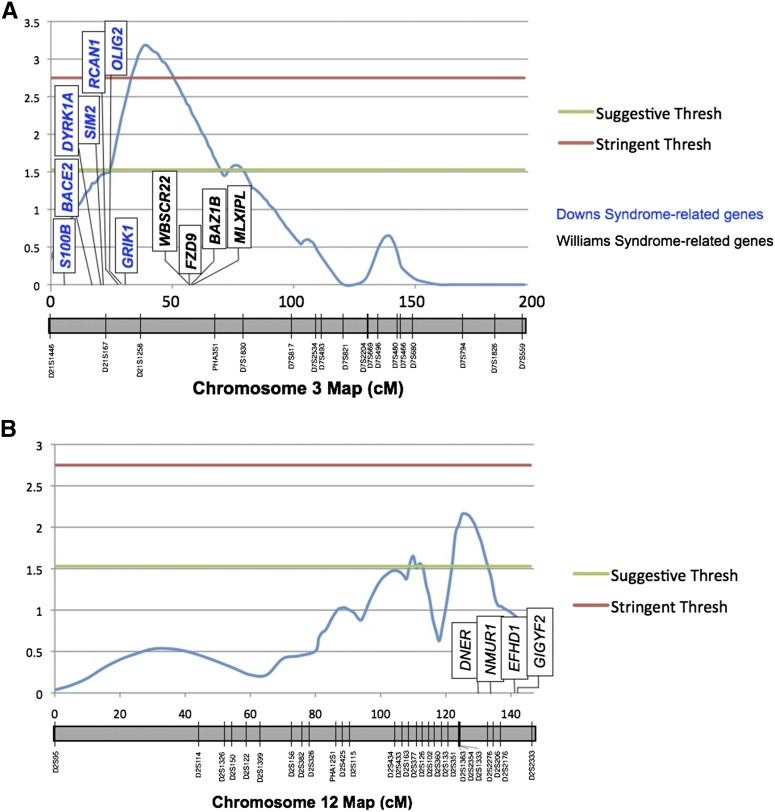
Figure 3.

Highest-priority QTL peaks. QTL maps for the lunate sulcus (lu) on (A) baboon chromosome 3 (orthologous to human 7_21) and (B) baboon chromosome 12 (orthologous to human 2q). Linkage map is shown in centimorgans. Marker names and positions are documented on the chromosome schematic along the x-axis. Location of candidate genes within the peak confidence intervals are labeled in boxes. Horizontal lines indicate suggestive and stringent genome-wide thresholds.

Table 6. Candidate genes contained within peak region of the top two QTL.

Trait	LOD score	Baboon chromosome	Human chromosome	Peak locus (cM)	Width (cM)	Candidate genes
lu	3.18	12	02q	126	16	DNER, NMUR1, EFHD1, GIGYF2, NGEF
lu	2.16	3	07_21	39	32	Williams syndrome gene cluster (WBSCR22, FZD9, BAZ1B, MLXIPL); Down syndrome-related genes (GRIK1, OLIG2, RCAN1, SIM2, DYRK1A, BACE2, S100B)

Peak characteristics for the two QTL of highest priority, including candidate genes within confidence interval regions, are given. Listed genes have been empirically implicated in affecting neurological development and/or function.

The highest peak obtained in the study, breaking the stringent genome-wide threshold, was for trait lu and appeared on baboon chromosome 3 (Figure 3A). This QTL contained two gene clusters associated with well-characterized neurological disorders: Williams and Down syndromes. Williams syndrome in particular is specifically associated with abnormal gyrification. Specifically, the Williams syndrome-associated genes within the confidence interval for chromosome 3 were the following: Williams Beuren Syndrome Chromosome Region 22 (WBSCR22), Frizzled Family Receptor 9 (FZD9), Bromodomain Adjacent to Zinc Finger Domain 1B (BAZ1B), and MLX Interacting Protein-Like (MLXIPL). The genes within the positionally relevant Down syndrome gene cluster were the following: Glutamate Receptor Ionotropic Kainate 1 (GRIK1), Oligodendrocyte Lineage Transcription Factor 2 (OLIG2), Regulator of Calcineurin 1 (RCAN1), Single-Minded Family bHLH Transcription Factor 2 (SIM2), Dual-specificity Tyrosine-(Y)-phosphorylation Regulated Kinase 1A (DYRK1A), Beta-site APP-Cleaving Enzyme 2 (BACE2), and S100 Calcium Binding Protein B (S100B) [National Center for Biotechnology Information (NCBI) genome database, http://www.ncbi.nlm.nih.gov/genome/].

The second-highest peak appeared on baboon chromosome 12 (Figure 3B). It was significant for numerous traits, indicating pleiotropic effects and its widespread role in cortical-folding development. This QTL additionally contained a handful of compelling candidate genes that make it of interest for further investigation. These genes were the following: Delta/Notch-like EGF Repeat Containing (DNER), Neuromedin U Receptor 1 (NMUR1), EF-Hand Domain Family Member D1 (EFHD1), GRB10 Interacting GYF Protein 2 (GIGYF2), and Neuronal Guanine Nucleotide Exchange Factor (NGEF), and all have also been implicated in affecting brain development or neuronal function.

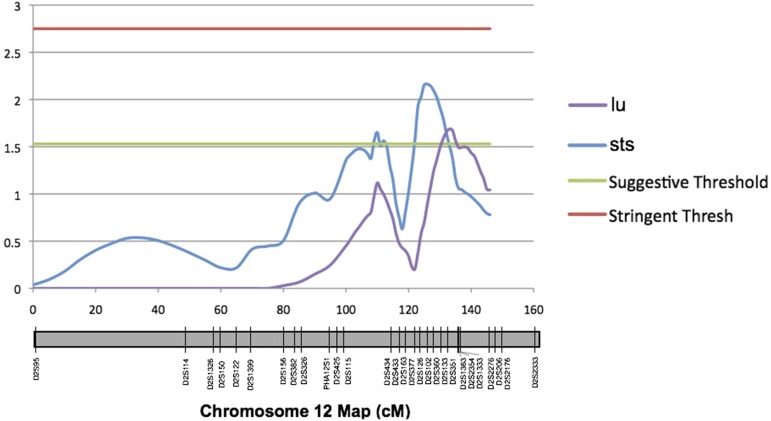
The genome-wide distribution of QTL peaks illustrates a complex genetic architecture underlying cortical gyrification in primates. First, a number of different traits mapped to the same chromosomal position. This is an indication of QTL pleiotropy, as the same gene or suite of genes present at the identified location is likely contributing to variation in the multiple significant phenotypes. An example of QTL pleiotropy on baboon chromosome 12 can be seen Figure 4. Further tests of the observed pleiotropy in this region were run in an effort to provide additional support for pleiotropy over coincident linkage. Analyses comparing QTL-specific ρ_G (additive genetic correlation) sets for polygenic traits did not reach statistical significance, but were near-significant (P ≈ 0.08) in the overlap region. This supports there being borderline-significant QTL-specific additive genetic correlations for putative pleiotropic traits and argues against the conclusion that these findings are due simply to coincident linkage. Larger pairwise trait sample sizes would be needed to boost ρ_Q values to the α = 0.05 level.

Figure 4.

Example of QTL pleiotropy. QTL map of baboon chromosome 12 (orthologous to human 2q) showing positional overlap of peaks for two distinct traits: lu and sts. Linkage map is shown in centimorgans. Marker names and positions are documented on the chromosome schematic along the x-axis. Horizontal lines indicate suggestive and stringent genome-wide thresholds.

The data additionally show indications of polygeny, the situation where one trait is affected by multiple genes. Nearly all traits mapped significantly to more than one position in the genome, supporting the postulate that most cortical phenotypes are controlled by a number of genes of small effect (Mackay 2001; Cookson et al. 2009) rather than a single gene of large effect determining gyrification pattern. The average number of significant QTL for those traits with at least one significant peak was 1.71, indicating that if traits were able to pass a threshold once, it was not uncommon for them to do so at least one more time. Often, subthreshold peaks were also visible, indicating the likely presence of additional affected traits or causative loci that did not pass the extremely conservative thresholds required for multiple comparisons.

Discussion

Quantitative genetics

It should first be noted that there are many interesting phenotypes associated with cortical morphology. In the current study, we aim to address the general question of the overall amount of gyrification across brain hemispheres by examining variation in the length of specific landmark sulci. Although these sulci were chosen to characterize a large portion of the cerebrum, there are many additional traits of interest that could be investigated further in future studies (e.g., depth of sulci, additional sulci not included here) that would complement these results.

The average significant heritability of 26.1% for metric traits falls into the range typical for morphological traits. This supports the hypothesis that brain cortical gyrification is not random but instead is under a significant, moderate degree of genetic control with additional environmental effects. Significant results even after removing the effects of cranial capacity and other size correlates support prior indications (Rogers et al. 2010) that gyrification has at least partial genetic control independent of brain volume. Gyrification thus has its own evolutionary history in primates and has potentially been influenced by natural selection separately but in tandem with forces selecting for larger brains.

Non-metric traits were also found to have significant heritability, but show a lower degree of genetic control over phenotypic variation. This implies that the finer details of shape within cortical-folding features are under some genetic control, but are more influenced by environmental effects than are the lengths of sulci. The fine-grained shape of sulci is apparently less genetically constrained than their length or overall degree of gyrification.

Modularity

The distribution of variation elucidated interesting trends regarding the boundaries of modules across different biological domains. There was a close relationship between genetic and phenotypic partitioning of brain features, consistent with our finding of genetic control over variation in sulcal length traits. This pattern is also consistent with past natural selection resulting in effective morphological integration of cortical traits. A strongly modular system of variation imposes constraints on morphological evolution (Cheverud 1984, 1995, 1996; Wagner et al. 2007; Klingenberg 2008; Gómez-Robles et al. 2014) as correlation among traits reduces the amount of variation available to selection along some morphological dimensions. Although constraints are often assumed to restrict the response to natural selection, some degree of constraint over the direction of evolution can actually lead to increased rates of adaptation in specific directions (Wagner and Altenberg 1996), and canalization of variance prevents traits from wandering into deleterious regions of phenotypic space. When variation in functionally related traits is restricted to a common set of genes, the coordinated evolution of these traits will result in a functionally compatible set of outcomes (Wagner 1984, 1988, 1996; Gibson and Wagner 2000). Restricting phenotypic variance into modules also allows systems to evolve patterns of correlation that facilitate future alteration of evolutionary traits through the convergence of genetic and functional modules (Cheverud 1996; Wagner 1996). The similarity of variation structure in genetic and phenotypic matrices thus illustrates the selective grouping of traits into related units in these two domains, providing a ready framework for future adaptive morphological change and an evolutionarily beneficial situation of increased morphological integration for traits that need to be functionally compatible with one another in an organism’s life.

The similarity in matrix variation structure between the anatomical location of the sulci and the day on which the sulcus first emerges during development parallels ontogenetic findings that the brain typically develops the primary and most deep-set folds first during development, with secondary folds developing next, and superficial wrinkles and projections off of the primary folds developing last (Huang et al. 2009; Sawada et al. 2012). The bulk of the primary folds are located toward the central region of the brain (lf, sts, cs), followed by the back of the brain (lu, ips), and finally the frontal folds (ps, spcd, iar). Superficial projections (arsp, sar) come last in development.

The final two significant results found from Mantel testing together provide indirect support for the propositions of the Van Essen model. The finding that strong similarity exists between the patterns of variation in connectivity and anatomical location of the sulci implies that connectivity is indeed paralleled by anatomical proximity (Markov et al. 2011). This theoretical result supports the mathematical models proposed concerning tension-based methods of cortical fold development (Mota and Herculano-Houzel 2012; Bayly et al. 2013) in an additional primate system. Moreover, the finding that there is significant similarity between the pattern of variation in connectivity and development hints at the interplay between the two factors in cortical formation. Tension imposed by white matter affects the emergence of sulci such that those dividing the most basal functional areas appear first in development (Kaymaz and Van Os 2009). Our results suggest that subsequent wrinkles and dimples might arise as the neural network becomes pruned and strengthened over the course of brain ontogeny. The modular patterns detected in these three domains therefore fall in line with the expectations of sulcal development theories based on axonal mechanical tension, rather than competing hypotheses for the origin of gyrification.

Turning to the structure of modules across biological domains, the first principal component for trait phenotypic variation, as determined by cluster analysis, roughly appears to correspond to orientation along the cortex. If we examine the hierarchical clustering network for the phenotypic data, the first sulcal group spans the frontmost portion of the endocast (Figure 2, A and B, blue). The next sulcal group that emerges has similar, roughly vertical orientations (Figure 2, A and B, green). The third main sulcal cluster consists of the sulci that cover the horizontal plane’s inferiofrontal–superioposterior axis (Figure 2, A and B, red). This overall grouping structure was very robust to different testing methods.

Despite best fitting with four modules rather than three, the genetic matrix clustering results (Figure 2, C and D) show a similar overall trend to the phenotypic pattern, as would be expected based on the similarity between these two matrices in the distribution of variation across phenotypic space as shown by Mantel testing. Specifically, the general trend of sulcal orientation across the cortex seems to hold for module determination, but with sar falling out into its own cluster and lu collapsed into the broader red group. This pattern is similar to that seen in the phenotypic matrix, and an examination of lower values of k for the genetic matrix matches phenotypic results even more closely. The borders to genetic modules in the brain have major implications as to the potential constraints imposed on the future evolutionary alteration of brain topology, including on selection acting on other biological domains. There could be selection focusing on developmental or connectivity phenotypes, but it is the DNA, the molecular substrate of evolution, that will reflect such pressures across generations.

Genetic architecture

The distribution of QTL peaks across the genome highlights the complex genetic architecture underlying cortical gyrification. We found multiple QTL peaks during linkage mapping, implying that numerous genes of small effect influence folding rather than a single gene of large effect. Additionally, through the recurrence of peak regions for distinct traits and the detection of numerous peaks for individual traits, we note both pleiotropy and polygeny for cortical features in this population.

One notable example of pleiotopy is for the traits of lu and sts on baboon chromosome 12 (Figure 4). This region is interesting for fine-mapping follow-up and candidate gene investigation, as a gene or gene cluster here seemingly has a relatively large effect on a number of different cortical sulci. It is interesting to note that these traits are all located toward the posterior portion of the cerebrum, behind the central sulcus (Figure 1). This could be an indication of these brain features sharing a common developmental pathway.

Candidate genes

A number of intriguing candidate genes are located in the peaks of highest interest (Table 6). The top two peaks identified in this study were for lu on baboon chromosomes 3 and 12. The peak for lu present on baboon 12 is of note due to its threshold-breaking recurrence for multiple cortical features (Figure 4). The region additionally contains a number of candidate genes of interest (Table 6) that have all been empirically shown to affect neuronal development and/or function in primates and are highly conserved across vertebrate species. There are therefore direct reasons to suspect that these genes could affect brain-fold development and adult cortical topology.

The second peak of interest was on baboon chromosome 3 (Table 6 and Figure 3A). This QTL attained LOD = 3.18, the highest score reached in this study, and was the only peak to break the rigorously stringent threshold for detecting genome-wide significance. Furthermore, it contains two extremely intriguing gene clusters with relevance to cortical gyrification and brain function (NCBI genome database). One gene suite on the periphery of the peak contains four genes that have been shown to be involved in Williams syndrome, a genetic disorder associated with abnormal cortical-folding patterns (Bellugi et al. 2000; Korenberg et al. 2000). A second gene cluster, located directly under the peak’s apex in the baboon chromosomal region orthologous to human chromosome 21, contains a cluster of Down syndrome-associated genes. All of these positional candidate genes have been empirically shown to affect nervous system development and function (Abdul-Hay and Sahara 2012; Hirata and Zai 2012; Lu et al. 2012; Streitbürger et al. 2012; Bhoiwala et al. 2013; Chatterjee and Dutta 2013; Hijazi et al. 2013). The genomic stretch containing this gene cluster has even been dubbed the “Down syndrome critical region” of human chromosome 21, making it a strong contender for playing a major role in brain development. The presence of these two gene clusters within this single peak makes this baboon chromosome 3 QTL of highest priority for future fine-mapping studies and candidate gene evaluation.

At this stage in our analyses, we have honed in on chromosomal regions of interest that are extremely likely to be involved in affecting baboon cortical folding. This provides a solid starting point for future work targeting specific positional candidate genes. To get from the QTL down to the quantitative trait gene (QTG), one would have to associate specific variants within genes of interest with variation in brain traits. Following such a step with functional testing of positional candidates would provide a robust demonstration of their effect on brain development and morphology.

Conclusions

Here, using CT-scan-based virtual endocasts from a pedigreed baboon population of unprecedented size for such research using nonhuman primates (n = ∼1000), we have characterized the heritability of cortical gyrification features, finding significant heritability for nearly all metric traits. Non-metric shape features additionally exhibited significant heritability estimates, but are more susceptible to environmental effects. We examine the module structure controlling cortical-folding traits and assess the interplay between numerous biological domains: development, genetics, morphology, and neural connectivity. This helps to characterize the evolutionary constraints imposed on the system, dramatically affecting the potential for future cortical alteration. We observe high morphological integration between phenotype and genotype, which would readily allow for adaptive alteration of the cortex as a whole. We also theoretically test tension-based models for cortical development, finding support for their predictions over competing models. Finally, we ran genome-wide linkage mapping tests for the 10 metric features, identifying QTL regions that contain the genes affecting variation in gyrification and parse out the genetic architecture for this complex phenotype. QTL peaks identified include stretches that contain genes that have been previously implicated in brain development and function, and we additionally discover novel areas that have not previously been shown to be associated with cortical topology phenotypes in primates. Brain folding is a significant and unique trait with a complex genetic architecture, involving polygeny, pleiotropy, and numerous genes of varying effect.

This interdisciplinary study characterizes gyrification’s underlying genetic makeup and elucidates the biological underpinnings contributing to structural and, ultimately, functional differences in the cerebral cortex between primate species. Our findings provide a foundation for further examination of the molecular basis for evolutionary changes in primate brain folding. Although this work was done in the baboon, the results are more widely applicable and can be used to inform human genetics and neuroscience, as there are numerous neurological disorders characterized by abnormal cortical gyrification.