Accurate theoretical prediction of vibrational frequencies in an inhomogeneous dynamic environment: A case study of a glutamate molecule in water solution and in a protein-bound form

Abstract

We propose a hierarchical approach to model vibrational frequencies of a ligand in a strongly fluctuating inhomogeneous environment such as a liquid solution or when bound to a macromolecule, e.g., a protein. Vibrational frequencies typically measured experimentally are ensemble averaged quantities which result (in part) from the influence of the strongly fluctuating solvent. Solvent fluctuations can be sampled effectively by a classical molecular simulation, which in our model serves as the first, low level of the hierarchy. At the second high level of the hierarchy a small subset of system coordinates is used to construct a patch of the potential surface (ab initio) relevant to the vibration in question. This subset of coordinates is under the influence of an instantaneous external force exerted by the environment. The force is calculated at the lower level of the hierarchy. The proposed methodology is applied to model vibrational frequencies of a glutamate in water and when bound to the Glutamate receptor protein and its mutant. Our results are in close agreement with the experimental values and frequency shifts measured by the Jayaraman group by the Fourier transform infrared spectroscopy [Q. Cheng et al., Biochem. 41, 1602 (2002)]. Our methodology proved useful in successfully reproducing vibrational frequencies of a ligand in such a soft, flexible, and strongly inhomogeneous protein as the Glutamate receptor.

I. Introduction

Vibrational spectroscopy is widely utilized to probe protein structure in solution at room temperature, to obtain information about the local interactions between a protein and its ligand, and to assess changes in the solute's environment (see Refs. 1 and 2 for recent reviews). However, from the spectral line shifts alone it is often difficult or sometimes impossible to decipher a detailed picture of changes in the medium surrounding a probe molecule. Theoretical modeling can, in principle, provide detailed understanding of physical factors responsible for experimentally observed line shifts and changes in a ligand binding strength. In protein systems, however, in order to have predictive power a theoretical method must account for the dynamical behavior of several hundreds atoms with a good accuracy. An attempt to directly use ab initio methods in such a big and fluctuating system seems impractical. For example, Kubo et al. have recently³ calculated frequency shifts for a carboxyl group of kainate ligand bound to a Glutamate receptor and in aqueous solution using the semiempirical PM3 method with only qualitatively satisfactory results. Note that high level ab initio methods capable of predicting spectra of molecules quantitatively are limited by the capabilities of computers and only applicable to systems with a small number of atoms. A typical vibrational spectroscopy experiment measures quantities that are averages of observables over a long time on a molecular time scale. Thus, the ideal computational methodology will describe a quantum mechanical system embedded in an inhomogeneous fluctuating environment with sufficient accuracy on an experimentally long time scale.

In this article we present a novel quantitatively reliable yet practical approach to the computational spectroscopic analysis of a ligand in a complex with a large biomolecule. While our approach can be qualified as a Quantum Mechanical/Molecular Mechanical (QM/MM⁴) model by the fact that a small part of the system is treated quantum mechanically while the majority of the atoms are represented by a classical force-field, we abandon the traditional QM/MM idea of propagating both parts of the system on the same time scale. Instead, we exploit a natural separation of vibrational modes in the system into the soft and the rigid ones to build a hierarchy of models. We initially use classical molecular simulations to quantitatively describe dynamical and structural properties of a fairly large system i.e., a protein in solution at room temperature, on a time scale spanning several nano-seconds or more. We then treat a part of the system potential surface, which is relevant to the vibrational motion of interest using an idea analogous to the partial Hessian vibrational analysis (PHVA) of Li and Jansen.⁵ As a result, our approach treats classically bath degrees of freedom that are populated to high levels at room temperature and thus are approximated appropriately by the classical mechanics; and it treats quantum mechanically intramolecular vibrational degrees of freedom that are present in low quantum states. (Apparent) success of such hierarchy is demonstrated in this article using several example applications.

Single amino acids such as glutamate and serine often serve as ligands to receptor proteins in neural system as well as in other regulatory functions,⁶ therefore, understanding their dynamics in an aqueous solution and in the protein environment is important for many biomedical purposes. The study of l-glutamate is particularly important, e.g., to understand the function of Glutamate receptors found in the human neural system.⁶ Under physiological conditions in water solution glutamate is present in a zwitterionic form characterized by a complex electric charge distribution dominated by two negative carboxylate groups and a positive amide group.⁷ Interactions in the binding site of the Glutamate receptor GluR2 are complex due to the charged ligand and the presence of water bridges.⁸ Furthermore, a binding site of this protein contains two charged residues, glutamate and arginine, in the close proximity to the ligand. Thus, electrostatic interactions in this system presumably play important role.⁸

In general, the electrostatic field in the binding site of a protein is a highly inhomogeneous function of space sensitive to small changes in the binding site geometry and composition. When a small ligand binds to a protein, the protein matrix induces Stark effect shifts in the ligand vibrational spectrum, which can be sensitive to polar interactions with the environment. For example, it has been shown that point mutations in a protein active site significantly affect Stark shifts of CO and NO stretch vibrations in various heme containing proteins.^9–12 The IR active asymmetric carboxylate stretch vibration is another example of an electric field sensitive spectral marker in biological systems.^13,14 Studies of the c-type cytochromes performed by Laberge et al.¹⁴ have demonstrated a strong correlation between the electrostatic environment of carboxylates and their frequency shifts. In this study we analyze the glutamate amino acid carboxylate frequencies in water solvent and when bound to a protein. We demonstrate that our proposed theoretical methodology is capable of predicting protein influenced frequency shifts and of achieving quantitative accuracy in calculating the ligand vibrational frequencies in a protein environment comparable in quality to the calculations reported for small molecules in the gas phase.

This article is organized as follows: In Sec. II we describe a computational method to calculate vibrational frequencies of a ligand bound to a protein. The solute vibrational frequencies are calculated on a QM level using a method analogous to the partial Hessian vibrational analysis.⁵ Sec. III describes simulation protocols used, and in Sec. IV we apply this composite methodology to model vibrational frequencies of glutamate in water and when bound to the Glutamate receptor and its mutant. Our conclusions are presented in Sec. V.

II. Theoretical approach

An adequate theoretical description of vibrational frequencies of a molecule in solution at room temperature must necessarily include its fluctuating environment. In order to make such computation plausible we utilize a hierarchical approach in which results of a classical molecular dynamics (MD) simulation of a ligand molecule with its molecular environment are incorporated into accurate quantum mechanical (QM) calculations of vibrational frequencies of interest. At this higher level of the hierarchy, the central part of the system is treated quantum mechanically while a bigger outer part of the system is taken into account via instantaneous distribution of partial point charges provided by the lower level of the hierarchy. Construction of a part of the potential surface needed to estimate particular vibrational frequencies is done in the spirit of the PHVA method previously used by Li and Jansen⁵

Let us consider an instantaneous configuration of all atoms n in the system. Near a stationary point the mass weighted Hessian matrix $K_{\mathit{\text{ij}}}^n$ is defined as

$$K_{\mathit{\text{ij}}}^n=\frac{1}{\sqrt{m_i{m}_j}}\left(\frac{{\partial }^2{E}^n}{\partial q_i\partial q_j}\right),$$ (1)

where the second derivative of energy E is taken with respect to the corresponding Cartesian coordinate displacements of atoms {∂q_i}. {m_i} are the masses of the corresponding atoms. The vibrational frequencies can then be found as ${\upsilon }_i^n=1/2\pi \sqrt{{\lambda }_i^n}$, where $\left\{{\lambda }_i^n\right\}$ are the eigenvalues of Hessian K̂.¹⁵ Often, only one or several frequency peaks are measured that represent vibrations of compact groups of atoms.

Li and Jensen⁵ proposed a strategy to construct only a part of the potential energy surface for a subset of coordinate space {q_i} involved in generating vibrations of interest. In their approach the total system (A) is separated into a central system (B) and the rest (C). The Hessian matrix then can be written in block form as

$$K_A=\left(\begin{array}{cc}{K}_{\mathit{\text{BB}}}& K_{\mathit{\text{BC}}}\\ K_{\mathit{\text{CB}}}& K_{\mathit{\text{CC}}}\end{array}\right).$$ (2)

Next, a matrix¹⁶

$$K_A=\left(\begin{array}{cc}{K}_{\mathit{\text{BB}}}& 0\\ 0& {\mathit{\text{K}}}_{\mathit{\text{CC}}}^{\prime }\end{array}\right),$$ (3)

is constructed where ${\mathit{\text{K}}}_{\mathit{\text{CC}}}^{\prime }$ corresponds to the same subsystem C as K_CC in Eq. (2) but with infinitely heavy atoms, thus efficiently removing the vibrational coupling between subsystems B and C. This approach was termed PHVA (partial Hessian vibrational analysis). Testing of the method⁵ indicated that the approximation holds for groups of several atoms and the error in predicting frequencies becomes negligibly small for subsystems separated by more than one chemical bond.

Let us now recall that the system A with the Hamiltonian Ĥ_A is embedded in a solvent or a protein environment. Thus, at room temperature this local subsystem is subjected to the influence of a strongly fluctuating environment. Considering that the experimental observation times are relatively long with respect to most of these fluctuations, the observed vibrational frequencies of a small subsystem, e.g., carboxylate vibrations, result from thermal averaging of instantaneous conformations of the external system. We can separate the total system with its environment into the three parts: B—a local chemical subsystem which contains all coordinates important for identifying a particular vibration, C—a part of the chemical system immediately coupled to the subsystem B and the rest of the environment. Only the lowest energy levels of rigid modes of the subsystem B, e.g., bond and angle stretching vibrations, are populated at room temperature and, therefore, these modes can be found as the lowest modes of a quantum mechanical harmonic oscillator. At the same temperature soft vibrational modes of the surrounding environment are excited to high energy levels, thus, the approximation of these modes by a quantum harmonic oscillator model is clearly inappropriate. Classical Newtonian dynamics, however, is known to be adequate for such soft systems. Therefore, different approaches are indicated for treating rigid and soft modes of the system of interest. Taking into account that thermal fluctuations of soft modes occur on significantly longer time scales than the bond-stretching vibrations of the small rigid subsystem B we utilize two simplifications. First, at any moment of time the vibrational motion of the subsystem B occurs under the influence of an instantaneous external field V_ext(t) imposed by the rest of the environment and the subsystem C. This approximation is used on the fine level of our hierarchy to express an instantaneous Hamiltonian of the total system as

$$\widehat{H}\left(t\right)=\widehat{H}\left(t\right)+V_{\text{ext}}\left(t\right).$$ (4)

V_ext(t) is evaluated at the lower first level of the hierarchy using the second consequence of the time scale separation of soft and rigid vibrational modes in the total system. Namely, the internal dynamics of the subsystem B is relatively unimportant for the long time scale dynamics of the whole system, which is dominated by the dynamics of the soft modes. Thus, a simulation in which the whole system is treated classically, i.e., H(t) ≈ H^MM(t) provides nearly correct Boltzmann sampling of soft modes to yield V_ext(t) in Eq. (4). The subsystem C may be treated quantum mechanically as needed at the higher level of the hierarchy according to Eq. (3).

Using this proposed two step hierarchy of modeling methods we then calculate a vibrational frequency ν_i of interest as the Boltzmann average

$${\upsilon }_i={\langle {\upsilon }_i\rangle }_0,$$ (5)

where 〈…〉₀ indicates averaging over the classical ensemble. One possible method to sample the classical ensemble is via a classical MD simulation of the whole system. An instantaneous ν_i is then calculated as prescribed by Eqs. (2)–(4).

In the next section we describe simulation protocols, which were used to implement the hierarchical method described above to model vibrational frequencies of glutamate carboxylates in water and in protein environment.

III. Simulation protocols and systems studied

We have performed classical MD simulations of three systems: a free glutamate molecule solvated in liquid water, a wild type (wt) S1S2 fragment of the GluR2 receptor solvated in water with the glutamate bound in the active site, and an E705D mutant of the S1S2 protein solvated in water with the glutamate ligand bound in the active site. The resulting MD trajectories were utilized in further theoretical analysis as described in the previous section. In this section we describe the construction of model systems and the MD protocols employed.

Under physiological pH both glutamate carboxyl groups are deprotonated and the amine group is protonated.⁷ Therefore, for MD simulation of a free glutamate in water a zwitterionic form of the glutamate was constructed. To calculate partial charges on the ionized glutamate ligand the Hartree–Fock method with the 6-31G basis set was used and partial charges were fitted with the Merz–Singh–Kollman algorithm.^17,18 Glutamate molecule thus constructed was solvated with TIP3P model water.¹⁹ The final size of the computational cell was 25×25×25 Å. After a short minimization and 150 ps equilibration simulation under constant pressure, the system was propagated as an NTV ensemble for ∼ 1 ns. The temperature was kept constant at 300 K using the Berendsen thermostat.²¹ The particle Mesh Ewald method²⁰ was used to treat long-range electrostatic forces. The coordinates of all atoms in the system were collected and used for further vibrational analysis as described in the previous section.

A crystal structure of a glutamate bound with the S1S2 protein construct⁸ was downloaded from the Protein Data Bank (PDB code-1FTJ). The residue numbering of Armstrong and Gouaux (2000) was employed. Crystallographic water molecules within 3 Å of the glutamate ligand were retained (five water molecules). The starting structure was solvated in a box of TIP3P water molecules with dimensions 60×70×65 Å. The protein–ligand complex was subjected to energy minimization followed by a restrained MD simulation of 150 ps, in which the protein and ligand were harmonically restrained with a harmonic force of 500 kcal/mol. Next, all restraints were removed and the equilibrium simulation was run for 500 ps at 300 K. An E705D mutant structure was generated by substituting the glutamate (Glu) 705 with aspartate (Asp) using the program harlem²² and was equilibrated as described above. The production simulation was performed for 600 ps.

All classical MD simulations were performed using the amber 6²³ software package with the Cornel et al. force field.²⁴ Electrostatic interactions were calculated using the particle mesh Ewald (PME) method with the 12 Å cut-off radius. The integration time step was 2 fs, and coordinates were saved every 0.5 ps. Bonds involving hydrogen atoms were constrained via the SHAKE algorithm. The root mean square deviation (RMSD) of all protein atoms calculated in the course of the MD simulation was no larger than 1.5 Å, indicating that the protein retained its structure.

All ab initio calculations were performed with partial optimization of carboxylate groups using Becke three parameter Lee–Yang–Parr (B3LYP) density functional theory (DFT) with basis set 6-31G*. To calculate vibrational frequencies via the PHVA approach, the masses of most common isotopes were used for carboxyl group atoms and masses of 1000 a.m.u. were used for other atoms in the glutamate molecule. We have also performed two gas-phase calculations of the glutamate vibrational frequencies in order to partially test our methodology. These test calculations were performed for the partly and the fully optimized structures. Normal modes for the partially optimized structure in vacuum were calculated using PHVA approach. The hydrogen atoms of the glutamate amino group were substituted with deuterium atoms for the fully optimized structure. The standard scaling factor 0.961 was used for a better fit of calculated values.²⁵ All ab initio calculations were performed using the gaussian 98 program.²⁶

IV. Results and discussion

A. Glutamate in a homogeneous liquid water

In this subsection, we apply our explicit solvent hierarchical approach to model asymmetric vibrational frequencies of the glutamate 1C and 5C carboxylates (see Fig. 1) in homogeneous D₂O solvent and compare our results with the corresponding frequencies measured by the FTIR experiment (provided in Table I).^27–29

FIG. 1.

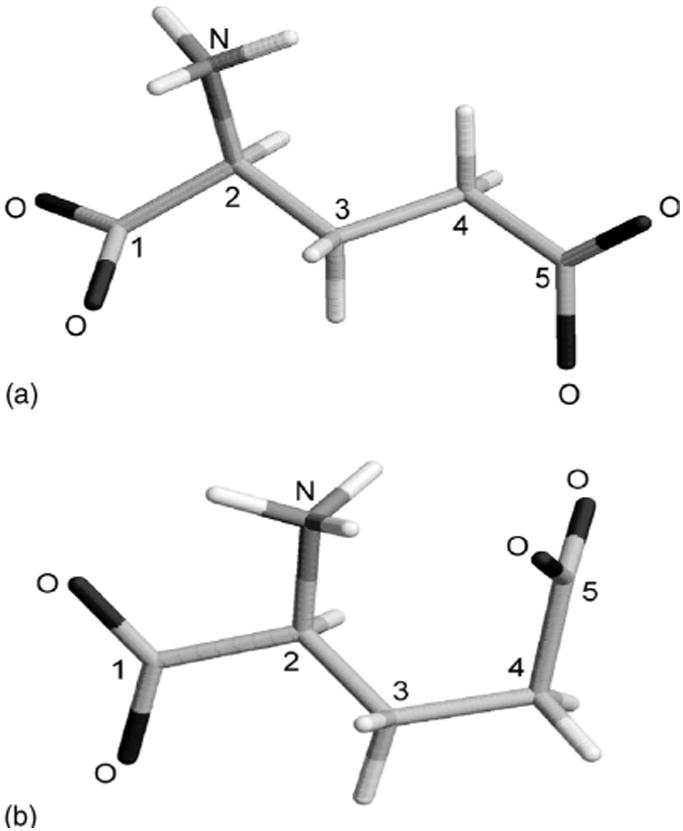
Extended (a) and fully optimized (b) structures of the glutamate zwitterion molecule.

TABLE I.

FTIR measured asymmetric stretch vibrational frequency of the glutamate COO⁻ groups at positions 1C and 5C (in cm⁻¹) (Refs. 27–29).

Ligand environment	1C	5C	1C	5C
D2O	1614	1565	…	…
	GluR0		GluR4
Wild-type protein S1S2	1612	1568	1610	1575
Mutant E705D	…	…	1609	1560

Several recently reported computational studies of spectroscopic properties of single amino acids in aqueous solution were nearly in quantitative agreement with the experimental results. Both continuum and molecular solvent models as well as various hybrid continuum/molecular approaches were employed.^30–38 One important conclusion which resulted from the prior theoretical analysis of the zwitterionic l-alanine, l-glycine, and l-glutamine in water solution was that both local hydrogen bonding and long-range electrostatic solvent effects must be taken into account in order to correctly predict their vibrational frequencies.^39–41 While the reaction field approach (PCM)⁴² in which the solvent is represented by dielectric continuum and the shape of the solute is taken into account is more computationally efficient than explicit solvent models, it cannot be applied in an inhomogeneous environment such as a protein binding site. We are thus interested in developing an explicit solvent approach. We report the results yielded by continuum solvent models for the purpose of comparison among several approaches.

In Table II calculated glutamate carboxylate vibrational frequencies are reported for several different representations of the surrounding solvent. In Fig. 2 some of these solvent models are shown schematically. According to Monte Carlo simulations reported elsewhere⁴³ a first solvation shell of a COO⁻ group is comprised of six water molecules on average. Therefore, using a single snapshot from the MD simulation of a glutamate molecule in water (described in Sec. III), we prepared two configurations of the glutamate molecule with its six nearest waters. In the first configuration waters form a first solvation shell around the 1C carboxylate as shown in Fig. 2(a), and in the second configuration waters surround the 5C carboxylate as shown in Fig. 2(b). We will further refer to models shown in Figs. 2(a) and 2(b) as Model I (see also Table II). In Model II, long-range electrostatic interactions are represented via the reaction field continuum approach with a spherical cavity [as shown in Fig. 2(c)]. The cavity radius for the continuum solvent model⁴⁴ was calculated using GAUSSIAN 98.²⁶ In Model IV partial charges associated with the outer solvating water molecules within the 12 Å radius from the solute were placed as shown in Fig. 2(e).³⁰ In Model III all solvent was represented by partial charges only [as shown in Fig. 2(d)]. Values and positions of partial charges for Models III and IV were taken from an MD simulation.

TABLE II.

Glutamate asymmetric vibrations (in cm⁻¹) in D₂O solvent calculated using partial optimization at the B3LYP/6-31G* level of theory and the different solvent representations (for model numbering definitions see the text and the caption to Fig. 2).

	1C		5C
Environment description	Single conformation	Average valuea/RMSD	Single conformation	Average valuea/RMSD
Partly optimized, gas phase	1716.2		1690.8
Fully optimized, gas phase	1701.7		1613.7
Model I	1676.5		1628.3
Model I with point charges	1644.6		1636.4
Model II	1623.9		1593.7
Model III	1617.6	1635.2± 12.4	1588.5	1589.5± 15.9
Model IV	1627.5	1653.2± 13.1	1588.0	1611.5±22.2
PCM model	1642.7		1588.2

^aAverage value is calculated according to the hierarchical methodology as described in the text.

FIG. 2.

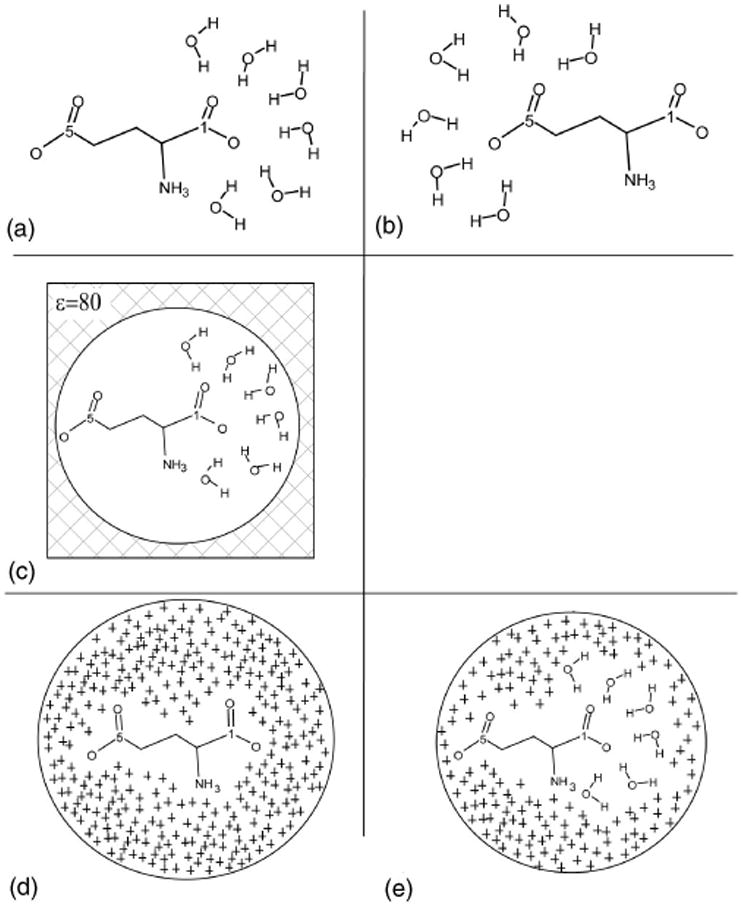
A schematic representation of several models with different description of the Glutamate environment: (a) Model I: six water molecules constituting a first solvation shell of the 1C carboxylate; (b) the same for the 5C carboxylate; (c) Model II is a spherical cavity model with the dielectric constant of water and six water molecules around the 1C carboxylate. An analogous model has been prepared for the system with water molecules surrounding the 5C carboxylate (not shown); (d) Model III: the ligand is treated quantum mechanically and the environment is represented as a sphere of partial charges taken from the MD simulation. The sphere radius is 12 Å. (e) Model IV is the same as Model III but the six water molecules which are the closest to the 1C carboxylate has been represented quantum mechanically. Similar model has been prepared with the six water molecules surrounding the 5C carboxylate (not shown).

Results shown in Table II for single configuration calculations reemphasize the importance of long-range solute–solvent interactions. Three calculations, Models II–IV (see Fig. 2), which take into account long-range electrostatic interactions by various approaches, produce similar results of about 1620 cm⁻¹ for 1C and 1590 cm⁻¹ for 5C carboxylate in D₂O. Calculated values differ from the experimental ones by only 5–10 and 25 cm⁻¹ respectively (see Table I). Deviations from the experimental data are higher in models with omitted long-range interactions, e.g., frequencies calculated using Model I, in which the first solvation shell water molecules are treated quantum mechanically but no long-range solvent effects are taken into account, differ from the experimental values by more than 60 cm⁻¹ for both 1C and 5C carboxylates. Although Model II performed well for the solute in water (see Table II) it utilizes continuum description of the solvent and cannot be used in an inhomogeneous dielectric environment, such as protein, and thus will not be considered in further discussion.

To test the performance of the PHVA methodology and for the sake of comparison we have also performed calculations of the glutamate carboxylate group vibrational frequencies in the gas phase. The partially and the fully optimized glutamate in the gas phase calculations exhibited different frequencies for both the 1C and 5C asymmetric vibrations but to a various degree (see Table II). These differences can be partially traced back to the substantial conformational change in the glutamate molecule that resulted from the full optimization [compare Figs. 1(a) and 1(b)]. Frequencies of the 1C carboxylate calculated for the extended (partially optimized) and the folded (fully optimized) structures differ by only ∼15cm⁻¹ indicating adequate performance of the PHVA method for the 1C vibration. The 5C carboxylate vibration is shifted by ∼ 77 cm⁻¹ in the fully optimized structure [Fig. 1(b)] with respect to the extended conformation [Fig. 1(a)]. Note that the 5C frequency in the fully optimized structure is comparable with the frequency in the extended structure in solvent when the first solvation shell is taken into account (Model I, see Table II). It seems that hydrogen bonds formed with the amino group in a collapsed structure serve as a “surrogate” first solvation shell for the carboxylate group in vacuum. In view of this result an honest comparison of the PHVA approach to conventional full diagonalization of Hessian matrix for the 5C carboxilate in vacuum proved impossible. PHVA method can be used successfully when the structure of the molecule is not greatly distorted as a result of optimization.

Further comparing results of calculations in vacuum and for the Model I (a system with only first solvation shell around the OOC1 and OOC5 carboxylate groups) we can assess how sensitive is the carboxylate vibration to its local electrostatic environment. The calculated downshifts of ∼ 40 and ∼60 cm⁻¹ for the 1C and 5C, respectively, indeed indicate the importance of local interactions. After considering next the long-range interactions (Models II–IV) we can conclude that both solute–solvent hydrogen bonds and the long-range interactions are important.

To calculate ensemble averaged glutamate frequencies we used the MD trajectory of a free glutamate in water as described in Sec. III. The ensemble average results, also reported in Table II, were obtained according to the Eq. (5) using 20 snapshots extracted from the MD trajectory with the interval of 10 ps, thus accounting for the thermal fluctuations of the environment and the solute. Ensemble average frequencies calculated with the solvent Model III are in good agreement with the experimental values within 20–25 cm⁻¹ with RMSD (root mean squared deviation) in the range of 12–20 cm⁻¹ (see Table II).

The frequencies calculated with Model IV are on average slightly higher than with Model III. In Model IV the six water molecules nearest to a respective carboxylate were treated quantum mechanically and thus Model IV seems superior to Model III. Possible reasons for a relatively worse performance of Model IV include overestimation of interaction between the solute and the QM waters insufficiently compensated by the outer solvation shell, possible slight vibrational coupling between the asymmetric stretch and the first solvation shell water (due to the deficiency of a PHVA model), or insufficient basis set used in our calculations. Therefore, given the impressive performance of Model III in a homogeneous solvent as well as its computational efficiency, we put it to further test in an inhomogeneous medium and apply it in the next section to calculate vibrational frequencies of a glutamate bound to a protein.

B. Glutamate in the protein-water environment

Each result reported in Table III is an average of 20 single DFT calculations for system configurations taken from a corresponding MD trajectory and constructed as defined for Model III in the previous section. The FTIR experimental asymmetric stretch vibrations of 1C and 5C carboxylates in GluR0, GluR4 proteins and the mutant GluR4/E705D are given in Table I.^27–29 The frequency of 1C is downshifted by four reverse cm with respect to a free glutamate in D₂O solution when the ligand binds to the wild-type protein. It is downshifted by 5 cm⁻¹ when glutamate binds to the GluR4/ E705D mutant. The 5C band is upshifted by 10 cm⁻¹ in the wild-type protein and it is downshifted by 5 cm⁻¹ in the GluR4/E705D mutant. Calculations predict the correct direction of the frequency shifts with the change of the glutamate environment from D₂O to a protein. Moreover, frequency shifts are predicted nearly quantitatively when the ligand binds with either the wild-type GluR4 or the mutant protein. For example, the calculated 1C frequency is downshifted by ∼6 cm⁻¹ and the 5C frequency is upshifted by ∼ 10 cm⁻¹ when glutamate binds to GluR2 protein (see Table III). The predicted mutant frequencies are downshifted by ∼9 and ∼16cm⁻¹, respectively. The downshift of the mutant frequencies can be traced to the rearrangement of hydrogen bonds and positions of water molecules in the active site of the mutated protein observed in the MD simulation. For example, Fig. 3 shows the formation of a strong hydrogen bond between the Ser654 hydroxyl group and the glutamate ligand 5C carboxylate during the MD simulations of the E705D mutant while this effect is absent in the wild-type protein. The mutation Glu705/Asp705 has also resulted in the shift in water positions near the ligand (see Fig. 4).

TABLE III.

Asymmetric vibrations (in cm ⁻¹) of the glutamate 1C and 5C carboxylates calculated by the hierarchical methodology.

Ligand environment	1C	5C
Glutamate—D2O	1635.2± 12.4	1589.5± 15.9
Glutamate—Wild-type protein S1S2	1628.8±9.8	1600.0± 8.7
Glutamate—Mutant E705D	1626.1± 10.9	1573.1 ± 15.0

FIG. 3.

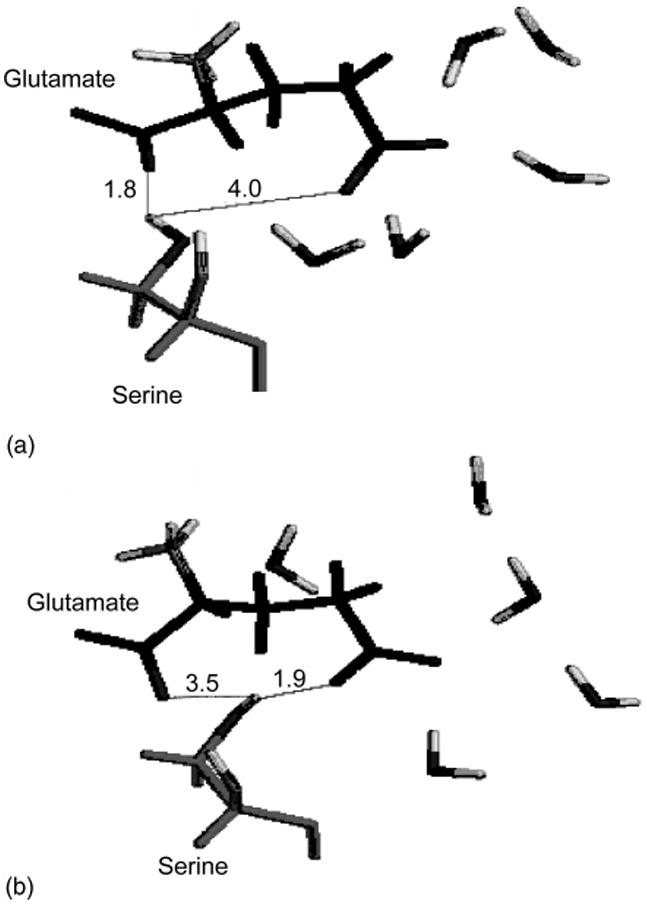
Shown are the fragments of the protein binding site with the Glutamate ligand bound. (a) the protein is the wild-type glutamate receptor and (b) the protein is the mutant E705D. Average distances in angstroms from the serine OH group hydrogen to both carboxylates of the ligand are shown. Also shown are positions of five water molecules which coordinate the 5C carboxylate of the ligand in the protein bound state.

FIG. 4.

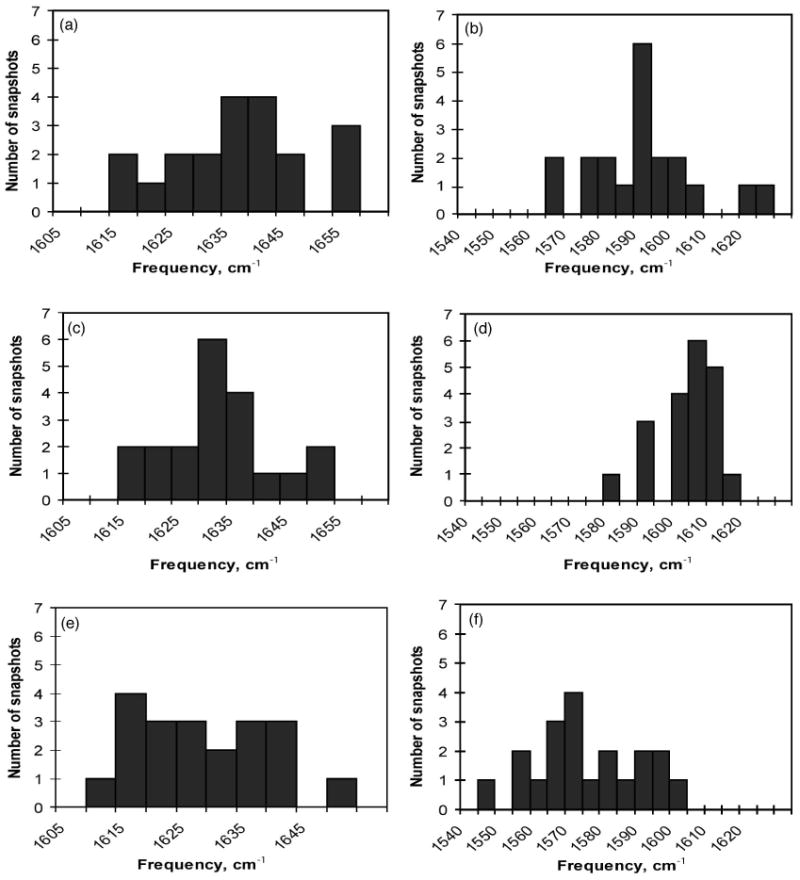
Histograms of the distributions of the calculated vibrational frequencies are plotted. These correspond to adsorption bands of (a) the 1C carboxylate in water solution, (b) the 5C carboxylate in water solution, (c) the 1C carboxylate of the glutamate bound with the wild-type protein, (d) the 5C carboxylate of the glutamate bound with the wild-type protein; adsorption band of (e) the 1C carboxylate of the glutamate bound with the E705D mutant protein and (f) the 5C carboxylate of the glutamate bound with the E705D mutant protein.

Although binding sites of the GluR2, GluR4, and GluR0 proteins are largely conserved the observed ligand frequency shifts upon binding to, e.g., GluR0 and GluR4 vary slightly (see Table I) and may be indicative of small variations in the ligand environment in the binding site.^27,28 Slight deviations between the experimental and predicted frequency shifts in the wild type and the mutant proteins (see Tables I and II) are within the experimental and theoretical errors and may be due to either small structural differences between the GluR2 and GluR4 proteins, insufficient sampling, or the quality of the theoretical model.

C. Spectral bandwidths

The calculated vibrational absorption bands are shown in Fig. 4. The histograms show distribution of frequencies calculated for 20 snapshots taken from the MD simulation as described above. In Figs. 4(a), 4(c), 4(e) the distributions of the 1C vibration are shown in the three solvent environments (water solution and when bound to two proteins). The C1 line shape is retained in all three environments indicating that it is mostly due to the presence of a positively charged amino group of the glutamate molecule itself. The influence of the environment on the line shape is stronger for the 5C vibration. The histogram of the distribution of the 5C vibrational frequencies in water [Fig. 3(b)] shows the broader spectral line in comparison to the line shape of the 5C vibration in the wt protein environment [Fig. 4(a)]. The mutation in the protein binding site from the glutamate residue to the aspartate residue, which has shorter side-chain, allowed the water molecules bound in the vicinity of the glutamate ligand to move slightly within the binding site. This increased water mobility resulted in a broader spectral line for the mutant 5C vibration as seen in Fig. 4(f). While the number of snapshots, which we used in these calculations is relatively small general trends in the spectral line shapes can be analyzed and traced back to the interatomic interactions. With the improved statistical sampling from the MD trajectory the proposed method can resolve the line shape due to the inhomogeneous broadening of the predicted IR spectra.

V. Conclusions

In this article we have introduced a novel hierarchical approach to compute vibrational frequencies of a ligand bound to a protein or in a liquid environment. We recognize that vibrational frequencies measured experimentally are ensemble average values which result from many instantaneous deformations of a small patch of the potential surface due to the strongly fluctuating environment. Moreover, we exploit the fact that soft modes of a surrounding bath are populated to high energetic levels at room temperature and therefore are adequately modeled by the classical approximation. At the same time the intramolecular vibrational modes, especially those corresponding to a valence bond stretching and angle bending, are in their ground state and thus are quantum mechanical and harmonic. This natural separation of the soft and rigid modes allowed us to construct a hierarchical methodology in which a classical MD simulation samples soft modes of the total system (at the low first level of the hierarchy). The amended potential surface for a subset of coordinates, which generate a vibration in question, is then calculated at the second level of the hierarchy using a sufficiently high level ab initio method. For this second level of the hierarchical approach we utilize an idea of a partial optimization of a small dimensional patch of the potential surface to calculate selected vibrational frequencies of interest. At this hierarchical level influence of the outer solvation shell is included as an external force extracted from the first level of a hierarchy. Since in our approach only a small part of the potential surface is constructed and used to evaluate the vibrational frequencies, only a small subsystem requires full optimization at ab initio level. Therefore, the method outlined in this work allows us to calculate selected vibrational frequencies at a moderate computational cost and with an impressive quality of predicted absolute values as well as shifts of frequencies.

We have tested the proposed methodology by calculating vibrational frequencies of a glutamate zwitterion in a D₂O liquid and when bound to the GluR2 Glutamate receptor protein and its mutant. Our results compare well with the experimental results.^27–29 While the simpler approaches such as a continuum reaction field approximation of the solvent work well in the homogeneous liquid environment, they are inadequate for the detailed modeling of a protein binding site characterized by a highly inhomogeneous distribution of an electric field and hydrogen bonds.

In testing this proposed approach for the glutamate in water we have found that representing the first solvation shell of a ligand explicitly quantum mechanically did not improve our results by comparison with a model in which all solvent was represented as a set of partial point charges. This may reflect the fact that the basis set employed in our DFT calculations was insufficient to adequately reproduce short range two body interactions. Another reason for such behavior of the model maybe that the solvent coupled modes may play a role. In the latter case a much more involved treatment of the potential surface which will include the first solvation shell molecules with appropriate corrections for anharmonicity may be needed.

The observed and calculated frequency shifts of the carboxylate vibrations in the three different systems reported in this work compare well with the experiment. Therefore, a closer look at the changes in the local environment of the carboxylate group is ensured. Our detailed computational analysis supplements experimental observations to provide a better understanding of the mechanism of the protein-ligand interactions. For example, slight frequency shifts were observed experimentally in the mutant protein with respect to the wild type protein. We were able to trace these frequency shifts in the protein-bound state to the shift in positions of nearest water molecules and to a conformational change in one amino acid, i.e., Ser654, in the binding site of the protein. Remaining important question is the degree of the correlation between the spectral shifts in the ligand and the ligand–protein affinity parameters.