Abstract
Despite general agreement on the effects of knee valgus and internal tibial rotation on anterior cruciate (ACL) loading, compelling debate persists on the interrelationship between these rotations and how they contribute to the multi-planar ACL injury mechanism. This study investigates coupling between knee valgus and internal tibial rotation and their effects on ACL strain as a quantifiable measure of injury risk. Nineteen instrumented cadaveric legs were imaged and tested under a range of knee valgus and internal tibial torques. Posterior tibial slope and the medial tibial depth, along with changes in tibiofemoral kinematics and ACL strain, were quantified. Valgus torque significantly increased knee valgus rotation and ACL strain (p<0.02), yet generated minimal coupled internal tibial rotation (p=0.537). Applied internal tibial torque significantly increased internal tibial rotation and ACL strain and generated significant coupled knee valgus rotation (p<0.001 for all comparisons). Similar knee valgus rotations (7.3° vs 7.4°) and ACL strain levels (4.4% vs 4.9%) were observed under 50 N-m of valgus and 20 N-m of internal tibial torques, respectively. Coupled knee valgus rotation under 20 N-m of internal tibial torque was significantly correlated with internal tibial rotation, lateral and medial tibial slopes, and medial tibial depth (R2>0.30; p<0.020). These findings demonstrate uni-directional coupling between knee valgus and internal tibial rotation in a cadaveric model. Although both knee valgus and internal tibial torques contribute to increased ACL strain, knee valgus rotation has the ultimate impact on ACL strain regardless of loading mode.
Introduction
Injuries to the anterior cruciate ligament (ACL) are one of the most common and devastating knee injuries sustained as a result of sports participation with over 125,000 injuries occur each year in the U.S. (Kim et al., 2011). Non-contact injuries (without direct blow to the knee) are the predominant mechanism of ACL injury, accounting for >70% of all ACL injuries (Griffin et al., 2000). These injuries often occur during landing from a jump or lateral cutting maneuvers during athletic activities such as basketball and soccer (Myklebust et al., 1998). Neuromuscular control deficits during dynamic movements are postulated to be the primary causal factors for ACL injury (Hewett et al., 2013). Deficits in dynamic active neuromuscular control manifest as excessive joint loads and ultimately lead to detrimental ACL stresses/strains and failure. Therefore, injury prevention strategies such as neuromuscular training are an appealing option to avoid long-term joint instability, pain and early development of osteoarthritis associated with ACL injury. Identification of high-risk maneuvers that lead to non-contact ACL injury is a major step in the development of new, as well as optimization of existing, neuromuscular training programs in an effort to prevent these devastating injuries more effectively.
Recent experimental studies support multi-planar loading, including knee valgus and internal tibial torques, as the most probable non-contact ACL injury mechanism (Kiapour et al., 2014a; Levine et al., 2013; Oh et al., 2012; Quatman et al., 2014). The presence of multi-planar loading at the time of non-contact ACL injury is also supported by the findings of systematic reviews of the ACL injury literature (Quatman et al., 2010; Shimokochi and Shultz, 2008). Despite general agreement on the multi-planar mechanism of these injuries and the well-characterized effects of isolated knee valgus and internal tibial rotation on ACL loading (Fukuda et al., 2003; Kiapour et al., 2014a; Levine et al., 2013; Meyer and Haut, 2008; Oh et al., 2012; Quatman et al., 2014; Shin et al., 2011; Withrow et al., 2006), there is a compelling and ongoing debate regarding the relationships between these rotations and the multi-planar injury mechanism. Therefore, the current study was designed to investigate the anatomical coupling between tibiofemoral frontal (valgus) and axial (internal tibial rotation) plane rotations, and how these rotations affect ACL strain, as a valid quantifiable measure of injury risk, in a cadaveric model. We hypothesized that frontal and axial rotations are coupled, and that knee valgus rotation mediates ACL loading, whether the knee is loaded under a valgus or internal tibial torque. We further hypothesized that coupling between knee frontal and axial plane rotations is significantly affected by tibial plateau topology, in particular posterior tibial slope and medial tibial depth.
Methods
Nineteen (10 females and 9 males) unembalmed fresh-frozen cadaveric lower limbs, with a mean age at death of 45 (SD= 7) years, were used in this study. Specimens were imaged using a 3T magnetic resonance (MR) imaging scanner (GE Signa Excite HD 3.0T, Waukesha, WI, USA) with a surface knee coil in sagittal, frontal and axial planes. An experienced, board certified orthopaedic surgeon inspected the specimens both visually and with MR-imaging to confirm that specimens were free from soft or hard tissue pathology including indications of prior surgery, mal-alignment deformities and ACL disruption. MR-imaging data were further used for anatomical index measurements. Specimens were then stored at −20°C for subsequent testing.
Quasi-Static Cadaveric Testing
Specimen Preparation
Frozen specimens were slowly thawed to room temperature 24 hours prior to testing. Specimens were sectioned at the mid-femoral diaphysis (30 cm above the joint line) and potted following removal of all soft tissues from femoral head to 15 cm proximal to the knee joint line. The quadriceps and hamstrings (medial and lateral) tendons were then isolated, and clamped to allow for simulation of trans-knee muscle loads. The remaining musculature and skin (from 15 cm above the knee joint line to toes) remained intact.
Instrumentation
ACL strain was calculated based on the measurements of a differential variable reluctance transducer (DVRT) (MicroStrain Inc., Williston, VT, USA) arthroscopically placed on the distal third of the anterior medial (AM) bundle through two para-patellar incisions. This system allows for quantification of displacement with an accuracy of 0.1% and the repeatability of 1 µm. Two rigid arrays of three non-collinear infrared light-emitting diodes (irLED), rigidly attached to the mid-shaft of the tibia and femur using bone screws, were used to quantify tibiofemoral kinematics via an Optotrak 3020 3D motion capture system (Northern Digital, Waterloo, Ontario, Canada). This system allows for the tracking of rigid body motion with a resolution of 0.01 mm and an accuracy of 0.1 mm.
Test Set-up and Loading Conditions
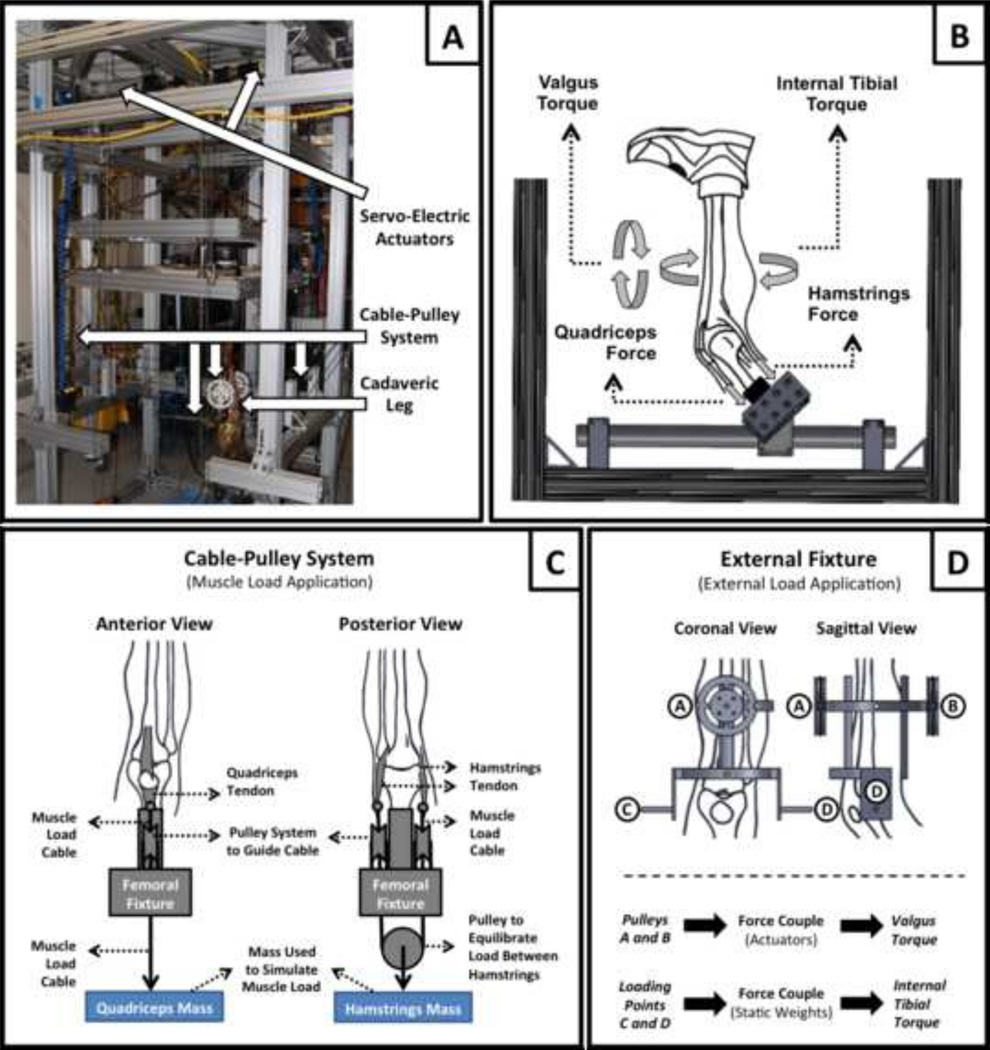
Specimens were tested using a custom, passive 6-DOF Force Couple Testing System (FCTS, Fig 1A) (Kiapour et al., 2011; Kiapour et al., 2012a; Kiapour et al., 2012b). This system utilized a combination of servo-electric actuators and static weights to drive multiple lightweight low friction cable-pulley systems that generate unconstrained forces and pure moments in all three anatomical planes (Fig 1B). The unconstrained nature of this setup allows for physiologic characterization of the joint with regard to kinematics and kinetics. The use of 6-DOF passive control offered by the FCTS results in natural join motion as defined by native geometry, particularly topology of the articular surfaces and surrounding soft tissue constraints. Each specimen was rigidly attached to the fixture at the proximal femur with the knee positioned at 25° of flexion, to simulate the orientation of the knee joint during ACL injury (Koga et al., 2010). Cable-pulley systems and static weights were used to apply constant forces to the quadriceps (400 N) and hamstrings (200 N; 100 N each to the medial and lateral sides) tendons in order to stabilize the knee joint and simulate trans-knee muscle forces. The simulated muscle forces have been derived from our previous unpublished work in order to provide a baseline joint stability under applied external loads with magnitudes used in this study without over protecting the knee joint or causing any soft tissue injuries. Adjustable pulley systems were used to maintain the physiologic line of action of each muscle group (Fig 1C). Knee extension due to quadriceps-to-hamstrings force imbalance was countered by preventing anterior translation of the foot using a high stiffness cable connecting the foot to the back of the test frame. This fixation constrained anterior translation of the foot while preserving the other five-degrees of freedom (2 translations and 3 rotations) across the ankle joint.
Figure 1.
Custom designed Force-Couple Testing System (FCTS) (A) and the diagram showing the application of external torques and muscle loads (B). Cable-pulley system used for application of the stimulated muscle loads (C) and the external fixation frame with the embedded cable-pulley system used for application of external loads (D).
An external fixation frame with an integrated pulley system was rigidly attached to the tibia in order to apply external loads (Fig 1D). Specimens were tested under 0–50 N-m knee valgus and 0–20 N-m of internal tibial torques using servo-electric actuators and static weights, respectively. As unconstrained force couples (free to move with the specimens) were used to generate pure rotational moments (torques), their action was independent of the point of application (Fig 1D). To allow for unconstrained application of external loads, the distal extremity (lower leg and foot) was free to rotate and translate in all degrees of freedom except knee extension during loading. Exposed tissue about the knee joint was kept moist with 0.9% buffered saline solution at all times during testing. After testing, specimens were inspected arthroscopically to document any tissue damage or failure of knee joint structures.
Data Acquisition and Processing
Data were collected at 100 Hz and all data acquisition systems were synchronized utilizing a simultaneous trigger. Data were processed using a custom macro developed in Matlab 7.1 (The MathWorks Inc., Natick, MA, USA). In order to calculate absolute strain values, ACL reference length was calculated based on established methods (Fleming et al., 1994; Howe et al., 1990) as the distinct inflection point in the force versus DVRT displacement curve. These data were collected by placing each specimen through four cycles of anterior-posterior shear prior to testing (Kiapour et al., 2014b). The selected inflection point was chosen as the proper reference between ligament taut and slack conditions. Therefore reference length is not dependent on initial DVRT gauge length at the time of insertion. Tibiofemoral joint kinematics was calculated from marker position data based on techniques previously described (Almosnino et al., 2013; Balasubramanian, 2006). Briefly, a digitizing pointed probe fitted with a cluster of six irLED markers was used to define virtual markers on standard anatomical landmarks of tibia and femur (Hewett et al., 2005) with respect to the rigidly attached tibial and femoral irLED marker arrays. The digitized bony landmarks (virtual markers) were used to define the joint center of rotation and anatomical coordinate system. The positional data of virtual landmarks was used to calculate instantaneous relative and absolute changes in tiobiofemoral joint rotations and translations in 3D.
Anatomical Index Measurement
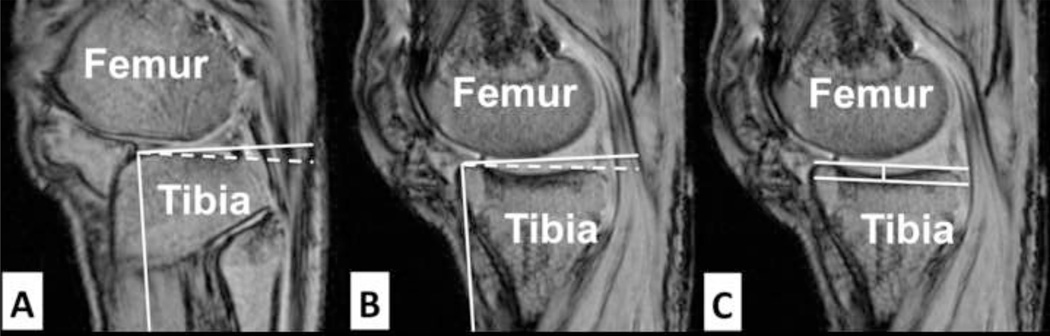
Medial and lateral posterior tibial plateau slopes and maximum depth of the medial tibial plateau were measured from MR image stacks according to the techniques described by Hashemi et al. (2008). Briefly, an axial plane slice of the tibiofemoral joint showing the dorsal aspect of the tibial plateau was selected and sagittal plane images from the midline of the medial and lateral tibial plateau were used to perform the tibial slope measurements. The longitudinal (diaphyseal) axis of the tibia was established by connecting the mid-points of the two horizontal lines, approximately 2 to 3 cm apart, in the sagittal plane across the mid-shaft of the tibia. Posterior slope of the tibial plateau across each compartment was measured as the angle between a line connecting the peak points on the anterior and posterior aspects of the plateau and the line perpendicular to the longitudinal axis (Fig 2A–B). This method has demonstrated the ability to quantify tibial slope with a sensitivity of 1° (Hashemi et al., 2008).
Figure 2.
Sagittal plane MR images used to measure the lateral tibial slope (A), medial tibial slope (B) and the medial tibial depth (C).
Medial tibial depth was measured by establishing a line connecting the superior and inferior crests of the tibial plateau on the same plane within which medial tibial slope was measured. A parallel line was then drawn tangent to the lowest point of concavity representing the lowest boundary of the subchondral bone. The medial tibial depth was defined as the perpendicular distance between the two lines (Fig 2C) (Hashemi et al., 2008). All dimensions were measured using Osirix (version 6.0.2 32-bit, open source, www.osirix-viewer.com) (Rosset et al., 2004) and were reported in mm or degrees.
Statistical Analysis
Tibiofemoral rotation, ACL strain and anatomical data were evaluated for normality using the Shapiro-Wilk test. Data were normally distributed for all quantified outcomes (p>0.2). The effect of applied knee valgus and internal tibial torques on tibiofemoral rotation and ACL strain were investigated using multiple general linear models. Loading magnitudes (valgus or internal tibial torques) were used as fixed factors with knee valgus rotation, internal tibial rotation and ACL strain as dependent variables. Changes in tibiofemoral rotation and ACL strain under 50 N-m of knee valgus torque versus 20 N-m of internal tibial torque were analyzed using paired t-tests. Univariate linear regression analysis was used to investigate the coupling between the knee valgus and internal tibial rotation. Relationships between tibial plateau anatomy and tibiofemoral coupled rotations in frontal and axial planes were also assessed using univariate linear regression analysis. The regression slope (β) and R2 coefficients along with p values were used to evaluate the linear relationships. Average values were reported as mean ± standard deviation (SD) and p≤0.05 was considered statistically significant.
Results
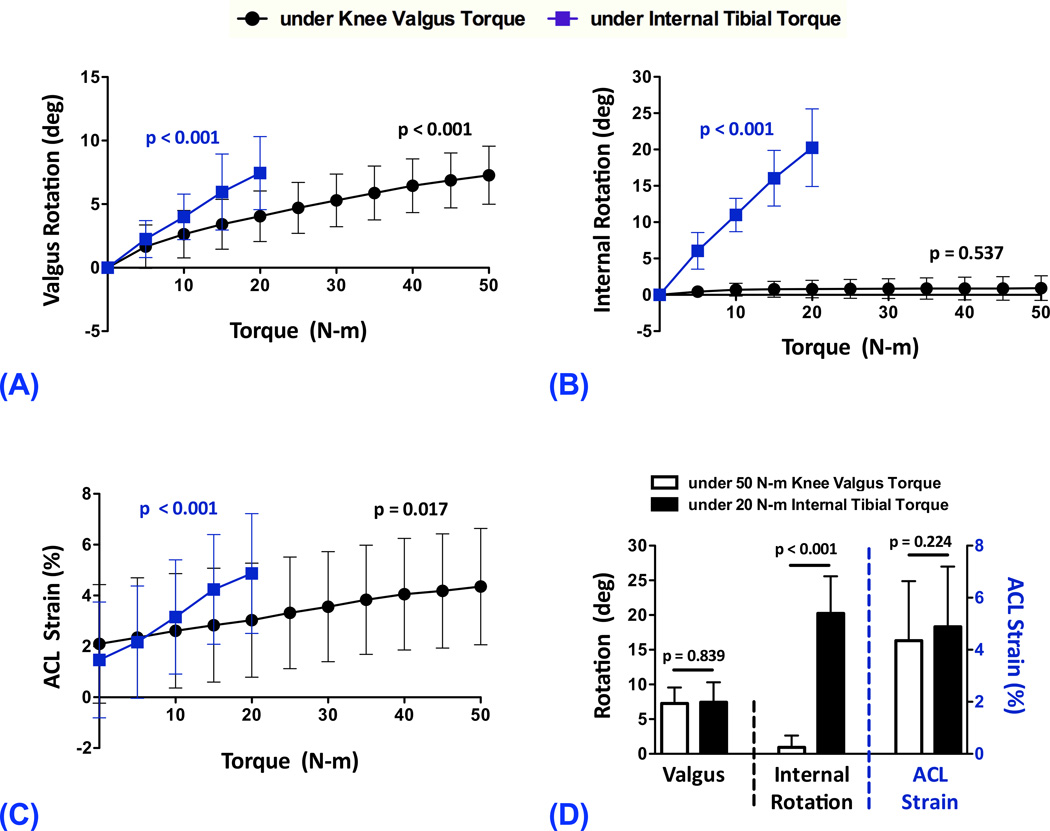
The specimens had an average posterior tibial slope of 7.8 (SD=2.4)° and 5.2 (SD=1.7)° across the lateral and medial tibial plateaus along with an average medial tibial depth of 2.5 (SD=0.7) mm. At 25° of knee flexion, and in presence of simulated muscle loads, gradually increased knee valgus torque, from 0 to 50 N-m, resulted in significant increases in knee valgus rotation (p<0.001) by up to 7.3 (SD=2.3)°; Fig 3A. Similarly, a significantly increasing trend (p<0.001) in coupled knee valgus rotation, by up to 7.4 (SD=2.9)°, was observed with incremental increases in internal tibial torque from 0 to 20 N-m (Fig 3A). Gradually increased knee valgus torque, from 0 to 50 N-m, resulted in almost no coupled internal tibial rotation (p=0.537, Fig 3B). However, the increased internal tibial torque, from 0 to 20 N-m, significantly increased the internal rotation of the tibia (p<0.001) by up to 20.3 (SD=5.3)°; Fig 3B. Increased magnitudes of knee valgus (0 to 50 N-m) and internal tibial (0 to 20 N-m) torques resulted in significant (p≤0.017) elevations in ACL strain by as much as 4.4 (SD=2.3)% and 4.9 (SD=2.4)%, respectively (Fig 3C). Similar knee valgus rotations were achieved under both the 50 N-m of knee valgus and 20 N-m of internal tibial torques (Difference: 0.2 (SD=3.6)°; p=0.839; Fig 3D). However, significantly greater internal tibial rotation was observed under 20 N-m of internal tibial torque than under 50 N-m of knee valgus torque (Difference: 19.3 (SD=5.1)°; p<0.001; Fig 3D). Knee valgus (50 N-m) and internal tibial (20 N-m) torques resulted in similar ACL strain levels (Difference: 0.5 (SD=1.8)%; p=0.224; Fig 3D).
Figure 3.
Changes in knee valgus rotation (A), internal tibial rotation (B) and ACL strain (C) under 0–50 N-m of knee valgus and 0–20 N-mo f internal tibial torques along with comparison between tibioremoral frontal and axial rotations and ACL strain under 50 N-m of knee valgus and 20 N-m of internal tibial torques (D).
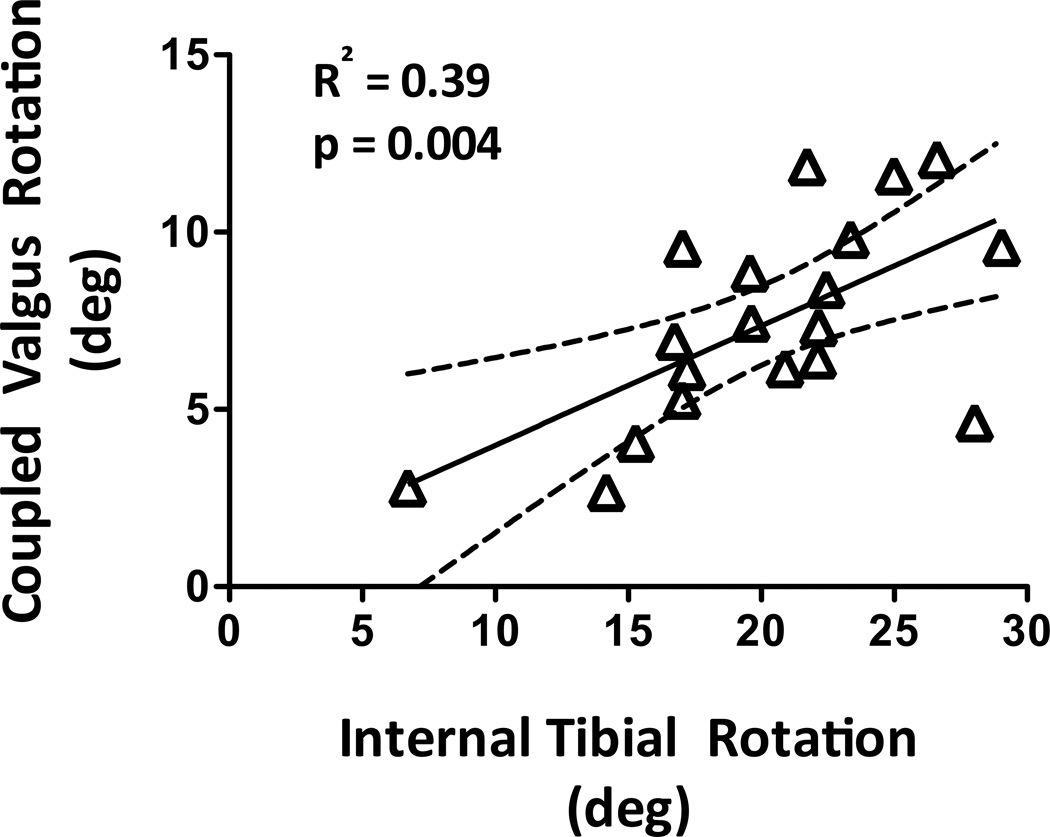
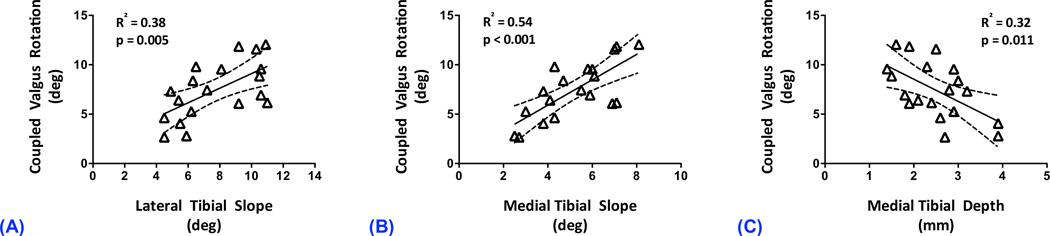
Regression coefficients for all linear models are presented in Table 1. Under 50 N-m of knee valgus torque, no significant correlations were observed between the knee valgus and coupled internal tibial rotations (R2=0.00; p=0.917). However, coupled knee valgus and internal tibial rotations were correlated under 20 N-m of internal tibial torque (R2=0.39; p=0.004; Fig 4). There were no significant correlations between any of the anatomical indices and coupled internal tibial rotation under 50 N-m of knee valgus torque (R2<0.02; p>0.650). In contrast, coupled knee valgus rotation under 20 N-m of internal tibial torque was significantly correlated with lateral tibial slope (R2=0.38; p=0.005), medial tibial slope (R2=0.55; p<0.001) and medial tibial depth (R2=0.32; p=0.011); Fig 5. Greater coupled knee valgus was observed in knees with steeper posterior slope of the tibial plateau (both lateral and medial) and with flatter medial tibial plateau (lower medial tibial depth).
Table 1.
Regression coefficients for univariate linear regression models.
| Variables | Loading | Model Coefficients | ||||
|---|---|---|---|---|---|---|
| Dependent | Independent | *β | t | R2 | +p-value | |
| Coupled Valgus Rotation | Internal tibial rotation | 20 N-m of Internal Tibial Torque | 0.34 (0.12–0.55) | 3.31 | 0.39 | 0.004 |
| Coupled Valgus Rotation | Lateral Tibial Slope (LTS) | 20 N-m of Internal Tibial Torque | 0.74 (0.26–1.22) | 3.25 | 0.38 | 0.005 |
| Coupled Valgus Rotation | Medial Tibial Slope (MTS) | 20 N-m of Internal Tibial Torque | 1.29 (0.69–1.88) | 4.55 | 0.55 | <0.001 |
| Coupled Valgus Rotation | Medial Tibial Depth (MTD) | 20 N-m of Internal Tibial Torque | −2.24 (−3.91 – −0.58) | −2.85 | 0.32 | 0.011 |
| Coupled Internal Tibial Rotation | Valgus Rotation | 50 N-m of Knee Valgus Torque | 0.02 (−0.36 – 0.40) | 0.11 | 0.00 | 0.917 |
| Coupled Internal Tibial Rotation | Lateral Tibial Slope (LTS) | 50 N-m of Knee Valgus Torque | 0.03 (−0.33 – 0.39) | 0.19 | 0.00 | 0.854 |
| Coupled Internal Tibial Rotation | Medial Tibial Slope (MTS) | 50 N-m of Knee Valgus Torque | 0.05 (−0.47 – 0.58) | 0.21 | 0.00 | 0.839 |
| Coupled Internal Tibial Rotation | Medial Tibial Depth (MTD) | 50 N-m of Knee Valgus Torque | −0.25 (−1.43 – 0.94) | −0.43 | 0.01 | 0.670 |
Slope (95% confidence intervals).
Significant correlations are presented in bold.
Figure 4.
Correlation between coupled knee valgus and internal tibial rotations under 20 N-m of internal tibial torque.
Figure 5.
Correlation between coupled knee valgus and lateral tibial slope (A), medial tibial slope (B) and medial tibial depth (C) under 20 N-m of internal tibial torque.
Discussion
A more complete understanding of the complex ACL injury mechanisms and associated risk factors is instrumental to improvement of prevention strategies aimed to reduce injury risk. Despite strong evidence supporting the knee valgus and internal tibial torques as integral components of multi-planar ACL injury mechanism, the mechanism through which these loadings interact, and jointly result in increased ACL loading, is not well understood. Thus, a combination of cadaveric experiments and imaging were used to investigate the anatomical coupling between knee valgus and internal tibial rotation and determine how they affect ACL strain as a measure of injury risk. Data revealed uni-directional coupling between these two rotations. Knee valgus rotation is tightly coupled to internal tibial rotation under externally applied tibial torque. Conversely, minimal coupled internal tibial rotation was observed under knee valgus torque. These results further support our first hypothesis that knee valgus rotation most significantly impacts ACL strain, whether the knee is loaded under a valgus or internal tibial torque. Findings also support our second hypothesis that there is significant correlation between coupled knee valgus rotation, and posterior slope of the tibial plateau (medial and lateral) and the concavity of the medial tibial plateau.
Uni-directional Coupling between Knee Valgus and Internal Tibial Rotation
As expected, significant increases in knee valgus and internal tibial rotation were observed under externally applied valgus and internal tibial torques, respectively. In addition to these observed in-plane rotations, the applied internal tibial torque generated a significant coupled knee valgus rotation. Under 20 N-m of internal tibial torque, greater degrees of coupled knee valgus rotation were observed in knees that demonstrated higher internal tibial rotations. Moreover, similar average knee valgus rotations (7.3° vs. 7.4°) were observed under 50 N-m of knee valgus or 20 N-m of internal tibial torques. This observed coupling might be associated with the interaction between the meniscus and the contour of the tibial plateau with the femoral condyles. The articular surfaces of the tibiofemoral joint consist of many unique features that play an important role in knee joint biomechanics (Hashemi et al., 2008; Sturnick et al., 2015). In particular, it has been demonstrated that the geometry of the tibial plateau has a direct influence on tibiofemoral joint translation, the location of instantaneous center of rotation, the screw-home mechanism and ACL strain (Lipps et al., 2012; McLean et al., 2010; McLean et al., 2011; Simon et al., 2010). The posterior slope of the tibial plateau (anterior elevation higher than posterior elevation) is one of the most widely studied morphological features of the tibia with respect to ACL loading and injury risk (Beynnon et al., 2014; Lipps et al., 2012; McLean et al., 2011; Sturnick et al., 2015). Previous studies have linked increased ACL strain and risk of injury in individuals with higher medial and lateral tibial slopes (Beynnon et al., 2014; Hashemi et al., 2010; Lipps et al., 2012; McLean et al., 2011). Smaller medial tibial depth, indicating a flatter medial tibial plateau, has also been associated with increased ACL injury risk (Hashemi et al., 2010; Sturnick et al., 2015). Moreover, posterior slope of the tibial plateau has also been associated with landing induced anterior tibial shear force (McLean et al., 2010) and acceleration (McLean et al., 2011), knee valgus (McLean et al., 2010) and internal tibial (McLean et al., 2010; Simon et al., 2010) rotations.
Under applied internal tibial torque, the lateral femoral condyle pivots around the medial knee compartment and translates posteriorly (Freeman and Pinskerova, 2003; Simon et al., 2010). This posterior translation of the lateral femoral condyle is coupled with inferior translation of the lateral point of articulation due to the posterior slope of the lateral tibial plateau. The externally applied internal tibial torque will also result in anterior translation of the medial femoral condyle relative to the medial tibial surface (Freeman and Pinskerova, 2003; Simon et al., 2010), which is coupled with superior medial condylar translation resulting from the posterior slope of the medial tibial plateau. Coupled inferior and superior translations of the lateral and medial femoral condyles result in a valgus knee alignment under internal tibial torque. This is supported by direct correlations between the coupled knee valgus rotation and posterior tibial slope across both the medial and lateral compartments. Additionally, a significantly greater coupled valgus rotation was observed in knees with flatter medial tibial plateau (lower medial depth). A flatter medial tibial plateau may facilitate anterior medial femoral condyle translation, thus generating greater coupled valgus rotation under externally applied internal tibial torque. In contrast, insignificant internal tibial rotation was generated under knee valgus torque. While this finding may appear counterintuitive, externally applied knee valgus torque predominantly results in medial joint distraction. This occurs in the absence of anterior-posterior translations of femoral condyles against the sloped tibial plateau, and thus, results in minimal coupled internal tibial rotation.
Change in ACL Strain due to Knee Valgus Rotation
Interestingly, similar mean ACL strain levels (4.4% vs. 4.9%) were observed under either 50 N-m of knee valgus or 20 N-m of internal tibial torque. The fact that similar knee valgus rotations and ACL strain levels generated under these torques indicates that ACL strain is mainly mediated by knee valgus rotation, regardless of the mechanism by which this valgus motion was generated. Knee valgus (Fukuda et al., 2003; Levine et al., 2013; Quatman et al., 2014; Shin et al., 2011; Withrow et al., 2006) and internal tibial (Meyer and Haut, 2008; Oh et al., 2012; Quatman et al., 2014; Shin et al., 2011) torques have been associated with increased ACL loading and potential risk of injury, particularly under dynamic impacts at shallow knee flexion angles. The findings of the current study and the established role of knee valgus and internal tibial torques on ACL loading indicate a direct causal relationship between the knee valgus rotation and ACL injury risk. This is supported by in vivo biomechanical and video analyses that show increased risk and/or frequency of non-contact ACL injuries in the presence of knee valgus rotation (Hewett et al., 2005; Koga et al., 2010; Krosshaug et al., 2007; Olsen et al., 2004). A prospective study by Hewett et al. (2005) demonstrated that subjects who subsequently went on to ACL injury had greater knee valgus angles at initial contact and at peak valgus torque compared to uninjured controls. Koga et al. (2010) showed significant knee valgus rotation within 40 ms of initial contact in 10 cases of non-contact ACL injuries during handball and basketball utilizing model-based image matching techniques. These findings are in agreement with those of Olsen et al. (2004) and Krosshaug et al. (2007) who reported dynamic knee valgus collapse as the most common mechanism for ACL injury in handball and basketball, respectively. A similar concept has been previously described by Stergiou et al. (1999) with regards to potential role of lack of coupling and coordination between subtalar and knee joints rotation in injuries during running.
Study Limitations
As with any experimental study, this study has its inherent limitations. Potential differences in tissue properties associated with cadaveric specimens compared with the in vivo tissue properties of young athletes might affect accuracy of the absolute reported values. This factor was minimized through the selection of relatively young specimens. The effect of knee flexion angle on observed anatomical coupling was not evaluated as all the specimens were tested at 25° of knee flexion. Yet, this flexion angle is within the reported range of in vivo ACL injury (Koga et al., 2010). ACL strain was represented by local strain measurements across the AM-bundle. However, the attachment of a second DVRT to the posterolateral bundle of the ACL would have compromised the posterior joint capsule and lead to potential measurement artifacts (Bach and Hull, 1998). The choice to place a single DVRT on the ACL AM-bundle was based on previous work that found AM-bundle strain to be representative of overall ACL strain (Markolf et al., 1990). Finally, specimens were only tested under non-injurious loading magnitudes (Shin et al., 2011) in a uni-planar and quasi-static manner. Further studies are needed to investigate the nature of the observed anatomical coupling and its role on ACL loading under multi-planar dynamic loading conditions with greater loading magnitudes and more realistic representation of muscle loads, simulating the injurious event. Care was taken to understand these limitations during interpretation of the findings.
Conclusions
To the authors’ knowledge, this is the first study of the complex interrelationships between tibiofemoral anatomy, frontal and axial plane rotational coupling, and ACL strain. The current findings support our hypotheses and highlight the role of knee valgus rotation, irrespective of the mode of loading, in ACL strain and potential injury risk. Overall, the results of this study help to explain the high incidence of knee valgus collapse at the time of non-contact ACL injury, as reported in prior in vivo studies. Improved understanding of the mechanism of non-contact ACL injury may provide insight that would improve current, and develop new, prevention and rehabilitation strategies, therein limiting the risk of these devastating injuries. Prevention strategies that neglect to address the multi-planar injury mechanisms may not be optimally suited to reduce ACL injury incidence. Intervention programs that address multiple planes of loading are needed to effectively mitigate the risk of ACL injury, in turn minimizing associated long-term clinical sequelae associated with these injuries, in particular, the devastating consequences of posttraumatic knee osteoarthritis.
Acknowledgements
The authors acknowledge funding support from the National Institutes of Health / National Institute of Arthritis and Musculoskeletal and Skin Diseases grants R01-AR049735 (THE) and R01-AR056259 (TEH). The content is solely the responsibility of the authors and does not necessarily represent the official views of the National Institutes of Health. The authors would also like to thanks American Society of Biomechanics (ASB) and Elsevier Inc. for the 2014 ASB Journal of Biomechanics Award. We also would like to thank Dr. Jason Levine for his assistance.
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
Conflict of Interest There are no conflicts of interest.
References
- Almosnino S, Kingston D, Graham RB. Three-dimensional knee joint moments during performance of the bodyweight squat: effects of stance width and foot rotation. Journal of applied biomechanics. 2013;29:33–43. doi: 10.1123/jab.29.1.33. [DOI] [PubMed] [Google Scholar]
- Bach JM, Hull ML. Strain inhomogeneity in the anterior cruciate ligament under application of external and muscular loads. J Biomech Eng. 1998;120:497–503. doi: 10.1115/1.2798020. [DOI] [PubMed] [Google Scholar]
- Balasubramanian S. Posterior cruciate ligament (PCL) injury and repair : A biomechanical evaluation of the human knee joint under dynamic posterior loading; kinematics and contact pressure measurements in normal, PCL deficient and PCL reconstructed knees. Wayne State University; 2006. [Google Scholar]
- Beynnon BD, Hall JS, Sturnick DR, Desarno MJ, Gardner-Morse M, Tourville TW, Smith HC, Slauterbeck JR, Shultz SJ, Johnson RJ, Vacek PM. Increased slope of the lateral tibial plateau subchondral bone is associated with greater risk of noncontact ACL injury in females but not in males: a prospective cohort study with a nested, matched case-control analysis. Am J Sports Med. 2014;42:1039–1048. doi: 10.1177/0363546514523721. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fleming BC, Beynnon BD, Tohyama H, Johnson RJ, Nichols CE, Renstrom P, Pope MH. Determination of a zero strain reference for the anteromedial band of the anterior cruciate ligament. Journal of orthopaedic research : official publication of the Orthopaedic Research Society. 1994;12:789–795. doi: 10.1002/jor.1100120606. [DOI] [PubMed] [Google Scholar]
- Freeman MA, Pinskerova V. The movement of the knee studied by magnetic resonance imaging. Clin Orthop Relat Res. 2003:35–43. doi: 10.1097/01.blo.0000063598.67412.0d. [DOI] [PubMed] [Google Scholar]
- Fukuda Y, Woo SL, Loh JC, Tsuda E, Tang P, McMahon PJ, Debski RE. A quantitative analysis of valgus torque on the ACL: a human cadaveric study. Journal of orthopaedic research : official publication of the Orthopaedic Research Society. 2003;21:1107–1112. doi: 10.1016/S0736-0266(03)00084-6. [DOI] [PubMed] [Google Scholar]
- Griffin LY, Agel J, Albohm MJ, Arendt EA, Dick RW, Garrett WE, Garrick JG, Hewett TE, Huston L, Ireland ML, Johnson RJ, Kibler WB, Lephart S, Lewis JL, Lindenfeld TN, Mandelbaum BR, Marchak P, Teitz CC, Wojtys EM. Noncontact anterior cruciate ligament injuries: risk factors and prevention strategies. The Journal of the American Academy of Orthopaedic Surgeons. 2000;8:141–150. doi: 10.5435/00124635-200005000-00001. [DOI] [PubMed] [Google Scholar]
- Hashemi J, Chandrashekar N, Gill B, Beynnon BD, Slauterbeck JR, Schutt RC, Jr, Mansouri H, Dabezies E. The geometry of the tibial plateau and its influence on the biomechanics of the tibiofemoral joint. J Bone Joint Surg Am. 2008;90:2724–2734. doi: 10.2106/JBJS.G.01358. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hashemi J, Chandrashekar N, Mansouri H, Gill B, Slauterbeck JR, Schutt RC, Jr, Dabezies E, Beynnon BD. Shallow medial tibial plateau and steep medial and lateral tibial slopes: new risk factors for anterior cruciate ligament injuries. Am J Sports Med. 2010;38:54–62. doi: 10.1177/0363546509349055. [DOI] [PubMed] [Google Scholar]
- Hewett TE, Di Stasi SL, Myer GD. Current concepts for injury prevention in athletes after anterior cruciate ligament reconstruction. Am J Sports Med. 2013;41:216–224. doi: 10.1177/0363546512459638. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hewett TE, Myer GD, Ford KR, Heidt RS, Jr, Colosimo AJ, McLean SG, van den Bogert AJ, Paterno MV, Succop P. Biomechanical measures of neuromuscular control and valgus loading of the knee predict anterior cruciate ligament injury risk in female athletes: a prospective study. Am J Sports Med. 2005;33:492–501. doi: 10.1177/0363546504269591. [DOI] [PubMed] [Google Scholar]
- Howe JG, Wertheimer C, Johnson RJ, Nichols CE, Pope MH, Beynnon B. Arthroscopic strain gauge measurement of the normal anterior cruciate ligament. Arthroscopy. 1990;6:198–204. doi: 10.1016/0749-8063(90)90075-o. [DOI] [PubMed] [Google Scholar]
- Kiapour AM, Quatman CE, Ditto RC, Levine JW, Wordeman SC, Hewett TE, Goel VK, Demetropoulos CK. Influence of Axial Rotation Moments on ACL Strain: A Cadaveric Study of Single- and Multi-Axis Loading of the Knee. Proceedings of the 35th ASB Annual Meeting; Long Beach CA. 2011. [Google Scholar]
- Kiapour AM, Quatman CE, Ditto RC, Levine JW, Wordeman SC, Hewett TE, Goel VK, Demetropoulos CK. Global Quasi-Static Mechanical Characterization of the Human Knee Under Single- and Multi-Axis Unconstrained Loading Conditions. Proceedings of 2012 ASME Summer Bioengineering Conference. 2012a;44809:1119–1120. [Google Scholar]
- Kiapour AM, Quatman CE, Goel VK, Ditto RC, Wordeman SC, Levine JW, Hewett TE, Demetropoulos CK. Knee articular cartilage pressure distribution under single-and multi-axis loading conditions: implications for ACL injury mechanism. Proceedings of the 36th ASB Annual Meeting; Geinsville FL. 2012b. [Google Scholar]
- Kiapour AM, Quatman CE, Goel VK, Wordeman SC, Hewett TE, Demetropoulos CK. Timing sequence of multi-planar knee kinematics revealed by physiologic cadaveric simulation of landing: implications for ACL injury mechanism. Clinical biomechanics. 2014a;29:75–82. doi: 10.1016/j.clinbiomech.2013.10.017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kiapour AM, Wordeman SC, Paterno MV, Quatman CE, Levine JW, Goel VK, Demetropoulos CK, Hewett TE. Diagnostic value of knee arthrometry in the prediction of anterior cruciate ligament strain during landing. Am J Sports Med. 2014b;42:312–319. doi: 10.1177/0363546513509961. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kim S, Bosque J, Meehan JP, Jamali A, Marder R. Increase in outpatient knee arthroscopy in the United States: a comparison of National Surveys of Ambulatory Surgery, 1996 and 2006. J Bone Joint Surg Am. 2011;93:994–1000. doi: 10.2106/JBJS.I.01618. [DOI] [PubMed] [Google Scholar]
- Koga H, Nakamae A, Shima Y, Iwasa J, Myklebust G, Engebretsen L, Bahr R, Krosshaug T. Mechanisms for noncontact anterior cruciate ligament injuries: knee joint kinematics in 10 injury situations from female team handball and basketball. Am J Sports Med. 2010;38:2218–2225. doi: 10.1177/0363546510373570. [DOI] [PubMed] [Google Scholar]
- Krosshaug T, Nakamae A, Boden BP, Engebretsen L, Smith G, Slauterbeck JR, Hewett TE, Bahr R. Mechanisms of anterior cruciate ligament injury in basketball: video analysis of 39 cases. Am J Sports Med. 2007;35:359–367. doi: 10.1177/0363546506293899. [DOI] [PubMed] [Google Scholar]
- Levine JW, Kiapour AM, Quatman CE, Wordeman SC, Goel VK, Hewett TE, Demetropoulos CK. Clinically relevant injury patterns after an anterior cruciate ligament injury provide insight into injury mechanisms. Am J Sports Med. 2013;41:385–395. doi: 10.1177/0363546512465167. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lipps DB, Oh YK, Ashton-Miller JA, Wojtys EM. Morphologic characteristics help explain the gender difference in peak anterior cruciate ligament strain during a simulated pivot landing. Am J Sports Med. 2012;40:32–40. doi: 10.1177/0363546511422325. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Markolf KL, Gorek JF, Kabo JM, Shapiro MS. Direct measurement of resultant forces in the anterior cruciate ligament. An in vitro study performed with a new experimental technique. J Bone Joint Surg Am. 1990;72:557–567. [PubMed] [Google Scholar]
- McLean SG, Lucey SM, Rohrer S, Brandon C. Knee joint anatomy predicts high-risk in vivo dynamic landing knee biomechanics. Clinical biomechanics. 2010;25:781–788. doi: 10.1016/j.clinbiomech.2010.06.002. [DOI] [PubMed] [Google Scholar]
- McLean SG, Oh YK, Palmer ML, Lucey SM, Lucarelli DG, Ashton-Miller JA, Wojtys EM. The relationship between anterior tibial acceleration, tibial slope, and ACL strain during a simulated jump landing task. J Bone Joint Surg Am. 2011;93:1310–1317. doi: 10.2106/JBJS.J.00259. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Meyer EG, Haut RC. Anterior cruciate ligament injury induced by internal tibial torsion or tibiofemoral compression. J Biomech. 2008;41:3377–3383. doi: 10.1016/j.jbiomech.2008.09.023. [DOI] [PubMed] [Google Scholar]
- Myklebust G, Maehlum S, Holm I, Bahr R. A prospective cohort study of anterior cruciate ligament injuries in elite Norwegian team handball. Scandinavian journal of medicine & science in sports. 1998;8:149–153. doi: 10.1111/j.1600-0838.1998.tb00185.x. [DOI] [PubMed] [Google Scholar]
- Oh YK, Lipps DB, Ashton-Miller JA, Wojtys EM. What strains the anterior cruciate ligament during a pivot landing? Am J Sports Med. 2012;40:574–583. doi: 10.1177/0363546511432544. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Olsen OE, Myklebust G, Engebretsen L, Bahr R. Injury mechanisms for anterior cruciate ligament injuries in team handball: a systematic video analysis. Am J Sports Med. 2004;32:1002–1012. doi: 10.1177/0363546503261724. [DOI] [PubMed] [Google Scholar]
- Quatman CE, Kiapour AM, Demetropoulos CK, Kiapour A, Wordeman SC, Levine JW, Goel VK, Hewett TE. Preferential loading of the ACL compared with the MCL during landing: a novel in sim approach yields the multiplanar mechanism of dynamic valgus during ACL injuries. Am J Sports Med. 2014;42:177–186. doi: 10.1177/0363546513506558. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Quatman CE, Quatman-Yates CC, Hewett TE. A 'plane' explanation of anterior cruciate ligament injury mechanisms: a systematic review. Sports Med. 2010;40:729–746. doi: 10.2165/11534950-000000000-00000. [DOI] [PubMed] [Google Scholar]
- Rosset A, Spadola L, Ratib O. OsiriX: an open-source software for navigating in multidimensional DICOM images. Journal of digital imaging. 2004;17:205–216. doi: 10.1007/s10278-004-1014-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shimokochi Y, Shultz SJ. Mechanisms of noncontact anterior cruciate ligament injury. J Athl Train. 2008;43:396–408. doi: 10.4085/1062-6050-43.4.396. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shin CS, Chaudhari AM, Andriacchi TP. Valgus plus internal rotation moments increase anterior cruciate ligament strain more than either alone. Med Sci Sports Exerc. 2011;43:1484–1491. doi: 10.1249/MSS.0b013e31820f8395. [DOI] [PubMed] [Google Scholar]
- Simon RA, Everhart JS, Nagaraja HN, Chaudhari AM. A case-control study of anterior cruciate ligament volume, tibial plateau slopes and intercondylar notch dimensions in ACL-injured knees. J Biomech. 2010;43:1702–1707. doi: 10.1016/j.jbiomech.2010.02.033. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Stergiou N, Bates BT, James SL. Asynchrony between subtalar and knee joint function during running. Med Sci Sports Exerc. 1999;31:1645–1655. doi: 10.1097/00005768-199911000-00023. [DOI] [PubMed] [Google Scholar]
- Sturnick DR, Vacek PM, DeSarno MJ, Gardner-Morse MG, Tourville TW, Slauterbeck JR, Johnson RJ, Shultz SJ, Beynnon BD. Combined Anatomic Factors Predicting Risk of Anterior Cruciate Ligament Injury for Males and Females. Am J Sports Med. 2015 doi: 10.1177/0363546514563277. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Withrow TJ, Huston LJ, Wojtys EM, Ashton-Miller JA. The effect of an impulsive knee valgus moment on in vitro relative ACL strain during a simulated jump landing. Clinical biomechanics. 2006;21:977–983. doi: 10.1016/j.clinbiomech.2006.05.001. [DOI] [PubMed] [Google Scholar]