Spatial variation in mortality risk for haematological malignancies near a petrochemical refinery: a population-based case-control study

Abstract

Introduction

The study investigated the geographic variation of mortality risk for hematological malignancies (HMs) in order to identify potential high-risk areas near an Italian petrochemical refinery.

Material and methods

A population-based case-control study was conducted and residential histories for 171 cases and 338 sex- and age-matched controls were collected. Confounding factors were obtained from interviews with consenting relatives for 109 HM deaths and 267 controls. To produce risk mortality maps, two different approaches were applied. We mapped (1) adptive kernel density relative risk estimation (KDE) for case-control studies which estimates a spatial relative risk function using the ratio between cases and controls’ densities, and (2) estimated odds ratios for case-control study data using generalized additive models (GAMs) to smooth the effect of location, a proxy for exposure, while adjusting for confounding variables.

Results

No high-risk areas for HM mortality were identified among all subjects (men and women combined), by applying both approaches. Using the adaptive KDE approach, we found a significant increase in death risk only among women in a large area 2–6 km southeast of the refinery and the application of GAMs also identified a similarly-located significant high-risk area among women only (global p-value<0.025). Potential confounding risk factors we considered in the GAM did not alter the results.

Conclusion

Both approaches identified a high-risk area close to the refinery among women only. Those spatial methods are useful tools for public policy management to determine priority areas for intervention. Our findings suggest several directions for further research in order to identify other potential environmental exposures that may be assessed in forthcoming studies based on detailed exposure modeling.

1. Introduction

Worldwide, on an annual basis, more than 850,000 patients are diagnosed with haematological malignancies (HMs) (Ferlay et al., 2010). HMs are a heterogeneous group of diseases classified according to International Classification of Disease, IX revision (World Health Organization, 1997) that includes Hodgkin lymphoma, non-Hodgkin lymphoma, multiple myeloma, and leukemia, and account for 6–8%, 40–44%, 15–16%, and 34–36% of total incident HMs in developed countries, respectively (GLOBOCAN, 2013). Little is known about the etiological mechanism of leukemias and lymphoma. Genetics factors, infectious disease, ionizing radiation, and smoking have been described in relation to leukemias (Rodriguez-Abreau et al., 2007). Emissions from petroleum refineries are considered one of the putative environmental risk factors in haematological cancers investigated. Those emissions include substances such as benzene, recognized as a carcinogen by the International Agency for Research on Cancer (IARC, 1987). Effects modulated by benzene-induced oxidative stress, aryl hydrocarbon receptor dysregulation and reduced immunosurveillance may lead to the generation of leukemic stem cells and subsequent clonal evolution to leukaemia (McHale et al., 2012).

Effects of occupational benzene exposure and of emissions from refineries on cancer have been widely investigated with different results both in terms of occurrence and mortality. Some studies have showed evidence that occupational exposure to benzene leads to an increased risk for acute myeloid leukemia (Schnatter et al., 2005), chronic lymphocytic leukemia (Khalade et al., 2010) and non-Hodgkin lymphoma (Steinmaus et al., 2008). Evidence of an association between emissions from refineries and HMs is weaker. A recent study in Sweden did not show any excess of incidence for leukemia or lymphoma (Axelsson et al., 2010). In Italy a case-control study showed a moderate, but not significant, risk of mortality for lymphohematopoietic neoplasms among residents living within 2 km from a petrochemical plant (Belli et al., 2004). In another case-control study, authors showed a 90% increased NHL risk of incidence associated with 10 years of proximity to petroleum refineries (OR=1.9, 95% C.I: 1.0–3.6) (De Roos et al., 2010).

Recently, in a population-based case-control study, we found a significant excess of HM-related death risk for women and participants who spent most of their time at their home resident in an area surrounding an Italian petrochemical refinery (Micheli et al., 2014). In that study, we combined distances and residency duration as a proxy of residential exposure for a long period of life before the event to analyze HMs death risk using conditional logistic regression. Participants who spent most of their time at home were identified using information on occupational status from interviews with consenting relatives. However, we were not able to specifically identify those areas (possibly influenced by the prevalent winds) where the risk was the highest.

In this paper, we conducted spatial analyses in order to detect geographic variation of risk for HMs mortality and to identify potential high-risk areas near the refinery. To reach the aim, we applied and compared two methods: (1) smoothing of location using Generalized Additive Models (GAMs) to produce risk maps adjusted for potential confounders (Vieira et al., 2002; Webster et al., 2006) and (2) adaptive kernel density relative risk estimation (KDE) (Davies and Hazelton, 2010).

2. Material and Methods

Details on the study area and participants in this spatial analysis are described in a previous paper (Micheli et al., 2014).

2.1 Study area and population

Briefly, the petrochemical refinery is located in the Municipality of Falconara Marittima (Province of Ancona, Region of the Marches, Central Italy) and has been operating since the early 1950s. A study funded by the Region of the Marches in 2003 found that mortality from leukemia and other HMs increased (non-significantly) from 1984 to 2000 in the municipality of Falconara and the adjacent municipality of Chiaravalle, in contrast to decreased or stable HM mortality in the Province of Ancona and Region of the Marches (Baili et al., 2007). However, monitoring data during that time period showed that known carcinogens were present in the atmosphere, and with support from the Region of the Marches (Giunta Regionale, 2004), an additional study was initiated to investigate mortality risk for leukemia, non-Hodgkin lymphoma, and other HMs (Micheli et al., 2014).

The study area included three municipalities (Falconara, Chiaravalle, Montemarciano) near the refinery with a geographic extent of approximately 65 km² (Fig. 1). Only cancer mortality can be investigated and not incidence because no population-based cancer registry is available in this region. Deaths for HM occurring between January 1, 1994 and December 31, 2003 were identified from death certificates, provided by the Italian National Institute of Statistics (ISTAT). A total of 177 deaths for HM (89 males and 88 females) were identified (Micheli et al., 2014).

Fig 1.

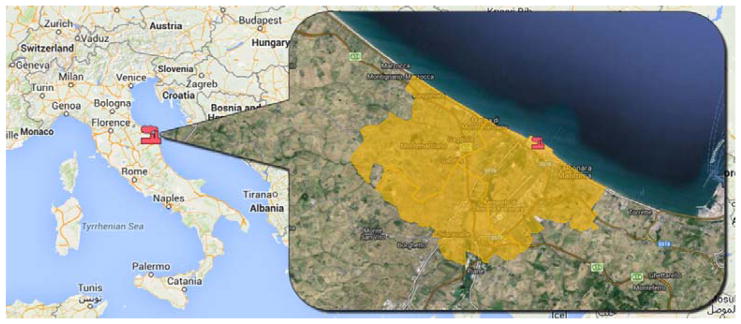
Map showing the location of the refinery (in red) and the study area in yellow.

For each case two controls were sampled from municipal records using the risk set sampling method (Rothman et al., 2008). Eligible controls (risk set) were identified among residents in the study area with the same sex and age (±2.5 years) and alive at the date of case death (index date).

2.2 Data collection

A complete residential history was traced for all 177 cases, and for 349 matched controls. The address with the longest residency duration (main residence) over a 15-year interval (time window) was used in the analysis. The time window was defined as the period preceding the index date by no more than 20 years to take into account latency between exposure and cancer mortality observed for workers exposed to benzene, and excluding the 5 years prior to the index date for persons ≥25 years (or 2 years prior to cancer death for 4 cases and index data for 8 controls under 25 years) to account for survival time between the unknown diagnosis date and the date of death (Micheli et al., 2014). Subjects with main residence outside the study area were excluded from the analysis, so only 171 cases and 338 controls (total 509 participants) were available for the analysis. The geographic coordinates of residences (latitude/longitude) were measured using a global positioning device (Garmin GPSMAPS 60CS). The distances of residences to the closest power lines were also calculated in order to consider the potential confounding effect of extremely low-frequency magnetic fields. The centroid of the refinery area was determined using the GIS MapInfo Professional software (release 8.0).

For a subgroup of 376 participants (109 cases and 267 controls) whose relatives consented to be interviewed, we collected information on life style, occupational history, and characteristics of residences. To avoid recall bias, relatives of both cases and controls were contacted by trained interviewers. Data on active and passive smoking, marital status, education, family history of HM, history of congenital or viral conditions potentially predisposing to HM, occupational history from age 15 and potential HM risks related to the characteristics and environment of habitations (urban area, resident on ground floor, rural area where pesticides used, proximity to traffic roads and to petrol stations) were collected as potential confounding factors.

2.3 Statistical analysis

To identify potentially high-risk areas, we applied two different approaches. First we used the adaptive KDE-based spatial relative function for case-control studies because of its minimal assumptions on the underlying data structure and flexibility of application (Bithell, 1990; Bithell, 1991; Kelsall and Diggle, 1995). This approach estimates the density of cases and the density of controls using kernel smoothing as follows. Let x₁, x₂, …, x_n be the geographical coordinates of n cases in the study area. The kernel density estimate of cases is written as (Davies and Hazelton, 2010),

$$\widehat{f}(x)=\frac{1}{n}{\sum }_{i=1}^n\frac{1}{h{(x_i)}^2}K\left(\frac{x-x_i}{h(x_i)}\right)$$ (1)

where K is a kernel density function and h(x_i) is the bandwidth controlling the smoothness of the density estimator. For a fixed-bandwidth density estimate, h(x_i) is a fixed value for each i. For the adaptive estimator, the bandwidths are calculated according to a theoretically beneficial function in Abramson (1982) as

$$h(x_i)=\frac{h_0}{f{(x)}^{1/2}\gamma }$$ (2)

where h₀ is the global bandwidth, which is a smoothing multiplier and γ is an arbitrary geometric mean term. These bandwidths are inversely related to the underlying population density, which is itself estimated in a pilot kernel estimation stage using a preliminary pilot bandwidth (Davies and Hazelton, 2010).

The spatial relative risk function is estimated as

$$\widehat{r}(x)=\frac{\widehat{f}(x)}{\widehat{g}(x)}$$ (3)

Where f̂(x) and ĝ(x) are the kernel density estimates of cases and controls respectively, calculated as in equation (1).

Adaptive relative risk surfaces are preferred over traditional fixed-bandwidth relative risk surfaces since the latter can perform poorly with highly heterogeneous populations (Abramson, 1982). As the selection of appropriate bandwidths, we used a common value for both case and control global bandwidths and left distinct the two pilot bandwidths, as suggested in Davies and Hazelton, 2010. Global and pilot bandwidths were both selected with a method based on the “oversmoothing” (OS) principle described by Terrell, because of its potential to control excess variability in the estimated densities (Terrel, 1990). We also computed a relative risk surface by using pilot bandwidths selected with a least-squares cross-validation (LSCV) approach (Bowman and Azzalini, 1997), as suggested in Davies and Hazelton, 2010, but the surface presented many small sub-regions highlighted as statistically significant (data not shown). Few isolates observations were likely responsible for such peaks, so we believed that the OS method is preferred to the LSCV for our dataset. In order to avoid an over interpretation of the results, the method allows for plotting of tolerance contours at given significance levels (we considered alpha=0.05), which highlights any identified extreme sub-regions of elevated risk (Davies et al., 2011). The adaptive KDE approach was applied for the entire dataset, for the subgroup of subjects whose relatives were interviewed and separately for men and women, in order to compare results with those produced by the GAMs approach. This method does not allow for simultaneous control of confounders, only stratification. For this reason comparisons were made with the unadjusted GAMs only.

The second approach we followed has been applied extensively to population-based health data by Vieira et al. (Vieira et al., 2002; Webster et al., 2006; Vieira et al., 2005; Vieira et al., 2008). With the application of this method, it was possible to map estimated odds ratios for case-control study data, by using generalized additive models (GAMs) (Kelsall and Diggle, 1998). This method models the effect of geolocation of the main residences (a proxy for exposure) as

$$\mathit{logit}[p(x_1,x_2)]=S(x_1,x_2)+\gamma z$$ (4)

with a two-dimensional smooth term, S(x₁, x₂) while adjusting for confounding variables, γz, which are modeled parametrically (Webster, 2006). The log of the odds at location (x₁, x₂) is modeled as it would be with an ordinary logistic regression on the covariates if there was no smooth term.

A Locally Weighted Regression Smoother (LOESS) was used in the analyses, because of the non-homogeneity of population densities. The loess smoother predicts the log odds by fitting a regression to data points closest to the prediction point and by weighting the data points with a tri-cube function of their distance from the prediction point (Hastie and Tibshirani, 1990).

The optimal span size (percentage of data points used for smoothing) was determined by minimizing Akaike’s Information Criterion which is a trade-off between bias and variance (Webster et al., 2006). By following this criterion of choice, a resulting large optimal span size indicates less spatial variability in mortality for HMs, compared to a small optimal span. A grid of 5,000 prediction points was generated approximately 0.5 km apart that extended across the latitude and longitude coordinates of subjects’ main residences. We do not predict spatial models in areas of low population density along the geographical edges of the study area, because GAMs may produce biased behavior at the edges of the data (Vieira et al., 2012). At each point on the grid, we predicted the log odds and calculated odds ratios by dividing the log odds at each point by the log odds from a reduced model which did not include the smooth of latitude and longitude. Odds ratios were mapped by using a continuous color scheme (dark red to dark blue) and the same range of odds ratios (0.25 –to 2.50) in order to compare different maps. We carried out 999 permutations of location in addition to the original. For each permutation, the model was refit and a global statistic (p-value) was computed (Webster et al., 2006; Vieira et al., 2005). A p-value cut-off of 0.025 was considered as a screening tool for any potential associations, as suggested in a previous study (Young et al., 2011). Areas of significantly increased or decreased odds were defined as points ranking in the extreme 2.5% of the distribution of permuted odds ratios at each point and were mapped using black contour bands. Results produced by the GAMs must include both areas of increased and decreased risk as the average log odds of the entire study area is used for calculating odds ratios (Vieira et al., 2012).

GAM models were fit for the entire dataset of 509 subjects, adjusting for the variables we could obtain without any interviews: sex, age at diagnosis (< 65, ≥65), and distance to the nearest power line.

GAMs were also fit for the subgroup of subjects where additional information on potential known risk factors was collected by interviews. These models were adjusted for age at diagnosis, sex and for those covariates positively associated with case/control status: smoking and living close (<200 m) to a petrol station for at least 10 years. Subjects with missing information on those covariates (n=26) were excluded; therefore only 350 subjects were available for spatial analysis. Changes in the model-selected optimal span of analysis with and without adjustment were observed and investigated, because a smaller optimal span size is selected when data presents more peaks. A change in optimal size after the inclusion of a covariate can indicate spatial confounding (Hoffman et al., 2012).

Also, for both of the approaches, we stratified by sex and fit separate models for women and men as women were significantly older than men. Because of this, they likely had different life style characteristics with most of their time spent at home, so we believe that sex is more an effect modifier rather than a confounder.

Spatial analyses were conducted in the R Package (version 3.0.1) using the “MapGam” (Vieira et al., 2014) package for the GAM approach and the “sparr” (Davies et al., 2011) package for the KDE approach.

3. Results

Table 1 shows the characteristics of the 509 study participants (171 cases and 338 controls). Most cases (46%) had leukemia, followed by non-Hodgkin lymphoma (30%). The sex distribution of cases was close to 50:50, while the ≥65 year age class contained proportionately more females. Only 25% were aged less than 65 years.

Table 1.

Distribution of characteristics of cases and controls included in analysis.

Characteristics		Cases (n = 171)		Controls (n = 338)
		No.	%	No.	%
HM (ICD-9 code) a	Leukaemia (204–208)	78	45.6	-	-
	Non-Hodgkin lymphoma (200, 202)	52	30.4	-	-
	Myeloma (203)	38	22.2	-	-
	Hodgkin’s disease (201)	3	1.8	-	-
Sex	Male	85	49.7	170	50.3
	Female	86	50.3	168	49.7
Age at diagnosis (years) or index year	Males ≤65	21	12.2	45	13.3
	Males >65	64	37.5	125	37.0
	Females ≤65	10	5.9	23	6.8
	Females >65	76	44.4	145	42.9
Distance to nearest power line, meters	≤200	44	25.7	80	23.7
	>200	127	74.3	258	76.3

^aICD-9 code: codes of International Classification of Diseases, ninth revision (WHO 1977)

Table 2 shows characteristics of the 376 subjects whose relatives were interviewed: education, marital status, smoking, passive smoking, occupational exposure, and characteristics and environment of habitations including urban area; rural area with pesticide use; and proximity to busy road and petrol station. Compared to controls, cases were more likely to have a first degree relative with HM (11.0% vs. 5.6%) and only living close to a petrol station for at least 10 years (39.5% vs. 26.6%) and smoking (for men) were positively associated with HM case-control status.

Table 2.

Characteristics of 376 subjects (109 cases and 267 controls) whose relatives were interviewed.

Participant characteristics		Cases		Controls
		n	%	n	%
Education: at least 8 years of schooling	No	89	81.7	226	84.6
	Yes	19	17.4	41	15.4
	missing	1	0.9	0	0.0
Marital status	Not married a	51	46.8	121	45.3
	Married	57	52.3	145	54.3
	missing	1	0.9	1	0.4
Smoking status b	Never smoked	57	52.3	161	60.3
	Former/current smoker	49	54.0	105	39.3
	missing	3	2.7	1	0.4
First degree relative with HM c	No	84	77.1	228	85.4
	Yes	12	11.0	15	5.6
	missing	13	11.9	24	9.0
Disease associated with increased HM risk d	No	105	96.3	264	98.9
	Yes	3	2.8	3	1.1
	missing	1	0.9	0	0.0
Occupational exposure (MAtline matrix)e	<10 years	94	86.2	231	86.5
	≥10 years	12	11.0	31	11.6
	missing	3	2.8	5	1.9
Resident in urban area	<10 years	10	9.2	35	13.1
	≥10 years	96	88.1	219	88.0
	missing	3	2.8	13	4.9
Resident on ground floor	<10 years	81	74.3	192	71.9
	≥10 years	25	22.9	63	23.6
	missing	3	2.8	12	4.5
Resident in rural area where pesticides are used	<10 years	88	80.7	216	80.9
	≥10 years	10	9.2	20	7.5
	missing	11	10.1	31	11.6
Passive smoking	<10 years	52	47.7	138	51.7
	≥10 years	54	49.5	113	42.3
	missing	3	2.8	16	6.0
Busy road <100 m	<10 years	49	45.0	98	36.7
	≥10 years	57	52.3	156	58.4
	missing	3	2.8	13	4.9
Petrol station <200 m	<10 years	63	57.8	183	68.5
	≥10 years	43	39.5	71	26.6
	missing	3	2.8	13	4.9

^aUnmarried, separated, divorced or widow/widower.

^bAt end of time window.

^cMother, father, sister, or brother with HM.

^dSpecifically: ataxia-telangiectasia, Down syndrome, neurofibromatosis type 1, inherited immunodeficiency, MLL rearrangement, TEL/AML1 rearrangement, hepatitis A, HIV infection or other RNA virus infection.

^ehttp://www.dors.it/matline_e.php

Figure 2 shows a point map of case and control main residences for 509 subjects (a) and for the 350 subjects available for spatial analysis whose relatives were interviewed (b).

Fig 2. Spatial distribution of main residences for cases and controls.

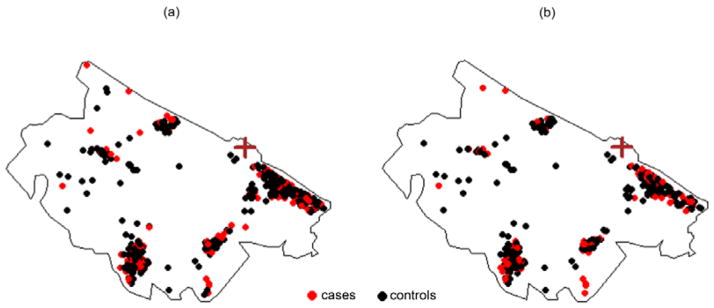
Each point represents the main residence of cases and controls. (a) All subjects, 171 cases and 338 controls. (b) Subjects whose relatives were interviewed and considered for the spatial analysis, 101 cases and 249 controls. The brown cross marks the location of the refinery

Figure 3 shows the spatial variation of death risk for the entire dataset of 509 subjects using GAMs. The association with location was not statistically significant at the 0.025 level in the crude model (p = 0.41, Figure 3a). When we considered age, sex and distance from power lines, the adjusted analysis produced a slightly wider range of OR predictions compared to the crude analysis (Table 3), but the map was very similar with location again not statistically significant (p=0.17, Figure 3b). The optimal span size was 0.95 for both the crude and adjusted models, indicating little spatial variability across the study region. Fig. 3c shows the estimated values of adaptive KDE-based relative risk function, obtained by using as optimal global bandwidth for the smoothing a value of 1.2 km based on the pooled dataset of both case and control points and as optimal pilot bandwidths a value of 1.5 km for cases’ density and 1.3 km for controls’ density. The map shows some higher, non-significant risk along the edge of the study area, and provides similar results to the GAM. When we only consider women (86 cases and 168 controls), the crude GAM model shows a sloped surface with statistically significantly increased ORs between 2 and 6 km southeast of the refinery and decreased risk over 6 km from the refinery (p=0.02, Figure 4a). When we adjusted for age and distance to the nearest power lines, analyses predicted similar statistically significant results (p=0.01), suggesting spatial confounding by these variables was not an issue (Figure 4b). Similar results were obtained when we applied the KDE approach (Figure 4c) where we observed a significantly increased risk of death for HMs in an area between 3 and 6 km south of the refinery. The global bandwidth was 1.4 Km, pilot bandwidths were 1.6 km for cases’ density and 1.5 km for controls’ density. No areas of statistically significant risk were found for men; a small area of decreased risk was found near the refinery (data not shown).

Fig 3. Spatial variation in mortality risk of HMs. All subjects (171 cases and 338 controls).

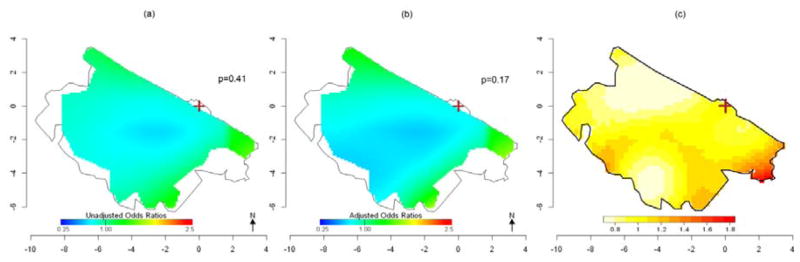
(a) Crude ORs for HM mortality using GAMs with optimal span=0.95. (b) ORs for HM mortality using GAMs adjusted for sex, age and distance from power lines. Optimal span=0.95. (c) Adaptive kernel Relative Risk of HM mortality estimation. The brown cross marks the location of the refinery.

Table 3.

Summary of HM mortality results using GAM models

	All subjects n=509 (172 cases)		Women n=254 (87 cases)
	Crude	Adjusteda	Crude	Adjustedb
OR range	0.7 – 1.6	0.7 – 1.7	0.3 – 2.8	0.2 – 3.0
Optimal Span size	0.95	0.95	0.70	0.65
Global p-value	0.41	0.17	0.02	0.01
Figure	2a	2b	3a	3b

	All subjects with interview n=350 (101 cases)		Women with interview n= 172 (49 cases)
	Crude	Adjustedc	Crude	Adjustedd
OR range	0.7 – 2.9	0.6 – 3.2	0.4 – 3.5	0.4 – 3.56
Optimal Span size	0.95	0.95	0.95	0.95
Global p-value	0.22	0.13	0.09	0.07
Figure	5a	5b	6a	6b

^aAdjusted for sex, age and distance to the nearest power line.

^bAdjusted for age and distance to nearest power line.

^cAdjusted for sex, age, smoking and proximity to petrol station.

^dAdjusted for sex, age and proximity to petrol station.

Fig 4. Spatial variation in of risk of HM death: Women only (86 cases and 168 controls).

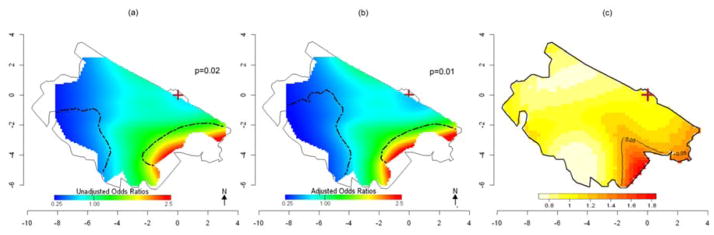
(a) Crude ORs for HM mortality using GAMs with optimal span=0.7. (b) ORs for HM mortality using GAMs adjusted for age and distance from power lines. Optimal span=0.65. Areas of significantly increased and decreased risk at the 0.025 level are denoted by black contour lines (c). Adaptive kernel Relative Risk of HM mortality estimation with 5% significant tolerance contours denoted by black contour lines. The brown cross marks the location of the refinery.

Crude and adjusted analyses with GAMs were also performed for the 350 (101 cases, 249 controls) subjects whose relatives were interviewed. The general patterns of the GAM results for the subset (Fig. 5a, 5b, 6a, 6b) were comparable to the full analysis, but predictions were less stable due to smaller numbers and did not reach statistical significance (Table 3). The smaller numbers also makes the subset analyses more prone to edge effects and wider fluctuations in predicted ORs. When we adjusted for age, smoking and proximity to a petrol station, analyses again predicted similar results, suggesting spatial confounding by these variables was not an issue. Because spatial confounding was minimal, we also applied the KDE approach for all the 350 subjects and for 172 women only to compare the two methods using the same data subset. Similar results were observed, and a significant high-risk area was identified south of the refinery (Fig. 5c, 6c). A summary of the results from all the spatial analyses by participant groups is displayed in Table 3.

Fig 5. Spatial variation in risk of HM death: Subjects whose relatives were interviewed (101 cases and 249 controls).

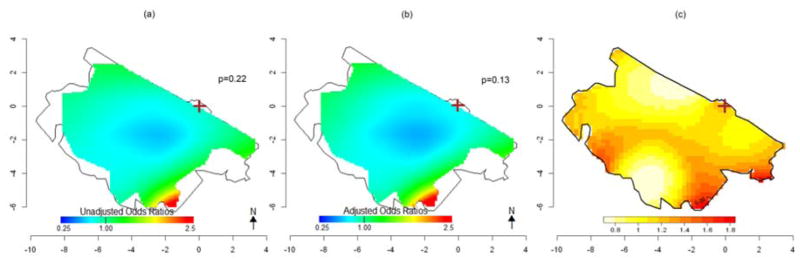
(a) Crude ORs for HM mortality using GAMs with optimal span=0.95. (b) ORs for HM mortality using GAMs adjusted for sex, age, smoking and proximity to petrol station. Optimal span=0.95. (c) Adaptive kernel Relative Risk of HM mortality estimation. The brown cross marks the location of the refinery.

Fig 6. Spatial variation of risk of HM death: Women whose relatives were interviewed (49 cases and 123 controls).

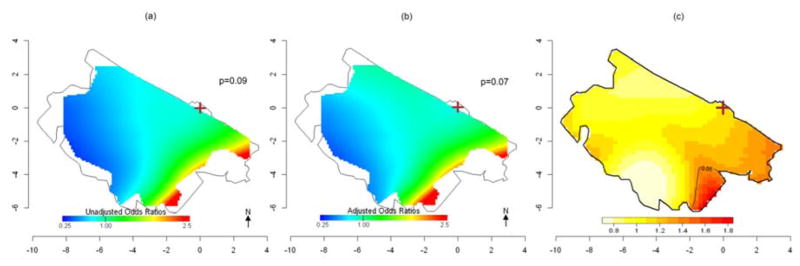
(a) Crude ORs for HM mortality using GAM with optimal span=0.95. (b) ORs for HM mortality using GAM adjusted for age and proximity to petrol station. Optimal span=0.95. c) Adaptive kernel Relative Risk of HM death estimation, with 5% significant tolerance contours, denoted by black contour lines. The brown cross marks the position of the refinery.

4. Discussion

The results of the spatial analyses suggest an increased risk of HM mortality among women located in an area southeast of the refinery. This is consistent with results from our previous conditional logistic regression, where we found increased risks, significant for the second but not for the third tertile of time-weighted average proximity to the refinery (Micheli et al., 2014). The current analyses provide an indication of where risk is higher, information that could not be determined in the prior analysis.

One likely reason why main residence location was a significant predictor of HM mortality among women but not men is that benzene may affect women more adversely. It is possible that absorbed benzene would be released more slowly from fat to blood in women, so that they may incur greater exposure effects than men (Brown et al., 1998).

Assessing exposure is a crucial issue in environmental studies. Generally, the data and information needed to fully assess exposure is not available. Often, without the benefit of detailed information on the quantity and quality of pollutant emissions necessary to formulate dispersion models or other related factors like the wind directions, distance has been very widely adopted as a proxy for exposure, i.e. exposure is assumed to be a function of distance (Zandbergen and Chakraborty, 2006). This method may provide a poor exposure surrogate, subject to major misclassification when compared with other strategies like dispersion modelling (Ashworth et al., 2013). In addition, dichotomous exposure measurements such as “living within a certain number of kilometers” of a pollutant source may not accurately reflect a continuous reduction of exposure with increasing distance, and changing the radius cut-off may drastically change results (Waller et al., 1999). That is why mapping spatial variation of disease/death risk could be a useful tool, in an exploratory analysis, to identify if high-risk regions exist near a pollution source.

In our study, we applied an adaptive kernel estimation of relative risk to explore the density ratio between cases and controls. This is a more intuitive approach compared to the fixed kernel estimation (Kelsall and Diggle, 1995) because the amount of smoothing is inversely related to the population density, which is never homogeneous in a study area. An important issue of this approach is the choice of the optimal bandwidth, which provides an overall level of smoothing for the density-ratio and is still the subject of much research in this field (Davies and Hazelton, 2010; Davies, 2013a). Regarding the selection of global and pilot bandwidths, in our study we computed and compared two relative risk surfaces based upon a common global bandwidth selected by the OS selector but with different pilot bandwidths. The first surface used two different pilot bandwidths calculated with the OS selector and the second surface used pilot bandwidths calculated with the LSCV selector. The second surface presented many small sub-regions highlighted as statistically significant, where probably one or few observations were responsible for such peaks. So we decided to compute and show relative risk surfaces with OS global and pilot bandwidths. Features observed in illustrative examples and simulation studies in Davies 2013 has indicated the promising performance of OS as a seemingly sensible option for selection of risk function bandwidths (Davies, 2013b). A limitation of the KDE method is that it does not support adjustment of known risk factors that may vary spatially and confound results. With the second approach, maps were obtained by plotting ORs predicted using Generalized Additive Models, after adjusting for potential risk factors. In our current analysis, we found that the mortality risk appears higher along the eastern edge of the study area. This could be due to an edge effect that GAMs may exhibit at the boundaries of the data (Hastie and Tibshirani, 1990). To limit this problem, we do not predict our spatial models in areas of low population density along the geographic edges of our study area (Webster et al., 2006). Maps produced by the KDE method were not trimmed because kernel estimations of relative risk were edge-corrected (Marshall and Hazelton, 2010) by an appropriate function implemented by Hazelton and Davies in R software (Davies et al., 2011).

As already specified, in this study we decided to fit separate models for women and men as women were significantly older than men, and because of this, they likely had different life style characteristics with most of their time spent at home. Moreover, in our previous analysis of men, we observed less HM deaths than expected (conditional logistic regression, not significant OR<1) for those living in proximity to refinery (Micheli et al., 2014). This may be due to mortality from other diseases linked to occupational exposure, which may bias results among men. So we believe that sex is more an effect modifier rather than a confounder.

Although spatial analyses are useful for generating new hypotheses or supporting existing ones, the location of significant hot and cold spots should be considered exploratory. In our study, the peak in risk we observed near the southern border might be due to wind direction, which we did not consider. We do not have adequate information on pollutants dispersion or wind direction, so the resulting maps may help support existing exposure hypotheses or identify new exposure hypotheses for future epidemiological investigations, for example by collecting more data on HMs outside the study region.

5. Conclusions

The first aim of this study was to explore spatial variation of HMs mortality risk near a refinery and to identify areas of significant increased risk. Using the adaptive KDE approach to produce maps, we found a significant increase in death risk only among women in a large area 2–6 Km southeast of the refinery. The application of generalized additive models, that allowed OR estimation adjusted for covariates, also identified a similarly-located significant high-risk area among women. Potential risk factors we considered in the models did not alter the results. Comparing the validity of the two methods was another aim of the study. The fact that both methods produced similar results provides more confidence in our findings.