Development and Application of a Nonbonded Cu²⁺ Model That Includes the Jahn–Teller Effect

Abstract

Metal ions are both ubiquitous to and crucial in biology. In classical simulations, they are typically described as simple van der Waals spheres, making it difficult to provide reliable force field descriptions for them. An alternative is given by nonbonded dummy models, in which the central metal atom is surrounded by dummy particles that each carry a partial charge. While such dummy models already exist for other metal ions, none is available yet for Cu²⁺ because of the challenge to reproduce the Jahn–Teller distortion. This challenge is addressed in the current study, where, for the first time, a dummy model including a Jahn–Teller effect is developed for Cu²⁺. We successfully validate its usefulness by studying metal binding in two biological systems: the amyloid-β peptide and the mixed-metal enzyme superoxide dismutase. We believe that our parameters will be of significant value for the computational study of Cu²⁺-dependent biological systems using classical models.

Most proteins function with metal ions such as copper, zinc, iron, calcium and magnesium ions being involved. They form complexes with surrounding residues of proteins and play significant roles including structural, electron transfer, and catalytic functions. For example, Cu–Zn superoxide dismutases (CuZnSODs) in complex with both Cu²⁺ and Zn²⁺ protect cells from oxygen toxicity by catalyzing the dismutaion of superoxide (O₂^–) into molecular oxygen and hydrogen peroxide.¹⁻³ On the other hand, dysregulation of metal ion homeostasis results in different kinds of diseases. Among these, Alzheimer’s disease (AD) is one of the most frequent age-related neurodegenerative pathologies with disorders in Zn²⁺ and Cu²⁺ homeostasis playing a pivotal role in the mechanisms of pathogenesis. The extracellular deposition of fibrils of the amyloid-β peptide (Aβ) is considered as a hallmark of AD, and it has been shown that the presence of substoichiometric levels of Cu²⁺ doubles the rate of production of amyloid fibers and promotes cell death.⁴⁻⁶ The N-terminal residues Aβ_1–16 encompass the metal binding region of Aβ.

Molecular dynamics (MD) simulations are commonly applied to investigate the dynamics and structural information of protein systems including metalloproteins. However, most of the widely used force fields do not have appropriate parameters for metal ions, presenting a practical obstacle to MD studies of metalloproteins. Various approaches have been developed to describe the interactions between metal ions and coordinated residues in classical MD simulations. They include representations of metal ions as simple van der Waals spheres,^7,8 nonbonded models with dummy atoms (called “dummy models” henceforth),⁹⁻¹³ and bonded models where artificial bonds between metal ions and ligands are introduced.¹⁴⁻¹⁷ Each of these methods has its own merits and limitations.^16,18 Modeling metal ions as simple spheres with electrostatic and van der Waals interactions is often successful for the description of alkali and alkaline-earth ions, but appears to be inadequate when it comes to more complex situations such as systems containing multinuclear metal centers with closely located metal ions, or for the correct treatment of transition metals. Bonded models, on the other hand, suffer from the fact that they include predefined covalent bonds between the metal and ligands, thus not allowing for ligand exchange and/or interconversion between different coordination geometries. For a more thorough discussion of the pros and cons of these approaches, the reader is referred to ref (13) and the references therein. The dummy model approach aims at resolving the aforementioned problems by providing a nonbonded description that captures both structural and electrostatic effects via the introduction of dummy atoms surrounding the metal ion. There have been several studies reporting dummy models for Zn²⁺, Ca²⁺, Mg²⁺, Fe²⁺, Ni²⁺, Co²⁺, and Mn²⁺ in tetrahedral, octahedral, or pentagonal bipyramid geometries.⁹⁻¹³ For the octahedral model shown in Figure 1, originally proposed by Åqvist and Warshel,¹² six dummy atoms with negligible van der Waals parameters and positive charge δ⁺ are placed around a central metal ion (n⁺) with a charge of n – 6δ. Such a charge distribution is particularly advantageous in systems with multiple metal centers,¹⁰ since the redistribution of charges reduces the excessive repulsion between metal sites. The dummy atoms are bonded and angled to the central atom, but there are no bonds to the ligands. No dummy model has yet been developed for Cu²⁺, most likely because of the Jahn–Teller distortion of Cu²⁺ (electron configuration d⁹) in water. In the present work, a Cu²⁺ dummy model (CuDum) that includes the Jahn–Teller effect is developed to facilitate computational studies of copper proteins.¹⁹ The major strength of this model is that it allows us to simultaneously reproduce the correct coordination properties of the metal, without the need for higher level quantum chemical calculations, while sampling the conformational properties of the peptide.²⁰ It should be noted that recently a polarizable force field for transition-metal ions was developed based on AMOEBA and the angular overlap model (AOM).²¹ This classical approach, which is similar in idea to previous AOM implementations for Cu²⁺,^22,23 can also handle the Jahn–Teller distortion yet is computationally more costly than the dummy model approach. Our CuDum model is implemented into the MD program Gromacs,²⁴ together with the previous Zn²⁺ dummy model (ZnDum),¹³ which was originally developed for Q.²⁵

Figure 1.

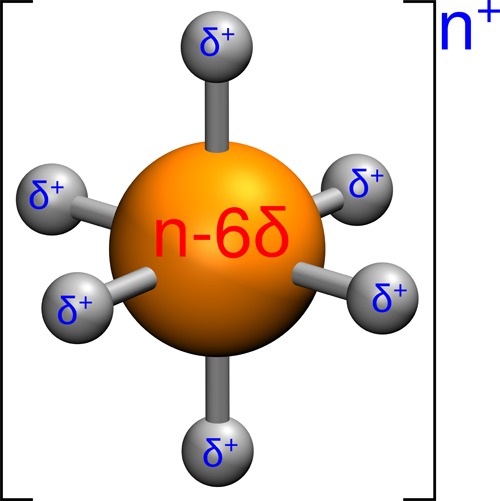
Schematic illustration of the dummy model.¹² Instead of a simple sphere, the point charge of the metal ion is distributed to six dummy atoms with partial charge δ⁺.

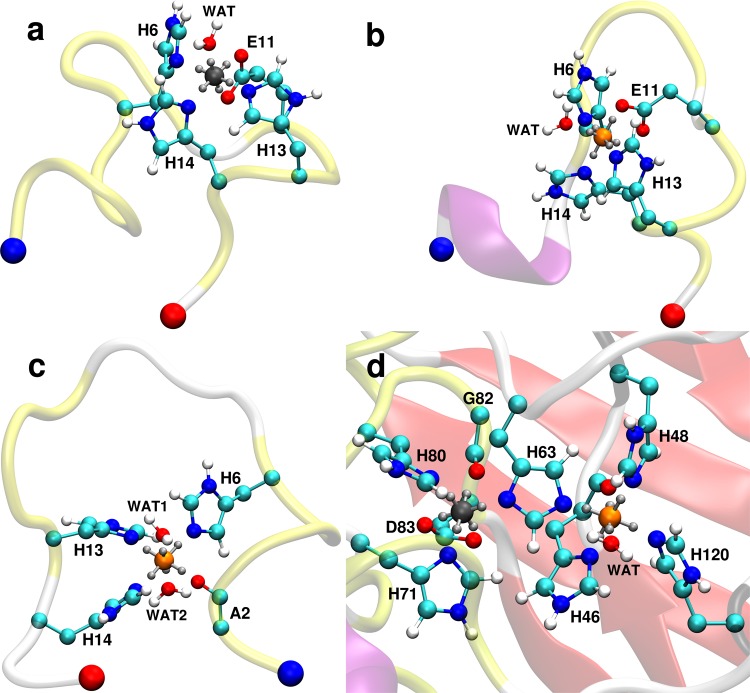
Full details about the MD simulations performed in this work and the adaptation of ZnDum for its use in Gromacs are given in the Supporting Information (SI). In short, the van der Waals distance σ_ZnO was systematically optimized (Table S1) in oder to reproduce both the experimental ion-oxygen distance (Zn–O) and the hydration free energy (ΔG_hyd) for Zn²⁺ in water. The calculation of ΔG_hyd is divided in two steps, decomposing it into the contributions from van der Waals (ΔG_LJ) and electrostatic (ΔG_elec) interactions^7,26,27 (Figure S1). For σ_ZnO = 2.034 Å, we found a compromise in terms of reproducing both ΔG_hyd and Zn–O with good accuracy (Figure S2). Furthermore, in subsequent 100 ns MD simulations for Aβ_1–16 in complex with ZnDum the metal binding site was maintained in a distorted square pyrimidal geometry (Figure 2a), in accordance with the NMR structure (PDB ID: 1ZE9).²⁸

Figure 2.

Final snapshots of dummy models in protein systems taken from 100 ns MD simulations of (a) Aβ_1–16^E11/ZnDum, (b) Aβ_1–16/CuDum, (c) Aβ_1–16^A2/CuDum, and (d) CuZnSOD/ZnDum/CuDum. The proteins are shown in cartoon presentation and colored red for β-sheet, purple for 3₁₀ helix, yellow for turn, and white for coil. The N- and C-terminus of Aβ_1–16 is indicated by a blue and red bead, respectively. The metal binding sites are shown in Corey–Pauling–Koltun (CPK) presentation using turquoise for C, blue for N, red for O, and white for H atoms, while Zn²⁺ is shown in gray and Cu²⁺ in orange.

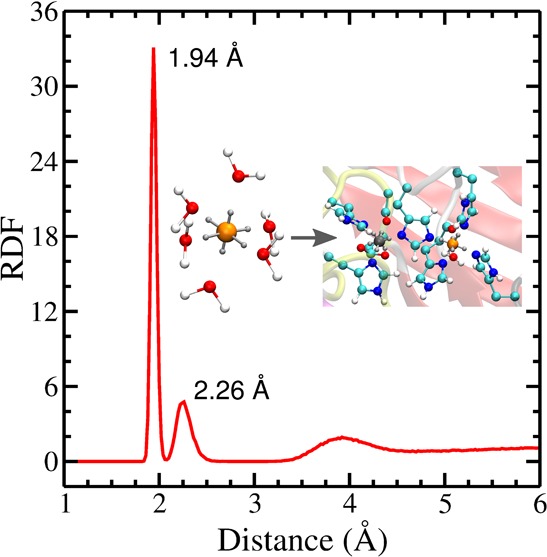
The results for ZnDum were then taken for the development of CuDum. As Zn–O calculated with σ_ZnO = 2.088 Å is quite close to the weighted mean distance between Cu²⁺ and oxygen (Cu–O, 2.07 Å), this σ together with the other ZnDum parameters were used as a starting point and systematically optimized for CuDum. In order to capture both the Jahn–Teller effect (i.e., different Cu–O distances for equatorial and axial ligands) and ΔG_hyd, we tested different charge and distance distributions for the dummy atoms (Figures S3 and S4). We found that reducing the charges for the axial and increasing them for the equatorial dummy atoms (based on q = 0.5e for the dummy atoms in ZnDum) is important for reproducing the Jahn–Teller effect (Figure S4). This reflects the fact that equatorial interactions are preferred over axial coordination for Cu²⁺ (d⁹) in aqueous solution. In combination with this charge disparity, a compressed octahedron performs better than elongated and regular octahedra. Despite the shorter distances between Cu²⁺ and the axial dummy atoms, due to the larger charges of the equatorial dummy atoms, the resulting Cu–O distances are shorter for the equatorial and not the axial ligands, in agreement with the Jahn–Teller distortion in water. The compressed octahedron combined with axial charges q_ax = 0.05e and equatorial charges q_eq = 0.725e (Table 1) was identified as being able to reproduce both the Jahn–Teller effect and ΔG_hyd. The calculated Cu–O distances (d_Cu–O^eq = 1.94 Å and d_Cu–O = 2.26 Å) agree almost perfectly with the corresponding experimental values of 1.96 and 2.28 Å,²⁹ and also the calculated ΔG_hyd = −496.1 kcal/mol deviates by less than 0.1 kcal/mol from the experimental finding (−496.16 kcal/mol)³⁰ (Figure 3). It should be noted, though, that the metal solvation free energies can largely deviate in different experimental studies. Following our earlier work,¹³ we use the data presented by Noyes,³⁰ which includes thermodynamic parameters for a wide range of metal centers, thus capturing the relative effect of the different metals (for further discussion of this choice, see ref (13)). This Cu²⁺ dummy model was further validated using MD simulations of metalloproteins, which are discussed below. The usage of six dummy atoms generally favors hexacoordinated complexes. However, since the current model is a nonbonded model, it has the flexibility to adopt other geometries, such as five- or four-coordinated geometries where relevant. In the latter case, square-planar geometries are favored due to the higher charges on the equatorial dummy atoms, which make them more attractive toward ligands than the axial dummy atoms. An alternative Cu²⁺ dummy model with larger charges on the axial dummy atoms is presented in the SI. As can be seen from the results (Figures S5 and S6) and the associated discussion, this model is also able to produce good results in the MD simulations. Yet, CuDum better reproduces the Jahn–Teller effect and ΔG_hyd for Cu²⁺ in water and is therefore our preferred model.

Table 1. Force Field Parameters for the Dummy Model of Cu²⁺ (CuDum).

bond type	b0 (Å)	Kb (kcal/mol Å2)
Cu–Deq	1.000	800.0
Cu–Dax	0.800	800.0

angle type	θ0 (degree)	Kθ (kcal/mol rad2)
Di–Cu–Di	180.0	250.0
Di–Cu–Dj	90.0	250.0

atom type	mass (au)	charge (e)	σCuO (Å)	ϵCuO (kcal/mol)
Cu	45.546	–1.00	2.043	4.1854
Deq	3.000	0.725	σD =0	ϵD = 0
Dax	3.000	0.050	σD =0	ϵD = 0

Dummy atoms are denoted by D with D_i being either D_eq or D_ax.

The bond potential is U_b = K_b(b – b₀)²; the angle potential is U_θ = K_θ(θ – θ₀)².

Figure 3.

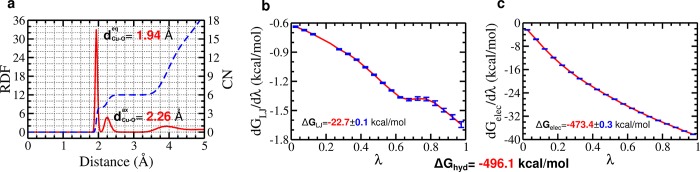
Jahn–Teller effect and ΔG_hyd for CuDum in water. (a) Radial distribution function (red, left y axis) and coordination number (blue, right y axis) for water around CuDum. The free energy contributions dG_LJ/dλ (b) and dG_elec/dλ (c) as a function of the coupling parameter λ. ΔG_LJ and ΔG_elec are calculated by summing over the 21 intermediate states ranging from λ = 0 to λ = 1 applying eq S7. The standard deviation for each state is shown by a blue bar (for some cases, it is <0.001 kcal/mol and thus not visible) while the interpolation between the states is shown in red. The experimental values are d_Cu–O^eq = 1.96 Å, d_Cu–O = 2.28 Å, and ΔG_hyd = −496.16 kcal/mol.

We performed MD simulations of both CuDum and ZnDum coordinated to Aβ_1–16 and tested the interplay of both metal ions in CuZnSOD. We studied Aβ_1–16 with two different coordination modes for CuDum (denoted Aβ_1–16^A2 and Aβ_1–16) and only Aβ_1–16^E11 for ZnDum. In Aβ_1–16 residues, H6, E11, H13, H14 act as ligands,^4,28,31 while in Aβ_1–16^A2 the ligands are A2, H6, H13, H14.^32,33 In CuZnSOD, there are one copper and one zinc ion in the active site.¹⁻³ The copper and zinc ions are bridged by the imidazole ring of H63. Copper is coordinated by another three His residues and a water molecule in a distorted square pyramidal geometry, while zinc is coordinated by two further His residues and an aspartic acid in a distorted tetrahedral geometry.³ More information about the choice of our starting structure can be found in the SI. For each test case, we performed two independent 100 ns MD simulations.

CuDum produces stable Cu²⁺ binding sites during the MD simulations of the Aβ_1–16/Cu²⁺ complex. The root-mean-square deviation (RMSD) of the metal binding site fluctuates around ∼0.42 Å for Aβ_1–16^E11/CuDum and it is only ∼0.15 Å greater for Aβ_1–16/CuDum (Table 2). The whole Aβ_1–16 peptide experiences larger flexibility with RMSD values of up to ∼2.6 Å, which is in agreement with Aβ being an intrinsically disordered peptide. For binding mode Aβ_1–16^E11 the stabilization for the interaction between Aβ_1–16 and CuDum is by more than 30 kcal/mol larger than for the Aβ_1–16/ZnDum complex (Table S3). Here the direct interactions between metal ion and Aβ_1–16 but also the interactions between the ion and solvent are considered. In either case, the main contribution is the Coulomb interaction between the metal center and Aβ_1–16, which is substantially stronger for CuDum than for ZnDum. This agrees with the fact that Cu²⁺ has a higher affinity for Aβ than Zn²⁺.^34,35 CuDum is able to maintain the coordination center of the Aβ_1–16^E11/Cu²⁺ complex in a distorted square pyramidal geometry (Figure 2b) with shorter distances between Cu²⁺ and the equatorial ligands (H6, atom OE1 of E11, H13, 14) and a longer distance for the single axial ligand (atom OE2 of E11) (Table S2). A water molecule is coordinated at the opposite axial position, that adds to the stability of the coordination center. In the simulations of Aβ_1–16 with CuDum, the four ligands prefer to interact with the equatorial dummy atoms producing a square planar coordination geometry (Figure 2c and Table S4), which agrees with findings from experiments^32,33,36 and other quantum-mechanics based calculations.^37,38 Furthermore, we successfully tested that this coordination geometry can also be obtained when the simulation is not initiated from a “perfect” starting conformation but from a distorted geometry (see Figure S7 and associated discussion). As for Aβ_1–16^E11, water coordinates to Cu²⁺. Yet for Aβ_1–16, there are two water molecules interacting with the two unoccupied axial dummy atoms. Again, the electrostatic interactions between Aβ_1–16 and ligands is the dominating contribution to the complex stability (Table S5). In summary, CuDum and ZnDum work well for modeling metal binding to Aβ_1–16.

Table 2. Time Averages of the RMSDs of the Protein Backbone Atoms and of the Metal Binding Sites of Aβ_1–16 and CuZnSOD.

system	backbone (Å)	metal site (Å)
Aβ1–16E11/ZnDum	1.34 ± 0.39	0.52 ± 0.08
Aβ1–16E11/CuDum	1.26 ± 0.43	0.42 ± 0.11
Aβ1–16A2/CuDum	2.64 ± 0.49	0.67 ± 0.11
CuZnSOD/ZnDum/CuDum	1.54 ± 0.16	0.71 ± 0.03

In the two 100 ns MD simulations of CuZnSOD, ZnDum and CuDum are both stable in the metal binding site (Figure 2d). Both overall structure and coordination geometry are conserved with the average RMSDs of the whole backbone and of the metal binding site being below 2.0 and 1.0 Å, respectively (Table 2). Throughout the simulation, the coordination geometry remains distorted square pyramidal for CuDum with the four His ligands interacting firmly with CuDum through the equatorial dummy atoms at distances of ∼2.0 Å. The distances to H46, H48, H120 are quite close to those in the crystal structure (PDB ID: 1HL5(3)) while the H63–CuDum distance is only 1.98 Å (Table S6), which is 0.48 Å shorter than the one in the crystal structure 1HL5. This discrepancy may be explained by the oxidation state of the copper ion in CuZnSOD. A distance increase for copper–H63 from ∼2.0 Å to ∼3.0 Å was observed when Cu²⁺ was reduced to Cu⁺.³ The state of the metal binding site in the crystal structure 1HL5 is considered to represent a mixture of the oxidized (Cu²⁺) and reduced (Cu⁺) states of CuZnSOD. Moreover, the distance between Zn²⁺ and Cu²⁺ calculated from our simulations (5.84 Å) is closer to the one in the oxidized (∼6.0 Å) than in the reduced state (∼6.8 Å). Interestingly, the carbonyl group of H46 is found to be close to CuDum and adds to the overall stability of the Cu²⁺ coordination center. Figure 2d shows that this carbonyl group and H48 compete for coordination to Cu²⁺. A water molecule binds to CuDum via an axial dummy atom as a fifth ligand. The distance Cu²⁺–O^water is 2.35 Å, which is slightly shorter than the one in the crystal structure 1HL5 (2.62 Å) but still falls in a reasonable range based on other crystal structures of CuZnSOD (i.e., PDB ID: 1CB4(1)). The coordination of water to CuDum is in good agreement with the experimental finding that the involvement of a water molecule is necessary for reactions to occur at the metal binding site. For the Zn²⁺ binding site, the distances Zn²⁺–His are 0.1–0.2 Å larger than the corresponding distances in the crystal structure 1HL5 (Table S6). Our findings are nonetheless satisfactory, as these distances vary upon chemical reactions.¹⁻³ It should be noted, though, that the tetrahedral Zn²⁺ coordination geometry cannot be maintained in CuZnSOD, as the carbonyl group from G82 coordinates to Zn²⁺ and D83 becomes bidentately coordinated, causing a 6-coordinated distorted octahedral geometry. This observation is not too surprising, as ZnDum was developed for octahedral geometries.¹³ This issue could be resolved by developing a tetrahedral Zn²⁺ dummy model,⁹ which, however, would have been beyond the scope of the current aim to develop and validate a Cu²⁺ dummy model with Jahn–Teller effect. Furthermore, it is a known fact that zinc coordination is flexible and can adopt multiple binding modes, including tetrahedral, as well as penta- or hexacoordinated geometries.³⁹ Especially for the zinc coordination to the carboxylate group, it could be either bidentate or monodentate,⁴⁰ which is exactly what happens to D83 during the MD simulation of CuZnSOD.

In conclusion, a nonbonded model of Cu²⁺ (CuDum) was developed in this study. This classical Cu²⁺ model captures both the Jahn–Teller effect and the experimental hydration free energy, and maintains stable coordination geometries during MD simulations of metalloproteins without the need for artificial bonds between metal center and ligands. Furthermore, parameters for a Zn²⁺ dummy model (ZnDum) were derived based on a previously reported dummy model.¹³ Our parameters can reproduce square planar Cu²⁺ geometries for our two test cases, the metal binding region of the amyloid-β peptide, Aβ_1–16, and the Cu–Zn superoxide dismutase (CuZnSOD). The comparison between Aβ_1–16/CuDum and Aβ_1–16/ZnDum reveals a lower binding affinity for ZnDum. This metal selectivity is in agreement with experimental findings.^34,35 The study of the bimetallo enzyme CuZnSOD further confirms that the two dummy models can be applied together without artificial repulsion between the two metal centers. We therefore believe that the dummy model of Cu²⁺ presented in this work is of great importance for future studies of the dynamics of copper proteins. A clear advantage of such nonbonded over bonded models is that they are able to model ligand exchange on the metal without the need for higher level quantum chemical calculations, while still performing conformational sampling on the peptide. For a peptide such as Aβ, this is of importance as the aggregation of Aβ is believed to be sped up by the formation of interpeptide coordination modes, which compete with the intrapeptide Cu²⁺ coordination discussed here.⁴¹

Supporting Information Available

Full details of the computational methods and starting structures, results for the parametrization of the Zn²⁺ dummy model (ZnDum) and an alternative Cu²⁺ dummy model, eight tables, and seven figures. The Supporting Information is available free of charge on the ACS Publications website at DOI: 10.1021/acs.jpclett.5b01122.

The authors declare no competing financial interest.