Efficient Estimation of Smooth Distributions From Coarsely Grouped Data

Abstract

Ungrouping binned data can be desirable for many reasons: Bins can be too coarse to allow for accurate analysis; comparisons can be hindered when different grouping approaches are used in different histograms; and the last interval is often wide and open-ended and, thus, covers a lot of information in the tail area. Age group–specific disease incidence rates and abridged life tables are examples of binned data. We propose a versatile method for ungrouping histograms that assumes that only the underlying distribution is smooth. Because of this modest assumption, the approach is suitable for most applications. The method is based on the composite link model, with a penalty added to ensure the smoothness of the target distribution. Estimates are obtained by maximizing a penalized likelihood. This maximization is performed efficiently by a version of the iteratively reweighted least-squares algorithm. Optimal values of the smoothing parameter are chosen by minimizing Akaike's Information Criterion. We demonstrate the performance of this method in a simulation study and provide several examples that illustrate the approach. Wide, open-ended intervals can be handled properly. The method can be extended to the estimation of rates when both the event counts and the exposures to risk are grouped.

Grouped data are omnipresent. In epidemiology, examples of grouped data are age-specific disease incidence rates and cause-of-death data by age. Ages are commonly grouped in bins of 5 years, followed by a broad or open-ended age class that includes all of the elderly starting at age 80 or 85 years. Many abridged life tables and data provided by the World Health Organization or EUROSTAT, the statistical office of the European Union situated in Luxembourg, follow this pattern (1–3). The data are grouped to facilitate compact presentation or to suppress small-scale fluctuations that occur in the sparsely occupied areas of a distribution.

Relying on coarsely grouped data may, however, hinder accurate data analysis. Thus, ungrouping binned data may be desirable. This is particularly true for the wide, open-ended interval that covers the highest ages. With increasing longevity, more people are reaching very high ages, and exploring health trends among the elderly is possible only if age-specific information can be made available for less heavily aggregated data. Another issue that can arise when using grouped data is that the bins may vary over time or across different geographical regions. Again, ungrouping or regrouping the data would facilitate comparisons.

In this paper, we propose a methodology for ungrouping data while making modest assumptions about the underlying (ungrouped) distribution. We assume only that the underlying distribution is smooth but otherwise let the data determine their actual shape. The method is based on the composite link model (4) with a penalty added to ensure smoothness, and estimation is achieved by maximizing a penalized likelihood (5). This approach essentially emulates the grouping process in a statistical model and estimates the most likely original distribution under the modest assumption of smoothness.

Different approaches to ungrouping histograms or abridged life tables have been proposed. Most early attempts were based on parametric assumptions for the underlying distribution (6, 7) or were developed for particular applications (8, 9). For fitting a nonparametric density to binned data histosplines (10), kernel density estimators (11) and local likelihood estimation (12) have been proposed. These approaches may, however, have some drawbacks, including a potential violation of nonnegativity, complications for open-ended intervals and for stretches of intervals with 0 counts, and an optimal choice of the smoothing parameter.

The method we propose is based on the idea that the counts in the coarse bins are indirect observations of a finer (i.e., ungrouped) but latent sequence of counts. This latent distribution has to be estimated, and estimation can be achieved by maximizing a penalized likelihood. First, we introduce this penalized composite link model and show how the latent distribution can be estimated. Nonparametric estimating procedures require the choice of a smoothing parameter, and we recommend minimizing Akaike's Information Criterion (AIC). We study the performance of the approach in a simulation study, and we also compare it with alternative methods. We apply our approach to age-at-death distributions for several causes of death in the United States in 2009 and pay particular attention to the last interval that is open ended. Furthermore, when analyzing age-specific rates, we note that just as events can be binned in intervals, exposures to risk can come in similar age groups. We demonstrate how our approach can be extended to ungroup both the event and the exposure distributions. We conclude with a discussion and give some R code.

METHODS

The statistical model for grouped counts

Consider a sequence of values a₁, …, a_J (i.e., ages a₁ = 0, a₂ = 1, …) and let γ_j, j = 1, …, J be the corresponding expected counts that constitute the distribution of the values a_j. In a sample of size N, each γ_j = Np_j, where p_j is the probability of the value a_j. If the sample were not grouped, then the number of observations at the a_j would follow Poisson distributions with means γ_j (13). However, although we would like to estimate the distribution γ = (γ₁, …, γ_J)^T, the actually observed grouped counts y_i are realizations from Poisson variables Y_i, i = 1, …, I, whose expected values μ_i = E(Y_i) result from grouping the original distribution γ into I < J bins (Figure 1). Each of the μ_i results from a sum of those values γ_j that contribute to bin i of the histogram, and the observed counts have the probability $P(Y_i=y_i)={{\mu }_i}^{y_i}{e}^{-{\mu }_i}/y_i!.$ If we combine the μ_i into a vector μ = (μ₁, …, μ_I)^T, we can write μ = Cγ, with C being the I × J composition matrix

$$C=\left(\begin{array}{ccccccccc}1& \cdots & 1& 0& \cdots & \cdots & \cdots & \cdots & 0\\ 0& \cdots & 0& 1& \cdots & 1& 0& \cdots & 0\\ ⋮& ⋮& ⋮& 0& \ddots & 0& 0& ⋮& ⋮\\ 0& \cdots & 0& 0& \cdots & 0& 1& \dots & 1\end{array}\right).$$

Figure 1.

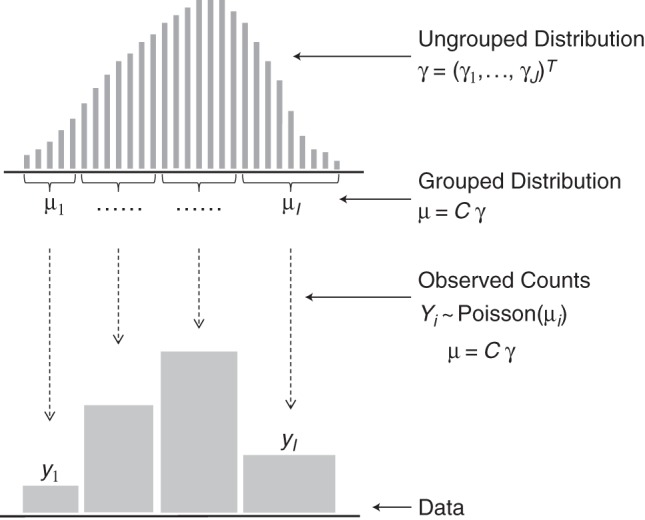
Statistical model for grouped data. The distribution of interest γ is defined on a fine scale. Grouping composes several values of γ to the values of μ, which are the expected counts for the grouped distribution. The observed data y are realizations of Poisson random variables with expected values μ. The latent distribution γ is to be estimated from the grouped counts y, which can be achieved by assuming that γ is smooth.

The number of rows I is the number of histogram bins, and the number of columns J corresponds to the length of the original, but unobservable distribution γ. Elements of C are 0 except for those c_ij = 1 that indicate the elements of γ that are aggregated into histogram bin i. This is a composite link model as it was introduced (4), which extends standard generalized linear models (14). To guarantee nonnegative values of γ, we write it as γ = e^Xβ and estimate the values of β = (β₁, …, β_J)^T. If the number of elements J in the original distribution γ is large, we can choose a design matrix X that represents a B-spline basis of dimension p < J to reduce the number of parameters to be estimated. As here we deal only with distributions of moderate length, we will always choose X to be the identity matrix of dimension J; that is, γ = e^β.

Estimation by penalized likelihood

To be able to estimate J elements in the original but latent distribution γ from I < J observed counts y_i, we must make additional assumptions, because otherwise the problem would be ill defined. We assume that the distribution γ is smooth, that is, that neighboring elements in γ do not differ drastically. This smoothness assumption is implemented in a roughness penalty on the coefficients β, which implies the smoothness of γ, since γ = e^β. Roughness here is measured by the second-order differences of the neighboring coefficients (15), and it is computed by the difference matrix D₂ (Appendix 1). The penalty is $P=D_2{\beta }^2={\beta }^T{D}_2^T{D}_2\beta .$ It is weighted by a parameter λ > 0 and subtracted from the Poisson log-likelihood, giving the penalized log-likelihood

$$l^{\ast }=l-\frac{\lambda }{2}P=\sum _{i=1}^I(y_i\ln {\mu }_i-{\mu }_i)-\frac{\lambda }{2}P,$$

where the μ_i are linearly composed from γ. For a fixed value of λ, the penalized likelihood l* can be maximized by a modified version of the iteratively reweighted least-squares algorithm, as was shown previously (5). The parameter λ balances fidelity to the data and smoothness of the solution β, and it has to be chosen optimally. To determine λ, we minimize AIC, which is equivalent to AIC(λ) = Dev(y|μ) + 2d, where Dev(y|μ) is the deviance and d is the effective dimension of the model (for details, refer to Appendix 1). AIC is computed for a sufficiently fine grid of λ values (on a log scale), and its minimal value is determined over this grid. The estimating procedure was implemented in R (16) (R Foundation for Statistical Computing, Vienna, Austria), and the code can be found in Appendix 2. In Appendix 1, we also discuss uncertainty estimates for $\hat{\beta }$ and $\hat{\gamma },$ respectively.

DATA AND APPLICATIONS

Simulation study

We conducted a simulation study to demonstrate the performance of the penalized composite link model approach. We applied it to various scenarios (distributions, grouping strategies, sample sizes), and we compared it with alternative methods for ungrouping (17, 18). The design of the simulation study and the summary of results are presented in Web Appendices 1 and 2 available at http://aje.oxfordjournals.org/, respectively. The quality of the results was assessed by producing plots of the estimates and boxplots for the integrated absolute error (Web Figures 1–4). The full details of the simulation study are reported in Web Appendices 3–5 (Web Figures 5–31). In several scenarios the penalized composite link model performs best. Most importantly for the purpose of our study, it prevails when unbinning histograms with wide bins and open-ended intervals.

Cause-of-death data

We now illustrate the proposed approach by studying age-at-death distributions for different causes of death for the United States in 2009. The death counts by underlying causes were taken from the Centers for Disease Control and Prevention Database (19). The data are classified according to the International Classification of Diseases, Tenth Revision. We look at the following distributions: deaths from diseases of the circulatory system (codes I00–I99), neoplasms (codes C00–D48), diseases of the blood and blood-forming organs and disorders involving the immune mechanism (codes D50–D89), and infectious and parasitic diseases (codes A00–B99).

The age-at-death distributions are documented by single year of age from 0 to 99 years, with a final open-age class for ages ≥100 years. To assess how well the proposed method works, we grouped the death counts into 5-year age classes up to age 84 years and created a wide, open-ended age interval starting at age 85 years. This grouping structure was used in many data sources until recently, and it is still used in some. We apply the penalized composite link model to the coarsely grouped data and compare the estimated ungrouped results with the empirical death counts.

The distribution of ages at death should be used with care in comparisons, as it conflates the size of past cohorts and mortality (20). Age-specific rates, which may require the ungrouping of deaths and exposures, are more appropriate, and we address this problem at the end of the section.

Ungrouping the age-at-death histograms

We first apply the approach to deaths from diseases of the circulatory system. The results are shown in Figure 2. The open-ended age class collects the observations made for individuals older than the starting age for the interval (here, age 85 years). Although in theory the tail area could be unlimited, in most applications there is a maximal number beyond which no observation is expected or is even possible. As the penalized composite link model smoothly redistributes the grouped observations into the tail area, such information, if available, should be provided. For the present application, the age of 115 years was set as the maximum, and the histogram was complemented with an age group from 115 to 130 years with 0 counts. The penalized composite link model can easily deal with longer stretches of 0 counts.

Figure 2.

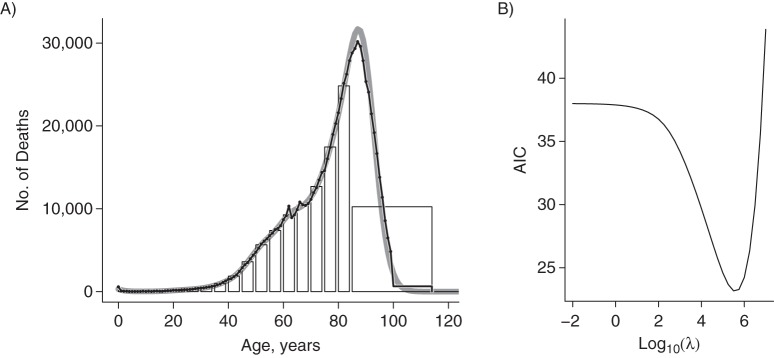
Ungrouping of the age-at-death distribution for diseases of the circulatory system, United States, 2009. The original data taken from the Centers for Disease Control and Prevention database were grouped in 5-year bins plus a wide class for ages ≥85 years. An additional bin with 0 counts between ages 115 and 130 years was added. This histogram was ungrouped by the penalized composite link model. A) Grouped histogram, original data (black line with overplotted points) and ungrouped data (solid gray line). B) The value of the smoothing parameter λ was chosen by minimizing Akaike's Information Criterion (AIC); λ varied on a fine grid, and the value that gave the minimum of AIC led to log₁₀(λ) = 5.5.

The model is estimated for a sequence of values for the smoothing parameter λ, and AIC is computed for each (Figure 2B). The minimal value is obtained for log₁₀(λ) = 5.5, and the corresponding estimate for the latent distribution γ (solid gray line) is shown, together with the grouped data (histogram) and the original counts (black line with overplotted points up to age 99 years, and the last age group from 100 to 115 years), in Figure 2A. The degree to which the original data and the estimates after ungrouping correspond is striking.

The same approach was applied to the age-at-death distribution for the other 3 causes of death. The results are illustrated in Figure 3. These 3 distributions were chosen because they allow us to demonstrate the performance of the method in various circumstances. The age-at-death distribution for neoplasms (Figure 3A) is unimodal, whereas the age-at-death distribution for infectious and parasitic diseases (Figure 3C) has a bimodal shape. Because we assume only that the latent distribution γ is smooth, the model performs well in either case, independent of the shape of the distribution. Furthermore, the sample sizes of these age-at-death distributions vary considerably: There were 9,643 deaths due to diseases of the blood and immune system (Figure 3B) but 582,219 deaths due to neoplasms—60 times as many. These differences in sample size do not undermine the accuracy of the obtained estimates. Because of the large sample sizes in these examples, standard errors were very narrow, and confidence intervals could hardly be seen, so we did not include them in the figures.

Figure 3.

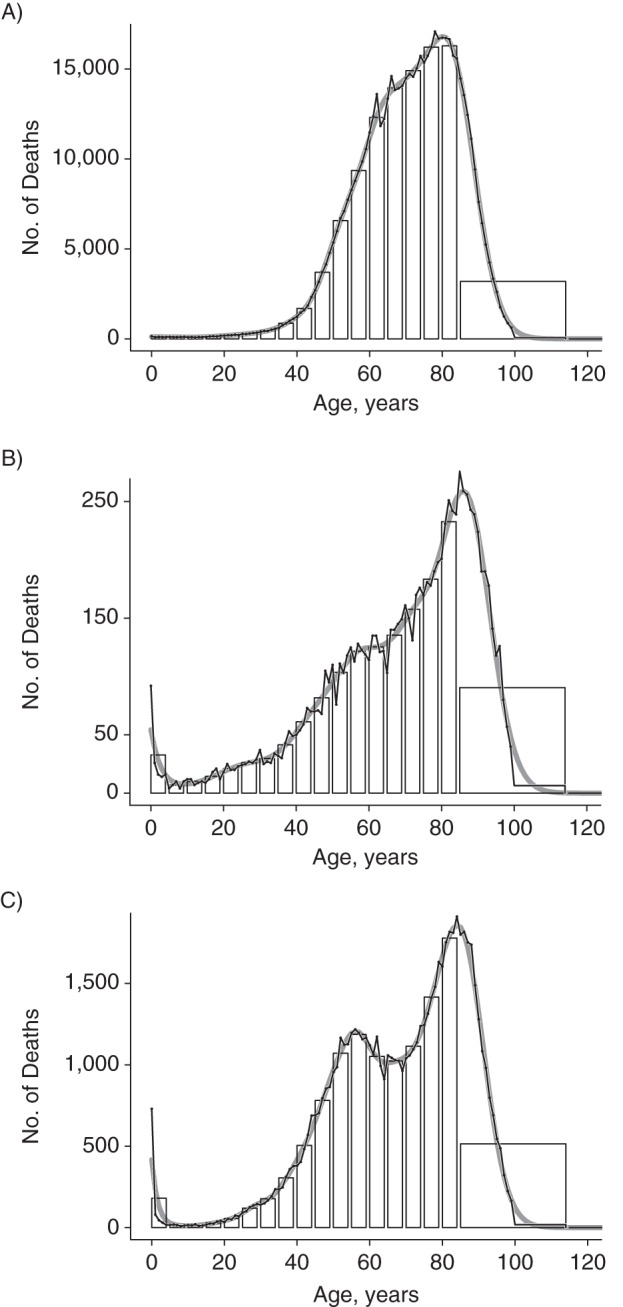
Ungrouping of the age-at-death distribution for neoplasms (A, log₁₀(λ) = 6.5), diseases of the blood and blood-forming organs and disorders involving the immune mechanism (B, log₁₀(λ) = 5.25), and infectious and parasitic diseases (C, log₁₀(λ) = 5.25), United States, 2009. Histogram, original data from the Centers for Disease Control and Prevention database (black line with overplotted points) and results from ungrouping (solid gray line). Optimal values of the smoothing parameter were chosen by minimizing Akaike's Information Criterion.

Appreciable differences between the original and ungrouped counts occur at age 0 years (infant deaths) for diseases of the blood and immune system, as well as for infectious and parasitic diseases. As infants constitute a group at particularly high risk for both causes of death, the assumption of smoothness is violated here. Explicitly including a point mass at age 0 years can remove this effect.

Extending the model to ungroup rates

In many cases, the age-specific rates, rather than the absolute numbers of events, are of interest. Thus, the counts of events as well as the numbers of exposures may be grouped into age classes. The parameters of interest are now the ungrouped latent rates, and we continue to denote the unknowns by γ = (γ₁, …, γ_J)^T; that is, the vector γ now represents rates, not counts. Consequently, the expected number of cases at age a_j is given by e_jγ_j, where e = (e₁, …, e_J)^T denotes the corresponding exposure numbers. As before, the expected number of events after grouping results from composing these e_jγ_j to obtain the μ_i. If we modify the composition matrix such that each column j is multiplied by the respective e_j, we again can write μ = Cγ and proceed in the same way as for ungrouping histograms. If the exposure numbers are available at a detailed resolution, as is often the case for population data at the national level (21), we directly use these e_j in the composition matrix C. If the exposures are also binned in age groups, we first ungroup them using the penalized composite link model and insert the estimates ${\hat{e}}_j$ into the composition matrix C.

To demonstrate the performance of the extended approach, we apply it to diseases of the circulatory system and compare estimated and original age-specific death rates. The exposure data were taken from the Human Mortality Database (21). They were provided by single year of age from 0 to 109 years, with a last age class of ≥110 years. We produced ungrouped estimates of the exposures after grouping them in the same age classes as the event counts. Again, the results are reassuring (Figure 4A). In Figure 4B and 4C, 2 versions of estimated death rates are shown. In Figure 4B, only the event counts were ungrouped, but the exposures were taken by single year of age from the Human Mortality Database. In Figure 4C, both the number of events and the exposures were ungrouped. First, the ungrouped exposures were inserted into the composition matrix C, and the rates were estimated from this second penalized composite link model. The model succeeds in producing accurate results not only when the events are binned in intervals but also when the exposure numbers come in age groups. In both cases, the steep decline in death rates after age 0 years counteracts the idea of smoothness that underlies the penalized composite link model; however, this feature could be captured by a single point component.

Figure 4.

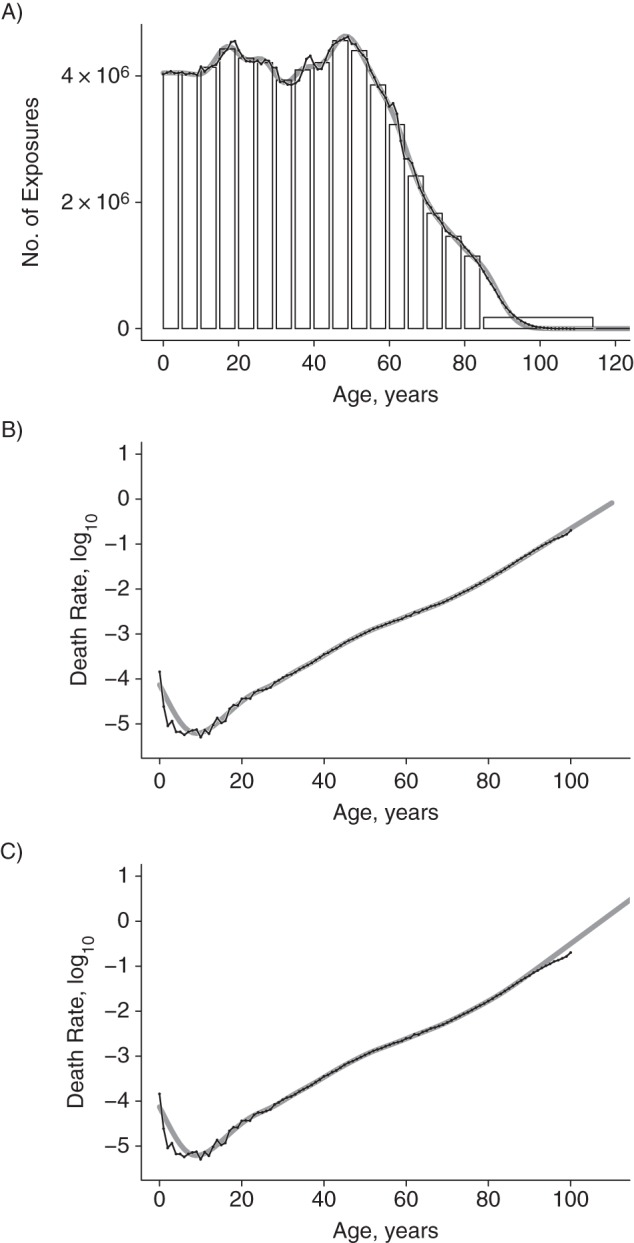
Ungrouping of the age-specific exposure to risk values and estimating age-specific death rates for diseases of the circulatory system, United States, 2009. A) The original exposures taken from the Human Mortality Database were grouped in 5-year bins plus a wide class for ages ≥85 years and an additional bin with 0 counts between ages 115 and 130 years. This histogram was ungrouped with the penalized composite link model. Histogram, original data (black line with overplotted points) and results from ungrouping (solid gray line). The optimal value of the smoothing parameter was log₁₀(λ) = 3.75. B) Death rates obtained from grouped death counts and original exposure to risk values. Death counts taken from the Centers for Disease Control and Prevention Database were grouped in 5-year bins plus an open-ended class for ages ≥85 years. The optimal value of the smoothing parameter was log₁₀(λ) = 5.75. C) Estimated death rates when both the death counts and the exposure numbers were grouped and then ungrouped by the penalized composite link model. The model for the rates had a composition matrix that contained the ungrouped exposures shown in A. The optimal value of the smoothing parameter was log₁₀(λ) = 5.75. In each panel, the original rates (black line with overplotted points) are compared with smoothly estimated rates (solid gray line).

A third and perhaps more straightforward approach turned out to be less successful: If the event counts and the exposures are ungrouped separately and the rates are estimated as the ratio of these 2 ungrouped sequences, then the resulting rates differ more strongly from the original estimates, particularly for wide intervals, such as the open-ended final age class. Inserting the ungrouped exposures into the composition matrix of the second step leads to a considerable improvement.

DISCUSSION

We have demonstrated how binned data can be efficiently ungrouped by using the penalized composite link model. The only assumption that is made about the original distribution is smoothness, which is usually met in practice. As no specific target model needs to be chosen, this approach is suitable for all kinds of applications and, as was shown in the examples, the method can recover features such as multimodality. It also is transparent because it essentially emulates the grouping process in a statistical model. The approach can easily deal with wide, open-ended intervals, and it can incorporate extra information about how the tail area may actually be occupied, if such information is available. As the estimation is based on a version of the iteratively reweighted least-squares algorithm, results are obtained in a few iterations, and computation is therefore fast. Selection of a smoothing parameter through the minimization of AIC was straightforward and generated appealing results in all of the examples. This approach works not only for histograms but also can be applied to rates if both the event counts and the exposures are grouped.

Here we presented a frequentist approach to the problem of ungrouping a histogram. A Bayesian version of the penalized composite link model was suggested previously (22), but open-ended last intervals and the treatment of rates were not discussed. A fully Bayesian approach has the advantage that all uncertainty is incorporated in the posterior distribution of the estimated parameters. In a frequentist setting, the estimated standard errors usually assume a fixed value of the smoothing parameter (23). We studied the performance of 2 common approaches to determine the variance of the estimates by simulation, and we present the details in Appendix 1. The results demonstrate that the additional uncertainty, which is introduced by the choice of the smoothing parameter but is not reflected in the common approaches to variance estimation, can be notable. Theoretical results on the asymptotic properties of the penalized composite link model have not been derived yet. However, the results of our simulation studies, which are presented in Web Appendices 2–5, underpin the good asymptotic properties (such as consistency) of the penalized composite link model approach. Analytical derivations of these properties are considered to be future work.

The model can be further extended to simultaneously ungroup several distributions, such as age-at-death distributions for adjacent years. It can also be used to ungroup 2-dimensional histograms, and a Bayesian version of the penalized composite link model for this problem was presented (24).

The estimation of the ungrouped distribution could be improved further if, in addition to the number of counts in each bin, the mean and possibly also the standard deviation were given for each interval. We are aware that such information is rarely provided, but if it were available, the penalized composite link model could be extended by 2 additional composition matrices to incorporate the 2 interval-specific moments. This could allow even very wide bins to be ungrouped more accurately and could offer a solution if data need to be grouped coarsely to prevent the identification of single individuals or households. The provision of extra information, such as the group means, would not reveal unwarranted details but would improve the estimates of the ungrouped distribution.

APPENDIX 1

Estimation Procedure of the Penalized Composite Link Model for Ungrouping

Here the roughness of the coefficients β is measured by second-order differences, which can be done by multiplying with the difference matrix D₂ of dimension (J − 2) × J:

$$D_2=\left(\begin{array}{cccccc}1& -2& 1& 0& \cdots & 0\\ 0& 1& -2& 1& \cdots & ⋮\\ ⋮& ⋮& \ddots & \ddots & \ddots & ⋮\\ 0& \cdots & \cdots & 1& -2& 1\end{array}\right).$$

The roughness penalty is $P=(D_2{\beta )}^2={\beta }^T{D}_2^T{D}_2\beta ,$ that is, the squared length of the vector of second-order differences. The penalty P is weighted by half the smoothing parameter, λ/2, and is subtracted from the Poisson likelihood. (Different penalty orders can be readily implemented by changing the difference matrix D accordingly.)

For a fixed value of λ, estimates of the coefficients β can be obtained by a modified version of the iteratively reweighted least-squares algorithm (14). The system of equations, in matrix notation, of the penalized composite link model becomes

$$({\breve{X}}^{\mathrm{\prime }}\tilde{W}\tilde{X}+\lambda D_2^T{D}_2)\beta ={\breve{X}}^{\mathrm{\prime }}\tilde{W}[{\tilde{W}}^{-1}(y-\tilde{\mu })+\breve{X}\tilde{\beta }],$$

where $\breve{X}$ has elements ${\breve{x}}_{ik}=\sum _j{c}_{ij}{x}_{ik}{\gamma }_j/{\tilde{\mu }}_i$ and can be interpreted as a “working X” in the iteratively reweighted least-squares algorithm, and $\tilde{W}=\text{diag(}\tilde{\mu }).$ The tilde indicates the current values in the algorithm. To start the algorithm, we chose an initial value, $\tilde{\beta }=\log (\sum _{i=1}^I{y}_i/I)$, and repeatedly calculated new values for β from the matrix equation until the absolute difference between 2 successive values of β was smaller than a threshold (e.g., 10⁻⁶).

To choose the value of λ, we minimized Akaike's Information Criterion (AIC),

$$\text{AIC}=\text{Dev}(y|\mu )+2d=2\sum _{i=1}^I{y}_i\text{ln}\left(\frac{y_i}{{\mu }_i}\right)+2d,$$

where Dev(y|μ) is the deviance, and d is the effective dimension of the model. Following the method of Hastie and Tibshirani (25), the effective dimension d is given by the trace of the so-called “hat matrix,” which is implicit in the linearized system of the iteratively reweighted least squares and is d = trace $\breve{X}({\breve{X}}^{\mathrm{\prime }}W\breve{X}+\lambda D_2^T{D}_2{)}^{-1}({\breve{X}}^{\mathrm{\prime }}W))$.

To obtain the variance-covariance matrix of $\hat{\beta }$, 2 approaches are commonly used as described by Wood (23): The so-called sandwich estimator can be used, which for our particular model is

$$\text{var}(\hat{\beta })=({\breve{X}}^{\mathrm{\prime }}W\breve{X}+\lambda D_2^T{D}_2{)}^{-1}({\breve{X}}^{\mathrm{\prime }}W\breve{X})({\breve{X}}^{\mathrm{\prime }}W\breve{X}+\lambda D_2^T{D}_2{)}^{-1}).$$ (A1)

An alternative estimate follows from a Bayesian approach, and for our model this estimator is

$$\text{var}(\hat{\beta })=({\breve{X}}^{\mathrm{\prime }}W\breve{X}+\lambda D_2^T{D}_2{)}^{-1}.$$ (A2)

In both cases, the value of the smoothing parameter λ is treated as fixed; uncertainty that is introduced by choosing an optimal value for λ is ignored. Standard errors are obtained by taking the square root of the diagonal elements of Equations A1 and A2, respectively. As $\hat{\gamma }=e^{\hat{\beta }},$ standard errors for the estimated $\hat{\gamma }$ are obtained by applying the delta method.

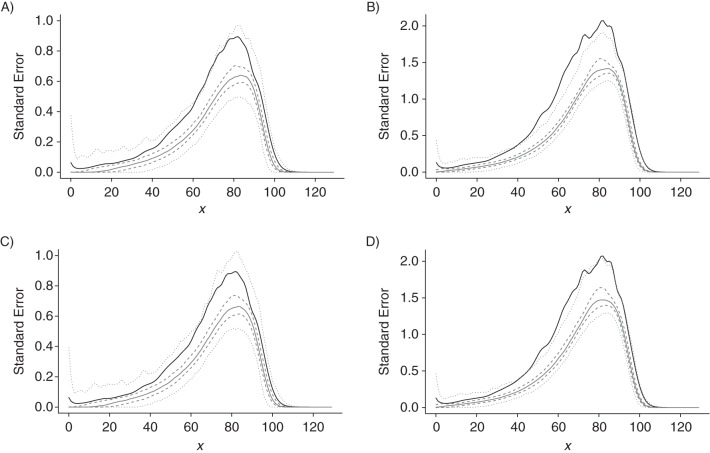
The performance of the 2 alternative variance estimators was evaluated by simulation in various scenarios. The penalized composite link model estimates ${\hat{\gamma }}_j$ were obtained for 500 replications in each scenario, and their empirical standard deviation was determined. Then, for each ${\hat{\gamma }}_j,$ the sandwich estimator (Equation A1) and the Bayesian estimate (Equation A2) were calculated for each of the 500 replications. As a general result, the standard deviation is larger than the values based on the equations. Therefore, the 2 common approaches provide a not very precise lower bound to the standard error. Appendix Figure 1 illustrates this result for 1 scenario.

Appendix Figure 1.

Gompertz distribution with grouping width 5 and sample size (A and C, n = 200; B and D, n = 1,000). The solid black line gives the standard deviation of 500 penalized composite link model estimates obtained in this setting. The gray lines summarize the distribution of the 500 estimates of the standard error derived from the sandwich estimator (A and B) and from the Bayesian estimator (C and D), with median (solid gray line), 25%–75% quantiles (dashed gray lines), and 1%–99% quantiles (dotted gray lines), respectively.

APPENDIX 2

R Code to Estimate the Penalized Composite Link Model

# Demo of the penalized composite link model (PCLM) for grouped counts

pclm <- function(y, C, X, lambda = 1, deg = 2, show = F){

 # Fit a PCLM (estimate b in ) E(y) = C %*% exp(X %*% b)

 # y = the vector of observed counts of length i

 # C = the composition matrix of dimension IxJ

 # X = the identity matrix of dimension JxJ; or B-spline basis

 # lambda = smoothing parameter

 # deg = order of differences of the components of b

 # show = indicates whether iteration details should be shown

 # Fit the penalized composite link model

 # Some preparations

 nx <- dim(X)[2]

 D <- diff(diag(nx), diff=deg)

 la2 <- sqrt(lambda)

 it <- 0

 bstart <- log(sum(y) / nx);

 b <- rep(bstart, nx);

 # Perform the iterations

 for (it in 1:50) {

  b0 <- b

  eta <- X %*% b

  gam <- exp(eta)

  mu <- C %*% gam

  w <- c(1 / mu, rep(la2, nx - deg))

  Gam <- gam %*% rep(1, nx)

  Q <- C %*% (Gam * X)

  z <- c(y - mu + Q %*% b, rep(0, nx - deg))

  Fit <- lsfit(rbind(Q, D), z, wt = w, intercept = F)

  b <- Fit$coef

  db <- max(abs(b - b0))

  if (show) cat(it, " ", db, "\n")

  if (db < 1e-6) break

 }

 cat(it, " ", db, "\n")

 # Regression diagnostic

 R <- t(Q) %*% diag(c(1 / mu)) %*% Q

 H <- solve(R + lambda * t(D) %*% D) %*% R

 fit <- list()

 fit$trace <- sum(diag(H))

 ok <- y > 0 & mu > 0

 fit$dev <- 2 * sum(y[ok] * log(y[ok] / mu[ok]))

 fit$gamma <- gam

 fit$aic <- fit$dev + 2 * fit$trace

 fit$mu <- mu

 fit

}

# Simulate latent data

m <- 130

x <- 1:m

xmean <- 80

xsd <- 10

set.seed(2012)

f <- dnorm(x, xmean, xsd)

mu <- 1e4 * f

z <- rpois(m, lambda = mu)

# Compute the group counts

gr <- seq(1, 86, by = 5)

bnd <- 114

ilo <- c(gr, bnd)

ihi <- c(seq(5,85,5),115,130)

n <- length(ihi)

ihi[n] <- m

y <- g <- 0 * ihi

for (i in 1:n) {

 y[i] <- sum(z[ilo[i]:ihi[i]])

}

y <- c(y[1:17],sum(y[18:19]),0)

for (i in 1:n) {

  g[i] <- y[i] / (ihi[i] - ilo[i] + 1)

}

# Make C matrix and (trivial) basis B

C <- matrix(0, n, m)

C[1:17, 1:85] <- kronecker(diag(17), matrix(1, 1, 5))

C[18, 86:115] <- 1

C[19, 116:130] <- 1

B <- diag(m)

# Solve PCLM

lambda <- 10^7

mod <- pclm(y, C, B,lambda = lambda, deg = 2)

cat("lambda, ED & AIC:", lambda, mod$trace, mod$aic, "\n")

# Plot data and fit

plot(x, mu, type = "l", xlim = c(50, m), ylim = range(mod$gamma), lwd = 2,

   xlab = "Age", ylab = "Number of events")

lines(x, z, col = "darkgreen")

 points(x, z, pch=20,cex=0.8, col="darkgreen")

lines(ihi, g, type = "S", col = "blue")

lines(x, mod$gamma, col = "orange", lwd = 2)