Scalable Multicore Motion Planning Using Lock-Free Concurrency

Abstract

We present PRRT (Parallel RRT) and PRRT* (Parallel RRT*), sampling-based methods for feasible and optimal motion planning designed for modern multicore CPUs. We parallelize RRT and RRT* such that all threads concurrently build a single motion planning tree. Parallelization in this manner requires that data structures, such as the nearest neighbor search tree and the motion planning tree, are safely shared across multiple threads. Rather than rely on traditional locks which can result in slowdowns due to lock contention, we introduce algorithms based on lock-free concurrency using atomic operations. We further improve scalability by using partition-based sampling (which shrinks each core’s working data set to improve cache efficiency) and parallel work-saving (in reducing the number of rewiring steps performed in PRRT*). Because PRRT and PRRT* are CPU-based, they can be directly integrated with existing libraries. We demonstrate that PRRT and PRRT* scale well as core counts increase, in some cases exhibiting superlinear speedup, for scenarios such as the Alpha Puzzle and Cubicles scenarios and the Aldebaran Nao robot performing a 2-handed task.

I. Introduction

INCREMENTAL sampling-based motion planners, such as the Rapidly-exploring Random Tree (RRT) and RRT*, are used in a variety of robotics applications including autonomous navigation, manipulation, and computational biology [1], [2]. The objective of these planners is to find a feasible or optimal path through the robot’s free configuration space from a start configuration to a goal configuration. We introduce PRRT (Parallel RRT) and PRRT* (Parallel RRT*), parallelized versions of the single-tree RRT and RRT* motion planners that are tailored to execute on modern multicore CPUs.

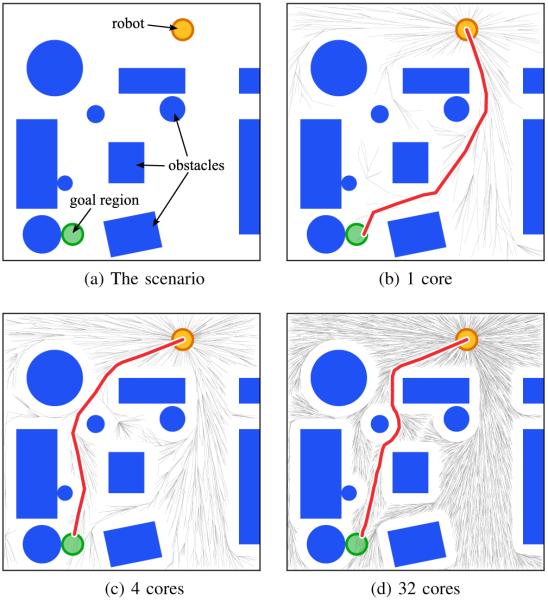
Most modern PCs and mobile devices have between 2 and 32 processing cores with shared memory, and the number of cores is increasing. PRRT and PRRT* are designed to scale and efficiently utilize all available cores concurrently, enabling substantial speedups in motion planning, as shown in Fig. 1. We have empirically observed that PRRT and PRRT* in some cases achieve a superlinear speedup: when p processor cores are used instead of 1 processor core, computation time is sped up by a factor greater than p.

Fig. 1.

We ran PRRT* for a 2D holonomic motion planning problem for a disc-shaped robot for 10 ms on 1, 4, and 32 processor cores. The red line shows the optimal path found. With the same wall clock time, adding more processor cores increases the size of the tree, enabling fast computation of higher quality motion plans on modern multicore computers.

Our focus is on challenging motion planning scenarios for which a large number (tens or hundreds of thousands) of configuration samples is necessary to find a feasible path or to compute a plan with the desired closeness to optimality. In RRT and RRT*, the time spent computing nearest neighbors grows logarithmically with each iteration as the number of samples rises, whereas the time spent per iteration on collision detection decreases as the expected distance between samples shrinks. Collision detection typically dominates computation time in the early iterations. But as the number of iterations rises and the number of samples increases, nearest neighbor search will dominate the overall computation.

To enable speedup regardless of the computational bottleneck (e.g. collision detection or nearest neighbor searching), we parallelize the outer loop of RRT and RRT*: we create multiple threads that each generate samples and incrementally extend the motion planning tree based on those samples. To parallelize at this level, independently working threads must share access to a common data nearest neighbor search and motion planning tree data structure.

Traditionally, shared access might be controlled using locks. In the lock-based approach, when a thread must access a shared data structure, it first locks the data structure, then accesses it, and finally unlocks it. When another thread attempts to access a locked data structure it waits (i.e. is blocked) until the data structure is unlocked. If the lock covers a large data structure, then one thread may unnecessarily block other threads. If instead many locks are used to cover smaller data structures, then threads will repeatedly lock data structures unnecessarily, leading to high overhead. As the number of processor cores increases and as the number of samples grows to handle more complex motion planning problems, more computation time must be spent on nearest neighbor checking and lock contention rises, causing sublinear speedup.

To reduce causes of sublinear speedup and create opportunities, but not a guarantee, for superlinear speedup, PRRT and PRRT* introduce three key components relevant to multicore concurrency. The first is lock-free concurrency using atomic operations. To eliminate slowdowns caused by lock overhead and contention, PRRT and PRRT* use lock-free shared data structures that are updated using an atomic compare-and-swap (CAS) operation, a universal primitive [3]. A CAS operation has three arguments: a location in shared memory, the expected value stored therein, and a new value to replace the previous. In a single atomic step, CAS loads the value stored in memory, compares it to the expected value and, only if they are the same, stores the new value in memory. Without the atomic guarantee, another concurrent thread would be able to store a different value between the CAS’s load and store. The atomic operation removes the need for locks when updates to shared data structures can be formulated into a single update. When a comparison fails due to a change made by another thread, the update is reformulated with the new information and tried again until it succeeds or is no longer necessary. In PRRT and PRRT* we observe that as the number of nodes n in a motion planning tree increases, the probability that any of the p threads are updating the same part of the motion planning tree decreases (lim_n→∞ O(p/n) = 0). As a consequence, CAS operations rarely fail and we avoid the unnecessary blocking and overhead associated with locks. Lock-free operations eliminate the need for locks and hence reduce the overhead that might otherwise be associated with concurrent access to a shared-memory data structure. Lock-free operations by themselves at best enable linear speedup, but can be used in conjunction with other components to create opportunities for superlinear speedup.

The second component introduced in PRRT and PRRT* that sets up conditions in which superlinear speedup might occur is cache-friendly partition-based sampling. To reduce the size of each thread’s working data set, we partition the configuration space into non-overlapping regions and assign a partition to each thread. Partitioning has two benefits. First, it reduces the likelihood that two threads will simultaneously attempt to modify the same part of the shared data structures, reducing CAS failures. Second, as each processor core is expected to work in a smaller subset of the nearest neighbor data structure, more of the relevant structure can reside in each core’s cache, thus creating an opportunity for superlinear speedup. Cache-efficiency, while not affecting the algorithmic complexity, can lead to significant real-world performance gains on modern CPU architectures.

The third component introduced to create opportunities for superlinear speedup in PRRT* is parallel work-saving. During the rewiring phase of RRT*, the algorithm evaluates the costs of paths to nearby nodes, rewires them through the new node if such routing would produce a shorter path, and percolates updates up the tree. To reduce the number of rewiring operations in RRT*, we ensure that when multiple threads attempt to rewire the same portion of the tree, only the one with the better update continues. This frees the other threads to continue expanding the RRT*, effectively reducing computation effort relative to single-threaded RRT* for percolating rewiring up the tree. Parallel work-saving can enhance an algorithm’s performance and can in some cases enable superlinear speedup.

PRRT and PRRT* are designed to run on standard shared-memory, multicore, CPU-based computing platforms (rather than, for example, a cluster or a GPU). This facilitates easy direct integration with existing libraries for collision detection, robot kinematics, and physics-based simulation [4], [5]. In this paper we provide a refined, archival version of our methods originally introduced in a conference paper [6] and generalize the lock-free kd-tree data structure to support configuration spaces such as SE(3) and include new evaluations. We also provide pseudocode sufficiently detailed to show where CAS operations are used, how they impact the surrounding instructions, and how we ensure correctness under concurrency. We demonstrate the fast performance and scalability of PRRT for feasible motion planning using the Alpha Puzzle scenario and a random spheres scenario, and we demonstrate PRRT* for optimal motion planning using the Cubicles scenario, a holonomic disc-shaped robot, and an Aldebaran Nao small humanoid robot performing a 2-handed task.

II. Related Work

Sampling-based motion planners include several components that can naturally be parallelized, and prior work has taken multiple avenues to exploit this parallelism using multicore and multi-processor CPUs, clusters, and GPUs. Early work by Amato et al. [7] showed that sampling-based probabilistic roadmaps (PRMs) can be parallelized. Our focus is on parallelizing RRT and RRT*.

Parallelizing RRT introduces new challenges since the validity of the tree must be maintained as it is updated by multiple processes. A direct approach on a shared-memory system is to use locks on shared data structures, which is one of the methods proposed by Carpin et al. [8] and implemented as pRRT in OMPL [5]. Parallelizing RRT has also been investigated for distributed-memory systems common in clusters. Devaurs et al. propose collaborative building of an RRT across multiple processes using message passing [9]. This approach achieves a sublinear speedup as the number of available processors increases. Jacobs et al. [10] recently introduced speedups by adjusting the amount of local computation before making an update to global data structures and by radially subdividing the configuration space into regions. Approaches targeting distributed-memory systems (e.g., [9], [10]) can also be run on shared-memory systems, but they do not take advantage of shared-memory primitives that can offer additional opportunities for speedup. KPIECE [11] prioritizes cells in a discretized grid for sampling based upon a notion of each cell’s importance to solving a difficult portion of the motion plan and has been demonstrated to parallelize on shared-memory systems using locking primitives. Our focus is on shared-memory systems (common in PC’s and mobile devices), which enables us to utilize atomic CPU operations and cache-friendly algorithms to set up conditions under which superlinear speedup might occur for a single RRT.

Several approaches to parallelizing motion planning across multiple cores/processors have utilized multiple tree-based data structures. Carpin et al. [8] propose an OR parallel algorithm in which several RRT processes run in parallel and the algorithm stops when the first RRT process finds a solution. Plaku et al. [12] introduced the Sampling-based Roadmap of Trees (SRT) algorithm, which subdivides the motion planning problem into subproblems that are distributed, solved by another planner, e.g. RRT, and connected together. SRT achieves near-linear speedup that slightly tapers at higher processor counts. Otte et al. [13] also distribute the generation of independent path planning trees among several processes and achieve significant speedups by sharing information between processes about the best known path. Unlike the above methods that rely on multiple trees, we focus on building a single motion planning tree as in RRT and RRT*. Hence, our approach is complementary to the above multi-tree methods, which utilize multiple single-tree data structures. Our lock-free methods for shared-memory, multicore concurrency resulted in an empirically observed superlinear speedup for some scenarios for both feasible and optimal single-tree motion planning.

Bialkowski et al. [14] parallelize RRT* and related methods by improving the rate of collision detection. This approach results in substantial speedups for environments where collision detection dominates processing time. But due to Amdahl’s law [15], parallel performance will taper as the number of samples increases and nearest neighbor checks begin to dominate as discussed in Sec. I.

Partitioning of configuration space has been used to various effect in motion planning. For example, Rosell et al. [16] hierarchically decomposes C-space to perform a deterministic sampling sequence that allows uniform and incremental exploration. Morales et al. [17] automatically decompose a motion planning problem into (possibly overlapping) partitions wellsuited for one of many (sampling-based) planners in a planning library. Yoon et al. [18] show how cache-efficient layouts of bounding volume hierarchies provide performance benefits in the context of collision detection.

GPU-based parallel computation has also been used to accelerate motion planning, including GPU-based methods for the PRM [19], rasterization-based planning [20], Voronoi diagram-based sampling [21], [22], and R* [23]. Implementing GPU-based algorithms is challenging in part because the single-instruction-multiple-data (SIMD) execution model of GPU’s constrains algorithm design. When each thread needs to do something different (inherently divergent), such as traversing a space partitioning tree, the SIMD model loses nearly all ability to parallelize [24]. Another challenge with GPU approaches is that, while they can gain the benefit of the high computational throughput associated with GPUs, they sacrifice some interoperability with standard systems and libraries based upon CPUs.

III. Problem Formulation

A. Parallel Computing Environment

Our target computing environment is the one available in almost every modern computer: a multicore/multi-processor concurrent-read-exclusive-write (CREW) shared-memory system with atomic operations that synchronize views of memory between threads running on different cores. This is the model in the current generation of x86-64 and ARM multicore processors as well as many other CPU architectures.

In this environment, a computer contains one or more processors. Each processor may contain one or more cores. Each core acts as an independent CPU capable of having a single thread running simultaneous to the threads running on the other cores. The total number of cores in the system is:

$$p=\left(\#\mathrm{of}\mathrm{cores}\mathrm{per}\mathrm{processor}\right)\times \left(\#\mathrm{of}\mathrm{processors}\right)$$

For example, a system with 4 processors, where each processor has 8 cores, has p = 32.

Speedup refers to how much a parallel algorithm is faster than a corresponding sequential algorithm. Let T_p be the execution time of a program that is executed using p cores. Formally, speedup S_p is the ratio of the sequential (single-threaded) execution time T₁ to parallel execution time T_p with p cores:

$$S_p=\frac{T_1}{T_p}$$

Linear speedup means S_p = p, and superlinear speedup means S_p > p.

To achieve large speedups, we will utilize several features that are common on modern multicore processors. First, we will use the atomic compare-and-swap (CAS) operation. Second, modern processors typically have a cache hierarchy between the core and RAM that includes one or more small but fast caches local to each core (L1 and L2) and a larger and slower cache shared among cores (L3). When the data set in use by a core is smaller, the core uses the faster local caches more often and gains a proportional speed benefit. CPU caches can be leveraged to gain superlinear speedups by distributing the working dataset into smaller chunks across multiple cores.

B. Problem Definition

Let C be the d-dimensional configuration space of the robot and C_free ⊆ C denote the subspace of the configuration space for which the robot is not in collision with an obstacle. Let q ∈ C denote a configuration of the robot. PRRT and PRRT* each require as input the start configuration q_init of the robot and a set of goal configurations Q_goal ⊆ C_free.

The objective of PRRT (feasible motion planning) is to find a path in the robot’s configuration space that is feasible (e.g., avoids obstacles) and reaches the goal region. Formally, the objective of PRRT is to compute a path Π : (q₀, q₁, q₂, … , q_end) such that q₀ = q_init, q_end ∈ Q_goal, and Π lies in C_free. The objective of PRRT* (optimal motion planning) is to compute a feasible path that reaches the goal region and minimizes a user-defined cost function. An example cost function is the minimum total Euclidean length of the segments in the planned path.

C. Problem-specific Functions

Similar to their sequential motion planning counterparts RRT and RRT*, PRRT and PRRT* require as input the definition of problem-specific functions. For two configurations q₁, q₂ ∈ C, the function STEER(q₁, q₂) returns a new configuration that would be reached if taking a trajectory from q₁ heading toward q₂ up to some maximum user-specified distance. The function FEASIBLE(q₁, q₂) returns false if the local path from q₁ to q₂ collides with an obstacle or violates some motion constraint, and true otherwise. For PRRT*, the function COST(q₁, q₂) specifies the cost associated with moving between two configurations q₁ and q₂, which can equal control effort, Euclidean distance, or any problem-specific user-specified metric that can be used with RRT* [2]. We also require a function GOAL(q) that returns true if q ∈ Q_goal and false otherwise.

The above problem-specific functions are standard in RRT and RRT*, which enables current implementations of these problem-specific functions to be used in PRRT and PRRT* largely unchanged. For the algorithm we present here, the only additional requirement we add is that the implementation of the problem-specific functions must be either (1) thread-safe and non-blocking or (2) capable of having multiple non-shared instances in the same program.

IV. PRRT

We present Parallel RRT (PRRT), a lock-free parallel extension of the RRT algorithm. We describe the algorithm in sufficient detail to show where atomic operations are used, how they impact the algorithm design, and how we ensure correctness under concurrency.

The PRRT algorithm maintains data structures that are shared across all threads, including the data structure for nearest neighbor searching, the RRT tree τ , the approximate iteration number, and whether or not a path to the goal has been found. As shown in Algorithm 1, PRRT begins by partitioning the configuration space into non-overlapping regions and launching an independent thread for each partition. For peak performance, each thread runs on a dedicated core. The impact of partitioning is that it localizes each thread’s operations (e.g. random sampling and nearest neighbor searching) to a smaller portion of the configuration space. This allows for more effective use of each core’s caches and contributes in some cases to our method’s empirically observed superlinear performance.

A. PRRT Threads

The algorithm for each thread of PRRT is shown in Algorithm 2. PRRT is nearly identical to the standard RRT algorithm except that (1) each thread only samples in its partition and (2) PRRT uses a lock-free nearest-neighbor data structure (introduced in Sec. IV-B). We note that although sampling is local to a partition, the nearest-neighbor data structure spans the entire configuration space and is shared by all threads.

As in the standard RRT algorithm, the function PRRT creates a new node for q_new and sets its parent pointer to the node of q_near (line 6) and then inserts the node into the lock-free kd-tree (line 7). The ordering is important since PRRT must ensure that other threads only see fully initialized nodes, and the new node will become visible as soon as it is inserted into the kd-tree.

Complicating matters, modern CPUs and compilers may speculatively execute memory reads and writes out-of-order as a performance optimization. These optimizations are done in a manner that guarantees correctness from the view of a single thread, but out-of-order writes may cause a thread executing concurrently on another core to see uninitialized or partially initialized values, resulting in an incorrect operation. The solution to this problem is to issue a memory barrier (also known as a memory fence) [25]. A memory barrier tells the compiler and CPU that all preceding memory operations must complete before the barrier, and similarly no memory operations may speculate ahead of the barrier until after the barrier completes. For PRRT_Thread to operate correctly, it must ensure that a memory barrier is issued before a new node becomes visible to another thread, which is done in the lock-free kd-tree insertion algorithm described next.

B. Building a Lock-Free kd-Tree

The RRT algorithm requires an algorithm Nearest(τ, q) for computing the nearest neighbor in τ to a configuration q in configuration space. Using a logarithmic nearest neighbor search rather than a brute-force linear algorithm often results in a substantial performance gain [26]. In PRRT, for nearest neighbor searches we use a variant of a kd-tree data structure [27] that we adapt to allow for concurrent lock-free inserts using CAS.

Each node of the kd-tree is a k-dimensional point (i.e., a configuration in PRRT), where k = d is the dimension of the configuration space. The kd-tree is a binary tree in which each non-leaf node represents an axis-aligned splitting hyperplane that divides the space in two; points on one side of this hyperplane are in the left subtree of that node and the other points are in the right subtree. The axis associated with a node is based on its depth (i.e., level) in the tree. For example, in 3D Euclidean space the hyperplane for a node in the first level of the kd-tree is perpendicular to the x-axis based on that node’s x dimension value. For successive layers, the splitting is perpendicular to the y-axis, then the z-axis, and then repeating x, y, z, x, y, z, … down the tree.

To insert a node in the kd-tree for fast nearest neighbor searching, PRRT_Thread calls the lock-free kd-tree insert function LockFreeKDInsert shown in Algorithm 3. It starts with a pointer to the root (line 4), then traverses down the kd-tree by different dimensions (lines 5, 6) until it finds an empty branch (line 7). Once found, it generates and records the split (line 8), performs a memory barrier, and then a CAS (lines 9, 10) to change the pointer from null to the new node that was allocated and initialized in line 1. If the CAS succeeds, the node is inserted and the algorithm returns. If another thread already updated the pointer, the CAS will fail, and the algorithm will continue to walk down the tree until it can attempt another insert. The memory barrier before the CAS ensures that the node is fully initialized before it is visible to other threads when the CAS succeeds.

In line 8, Split denotes a function that generates the hyperplane. The split is generated based upon the bounds of the region of the node’s parent. The bounds are initialized in lines 2 and 3 and updated in lines 15 and 18. If the bounds are known and finite, Split forces a mid-point split [28] by returning (q_min + q_max)/2. If the bounds are not known, as might happen with the initial values at the root of the tree, Split returns q_new [a], causing the inserted value to define the split.

The kd-tree handles most spaces relevant to motion planning in configuration spaces, including Rⁿ, T ⁿ, and combinations thereof with an appropriate distance metric [26]. For Rⁿ spaces, we consider Euclidean distance metrics. For T ⁿ spaces (with unbounded revolute joints where θ = θ + 2nπ for any integer n) we consider distance metrics based on a circular distance in the form dist_S1 (θ₁, θ₂) = min(|θ₁ − θ₂|, 2π − |θ₁ − θ₂|). For a combination of these spaces, we consider the root sum of squares.

We augment the lock-free kd-tree to support SE(3) and SO(3) by defining splits based on the approach of vantagepoint trees (vp-trees) [29]. The kd-tree defines a split on an SO(3) component using an orientation a_split in space and a pre-defined distance φ from the orientation. The distance function is the shortest arc-length between two orientations and thus ranges from 0 to π. Representing orientations using quaternions [30], dist_SO3(a₁, a₂) = arccos |a₁ · a₂|. Orientations that are less than φ away from a_split are on one side of the split, and orientations greater than φ away are on the other side. We preselect φ as sec 30°, as that produces an even split on the orientations in SO(3). The Split function on the SO(3) component generates a split orientation by rotating the orientation component a_new of the inserted point by φ about an arbitrary axis. This causes a_new to lie exactly on the split. This vp-tree-based approach enables the lock-free kd-tree to efficiently support the SE(3) and SO(3) configuration spaces.

PRRT and PRRT* builds up the lock-free kd-tree on the fly by inserting randomly generated configuration samples. The resulting tree remains relatively balanced. It can be shown that the expected number of comparisons required to insert a random sample into a binary tree generated with uniform random insertions is about 2 ln n [31, p. 430–431].

The kd-tree can be used for any number of dimensions, but may become inefficient in very high dimensional spaces [26]. Even in such cases, kd-trees distribute random updates throughout the tree, leading to low contention over insertion points. In brute-force approaches based upon arrays or lists, inserts at a single insertion point (e.g. the tail of the list/array) may result in contention.

C. Querying a Lock-Free kd-Tree

For a given query sample, Nearest and Near search the lock-free kd-tree for the sample closest to it, or all samples within a radius of it, respectively. They successively compare the query to each traversed node’s splitting hyperplane, and recurse down the side on which the query sample lies (the “near” side). Recursion ends when encountering empty branches. Upon return from the near side, the methods traverse the “far” side of the hyperplane only if it is possible that points in that part of the tree would be closer than the closest found so far (Nearest) or within the search radius (Near).

In practice PRRT can be used with other nearest-neighbor search approaches that allow for non-blocking searches and low-contention updates, and provide partitioned locality properties. The alternative of using a nearest-neighbor data structure with locks is also possible, but as shown in the results in Sec. VI, unlike the lock-free kd-tree, a lock-based kd-tree will result in sublinear speedup as different threads contend for access to the structure.

In our implementation, we consider two schemes for configuration space partitioning that naturally align with the nearest neighbor search kd-tree: (1) an even subdivision created by “slicing” along the first dimension of configuration space, and (2) a multi-dimensional grid created by recursively partitioning along successive axes. While more sophisticated partitioning approaches (e.g. [11], [16], [17]) might look for ways to focus sampling on regions of difficulty (such as regions containing narrow passages), our motivation in partitioning is to create locality with sampling and nearest neighbor searches, and thus improve CPU cache utilization. As seen in the results, the choice of partitioning scheme has an impact on the overall performance of the motion planner depending on the scenario.

V. PRRT*

We present Parallel RRT* (PRRT*), a lock-free parallel extension of the RRT* algorithm. The PRRT* algorithm shares across all threads the data structure for nearest neighbor searching, the RRT* tree τ , the approximate iteration number, and the best path to the goal found by any of the threads. PRRT*, shown in Algorithm 4, begins just like PRRT except it launches threads of PRRT*_Thread(τ, s).

A. PRRT* Threads

PRRT* expands the motion planning tree much like PRRT except that it includes the additional step of “rewiring” a small neighborhood of the tree to enable finding optimal paths. PRRT*_Thread, shown in Algorithm 5, is the main loop of a thread of PRRT*.

At a high level, PRRT* works much like standard RRT*. In the outer loop, it randomly samples a configuration, finds the sample’s nearest neighbor in the motion planning tree, and computes a new configuration by steering from the nearest neighbor toward the sampled configuration (lines 2–5). PRRT* then searches for all the configurations in a ball around the new configuration (line 6) using the ball radius defined in [2]. PRRT* then connects the new configuration to the configuration in the ball that produces the shortest path (lines 8–17), and then inserts the newly connected configuration into the nearest neighbor structure (line 21). Finally, it rewires any configuration in the ball radius that produces a shorter path to goal through the newly added configuration.

The notable differences from standard RRT* are: (1) each thread samples within a partition of the configuration space (line 2), (2) nearest neighbors are found using a lock-free kd-tree (lines 3 and 6), (3) new configurations are added to the RRT* tree in a manner that accounts for parallelism by fully initializing them before adding them to the nearest-neighbor structure (lines 18–20), and (4) rewiring is accomplished entirely via lock-free operations.

B. PRRT* Rewiring

During the rewiring phase of RRT*, the algorithm considers paths to configurations nearby the newly added configuration, and it rewires the RRT* tree if re-routing those paths through the newly added configuration is both FEASIBLE and results in a shorter path. Following the approach of prior implementations of RRT* [2], [5], we cache with each RRT* node the the path cost to that node’s configuration and push updates down the tree when a node is rewired.

PRRT* formulates rewiring (Algorithm 6) into a CAS operation that guarantees rewiring is completed correctly, even if another thread is concurrently accessing or rewiring the same node. If the CAS update fails, the assertion about the new trajectory being shorter may now be incorrect. In that case, the update is re-evaluated and tried again if the rewiring would still result in a shorter path.

CAS operations only work on single memory operands. The rewiring assertion however is made about two pieces of information: the trajectory and the cost of that trajectory. We thus modify the data structures to encapsulate both trajectory and cost into a single unit making it suitable for a CAS. The data structures we define are nodes, representing reachable valid configurations, and edges, representing trajectories from one node to another. The edges form a linked tree structure that represents known trajectories to any nodes. To get from the initial configuration to any node’s configuration, the edge structure is followed (in reverse) from the node back to the root of the tree where the initial configuration is stored. An edge’s path to root never changes, and thus its computed trajectory cost never changes. When PRRT* finds a shorter path to a node, the node’s edge is CAS with the better edge. Here again, we issue a memory barrier and ensure that the new edge is fully initialized before the CAS. The old edge will still essentially be present in the edge tree, but is no longer referenced from the node. We call an edge in this state “expired”, and detect it when edge.node.edge ≠ edge. Expired edges can be garbage collected and their associated memory reused, but care must be taken to avoid the “ABA” problem [3]. (The ABA problem occurs when a thread reads ‘A’ from a shared memory location and, before it performs the CAS, another thread modifies the shared location to ‘B’ and back to ‘A’, which causes the first thread to treat the shared memory location as unmodified.)

By computing CAS operations around an edge, PRRT* guarantees that any update it makes results in an equal or better path, a requirement for the solution to converge towards optimality. After rewiring a node through a better path, the new shorter path is recursively percolated to the nodes that link in to the rewired node. This update process (Algorithm 7) atomically replaces edges to the expired parent with shorter ones. It repeatedly removes the old children one at a time (line 4) from a lock-free list structure (e.g. [32], [3]) until no more children remain (line 5). It then creates the new child edge with the updated cost, and CAS it into place (line 15). A memory barrier before the CAS ensures that the edge is fully initialized before another thread can access it. Note that by using the lock-free list removal, the algorithm ensures that only one thread is updating a particular child at any time. In the case in which two threads are competing to update the same portion of the tree, the thread(s) producing the longer update terminate early (lines 10, 13), and only the thread producing the shorter update proceeds, thus providing work savings and improving speedup.

C. Asymptotic Optimality of PRRT*

In the case of single-threaded execution, PRRT* runs exactly like sequential RRT* and hence is asymptotically optimal.

Next, let us consider PRRT* running with multiple threads and without partitioning. Each of the p threads is operating independently on a shared RRT* graph. Each thread begins its computation by observing the size n_t of the current graph and ends an iteration adding a configuration to the graph that is of size $n_t^{\prime }$. When a single thread is running, $n_t^{\prime }=n_t$. When multiple threads are running concurrently, $n_t^{\prime }\ge n_t$ due to updates from other threads. Since the ball radius used in iteration t is based on n_t, as t increases and the ball radius shrinks, each thread is operating with a ball radius greater than or equal to what is necessary for asymptotic optimality according to the proofs from RRT* [2]. Thus it follows from the proof of asymptotic optimality of RRT* [2] that PRRT* when running without partitioning is asymptotically optimal.

Finally, let us consider PRRT* running with multiple threads and with partitioning. The impact of partitioning on the sampling distribution is that (1) PRRT* samples uniformly in independent static partitions rather than globally, and (2) each partition (due to the nature of the underlying planning problem) may sample at a different rate. If all threads sample their partition at the same rate, the sampling distribution of the entire space, in the limit, is uniform. We will denote this RRT* graph resulting from these samples at iteration t as G_t. If the sampling rate differs between threads, then we can consider G_t as the graph that results from running all the threads at the sampling rate of the slowest thread. Samples added by the threads with a faster sampling rate result in a graph $G_t^{\prime }$ that is a superset of G_t. The rewiring step of PRRT* guarantees that the quality of plans found on $n_t^{\prime }$ are at least as good as the plans found on G_t. If the ball radius of PRRT* is thus defined to guarantee asymptotic optimality of the slowest thread’s partition, we guarantee asymptotic optimality of G_t as t increases. The graph $n_t^{\prime }$, as a superset, is thus also guaranteed to be asymptotically optimal as t increases. Hence, PRRT* carries the same asymptotic optimality guarantee as RRT*.

VI. Results

We evaluate our method with five scenarios: (1) PRRT on the Alpha Puzzle scenario, (2) PRRT on a 10,000 random spheres scenario, (3) PRRT* on the Cubicles scenario, (4) PRRT* on a holonomic disc-shaped robot moving in a planar environment, and (5) PRRT* on an Aldebaran Nao small humanoid robot performing a 2-handed task using 10 DOF. Results are computed on a system with four Intel x7550 2.0GHz 8-core Nehalem-EX processors for a total of 32 cores. Each processor has an 18MB shared L3 cache and each core has a private 256KB L2 cache as well as 32KB L1 data and instruction caches.

A. PRRT on the Alpha Puzzle Scenario

The Alpha Puzzle scenario [33] is a motion planning problem containing a narrow passage in the configuration space. The puzzle consists of two tubes, each twisted into an alpha shape. The objective is to separate the intertwined tubes, where one tube is considered a stationary obstacle and the other tube is the moving object (robot), as shown in Fig. 2. We specifically use the Alpha 1.2 variant included in OMPL [5], where different variants scale the size of the narrow passage (with smaller numbers being more difficult to solve).

Fig. 2.

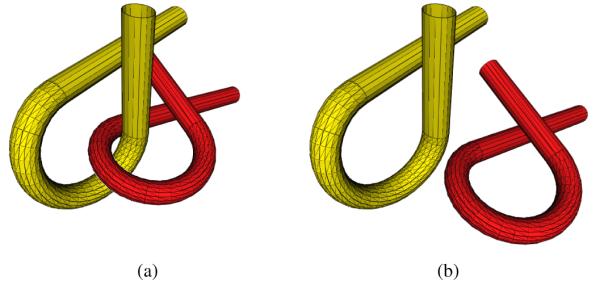
The Alpha 1.2 scenario. The yellow alpha is the obstacle, and the red alpha is the robot in SE(3). The robot must move from inside the obstacle (a) to outside the obstacle (b) by sliding through the narrow passage at an appropriate orientation.

Using the Alpha 1.2 scenario, we evaluate PRRT’s ability to speed up computation as the number of available CPU cores rises. We note that there has been much work on developing sampling strategies that improve RRT’s ability to solve the Alpha Puzzle scenario quickly—we however used the standard uniform sampling (with and without partitioning) to demonstrate the multicore performance of PRRT. As with other RRT variants, customized sampling strategies could be used with PRRT (with and without partitioning) to obtain results even more quickly. We evaluated PRRT (for both slice and grid-based partitioning) on different numbers of processor cores up to 32. For each core count, we ran 500 trials. We also consider PRRT with lock-free data structures but without partition-based sampling. We plot the median computation times and speedups in Fig. 3(a) and (b), respectively. For comparison, we include results from multi-threaded locked variants of RRT in which each thread independently samples and computes feasibility, but the shared kd-tree is locked either at the tree level (“coarse-grain locking”) or at the node level (“fine-grain locking”). We also compare to the multi-tree OR parallel RRT in which each thread creates its own tree and all threads stop as soon any find a solution [8].

Fig. 3.

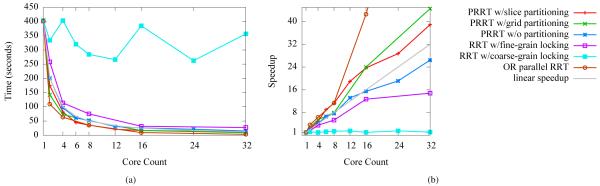
Performance of PRRT and related methods run on the Alpha Puzzle scenario. PRRT finds a solution with superlinear speedup with respect to the number of processor cores. PRRT without partition-based sampling finds solutions with a slightly sublinear speedup but good scalability. In contrast, RRT using a locked kd-tree does not scale as well. Coarse-grain locking causes too much lock-contention, and fine-grain avoids some lock-contention but adds the overhead of repeated locking. For this scenario, the multi-tree OR parallel RRT acheives greater speedups than accelerating the construction of a single tree.

As shown in Fig. 3, PRRT achieves a superlinear speedup for the Alpha 1.2 scenario for all processor counts. PRRT’s speedup for 32 cores was 39.4x. PRRT without partitioning achieves sublinear speedup, but due to the lock-free data structures still scales well as the number of cores rises. In contrast, RRT with a locked nearest neighbor data structure scales poorly; lock contention is very high due to the large number of configuration samples necessary to solve this motion planning problem. PRRT’s use of lock-free data structures and partitioning enable a superlinear speedup for the Alpha 1.2 scenario on the multicore computer. OR parallel RRT performs best on this scenario, which requires creating samples inside a short, narrow passage. We hypothesize that the independence of the RRT’s in OR parallel RRT facilitates landing the critical samples inside the short, narrow passage, and hence is better for this scenario than an approach that accelerates construction of a single RRT.

B. PRRT on 6-DOF, 10,000 Random Spheres

We apply PRRT and related methods to a random spheres scenario in which a holonomic spherical robot must navigate through an obstacle course of 10,000 randomly placed spheres in 6-dimensional C-space. The objective for the robot is to navigate from the center of the C-space to a corner while avoiding collision with the obstacles. The problem does not have a single difficult narrow passage like the Alpha problem, but the problem is still difficult because solutions necessarily have many segments.

In the random spheres scenario, OR parallel RRT does not perform as well as in the Alpha Puzzle scenario, likely because this scenario does not include a short, narrow passage requiring a “lucky” few samples to solve. In contrast, PRRT scales well with additional cores, which allow it to rapidly generate configuration samples and make progress towards the goal. The results are plotted in Fig. 4.

Fig. 4.

PRRT and related methods run on the 6-DOF random spheres scenario. PRRT scales well with additional cores, which allow it to rapidly generate configuration samples and make progress towards the goal.

C. PRRT* on the Cubicles Scenario

The Cubicles scenario, included in OMPL [5], is a motion planning problem in which an “L”-shaped robot must move in SE(3) through a 2-story office-like environment. As shown in Fig. 5, to move from the start pose to the goal pose, the robot must find a path through SE(3) that includes traveling through a different floor. For computing path cost, we use OMPL’s configuration space distance metric that sums the weighted spatial and orientation components. The objective is to compute a feasible path from the start pose to the goal pose that minimizes path cost.

Fig. 5.

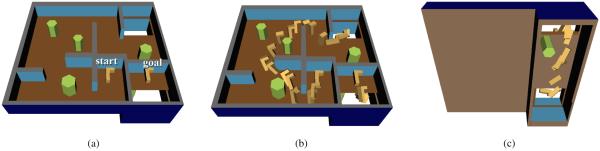
We evaluate PRRT* on the Cubicles scenario. The “L”-shaped robot must move from its start pose on one side of a wall to the goal pose on the other side of the wall by moving through a lower floor (a). We illustrate an example path produced with 50,000 configurations (b, c).

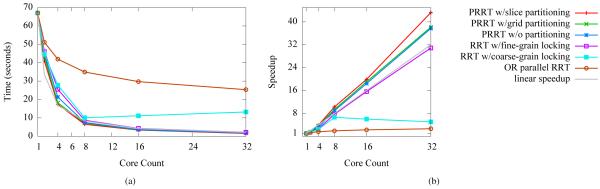
Using the Cubicles scenario, we evaluate PRRT*’s ability to speed up computation as the number of available CPU cores rises. We evaluated PRRT* with and without partition-based sampling on different numbers of processor cores up to 32. For each core count, we ran 100 trials of each method, generating trees with 50,000 configurations in each trial. We plot the median computation times and speedups in Fig. 6(a) and (b), respectively. For comparison, as with RRT, we compare against multi-threaded locked variants of RRT*. In the locked-RRT* fine-grain variant, access to the kd-tree and the rewiring updates of the tree are locked at the node (i.e. configuration) level—at most times multiple locks must be acquired to guarantee only one thread is updating a portion of the graph at any given moment, and locks are always acquired in the same order to avoid deadlock. We also compare against a multi-threaded “OR” parallel RRT*, in which each thread computes an independent RRT* graph, and the final computed path is the one with the minimum cost selected from all graphs.

Fig. 6.

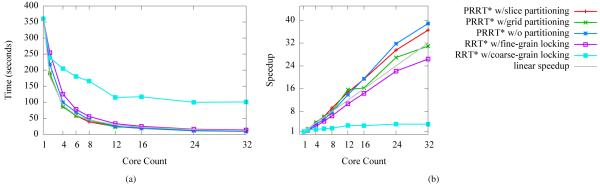
Performance of PRRT* and related methods run to 50,000 configurations on the Cubicles scenario. PRRT* without partitioning and with slice partitioning both achieve superlinear speedups with respect to the number of processor cores. PRRT* with grid partitioning suffers in performance as some cores are confined to sampling inside partitions that are disconnected by obstacles from the start and goal. RRT* with a locked kd-tree nearest neighbor data structure scales poorly due to lock contention.

PRRT* with slice partitioning and PRRT* without partitioning achieve superlinear speedup on the Cubicles scenario. On 32 cores, PRRT* with slice partitioning achieves a speedup of 36.6x and PRRT* without partitioning achieves a speedup of 38.9x. All methods achieved median solution path costs that are within 1% of one another, indicating that parallelization and partitioning do not significantly affect path quality when the size of the tree (50,000 configurations in this case) is held constant. In this scenario, PRRT* with grid partitioning does not perform as well as other PRRT* variants because some of the threads sample in partitions that are unreachable (i.e., the space on the left of Fig. 5(c)) from the start and goal configurations. At 32 cores, grid partitioning allocates 8 cores to partitions entirely in the unreachable space. PRRT* performs substantially better than RRT* with a locked kd-tree for nearest neighbor searching, which achieved sublinear speedup for both fine and coarse grain locking due to lock overhead and contention.

D. PRRT* for a 2D Holonomic Disc-shaped Robot

We executed PRRT* for a 2D holonomic disc-shaped robot that must move to the goal in the environment shown in Fig. 1(a). We executed RRT* on 1 core and PRRT* on 4 and 32 cores for 10 ms of wall clock time. The quality of paths is shown visually in Fig. 1 and quantitatively in Fig. 7. With more cores, the size of the constructed tree in the 10 ms increases substantially, visibly improving the quality of the computed motion plan. More space is explored and more narrow passages are discovered.

Fig. 7.

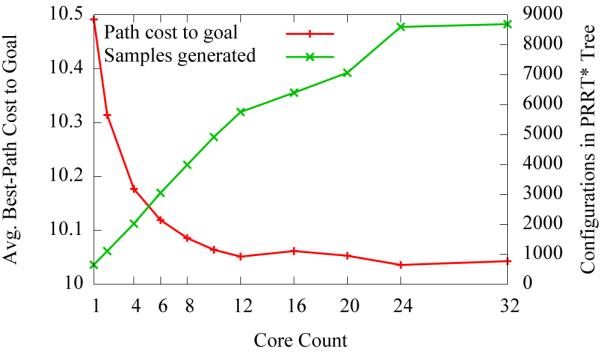
PRRT* run for 10 ms on the 2D holonomic disc-shape robot scenario. PRRT* generates more samples, and produces a better quality solution with more cores, even in this short time interval.

As stated in section I, the focus of PRRT and PRRT* is on challenging scenarios requiring tens or hundreds of thousands of samples, and this 10 ms scenario does not fall into that category. In Fig. 7, we see that as we add more cores above 12, PRRT* begins to show a diminishing return on samples generated and quality of solution due to several factors: (1) the PRRT* tree grows faster thus causing the per-query time for nearest neighbor to also increase, (2) PRRT* is rapidly converging towards the optimal solution, and (3) 10 ms is a short enough interval that we observe the overhead of startup. In the early growth of the roadmap, where the number of samples n is small, as we add more cores p, the expected contention rises (lim_p→∞ O(p/n) = ∞). As we show in Sec. VI-E, the PRRT* startup overhead quickly disappears with additional computation time. We also note that this 10 ms scenario performs well for current readily available multicore systems (typically in the range of 2–12 cores), producing the significant and visible improvements shown in Fig. 1.

E. PRRT* for a 2-handed Aldebaran Nao 10 DOF Task

We evaluated PRRT* on an Aldebaran Nao small humanoid robot [34] with the task of dropping an object held in one hand into a cup held in the other hand while avoiding obstacles. Each arm of the Nao robot has 5 degrees of freedom (shoulder pitch/roll, elbow yaw/roll and wrist yaw), resulting in a 10 dimensional configuration space for this problem. All joints are bounded revolute joints, and we define COST as a Euclidean distance in configuration space. The robot must avoid obstacles on the table in front of it while keeping the cup upright throughout its motion—i.e. the function FEASIBLE tests if the robot will collide with objects in the environment and also tests if the robot’s joint angles will result in the cup being upright subject to a tolerance. We define GOAL to return true for configurations that satisfy the following constraints within a tolerance: (1) the (x, y) coordinates for the left hand and the right hand are the same, (2) the left hand’s z coordinate is higher than the right hand, (3) the object in the left hand is pointing down, and (4) the cup in the right hand is held upright. We show the Nao robot using PRRT* successfully performing the task in Fig. 8.

Fig. 8.

An example PRRT* motion plan created for the Aldebaran Nao robot. The robot carries an effervescent antacid in one hand and places it over a glass of water held in the other hand, all while avoiding the bottles on the table and not spilling the water (i.e. FEASIBLE is constrained to keep the glass mostly level). In the last frame, after the robot reaches the goal configuration, it drops the antacid into the water.

To demonstrate PRRT*’s ability to compute high quality solutions faster on multiple cores, we executed the Nao 10 DOF task for n = 100, 000 configurations with varying core counts and averaging over 10 runs. As shown in Fig. 9, we observe superlinear speedup with PRRT*. Executing PRRT* on 1 core (thus making it equivalent to standard RRT*) requires 420 seconds. On 32 cores, PRRT* required only 11.6 seconds for the same number of samples. PRRT* was 36x faster with no significant difference in the quality of the computed paths.

Fig. 9.

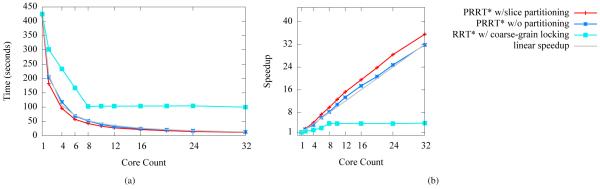
Performance of PRRT* and related methods run on the Nao 10 DOF task for 100,000 configurations. PRRT* achieves superlinear speedups with respect to the number of processor cores. In contrast, RRT* with a course-grain locked kd-tree nearest neighbor data structure cannot exceed 4x speedup due to lock contention.

The use of lock-free data structures and partitioning in PRRT* both have an impact on performance. PRRT* without partition-based sampling performed slightly worse than PRRT*, achieving approximately a linear speedup as shown in Fig. 9. We also executed RRT* parallelized by locking the kd-tree. At 100,000 configurations, nearest neighbor searches dominate the computation time, so threads spend most of their time waiting for access to the kd-tree when using locks. Consequently, the lock-based approach cannot exceed 4x speedup.

In Fig. 10, we plot the average time for PRRT* and RRT* variants to reach a prespecified target path cost. In this experiment we see that PRRT* with and without partitioned sampling consistently outperforms the lock-based and OR parallel RRT* versions by at least a factor of 1.7x.

Fig. 10.

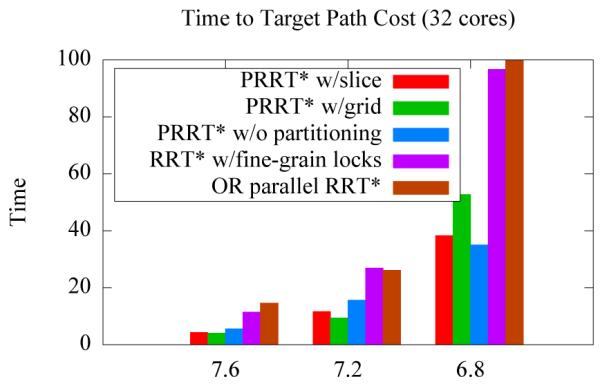
We give PRRT* and RRT* variants a specified target path cost and show the time it takes to reach the target in the Nao scenario. In this graph we also include OR parallel RRT*, a multi-tree RRT* in which 32 RRT* trees are built in parallel and the best result is chosen from among them. For target path cost 6.8, OR parallel RRT* exceeded the allotted time and is plotted only to 100 seconds. We do not include the coarse-grained locking in this graph—in all cases it exceeded the allotted time.

We note that the relative performance of motion planning using lock-free and lock-based nearest neighbor searching varies with the size of the motion planning tree τ . When the size of the tree τ is smaller, collision-detection dominates computation time and the lock-based approach achieves a more reasonable speedup. At 2,000 samples on 32 cores, we observe a 16.4x speedup with locked kd-trees, although PRRT* still outperforms with a 28.9x speedup. The locked version’s speedup diminishes as more samples are added, as shown in Fig. 11. In contrast, the lock-free PRRT* overcomes thread startup overhead and reaches 32x speedup by the 20,000th configuration before increasing to 36x speedup by 100,000 configurations.

Fig. 11.

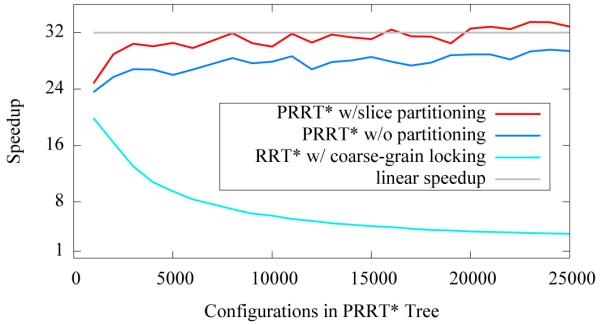
PRRT* running on 32 cores overcomes startup overhead and speedup increases as the number of configurations increases. In contrast, using a locked nearest neighbor structure shows good speedup initially, but as the number of configurations increases, contention over locked data structures slows the algorithm down.

To demonstrate how PRRT* can be used to produce better results per unit time, we also ran the Nao 10 DOF task 50 times for 3 seconds at various processor core counts. As shown in Fig. 12, increasing the number of processor cores enables us to build trees with more samples per second and find better solutions. The path cost from the initial configuration to the goal shows convergence to an optimal solution as the number of samples increases, as expected with RRT*. In contrast to the 10 ms runs for the holonomic disc-shaped robot, in these 3-second runs for the Nao robot the impact of startup overhead is no longer significant and we see the number of samples generated scale well with the number of cores. We also observed that RRT* would find paths to the goal in only 80% of the 3-second runs on 1 core. With 2 cores, PRRT* found solutions in 98% of the runs. At higher core counts, PRRT* found solutions in all runs.

Fig. 12.

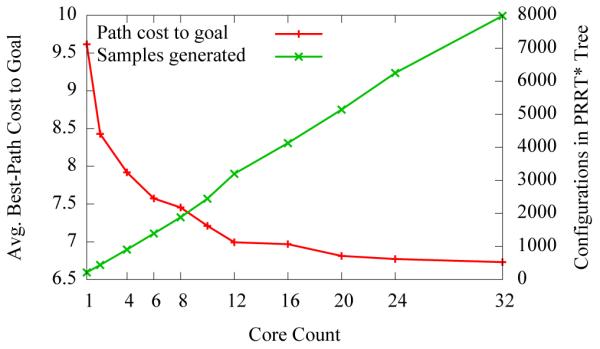
PRRT* run for 3 seconds on the Nao 10 DOF task. Increasing the number of processor cores results in samples being generated at a higher rate and better quality solutions.

VII. Conclusion

We presented PRRT (Parallel RRT) and PRRT* (Parallel RRT*), single-tree sampling-based methods for feasible and optimal motion planning that are tailored to execute on modern multicore CPUs. Using atomic updates and lock-free data structures, PRRT and PRRT* remove barriers to scaling to higher processor core counts. We further observe that using a non-overlapping partition-based sampling strategy increases cache efficiency by localizing each thread’s computation to a region of memory. While not guaranteed, we empirically observed that these contributions enable PRRT and PRRT* in some scenarios to achieve superlinear speedup.

Our method is best suited for challenging motion planning problems in which a large number of samples is required to find a feasible or near optimal solution. As the number of samples increases, computation time gradually changes from being dominated by collision detection to being dominated by nearest neighbor search. PRRT and PRRT* parallelize the entire computation of the motion planning tree and thus maintain speedup ratios regardless of which portion of the computation is dominating. We demonstrated fast performance and significant speedups in 5 scenarios including the Alpha Puzzle and Cubicles scenarios and an Aldebaran Nao small humanoid robot performing a 2-handed, 10 DOF task.

In ongoing and future work we would like to adapt PRRT and PRRT* to other commonly-available hardware architectures and new applications. Some computing architectures provide hardware support for simultaneous multithreading (SMT)—running two or more threads simultaneously within each core by sharing cache and execution units within the core. Additional speedups may be achievable by scheduling such threads in a manner that coordinates with the partitioning scheme. The static partitioning in our implementation, while having an impact on many real-world level problems, does not produces a sustainable cache-locality in the limit. Eventually, the cache-benefit of the static partitioned locality will run out. Other work in the field of cache-aware and cacheoblivious algorithms (e.g. [35], [36]) has shown how to create a sustained cache-based performance improvement, regardless of problem size. More sophisticated partitioning approaches, such as approaches that focus sampling on regions of difficulty, could potentially by used with PRRT and PRRT* to provide both the benefits of improved partitioned sampling and of localizing computations to better fit in a core’s cache. We also plan to investigate adapting the algorithmic approaches of PRRT and PRRT* to applications in dynamic environments and other challenging scenarios. Included in this investigation will be reducing the overhead associated with startup to allow PRRT and PRRT* to make more effective use of additional cores in shorter time periods. The speedups gained through utilizing existing and readily available multicore concurrency in conjunction with lock-free data structures could enable new robotic applications in scenarios that are currently considered too computationally expensive when run in a single thread or using lock-based data structures.

Biographies

Jeffrey Ichnowski received his B.A. degrees in Computer Science and Asian Studies with honors from the University of California, Berkeley, CA in 1998. He since has had a successful career as a founder, engineer, architect, and technical advisor in software-as-a-service (SaaS) startups and enterprises. He has received several patents related to SaaS architecture, and is an active contributor to open-source projects. In 2010, he joined the Department of Computer Science at the University of North Carolina at Chapel Hill, NC, where, as a Ph.D. candidate, his research focus is on high-performance computing in robot motion planning algorithms.

Ron Alterovitz received his B.S. degree with Honors from Caltech, Pasadena, CA in 2001 and the Ph.D. degree in Industrial Engineering and Operations Research at the University of California, Berkeley, CA in 2006.

In 2009, he joined the faculty of the Department of Computer Science at the University of North Carolina at Chapel Hill, NC, where he leads the Computational Robotics Research Group. His research focuses on motion planning for medical and assistive robots. Prof. Alterovitz has co-authored a book on Motion Planning in Medicine, was awarded a patent for a medical device, has received multiple best paper finalist awards at IEEE robotics conferences, and is the recipient of the NIH Ruth L. Kirschstein National Research Service Award and the NSF CAREER Award.