Abstract
A natural way to study protein sequence, structure, and function is to put them in the context of evolution. Homologs inherit similarities from their common ancestor, while analogs converge to similar structures due to a limited number of energetically favorable ways to pack secondary structural elements. Using novel strategies, we previously assembled two reliable databases of homologs and analogs. In this study, we compare these two data sets and develop a support vector machine (SVM)-based classifier to discriminate between homologs and analogs. The classifier uses a number of well-known similarity scores. We observe that although both structure scores and sequence scores contribute to SVM performance, profile sequence scores computed based on structural alignments are the best discriminators between remote homologs and structural analogs. We apply our classifier to a representative set from the expert-constructed database, Structural Classification of Proteins (SCOP). The SVM classifier recovers 76% of the remote homologs defined as domains in the same SCOP superfamily but from different families. More importantly, we also detect and discuss interesting homologous relationships between SCOP domains from different superfamilies, folds, and even classes.
Keywords: homology, analogy, discrimination, protein structures, support vector machines
Introduction
Three-dimensional structural similarities among proteins are explained by either divergence or convergence. In divergent evolution, homologs inherit similar structures from their common ancestor. In convergent evolution, proteins from distinct evolutionary lineages arrive independently at similar structures due to a limited number of energetically favorable ways to pack secondary structural elements (SSEs),1–3 and such proteins are called analogs. Judging if two structurally similar proteins are homologous or analogous remains a difficult task. Statistically significant sequence similarity, as detected by sequence search tools such as PSI-BLAST,4 is generally accepted as adequate evidence for homology.5,6 In the absence of significant sequence similarity, remote homology inference can be based on overall structural similarity, augmented by other properties such as similar arrangements of functional residues, common ligand-binding modes, shared unusual structural features, and similar domain organizations.7,8 However, capturing these features often requires visual inspection by human experts and is more in the realm of art than science.
The Structural Classification of Proteins (SCOP) database9 represents a comprehensive collection of manually curated homologous superfamilies of protein domains with known structures. In the SCOP hierarchy, domains with significant sequence similarity or overwhelming structural and functional similarity (close homologs) are grouped into the same family; families with convincing structural and/or functional evidence for common ancestry are grouped into the same superfamily; superfamilies with the same overall three-dimensional structure and topology but without very strong evidence for homology are grouped into the same fold; and folds are grouped into classes based on their SSE compositions. SCOP is manually maintained by human experts, and its superfamily level is regarded as the most reliable standard for remote homologs.10
Several efforts have been made to discern the boundary between homology and analogy in an automated and quantitative way. Russell et al.11 statistically analyzed structurally aligned homologous and analogous pairs and found that homologs generally retain higher sequence identity, more conserved SSEs, and solvent accessibility compared to analogs. Matsuo and Bryant12 defined a homologous core structure representing the consensus substructure in a protein family, and used the overlap of homologous core structure to distinguish homologs and analogs. Dietmann and Holm13 trained a neural network to discriminate homologs and analogs based on sequence, structure, and functional similarities. All three studies used domains in the same SCOP superfamily as homologs and domains in different SCOP superfamilies as analogs in their analysis. Given the conservative nature of the SCOP hierarchy, a potential flaw of this approach is the contamination of the analog data set by homologs. Domains in different superfamilies are not necessarily analogs and may in fact be homologous when new evidence emerges.9 For instance, through careful analysis, Ponting and Russell14 suggested that at least five SCOP superfamilies under the β-trefoil fold were actually homologous and had descended from a common ancestor.
To avoid the aforementioned ambiguity, we approach the problem of discriminating between homologs and analogs with more clear-cut and reliable data sets. Previously, we manually constructed a homolog database (MALIDUP15) composed of duplicated domain pairs and an analog database (MALISAM16) composed of three categories of analogous pairs (a hybrid motif and a core motif, an interface motif and a core motif, and an artificial protein and a natural protein). Each pair in MALIDUP or MALISAM is carefully inspected to convincingly support homology or analogy and then manually superimposed and aligned to ensure good alignment quality. In this study, we use pairs from these two databases as reliable homologs and analogs to understand the differences as well as to develop a discriminator between homology and structural analogy.
We first characterize and compare the MALIDUP and MALISAM pairs in terms of structure, sequence, and profile scores. Combining these scores, we train support vector machines (SVMs) to discriminate between the homologs in MALIDUP and the analogs in MALISAM. Since MALIDUP and MALISAM are quite small in size and may not be representative of the total protein variety found in nature, we test the resulting SVM-based classifier on the comprehensive SCOP database. We show that although the classifier is trained on the manually constructed data sets with particular statistical properties, it can recover the majority of distant homologs classified in the same SCOP superfamily but different families. Moreover, the classifier is capable of finding more distantly related pairs between SCOP superfamilies, folds, and classes. We discuss some of these interesting pairs and argue that many of them indeed represent remote homologs.
Results and Discussion
Comparison of homologs and analogs in the manually constructed data sets
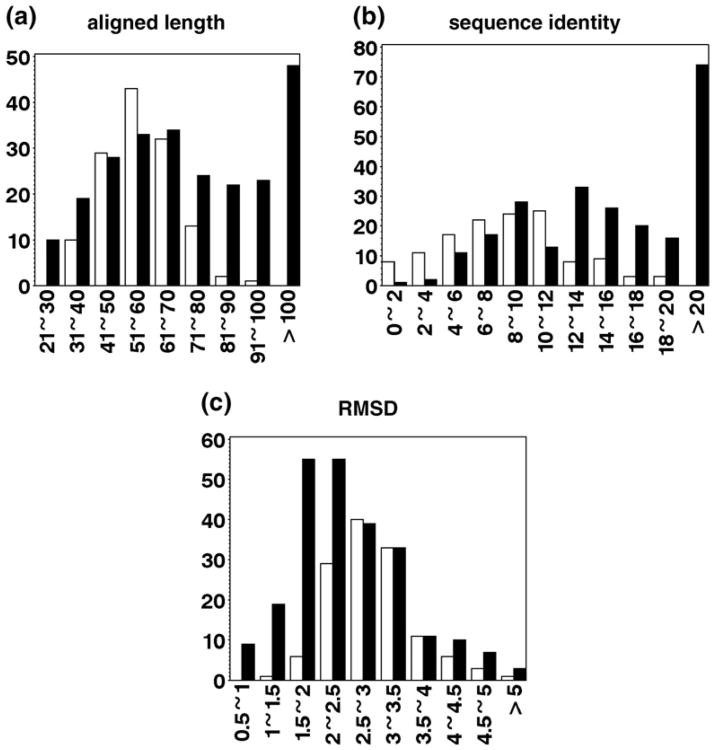
To better understand the differences between homology and analogy, we compare the homologous pairs in MALIDUP and the analogous pairs in MALISAM in terms of aligned length, sequence identity, and RMSD of structure superposition (Fig. 1). Apparently, MALIDUP includes more pairs with longer alignments, higher sequence identity, or lower RMSD. To focus on the differences between remote homologs and structural analogs as well as to obtain balanced data sets for developing the classifier, we partitioned MALIDUP and MALISAM into three nonoverlapping data sets: “close,” “comparable,” and “remaining” (summarized in Table 1). The “close” data set consists of similar MALIDUP pairs and is used as a positive control to monitor the classifier's performance on relatively close homologs. Pairs that do not belong to “close” form a data set called “remote” and have average sequence identity in the “twilight zone” (0–20%). The “remote” data set is further partitioned into “comparable” and “remaining.” The “comparable” data set, in which homologous and analogous pairs possess comparable aligned length and sequence identity, serves as the most challenging set in developing the classifier (see Methods for details in partitioning the data sets).
Fig. 1.
Aligned length, sequence identity, and RMSD distributions of the manually prepared homologs and analogs. (a) Aligned length in number of residues. (b) Sequence identity in percent. (c) RMSD in angstroms. In all three histograms, filled bars represent homologous pairs and open bars represent analogous pairs. The horizontal axis shows the range of each bin and the vertical axis shows the number of pairs that fall into each bin.
Table 1. Summary of the manually constructed data sets.
| No. of pairs | Aligned length (amino acids) | Average identity (%) | Average RMSD (Å) | |||||
|---|---|---|---|---|---|---|---|---|
|
|
|
|
|
|||||
| Data set | Homologs | Analogs | Homologs | Analogs | Homologs | Analogs | Homologs | Analogs |
| Close | 111 | 0 | 91/101 | N/A | 24.9/23.6 | N/A | 2.2/2.2 | N/A |
| Remote | 130 | 130 | 67/72 | 57/57 | 12.1/11.5 | 8.5/8.1 | 2.7/2.7 | 2.9/2.8 |
| Comparable | 65 | 65 | 58/62 | 58/59 | 10.1/9.8 | 10.1/9.5 | 2.6/2.7 | 2.9/2.8 |
| Remaining | 65 | 65 | 77/83 | 56/56 | 14.1/13.2 | 7.0/6.8 | 2.8/2.8 | 3.0/2.8 |
Numbers before the slashes are based on manual alignments, while numbers after the slashes are based on DALI alignments.
To characterize a homologous or analogous pair, we compute 13 scores based on the manual structural alignment. These scores represent four major score types that are developed in computational studies of proteins: pairwise sequence scores (comparing two single sequences), profile sequence scores (comparing two multiple sequence alignments), intramolecule structure scores (comparing corresponding Cα–Cα distances within the two domains), and intermolecule structure scores (measuring interdomain distances between corresponding Cα atoms in the structural superposition). In addition to these structural-alignment-based scores, each pair is aligned and scored regardless of the structures by the sequence profile comparison program, HHsearch.17 Inclusion of this HHsearch score is intended to detect sequence motifs that frequently reside in loop regions. In remote homologs, such loop regions often assume variable conformations and tend to be ignored or misaligned in structural alignments. See Methods and Appendix A for details in score calculations.
Using the manually constructed data sets (Table 1), we study different scores' ability to discriminate between remote homologs and structural analogs. For an individual score, one can measure this ability by its “separation parameter” as well as its performance as a single-score classifier. Separation parameter measures the distance between the centers of the score distributions of homologs and analogs. A single-score classifier predicts a pair as homologous if the pair's score is above a predefined threshold, or as nonhomologous if its score is below that threshold (see Table 3 legend for details). As shown in Table 3, profile sequence scores (compass-like, correl, and HHsearch) have better separations than pairwise sequence scores or structure scores and are more effective as single-score classifiers. The compass-like score, which is a profile score calculated on structure-based alignments, displays the largest separation parameter and the highest accuracy on the difficult set “comparable” when used as a single-score classifier.
Table 3. Each individual score's separation parameter and performance as a one-score classifier.
| Score | Type | Separationa | Optimal thresholdb | Accuracy (%) | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
|
| ||||||||||
| Remaining | Comparable | Close | SF | FD | CL | RT | ||||
| Dali | Intra | 0.42 | 0.75 | 67.69 | 70.00 | 73.87 | 24.60 | 93.18 | 90.04 | 92.15 |
| Daliz | Intra | 0.36 | 0.52 | 70.77 | 63.08 | 71.17 | 20.87 | 95.57 | 97.35 | 98.55 |
| GDT_S | Inter | 0.28 | 0.66 | 66.92 | 63.08 | 67.57 | 12.95 | 96.35 | 98.99 | 99.36 |
| TM score | Inter | 0.42 | 0.56 | 74.62 | 63.08 | 83.78 | 69.96 | 54.92 | 96.67 | 99.59 |
| RMSD | Inter | 0.38 | 0.77 | 70.00 | 60.00 | 86.49 | 59.02 | 77.08 | 96.31 | 98.32 |
| AHM | Inter | 0.39 | 0.64 | 73.85 | 63.85 | 77.48 | 74.44 | 46.05 | 80.45 | 85.74 |
| LBa | Intra | 0.29 | 0.36 | 61.54 | 56.92 | 96.40 | 84.03 | 37.95 | 47.02 | 60.04 |
| LBb | Intra | 0.24 | 0.48 | 58.46 | 60.00 | 92.79 | 87.04 | 29.22 | 48.05 | 64.52 |
| LHM | Inter | 0.11 | 0.52 | 63.08 | 52.31 | 74.77 | 21.07 | 94.03 | 99.91 | 99.98 |
| Id | Pair | 0.41 | 0.06 | 80.00 | 51.54 | 88.29 | 46.40 | 81.42 | 86.13 | 87.44 |
| Blosum | Pair | 0.53 | 0.07 | 79.23 | 56.92 | 95.50 | 76.21 | 52.76 | 72.37 | 77.09 |
| Compass-like | Profile | 0.86 | 0.18 | 86.15 | 76.92 | 93.69 | 45.06 | 82.40 | 95.72 | 97.87 |
| Correl | Profile | 0.70 | 0.19 | 83.08 | 70.77 | 91.89 | 57.69 | 75.96 | 92.26 | 95.33 |
| HHsearch | Profile | 0.75 | 0.02 | 86.15 | 66.15 | 90.09 | 70.17 | 58.21 | 87.10 | 95.08 |
| SVM scorec | 0.93 | 0.40 | 94.62 | 76.15 | 90.99 | 75.04 | 56.59 | 80.63 | 84.01 | |
Separation of a score is calculated by the following equation: separation=(μh − μa)/(σh + σa), where μh, σh, μa, and σa are the mean and standard deviation for homologs and analogs in the “remote” data set, respectively.
The optimal threshold for a single-score classifier is found by scanning a wide range of thresholds and identifying the one at which the accuracy on “remaining” is the highest.
This is the SVM prediction score given by the final classifier.
Comparison of the manually constructed data sets with the SCOP-based data sets
We assemble four large data sets using domains from SCOP9 as a comprehensive representation of the protein world. Table 2 summarizes these four SCOP-based data sets. As the two domains in a pair differ in higher levels of the SCOP hierarchy, they share lower sequence and structure similarity: in Table 2, the average aligned length and sequence identity decrease, while the average RMSD increases from SF to RT. Many class-level (CL) or root-level (RT) pairs do not share overall structural similarity, and their alignments are limited to a couple of SSEs and reflect some local similarities that have arisen by chance.
Table 2. Summary of the SCOP-based data sets.
| Data set | Differed SCOP level | Shared SCOP level | No. of pairs | Labeled as | Average aligned length (amino acids) | Average identity (%) | Average RMSD (Å) |
|---|---|---|---|---|---|---|---|
| SF | Family | Superfamily | 6920/6323 | Homologs | 113/118 | 11.8/12.0 | 3.3/3.2 |
| FD | Superfamily | Fold | 15,416/12,380 | Nonhomologs | 96/107 | 9.0/9.2 | 3.5/3.5 |
| CL | Fold | Class | 80,599/8346 | Nonhomologs | 51/77 | 7.6/8.7 | 5.0/4.1 |
| RT | Class | Root | 202,294/2353 | Nonhomologs | 45/60 | 7.2/8.1 | 5.4/4.6 |
SF pairs are from different families but the same superfamily. FD pairs are from different superfamilies but the same fold. CL pairs are from different folds but the same class. RT pairs are from different classes but the same root. Scores are calculated based on DALI18 alignments. Numbers before the slashes are based on the whole data sets, while numbers after the slashes are based on the filtered data sets that only include pairs with DALI z-scores more than 2.
To compare the manually constructed and the SCOP-based data sets, we also align the pairs in the manually constructed data sets automatically with the DALI18 program and calculate aligned length, sequence identity, and RMSD based on the DALI alignments (shown as numbers after the slashes in Table 1). Comparing Tables 1 and 2, we observe that MALIDUP remote homologs (homologs in “remote”) are much shorter but structurally more similar than SCOP remote homologs (SF pairs). Also, the manually prepared analogs (analogs in “remote”) are close to the SCOP CL pairs in terms of average aligned length, but are much more structurally similar than the CL pairs. In general, this comparison reflects the way the manual data sets are constructed: homologs come from duplicates, which are often structural repeats, and analogs come from similar structural motifs.
The accuracies of each single-score classifier on the four SCOP-based data sets are also shown in Table 3. As mentioned above, the compass-like score displays the highest accuracy on the manually constructed data set “comparable.” However, TM score outperforms compass-like score on the SCOP-based data sets with higher accuracies on both SF and RT, indicating its good ability to discriminate between overall and sporadic structural similarities. Apparently, different scores offer varied advantages. Hence, combining these scores to obtain a better classifier on all data sets seems sensible. Meanwhile, accuracies in Table 3 serve as a baseline for evaluating the performance of the SVM classifiers obtained by combining different scores.
Development of the classifier
In developing the classifier, we first use the simplest linear SVM, then try the more complex and powerful nonlinear SVM, and last add a filter to boost the performance on the SCOP-based data sets. Based on the final classifier, a probability model is built to estimate the probability of being homologous for a pair with a certain SVM prediction score.
Performance of a classifier
The performance of a classifier is monitored by its accuracies on the manually constructed (Table 1) as well as the SCOP-based (Table 2) data sets. However, the accuracies on the four SCOP-based data sets are not equally informative when it comes to comparing the performance of various classifiers. Particularly, we usually ignore the accuracies on the fold-level (FD) and CL sets because, although these pairs are labeled as “nonhomologs,” many of them may actually be homologous. Also, since a classifier can almost always increase its accuracy on a set composed entirely of homologs (SF) by sacrificing its accuracy on a set composed entirely of nonhomologs (RT), we need to consider the accuracies on these two sets together in order to obtain balanced classifiers.
Linear SVM models
We compute 13 structural alignment-based scores as well as the HHsearch score to characterize each domain pair. However, these scores almost certainly carry redundant information. Hence, all of them may not be needed to build a good classifier. In order to find the most effective score subset, we try all the possible combinations with two or more scores. For each score combination, we train linear SVM using the procedure described in Methods. From the resulting thousands of SVM models, we select the ones with the highest performance (Model L1 to L4 in Table 4). Interestingly, these selected models are all built of only five to seven scores. This result confirms our speculation that these scores are redundant to some extent and, more important, suggests that redundant scores lead to overtraining and inferior models.
Table 4. Best classifiers.
| Scoresb and weights | Accuracy (%)c | |||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
|
|
|||||||||||||||||||||||||||
| Remainingd | Comparabled | |||||||||||||||||||||||||||
|
|
|
|||||||||||||||||||||||||||
| Model name |
Selection criteriaa |
C/gamma | Dali | Daliz | GDT_TS | TM score | RMSD | AHM | LBa | LBb | LHM | Id | Blossom | Compass-like | Correl | HHsearch | Threshold b | H | A | T | H | A | T | Close | SF | FD | CL | RT |
| L1 | a | 1/ | 0.02 | 0.31 | 0.13 | 0.09 | 0.13 | 0.32 | −0.35 | 80.0 | 86.2 | 83.1 | 66.2 | 86.2 | 76.2 | 95.5 | 68.1 | 70.8 | 97.1 | 99.5 | ||||||||
| L2 | a | 1/ | 0.31 | 0.04 | 0.12 | 0.09 | 0.13 | 0.32 | −0.35 | 78.5 | 84.6 | 81.5 | 66.2 | 86.2 | 76.2 | 95.5 | 68.3 | 70.8 | 97.2 | 99.5 | ||||||||
| L3 | a | 1/ | 0.33 | 0.13 | 0.09 | 0.13 | 0.32 | −0.36 | 80.0 | 86.2 | 83.1 | 66.2 | 87.7 | 76.9 | 95.5 | 68.7 | 69.6 | 97.1 | 99.5 | |||||||||
| L4 | a | 1/ | 0.01 | 0.30 | 0.04 | 0.12 | 0.09 | 0.13 | 0.32 | −0.34 | 78.5 | 84.6 | 81.5 | 66.2 | 86.2 | 76.2 | 95.5 | 67.9 | 71.3 | 97.2 | 99.5 | |||||||
| R1 | a | 1/.5 | 0.63 | 0.75 | 0.62 | 0.64 | 0.77 | 0.86 | 78.5 | 87.7 | 83.1 | 64.6 | 87.7 | 76.2 | 95.5 | 67.3 | 72.2 | 97.4 | 99.6 | |||||||||
| R2 | a | 1/.5 | 0.76 | 0.71 | 0.63 | 0.64 | 0.77 | 0.85 | 78.5 | 86.2 | 82.3 | 66.2 | 87.7 | 76.9 | 95.5 | 68.0 | 71.2 | 97.3 | 99.5 | |||||||||
| R3 | a | 1/.5 | 0.75 | 0.63 | 0.64 | 0.77 | 0.86 | 80.0 | 86.2 | 83.1 | 66.2 | 87.7 | 76.9 | 95.5 | 68.4 | 70.2 | 97.2 | 99.5 | ||||||||||
| LF1 | a | 1/ | 0.02 | 0.31 | 0.13 | 0.09 | 0.13 | 0.32 | −0.35 | 80.0 | 86.2 | 83.1 | 66.2 | 86.2 | 76.2 | 95.5 | 67.3 | 71.5 | 98.1 | 99.9 | ||||||||
| LF2 | a | 1/ | 0.31 | 0.04 | 0.12 | 0.09 | 0.13 | 0.32 | −0.35 | 78.5 | 84.6 | 81.5 | 66.2 | 86.2 | 76.2 | 95.5 | 67.6 | 71.4 | 98.1 | 99.9 | ||||||||
| LF3 | a | 1/ | 0.33 | 0.13 | 0.09 | 0.13 | 0.32 | −0.36 | 80.0 | 86.2 | 83.1 | 66.2 | 87.7 | 76.9 | 95.5 | 68.0 | 70.1 | 98.1 | 99.9 | |||||||||
| LF4 | a | 1/ | 0.01 | 0.30 | 0.04 | 0.12 | 0.09 | 0.13 | 0.32 | −0.34 | 78.5 | 84.6 | 81.5 | 66.2 | 86.2 | 76.2 | 95.5 | 67.2 | 71.9 | 98.2 | 99.9 | |||||||
| LF5 | a | 0.25/ | 0.08 | 0.18 | 0.15 | 0.16 | 0.42 | −0.38 | 87.7 | 76.9 | 82.3 | 81.5 | 70.8 | 76.2 | 97.3 | 68.4 | 71.3 | 97.6 | 99.9 | |||||||||
| RF1 | b | 1000/1 | 0.26 | 0.42 | 0.53 | 0.25 | 0.18 | 0.84 | 92.3 | 87.7 | 90.0 | 81.5 | 81.5 | 81.5 | 96.4 | 77.0 | 49.8 | 94.6 | 99.6 | |||||||||
| RF2 | b | 100/2 | 0.35 | 0.51 | 0.64 | 0.09 | 0.66 | 0.81 | 93.9 | 90.8 | 92.3 | 75.4 | 84.6 | 80.0 | 95.5 | 75.2 | 50.5 | 95.7 | 99.8 | |||||||||
| RF3 | b | 100/1 | 0.35 | 0.56 | 0.15 | 0.66 | 0.81 | 0.81 | 95.4 | 92.3 | 93.9 | 74.9 | 84.6 | 79.2 | 95.5 | 76.3 | 52.4 | 95.6 | 99.8 | |||||||||
A linear classifier's name begins with an “L,” while a nonlinear classifier's name begins with an “R.” If a classifier uses the filter, the second letter in its name is “F.” For a linear model, the weights and threshold b in the transformed function for z-scores are shown. For a nonlinear model, the Pearson's correlation coefficients between the SVM prediction score and each individual score used in that model are shown (correlation coefficients are calculated on the data set “remote”).
Selection criteria: a, percent accuracies on “remaining,” “comparable,” “close,” SF, and RT above 80, 76, 95, 67, and 99.5, respectively; b, percent accuracy on “remaining,” “comparable,” “close,” SF, and RT above 80, 79, 95, 75, and 99.5, respectively.
See Methods and Appendix A for the equations, abbreviations, and references of these scores.
Accuracy is defined as the percentage of the data set that is correctly classified. A pair is considered to be correctly classified if the classification agrees with its label.
In the “Remaining” or “Comparable” column, “H,” “A,” and “T” stand for “homologs,” “analogs,” and “total,” respectively.
To better understand and interpret these models, we deduce the explicit linear decision function for each model and transform the function into an equivalent function for the standard z-scores as described in Methods. In the transformed function for z-scores, the components of the weight vector indicate the relative importance of the individual scores: a score with a large weight is more influential in the decision function than a score with a small weight. Comparing the transformed decision functions in Table 4, we observe that the four high-performance linear models (L1 to L4) are very similar in terms of the scores used and their weights. In these models, the TM score measuring intermolecular structural similarity and the structure-alignment-based Pearson's correlation coefficient between sequence profiles (correl) are the most influential as they have the largest weights.
Nonlinear SVM models
Although linear SVM offers the convenience of deducing the explicit decision function, it only has limited capacity as a discriminator. To improve our classifier, we move to the more complex nonlinear SVM using the radial basis function kernel. For each of the combinations with two or more scores, we train SVM using the procedure described in Methods. From the resulting models, we select the ones with the highest performance (R1 to R3 in Table 4). Although a nonlinear model does not allow inference of the explicit decision function, we can calculate the Pearson's correlation coefficient between the SVM prediction score and each individual score used in that model in order to gain a better understanding of the model. As shown in Table 4, the three selected high-performance models (R1 to R3) are quite similar in terms of the scores used, the correlation coefficients, and the performances.
If we only consider the accuracies on the manually constructed data sets, nonlinear models perform much better than the linear ones, e.g., 1986 nonlinear models have accuracies on “remaining,” “comparable,” and “close” above 80%, 80%, and 95%, respectively, while only 172 linear models meet the same criteria. However, when we consider the accuracies on both the manual and the SCOP-based data sets, the selected nonlinear models (R1 to R3) display very similar performance as the linear models (L1 to L4). It seems that some models, especially nonlinear ones, perform well on the manual data sets but poorly on the SCOP-based data sets. We speculate that this effect is due to the different statistical properties of the manual and the SCOP-based data sets. Particularly, the RT data set has shorter aligned length and much larger RMSD than both homologs and analogs in the manually constructed data sets (Tables 1 and 2). Although most RT pairs only share limited or sporadic structural similarities involving a couple of SSEs, the aligned parts in these pairs may have similar hydrophilicity/hydrophobicity patterns resulting in high sequence profile scores. Since the SVM models are trained on pairs with global structural similarity, they may not be applicable to alignments involving only local similarity. To approach the problem of discriminating between globally similar and dissimilar proteins, we impose a filter to remove pairs lacking overall structural similarity. Because we choose the DALI program to align the pairs in the SCOP-based data sets, we simply follow the observations made by the DALI authors19 and use a DALI z-score cutoff (> 2) as the filter for global structural similarity.
Classifiers with the filter
We add the “DALI z-score above 2” filter before each SVM model and recalculate the accuracies as described in Methods. Based on the recalculated accuracies, we reselect the best linear classifiers (LF1 to LF5 in Table 4) and the best nonlinear classifiers (RF1 to RF3 in Table 4). LF1 to LF4 are actually the same models as L1 to L4. Comparing their performances on the SCOP-based data sets with and without filtering, we see that filtering decreases the accuracy of remote homology inference (accuracy on SF), but increases the accuracies on all other sets (FD, CL, and RT), making the models more conservative and probably more realistic. The best nonlinear classifiers with (RF1 to RF3) and without (R1 to R3) filtering are very different: RF1 to RF3 do not use TM score or sequence identity, and are obtained with larger C values (a larger C means a heavier penalty on training errors20). While the filter does not affect much the performance of the best linear models, it does improve the performance of the best nonlinear models on the SCOP-based data sets. We consider the nonlinear models with filtering to be our best classifiers, for they achieve the highest overall accuracy on the difficult set “comparable” as well as on the SCOP-based data sets SF and RT.
Final classifier
Out of the three nonlinear classifiers with filtering (RF1 to RF3 in Table 4), we chose RF3 as the final classifier, because it appears more conservative with the highest accuracy on the analogs in “remaining” and “comparable” and it has reasonable accuracies on SCOP-based data sets. Shown in Table 4, the Pearson's correlation coefficients between the SVM prediction score and each individual score used in this final classifier suggest that profile sequence scores (correl and HHsearch) contribute the most to discriminating homologs and analogs. The separation parameter of the SVM score between the homologs and analogs in “remote” is 0.93, larger than any individual score (Table 3).
We studied some of the pairs in the manually constructed data sets that are misclassified by the final classifier. The analogous pair that is misclassified as homologous with the highest prediction score (7.3) is composed of a de novo designed enzyme [Protein Data Bank (PDB) code 1lq721] and a natural protein (domain 1 of the bacterial polypeptide release factor RF2, PDB code 1gqe22). These two proteins are both three-helical bundles and can be aligned on 61 residues with an RMSD of 1.5 Å. In addition to considerable structural similarity, they show similar hydrophobicity/hydrophilicity patterns so that their sequence scores are quite high. For instance, HHsearch probability for this pair is 0.61, although the de novo protein's multiple sequence alignment contains only its own sequence.
The homologous pair that is misclassified as analogous with one of the lowest predictions scores (−4.3) is composed of the two barrels in the chymotrypsin-like protease, elastase (PDB code 1haz23). Despite the fact that these two barrels share the same overall structure and most likely result from a duplication event,24 they can only be aligned over 58 residues with an RMSD of 3.0 Å. Moreover, their sequence scores are very low (HHsearch probability is 0.015). Indeed, this pair is so diverged that their alignment could have a register problem.25,26 Thus, the final SVM model appears to make reasonable mistakes, and correct classification of such pairs based only on the current score set may be very difficult, if not impossible. Perhaps more scores carrying additional information (e.g., functional information) are needed to discriminate such distant homologs and similar analogs.
Probability model
To quantify the reliability of the SVM scores, we develop an empirical statistical model. As described in Methods, we estimate the probability of being homologous (p) for a pair with an SVM prediction score x as:
According to this model, at prediction score 3.5, the probability of being homologous is about 0.95. A higher prediction score corresponds to a larger likelihood for a pair to be homologous.
High-scoring pairs between SCOP classes, folds, or superfamilies
Pairs from different SCOP classes, folds, or superfamilies that are classified as homologs are sorted by their probability of being homologous, and we manually examined some pairs with high probabilities from the top of the lists. For many of them, evidence supporting homology has been published; and some of them are even classified within the same superfamily in the latest version of SCOP. Below, we discuss several typical examples of the top-scoring pairs and the performance of the final classifier.
High-scoring pairs between classes
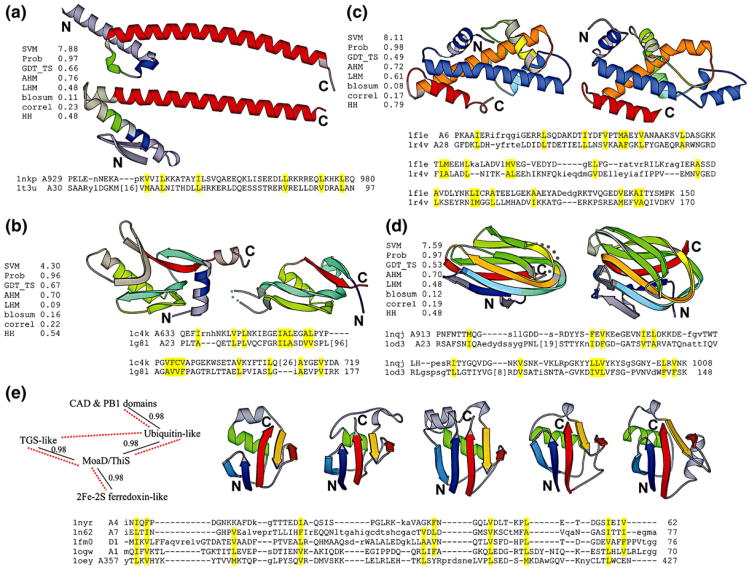
The highest-scoring pair between SCOP classes is composed of the transcription factor Myc27 and the cell-division regulator ZapA28 (Fig. 2a). SCOP classifies Myc in the all α-class and ZapA in the α+β class, respectively. Although this pair has a high prediction score (7.88, probability 0.97) as well as a reasonably high HHsearch score (probably 0.48), we suspect that this link is fortuitous because the aligned part is basically a single, although very long, helix (red in Fig. 2a). Coiled coils are known to create problems for various sequence analysis techniques and, being quite low in amino acid complexity and very similar in structure, represent a case of unclear evolutionary origin.
Fig. 2.
High-scoring pairs between SCOP classes, folds, or superfamilies. In (a–d), based on DALI alignments, aligned residues are shown in bright colors, while unaligned residues are shown in dark, grayish colors. Structurally equivalent regions are shown in the same color. The SVM prediction score, probability value, and the individual scores used in the final classifier are shown to the left of each pair. In (e), major SSEs are in bright colors, while other parts of the structures are in gray, and corresponding SSEs are in the same color. In the linkage diagram on the left, the probability values between two superfamilies are shown, and the superfamilies that are considered to be “possibly related” by SCOP are linked by red dotted lines. In all panels, each domain is colored in a spectrum from blue (N-terminus) to red (C-terminus). Discontinuous regions are represented as dotted curves. Diagrams are generated by MOLSCRIPT29. (a) Top: transcription factor Myc (PDB code 1nkp, chain A, residues 907–984). Bottom: bacterial cell division protein ZapA (PDB code 1t3u, chain A, residues 6–97). (b) Left: ornithine decarboxylase C-terminal domain (PDB code 1c4k, chain A, residues 616–730). Right: MoeA domain I (PDB code 1g8l, chain A, residues 23–53 and 139–177). (c) Left: archaeal histone (PDB code 1f1e, chain A, residues 4–154). Right: hypothetical protein Aq_328 (PDB code 1r4v, chain A, residues 21–171). (d) Left: collagenase collagen-binding domain (PDB code 1nqj, chain A, residues 909–1008). Right: carbohydrate-binding module CBM6-3 (PDB code 1od3, chain A, residues 19–149). (e) From left: threonyl-tRNA synthetase, N1 domain (PDB code 1nyr, chain A, residues 4–62); CO dehydrogenase N-terminal domain (PDB code 1n62, chain A, residues 4–77); molybdopterin synthase subunit MoaD (PDB code 1fm0, chain D, residues 1–76); ubiquitin (PDB code 1ogw, chain A, residues 1–70); PB1 domain (PDB code 1oey, chain A, residues 352–427). In each panel, DALI alignment of the diagramed structures are shown with hydrophobic positions highlighted in yellow. PDB identifiers, chain identifiers, and beginning and ending residue numbers are shown for each sequence.
Another highest-scoring pair (SVM score 4.30, probability 0.96) between classes consists of the ornithine decarboxylase C-terminal domain (OrnDC-C) and the molybdenum cofactor biosynthesis protein MoeA domain I (MoeA-I), which are classified in the α+β and the all-β SCOP classes, respectively. OrnDC-C contributes in channeling the cofactor pyridoxal-5′-phosphate,30 while MoeA-I plays an important role in MoeA dimerization31. As shown in Fig. 2b, these two domains share four β-strands and two α-helices connected as βαββαβ. (The first helix in OrnDC-C is much deteriorated.) This topology and its circular permutations are characteristic of the recently defined RAGNYA fold.32 However, unlike the RAGNYA domains, there is a deep cleft between the second (cyan) and the fourth (red) β-strands that is covered by an additional β-strand (gray) in OrnDC-C but is open in MoeA-I. Though the RAGNYA article32 mentioned neither OrnDC-C nor MoeA-I, we suggest including these two domains in the RAGNYA fold based on the shared topology. The study reporting the Escherichia coli MoeA structure31 noted that MoeA-I has the same fold as OrnDC-C based on a decent superposition (DALI z-score 4.2, RMSD 1.8 Å over 51 residues), yet evolutionary implications of this similarity were not discussed. Manual superposition and inspection reveal that although their β-sheets are both irregular and split with the cleft, these two domains can be aligned closely with few indels over almost their entire lengths. Moreover, the alignment includes unusual structural features such as β-bulges that are regarded as evidence for homology.8 Thus, we believe that they are most likely homologous.
High-scoring pairs between folds
Most of the high-scoring pairs between folds belong to the α/β class and adopt the Rossmann-like structure. Many of these links have been noticed and commented upon before. For instance, the links between the NAD(P)-binding Rossmann fold, the flavin adenine dinucleotide/NAD(P)-binding domain fold, the preATP-grasp domain fold, and the nucleotide-binding domain fold are mentioned on the SCOP Web site and in the literature.33,34
In the all-α class, the highest-scoring pair (SVM score 8.11, probability 0.98) is archaeal histone35 and hypothetical protein Aq_32836 (Fig. 2c). This homologous link has been previously reported,36,37 and in fact, the updated SCOP 1.71 moves Aq_328 to the same superfamily as the histones, thus eliminating the “hypothetical protein Aq_328” fold present in the previous SCOP version.
In the all-β class, the highest-scoring pair (SVM score 7.59, probability 0.97) is the Clostridium histolyticum class I collagenase collagen-binding domain (CBD)38 and the Clostridium stercorarium putative xylanase carbohydrate-binding module CBM6-3.39 As shown in Fig. 2d, both CBD and CBM6-3 adopt a β-sandwich structure with the so-called jelly roll topology. Although these two domains have somewhat different sheet-to-sheet packing angles, DALI aligns them with z-score 5.2 and RMSD 2.7 Å over 80 residues (83% of CBD and 61% of CBM6-3). Both CBD and CBM6-3 bind metal ions at their N-terminal region, but they use different residues to coordinate the ions. The proposed collagen-binding site in CBD and the observed sugar-binding site in CBM6-3 do not overlap, although they are located on the same side in both molecules. Thus, we are not sure if these two domains are indeed homologous. In addition, it is worth noting that the β-propeller folds with different numbers of blades are scored to be homologous by our classifier, in line with previous reports.40,41
High-scoring pairs between superfamilies
A significant fraction of the high-scoring pairs between superfamilies but within the same fold are the TIM β/α-barrels, and many of these links have been previously reported in the literature.42,43 Additionally, different superfamilies in the following SCOP folds are found to be homologous by our classifier: DNA/RNA-binding three-helical bundle, α-α superhelix, α/α toroid, immunoglobulin-like β-sandwich, β-propellers, and β-trefoil. Many of these relationships have been discussed in previous studies.14,33,44,45
The top-scoring pairs outside of these well-known examples of homology between SCOP superfamilies come from the β-grasp fold. Five superfamilies (TGS-like, 2Fe–2S ferredoxin-like, MoaD/ThiS, ubiquitin-like, and CAD and PB1 domains) in this fold are linked by single linkage with high probabilities (Fig. 2e). As shown by the representative structures of these five superfamilies in Fig. 2e, the β-grasp fold is composed of five major SSEs: four β-strands and one α-helix connected as ββαββ Ubiquitin is a highly conserved eukaryotic protein functioning as a “tag” in protein degradation.46 MoaD and ThiS are both sulfur carrier proteins involved in small-molecule biosynthesis pathways.47,48 2Fe–2S ferredoxins (also referred to as β-grasp ferredoxins) are electron transporters in photosynthesis and nitrogen fixation.49,50 TGS domain is named after three proteins [ThrRS, guanosine 5′-triphosphatase (GTPase), and SpoT] in which it is found,51 and the TGS-like superfamily is represented by the N1 domain of the threonyl-tRNA synthetase52 that may participate in the proofreading activity of this enzyme.53 CAD and PB1 domains mediate protein complex formation through heterodimerization.54,55 The evolutionary relatedness between MoaD/ThiS and ubiquitin has been convincingly argued based on structural and functional similarities.47 Using transitive PSI-BLAST, Iyer et al.56 linked MoaD/ThiS, TGS domains, and β-grasp ferredoxins. Our links between these five superfamilies agree with SCOP annotations (in Fig. 2e, the superfamilies that are considered to be “possibly related” by SCOP are linked by red dotted lines) as well as the suggestion in a recent study57 that all five-stranded β-grasp domains “form a monophyletic assemblage”.
Methods
Manually constructed data sets
The MALIDUP database contains manual structure-based alignments of 241 homologous pairs, while the MALISAM database contains 130 analogous pairs. As shown in Fig. 1, MALIDUP includes many close homologous pairs whose long aligned length, high sequence identity, or low RMSD is not matched by any analogous pairs in MALISAM. Since we are interested in discriminating remote homologs and analogs, we divide MALIDUP into two parts: 111 close homologous pairs (aligned length above 100 residues, sequence identity above 20%, or RMSD below 1.5 Å) and 130 remote homologous pairs (those that do not pass any of the above three conditions). The 111 close homologous pairs compose the data set “close,” while the 130 remote homologous pairs together with the 130 analogous pairs from MALISAM compose the data set “remote.” Furthermore, 65 homologous pairs and 65 analogous pairs that have comparable aligned lengths and sequence identities are manually selected from “remote” to form another data set called “comparable,” and the remaining 65 homologous pairs and 65 analogous pairs form the data set “remaining.” Table 1 summarizes the four manually prepared data sets.
SCOP-based data sets
Using SCOP domains in the ASTRAL58 1.69 less than 40% sequence identity set, we construct four large data sets: SF, FD, CL, and RT (summarized in Table 2). Each pair in SF consists of domains from different SCOP families but the same superfamily; each pair in FD consists of domains from different SCOP superfamilies but the same fold; each pair in CL consists of domains from different SCOP folds but the same class; and each pair in RT consists of domains from different SCOP classes. We limit ASTRAL domains to those belonging to the four major SCOP classes [all-alpha proteins, all-beta proteins, alpha and beta proteins (a/b), and alpha and beta proteins (a+b)]. From these domains, we select one structure with the best resolution from each SCOP family to serve as that family's representative and one structure with the best resolution from each SCOP fold to serve as that fold's representative. From the family representatives, we exhaustively select domain pairs for SF and FD. From the fold representatives, we exhaustively select domain pairs for CL and RT. We use the program DALI59 to align the pairs in these four SCOP-based data sets. Pairs for which DALI fails to output any alignments are discarded.
Scores
We use 13 structural alignment-based scores to characterize each pair in the manually constructed and the SCOP-based data sets. These scores belong to four different types: (1) pairwise sequence scores, including sequence identity (id) and blosum score (blosum)60; (2) profile sequence scores, including compass-like61 and Pearson's correlation coefficient (correl)62; (3) intramolecule structure scores, including DALI score (dali),18 DALI z-score (daliz),19 LiveBench contact score A (LBa),63 and Live-Bench contact score B (LBb)63; and (4) intermolecule structure scores, including TM score,64 RMSD, GDT_TS,65 alignment-based Hausdorff measure (AHM),66 and loop-based Hausdorff measure (LHM).66 For the manually constructed data sets, all 13 scores are calculated based on manual structural alignments; for the SCOP-based data sets, all 13 scores are calculated based on DALI alignments. Equations of these scores are given in Appendix A. Particularly, to calculate the profile sequence scores for a pair, we first generate a multiple-sequence alignment for each domain by running PSI-BLAST4 (-j 1, -m 6, -e 0.002, -b 5000, nr database), then align the two multiple sequence alignments of the two domains according to their structural alignment (positions that are not aligned in the structure alignment are discarded), then score the aligned columns according to the equations in Appendix A.
In addition, we run the HHsearch17,67 program for each pair. The HHsearch score using domain 1 as query and the HHsearch score using domain 2 as query are compared, and the larger one is used as the HHsearch score of the pair.
Score scaling
Since the raw scores are in different orders of magnitude, they have to be properly scaled before SVM training.68 We use the following scaling method: S =(S12 − Srandom)/(Sself − Srandom). S12 is the raw score calculated from the alignment between domain 1 and domain 2. In calculating Srandom, we circularly permute the domain 1 sequence relative to the domain 2 sequence in the alignment 10 times, reconstruct the structural superposition for each permutation, calculate the score based on the reconstructed superposition, and take the median of the resulting 10 scores as Srandom. (The Srandom for compass-like and correl is calculated in a different way.) Sself is the average of the two self scores S11 and S22, which are calculated from domain 1 aligned to itself and domain 2 aligned to itself, respectively. Since S12 generally falls between Srandom and Sself, the scaled score S generally falls between 0 and 1. Moreover, after scaling, all the scores have the same directionality: the larger the score, the higher the similarity.
SVM training
We use the SVM package SVM-light (version 6.01)†. Different subsets or combinations of the 14 scores are used to train SVM. We try all the possible score combinations with two or more scores (16,369 combinations in total). All SVM models are trained on the manually constructed data sets.
In linear SVM training, we optimize the parameter C (-c option in SVM-light) in the following steps: (1) set an appropriate initial value Cinitial and a proper multiplier m; (2) train SVM on the “remaining” data set at three C values (Cinitial/m, Cinitial, ); (3) apply the three resulting models on the “comparable” data set; (4) check the weight vector w (see the next section) of each model and change a model's accuracy on the “comparable” data set to zero if its w has negative components (This step is to avoid overfitting, because we observed that negative weights usually occurred simultaneously with overfitting69); (5) denote the C value whose model has the highest accuracy on the “comparable” data set as Coptimal; (6) if Coptimal equals Cinitial, stop and use Coptimal as the optimal C value; otherwise, use Coptimal as Cinitial and repeat the whole procedure. The model trained at the optimal C value is regarded as the optimal model given the particular score combination.
Two key parameters in nonlinear SVM training using the radial basis function kernel are C and γ68 (-c and -g options in SVM-light). Using a simple extension of the above method, we optimize the parameters C and γ in the following steps: (1) set appropriate initial values for C (Cinitial) and γ(γinitial) and proper multipliers for C (mc) and γ (mγ); (2) train SVM on “remaining” at nine (C, γ), combinations (Cinitial/mc, γinitial/mγ), (Cinitial/mc, γinitial), (Cinitial/mc, , (Cinitial, γinitial/mγ), (Cinitial, γinitial), (Cinitial, , ( , γinitial/mγ), ( , γinitial), and ; (3) apply the resulting nine models on “comparable”; (4) denote the (C, γ) combination whose model has the highest accuracy on “comparable” as (Coptimal, γoptimal); (5) if (Coptimal, γoptimal) equals (Cinitial, γinitial), stop and use (Coptimal, γoptimal) as the optimal C and γ values; otherwise, use (Coptimal, γoptimal) as (Cinitial, γinitial) and repeat the whole procedure. The model trained at the optimal C and γ values is regarded as the optimal model given the particular score combination.
Deducing and transforming the decision function of a linear SVM model
The decision function of a linear SVM model can be written as , where x, w, b, and n are the score vector, the weight vector, the threshold scalar, and the number of scores, respectively. A pair with f(x) > 0 is classified as homologous, while a pair with f(x) < 0 is classified as nonhomologous. The specific value of f(x) is called the “prediction score” in this study. The decision function can be explicitly deduced from a linear SVM model: the weight vector w can be calculated by the program “svm2weight.pl”‡, and the threshold b is specified in the model file.
If standard z-scores were used in SVM training, the components of the weight vector w in the decision function would indicate the relative importance of each individual score. However, the SVM-light package recommends that the input data be within [−1, +1], and it is also our own experience that using scaled scores instead of z-scores in SVM training usually yields better models. Therefore, we train SVM on scaled scores, deduce the decision function from the resulting model, and then transform the decision function into an equivalent function for z-scores. The following example with two scores explains how to transform the decision function. Here, x1 and x2 are the scaled scores, while z1 and z2 are their respective standard z-scores. μ1 and σ1 are the mean and standard deviation, respectively, of score 1, and μ2 and σ2 are the mean and standard deviation, respectively, of score 2.
Initial decision function of the linear SVM model:
| (1) |
Since z1 =(x1 − μ1)/σ1 and z2 =(x2 − μ2)/σ2, we have the following:
| (2) |
| (3) |
Plugging (2) and (3) into (1), we get:
which is equivalent to:
| (4) |
Defining w1z =w1σ1, w2z = w2σ2, bz = b − w1μ1 − w2μ2, we can rewrite (4) into
| (5) |
Equation (5) is the equivalent decision function for the standard z-scores: w1z and w2z are the weights for score 1 and score 2, respectively, and bz is the threshold. We use the data set SF to calculate the mean and standard deviation for each score.
Filter
To remove pairs that lack overall structural similarity, we apply the “DALI z-score above 2” filter. Pairs with DALI z-score less than or equal to 2 do not pass the filter and are automatically classified as nonhomologs. Pairs that pass the filter are classified as homologs or nonhomologs according to their prediction scores given by the SVM model. The filter is only applied to the four SCOP-based data sets. After the filter is incorporated, a classifier's accuracies are calculated as follows:
for a data set composed entirely of homologs, Accuracy = p/(p + q + f);
for a data set composed entirely of nonhomologs, Accuracy = (q + f)/(p + q + f).
Here, p is the number of pairs classified as homologs by the SVM model, q is the number of pairs classified as nonhomologs by the SVM model, and f is the number of pairs that do not pass the filter.
Probability model
Given an SVM prediction score x, we count the number of homologous pairs whose prediction scores are above x (nh) and the number of analogous pairs whose prediction scores are above x (na). Then we define p[x] = nh[x]/(nh[x] + na[x]). p[x] can be interpreted as the probability of being homologous for a pair with prediction score at least x. We plot p against x using the homologs and analogs in the manually constructed data set “remote.” The resulting curve can be mimicked by the function p = (1 + cdf[x]*r)/(1 + r), where cdf[x] is any cumulative density function, and r is the ratio of analogs to homologs. This function ensures that when x→−∞, p → 1/(1 + r), and that when x→+∞, p → 1. Taking Cauchy distribution for the cdf[x] and assuming r→+∞, we fit the curve to the following function:
where arctan is the inverse function of the tangent.
Acknowledgments
We thank Lisa Kinch for critical reading of the manuscript and helpful discussions. This work was supported by National Institutes of Health grant GM67165 and Welch foundation grant I-1505 to N.V.G.
Abbreviations used
- PDB
Protein Data Bank
- SCOP
Structural Classification of Proteins
- SSE
secondary structural element
- SVM
support vector machine
- OrnDC-C
ornithine decarboxylase C-terminal domain
- MoeA-I
molybdenum cofactor biosynthesis protein MoeA domain I
- CBD
collagen-binding domain
- CBM
carbohydrate-binding module
- AHM
alignment-based Hausdorff measure
- LHM
loop-based Hausdorff measure
Appendix A. Score Equations
Scores are organized in four groups: pairwise sequence scores, profile sequence scores, intramolecule structure scores, and intermolecule structure scores. The abbreviation we use in this study is given in the parentheses after each score name.
A.1. Pairwise sequence scores
(1) Sequence identity (id)
where Ialigned is the number of identical residue pairs in aligned positions and Laligned is the aligned length.
(2) Blosum score (blosum)
Where , are the amino acids at the ith aligned position in domain 1 and domain 2, respectively. BLOSUM62( , ) is the substitution score of and given by the blosum62 matrix.60
A.2. Profile sequence scores
In the equations for profile sequence scores, pa is the background frequency of residue a, Qa is the target frequency of residue a, and and .62
(1) COMPASS-like (compass-like)61
(2) Pearson's correlation coefficient (correl)
A.3. Intramolecule structure scores
(1) DALI score (dali)
Residue i in domain 1 and residue i in domain 2 are structurally equivalent to each other, and so are residue j in domain 1 and residue j in domain 2. d1ij and d2ij are the intramolecular Cα − Cα distances between residues i and j in domain 1 and domain 2, respectively. d*ij is the average of d1ij and d2ij. This scoring function was used in the structure superposition program DALI.18
(2) DALI z-score (daliz)
where μ = 7.95 + 0.71x + 0.00026x2 − 0.0000019x3, x=aligned length, and σ=μ/2. This equation is modified from Eqs. (3) and (4) in Ref. 19.
(3) LiveBench contact score A (LBa)
(4) LiveBench contact score B (LBb)
LBcontacta and LBcontactb were developed in the LiveBench experiments.63
A.4. Intermolecule structure scores
(1) TM score (TM score)
where di is the Cα−Cα distance of the ith aligned residue pair. d0 is a normalization factor.64
(2) Root mean square deviation (RMSD)
where di is the Cα−Cα distance of the ith aligned position in the superposition of domain 1 and domain 2.
(3) GDT_TS (GDT_TS)
where n1, n2, n4, n8 are the number of aligned residues within 1, 2, 4, and 8 Å, respectively.65
(5) Alignment-based Hausdorff measure (AHM)
(6) Loop-based Hausdorff measure (LHM)
In AHM and LHM equations, ns is the total number of aligned segments and hi is the Hausdorff distance for the ith aligned segment (in AHM) or for the ith unaligned segment (in LHM).66
Footnotes
Downloaded from http://svmlight.joachims.org/
Found in the FAQ page at http://svmlight.joachims.org/
Supplementary Material: Lists of pairs between SCOP superfamilies, folds, and classes that are classified as homologous with high scores can be accessed via the Web page http://prodata.swmed.edu/HorA/.
References
- 1.Finkelstein AV, Ptitsyn OB. Why do globular proteins fit the limited set of folding patterns? Prog Biophys Mol Biol. 1987;50:171–190. doi: 10.1016/0079-6107(87)90013-7. [DOI] [PubMed] [Google Scholar]
- 2.Krishna SS, Grishin NV. Structurally analogous proteins do exist! Structure (London) 2004;12:1125–1127. doi: 10.1016/j.str.2004.06.004. [DOI] [PubMed] [Google Scholar]
- 3.Orengo CA, Sillitoe I, Reeves G, Pearl FM. Review: what can structural classifications reveal about protein evolution? J Struct Biol. 2001;134:145–165. doi: 10.1006/jsbi.2001.4398. [DOI] [PubMed] [Google Scholar]
- 4.Altschul SF, Madden TL, Schaffer AA, Zhang J, Zhang Z, Miller W, Lipman DJ. Gapped BLAST and PSI-BLAST: a new generation of protein database search programs. Nucleic Acids Res. 1997;25:3389–3402. doi: 10.1093/nar/25.17.3389. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Doolittle RF. Similar amino acid sequences: chance or common ancestry? Science. 1981;214:149–159. doi: 10.1126/science.7280687. [DOI] [PubMed] [Google Scholar]
- 6.Doolittle RF. Similar amino acid sequences revisited. Trends Biochem Sci. 1989;14:244–245. doi: 10.1016/0968-0004(89)90055-8. [DOI] [PubMed] [Google Scholar]
- 7.Kinch LN, Grishin NV. Evolution of protein structures and functions. Curr Opin Struct Biol. 2002;12:400–408. doi: 10.1016/s0959-440x(02)00338-x. [DOI] [PubMed] [Google Scholar]
- 8.Murzin AG. How far divergent evolution goes in proteins. Curr Opin Struct Biol. 1998;8:380–387. doi: 10.1016/s0959-440x(98)80073-0. [DOI] [PubMed] [Google Scholar]
- 9.Murzin AG, Brenner SE, Hubbard T, Chothia C. SCOP: a structural classification of proteins database for the investigation of sequences and structures. J Mol Biol. 1995;247:536–540. doi: 10.1006/jmbi.1995.0159. [DOI] [PubMed] [Google Scholar]
- 10.Lichtarge O. Getting past appearances: the many-fold consequences of remote homology. Nat Struct Biol. 2001;8:918–920. doi: 10.1038/nsb1101-918. [DOI] [PubMed] [Google Scholar]
- 11.Russell RB, Saqi MA, Sayle RA, Bates PA, Sternberg MJ. Recognition of analogous and homologous protein folds: analysis of sequence and structure conservation. J Mol Biol. 1997;269:423–439. doi: 10.1006/jmbi.1997.1019. [DOI] [PubMed] [Google Scholar]
- 12.Matsuo Y, Bryant SH. Identification of homologous core structures. Proteins. 1999;35:70–79. [PubMed] [Google Scholar]
- 13.Dietmann S, Holm L. Identification of homology in protein structure classification. Nat Struct Biol. 2001;8:953–957. doi: 10.1038/nsb1101-953. [DOI] [PubMed] [Google Scholar]
- 14.Ponting CP, Russell RB. Identification of distant homologues of fibroblast growth factors suggests a common ancestor for all betatrefoil proteins. J Mol Biol. 2000;302:1041–1047. doi: 10.1006/jmbi.2000.4087. [DOI] [PubMed] [Google Scholar]
- 15.Cheng H, Kim BH, Grishin N. MALIDUP: a database of manually constructed structure alignments for duplicated domain pairs. Proteins. 2007 doi: 10.1002/prot.21783. [DOI] [PubMed] [Google Scholar]
- 16.Cheng H, Kim BH, Grishin N. MALISAM: a database of structurally analogous motifs in proteins. Nucleic Acids Res. 2008;36:D211–D217. doi: 10.1093/nar/gkm698. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Soding J. Protein homology detection by HMM–HMM comparison. Bioinformatics. 2005;21:951–960. doi: 10.1093/bioinformatics/bti125. [DOI] [PubMed] [Google Scholar]
- 18.Holm L, Sander C. Protein structure comparison by alignment of distance matrices. J Mol Biol. 1993;233:123–138. doi: 10.1006/jmbi.1993.1489. [DOI] [PubMed] [Google Scholar]
- 19.Holm L, Sander C. Dictionary of recurrent domains in protein structures. Proteins. 1998;33:88–96. doi: 10.1002/(sici)1097-0134(19981001)33:1<88::aid-prot8>3.0.co;2-h. [DOI] [PubMed] [Google Scholar]
- 20.Burges CJC. A tutorial on support vector machines for pattern recognition. Data Min Knowl Discovery. 1998;2:121–167. [Google Scholar]
- 21.Dai QH, Tommos C, Fuentes EJ, Blomberg MR, Dutton PL, Wand AJ. Structure of a de novo designed protein model of radical enzymes. J Am Chem Soc. 2002;124:10952–10953. doi: 10.1021/ja0264201. [DOI] [PubMed] [Google Scholar]
- 22.Vestergaard B, Van LB, Andersen GR, Nyborg J, Buckingham RH, Kjeldgaard M. Bacterial polypeptide release factor RF2 is structurally distinct from eukaryotic eRF1. Mol Cell. 2001;8:1375–1382. doi: 10.1016/s1097-2765(01)00415-4. [DOI] [PubMed] [Google Scholar]
- 23.Wilmouth RC, Edman K, Neutze R, Wright PA, Clifton IJ, Schneider TR, et al. X-ray snapshots of serine protease catalysis reveal a tetrahedral intermediate. Nat Struct Biol. 2001;8:689–694. doi: 10.1038/90401. [DOI] [PubMed] [Google Scholar]
- 24.McLachlan AD. Gene duplications in the structural evolution of chymotrypsin. J Mol Biol. 1979;128:49–79. doi: 10.1016/0022-2836(79)90308-5. [DOI] [PubMed] [Google Scholar]
- 25.Godzik A. The structural alignment between two proteins: is there a unique answer? Protein Sci. 1996;5:1325–1338. doi: 10.1002/pro.5560050711. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Cheng H, Grishin NV. DOM-fold: a structure with crossing loops found in DmpA, ornithine acetyltransferase, and molybdenum cofactor-binding domain. Protein Sci. 2005;14:1902–1910. doi: 10.1110/ps.051364905. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Nair SK, Burley SK. X-ray structures of Myc-Max and Mad-Max recognizing DNA. Molecular bases of regulation by proto-oncogenic transcription factors. Cell. 2003;112:193–205. doi: 10.1016/s0092-8674(02)01284-9. [DOI] [PubMed] [Google Scholar]
- 28.Low HH, Moncrieffe MC, Lowe J. The crystal structure of ZapA and its modulation of FtsZ polymerisation. J Mol Biol. 2004;341:839–852. doi: 10.1016/j.jmb.2004.05.031. [DOI] [PubMed] [Google Scholar]
- 29.Kraulis PJ. MOLSCRIPT: a program to produce both detailed and schematic plots of protein structures. J Appl Crystallogr. 1991;24:946–950. [Google Scholar]
- 30.Momany C, Ernst S, Ghosh R, Chang NL, Hackert ML. Crystallographic structure of a PLP-dependent ornithine decarboxylase from Lactobacillus 30a to 3.0 Å resolution. J Mol Biol. 1995;252:643–655. doi: 10.1006/jmbi.1995.0526. [DOI] [PubMed] [Google Scholar]
- 31.Xiang S, Nichols J, Rajagopalan KV, Schindelin H. The crystal structure of Escherichia coli MoeA and its relationship to the multifunctional protein gephyrin. Structure. 2001;9:299–310. doi: 10.1016/s0969-2126(01)00588-3. [DOI] [PubMed] [Google Scholar]
- 32.Balaji S, Aravind L. The RAGNYA fold: a novel fold with multiple topological variants found in functionally diverse nucleic acid, nucleotide and peptide-binding proteins. Nucleic Acids Res. 2007;35:5658–5671. doi: 10.1093/nar/gkm558. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Shah PK, Aloy P, Bork P, Russell RB. Structural similarity to bridge sequence space: finding new families on the bridges. Protein Sci. 2005;14:1305–1314. doi: 10.1110/ps.041187405. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Grishin NV. Fold change in evolution of protein structures. J Struct Biol. 2001;134:167–185. doi: 10.1006/jsbi.2001.4335. [DOI] [PubMed] [Google Scholar]
- 35.Fahrner RL, Cascio D, Lake JA, Slesarev A. An ancestral nuclear protein assembly: crystal structure of the Methanopyrus kandleri histone. Protein Sci. 2001;10:2002–2007. doi: 10.1110/ps.10901. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Qiu Y, Tereshko V, Kim Y, Zhang R, Collart F, Yousef M, et al. The crystal structure of Aq_328 from the hyperthermophilic bacteria Aquifex aeolicus shows an ancestral histone fold. Proteins. 2006;62:8–16. doi: 10.1002/prot.20590. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Alva V, Ammelburg M, Soding J, Lupas AN. On the origin of the histone fold. BMC Struct Biol. 2007;7:17. doi: 10.1186/1472-6807-7-17. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Wilson JJ, Matsushita O, Okabe A, Sakon J. A bacterial collagen-binding domain with novel calcium-binding motif controls domain orientation. EMBO J. 2003;22:1743–1752. doi: 10.1093/emboj/cdg172. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Boraston AB, Notenboom V, Warren RA, Kilburn DG, Rose DR, Davies G. Structure and ligand binding of carbohydrate-binding module CsCBM6-3 reveals similarities with fucose-specific lectins and “galactose-binding” domains. J Mol Biol. 2003;327:659–669. doi: 10.1016/s0022-2836(03)00152-9. [DOI] [PubMed] [Google Scholar]
- 40.Chaudhuri I, Soding J, Lupas AN. Evolution of the beta-propeller fold. Proteins. 2007 doi: 10.1002/prot.21764. [DOI] [PubMed] [Google Scholar]
- 41.Ponting CP, Pallen MJ. A beta-propeller domain within TolB. Mol Microbiol. 1999;31:739–740. doi: 10.1046/j.1365-2958.1999.01168.x. [DOI] [PubMed] [Google Scholar]
- 42.Nagano N, Orengo CA, Thornton JM. One fold with many functions: the evolutionary relationships between TIM barrel families based on their sequences, structures and functions. J Mol Biol. 2002;321:741–765. doi: 10.1016/s0022-2836(02)00649-6. [DOI] [PubMed] [Google Scholar]
- 43.Copley RR, Bork P. Homology among (betaalpha)(8) barrels: implications for the evolution of metabolic pathways. J Mol Biol. 2000;303:627–641. doi: 10.1006/jmbi.2000.4152. [DOI] [PubMed] [Google Scholar]
- 44.Aravind L, Anantharaman V, Balaji S, Babu MM, Iyer LM. The many faces of the helix–turn–helix domain: transcription regulation and beyond. FEMS Microbiol Rev. 2005;29:231–262. doi: 10.1016/j.femsre.2004.12.008. [DOI] [PubMed] [Google Scholar]
- 45.Ponting CP, Pallen MJ. Beta-propeller repeats and a PDZ domain in the tricorn protease: predicted self-compartmentalisation and C-terminal polypeptide-binding strategies of substrate selection. FEMS Microbiol Lett. 1999;179:447–451. doi: 10.1111/j.1574-6968.1999.tb08761.x. [DOI] [PubMed] [Google Scholar]
- 46.Vijay-Kumar S, Bugg CE, Wilkinson KD, Vierstra RD, Hatfield PM, Cook WJ. Comparison of the three-dimensional structures of human, yeast, and oat ubiquitin. J Biol Chem. 1987;262:6396–6399. [PubMed] [Google Scholar]
- 47.Wang C, Xi J, Begley TP, Nicholson LK. Solution structure of ThiS and implications for the evolutionary roots of ubiquitin. Nat Struct Biol. 2001;8:47–51. doi: 10.1038/83041. [DOI] [PubMed] [Google Scholar]
- 48.Rudolph MJ, Wuebbens MM, Rajagopalan KV, Schindelin H. Crystal structure of molybdopterin synthase and its evolutionary relationship to ubiquitin activation. Nat Struct Biol. 2001;8:42–46. doi: 10.1038/83034. [DOI] [PubMed] [Google Scholar]
- 49.Im SC, Liu G, Luchinat C, Sykes AG, Bertini I. The solution structure of parsley [2Fe–2S] ferredoxin. Eur J Biochem. 1998;258:465–477. doi: 10.1046/j.1432-1327.1998.2580465.x. [DOI] [PubMed] [Google Scholar]
- 50.Jacobson BL, Chae YK, Markley JL, Rayment I, Holden HM. Molecular structure of the oxidized, recombinant, heterocyst [2Fe–2S] ferredoxin from Anabaena 7120 determined to 1.7-Å resolution. Biochemistry. 1993;32:6788–6793. doi: 10.1021/bi00077a033. [DOI] [PubMed] [Google Scholar]
- 51.Wolf YI, Aravind L, Grishin NV, Koonin EV. Evolution of aminoacyl-tRNA synthetases—analysis of unique domain architectures and phylogenetic trees reveals a complex history of horizontal gene transfer events. Genome Res. 1999;9:689–710. [PubMed] [Google Scholar]
- 52.Sankaranarayanan R, Dock-Bregeon AC, Romby P, Caillet J, Springer M, Rees B, et al. The structure of threonyl-tRNA synthetase–tRNA(Thr) complex enlightens its repressor activity and reveals an essential zinc ion in the active site. Cell. 1999;97:371–381. doi: 10.1016/s0092-8674(00)80746-1. [DOI] [PubMed] [Google Scholar]
- 53.Dock-Bregeon AC, Rees B, Torres-Larios A, Bey G, Caillet J, Moras D. Achieving error-free translation; the mechanism of proofreading of threonyl-tRNA synthetase at atomic resolution. Mol Cell. 2004;16:375–386. doi: 10.1016/j.molcel.2004.10.002. [DOI] [PubMed] [Google Scholar]
- 54.Wilson MI, Gill DJ, Perisic O, Quinn MT, Williams RL. PB1 domain-mediated heterodimerization in NADPH oxidase and signaling complexes of atypical protein kinase C with Par6 and p62. Mol Cell. 2003;12:39–50. doi: 10.1016/s1097-2765(03)00246-6. [DOI] [PubMed] [Google Scholar]
- 55.Uegaki K, Otomo T, Sakahira H, Shimizu M, Yumoto N, Kyogoku Y, et al. Structure of the CAD domain of caspase-activated DNase and interaction with the CAD domain of its inhibitor. J Mol Biol. 2000;297:1121–1128. doi: 10.1006/jmbi.2000.3643. [DOI] [PubMed] [Google Scholar]
- 56.Iyer LM, Burroughs AM, Aravind L. The prokaryotic antecedents of the ubiquitin-signaling system and the early evolution of ubiquitin-like beta-grasp domains. Genome Biol. 2006;7:R60. doi: 10.1186/gb-2006-7-7-r60. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 57.Burroughs AM, Balaji S, Iyer LM, Aravind L. Small but versatile: the extraordinary functional and structural diversity of the beta-grasp fold. Biol Direct. 2007;2:18. doi: 10.1186/1745-6150-2-18. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 58.Brenner SE, Koehl P, Levitt M. The ASTRAL compendium for protein structure and sequence analysis. Nucleic Acids Res. 2000;28:254–256. doi: 10.1093/nar/28.1.254. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 59.Holm L, Sander C. Mapping the protein universe. Science. 1996;273:595–603. doi: 10.1126/science.273.5275.595. [DOI] [PubMed] [Google Scholar]
- 60.Henikoff S, Henikoff JG. Amino acid substitution matrices from protein blocks. Proc Natl Acad Sci USA. 1992;89:10915–10919. doi: 10.1073/pnas.89.22.10915. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 61.Sadreyev R, Grishin N. COMPASS: a tool for comparison of multiple protein alignments with assessment of statistical significance. J Mol Biol. 2003;326:317–336. doi: 10.1016/s0022-2836(02)01371-2. [DOI] [PubMed] [Google Scholar]
- 62.Wang G, Dunbrack RL., Jr Scoring profile-to-profile sequence alignments. Protein Sci. 2004;13:1612–1626. doi: 10.1110/ps.03601504. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 63.Rychlewski L, Fischer D, Elofsson A. LiveBench-6: large-scale automated evaluation of protein structure prediction servers. Proteins. 2003;53(Suppl. 6):542–547. doi: 10.1002/prot.10535. [DOI] [PubMed] [Google Scholar]
- 64.Zhang Y, Skolnick J. TM-align: a protein structure alignment algorithm based on the TM-score. Nucleic Acids Res. 2005;33:2302–2309. doi: 10.1093/nar/gki524. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 65.Zemla A. LGA: a method for finding 3D similarities in protein structures. Nucleic Acids Res. 2003;31:3370–3374. doi: 10.1093/nar/gkg571. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 66.Panchenko AR, Madej T. Analysis of protein homology by assessing the (dis)similarity in protein loop regions. Proteins. 2004;57:539–547. doi: 10.1002/prot.20237. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 67.Soding J, Biegert A, Lupas AN. The HHpred interactive server for protein homology detection and structure prediction. Nucleic Acids Res. 2005;33:W244–W248. doi: 10.1093/nar/gki408. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 68.Hsu CW, Chang CC, Lin CJ. A practical guide to support vector classification. http://www.csie.ntu.edu.tw/∼cjlin/papers/guide/guide.pdf.
- 69.Cheng H. Ph D Dissertation. The University of Texas Southwestern Medical Center at Dallas; 2007. Classification and Differentiation of Homologs and Structural Analogs. http://www4.utsouthwestern.edu/library/ETD/etdSearch.cfm. [Google Scholar]