Application of a genetic algorithm and an artificial neural network for global prediction of the toxicity of phenols to Tetrahymena pyriformis

Abstract

Abstract

Genetic algorithm (multiparameter linear regression; GA-MLR) and genetic algorithm–artificial neural network (GA-ANN) global models have been used for prediction of the toxicity of phenols to Tetrahymena pyriformis. The data set was divided into 150 molecules for training, 50 molecules for validation, and 50 molecules for prediction sets. A large number of descriptors were calculated and the genetic algorithm was used to select variables that resulted in the best-fit to models. The six molecular descriptors selected were used as inputs for the models. The MLR model was validated using leave-one-out, leave-group-out cross-validation and external test set. A three-layered feed forward ANN with back-propagation of error was generated using six molecular descriptors appearing in the MLR model. Comparison of the results obtained using the ANN model with those from the MLR revealed the superiority of the ANN model over the MLR. The root mean square error of the training, validation, and prediction sets for the ANN model were calculated to be 0.224, 0.202, and 0.224 and correlation coefficients (r ²) of 0.926, 0.943, and 0.925 were obtained. The improvements are because of non-linear correlations of the toxicity of the compounds with the descriptors selected. The prediction ability of the GA-ANN global model is much better than that of previously proposed models.

Graphical Abstract

Introduction

Toxicological assessment of phenolic compounds is essential for risk-assessment purposes. Compounds with a single aromatic ring substituted with a hydroxyl group (the phenols) are ubiquitous in nature and are used in many industries including those involving textiles, leather, paper, and oil. They are also commonly used food additives and frequently utilized in agriculture [1]. There has therefore been great interest in assessing the toxicity of such compounds. The impact of the potential hazard of untested chemicals, a challenge confronting national and international regulatory agencies [2–5], can be measured by experimental investigations, but this approach is both quite expensive and time-consuming. This has meant that the development of computational methods as an alternative tool for predicting the properties of chemicals has been a subject of intensive study. Among computational methods quantitative structure–activity relationships (QSAR) have found diverse applications for predicting compounds’ properties, including biological activity prediction [6], physical property prediction [7], and toxicity prediction [8, 9]. QSPR/QSAR models are essentially calibration models in which the independent variables are molecular descriptors that describe the structure of molecules and the dependent variable is the property/activity of interest. In QSAR studies, techniques which can be used for model construction, for example multiple linear regression (MLR) and artificial neural networks (ANN), have been used for inspection of linear and nonlinear relationships between the activity of interest and molecular descriptors. Artificial neural networks have become popular in QSPR/QSAR models because of their success where complex non-linear relationships exist amongst data [10, 11]. An ANN is formed from artificial neurons connected with coefficients (weights), which constitute the neural structure and are organized in layers. The layers of neurons between the input and output layers are called hidden layers. Neural networks do not need explicit formulation of the mathematical or physical relationships of the problem handled. These give ANNs an advantage over traditional fitting methods for some chemical applications. For these reasons, in recent years ANNs have been applied to a wide variety of chemical problems [12–20]. Application of these techniques usually requires selection of variables to build well-fitting models. Nowadays, genetic algorithms (GA) are well-known as interesting and more widely used methods for variable selection [21–23]. GA are stochastic methods used to solve optimization problems defined by fitness criteria, by applying the evolution hypothesis of Darwin and different genetic functions, i.e., crossover and mutation.

QSAR models have been used to predict the toxicity of phenols [1, 24, 25]. Two approaches have been suggested in this modeling and in similar QSAR modeling. The first of these is the development of “global” models which are defined as QSAR models that cover a number of different mechanisms of action for a given toxicological endpoint. The use of the term “global model” in this study is distinct from that used to define QSAR models based on chemicals with similar modes of action allowing interspecies correlations. The second is the development of a number of “local” models, each covering a single mechanism of action present in the database [26]. Very recently, Enoch et al. [26] used a global QSAR method for prediction of the toxicity of phenols. The ability of the proposed global QSAR model to predict the toxicity of phenols is poor (correlation coefficients (r ²) of the model are 0.71 and 0.73 for training and test sets) [26].

In order to predict accurately the toxicity of these compounds, in this work genetic algorithm–multiparameter linear regression (GA-MLR) and genetic algorithm–artificial neural network (GA-ANN) global models were used to generate QSAR models between the descriptors and toxicity of 250 phenols with diverse chemical structures. The results obtained were compared with each other, with those from previous work [26], and with the experimental values.

Results and discussion

For selection of the most important descriptors the genetic algorithm technique was used. To select the optimum number of descriptors, the influences of the number of the descriptors were investigated for one to ten descriptors.

The R ² value can be generally increased by adding the additional predictor variables to the model, even if the added variable does not contribute to the reduction of the unexplained variance of the dependent variable. Therefore, the R ² usage requires special attention. For this reason, it is better to use another statistical parameter, called the adjusted R ² (R ²_adj), were R ²_adj is defined by Eq. 1.

\documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$ R^{2}_{\text{adj}} = 1- \left( { 1- R^{2} } \right)\left( {{\frac{n - 1}{n - p - 1}}} \right) $$\end{document} 1

R ²_adj is interpreted similarly to the R ² value, considering the number of degrees of freedom also. It is adjusted by dividing the residual sum of squares and total sum of squares by their respective degrees of freedom. The R ²_adj value diminishes if an added variable to the equation does not reduce the unexplained variance [27]. Subsequently, R ²_adj is used to compare models with different numbers of predictor variables.

Another statistical parameter is the standard error of the estimate(s) that measures the dispersion of the observed values about the regression line. When the s value is low, the reliability of the prediction is higher. Figure 1 shows plots of R ², R ²_adj, and s for the training set as a function of the number of descriptors for the 1–10 descriptors in the models. R ² and R ²_adj increased with increasing number of descriptors. However, the values of s decreased with increasing number of descriptors. As models with 7–10 descriptors did not significantly improve the statistics of the models, it was determined that the optimum subset size had been achieved with a maximum of 6 descriptors.

Fig. 1.

Influences of the number of descriptors on R ² (filled circle), R ²_adj (open circle), and s (filled triangle) of the regression model

The selected variables and the correlation matrix of the descriptors are listed in Table 1, from which it can be seen that the correlation coefficient value of each pair of descriptors was less than 0.65, which meant that the selected descriptors are independent.

Table 1.

Correlation coefficient matrix of the selected descriptors

	Xt	MATS1m	PJI3	Mor23u	nCs	H-046
Xt	1	0.183	−0.489	0.323	−0.401	−0.226
MATS1m		1	−0.528	0.396	−0.374	−0.613
PJI3			1	−0.449	0.364	0.206
Mor23u				1	−0.648	−0.287
nCs					1	0.421
H-046						1

To examine the relative importance, and the contribution of each descriptor in the model, for each descriptor the value of the mean effect (MF) was calculated. This calculation was performed by use of Eq. 2.

\documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$ {\text{MF}}_{j} = {\frac{{\beta_{j} \sum\nolimits_{i = 1}^{i = n} {d_{ij} } }}{{\sum\nolimits_{j}^{m} {\beta_{j} \sum\nolimits_{i}^{n} {d_{ij} } } }}} $$\end{document} 2

MF_j represents the mean effect for the considered descriptor j, β _j is the coefficient of the descriptor j, d _ij stands for the value of the target descriptors for each molecule, and m is the descriptor’s number in the model. The MF value indicates the relative importance of a descriptor, compared with the other descriptors in the model. Its sign shows the direction of variation in the toxicity values as a result of the increase (or reduction) of the descriptor values. The mean effect values are −0.043, 1.071, −0.081, 0.035, −0.004, and 0.023 for Xt, MATS1m, PJI3, Mor23u, nCs, and H-046. By interpreting the descriptors contained in the model, it is possible to gain useful chemical insights into the toxicity of phenols. For this reason, an acceptable interpretation of the QSAR results is provided below.

The first descriptor which has appeared in the model is Xt (total structure connectivity index). Connectivity indices are among the most popular topological indices and are calculated from the vertex degree of the atoms in the H-depleted molecular graph. Xt is a connectivity index contemporarily accounting for all the atoms in the graph. Also the total structure connectivity index is the square root of the simple topological index that is proposed for measuring molecular branching [28]. The mean effect of Xt has a negative sign, which indicates that an increase in the molecular branch leads to a decrease in its pIG ₅₀ value.

The second descriptor is MATS1m (Moran autocorrelation—lag 1/weighted by atomic masses), which is a 2D autocorrelation descriptor. In this descriptor the Moran coefficient is a distance-type function, and is any physicochemical property calculated for each atom of the molecule, for example atomic mass, polarizability, etc. The Moran coefficient usually takes a value in the interval [−1, +1]. Positive autocorrelation corresponds to positive values of the coefficient whereas negative autocorrelation produces negative values. Therefore, the molecule atoms represent a set of discrete points in space and the atomic property is the function evaluated at those points. The physicochemical property in this case is the atomic mass. MATS1m has a positive sign, illustrating a greater mean effect value than that of the other descriptors, which indicates that this descriptor had a significant effect on the toxicity and that the pIG ₅₀ value is directly related to this descriptor. Hence, it was concluded that by increasing the molecular mass the value of this descriptor increased, causing an increase in its pIG ₅₀ value.

The third descriptor is PJI3 (3D Petijean shape index), which is a geometrical descriptor. The Petitjean shape index is a topological anisometry descriptor also called a graph-theoretical shape coefficient that is calculated from the topological radius and the topological diameter obtained from the distance matrix representing the considered molecular graph. PJI3 has a negative sign, which indicates that the pIG ₅₀ is inversely related to this descriptor.

Mor23u is the fourth descriptor appearing in the model. It is a 3D-MoRSE descriptor. 3D MoRSE descriptors (3D molecule representation of structures based on electron diffraction) are derived from infrared spectra simulation using a generalized scattering function [28]. This descriptor was proposed as signal 23/unweighted. Mor23u has a positive sign, which indicates that the pIG ₅₀ is directly related to this descriptor.

The fifth descriptor is nCs which is one of the functional groups. nCs represents the number of total secondary C(sp³). The mean effect of nCs has a negative sign, which indicates that an increase in the number of secondary C(sp³) of the molecule leads to a decrease in its pIG ₅₀ value.

The final descriptor of the model was the H-046 (H attached to C0 (sp³)). It is one of the atom-centered fragment descriptors that describe each atom by its own atom type and the bond types and atom types of its first neighbors. This descriptor represents the first neighbor (hydrogen) of carbon atoms. This descriptor has a positive sign, which indicates that the pIG ₅₀ is directly related to this descriptor.

In summary, it is concluded that the molecular branching, the molecular mass, the molecular shape, the number of secondary C(sp³) of molecules, and the first neighbor (hydrogen) of carbon atoms are of major importance in the toxicity of the compounds studied.

Genetic algorithm: multiparameter linear regression

We used a GA for selection of the most relevant descriptors. Multiparameter linear correlation of pIG ₅₀ values for 150 different phenolic compounds in the training set was achieved by the GA by use of the six descriptors selected, and the following equation was obtained:

\documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$ \begin{aligned} pIG_{50} = & - 1 5.0 5\left( { \pm 1. 6 6} \right) - 1 5. 7 7\left( { \pm 2.00} \right){\text{Xt}} + 1 7. 8 4\left( { \pm 1. 5 8} \right){\text{MATS1m}} \\ & \quad - 1. 8 4\left( { \pm 0. 3 1} \right){\text{PJI3}} - 1. 2 3\left( { \pm 0. 1 8} \right){\text{Mor23u}} - 0. 1 2\left( { \pm 0.0 4} \right){\text{nCs}} \\ & \quad + 0. 1 4\left( { \pm 0.0 1} \right){\text{H}} - 0 4 6\\ \end{aligned} $$\end{document} 3

The model was then used to predict pIG ₅₀ values for the compounds in the validation and prediction sets. The prediction results are given in Table 2. The calculated values of pIG ₅₀ for the compounds in the training, validation, and prediction sets using the GA-MLR model have also been plotted versus their experimental values (Fig. 2). The correlation coefficients, r ², obtained were 0.747 for the training set, 0.721 for the validation set, and 0.516 for the prediction set. Table 3 shows the root mean square error (RMSE) and r ² of the model for total, training, validation, and prediction sets.

Table 2.

Experimental values of the toxicity of phenols to Tetrahymena pyriformis (pIG ₅₀) and the values calculated by the GA-MLR and GA-ANN global models

No.	Compound	pIG 50 (exp)	MLR	ANN
Training
1	4-Hydroxyphenylacetic acid	−1.50	0.10	−1.43
3	3-Hydroxybenzyl alcohol	−1.04	−0.51	−0.97
5	3-Hydroxy-4-methoxybenzyl alcohol	−0.99	0.07	−0.50
6	4-Hydroxy-3-methoxybenzylamine HCl	−0.97	−0.41	−0.83
8	4-Hydroxyphenethylalcohol	−0.83	−0.69	−0.86
10	3-Hydroxybenzoic acid (3-carboxylphenol)	−0.81	0.45	−0.27
11	4-Hydroxybenzamide	−0.78	−0.33	−0.76
13	Resorcinol	−0.65	−0.14	−0.05
15	2,4,6-Tris(dimethylaminomethyl)phenol	−0.52	−0.52	−0.54
16	3-Aminophenol (3-hydroxyaniline)	−0.52	−0.40	−0.82
18	2-Methoxyphenol (guaiacol)	−0.51	−0.24	−0.17
20	5-Methylresorcinol	−0.39	0.09	−0.20
21	4-Hydroxybenzylcyanide (4-cyanomethylphenol)	−0.38	0.01	−0.64
23	2-Ethoxyphenol	−0.36	−0.28	−0.28
25	4-Hydroxyacetophenone (4-acetylphenol)	−0.30	−0.30	−0.30
26	3-Ethoxy-4-methoxyphenol	−0.30	−0.06	−0.28
28	Salicylamide (2-hydroxybenzamide)	−0.24	0.04	−0.33
30	Phenol	−0.21	−0.22	−0.22
31	p-Cresol (4-methylphenol)	−0.18	−0.33	−0.19
33	3-Acetamidophenol (3-hydroxyacetanilide)	−0.16	0.10	−0.08
35	4-Methoxyphenol	−0.14	−0.47	−0.17
36	Isovanillin (3-hydroxy-4-methoxybenzaldehyde)	−0.14	0.38	0.02
38	3,5-Dimethoxyphenol	−0.09	0.31	−0.09
40	4-Aminophenol (4-hydroxyaniline)	−0.08	−0.56	−0.15
41	3-Cyanophenol	−0.06	0.27	0.29
43	Methyl 3-hydroxybenzoate	−0.05	−0.04	−0.51
45	4-Hydroxy-3-methoxybenzonitrile	−0.03	0.33	0.09
46	4-Ethoxyphenol	0.01	−0.41	−0.16
48	4-Fluorophenol	0.02	0.30	0.08
50	5′-Fluoro-2′-hydroxyacetophenone	0.04	0.02	0.15
51	4′-Hydroxypropiophenone	0.05	−0.21	0.08
53	2-Hydroxyacetophenone	0.08	−0.25	−0.18
55	Methyl 4-hydroxybenzoate	0.08	0.16	0.05
56	3-Hydroxybenzaldehyde	0.09	0.18	−0.05
58	4′-Hydroxypropiophenone	0.12	−0.21	0.08
60	3,4-Dimethylphenol	0.12	0.36	0.07
61	4-Chlororesorcinol	0.13	0.65	−0.27
63	2-Ethylphenol	0.16	0.10	0.12
65	Salicylhydrazide	0.18	0.30	0.33
66	2-Chlorophenol	0.18	0.76	0.09
68	4′-Hydroxy-2′-methylacetophenone	0.19	0.04	0.38
70	3-Ethylphenol	0.23	0.17	0.20
71	Salicylaldoxime	0.25	0.13	0.22
73	3,4-Dinitrophenol	0.27	0.84	0.34
75	2,3,6-Trimethylphenol	0.28	0.64	0.28
76	2,4,6-Trimethylphenol	0.28	0.84	0.27
78	2′-Hydroxy-5′-methylacetophenone	0.31	0.19	0.20
80	5-Hydroxy-2-nitrobenzaldehyde	0.33	0.73	0.63
81	2-Allylphenol	0.33	0.22	0.33
83	2,3,5-Trimethylphenol	0.36	0.73	0.38
85	4-Methylcatechol	0.37	0.34	0.32
86	o-Vanillin (3-methoxysalicylaldehyde)	0.38	0.26	0.03
88	3-Fluorophenol	0.38	0.40	0.36
90	4-Allyl-2-methoxyphenol (eugenol)	0.42	0.53	0.42
91	Salicylaldehyde (2-hydroxybenzaldehyde)	0.42	0.34	0.68
93	5-Amino-2-methoxyphenol	0.45	−0.12	−0.49
95	2,6-Difluorophenol	0.47	0.99	0.39
96	Hydroquinone	0.47	−0.12	0.13
98	Ethyl 3-hydroxybenzoate	0.48	0.33	0.34
100	3-Nitrophenol	0.51	0.61	0.80
101	4-Cyanophenol	0.52	0.05	0.52
103	2,6-Dinitrophenol	0.54	0.82	0.54
105	2′-Hydroxy-4′-methoxyacetophenone	0.55	0.31	0.54
106	Ethyl 4-hydroxybenzoate	0.57	0.14	0.41
108	5-Methyl-2-nitrophenol	0.59	0.95	1.05
110	2,4-Difluorophenol	0.60	0.81	0.73
111	3-Isopropylphenol	0.61	0.70	0.62
113	3-Methyl-2-nitrophenol	0.61	0.77	0.35
115	α,α,α-Trifluoro-p-cresol	0.62	1.01	0.62
116	Methyl 4-methoxysalicylate	0.62	0.31	0.90
118	4-Propylphenol	0.64	0.40	0.54
120	2-Nitroresorcinol	0.66	0.94	1.35
121	2-Nitrophenol	0.67	0.86	0.54
123	2-Chloro-4,5-dimethylphenol	0.69	1.14	1.12
125	4-Chloro-2-methylphenol	0.70	0.82	0.63
126	2′-Hydroxy-4′,5′-dimethylacetophenone	0.71	0.25	0.96
128	2,6-Dichlorophenol	0.74	1.38	0.97
130	2-Methoxy-4-propenylphenol	0.75	0.55	0.75
131	Catechol	0.75	0.17	0.80
133	3-Chloro-5-methoxyphenol	0.76	0.53	0.76
135	5-Chloro-2-hydroxyaniline (2-amino-4-chlorophenol)	0.78	0.55	0.67
136	4-Chloro-3-methylphenol	0.80	0.75	0.86
138	2,6-Dichloro-4-fluorophenol	0.80	1.56	0.91
140	1,2,3-Trihydroxybenzene	0.85	0.49	0.87
141	3-Chlorophenol	0.87	0.60	0.31
143	4-Amino-2-nitrophenol	0.88	0.71	0.84
145	6-Amino-2,4-dimethylphenol	0.89	0.59	0.94
146	4-tert-Butylphenol	0.91	1.18	0.94
148	3-Fluoro-4-nitrophenol	0.94	0.72	0.93
150	2,5-Dinitrophenol	0.95	1.40	0.61
151	2,2′,4,4′-Tetrahydroxybenzophenone	0.96	1.08	1.04
153	4-sec. Butylphenol	0.98	0.86	0.85
155	3-Hydroxydiphenylamine	1.01	1.19	0.97
156	4-Hydroxybenzophenone	1.02	1.27	1.13
158	2,4-Dichlorophenol	1.04	1.11	1.48
160	4-Chlorocatechol	1.06	0.72	0.97
161	Benzyl 4-hydroxyphenyl ketone	1.07	1.30	1.01
163	4-Chloro-3-ethylphenol	1.08	0.98	1.03
165	2-Phenylphenol	1.09	1.27	1.30
166	3-Iodophenol	1.12	0.90	1.12
168	3-Chloro-4-fluorophenol	1.13	1.02	1.09
170	3-Bromophenol	1.15	0.79	1.15
171	6-tert-Butyl-2,4-dimethylphenol	1.16	1.31	1.20
173	2,3,5,6-Tetrafluorophenol	1.17	1.73	1.42
175	2-Amino-4-chloro-5-nitrophenol	1.17	1.03	1.04
176	4-Chloro-3,5-dimethylphenol	1.20	1.15	1.21
178	4-tert-Pentylphenol	1.23	1.23	1.38
180	Chlorohydroquinone	1.26	0.75	0.78
181	4-Bromo-3,5-dimethylphenol	1.27	1.50	0.99
183	4-Bromo-6-chloro-o-cresol	1.28	1.64	1.32
185	p-Cyclopentylphenol	1.29	1.20	1.58
186	2-tert-Butylphenol	1.30	1.00	0.92
187	2-tert-Butyl-4-methylphenol	1.30	1.40	1.30
190	2-Hydroxydiphenylmethane	1.31	1.09	1.29
191	Butyl 4-hydroxybenzoate	1.33	0.92	1.35
193	3-Phenylphenol	1.35	1.32	1.42
195	n-Pentyloxyphenol	1.36	0.95	1.33
196	4-Fluoro-2-nitrophenol	1.38	1.11	1.06
198	2,4-Dibromophenol	1.40	1.46	1.49
200	2,3-Dimethylhydroquinone	1.41	0.82	1.31
201	2-Hydroxy-4-methoxybenzophenone	1.42	1.06	1.42
203	4-Amino-2,3-dimethylphenol HCl	1.44	0.65	1.21
205	Benzyl 4-hydroxybenzoate	1.55	1.43	1.57
206	3,5-Dichlorosalicylaldehyde	1.55	1.44	1.55
208	3,5-Dichlorophenol	1.57	1.24	1.69
210	4-Bromo-2-fluoro-6-nitrophenol	1.62	1.56	1.92
211	4-Hexyloxyphenol	1.64	1.42	1.76
213	3,5-Dibromosalicylaldehyde	1.64	1.72	1.39
215	4-Chloro-6-nitro-m-cresol	1.64	1.42	1.46
216	4-Nitro-3-(trifluoromethyl)-phenol	1.65	1.53	1.69
218	Tetrachlorocatechol	1.70	2.30	1.88
220	4,6-Dinitro-o-cresol (4,6-dinitro-2-methylphenol)	1.72	1.51	1.58
221	3-Methyl-4-nitrophenol	1.73	0.83	1.27
223	2,4-Dichloro-6-nitrophenol	1.75	1.52	1.87
225	4-Hexylresorcinol	1.80	1.74	1.72
226	2,6-di-tert-Butyl-4-methylphenol (BTH)	1.80	1.98	1.72
228	4-Chloro-2-isopropyl-5-methylphenol	1.85	1.55	1.81
230	4-Bromo-2-nitrophenol	1.87	1.47	1.84
231	Phenylhydroquinone	2.01	1.38	1.74
233	4-Heptyloxyphenol	2.03	2.01	2.03
235	4-Chloro-2-nitrophenol	2.05	1.25	1.64
236	2,4,5-Trichlorophenol	2.10	1.55	2.08
238	3,5-di-tert-Butylcatechol	2.11	2.25	1.70
240	Methoxyhydroquinone	2.20	0.31	1.66
241	2,3,5,6-Tetrachlorophenol	2.22	1.95	2.20
243	3,5-Diiodosalicylaldehyde	2.34	1.96	2.29
245	4-Nonylphenol	2.47	2.98	2.55
246	2-Ethylhexyl 4′-hydroxybenzoate	2.51	2.14	2.51
248	Nonyl 4-hydroxybenzoate	2.63	2.65	2.51
250	2,3,4,5-Tetrachlorophenol	2.71	2.11	2.37
Validation
2	1,3,5-Trihydroxybenzene	−1.26	0.08	−0.92
7	2-Hydroxybenzylalcohol (salicylalcohol)	−0.95	−0.01	−0.93
12	4-Hydroxy-3-methoxybenzyl alcohol	−0.70	−0.27	−0.40
17	Salicylic acid	−0.51	0.42	−0.23
22	3-Hydroxyacetophenone	−0.38	−0.11	−0.48
27	o-Cresol (2-methylphenol)	−0.30	0.14	−0.34
32	4-Hydroxy-3-methoxyphenethylalcohol	−0.18	−0.31	−0.19
37	4-Hydroxy-3-methoxyacetophenone (acetovanillone)	−0.12	−0.08	−0.05
42	m-Cresol(3-methylphenol)	−0.06	−0.16	−0.06
47	3-Ethoxy-4-hydroxybenzaldehyde	0.02	−0.17	−0.02
52	2,4-Dimethylphenol	0.07	0.44	0.13
57	3,5-Dimethylphenol	0.11	0.47	0.24
62	2,4-Diaminophenol 2HCl	0.13	−0.16	0.11
67	2-Fluorophenol	0.19	0.51	0.32
72	4-Hydroxybenzaldehyde	0.27	−0.02	0.35
77	3-Methylcatechol	0.28	0.14	0.58
82	5-Bromo-2-hydroxybenzylalcohol	0.34	0.86	0.31
87	Salicylhydroxamic acid	0.38	0.23	0.15
92	1,2,4-Trihydroxybenzene	0.44	0.46	0.48
97	4-Isopropylphenol	0.47	0.65	0.69
102	4-Propyloxyphenol	0.52	0.46	0.54
107	4-Methyl-2-nitrophenol	0.57	0.96	0.98
112	4-Hydroxy-3-nitrobenzaldehyde	0.61	1.00	0.73
117	2,6-Dichloro-4-nitrophenol	0.63	1.75	1.21
122	4-Bromophenol	0.68	0.62	0.71
127	3-tert-Butylphenol	0.73	1.00	0.98
132	2-Chloromethyl-4-nitrophenol	0.75	1.06	0.64
137	2-Isopropylphenol	0.80	0.57	0.60
142	2-Bromo-2′-hydroxy-5′-nitroacetanilide	0.87	0.91	0.89
147	3,4,5-Trimethylphenol	0.93	0.84	0.93
152	4,6-Dichlororesorcinol	0.97	1.20	0.60
157	4-Benzyloxyphenol	1.04	1.66	0.99
162	2-Fluoro-4-nitrophenol	1.07	1.06	0.93
167	2,5-Dichlorophenol	1.13	1.13	1.44
172	4-Bromo-2,6-dimethylphenol	1.17	1.49	1.04
177	2-Hydroxybenzophenone	1.23	1.06	1.14
182	2,3-Dichlorophenol	1.28	1.29	1.10
188	5-Pentylresorcinol	1.31	1.70	1.37
192	Trimethylhydroquinone	1.34	0.97	1.11
197	4-Phenylphenol	1.39	1.06	1.54
202	4-Nitrophenol	1.42	0.51	0.95
207	4-Cyclohexylphenol	1.56	1.81	1.56
212	3,5-di-tert-Butylphenol	1.64	2.44	1.70
217	Bromohydroquinone	1.68	1.11	1.47
222	3,4-Dichlorophenol	1.75	1.08	1.54
227	Tetrafluorohydroquinone	1.84	1.81	1.55
232	2,4,6-Tribromophenol	2.03	1.88	1.81
237	4-tert-Octylphenol	2.10	2.10	2.18
242	4-(4-Bromophenyl)phenol	2.31	1.74	2.20
247	3,4,5,6-Tetrabromo-o-cresol	2.57	2.59	2.57
Prediction
4	4-Hydroxybenzoic acid (4-carboxylphenol)	−1.02	0.08	−0.70
9	4-Acetamidophenol (4-hydroxyacetanilide)	−0.82	−0.07	−0.63
14	2,6-Dimethoxyphenol	−0.60	0.02	−0.60
19	4-(4-Hydroxyphenyl)-2-butanone	−0.50	0.47	−0.35
24	3-Methoxyphenol	−0.33	−0.07	−0.33
29	Ethyl 4-hydroxy-3-methoxyphenylacetate	−0.23	0.47	−0.13
34	2,4,6-Trinitrophenol	−0.16	1.61	0.06
39	2-Hydroxyethyl salicylate	−0.08	0.20	−0.17
44	Vanillin (3-methoxy-4-hydroxybenzaldehyde)	−0.03	0.20	−0.01
49	2-Cyanophenol	0.03	0.43	0.39
54	2,5-Dimethylphenol	0.08	0.22	−0.09
59	2,3-Dimethylphenol	0.12	0.32	0.12
64	Syringaldehyde	0.17	0.82	0.19
69	4-Ethylphenol	0.21	−0.01	0.18
74	3-Hydroxy-4-nitrobenzaldehyde	0.27	1.03	0.41
79	2-Bromophenol	0.33	0.95	0.65
84	2-Amino-4-tert-butylphenol	0.37	1.21	0.26
89	2-Chloro-5-methylphenol	0.39	0.66	0.69
94	2,3-Dinitrophenol	0.46	1.23	0.52
99	2-Amino-4-nitrophenol	0.48	0.81	0.73
104	4-Chlorophenol	0.55	0.42	0.55
109	2-Bromo-4-methylphenol	0.60	1.11	0.65
114	5-Bromovanillin	0.62	1.16	0.29
119	4-Nitrosophenol	0.65	0.36	0.28
124	4-Butoxyphenol	0.70	0.66	0.69
129	4-Methyl-3-nitrophenol	0.74	0.89	1.11
134	2-Methyl-3-nitrophenol	0.78	0.75	0.43
139	4-Iodophenol	0.85	0.70	0.87
144	2,2′-Biphenol	0.88	1.14	0.82
149	2-Aminophenol (2-hydroxyaniline)	0.94	−0.13	0.99
154	Tetrabromocatechol	0.98	2.45	1.05
159	2,4,6-Tribromoresorcinol	1.06	2.00	1.72
164	2,4-Dinitrophenol	1.08	1.24	0.98
169	5-Fluoro-2-nitrophenol	1.13	1.00	0.72
174	4-Nitrocatechol	1.17	0.98	0.89
179	2,6-Dinitro-p-cresol	1.23	1.47	1.09
184	Tetramethylhydroquinone	1.28	1.35	1.52
189	4-Amino-2-cresol	1.31	0.18	1.31
194	2,6-Dibromo-4-nitrophenol	1.36	1.99	1.46
199	2,4,6-Trichlorophenol	1.41	1.57	2.00
204	Isoamyl 4-hydroxybenzoate	1.48	1.22	1.54
209	2-Chloro-4-nitrophenol	1.59	1.30	1.54
214	Pentafluorophenol	1.64	2.15	1.71
219	2,6-Diiodo-4-nitrophenol	1.71	2.09	1.52
224	4-Bromo-2,6-dichlorophenol	1.78	1.66	1.51
229	Methylhydroquinone	1.86	0.51	1.75
234	Pentachlorophenol	2.05	2.46	1.99
239	Tetrachlorohydroquinone	2.11	2.24	1.93
244	2,3,5-Trichlorophenol	2.37	1.53	2.20
249	Pentabromophenol	2.66	2.69	2.66

Fig. 2.

Plot of the calculated values of pIG ₅₀ from the GA-MLR model versus the experimental values for the training (open circle), validation (filled circle), and prediction (filled triangle) sets

Table 3.

Comparison of statistical data obtained by the GA-MLR and GA-ANN models for the toxicity (pIG ₅₀) of phenols

Model	RMSEtot	RMSEtrain	RMSEvalid	RMSEpred	r 2tot	r 2train	r 2valid	r 2pred
GA-MLR	0.475	0.415	0.456	0.634	0.681	0.748	0.721	0.517
GA-ANN	0.220	0.224	0.202	0.224	0.929	0.927	0.944	0.926

Subscripts: “train” refers to the training set, “valid” refers to the validation set, “pred” refers to the prediction set, and “tot” refers to the total data set

RMSE is the root mean square error and r ² is the square of the correlation coefficient

The model obtained was validated using the leave-one-out (LOO) and leave-group-out (LGO) cross-validation processes. For LOO cross-validation, a data point is removed from the set and the model is recalculated. The predicted activity for that point is then compared with its actual value. This is repeated until each data point has been omitted once. For LGO, 20% of the data points are removed from the dataset and the model refitted; the values predicted for those points are then compared with the experimental values. Again, this is repeated until each data point has been omitted once. The crossvalidated correlation coefficient (Q ²) was 0.620 for LGO and 0.728 for LOO. This indicates that the regression model obtained has good internal and external predictive power.

Genetic algorithm–artificial neural network

To process the non-linear relationships between the toxicity and the descriptors the ANN modeling method combined with GA for feature selection was employed. The input vectors were the set of descriptors which were selected by the GA, and therefore the number of nodes in the input layer was dependent on the number of selected descriptors. In the GA-MLR model it is assumed that the descriptors are independent of each other and have truly additive relevance to the property under study. ANNs are particularly well-suited for QSAR/QSPR models because of their ability to extract non-linear information present in the data matrix. For this reason the next step in this work was generation of the ANN model. There are no rigorous theoretical principles for choosing the proper network topology; so different structures were tested in order to obtain the optimum number of hidden neurons and training cycles [17–20]. Before training the network, the number of nodes in the hidden layer was optimized. In order to optimize the number of nodes in the hidden layer, several training sessions were conducted with different numbers of hidden nodes (from 1 to 18). The root mean square error of training (RMSET) and validation (RMSEV) sets were obtained at various iterations for different numbers of neurons in the hidden layer and the minimum value of RMSEV was recorded as the optimum value. A plot of RMSET and RMSEV versus the number of nodes in the hidden layer is shown in Fig. 3. It is clear that fifteen nodes in the hidden layer is the optimum value.

Fig. 3.

Plot of RMSE for training (open circles) and validation (filled circles) sets versus the number of nodes in the hidden layer

This network consists of six inputs, the same descriptors as in the GA-MLR model, and one output for pIG ₅₀. Then an ANN with architecture 6-15-1 was generated. It is noteworthy that training of the network was stopped when the RMSEV started to increase, i.e., when overtraining begins. The overtraining causes the ANN to lose its prediction power [11]. Therefore, during training of the network, it is desirable that iterations are stopped when overtraining begins. To control the overtraining of the network during the training procedure, the values of RMSET and RMSEV were calculated and recorded to monitor the extent of learning in the various iterations. Results showed that overtraining did not occur in the optimum architecture (Fig. 4).

Fig. 4.

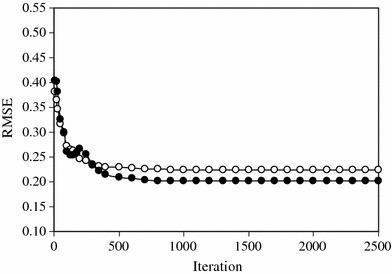
Plot of RMSE for training (open circles) and validation (filled circles) sets versus the number of iterations

The generated ANN was then trained using the training and validation sets for optimization of the weights and biases. For evaluation of the predictive power of the generated ANN, an optimized network was used for prediction of the pIG ₅₀ values in the prediction set, which were not used in the modeling procedure (Table 2). The calculated values of pIG ₅₀ for the compounds in the training, validation, and prediction sets using the ANN model have been plotted versus their experimental values in Fig. 5. A plot of the residuals for the calculated values of pIG ₅₀ in the training, validation, and prediction sets versus their experimental values is presented in Fig. 6. As can be seen, the model did not show proportional and systematic error, because the distribution of the residuals on both sides of zero are random.

Fig. 5.

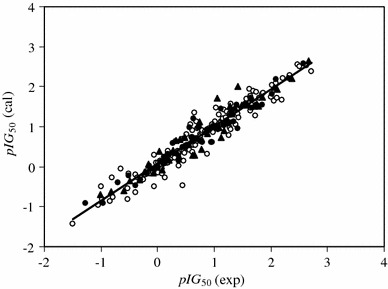
Plot of the calculated values of pIG ₅₀ from the GA-ANN model versus their experimental values for the training (open circles), validation (filled circles), and prediction (filled triangles) sets

Fig. 6.

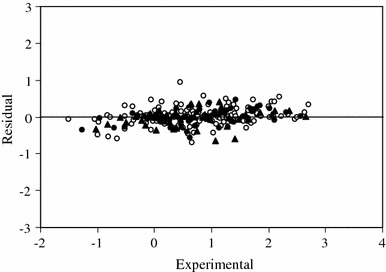
Plot of the residuals for calculated values of pIG ₅₀ from the GA-ANN model versus their experimental values for the training (open circles), validation (filled circles), and prediction (filled triangles) sets

As expected, the calculated values of pIG ₅₀ are in good agreement with the experimental values. The correlation equation for all of the calculated values of pIG ₅₀ from the ANN model and the experimental values is given by Eq. 4.

\documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$ pIG_{50} \left( {\text{cal}} \right) = 0. 9 2 7\,pIG_{50} \left( { \exp } \right) + 0.0 5 4\\ \left( {r^{2} = 0. 9 2 9;{\text{ RMSE}} = 0. 2 20; \, F = 3 2 5 7. 5 2 3} \right)\\ $$\end{document} 4

Similarly, the correlation of pIG ₅₀ (cal) versus pIG ₅₀ (exp) values in the prediction set is given by Eq. 5.

\documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$ pIG_{50} \left( {\text{cal}} \right) = 0. 9 2 7\, pIG_{50} \left( { \exp } \right) + 0.0 7 9\\ (r^{2} = 0. 9 2 6;{\text{ RMSE}} = 0. 2 2 4; \, F = 5 9 9.0 7 5) \\ $$\end{document} 5

Table 3 compares the results obtained using the GA-MLR and GA-ANN models. The r ² and RMSE of the models for the total, training, validation, and prediction sets show the potential of the ANN model for prediction of pIG ₅₀ values of phenolic compounds using a global QSAR model. As a result, it was found that a properly selected and trained neural network could fairly represent the dependence of the toxicity of phenols on the descriptors. The optimized neural network could then simulate the complicated nonlinear relationship between pIG ₅₀ value and the descriptors. The RMSE of 0.634 for the prediction set by the GA-MLR model should be compared with the value of 0.224 by the GA-ANN model. As can be seen, the ability of the proposed model to predict the pIG ₅₀ is better than the QSAR models proposed recently [26]. It can be seen from Table 3 that although parameters appearing in the GA-MLR model are used as inputs for the generated GA-ANN model, the statistics indicate substantial improvement. These improvements are because of the non-linear correlation of the toxicity of phenols to Tetrahymena pyriformis with the selected descriptors.

Data and methodology

The data set of toxicity values (pIG ₅₀, or Log (1/IGC ₅₀)) for the 250 phenolic compounds used for the QSAR models was selected from literature [1]. The data set was randomly split into training, validation, and prediction sets (150, 50, and 50 compounds, Table 2). The z-matrices (molecular models) were constructed with HyperChem 7.0 and molecular structures were optimized using the AM1 algorithm [29]. In order to calculate the theoretical descriptors, Dragon package version 2.1 was used [30]. For this purpose the output of the HyperChem software for each compound was fed into the Dragon program and the descriptors were calculated. As a result, a total of 1,481 theoretical descriptors were calculated for each compound in the data sets (250 compounds).

The theoretical descriptors were reduced by the following procedure:

1. descriptors that were constant were eliminated (394 descriptors); and

2. to reduce the redundancy existing in the descriptors, the correlation of the descriptors with each other and with pIG ₅₀ of the molecules were examined, and collinear descriptors (R > 0.9) were detected. Among the collinear descriptors, that with the highest correlation with toxicity values was retained, and the others were removed from the data matrix (703 descriptors).

The genetic algorithm (GA)

To select the most relevant descriptors, evolution of the population was simulated [31–35]. Each individual of the population defined by a chromosome of binary values represented a subset of descriptors. The number of genes on each chromosome was equal to the number of descriptors. The population of the first generation was selected randomly. A gene took a value of 1 if its corresponding descriptor was included in the subset; otherwise, it took a value of zero. The number of genes with a value of 1 was kept relatively low to furnish a small subset of descriptors [35], that is, the probability of generating 0 for a gene was set greater (at least 60%) than that of generating 1. The operators used here were crossover and mutation. The probability of the application of these operators was varied linearly with generation renewal (0–0.1% for mutation and 60–90% for crossover). The population size was varied between 50 and 250 for different GA runs. For a typical run, the evolution of the generation was stopped when 90% of the generations took the same fitness [21]. The GA program was written in Matlab 6.5 [36].

The artificial neural network (ANN)

A feed-forward artificial neural network with a back-propagation (BP) of error algorithm was used to process the non-linear relationship between the selected descriptors and the toxicity (pIG ₅₀). The number of input nodes in the ANN was equal to the number of descriptors appearing in the MLR model. The ANN model is confined to a single hidden layer, because a network with more than one hidden layer would be harder to train. A three-layer network with a sigmoidal transfer function was designed. The initial weights were randomly selected between 0 and 1. Optimization of the weights and biases was carried out according to Levenberg–Marquardt algorithms for BP of error, which, although requiring far more extensive computer memory, are significantly faster than other algorithms based on gradient descent [37]. The data set was randomly divided into three groups: a training set, a validation set, and a prediction set consisting of 150, 50, and 50 molecules. The training and validation sets were used for generation of the model and the prediction set was used for evaluation of the generated model. The performances of the training, validation, and prediction of models were evaluated as the root mean square error (RMSE), which is defined by Eq. 6.

\documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$ {\text{RMSE}} = \sqrt {\sum\limits_{i = 1}^{N} {{\frac{{(P_{i}^{ \exp } - P_{i}^{\text{cal}} )^{2} }}{N}}} } $$\end{document} 6

where P ^exp_i and P ^cal_i are experimental values of pIG ₅₀ and calculated with the models and N denotes the number of data points. The residual is defined by Eq. 7.

\documentclass[12pt]{minimal} \usepackage{amsmath} \usepackage{wasysym} \usepackage{amsfonts} \usepackage{amssymb} \usepackage{amsbsy} \usepackage{mathrsfs} \usepackage{upgreek} \setlength{\oddsidemargin}{-69pt} \begin{document}$$ {\text{Residual}} = P_{i}^{ \exp } - P_{i}^{\text{cal}} . $$\end{document} 7

The processing of the data was carried out using Matlab 6.5 [38]. The neural networks were implemented using Neural Network Toolbox Ver. 4.0 for Matlab [39].

Conclusion

In this study, linear (GA-MLR) and nonlinear (GA-ANN) global QSAR models were used to construct quantitative relationships between the toxicity of phenols to Tetrahymena pyriformis and their calculated descriptors. Comparison of the results obtained by use of the GA-ANN and the GA-MLR confirmed the superiority of the GA-ANN model as a more powerful method to predict pIG ₅₀. A suitable model with high statistical quality and low prediction errors was eventually derived. Because the improvement of the results obtained by use of the non-linear model (GA-ANN) is substantial, it can be concluded there is a non-linear correlation between the descriptors and the pIG ₅₀ values of the phenols.