Virtual experiments in megastudies: a case study of language and emotion

Abstract

A recent dramatic increase in the number and scope of chronometric and norming lexical megastudies offers the ability to conduct virtual experiments, that is, to draw samples of items with properties that vary in critical linguistic dimensions. This paper introduces a bootstrapping approach which enables testing research hypotheses against a range of samples selected in a uniform, principled manner and evaluates how likely a theoretically motivated pattern is in a broad distribution of possible outcome patterns. We apply this approach to conflicting theoretical and empirical accounts of the relationship between the psychological valence (positivity) of a word and its speed of recognition. To this end, we conduct three sets of multiple virtual experiments with a factorial and a regression design, drawing data from two lexical decision megastudies. We discuss the influence that criteria for stimuli selection, statistical power, collinearity and the choice of dataset have on the efficacy and outcomes of the bootstrapping procedure.

1 Introduction

The last decade has witnessed a dramatic increase in the number and scope of large-scale chronometric and norming lexical megastudies, granting access to behavioral responses to thousands of words obtained from hundreds and thousands of participants. Among other advantages, megastudies offer the ability to conduct virtual experiments, that is, to draw samples of items with properties that vary in critical linguistic dimensions. Behavioral responses to the items in such a virtual experiment can then be treated as if they were the outcomes of an experiment designed with the critical manipulation in mind (Balota, Yap, Hutchinson, & Cortese, 2013; Keuleers, Diependaele, & Brysbaert, 2010; Sibley, Kello, & Seidenberg, 2009). The benefits of virtual experiments are many. Once the megastudies are made accessible, an infinite number of virtual experiments can be conducted without any extra data collection. While many practical factors such as time and personnel limitations constrain the duration of small-scale experiments, virtual experiments face no such restrictions on the number of items they can include. In addition, smaller-scale experimental lists are typically created to implement specific manipulations resulting in an overrepresentation of items with extreme values of lexical properties. Because megastudies are not created to implement such manipulations, they arguably provide more naturalistic ranges (see Balota, Cortese, Sergent-Marshall, Spieler, & Yap, 2004 and Keuleers et al., 2010 for extensive discussions).

Importantly, the utility of virtual experiments as replications of small-scale studies hinges on the assumption that task differences between these formats of data collection do not affect Type I and Type II error rates when testing statistical hypotheses on the same stimuli list. This assumption has been debated. Sibley et al. (2009) analyzed naming latencies reported in the English Lexicon Project megastudy (Balota et al., 2007) as well as in Kessler, Treiman, & Mullennix (2002) and Seidenberg and Waters (1989), and failed to replicate the frequency by regularity interaction that had previously been robustly presented in 5 experimental studies, thereby attesting to the inflated Type II error rates when using megastudies. Possible explanations for this failure to replicate include task demands (participants usually respond to a much larger number of words over time in a megastudy than in a small-scale experiment leading to different fatigue and practice effects, and priming and list effects), and item-wise correlations between megastudies. Conversely, Keuleers et al. (2010) reported a perfect convergence between the results of over 10 small-scale lexical decision experiments, covering a range of word processing phenomena, and the data patterns obtained by analyzing lexical decision RTs to the same sets of stimuli, as reported in their Dutch Lexicon Project megastudy. Moreover, Balota et al. (2013) replicated results of published studies on word frequency and regularity, contra Sibley et al. (2009), using by-participant z-scores and accuracy estimates from the English Lexicon Project. To sum up, the relationship between actual and virtual experiments remains contested, and the sole tool used so far to (in)validate this relationship appears to be the cross-study comparison of responses to the same stimuli list.

The present study introduces a different utilization of virtual experiments as a robust tool for validating novel or well-established experimental effects. The proposed procedure is to (a) identify selection criteria for stimuli that put to the test a research hypothesis with sufficient statistical power as well as control for undesirable variance, (b) draw multiple random samples from a set of items for which requisite behavioral and norming data are available, (c) retain for analyses those samples that satisfy criteria predefined in (a), and finally (d) evaluate the probability of theoretically motivated response patterns across the individual samples. We illustrate this approach by conducting several series of virtual experiments organized around a well-established experimental finding in the area of language and emotion that words with relatively extreme values of psychological valence (rated as very pleasant or very unpleasant) elicit shorter lexical decision RTs than neutral words (Kousta, Vinson, & Vigliocco, 2009).

The effect of valence on word processing

An influential theoretical account of how emotionality of lexical meaning affects word recognition argues that emotionally loaded stimuli benefit from a preferential allocation of attention, as such stimuli are crucial for avoiding danger or gathering resources necessary for survival, cf. Lang, Bradley, and Cuthbert (1990, 1997). Thus, stimuli associated with extreme affective states are predicted to elicit faster processing than relative neutral stimuli due to their relevance for the approach-avoidance motivational systems. So both positive and negative words are expected to elicit faster responses in lexical decision. Moreover, as motivational systems are argued to influence behavioral responses equally strongly, no difference between the speed of responding to positive versus negative words is expected.

The predicted inverse U-shape of the functional relationship between a word’s valence and the lexical decision RT to that word was originally observed in Koustaet al.’s (2009) small-scale experiment with 120 (i.e., 40 triplets) critical words. The triplets represented the positive, neutral and negative ranges of valence and were matched triplet-wise on a comprehensive range of lexical and sublexical properties (see below). Later studies using the same stimuli list with different participant cohorts replicated this inverse U-shaped effect of valence on RTs in two standard lexical decision experiments (Vigliocco, Clarke, Ponari, Vinson, & Fucci, 2013; Experiment 1 in Yap & Seow, 2014) and one go/no-go lexical decision experiment (Experiment 2 in Yap & Seow, 2014). Moreover, Kousta et al. (2009) found the same qualitative pattern of shorter lexical decision RTs to positive and negative words in a sample of 1446 words from the English Lexicon Project (ELP; Balota et al., 2007), and Vinson, Ponari, and Vigliocco (2014) in a sample of 1373 words from the British Lexicon Project megastudy (Keuleers, Lacey, Rastle, & Brysbaert, 2012). The inverse-U effect of valence characterizes the statistical behavior of the mean RT across the range of valence. Yap and Seow (2014) substantially complemented this finding with a distributional analysis of RTs to the same set of 120 words, observing differences between valence levels both in the overall distributional shift and particularly long responses.

The “motivated attention” account, along with the body of evidence supporting the inverse-U effect of valence on response times, is not uncontested: see Larsen, Mercer, Balota, and Strube (2008) and references below. Estes and Adelman (2008a) and Kuperman, Estes, Brysbaert, and Warriner (2014) propose that the interaction of language and emotion is regulated by the automatic vigilance mechanism (Erdelyi, 1974; Pratto & John, 1991). The central tenet of this account is that the perceptive system is attuned to potentially dangerous, negative stimuli which both capture one’s attention faster and for a longer time than positive stimuli do (Fox, Russo, Bowles, & Dutton, 2001; Öhman & Mineka, 2001). As negative words are “released” for processing later than positive ones, they elicit longer processing times. If one further assumes that automatic vigilance is gradient (Kuperman et al., 2014), the account predicts a monotonic decrease in RTs as a word’s valence increases. This pattern was indeed observed in a regression study by Kuperman et al. of lexical decision and naming RTs to over 13,000 words from ELP (Balota et al., 2007): more positive words elicited faster responses. Moreover, as first shown by Larsen, Mercer, and Balota (2006), word frequency was found to play a modulating role, with the effect of valence being stronger in low-frequency words (for other reports of the valence by frequency interaction, see Larsen et al., 2008; Scott, O’Donnell, & Sereno, 2012, and Sheikh & Titone, 2013). Given the larger sample of words in their regression analysis (12324 vs 1446 words in Kousta et al., 2009) with its naturalistic range of valence, Kuperman et al. (2014) concluded that the monotonic near-linear negative relationship between valence and lexical decision RTs finds stronger support in the data than the inverse U-shaped relationship observed in Kousta et al.’s (2009) analysis of stimuli from the same ELP megastudy.

An adjudication between these conflicting theoretical accounts and accompanying bodies of empirical data is currently incomplete. Only one large-scale regression study exists that supports the automatic vigilance account and the gradient negative relationship between valence and behavioral RTs (Kuperman et al., 2014), while the “motivated attention” model and the predicted inverse U-shaped relationship are replicated in three tightly controlled experiments using the same stimulus set (Kousta et al., 2009; Vigliocco et al., 2013; Yap & Seow, 2014), as well as regression analyses of ELP and BLP data by Kousta et al. and Vinson et al. (2014). To contribute to this debate and demonstrate the merit of virtual experiments, the present paper harnesses the power of available megastudies: ELP (Balota et al., 2007), BLP (Keuleers et al., 2010), frequency lists from US and UK films and media (Brysbaert & New, 2009; Van Heuven, Mandera, Keuleers, & Brysbaert, 2014), and recent datasets of affective ratings, concreteness ratings and age-of-acquisition ratings (Brysbaert, Kuperman, & Warriner, in press; Kuperman, Stadthagen-Gonzales, & Brysbaert, 2013; Warriner, Kuperman, & Brysbaert, 2013).

The gist of our bootstrapping procedure is as follows. We establish selection criteria for stimuli, draw a large number of random samples of lexical items from ELP and BLP megastudies, retain only those samples that satisfy these criteria, and estimate the probability of observing the patterns predicted by different theoretical accounts in the retained pool of samples. In Study 1 we use the original factorial design, including the matching criteria for stimuli, of Kousta et al. (2009). Study 2 changes both the selection criteria and the sample size, while still implementing a factorial manipulation of lexical variables. Study 3 implements a regression design, with less tightly controlled samples drawn from ELP and BLP datasets and analyzed with regression models.

2 Study 1: Factorial design with Kousta et al.’s selection criteria

2.1 Methods

We obtained average ELP lexical decision latencies for all correct responses to existing words. The set was further restricted to words for which all of the following lexical variables were available: affective ratings of valence and arousal (Warriner et al., 2013), frequency counts in the 51 million-token SUBTLEX-US corpus based on subtitles to US films and media (Brysbaert & New, 2009), age-of-acquisition ratings (Kuperman et al., 2013), concreteness ratings (Brysbaert et al., in press) and several form-related lexical measures available from the ELP (see the full list below). The resulting set of 12324 words was split into three subranges, using the original cut-off points of Kousta et al.’s study (Vinson, personal communication): negative (valence below 3.5), neutral (valence between 4.5 and 5.5) and positive (valence above 6.5). A similar procedure, including the criteria for valence bins, was applied to the British Lexicon Project using the 201.3 million-token SUBTLEX-UK (Van Heuven et al., 2014) as a source of frequency counts. Average lexical decision latencies were calculated for 6742 words from BLP, for which all other lexical variables were available.

We set out to test the generalizability of the inverse-U pattern of the valence effect by conducting a series of virtual experiments, each satisfying the matching criteria proposed by Kousta et al. (2009). We drew 5000 samples with replacement from the ELP and, separately, the BLP datasets, such that each sample contained 40 words from each of the positive, neutral and negative ranges of valence (see above for valence cut-off points), for a total of 120 words. In every sample, each pair of 40-word subsets (positive-negative, positive-neutral and negative-neutral) was tested for a significant difference between means in each of the following lexical dimensions: concreteness, age of acquisition, familiarity, log frequency, orthographic neighborhood, number of letters, number of syllables, number of morphemes, and mean positional bigram frequency. Positive and negative words within each 120-word sample were further tested for differences in arousal. Two-tailed paired t-tests were used in all comparisons. Only those samples in which each individual t-test failed to reject the null hypothesis for each pair of lexical subsets at the 5% level were considered matched (see below for more detail).

The list of variables that positive, neutral and negative words were matched on was virtually identical to the one used for stimuli creation in Kousta et al. (2009) with two exceptions. First, we used pairwise matching rather than triplet matching, as established statistical tests tend to operate on pairs of samples. Second, we omitted imageability as a matching criterion: because imageability ratings exist for a relatively small number of words (on a megastudy scale), using them would halve the number of words available to us and reduce the statistical power of the bootstrapping procedure considerably. However, because imageability is strongly correlated with concreteness (Brysbaert et al., 2014), this source of variability was at least partly taken into account.

Statistical considerations

Study 1 with its bootstrapping procedure inherits two important statistical properties of the original experimental design, namely, low statistical power and collinearity of predictors. To estimate statistical power and a related measure of effect size, we first re-analyzed RT means and standard deviations reported for each level of valence (negative, neutral and positive) in Kousta et al. (2009) and Experiment 1 by Yap and Seow (2014). A common metric of effect size for two-tailed t-tests (i.e., the tests used by both studies for post-hoc comparisons) is Cohen’s d, defined as $\frac{{\mathrm{\mu }}_1-{\mathrm{\mu }}_2}{{\mathrm{\sigma }}_{12}}$, e.g. the difference between RT means µ of two samples divided by the pooled standard deviation of the RT (σ₁₂) of the two samples. For equal-size samples, ${\mathrm{\sigma }}_{12}=\sqrt{\frac{{{\mathrm{\sigma }}_1}^2-{{\mathrm{\sigma }}_2}^2}{2}}$ (Cohen, 1988). Small, medium and large effects are estimated by Cohen (1988) at d = 0.2, 0.5 and 0.8, respectively. In all pairwise comparisons of Kousta et al. and Yap and Seow’s data, Cohen’s d ranged between 0.35 and 0.39, indicating fairly small effect sizes. Statistical power of detecting an effect of d = 0.35 in a two-sample paired t-test with 40 items in each of the two samples and the 0.05 significance level amounts to as little as 0.58. In other words, the original factorial design will successfully detect an effect of this size and reject the null hypothesis only about half of the time. If an effect size is closer to the lower boundary of what Cohen (1988) classified as a small effect size (d = 0.2), as is commonly the case in our Study 1 and Study 2, the situation is more drastic. The probability of a two-tailed paired t-test to detect an effect of such magnitude – with the given sample size and significance level – drops to a mere 23%. Another statistical test used in Kousta et al.’s study is the one-way ANOVA. The statistical power of this test to detect a small effect size (η² = 0.01) when applied to three samples of 40 items each is only 0.15 (Fritz, Morris, & Richler, 2011), i.e. the test is expected to fail to detect a small valence effect 85% of the time¹. This low statistical power – reduced due to discretizing continuous variables like valence to create bins (Baayen, 2004, 2010; Cohen, 1992; MacCallum, Zhang, Preacher, & Rucker, 2002) – is a hallmark of the factorial approach and makes generalizability of its findings less than reliable.

Another important issue is collinearity of psycholinguistic variables. The correlation of concern here is one between valence and (log-transformed) frequency: r = 0.18 in our subset of the ELP dataset and r = 0.28 in the BLP dataset (both ps < 0.0001). The matching procedure of a factorial design only verifies, with a given confidence, that the mean values of a matched variable (here, log frequency) are not reliably different across levels of a critical variable (here, valence). However, as will become evident below, this matching does not test, nor does it rule out, a correlation between raw (rather than discrete) values of valence and frequency in a given sample. In what follows, we highlight implications of both statistical power and collinearity for our results. Sampling, regression modeling and power analyses reported below were done using functions in the base, rms and pwr packages of the statistical programming language R version 3.0.1 (R Core Team, 2014).

2.2 Results and discussion

The procedure that followed Kousta et al.’s selection criteria (see Methods above) yielded 3 matched samples of 120 words drawn from the 12324 words in the ELP database and 1 matched sample from the 6742 words in the BLP database. No two samples drawn from ELP shared more than two words, and thus they were practically independent. The low number of samples we yielded is a testimony to how unrewarding the task of factorial matching is, even if done in an automatized way (Balota et al., 2013). The mean RTs (SDs in parentheses) in the negative, neutral, and positive conditions in the three ELP samples respectively were 759 (102), 745 (110), and 710 (90) ms; 728 (124), 728 (100), and 681 (75); and 731 (99), 718 (98), and 709 (98) ms. All samples showed positive correlations between valence and log frequency: the correlation reached statistical significance in the first sample (r = 0.23, p = 0.01). The means (SDs) in the one BLP sample were 599 (58), 618 (70), and 587 (57) ms: the positive correlation between valence and log frequency was marginally significant (r = 0.16, p = 0.07). Even though all 40-word word groups were matched on frequency, more positive words were still reliably associated with higher frequency of occurrence in several samples, and thus the effect on RTs that would be ascribed to valence may in fact mask a robust and well-reported effect of word frequency. Due to the small number of samples obtained, we do not report descriptive statistics on other lexical variables, averaged across samples, see however Table 1 for Study 2 below.

Table 1.

Descriptive statistics of critical lexical properties averaged across ELP and BLP samples.

	valence mean	valence sd	frequency mean	frequency sd	AoA mean	AoA sd	length mean	length sd	concrete mean	concrete sd
ELP
negative	3.61	0.12	2.09	0.07	9.54	0.29	7.23	0.32	3.19	0.13
neutral	5.20	0.05	2.13	0.08	9.33	0.33	7.18	0.30	3.43	0.12
positive	6.42	0.08	2.26	0.09	8.74	0.30	7.32	0.33	3.29	0.14
BLP
negative	3.72	0.12	2.85	0.09	8.55	0.36	5.86	0.23	3.47	0.12
neutral	5.25	0.05	2.93	0.11	8.49	0.34	5.82	0.23	3.69	0.14
positive	6.43	0.08	3.10	0.08	7.89	0.31	5.97	0.22	3.55	0.14

To examine differences between negative, neutral and positive words, and their conformity with theorized patterns, we followed the recommendations of Fritz et al. (2012) and calculated Cohen’s d for all pairs of value levels in all ELP and BLP samples. We considered a sample as a confirmation of Kousta et al.’s motivated attention account if the following three conditions were met simultaneously: on average, RTs to negative words and positive words were faster than to neutral ones with the difference showing at least a small effect size (d < −0.2), and RTs to positive and negative words did not differ from each other (|d| < 0.2). None of the ELP or BLP samples conformed to this the hypothesized inverse-U shape. The single BLP sample appeared to follow the trend numerically, but its negative words were slower than positive ones (d = 0.21). An alternative pattern of a monotonic negative relationship between valence and RTs by Kuperman et al. (2014) is construed as a gradient pattern rather than a categorical contrast between discrete levels of valence. Yet, to estimate it in comparable categorical terms, we calculated Cohen’s d to assess how many samples showed a simultaneous small or larger (d < −0.2) advantage of positive words over neutral and negative ones, and of neutral words over negative ones. While all three ELP samples appeared to follow this pattern numerically and all these samples showed the advantage of positive over negative words to be noticeable (all d < −0.3), none of the ELP or BLP samples showed all three pairwise differences in RTs to simultaneously produce effects that would be considered small. Nonsignificant results of post-hoc t-tests applied to pairwise RT comparisons between valence levels in all samples confirmed this observation.

We further examined the obtained samples using standardized RTs (calculated as the mean of per-participant z-transformed RTs) to words as provided in ELP and BLP datasets. As argued in Balota et al. (2007; Balota et al., 2013), z-scores allow for a direct comparison of responses to different words, while minimizing the individual variability in processing speed and accuracy. Results of the RT analyses reported below were virtually identical when z-scores of RTs were used.

Why is there such a drastic discrepancy between the present results and results of the original experimental study (Kousta et al., 2009) and subsequent replications (Vigliocco et al., 2013; Yap & Seow, 2014)? One possibility is the cross-study differences in the list and context effects: pseudowords varied between the ELP, BLP and Kousta et al.’s study, as did the participants, the length of the stimulus list presented for lexical decision, and the probability of encountering a positive, neutral or negative word in the stimulus list. It is possible then that discrepancies in the task or the population altered the responses such that the effect of valence elicited by the original word list in the laboratory setting is no longer present among megastudy participants. We ruled out this possibility by considering RTs to words from Kousta et al.’s 120-word list in both the ELP and BLP databases. The overlapping sets included 112 words from the ELP database, and 92 words from the BLP database. In both databases, RTs to the original word list replicated the critical findings of Kousta et al. RTs to negative and positive words were not significantly different from each other in the ELP (a two-tailed t-test: t = −0.77, df = 71.8, p = 0.44; Cohen’s d = −0.18) and the BLP sample (t = 0.18, df = 57.0, p = 0.86; d = −0.04). Positive words elicited faster responses than neutral ones (one-tailed two-sample t-test, ELP: t = −1.97, df = 70.5, p = 0.03; d = −0.45; BLP: t = −2.00, df = 50.0, p = 0.03; d = −0.52). RTs to negative words were significantly shorter than to neutral words in the BLP sample (one-tailed two-sample t-test: t = −2.35, df = 56.0, p = 0.01; d = −0.59) and there was a numerical tendency in the expected direction in the ELP sample (one-tailed two-sample t-test: t = −1.19, df = 73.3, p = 0.12; Cohen’s d = −0.27). Thus, the inverse-U shape of the valence effect observed in studies using one and the same word list (Kousta et al., 2009; Vigliocco et al., 2013; Yap & Seow, 2014) was also found in the ELP and BLP data. That is, this specific set of stimuli is confirmed to elicit the same qualitative pattern of speedier responses to positive and negative words than to neutral ones in two more datasets, the ELP and the BLP megastudies. Thus, whatever the discrepancies were in the administration, participant cohorts, or stimuli of the small-scale and large-scale experiments we discuss, they were not responsible for the change in a magnitude or direction of the valence effect.

To sum up, samples generated from large-scale behavioral datasets using the same matching and binning criteria as in Kousta et al.’s study are too few, and the effects they show are too weak, to reach definitive conclusions about the stability and prevalence of conflicting response patterns. Study 1 highlights the importance of statistical power and collinearity as issues that the original factorial design, and the bootstrapping procedure that adopts it, may be vulnerable to.

3 Study 2: Factorial design with relaxed selection criteria

In this series of virtual experiments, we aimed to address collinearity between frequency and valence by relaxing the selection criteria of Kousta et al.’s (2009) experimental design: at the end of this section, we also address the issue of statistical power. Instead of maximizing contrasts in the values of valence (negative below 3.5, neutral between 4.5 and 5.5, positive above 6.5) as in the original study, here we binned valence into discrete categories based on tertiles (33% and 66%) of the valence distribution in the ELP and BLP datasets. Since contrasts between valence conditions are less extreme in this setup, we expected to yield a larger number of matched samples overall, and particularly a larger number of samples with fairly weak correlations between valence and log frequency. Retaining only those samples in which valence and frequency are near-orthogonal offers one way of eradicating the problem of collinearity. Also, an expected increase in the number of matched samples would help assess probabilities of opposing theoretical patterns in the outcomes of virtual experiments.

3.1 Methods

A set of 12324 words from the ELP dataset for which lexical decision RTs and other lexical variables were available was split into negative, neutral and positive conditions with tertiles of valence (4.65 and 5.68) as cut-off points. A set of 6742 words from the BLP dataset was split into conditions with tertile valence cut-off points of 4.71 and 5.7. We drew 5000 samples with replacement from the ELP and, separately, the BLP datasets, such that each sample contained 40 words from the positive, neutral and negative ranges of valence (see above for tertiles as new cut-off points for valence bins), for a total of 120 words. Matching criteria on lexical variables other than valence were as described in Study 1. No two samples drawn from ELP or BLP shared more than three words, and thus they were practically independent.

3.2 Results and discussion

This bootstrapping procedure retrieved 163 samples from ELP and 46 from BLP. Table 1 summarizes descriptive statistics for critical lexical properties averaged across resulting samples: Each sample was matched on the same set of lexical variables, and using the same criteria as in Kousta et al. (2009) and Study 1. The pattern of behavioral responses in each sample can be considered an outcome of an experiment, irrespective of other samples, and thus the result of the bootstrapping amounts to a 163-fold and 46-fold replication of the original study.

First, we estimated correlations between valence and log frequency of 120 words in each sample. Pearson’s correlation coefficients ranged between −0.06 and 0.27 in ELP samples, and between 0.03 to 0.26 in BLP samples. Eighteen ELP samples (11%) and 15 BLP samples (33%) showed a significant positive correlation (p < 0.05) between valence and log frequency. Even though all our samples were frequency-matched (i.e. the means of log frequency were no different between negative, neutral and positive words, as established with two-tailed paired t-tests using the 5% significance level), in a substantial percent of samples, more positive words were reliably more frequent, and so any comparison of RTs between valence levels in such samples could be confounded by this frequency bias. Our further consideration was then confined to 145 and 31 samples from ELP and BLP datasets that did not show a significant correlation between valence and frequency. (This method can be expanded to remove samples with any number of undesired correlations between variables.) The mean RTs (SDs in parentheses) of the negative, neutral and positive conditions across ELP samples were 740 (103), 722 (98), and 705 (95) ms. In BLP samples, respective values were 605 (59), 604 (60), and 589 (57) ms. As in Study 1, RTs aggregated across ELP samples were consistent with the linear negative effect advocated by Kuperman et al. (2014), while those aggregated across BLP samples were more ambiguous about a contrast between negative and neutral words, not lending unequivocal support to either of the hypothesized patterns.

Our primary interest was in probabilities of two patterns of differences between RTs as a function of valence: an inverse-U shape of the valence effect on RTs vs a monotonic near-linear negative relation between valence and RT. We operationalized pairwise differences between RTs to negative, neutral and positive words in each sample as the effect size d (Cohen, 1988), see above for definition. As in Study 1, we considered a sample to fit the inverse U-shape if the standardized difference between positive and negative words that d represents was below the threshold that Cohen (1988) assigned to a small effect (|d| < 0.2), while both positive and negative words were responded to faster than neutral ones with the effect size equal to or exceeding that threshold (d < −0.2). For a sample to provide support for the gradient negative effect of valence, we required that all three differences (positive vs negative, positive vs neutral, neutral vs negative) produce effects above the small-effect threshold (d < −0.2) with increased word positivity eliciting faster responses.

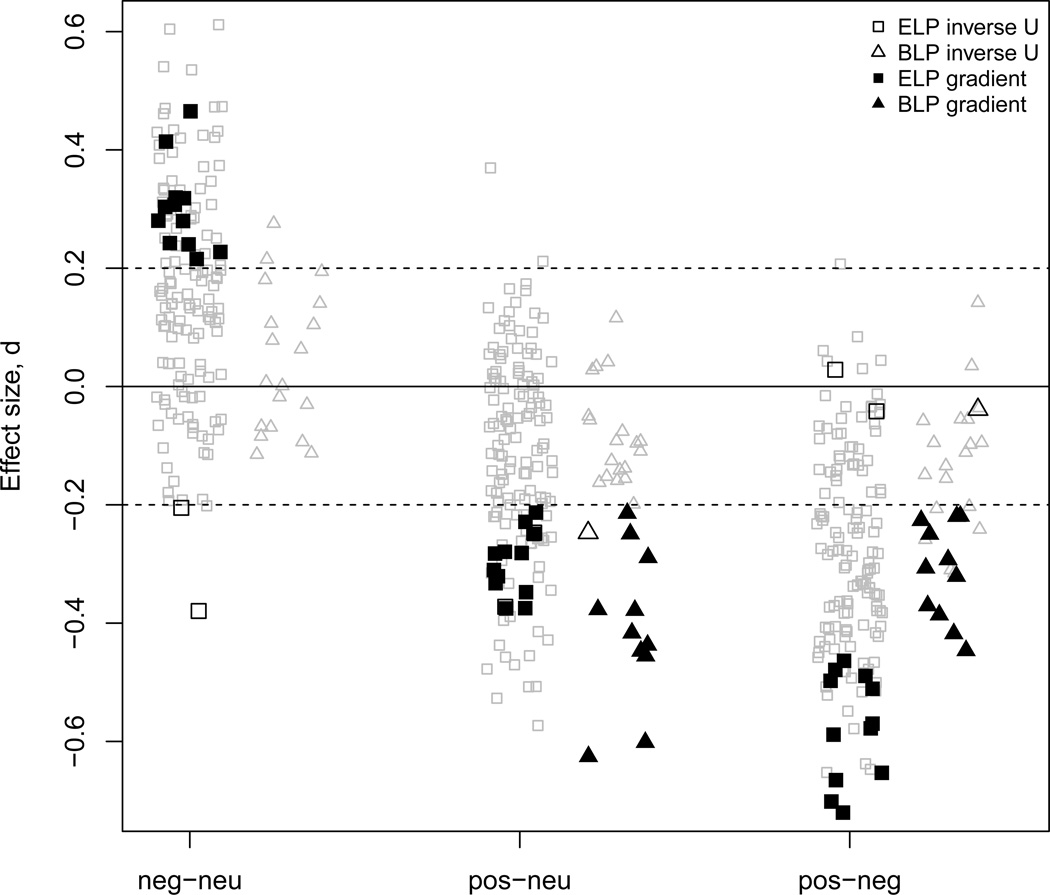
Figure 1 visualizes the spread in pairwise differences between all valence levels for each ELP and BLP sample, by plotting respective estimates of d. An individual sample is then represented in Figure 1 by three points, one for each pairwise difference between three valence levels. We calculated the number of sets in which (a) the difference between mean negative and mean neutral RTs was below d = −0.2 (the lower dotted line), (b) the difference between mean positive and mean neutral RT was also below d = −0.2, and (c) the absolute value of the difference between mean negative and mean positive RT was smaller than 0.2 (between the dotted lines). Only 2 out of 145 samples from the ELP dataset satisfied these requirements, shown as unfilled black squares in Figure 1. Alternatively, Kuperman et al.’s (2014) account suggests a gradient decrease in RTs related to higher positivity of the word. We calculated the number of datasets in which (a) the difference between mean negative and neutral RTs was above d = 0.2 (the upper dotted line), (b) the difference between mean positive and mean neutral RTs was below d = −0.2 (the lower dotted line), and (c) the difference between mean positive and mean negative RTs was below −0.2 (the lower dotted line). Twelve out of 145 ELP samples followed this pattern, shown as filled black squares in Figure 1.

Figure 1.

Pairwise differences in RTs between valence levels presented as effect sizes d for each ELP and BLP sample (horizontal jitter added for legibility). Squares indicate d values for ELP samples, and triangles for BLP samples. Unfilled black symbols indicate samples supporting the inverse-U shape of the valence effect on RTs in all three differences. Filled black symbols indicate samples supporting the gradient negative relationship of RT with valence in all three pairwise differences. Differences in remaining samples are shown in gray. Dotted lines represent the 0.2 effect size.

Since negative and neutral words elicited very similar RTs in samples from BLP, we only used criteria (b) and (c) from respective accounts to estimate the likelihood of the patterns they predict in BLP samples. Thus, the inverse-U functional form is only one of several that could be compatible with these criteria. Only one out of 31 BLP samples (unfilled black triangles in Figure 1) were consistent with Kousta et al.’s predictions, and 11 (filled black triangles) with Kuperman et al.’s predictions.

We also estimated whether there was an overall tendency for the pairwise differences in RTs between valence levels to be positive or negative. Two-tailed Wilcoxon rank sum tests compared the central tendency in the distribution of d values against zero for each of three pairwise comparisons between negative, neutral and positive words in the ELP- and BLP-derived samples. None of the distributions as a whole showed a significant location shift in either a positive or negative direction. This suggests that while a small percentage of individual samples showed a tendency towards an inverse-U shape or a gradient negative slope, standardized differences between RT means gauged by Cohen’s d were too small in the majority of samples and too unreliable to indicate a larger cross-sample trend. All the findings above were replicated when z-transformed RTs were used instead of raw RTs.

To sum up, the pattern of a gradient decrease in RTs that comes with increasing valence finds a somewhat stronger support in the variety of virtual experiments that adopted the original experimental manipulation (with less stringent binning of valence): 12 vs 2 samples from ELP and 11 vs 1 samples from BLP are consistent with this negative relationship. Also, we lessened the potential confounding role of word frequency by excluding samples in which it strongly correlated with valence: such a correlation affected over 10% of ELP samples and over 30% of BLP samples despite the matching procedure. Yet, the number of samples that fully converged with either set of predictions was essentially at the chance level and thus does not provide the grounds for an unequivocal preference for any theoretical account. We believe this to be a direct consequence of a very low level of statistical power (i.e. power of 0.23 for d = 0.2) that a factorial design with discretization of continuous dependent variables and matching of continuous independent variables offers for detection of small- and mid-size effects (Baayen, 2004; Cohen, 1983; MacCallum et al., 2002). It is worth reminding the reader that such designs - and the concomitant problems of low power and uncontrolled collinearity - are still standard and prevalent in psycholinguistic research (see Balota et al., 2013 for discussion).

We explored whether statistical power could be feasibly increased as part of the present bootstrapping procedure. Power analysis indicated that each item set needed to contain 198 words to afford an 80% probability of detecting a small effect (d = 0.2) in a two-tailed paired t-test comparing means of RTs between any two sets, with a 5% significance threshold. We drew 5000 samples with replacement from the ELP and, separately, the BLP datasets, such that each sample contained 200 words from the positive, neutral and negative ranges of valence (see above for valence cut-off points), for a total of 600 words. Matching criteria on lexical variables other than valence were as described in Study 1. Critically, there was not a single 600-word sample drawn from either dataset that would satisfy the present selection criteria. Our inspection of lexical characteristics of obtained samples revealed a variety of reasons for their failing to match, but most samples varied too strongly on average log frequency across valence bins. This outcome illustrates an extreme difficulty of coming up with a factorial design that provides both the experimental control over a broad range of lexical variables and substantial statistical power to detect a small effect. We note that the problem is serious even with large-scale megastudies at one’s disposal as a resource for sampling. In line with Baayen (2004, 2010) and Balota et al. (2004), we argue in Study 3 that this difficulty can be avoided if regression design and regression modeling are used.

4 Study 3

This study evaluates the probability of conflicting theoretical patterns by implementing a series of virtual experiments using a regression design. The statistical technique of regression is designed to estimate the relation between an independent and a dependent variables, over and above contributions of other independent variables. As such, it enables us to estimate the valence effect (and the shape of its functional relation with the RT) over and above the confounding effect of frequency (Larsen et al., 2006) and other variables in each sample.

4.1 Methods

To test theoretical patterns of the motivated attention account (an inverse-U shaped effect of valence) and the gradient automatic vigilance account (a negative monotonic slope of valence), we fitted RTs to words in each sample with three kinds of regression models, using two or three predictors. Model A contained log word frequency and valence as independent predictors, Model B had a valence by log frequency interaction as a predictor, while Model C had log frequency and the linear and quadratic terms for valence as predictors (using restricted cubic splines to approximate nonlinearity led to same results). To avoid the confounding impact of word frequency, this predictor was included in each model type either as a main effect (A and C) or – in accordance with findings of Kuperman et al. (2014), Scott, O’Donnell, & Sereno, (2012), and Sheikh and Titone (2013) – in an interaction with valence (B)². A negative effect of valence in Models A or B would be consistent with the gradient automatic vigilance account of Kuperman et al.’s (2014) large-scale regression study, which was based on ELP data and reported a monotonic negative relation of valence with RT that was additionally found to decrease in magnitude in higher-frequency words. A nonlinear (inverse-U) functional relationship between valence and RT, estimated over and above the contribution of frequency in Model C, would instead indicate convergence with the motivated attention account of Kousta et al. (2009) and experimental results of Kousta et al., Yap and Seow (2014), Vigliocco et al. (2013) and Vinson et al. (2014).

Statistical considerations

We conducted power analyses to estimate a sample size that would allow for a reliable detection of effects in regression models. Prior research (Kuperman et al., 2014) estimated the amount of variance explained by valence at about 2%: a regression model with multiple other lexical predictors including valence (R²_ab was 60% and the amount of variance explained by the regression model without valence (R²_a) was 58%. We used Cohen’s (1988) formula for estimating effect size associated with valence: $f^2=\frac{{R^2}_{ab}-{R^2}_a}{1-{R^2}_{ab}}$ Thresholds suggested by Cohen for small, medium and large effects are f²=0.02, 0.15, and 0.35, respectively. The f² of 0.05 obtained in the power analysis of Kuperman et al.’s data qualified the effect of valence in the regression model as small. For the present bootstrapping procedure, we adopted Cohen’s conservative threshold of a small effect (f²= 0.02). To reiterate, our goal is to identify the sample size that would allow a regression model with up to three predictors (see above for description of models A–C) to detect a small effect with 80% probability (power) using the 0.05 significance threshold. Power analysis indicated 549 data points (or 545 degrees of freedom in the denominator) as the optimal sample size for the regression model with the given set of parameters. To accommodate this power conservatively, we chose 600 observations (i.e. words with their mean RTs) to be the size of each of 5000 samples drawn with replacement from ELP and BLP datasets.

Collinearity might affect the accuracy of estimates of a regression model (e.g. Cohen, Cohen, West, & Aiken, 2003). However, its harmful influence is expected to be noticeable when predictors show much stronger correlations (r > 0.5) than the correlation between frequency and valence that we observed in the samples from ELP and BLP datasets (r < 0.3). We concluded that collinearity is immaterial for the purposes of this study.

4.2 Results

We drew 5000 random samples of 600 datapoints with replacement from ELP and BLP datasets. No binning or matching criteria were applied to how words were sampled. On average, 32 words (or 5%), and no more than a total of 55 words (9% of the sample size), overlapped between any two samples, making it unlikely that the observed effects are driven by a small set of overutilized items. Three regression models (A–C) were fitted to RTs in each sample. A critical result was a significant effect (at the 5% level) of either valence as a linear main effect (Model A), the interactive term of the valence by frequency interaction (Model B), or the quadratic term of valence (Model C). In cases where more than one pattern elicited a significant effect, the model with the lowest AIC was chosen to represent the sample as the best fit to the data.

Out of 5000 samples from the ELP database, 1084 samples did not show a significant critical effect in any of the three models. The observed percentage of null effects (21%) is consistent with the value of statistical power (0.8) that we chose for the experiment. The distribution of patterns over the remaining 3916 samples was as follows: 1136 (29%) samples showed a linear negative effect of valence, 2553 (65%) a linear negative effect of valence that decreased in its slope as frequency increased (e.g. showed a significant valence by frequency interaction), and 227 (6%) demonstrated quadratic nonlinearity which, upon further inspection of relevant samples, had an inverse-U shape. To sum up, in the vast majority (94%) of samples that showed any effect of valence, shorter RTs were associated with positive words rather than with valenced (positive or negative) ones. Findings were very similar with z-scores of RTs as dependent variables: 591 samples (12%) did not show a significant effect in any of the models. The distribution in the remaining samples was as follows: 891 (20%) showed an independent linear negative effect of valence, 3393 (77%) revealed a significance valence by frequency interaction, and the remaining 125 (3%) demonstrated an inverse-U shaped relationship between valence and z-transformed RTs. Again, the vast majority of samples (97%) supported the monotonic negative slope of the effect of valence on response latencies.

This set of findings dovetails perfectly with the gradient automatic vigilance account advocated by Kuperman et al. (2014). Additionally, the interactive pattern (the negative effect of valence on RTs attenuated in higher-frequency words) reported by Kuperman et al. in their analysis of the entire ELP dataset emerged as a dominant, if not ubiquitous, pattern in the present bootstrapping study, pointing to the stability of this empirical finding. Why the negative effect of valence is modulated by frequency in only a majority but not all of the samples is a topic for further investigation. We note however that samples giving rise to a significant interactive pattern tend to have broader ranges of both log frequency values and values of valence than the samples in which independent linear effects of valence and frequency were observed.

A very different set of results emerged in the 5000 samples drawn from the BLP dataset. One or more critical effects reached significance in 3461 (69%) samples. Within those samples, the distribution of patterns was as follows: 72 (2%) samples showed a linear negative effect of valence, 1414 (41%) an interaction between valence and frequency (with a flatter negative slope of valence in higher-frequency words), and 1975 (57%) a nonlinear effect, which invariably took an inverse-U shape. A similar pattern emerged when using z-scores. In 3712 (74%) of the samples, at least one of the models reached significance. Within this set, 42 samples (1%) showed an independent linear negative effect of valence, 1577 (42%) showed a significance valence by frequency interaction, and the remaining 2093 (57%) were in line with the inverse-U shape of the valence effect.

Thus, the prevalent nonlinear pattern replicated the one observed in the regression study of Vinson et al. (2014) which used 1313 words from the same source of RTs, i.e. the BLP dataset. This pattern also converged with well-replicated findings of smaller-scale experiments by Kousta et al. (2009), Yap and Seow (2014) and Vigliocco et al. (2013). This stands in stark contrast with the dominance of the negative linear effect of valence observed in both the samples from ELP (see above) and the entire ELP dataset (Kuperman et al., 2014). Importantly, however, results of this virtual regression experiment provide substantial support for both theorized patterns, with only a slight bias (57 vs 43%) towards a speed-up in RTs to very positive and very negative words.

The discrepancy between the valence effects in ELP- and BLP-derived samples could be due to the differences in words that were randomly and independently drawn from ELP and BLP. To eliminate this possibility, we drew an additional 5000 samples of 600 words from a list of 6736 words that are found in both ELP and BLP datasets. This time, in any given sample we analyzed z-transformed RTs from ELP and BLP to the same set of lexical items. Furthermore, for each sample we calculated a correlation between ELP and BLP RTs. Across samples (N = 600), the Pearson’s correlation coefficients ranged from 0.64 to 0.78, while the correlation between full overlapping data sets (N = 6736) was r = 0.72 (all ps < 0.0001): thus, one set of RTs explained 40 to 60% of variance in another set.

The pattern of the valence effects across samples was virtually identical to the one reported above: of the 4274 samples of ELP RTs that showed significance in any of the patterns, 98% demonstrated the negative monotonous relation of valence and RTs (with or without an interaction with frequency) and 2% were compatible with the inverse-U shaped valence effect on RTs. Within 3938 samples of BLP RTs that showed a significant pattern, 58% showed the inverse-U shape and 42% a negative linear shape of the valence effect. To conclude, the cross-study discrepancy in the functional form of effects did not come from differences in word sampling. Below we discuss both the discrepancies between datasets of behavioral latencies, and the utility of the probability distribution of data patterns that our bootstrapping procedure affords.

5 General Discussion

This paper explores the potential of behavioral and norming megastudies to bootstrap psycholinguistic studies with factorial and regression designs, via series of virtual experiments. The usual notion of a virtual experiment is that of a one-time replication of a completed experimental study through the cross-check of behavioral responses to its stimuli list made in that study and a response database. A comparison of the responses obtained in a hypothesis-driven small-scale experiment and a hypothesis-blind large scale megastudy is typically interpreted as (in)validation of the results of that small-scale experiment or, more commonly, of that megastudy. We propose a more robust validation procedure that is predicated on availability – through megastudies – of both extensive collections of behavioral data (represented for the lexical decision in English by the English and British Lexicon Projects, Balota et al., 2007, Keuleers et al., 2010), and equally broad collections of objective or subjective norms for a variety of lexical variables. The core of this approach is in drawing multiple random samples of lexical items from a database of behavioral responses and retaining only those that satisfy the demands of statistical power and selection criteria of the chosen (existing or novel) manipulation. Responses to resulting samples of the items can be analyzed to identify the presence and the functional form of the effect of critical variables in each sample and across samples. Moreover, the procedure generates the distribution of characteristic patterns of effects, which is indicative of how probable each pattern is and what statistical properties of the samples contribute to the prevalence of one pattern over others. If conflicting theories motivate specific functional forms for effects of interest, the probability distribution of patterns can point to how accurate one’s theorizing might be if it is based on a behavioral pattern observed in a single sample. In what follows we first summarize our three studies, with an emphasis on issues of statistical power and collinearity, and then discuss what multiple virtual experiments can and cannot achieve as a methodological paradigm.

Validation of the valence effect on lexical decision latencies

Recent work reporting an effect of valence on lexical decision latencies provided the focus of this study. A series of factorial studies (Kousta et al., 2009; Vigliocco et al., 2013, Yap & Seouw, 2013) used the same stimulus list and reported an inverse U-shaped relationship between valence and RTs, such that positive and negative words elicited equally fast responses, and both conditions were responded to significantly faster than neutral words. The inverse-U pattern was also reported in a regression study of the BLP dataset by Vinson et al. (2014). This body of evidence supports the “motivational relevance” account, with very positive and negative words benefitting from allocation of additional attentional resources associated with the approach or avoidance motivational systems (Lang, Bradley, & Cuthbert, 1990, 1997). Conversely, the regression analysis of the ELP data in Kuperman et al. (2014) attested a negative monotonic near-linear relationship with more positive words responded to faster across the entire valence range, rather than an equal advantage to positive and negative words. While no specific prediction regarding an interaction of valence and frequency was made on theoretical grounds, the negative effect of valence was attenuated in higher-frequency words. Kuperman et al. linked their findings to the gradient nature of the automatic vigilance mechanism that makes human perception more attuned to threatening negative stimuli (Erdelyi, 1974; Pratto & John, 1991), in proportion to how threatening or negative they are.

To establish probabilities of the two alternative patterns of the valence effect on RTs (an inverse-U shape vs negative slope), three studies were conducted, each drawing multiple random samples of words and RTs from ELP and BLP lexical decision datasets and looking up additional lexical variables in a broad range of norming studies (see above). Study 1 adopted all essential aspects of the stimulus selection procedure proposed in Kousta et al. (2009), including the binning of valence into negative, neutral and positive discrete groups of words and pairwise matching of all groups on means of multiple lexical variables. Of 5000 samples, Study 1 only yielded 3 required samples from the ELP and 1 sample from the BLP that matched the original selection criteria. That is, our hypothesis-blind automatic bootstrapping procedure, which has at its disposal thousands of lexical items to choose from, was only able to generate about as many satisfactory samples as did the painstaking elaborate manual selection of a sample done in the original study. This result corroborates the long-standing notion that the compilation of lists of stimuli with required characteristics may be non-random and critically depends on experimenters’ intuitions and experience, leaving the door open to experimenter bias (Cutler, 1981; Forster, 2000).

Study 1 also highlighted two statistical issues that are difficult for factorial experimental designs to tackle: low statistical power and collinearity. As our reanalysis of prior studies indicated, the size of the effect of valence on lexical decision RTs was small. Further power analysis of the factorial design, as implemented in Kousta et al. and adopted in a number of follow-up studies and in Study 1, demonstrated that it would fail to detect a small effect in 50 to 77% of cases. In line with this observation, none of the samples that we retrieved in Study 1 showed all the pairwise differences between negative, neutral and positive words that were predicted under either theoretical account. The issue of collinearity stemmed from the fact that valence and frequency showed a moderate positive correlation in both ELP and BLP datasets, as well as in a substantial percent of samples from these datasets in both Study 1 and Study 2. Thus, an apparent effect of valence might in fact be due to a well-established word frequency effect on lexical decision RTs. While the matching procedure ensures that mean log frequency does not differ significantly between negative, neutral and positive words in each retained sample, it does not rule out a correlation between valence and frequency if all words in the sample are considered jointly, across levels of valence. The given study design with discretization of valence and matching of valence levels on frequency cannot dis-confound the contribution of the two variables in question. Indeed, a positive correlation between valence and frequency was observed in all samples, reaching statistical significance in some of them. To sum up, low power and collinearity rendered patterns observed within samples unreliable, and due to the paucity of retained samples the probability distribution of conflicting patterns across samples could not be utilized either.

Study 2 increased the number of samples obtained through bootstrapping by using less rigid criteria for including words into negative, neutral and positive groups: all matching criteria were maintained as defined in Kousta et al. (2009) and Study 1. Study 2 also addressed the issue of collinearity by only retaining samples that did not show a statistically reliable correlation between valence and log frequency. The multiple samples generated by the bootstrapping procedure can be considered independent and represent a multifold replication of the original experiment. While the resulting number of samples was substantial (145 and 31 from ELP and BLP respectively), very few samples showed valence effects that supported either the motivational attention account (2 in ELP and 1 in BLP) or the gradient automatic vigilance account (12 in ELP and 11 in BLP). Figure 1 and analyses of the probability distributions of pairwise differences between valence levels demonstrate that the vast majority of samples produced very weak effects of valence, well below the “small effect size” threshold. We link this to the reduction in statistical power of detecting small effects in a factorial experiment that is caused by a sample size limited by the matching procedure and the binning of continuous variables of interest into discrete categories (cf. Baayen, 2004; 2010, and references therein). Again, low statistical power and concomitant weakness of effects made probability distributions of effects over samples unusable.

Another important finding of Study 2 is the virtual impossibility of creating samples that would both satisfy the item selection criteria and have a size that affords sufficient statistical power. Our power analysis indicated 600 (200 triples of negative, neutral and positive) words as a sample size that would lead to a 80% probability of detecting a small size effect of valence in Study 2. Not one of the 5000 samples of this size, drawn from either ELP or BLP, was found to satisfy the matching criteria of Study 2, i.e. the slightly relaxed criteria of Kousta et al.’s design. Given the wealth of resources available and the large number of random samples drawn, this finding suggests that the problem of providing required statistical power to one’s study is practically unsolvable in the situation of an expected small effect size, and a factorial design that requires extensive matching of control variables.

Finally, Study 3 implemented recommendations of Baayen (2004; 2010), Balota et al. (2004) and Cohen (1983, 1988), among others, and adopted a regression design, which eschewed discretization of continuous variables and used statistical control over potential confounds instead of their experimental control through matching. The issue of statistical power was addressed by setting a sufficient sample size as indicated by power analysis. Also, in all samples collinearity was below a level that is harmful for the accuracy of regression models. Most samples from both ELP and BLP datasets (79% and 69% of 5000 samples respectively) showed a reliable effect of valence on RTs in one of the three forms: an independent negative effect, a negative effect modulated by log frequency (a steeper slope of valence in lower-frequency words), or a nonlinear inverse-U effect. To reiterate, when applied to either ELP or BLP, this bootstrapping procedure amounts to a multifold replication of one-sample regression studies like Kousta et al. (2009), Kuperman et al. (2014) and Vinson et al. (2014). The gradient automatic vigilance account of Kuperman et al. (2014) and their regression analysis received decisive support in the pool of samples drawn from the ELP dataset: the probability of observing the linear negative effect of valence on RTs in samples that showed a reliable behavioral pattern was 94%.

A pool of samples from BLP revealed that probabilities of an inverse-U pattern and of a negative linear pattern (with or without an interaction with frequency) were split more evenly, 57% vs 43%. The motivated attention account of Kousta et al. (2009) receives the majority vote in this dataset. At the same time, the resulting probability distribution illustrates the risk of basing one’s conclusions about the link between language and emotion on any one sample. Picking either the motivated attention model or the gradient automatic vigilance model on the basis of a single sample from BLP would fail to account for close to 50% of samples from the same statistical population. Skewness of results may be even more drastic if the single sample that one chooses for theory testing happens to represent a minority pattern (e.g. the 6% of samples with an inverse-U shaped valence effect in ELP samples, or the 2% with the linear negative valence effect in BLP samples). It is in such cases of indeterminacy that the utility of the bootstrapping procedure, and the probability distributions that it generates, is paramount.

Our bootstrapping approach is equally useful in enabling an inspection of samples from the same data population that support opposite theoretical patterns and identification of lexical properties that give rise to the discrepancy possibility. Distributions of most lexical variables (e.g., valence, arousal, length, AoA) did not vary between BLP samples giving rise to an inverse-U shape and those with a negative valence effect. However, average log frequency was significantly higher (p = 0.04 in a two-sample t-test) in the samples supporting the monotonic negative valence effect. Thus, the shape of the valence effect, especially in very negative words, appears to be contingent on how frequent these words are in each sample: this is in line with an observation of Larsen et al. (2006, 2008).

To sum up, factorial experiments (Study 1 and 2) do not appear to provide sufficient statistical grounds for adjudicating between conflicting theoretical accounts. Multifold replications of a regression-based Study 3 showed that an answer to the question of which pattern characterizes the link between language and emotion best is specific to the dataset. Thus, support for the negative effect of valence ranges from sweeping in the ELP dataset to below-average in BLP-derived samples. In what follows we rule out several possible explanations and speculate on a few others that require further investigation.

One potential source of variability is our bootstrapping procedure. However, in Study 3 we replicated the divergent patterns of valence effects in the samples of words that occurred in both ELP and BLP and thus ruled out differences in random sampling as a relevant factor. Another source might be the difference in samples of participants, lists of stimuli, and testing conditions between ELP and BLP megastudies. In Study 3 we report strong correlations between mean z-transformed ELP and BLP RTs to the same words (r = 0.72, p < 0.0001). Still, even though averaging and z-scoring attenuate individual and task differences (Balota et al., 2007), about half of the variance in one dataset is unexplained by another, leaving room for either potential systematic differences between datasets, or noise inherent in lexical decision studies (Diependaele & Brysbaert, 2012). All in all, we consider differences between lexical decision megastudies to be an unlikely cause of the discrepancy in valence effects. Such differences would have to specifically influence response behavior to very negative words (which is where the negative linear form and the inverse-U shape diverge) and not to the words from the remainder of the valence range.

A final, and more likely, explanation stems from the fact that ratings of valence that we used here and in Kuperman et al. (2014) were collected from US responders rather than British ones, yet they were applied for analyses of both the ELP and BLP data, thus overlooking potential regional variation in either lexical semantics or affective reactivity. The lack of a sufficiently large pool of affective ratings for UK participants may account for the apparent lack of difference between negative and neutral words in BLP data and for the variability in responses to very negative words by BLP participants. We leave the methodological scrutiny of the discrepancy between effects of valence on the ELP and BLP data to future research. It also stands to reason that an ultimate determination of the relationship between valence, frequency and the effort of word recognition will require data from multiple experimental paradigms, beyond lexical decision datasets.

What virtual experiments can and cannot do

As demonstrated above, virtual experiments enable an estimation of how probable a certain pattern is when pitted against similarly selected samples of items. The procedure can easily incorporate any set of selection criteria that a researcher wishes to impose on the stimuli, by retaining only those samples that satisfy these criteria. While we only demonstrated this ability in factorial Studies 1 and 2, one may require certain properties of a sample used in a regression analysis too, e.g. a specific distribution of the dependent or independent variables, a presence or absence of a correlation between variables, and others. An important outcome of the bootstrapping approach is quantification of how rigid the criteria are, and how likely researchers are to come about a valid sample randomly, without using their intuitions. The technique we propose can also be readily used for bootstrapping participants of a megastudy, thus ensuring that the resulting patterns are not specific to a participant cohort. The procedure is valuable insofar as it protects researchers from experimenter bias (Forster, 2000) and from building theoretical models based on a sample that represents a rare mixture of lexical properties or represents a minority pattern.

There are several methodological issues that multifold sampling from megastudies is not designed to resolve. For instance, this technique may not be helpful if the research question crucially hinges on the context in which items occur, such as list or block effects, short- or long-distance priming, or any other manipulation which requires a certain order of and distance between experimental items. Samples from stimuli lists of the megastudy will not generally comply with specifications like these. Moreover, drawing multiple samples does not decrease the probability of a Type II error in any individual sample, i.e. it does not increase statistical power. As discussed in Studies 1 and 2, the limitations of an original design, such as reduced statistical power and collinearity of predictors, are not removed by virtue of bootstrapping that design multiple times.

To conclude, one of the currently underutilized benefits that megastudies afford is the ability to test one’s hypothesis against a range of samples selected in a uniform, principled manner. Virtual experiments can be fruitfully used not only for replicating the results of a small-scale laboratory experiment, but also for shedding light on how likely the results of that experiment are in a much broader distribution of possible outcome patterns.