Computing the functional proteome: recent progress and future prospects for genome-scale models

Abstract

Constraint-based models enable the computation of feasible, optimal, and realized biological phenotypes from reaction network reconstructions and constraints on their operation. To date, stoichiometric reconstructions have largely focused on metabolism, resulting in genome-scale metabolic models (M-Models). Recent expansions in network content to encompass proteome synthesis have resulted in models of metabolism and protein expression (ME-Models). ME-Models advance the predictions possible with constraint-based models from network flux states to the spatially resolved molecular composition of a cell. Specifically, ME-Models enable the prediction of transcriptome and proteome allocation and limitations, and basal expression states and regulatory needs. Continued expansion in reconstruction content and constraints will result in an increasingly refined representation of cellular composition and behavior.

Introduction

Building computational whole cell models has been a long-standing goal of theoretical biology. In the 1980s, serious attempts to build large-scale models of a whole bacterium were undertaken [1]. A few years later, an attempt to build whole cell models for the human red cell represented a culmination of decades of work [2–6]. Perhaps the most comprehensive whole organism model appeared in the mid 1990s for the lambda-bacteriophage [7,8]. Time scale decomposition of these early models showed that their effective dynamic order was low [9] and that their dynamic structure was relatively condition invariant [10], motivating the development of constraint-based models that minimized the need for kinetic information [11].

After the first full genome sequences appeared, constraint-based models could be scaled up to the genome-scale [12]. As the first genome-scale models (GEMs) proved their ability to predict biological functions [12,13], a vision was laid out in 2003 [14] that all cellular functions could be reconstructed in biochemical terms and seamlessly integrated. A decade later, some of this vision has been realized [15–19]. With these achievements, we can now assess what might be ahead with genome-scale models over the coming decade. We lay out some of our thoughts in this commentary.

The expanding scope of reconstructions: synthesis and function of the proteome

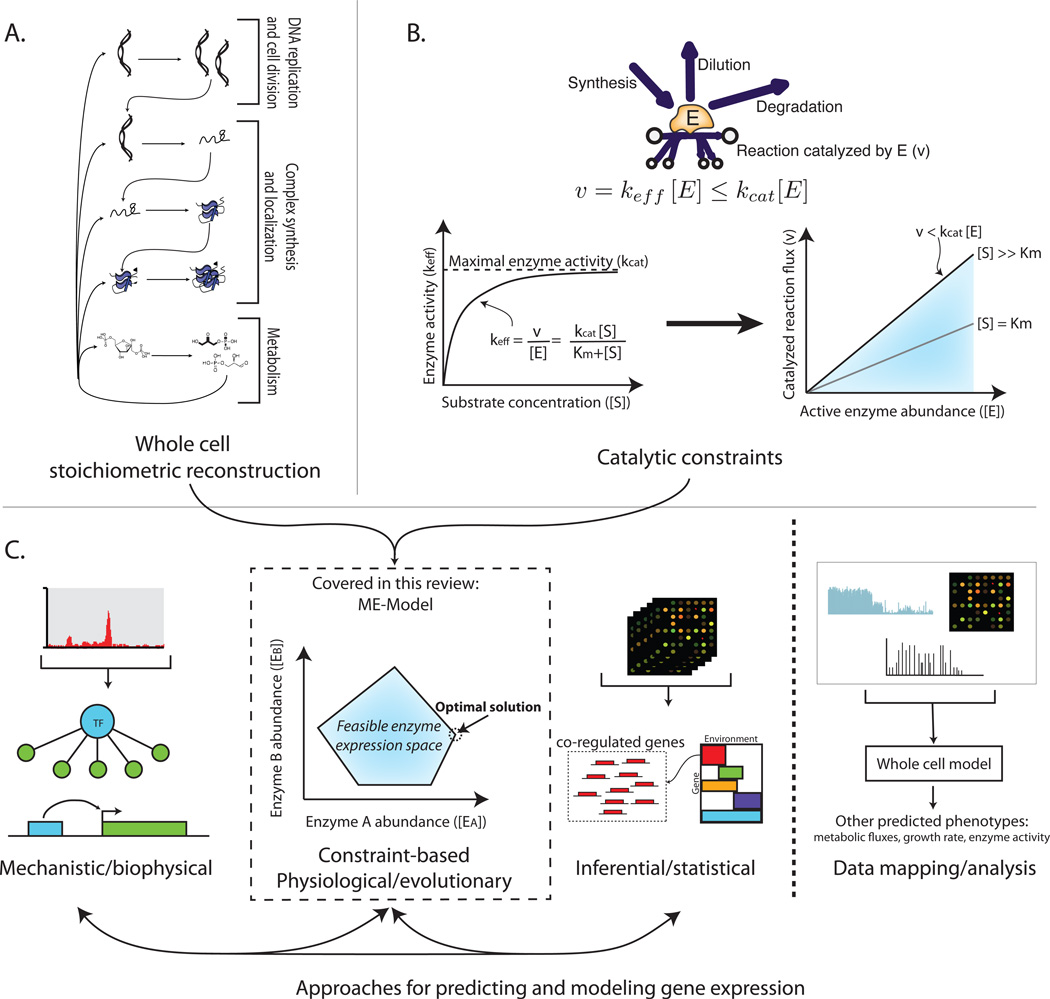
To date, stoichiometric reconstructions have largely focused on metabolism, resulting in genome-scale metabolic models, M-Models. The processes of enzyme synthesis including transcription, translation, protein folding, complex formation, and prosthetic group integration were formalized in a gene expression reconstruction [20]. Protein translocation and localization pathways [18,21] and DNA replication, repair, and cell division have also been reconstructed [19]. These networks have been merged with metabolic reconstructions to create integrated reaction networks [15–19] that formalize the primary chemical transformations that occur in cell (Figure 1A). Models integrating metabolism with protein expression are called ME-models.

Figure 1. The expanding scope of reconstructions: synthesis and function of the proteome.

A) Stoichiometric reconstructions represent the chemical transformations that can occur in a cell and form the base of whole cell models. Recent reconstructions represent all of the major steps in the central dogma of molecular biology in biochemical detail [15–19].

B) Constraints on network operation are utilized to predict functional states. For reconstructions that encompass enzyme synthesis and function, catalytic constraints are necessary [15,20]. Catalytic constraints relate enzyme abundance to its dilution (to daughter cells), degradation, and catalyzed flux with kinetic and/or thermodynamic relationships.

C) Several general approaches exist to predict and model gene expression. Mechanistic/biophysical approaches first start from bottom-up reconstructions of transcription factor interactions and promoter architectures [56], aided by high-throughput data types [95]; models of regulatory logic can then be reconstructed and imposed [71,96]. Constraint-based models are built from reconstructions of biochemical networks and constraints on their operation and can then be used to compute feasible and optimal physiological states [15–18]. Importantly, the constraint-based approach enables prediction of gene expression states without any previous gene expression measurements. Inferential/statistical approaches are based on large gene expression datasets across environmental and genetic perturbations to identify co-regulated gene sets and their expression under novel perturbations. These general approaches can also be combined into hybrid models [24,25]. Finally, we distinguish approaches that predict gene expression from those that use gene expression data from a particular state to predict other phenotypes [19,22]—another important capability of genome-scale models.

To enable prediction of biological phenotypes, stoichiometric reconstructions are combined with constraints on their operation. Stoichiometric networks are subject to (dynamic or steady-state) mass balance constraints on the production and consumption of molecules. For ME-Models, enzyme catalytic constraints are also necessary. In contrast to the typical use of kinetic equations to simulate system dynamics, the catalytic constraints in ME-Models are approximate stoichiometric relationships between enzyme abundance and catalyzed flux (Figure 1B). Adding these catalytic ‘coupling’ constraints [20] enables the computation of feasible and optimal proteome and transcriptome states.

Most models encompassing gene expression have used measured expression states as a prerequisite for simulations. Often, gene expression measured under a particular condition is used to predict other molecular and physiological phenotypes [19,22]. Alternatively, some approaches utilize gene expression data under environmental or genetic perturbations to build regulatory models [23]. These two approaches can be combined to predict molecular and physiological phenotypes subject to a transcriptional regulatory model [24,25]. These are undoubtedly invaluable types of models and predictions; similar methods will likely be applied to ME-Models (Figure 1C).

ME-Models can predict gene expression with no previous input expression measurements: they can compute protein abundances that are required to (optimally) achieve integrated physiological functions (Figure 1C). Enzymes have an optimal expression level subject to their (biosynthetic) cost and (physiological) benefit [26]. The ME-Model solves this cost-benefit optimization to compute genome-scale proteome states. Thus, compared to other methods for prediction and analysis of gene expression, predictions of gene expression in the ME-Model are based on fundamental constraints and optimality principles (as are the predictions of flux states in M-Models). ME-models can therefore be used to predict optimal expression and regulatory states.

Prediction of the molecular composition of a cell

An important distinction between M- and ME-Models is the prediction of cellular biomass composition. Instead of having protein and RNA biomass composition as an input (in the form of a biomass objective function [27]), biomass composition is an output that is predicted by ME-models. The expressed molecular machinery, such as the proteome, must support the integrated physiological functions of the cell. Rather than processes being coupled stoichiometrically through the biomass function, demands for vitamins and cofactors, chaperones, amino acids, nucleotides, tRNAs, etc. are derived directly from the computed proteome state.

Furthermore, a recent expansion of the ME-Model to include protein translocation enables predictions of a cell’s coarse-grained spatial organization [18]. Protein complexes are localized in cellular compartments required for enzyme function. With this expansion in scope, aspects of compartmentalized proteome abundance and molecular crowding can be assessed [18].

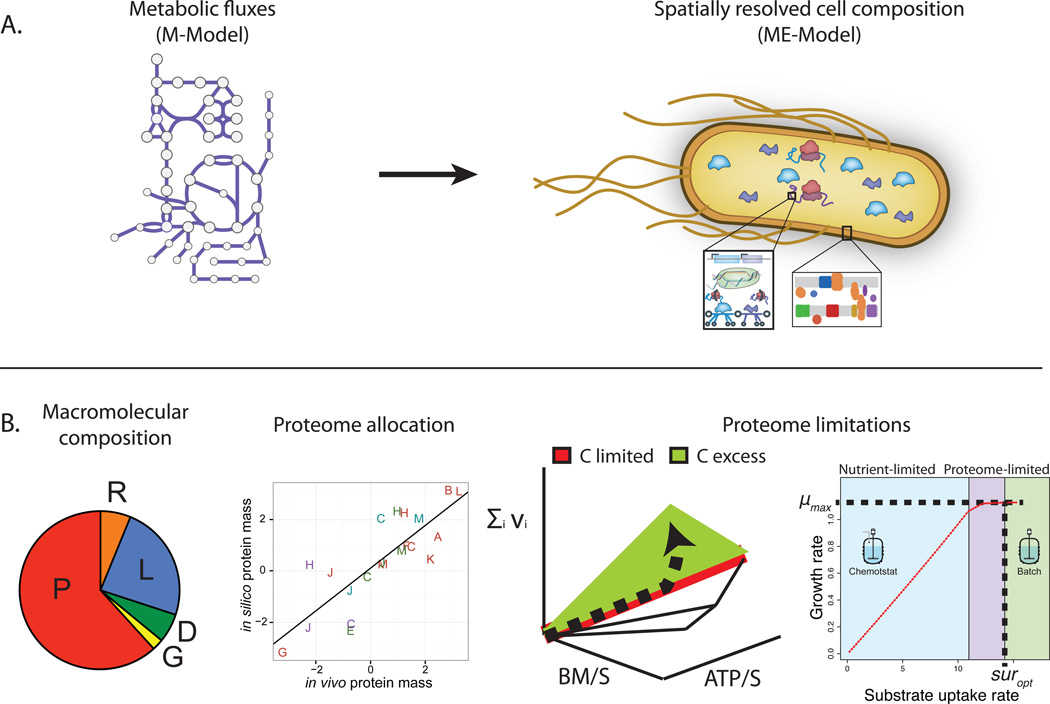
Thus, ME-Models advance the predictions possible with constraint-based models from network flux states to the spatially resolved molecular composition of a cell (Figure 2A).

Figure 2. Prediction of spatially resolved proteome allocation and limitations.

A) The expanded scope of reconstruction content advances the predictions possible with constraint-based models from network flux states (with M-Models) to the spatially resolved molecular composition of a cell (with ME-Models).

B) ME-Models predict the gross macromolecular composition of the cell and the detailed allocation of the proteome. Additionally, the effects of proteome limitations can be accounted for, including the prediction of optimal substrate uptake rates and specific pathway shifts from carbon-limited to carbon-excess environments.

Phenotypic effects of proteome allocation constraints

In addition to satisfying flux balance constraints, ME-Models are subject to proteome allocation constraints. While M-Models account for the ‘operating expenses’ (i.e., metabolic requirements) to carry flux through pathways, ME-Models also account for the ‘capital expenses’ (i.e., enzyme machinery) needed to catalyze all network reactions. Therefore, in addition to cellular functions being limited by nutrients, they can also be limited by properties of the proteome (i.e., due to limited protein synthesis capacity and enzyme catalytic rates). Proteome allocation constraints govern integrated cell functions and, combined with growth-optimality assumptions, can explain several aspects of cell behavior not encompassed by previous models (Figure 2B).

First, the change in ribosomal protein abundance can be explained by growth-optimization subject to proteome allocation constraints [15,17,20,28,29]. At faster growth rates, more ribosomes are required to sustain the faster dilution of protein to daughter cells. Previous models have taken this growth rate dependent relationship as an observed (and subsequently assumed and fixed) phenomenological relationship [30], rather than a prediction.

Second, specific pathway shifts in central carbon metabolism from carbon-limited to carbon-excess environments (i.e., batch culture or non-carbon limitations), can be explained as a consequence of proteome allocation constraints. Specific pathway shifts from carbon-limited to proteome-limited growth are consistent with pathway shifts observed between chemostat and batch cultures [17]. Whereas previous approaches required the invocation of multiple competing objectives [31], now a single objective of maximal growth rate subject to proteome allocation constraints can explain the same phenomenon.

Third, the constraints limiting absolute growth rates and substrate uptake rates have remained elusive. Proteome-limitations in the ME-Model result in a maximal growth rate and optimal substrate uptake rate that is consistent with experimental data when nutrients are available in excess [17]. The limitations placed on substrate uptake by the proteome significantly expand the scope of environments that can be simulated with constraint-based models to include nutrient-excess and complex media conditions.

Fourth, spatial limitations on the membrane proteome further refine predictions of pathway shifts and substrate uptake rates in nutrient-excess environments [18]. Limitations on protein synthesis and protein space result in similar phenotypic responses, but have some differences in enzyme utilization; membrane proteomics data and experimental evolution can help to illuminate which constraints are dominant.

The phenotypic effects of proteome allocation constraints are just beginning to be uncovered and will likely change our conception of optimal behavior and pathway use [32].

Gene expression states and molecular phenotypes can now be computed

The prediction of proteome composition is an ambitious endeavor. To date, a few predictions of absolute gene expression have been validated. The ME-Model accurately predicts ribosomal [15,17] and translocase [18] protein abundances, which have well-known catalytic rates. In general, however, catalytic rates of specific enzymes in vivo are not known. Nonetheless, the relatively accurate prediction of overall proteome abundance of different cellular compartments and functional subsystems is possible [18]. Furthermore, genome-scale predicted and measured mRNA abundance correlate significantly [15]. These early predictions provide support for the genome-scale prediction of absolute gene expression from evolutionary optimality principles (Figure 2B).

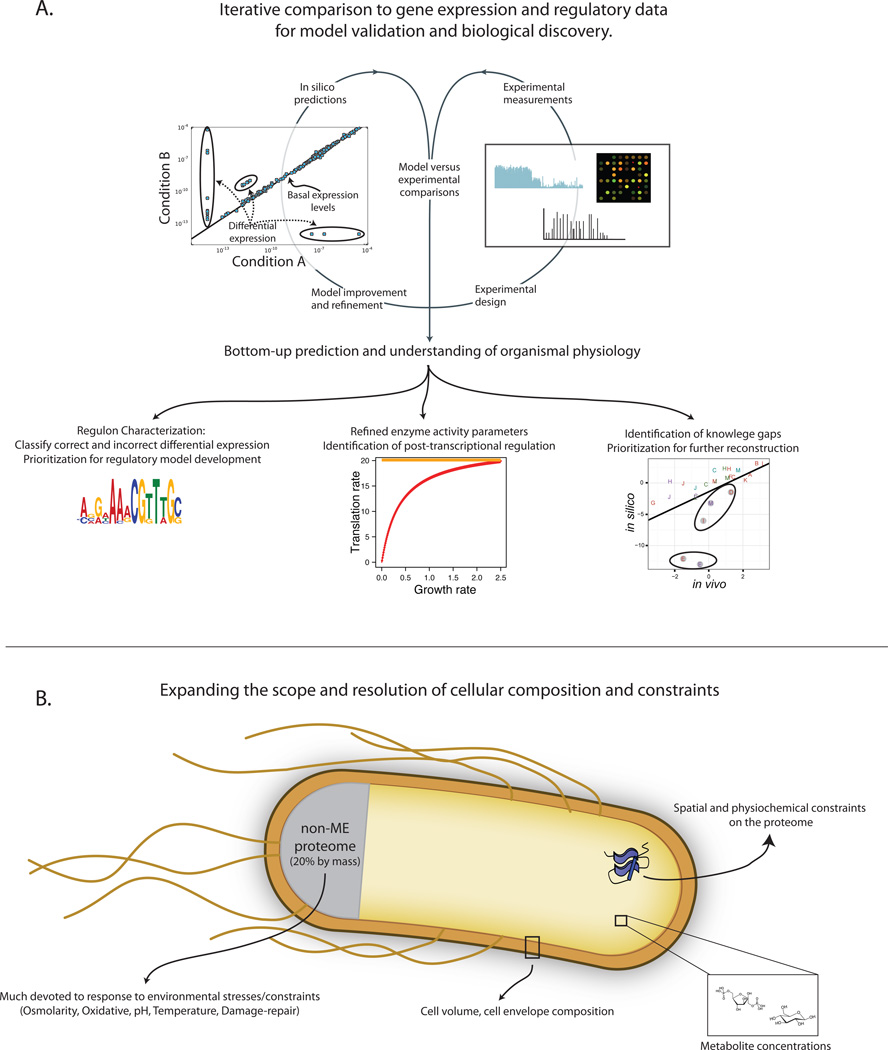
As with false predictions from M-Models [33], discrepancies between predicted and observed expression levels have led to discovery (Figure 3A). First, the quantitative difference between predicted and measured gross RNA and protein biomass composition has led to the realization that translation rate is a hyperbolic function of growth rate [17], which has been independently validated [34]. Second, comparing predicted and measured abundance of functional subsystems identified the processes of protein folding and metal ion and prosthetic group integration as under-predicted [18]. These under-predictions are consistent with known knowledge gaps of chaperone targets [35] and metal ion usage by proteins [36] and prioritizes these processes for further reconstruction.

Figure 3. Iterative model validation and biological discovery enabled by expanded scope.

A) The prediction of basal gene expression states and regulatory needs upon environmental shifts enables comparisons to gene expression datasets. Like M-Model predictions of gene essentiality [64] and metabolic flux [97], comparison of in silico and in vivo gene expression states will enable model validation and biological discovery.

B) To increase the scope and resolution of predicted cellular composition and organization, there are several prioritized areas for model expansion. These include metabolite concentrations, the non-ME proteome, cell envelope composition, and the spatial organization and physiochemical constraints on the proteome (aided by protein structures).

Given the discordance between measured RNA and protein abundances [37], the moderate correlation between genome-scale predicted and measured gene product abundance is unsurprising. The factors contributing to the discrepancy between RNA and protein abundances are beginning to be uncovered [38,39], aided by diverse data types on the various steps of gene expression, including promoter activity [40,41], RNA abundance, RNA degradation rates, ribosome occupancy [42], and protein abundance [43]. These data types and gene-specific rates on the steps of gene expression can readily be integrated into ME-Models. Parameterizing the steps of gene expression with these data types, biophysical models [44,45] or synthetic ‘parts characterization’ [46–49] will help understand the gap between RNA and protein abundance as well as in silico and in vivo gene expression levels.

Precise prediction of protein abundance is also limited by knowledge of enzyme catalytic rates. However, even though data on individual enzyme rates is noisy and sparse [50,51], statistics on the distributions of catalytic rates are robust [52], enabling confident distributions of expression levels to be computed. Furthermore, model-driven approaches can be used to infer catalytic rates that are consistent with in vivo data [53–55]. These efforts will iteratively result in more precise predictions of protein expression.

Bottom-up prediction of gene expression will truly test our understanding of the biological demand and activity of enzymes. We believe that quantitative proteome levels will not fully be understood until we are able to predict them from the bottom-up with GEMs. Given the early successful uses of ME-models it seems clear that there is much more discovery that lies ahead. Just as the community has become accustomed to flux balances, and thus the uses of metabolic networks, ME-models are likely to help us understand how the composition of the proteome is optimally balanced.

Defining and understanding regulatory needs

Prediction of regulatory needs during shifts in homeostatic states is another important challenge for ME-Models. Differential expression data is more abundantly available than absolute expression data, and will aide in ME-Model validation and model-driven discovery. We anticipate that this comparison and, more generally, a physiological needs perspective on gene expression will help reveal the principles underlying transcriptional regulation.

Recent examples of bottom-up prediction of differential expression include the use of an M-Model to predict transcriptional changes after redox shifts [56] and the use of a ME-Model to predict differential expression after a shift in carbon sources [15]. Furthermore, the principle of simplest pathway structure can predict gene co-expression and transcriptional regulatory relationships [57]. These examples provide evidence that transcriptional regulation is somewhat predictable based on optimality principles.

There are various reasons as to why transcriptional regulation may seem non-optimal [58]. First, there could be errors in the reaction network reconstruction, which can be rectified by systematic comparison of computational predictions and experimental data [33]. Second, discrepancies could be due to constraints or optimality principles that are not yet modeled or understood (such as proteome constraints added in moving from M- to ME-Models). Third, the environmental history of the organism may have coupled seemingly unrelated biological processes [59], or be optimized for fluctuating rather than static environments [60–63]. Finally, it is likely that transcriptional regulation is ‘moderately efficient’ rather than perfectly optimal. Enumerating and classifying these discrepancies can drive biological discovery as has occurred through classifying the false predictions of gene essentiality [33,64]. Identified discrepancies can provide insight into organismal physiology and prioritize the development of explicit transcriptional regulatory models.

Parallel to the prediction of transcriptional regulation with constraint-based models, a physiological perspective has revealed striking simplicity and optimality in transcriptional regulation [56,65]. In several studies, the mass fractions of large protein subsystems and the activity of transcription factors have been shown to change linearly with growth rate or specific metabolic fluxes [66–69]. Furthermore, linear models covering several genes have been shown to capture the variation in their expression with relative accuracy [41,70]. The simplicity of these regulatory relationships (despite the complex topology and biophysical relationships [71] underlying regulatory networks) provides promise for accurate genome-scale regulatory models. However, the cross-talk and competition between transcription factors is still not generally understood; in the meantime, top-down approaches [23] may be necessary to capture the essence of these more complex relationships.

Importantly, the explicit representation of transcription in the ME-Model allows for the molecular details of transcription factor targets to be combined with the physiological principles underlying transcription factor activity. This will enable new approaches to model transcriptional regulation that move beyond binary representations of transcription factor activity [25]. Regulatory model development can be prioritized by the physiological importance of regulatory shifts and failure modes identified through comparison of predicted and measured differential expression.

Though we have focused on transcriptional regulation here, optimality and physiological principles will likely apply to translational (e.g., by sRNAs) and post-translational regulation (e.g., by post-translational modifications and allosteric interactions) as well. These regulatory networks have received less attention, partially due to the difficulty in identifying the underlying interactions networks (compared to transcriptional regulatory networks [72]). However, new computational [73,74] and experimental [45,75] methods are emerging, and optimality principles are being uncovered [76,77] to elucidate these regulatory networks. Like transcriptional regulation, we anticipate that the explicit representation of enzyme abundance and activity in ME-Models will aid in the genome-scale modeling of post-transcriptional regulation.

Seeking a comprehensive biophysical representation of cellular composition

The conceptual change in GEMs to enable the prediction of proteome abundance, localization, and limitations affords numerous opportunities for model application and expansion. The E. coli ME-Model currently encompasses ~80% of the proteome and transcriptome by mass in environments of exponential growth [17]; this equates to ~60% of the cell’s entire mass. While the requirements for biosynthesis of a whole cell are encompassed by the model, not all molecular abundances are predicted; gaps include: 1) the non-ME proteome, 2) the cell envelope, 3) metabolite concentrations, 4) DNA replication and gene copy number, and 5) glycogen. We briefly cover factors that may enable prediction of these molecular abundances deemed most important (Figure 3B).

Metabolite concentrations are beginning to be predicted with genome-scale models using thermodynamic considerations. By extending a method to ensure metabolic fluxes are thermodynamically feasible [78], thermodynamic constraints were used to predict steady-state metabolite concentrations that are consistent with a given flux state [79]. Later, an objective to minimize metabolite concentrations over the thermodynamically feasible space was shown to increase prediction accuracy [80]. Additional constraints on osmolarity, metabolite toxicity, and correlations observed between metabolite concentrations and their enzyme affinities [81] and chemical properties [82] may improve predictions further. Then, the effects of these concentrations on enzyme and transcription factor activity may be accounted for in future genome-scale models.

A first requirement for the prediction of cell envelope composition is the prediction of cell size and shape, which determines the surface area of the cell that must be covered. The consistent growth rate dependence of cell size [83] suggests that simple principles may underlie the determination of cell size (for example, the balance between cytosolic and membrane proteome abundance [84]). However, the constraints underlying the exact composition of membrane lipid, glycans, LPS, and murein (together accounting for 15% of cell dry weight) are not well understood. Perhaps data on cell envelope composition will aide in understanding when and how it varies across environments and strains (an important characteristic of particular E. coli serotypes).

Expanding the proteome coverage to the remaining 20% of the proteome not encompassed by the ME-Model will require expansion of reconstruction content. Proteome abundance can be used to prioritize model expansion [85]. Many of these non-ME proteins can be broadly categorized as non-growth and stress response genes (e.g., biofilm and flagella formation and pH, osmolarity, and temperature responses). Therefore, modeling of stress responses is important to increase the coverage of the proteome and environments that can be simulated. Importantly, the ME-Model already accounts for the biosynthetic costs of synthesizing stress response proteins; however, the constraints imposed by environmental stresses will be needed to understand the protein’s physiological benefit.

Protein structures will aide in formalizing the constraints on the proteome. Genome-scale models integrated with protein structures (GEM-PRO) enable simulation of the effects of temperature: structure-based predictions of protein thermostability and the subsequent limitations on metabolic fluxes result in accurate predictions of growth and nutrient supplementations at high temperatures [86]. As other cellular stresses (e.g., pH) also affect protein catalytic capacity, protein structures may enable the simulation of other physiochemical stresses as well. Protein structures combined with ME-Models will also approach a more detailed biophysical representation of a cell. Spatial resolution can be refined further with protein-protein interaction data [87] (or prediction of protein-protein interactions with protein structures themselves [88]). Spatial considerations may be important for understanding co-localization of sequential catalytic steps [89,90] and the effects of molecular crowding [91,92] in the cytosol and membranes.

Conclusion

Building whole cell computational models has been a long-standing goal. Genome-scale metabolic models, M-Models, have become widely used due to the numerous actionable predictions they can make [93], and the ease of draft model construction from readily available genome sequences and annotations [94]. Here we reviewed recent advancements expanding the scope of whole cell computational models to encompass the synthesis and localization of the proteome. The constraint-based philosophy underlying ME-Models parallels that of M-Models. However, the expanded scope of components and constraints enables the prediction of enzyme abundance and activity. Already, ME-Models have revealed how constraints on proteome allocation explain aspects of cell behavior that have remained elusive or require invocation of phenomenological relationships. Furthermore, several cases demonstrate that ME-Models enable accurate prediction of protein abundance and differential expression. As the basic capabilities of M-Models to predict flux states have led to numerous applications, future work will capitalize on the new capabilities of GEMs to compute proteome allocation and limitations. Optimality-based predictions will no doubt be imperfect, but they form a strong conceptual base to drive biological discovery, bioengineering, and further model development.

• Models of metabolism and gene expression (ME-Models) now exist for model organisms.

• ME-Models account for ~80% of the proteome mass.

• ME-Models enable prediction of proteome allocation and limitations.

• ME-Models enable prediction of basal expression states and regulatory needs.

• Increased scope and resolution will be achieved with further model expansion.