Selective Gating of Neuronal Activity by Intrinsic Properties in Distinct Motor Rhythms

Abstract

Many neural circuits show fast reconfiguration following altered sensory or modulatory inputs to generate stereotyped outputs. In the motor circuit of Xenopus tadpoles, I study how certain voltage-dependent ionic currents affect firing thresholds and contribute to circuit reconfiguration to generate two distinct motor patterns, swimming and struggling. Firing thresholds of excitatory interneurons [i.e., descending interneurons (dINs)] in the swimming central pattern generator are raised by depolarization due to the inactivation of Na⁺ currents. In contrast, the thresholds of other types of neurons active in swimming or struggling are raised by hyperpolarization from the activation of fast transient K⁺ currents. The firing thresholds are then compared with the excitatory synaptic drives, which are revealed by blocking action potentials intracellularly using QX314 during swimming and struggling. During swimming, transient K⁺ currents lower neuronal excitability and gate out neurons with weak excitation, whereas their inactivation by strong excitation in other neurons increases excitability and enables fast synaptic potentials to drive reliable firing. During struggling, continuous sensory inputs lead to high levels of network excitation. This allows the inactivation of Na⁺ currents and suppression of dIN activity while inactivating transient K⁺ currents, recruiting neurons that are not active in swimming. Therefore, differential expression of these currents between neuron types can explain why synaptic strength does not predict firing reliability/intensity during swimming and struggling. These data show that intrinsic properties can override fast synaptic potentials, mediate circuit reconfiguration, and contribute to motor–pattern switching.

Introduction

There has been much debate about how specific neural networks can generate different types of motor outputs (Getting, 1989; Morton and Chiel, 1994; Marder and Calabrese, 1996; Marder and Bucher, 2007; Briggman and Kristan, 2008; Frigon, 2009; Berkowitz et al., 2010). When motor patterns switch, circuit reconfiguration takes place involving changes in the firing frequency of different neurons, and often there is a recruitment of specialized neurons (Weimann et al., 1991; Weimann and Marder, 1994; Briggman and Kristan, 2006; Li et al., 2007; Berkowitz, 2008; Liao and Fetcho, 2008; White and Nusbaum, 2011). Such reconfiguration is possible because these circuits do not appear to be synaptically connected with strict specificity. We normally consider neurons that spike in electrophysiology recordings, or have strong Ca²⁺ signals in Ca²⁺ imaging experiments, to be part of a functional network. However, subthreshold membrane potential (MP) oscillations are often present in many neurons that do not spike (Berkowitz, 2007; Li et al., 2007; Liao and Fetcho, 2008). Although synaptic connections to such nonspiking neurons may be functionally redundant for one motor pattern, these neurons can start spiking in a different motor pattern following circuit reconfiguration.

Several factors can influence the activity flow and mediate circuit reconfiguration. Altered sensory transmission (Soffe, 1993; Combes et al., 1999b; Blitz et al., 2004; Berkowitz, 2008) and higher-order descending projections (Combes et al., 1999a; Ritter et al., 2001) can trigger changes in motor patterns. Different neuromodulatory states can affect both synaptic transmission and ion channels (Marder and Bucher, 2007; Briggman and Kristan, 2008; Sillar et al., 2008; Rauscent et al., 2009) and differentially influence neuronal firing. Time constant differences in larval zebrafish motoneurons have recently been shown to play a role in their recruitment (Wang and McLean, 2014). Various voltage-dependent ionic channels, such as low voltage-gated Ca²⁺ or Ca²⁺-dependent K⁺ channels, have been extensively studied in motor rhythm generation (Hess and El Manira, 2001; Harris-Warrick, 2002; Grillner, 2003). Among them, transient K⁺ currents (Hoffman et al., 1997; Harnett et al., 2013; Takahashi et al., 2013) and the inactivation of fast sodium currents (I_Na⁺; Hodgkin and Huxley, 1952; Bostock and Grafe, 1985; Wilent and Contreras, 2005; Snape et al., 2010) can particularly alter firing thresholds. Since firing thresholds directly affect excitability and neuronal responses to synaptic inputs, these currents may dynamically gate neuronal activity and contribute to the fast reconfiguration of circuits driving different motor rhythms.

Xenopus tadpoles are capable of generating two types of motor rhythm, swimming and struggling. Swimming is evoked by a brief touch to the skin, whereas struggling requires sustained skin stimulation (Soffe, 1993). We previously showed that a switch from swimming to struggling involved reconfiguration of the tadpole spinal–hindbrain circuit (Li et al., 2007). During struggling, two special types of excitatory interneurons are recruited, whereas descending interneurons (dINs), critical in swimming rhythmogenesis, are only weakly active. I report here that fast transient K⁺ currents and I_Na⁺ inactivation, important in neuronal firing properties, also gate activity flow during swimming and struggling by dynamically resetting firing thresholds.

Materials and Methods

Human chorionic gonadotropin was injected twice a week to induce mating between pairs of adult Xenopus of either sex. All experimental procedures were approved by the local Animal Welfare Ethics committee and comply with the UK Home Office regulations. Tadpoles at stage 37/38 (Nieuwkoop and Faber, 1956) were anesthetized using 0.1% MS222 (3-aminobenzoic acid ester; Sigma-Aldrich), then immobilized using 12.5 μm α-bungarotoxin (Tocris Cookson) and mounted onto a sylgard stage for dissections (Moult et al., 2013). The saline contained the following (in mm): NaCl 115, KCl 3, CaCl₂ 2, NaHCO₃ 2.4, MgCl₂ 1, and HEPES 10, with pH adjusted to 7.4. Fine dissections were performed to expose muscle clefts for motor nerve recordings and neuronal somata in the caudal hindbrain and rostral spinal cord for whole-cell recordings (between the fifth rhombomere segments and the seventh postotic muscle segment).

In immobilized tadpoles, fictive swimming was evoked by electrical stimulation to the skin (0.2–1 ms current pulse) or dimming the microscope light. Struggling was evoked by electrically stimulating the head skin at 30–40 Hz (10–40 pulses). Recordings from motor nerves were made by placing a glass suction electrode on the segmented swimming muscle clefts to monitor spinal cord outputs. Whole-cell recording pipettes were filled with a solution of 100 mm K-gluconate, 2 mm MgCl₂, 10 mm EGTA, 10 mm HEPES, 3 mm Na₂ATP, and 0.5 mm NaGTP with 0.1% neurobiotin (pH adjusted to 7.3; Vector Laboratories). Intracellular signals were amplified with an Axon Multiclamp 700B (Molecular Devices), digitized with a Power 1401 mkII and sampled with Signal (version 5; CED). The identification of neurons was based on their activity patterns during fictive swimming and struggling (Li et al., 2007), and their anatomy revealed after neurobiotin staining (Li et al., 2001). Some neurons were chosen from previous paired whole-cell recordings (Li et al., 2007), where their synaptic outputs were also needed for identification. Microperfusion of 4-aminopyridine (4-AP) and Anemone toxin (ATX II, Sigma-Aldrich) was performed by positioning a glass pipette with a tip opening of ∼10 μm more than 30 μm upstream to the recorded soma (Li and Moult, 2012). Gentle pressure was applied inside the pipette by compressing a connected 50 ml syringe for 100 μl (∼200 Pa) to eject the solution. The pipette was moved >200 μm away from the preparation, and gentle suction (approximately −100 Pa) was applied inside to stop gravity-driven leakage, when not in use. Each application typically used a few microliters of drugs.

To analyze K⁺ currents in voltage-clamp recordings, tetrodotoxin (TTX) at 0.4 μm (Sigma-Aldrich) and Cd²⁺ at 150 μm were used to block Na⁺ and Ca²⁺ currents, respectively. Series resistance was consistently high (30–50 MΩ) and compensated for 70–80%. Recordings with a series resistance change of >20% were not included for analyses. Measuring series resistance in current-clamp mode (bridge balance, resistance between electrolyte and cytoplasm) and voltage-clamp mode (resistance between electrolyte and cellular membrane) using the Multiclamp700B revealed a difference of ∼20 MΩ. The higher resistance in voltage-clamp mode may arise from the cytoplasmic yolk platelets present in all developing Xenopus cells. A one- or two-exponent fitting was applied to the rise and fall of the current traces recorded when the clamping voltage was stepped from −80 to 0 ± 20 mV. Although the rising phase of currents has a sigmoid shape, exponential time constants could provide rough estimates of channel activation and inactivation dynamics. The fitting was performed on tests in both control and with a pre-depolarization step to −30 mV, which inactivated transient K⁺ currents. A junction potential of 14.7 mV in standard saline solution was calculated using the Clampex 10.2 junction potential formula. This was not corrected in all measurements of voltage-clamp recordings. Leak currents were subtracted during experiments.

To estimate firing thresholds, brief triangular ramp currents (10 ms in duration with peaks stepped) were injected into neurons to simulate phasic EPSCs in swimming. A long step current (500–1000 ms) was injected to set membrane potentials before the ramp currents. To reveal synaptic potentials during swimming and struggling, sequential whole-cell recordings were made from individual neurons. The first electrode contained a normal pipette solution, and recordings were used to estimate firing thresholds, firing reliability during swimming, and the number of spikes per struggling cycle. The pipette solution during the second recording contained 2 mm QX314 to block Na⁺ channels intracellularly. Some repetitive, brief suprathreshold current pulses were often used to speed up the blockade, which took from 15 s to 1 min to establish.

Data processing and analyses were performed using Dataview (version 8; courtesy of Dr. W.J. Heitler, University of St. Andrews) and Excel. Statistical analyses were performed using SPSS (IBM). Averages were given with SEs when the data were normally distributed. Otherwise, a median with a range was given. Averages were compared using either a paired or an independent-samples t test, or a repeated-measures one-way ANOVA, depending on the data structure. Medians were compared using Wilcoxon signed-rank test unless otherwise stated. Any p value <0.05 was considered significant.

Results

Tadpole swimming and struggling rhythms differ in their burst duration, frequency of bursts, and sequence of activity in the rostral–caudal axis (Soffe, 1993; Li et al., 2007; Roberts et al., 2010). Swimming central pattern generator (CPG) comprises dINs, reciprocal inhibitory commissural interneurons (cINs), inhibitory interneurons with ipsilateral ascending axons (aINs), and motoneurons (MNs). These neurons typically fire one spike per cycle during swimming. Unlike swimming, the slower but stronger struggling activity starts earlier in the caudal end of the nervous system than the rostral segments. During struggling, most swimming CPG neurons are also active. Repetitive activation of sensory Rohon–Beard (RB) neurons recruits excitatory commissural interneurons (ecINs), repetitive-firing dINs (dINrs), and some additional cINs. All rhythmic neurons fire multiple spikes on each cycle, generating prolonged bursts of activity in the motor nerves during struggling (Soffe, 1993; Li et al., 2007). In this study, I first determined how some voltage-dependent currents set firing thresholds in different neurons, and then examined how this affected neuronal activity during swimming and struggling.

Many rhythmic neurons except for dINs show delayed firing properties

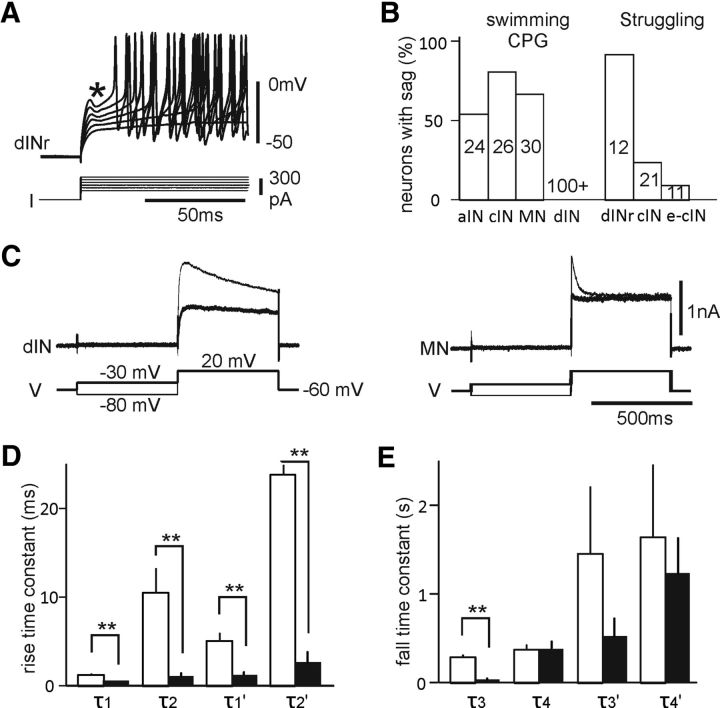
Ionic currents directly determine neuronal spiking. Therefore, by examining firing properties at rest, differences in ionic currents between different types of neuron may be initially identified. Neuronal firing properties were tested by injecting positive step currents. With the significant exception of excitatory dINs (see below), most neurons that are active during rhythmic motor activity fired repetitively when depolarized. In many of these, including some cINs and MNs, this repetitive firing was preceded by a delay (Sautois et al., 2007), during which there was typically a sag (Fig. 1A). The proportion of neurons with delayed firing was 54% in 24 aINs, 81% in 26 cINs, and 67% in 30 MNs. It was highest in dINrs (92%; 11 of 12; Fig. 1B), which are typically active only during struggling.

Figure 1.

Delayed firing and K⁺ currents in neurons involved in swimming and struggling. A, Responses of a dINr to DC steps. *The sag before spiking increases with bigger DCs. B, Percentage of neurons with delayed firing. Numerals in bars indicate numbers of neurons examined. Struggling-specific neurons are active only in struggling and are identified in paired recordings (Li et al., 2007). Swimming CPG neurons are also active in struggling. C, Example K⁺ currents in a dIN and a MN. Inactivation voltage step is −30 mV before the final test step of 20 mV (thick lines). D, E, Comparing rise (D) and fall (E) time constants between dINs (unfilled bars) and non-dIN (solid bars). τ₁–τ₄ exponential constants measured in control (thin traces in C). τ₁′–τ₄′ are constants in tests with −30 mV inactivation steps. **Significance levels at p < 0.01.

In contrast, none of a large sample (n > 100) of dINs, which play a critical excitatory role during swimming, showed delayed firing. It was previously shown that dINs typically fired a single spike at the onset of current injections (Li et al., 2006). Although the functional significance of the delayed firing is unclear, these results suggest an important difference between dINs and other motor and premotor neurons in the ionic conductances that control firing, and which could be important in the expression of different motor patterns.

Motor and premotor neurons typically have fast transient K⁺ currents

Transient K⁺ currents have been previously shown to be a cause of delayed firing (Dekin and Getting, 1987; Pulver and Griffith, 2010). Adding transient K⁺ currents (I_A) in modeled tadpole neurons could make repetitive-firing neurons fire with delays (Sautois et al., 2007). I therefore investigated transient K⁺ currents experimentally by making voltage-clamp recordings of K⁺ currents in the presence of 0.4 μm TTX and 150 μm Cd²⁺. Whole-cell K⁺ currents were recorded by stepping the membrane potential to 0–20 mV (depending on the amplitude of K⁺ currents) from either −80 mV (control) or −30 mV to produce inactivation (Fig. 1C). The K⁺ currents, recorded in all neurons, showed different kinetics. The rise and fall of K⁺ currents was quantified in 26 non-dIN neurons (10 MNs, 7 aINs, 5 cINs, and 4 dINrs) by fitting one or two exponentials. One exponential gave the best fit for the rise of K⁺ currents in most neurons (25 of 26 in control, 19 of 26 with inactivation), and fall in some neurons with inactivation (10 of 26). In these cases, a single value was used for both first and second time constants to simplify comparisons between neurons (Fig. 1D,E). Currents were also measured in 10 dINs. A single exponential gave the best fit to the fall in currents on most of these (7 of 10 in control and following inactivation).

These time constant measurements showed that K⁺ currents in dINs have kinetics that are different from those in other neurons. For the rising phase of the current, time constants in dINs were longer than those in non-dINs (p < 0.01). In accord with this, currents in dINs took longer to peak than in non-dINs (dINs: 36.8 ± 2.2 ms, n = 7 measured; non-dINs: 4.1 ± 0.4 ms, n = 10 measured; p < 0.001). Even after inactivation (stepping from −30 mV), this difference remained (p < 0.01), suggesting the presence of fast nondecaying K⁺ currents in non-dINs. For the falling phase of the current, the first time constants in control were also longer in dINs than that for non-dINs (p < 0.01, independent-samples t test in these cases; Fig. 1D,E). These data show that dINs and non-dINs possess different transient K⁺ currents: dINs typically possess slow transient K⁺ currents, while non-dINs possess fast currents. The −30 mV inactivation steps show that these currents are voltage dependent. Fast transient K⁺ currents like those in non-dINs have previously been designated I_A (Yuan et al., 2005), and this terminology will be used throughout the following text.

Firing thresholds change with pretest membrane potentials

In neurons with delayed firing properties, an increase of DC injection is often required to evoke initial spiking before the sag, suggesting thresholds for the initial firing are high. During swimming, CPG neurons receive fast phasic EPSCs on each swimming cycle (Li and Moult, 2012). I therefore injected brief ramp currents to simulate these EPSCs to estimate their firing thresholds. To test whether voltage-dependent currents like I_A could affect firing thresholds, these ramps were superimposed on longer step currents to alter background, pretest membrane potentials. Firing threshold was defined as the peak of the biggest EPSP-like ramp depolarization before firing occurred (Fig. 2). Neurons with delayed firing were grouped together as non-dINs, and their thresholds were compared with those of dINs.

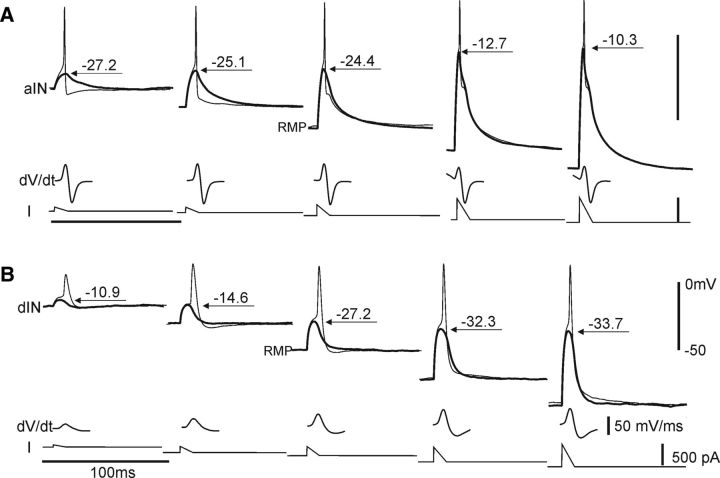
Figure 2.

Firing thresholds tested with brief ramp currents and derivatives of spiking (dV/dt). A, In an aIN, thresholds (arrows with numerals) are increased by hyperpolarized pretest membrane potentials. B, In a dIN, thresholds are lowered by hyperpolarization.

In 30 non-dINs (n = 15 cINs, 11 MNs, and 4 aINs), 21 neurons had higher thresholds when depolarized from relatively hyperpolarized pretest potentials than when depolarized from rest (70% Figs. 2A, 3A,B). In contrast, hyperpolarization in the pretest membrane potential lowered thresholds in all dINs (n = 16; Figs. 2B, 3A,B) compared with their value from rest (i.e., following a period of relative hyperpolarization, thresholds became less depolarized and dINs gained higher excitability). Figure 3B shows examples of neurons whose threshold varied by >10 mV across the range of pretest membrane potentials (n = 14 dINs, 13 non-dINs). Measured from rest, the average threshold for dINs was significantly lower than that for non-dINs (dINs: −29.2 ± 0.6 mV, n = 16; non-dINs: −21.6 ± 1.4 mV, n = 30; p < 0.001, independent-samples t test). Interestingly, resting MPs (RMPs) of both dINs and non-dINs (Fig. 3B, circles) are located about halfway through the range of possible thresholds, suggesting that thresholds should be particularly sensitive to changes at RMPs.

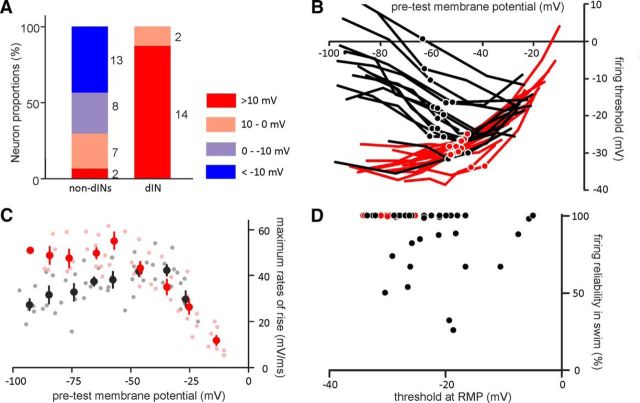
Figure 3.

Properties of neuronal firing thresholds and derivatives of spiking. A, Proportion of neurons with indicated threshold ranges (= threshold at depolarization − threshold at hyperpolarization). Numerals right to columns are neuron numbers. B, Firing thresholds as a function of membrane potential. Examples of neurons with absolute threshold ranges ≥10 mV. Filled circles indicate thresholds at RMPs. C, Maximum rates of rise plotted against pretest membrane potentials. Light symbols are individual measurements from 9 dINs and 9 non-dINs. Dark circles with error bars are binned averages (every 10 mV between 0 and −100 mV). D, Thresholds at RMPs plotted against the firing reliability in swimming. Black lines and symbols are for non-dINs, and red lines and symbols are for dINs in A–D.

Firing thresholds are known to be affected by the inactivation of voltage-gated Na⁺ channels (Wester and Contreras, 2013). The availability of Na⁺ channels is often measured using the maximal rate of rise of spikes (Seutin and Engel, 2010), and I_Na⁺ inactivation can be detected as a reduction in this maximal rate of rise. Therefore, I measured the maximal rate of rise in just-above-threshold spikes as an indirect measurement for I_Na⁺ inactivation. Neurons whose thresholds could vary by >10 mV (Fig. 3B) were chosen for comparison. From rest, the maximal rate of rise for dIN spikes was higher than that for non-dINs (dINs: 47.9 ± 2.3 mV/ms; non-dINs: 37.6 ± 1.9 mV/ms; p < 0.01, independent-samples t test). In dINs, it was negatively correlated with pretest membrane potentials, decreasing at membrane potentials more depolarized than −60 mV (p < 0.01, two-tailed Pearson; Fig. 3C, red symbols). Non-dINs showed a broadly opposite effect: maximal rates of rise were still correlated with pretest membrane potentials, but in this case they decreased with membrane potentials below −30 mV (p < 0.01, two-tailed Pearson; Fig. 3C, black symbols). Only for pretest membrane potentials more depolarized than −30 mV is there any indication of a decrease in the maximal rate of rise. These data show that I_Na⁺ inactivation increases in dINs with increasing pretest depolarization, but in non-dINs, I_Na⁺ inactivation decreases, at least until they are very depolarized.

At membrane potentials more depolarized than −40 mV, there was also a 5–11 mV upward shift of thresholds in 15 of the 30 non-dINs, giving the overall curves a v shape (Fig. 3B, black lines). In non-dINs, threshold ranges were correlated with thresholds at RMPs (p < 0.01, n = 30, two-tailed Pearson). This correlation implies that both features may result from the same source (i.e., the activation of I_A). Firing thresholds at RMPs were not correlated with the neuronal firing reliability during swimming in either dINs or non-dINs (Fig. 3D).

Blocking I_A using 4-AP

Transient K⁺ currents in tadpole sensory interneurons (Winlove and Roberts, 2012) and cultured neurons (Ribera and Spitzer, 1990) can be blocked preferentially by 4-AP. Neurons were therefore locally microperfused with 2 mm 4-AP to look for changes in their firing thresholds. Thresholds in dINs were not altered by 4-AP (n = 6, p = 0.25, Wilcoxon signed-rank test). However, for non-dINs, they were lowered from −21.5 ± 2.3 to −24 ± 2.2 mV (n = 13, paired t test, p < 0.01; Fig. 4A,B). The change in thresholds following 4-AP was clear in non-dINs with delayed firing (Fig. 4A) but was small in others when they did not show sags in depolarization from DC injections (Fig 1B). This shows how the activation of I_A could be a major determinant of firing thresholds in many non-dINs, and is likely to be responsible for their increase in threshold (and therefore reduced excitability) when depolarized by EPSPs from relative hyperpolarization.

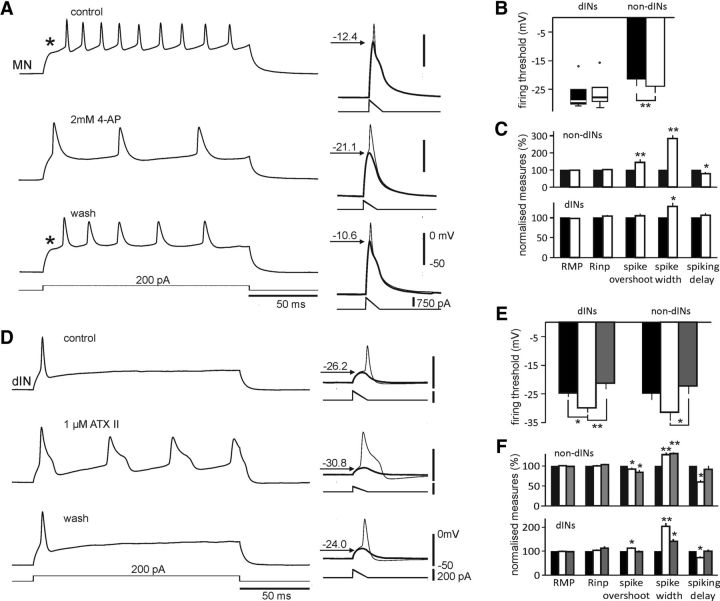
Figure 4.

Effects of 4-AP and ATX II on neuronal spiking properties. A, The firing of a MN in control, 2 mm 4-AP and wash to step and ramp current injections. *Delay in firing. The MN is injected with −100 pA DC to set membrane potentials during threshold tests (right). B, Effects of 4-AP on dIN and non-dIN firing thresholds. C, Effects of 4-AP on other parameters normalized to their controls. Rinp, Cellular input resistance. D, Firing of a dIN in control, 1 μm ATX II, and wash (left). The dIN is injected with 50 pA to set membrane potential at approximately −40 mV during threshold tests (right). Thresholds are shown in thick traces with arrows and numbers in A and D. Saline solution contains 150 μm Cd²⁺ to prevent swimming. E, Effects of ATX II on thresholds. F, Effects of ATX II on other normalized parameters. B, C, E, and F: *p < 0.05 and **p < 0.01; black bars are controls, empty bars are for 4-AP or ATX II, and gray bars are for the wash. Comparisons are against controls in F.

The blockade of I_A also allowed non-dINs (n = 13) to depolarize faster to threshold current injections and fire their first spikes sooner (time measured from onset of currents, p < 0.05). Meanwhile, spike widths in non-dINs were broadened by 184 ± 19% (measured at 0 mV crossing points, p < 0.001), indicating that I_A contributes to the fast membrane repolarization after spike peaks. As a consequence of this, overshoots of non-dIN spikes were higher in 4-AP (p < 0.01). There was no change in RMPs and cellular input resistances in 4-AP. In dINs (n = 6), 4-AP only increased spike widths (p < 0.05, Wilcoxon matched-pair signed-rank tests after normalization in these cases). The changes all took place within 2 min after 4-AP application; they did not wash off after up to 10 min, so wash measurements are not shown in Figure 4, B and C. These results are consistent with a much smaller role for I_A in dINs than in non-dINs.

Slowing down I_Na⁺ inactivation by ATX II

The lowered firing thresholds (and increased excitability) by hyperpolarization can result from the removal of I_Na⁺ inactivation (Snape et al., 2010; Wester and Contreras, 2013; Fig. 3C). To test this, ATX II at 1 μm was microperfused to the recorded neurons to weaken the I_Na⁺ inactivation. Maximal rates of rise in spiking (shown above to be a good indicator of I_Na⁺ inactivation) increased in all neurons tested (from 56.8 ± 1.7 to 61.7 ± 1.7 mV/ms in ATXII; p < 0.05) and decreased to 48.7 ± 1.6 mV/ms in wash (p < 0.001, n = 7 dINs and 9 non-dINs, paired t tests). This showed that the ATX II was indeed weakening I_Na⁺ inactivation. In ATX II, the dIN firing pattern changed from single spiking to repetitive firing during step current injections (Fig. 4D). As predicted, dIN firing thresholds were lowered in ATX II (from −24 ± 1.2 to −29.2 ± 1.4 mV, n = 9; p < 0.01, one-way ANOVA). In non-dINs (three MNs, two aINs, and four dINrs), firing thresholds were also lowered in ATX II (from −24.3 ± 2 to −30.7 ± 2.8 mV; p < 0.05, one-way ANOVA; Fig. 4E). These data show that I_Na⁺ inactivation normally raises dIN firing thresholds and lowers their excitability. In agreement with the analysis of maximal rates of rise, I_Na⁺ inactivation may also play a role in raising non-dIN firing thresholds at more hyperpolarized membrane potentials.

ATX II also increased dIN spike overshoot and spike width, and shortened the spiking delay from current onset (p < 0.05, n = 7). In non-dINs, spike width increased from 0.81 ± 0.07 to 1.04 ± 0.11 ms in ATX II (p < 0.01), suggesting some I_Na⁺ inactivation. There was a decrease of spike overshoot and spiking delay (p < 0.05, n = 9). Neither RMPs nor cellular input resistances were affected by ATX II in both dINs and non-dINs (Wilcoxon matched-pair signed-rank tests after normalization in these cases; Fig. 4F).

Fast synaptic drive is insufficient in driving non-dIN activity during swimming

The data above show that the activation of I_A and inactivation of I_Na⁺ can both shift firing thresholds in a voltage-dependent manner, but in broadly opposite directions. To test how this affects the reliability and/or strength of neuronal spiking during swimming and struggling, I first tested whether fast synaptic potentials were themselves sufficient to account for neuronal firing. Neurons were first recorded with a normal electrode to measure firing thresholds using ramp currents and firing reliability during swimming. To measure EPSP peaks during swimming, the same neurons were sequentially recorded with a second electrode containing 2 mm QX314 to block spiking. Although QX314 also blocks some ionic channels other than Na⁺ currents at 10 mm (Talbot and Sayer, 1996), its use at ≤2 mm provides the best estimates of synaptic drives without affecting network activity (Hu et al., 2002; Pace et al., 2007).

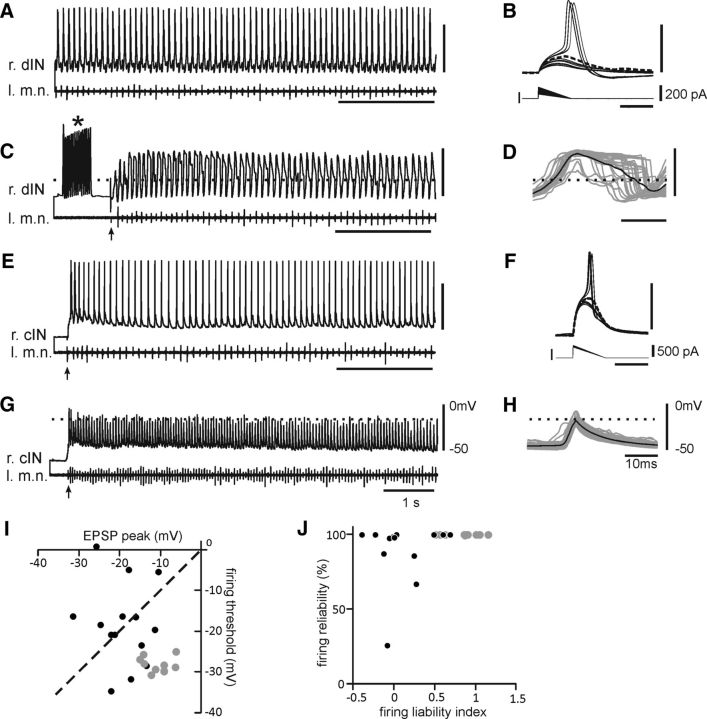
Measured at their peaks, phasic EPSPs during swimming depolarized dINs to −10.5 ± 1 mV (n = 10 episodes from 10 dINs). Since this was well above their firing thresholds of −28.5 ± 0.6 mV (measured when depolarizing them from rest; Fig. 5A–D; paired t test, p < 0.0001), dINs would be expected to fire reliably during swimming, which is what is observed. Phasic EPSPs depolarized non-dINs to −18.8 ± 1.6 mV (n = 14 episodes from 14 non-dINs), which is less positive than that in dINs (p < 0.001, independent-samples t test). Although phasic EPSP depolarization in non-dINs is similar to their firing thresholds measured from rest (−18.6 ± 2.7 mV; p = 0.93, paired t test; Fig. 5E–H), in half of them (7 of 14) phasic EPSP peaks were actually below their corresponding thresholds (Fig. 5I, black symbols above the dashed line). This makes it likely that firing will be less reliable in non-dINs than in dINs. The EPSP differences between these dINs and non-dINs may not simply arise from differences in their cellular input resistances, which are similar (median: 9 dINs, 216 MΩ; 13 non-dINs, 245 MΩ; p = 1, independent-samples median test).

Figure 5.

Comparing neuronal activities and EPSPs in swimming and firing thresholds at RMPs. A, Reliable firing of a right-side dIN. B, Threshold tests of the dIN in A. C, dIN in A recorded with an electrode containing 2 mm QX314. *Period with 15 DC steps (500 pA, 10 ms at 50 Hz) used to facilitate the QX314 blockade of I_Na⁺. D, Overlapped phasic EPSPs on individual swimming cycles (gray lines) and their average (black). E, Activity of a right side cIN. F, Threshold tests for the cIN in E. G, cIN in E recorded with a QX314 electrode. H, Overlapped EPSPs in the cIN in G and the average. I, Average EPSP peaks plotted against thresholds at RMPs with a dashed identity line. Black circles above the identity line are from non-dINs with EPSP peaks below their firing thresholds. J, Firing liability indices plotted against the firing reliability in swimming. Gray circles are for dINs and black circles are for non-dINs in I and J. Dashed lines in C, D, G, and H mark thresholds revealed in B and F, respectively. r, Right; l, left; m.n., motor nerve.

dINs have more depolarized RMPs than non-dINs (Li et al., 2006). To explore firing reliability more closely, I used a firing liability index, which equals (EPSP peak − threshold)/(threshold − RMP), as a predictor of the likelihood of spiking during swimming. This could then be compared with the observed firing reliability during swimming. The firing liability index for dINs (0.84 ± 0.08, n = 10) was higher than that for non-dINs (0.07 ± 0.09, n = 14; p < 0.001, independent-samples t test). Importantly, though, the index for non-dINs could be small or negative, predicting little or no firing, even when their observed firing reliabilities during swimming were at or near 100% (Fig. 5J). Consistent with this, the percentage of individual swimming cycles with EPSP peaks above thresholds (median, 48.8%; range, 0–100%) was lower than firing reliabilities in these same non-dINs (median, 99.3%; range, 26–100%; p < 0.01, Wilcoxon matched-pair signed-rank test, n = 14). Firing during swimming in non-dINs is therefore significantly more reliable than predicted by the peak depolarization of their phasic excitation compared with their spike thresholds at rest. This discrepancy was not observed in dINs (p = 0.655, Wilcoxon matched-pair signed-rank test; n = 10).

The data on ionic currents (outlined above) may provide an explanation here in that the depolarization produced by the combination of phasic and background excitation (see below), like artificial depolarization from rest (Fig. 2A), will inactivate I_A and reduce the spike threshold in non-dINs, making them more likely to fire.

The activity of dINs is weak for the strong synaptic drive during struggling

Our previous study found that dINs were only weakly active during struggling, while most non-dINs were vigorously active (Li et al., 2007). I investigated whether the depolarization provided by synaptic potentials in these neurons was sufficient to explain their firing during struggling.

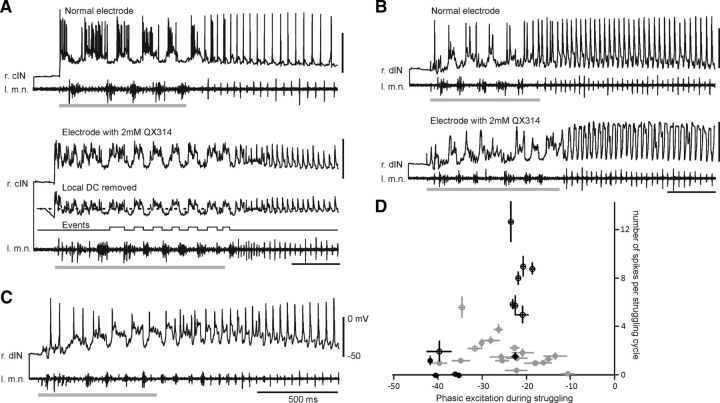
Successful sequential recordings were made from 16 non-dINs, but good struggling activity was evoked in only 8 of them (5 cINs, 1 dINr, 1 aIN, and 1 unidentified; Fig. 6A,D, empty black circles). Recordings with normal electrodes were first used to calculate the average number of spikes per struggling cycle, which was used to quantify the intensity of spiking. The phasic excitation was then measured in the subsequent recordings with QX314 electrodes from the same neurons. The active (bursting) phase of each struggling cycle was determined by threshold crossing in the whole-cell recording trace after removing the local DC using Dataview (Fig. 6A). All eight neurons except for the aIN showed vigorous firing during struggling. To look at the relation between phasic excitation and spiking intensity, I also chose five non-dINs (two MNs, one aIN, and two unidentified neurons) recorded with normal electrodes, which showed little/weak spiking during struggling. The weak activity allowed appropriate approximation of phasic excitation by averaging membrane potentials excluding spiking periods (Fig. 6D, filled black circles). The distribution of phasic excitation size was not normal, so I did not correlate it with spike numbers. However, dividing the non-dINs into two groups based on firing strength showed that the phasic excitation of −21.7 ± 0.6 mV in seven vigorously spiking non-dINs (7.9 ± 1 spikes per cycle) was stronger than that in the six weakly spiking neurons (−36.1 ± 2.9 mV, 0–1.6 spikes per cycle; p < 0.01, independent-samples t test; Fig. 6D, black symbols).

Figure 6.

Neuronal activities and phasic excitation during struggling. A, The activity of a cIN in sequential recordings. Inset shows the QX314 trace with its local DC removed. Dashed line indicates the threshold for event triggering. Event channel illustrates periods for phasic excitation averaging after merging within-cycle events. B, The activity of a dIN in sequential recordings. C, A dIN with typically weak firing in struggling. D, Numbers of spikes per cycle plotted against the average phasic excitation. Symbols are for individual neurons (gray, dINs; black, non-dINs; bars indicate the SE). Empty circles are from sequential recordings, and filled circles are from normal recordings (e.g., C). Struggling is evoked by skin stimulation at 25–40 Hz (gray bars, artifacts removed). r, Right; l, left; m.n., motor nerve.

Similar sequential recordings were made from seven dINs, but struggling activity was only evoked in three of them (Fig. 6B,D, empty gray circles). Fifteen additional dINs recorded with normal electrodes were used because dIN firing during struggling was generally weak with small spikes (Fig. 6C). The average phasic excitation was −24.7 ± 1.8 mV, ranging from −39.8 to −10.7 mV (Fig. 6D, gray symbols). In contrast to the situation in non-dINs, there was a negative correlation between phasic excitation amplitude and the numbers of spikes per cycle (n = 18 dINs; p < 0.05, two-tailed Pearson). The properties of I_Na⁺ inactivation described above mean that this reversed relationship between phasic excitation and spiking intensity in dINs, in which strong dIN excitation is associated with weaker firing, may result from increased I_Na⁺ inactivation during the strong excitation that is a feature of struggling.

Background depolarization during swimming and struggling

The data above have revealed that fast synaptic potentials alone are insufficient to account for the activity of many non-dINs during swimming, and dIN activity during struggling. Background depolarization can inactivate I_Na⁺ and I_A, cause shifts in firing thresholds at rest (Figs. 2, 3B), and may explain the discrepancies. I next estimated the background excitation neurons received during swimming and struggling. There is no completely satisfactory way of isolating the background depolarization from phasic synaptic potentials to measure it. In this study, a simple estimate was made by averaging the overall membrane potential of neurons during sequences of swimming or struggling after blocking their firing intracellularly with QX314 (averaged MP). To relate the averaged MP to a wider range of neuronal activity, some neurons with weak spiking recorded with normal electrodes were also included. These included some non-dINs with <20% firing reliability during swimming (Fig. 7A) and some dINs with weak spiking during struggling (see above).

Figure 7.

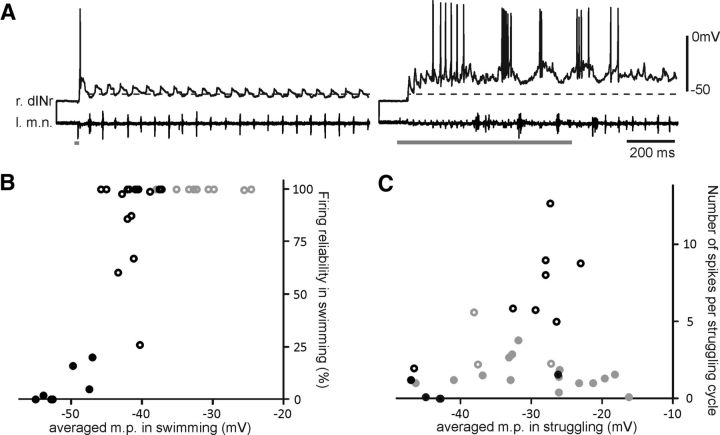
Averaged membrane potential (m.p.) in swimming and struggling. A, The activity of a dINr in swimming (left traces) and struggling (right traces). The dashed line is the average MP for the shown swimming episode (−52.7 mV). B, Averaged MP drawn against firing reliabilities in swimming. C, Averaged MP against number of spikes per struggling cycle. Gray symbols represent dINs, and black symbols represent non-dINs in B and C. Empty circles are from sequential recordings, and filled circles are from normal recordings with weak activity. Gray bars show time of skin stimulation. r, Right; l, left; m.n., motor nerve.

During swimming, the averaged MP was higher in 10 dINs than in 24 non-dINs (4 aINs, 4 MNs, 10 cINs, 6 dINrs; Table 1). This was still true if the comparison was only between dINs and non-dINs, which also fired 100% reliably (Table 1; p < 0.001, independent-samples t test in both cases). In non-dINs, higher levels of averaged MP were associated with more reliable firing (Fig. 7B; p < 0.001, two-tailed Pearson); no such relationship was detectable in dINs as they all fire 100% reliably during swimming.

Table 1.

Averaged membrane potentials during swimming and struggling

	Total record	QX314 record	Mean/median (mV)	SE/range (mV)
Swimming
dIN	10	10	−31.8	1.3
Non-dIN	24	17	−44.2	1.1
100% reliable non-dIN	12	12	−41.2	0.8
Struggling
dIN	18	3	−29.7	2.0
Non-dIN	13	8	−29.5	−47.1 to −23.1

Unlike swimming, the averaged MP during struggling was similar for dINs and non-dINs, but in both cases was more depolarized than during swimming (Table 1; p < 0.05, independent-samples t test or Wilcoxon signed-rank test). Among non-dINs, the averaged MP in neurons with vigorous firing (−27.9 ± 1.1 mV) was higher than that in weakly firing neurons (−41.8 ± 3.2 mV; p < 0.05, Wilcoxon Signed-rank test; Fig. 7C). This suggests that, during struggling, non-dIN firing is stronger in neurons that are more strongly depolarized (when their firing threshold would be reduced; Fig. 2), paralleling their increased firing reliability when more strongly depolarized during swimming.

These analyses show that reliable/intense non-dIN firing is likely driven by both strong phasic and background excitation in both swimming and struggling. Phasic and background excitation remain strong in all dINs in swimming. In struggling, dINs with weak firing receive strong phasic excitation.

Discussion

Firing thresholds directly control neuronal excitability and can gate activity flow through neural networks. I have looked at how two intrinsic properties set firing thresholds, and how they may dynamically interact with synaptic drives and influence spiking in two different modes of rhythmic motor behavior (i.e., swimming and struggling).

The first property concerns the delayed firing in non-dINs mediated by I_A, which has fast activating and inactivating kinetics. I_A was suggested to prevent repetitive firing in cultured Xenopus spinal neurons (Ribera and Spitzer, 1990) but was mostly absent in acutely isolated neurons (Dale and Kuenzi, 1997). In this study, neurons with I_A recorded in situ still fire repetitively at RMPs to step current injections but with a delay. With brief ramp current injections, the activation of I_A raised non-dIN firing thresholds and reduced excitability. “D-currents,” which have fast activation but slow inactivation, also affect spiking thresholds in a similar way (Storm, 1988; Bekkers and Delaney, 2001). In hippocampal pyramidal cells, I_A was reported to lower neuronal excitability (Hoffman et al., 1997; Magee and Carruth, 1999; Johnston et al., 2000; Hara et al., 2012). A similar influence of I_A over firing thresholds has been found in rat bladder afferent dorsal root ganglion neurons with spinal injury (Takahashi et al., 2013) and cortical pyramidal neurons (Harnett et al., 2013). The consistent role of I_A in motor systems is the regulation of motor firing frequency. I_A renders neurons with high firing thresholds and delayed firing at rest in Drosophila, and mutants lacking I_A have slower rhythmic movements (Ping et al., 2011). In the crustacean stomatogastric ganglion, I_A was proposed to lower neuronal excitability, slow pyloric motor rhythm frequency, and alter phasing of firing in the follower cells (Tierney and Harris-Warrick, 1992; Harris-Warrick et al., 1995). The role of I_A was also examined in lamprey spinal neurons (Hess and El Manira, 2001; Huss et al., 2007). Blocking I_A with catechol led to fewer spikes in motoneurons on each cycle, which in turn sped up fictive swimming. Data in this study show that upon I_A activation, non-dINs require larger depolarization to reach firing thresholds (Figs. 2, 3). Interestingly, large depolarization can inactivate I_Na⁺ at the same time and also contribute to lowering neuronal excitability (Fig. 4E).

The second property is related to dIN firing. The dependence of spiking threshold on I_Na⁺ inactivation was expressed in many preparations, such as the squid axon (Hodgkin and Huxley, 1952; Noble and Stein, 1966), rat barrel cortex neurons (Wilent and Contreras, 2005; Wester and Contreras, 2013), and some primary sensory neurons (Bostock and Grafe, 1985; Snape et al., 2010). Tadpole dINs typically only fire a single action potential at the onset of step current injections (Li et al., 2006). Depolarized membrane potential is correlated with more I_Na⁺ inactivation and higher firing thresholds in dINs (Fig. 3). It is not known whether the Na⁺ currents in dINs have different properties from those in the non-dINs, but a relatively high level of I_Na⁺ inactivation may result from the observed lack of fast K⁺ currents in dINs (Fig. 1), which also helps to shape the distinct, broad dIN action potentials. The slow kinetics of transient K⁺ currents in dINs also endows dIN spikes with long AHPs, allowing only slow recovery of depolarization after spiking. Such slowly rising depolarization in turn can progressively inactivate Na⁺ currents and stop dINs from firing again (Li et al., 2010), and explain their single firing property.

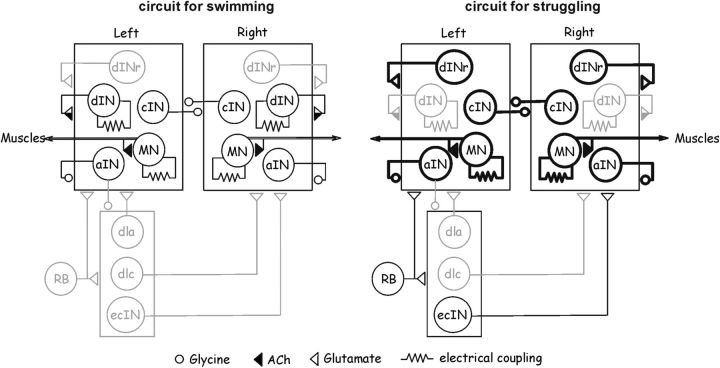
How do I_A and I_Na⁺ selectively gate neuronal activity during swimming and struggling, and contribute to circuit reconfiguration? The activation and inactivation of both currents is voltage dependent, allowing nonlinear conversion of fast EPSPs to spiking reliability/intensity. Neuronal firing during swimming and struggling therefore will be differentially regulated by these currents based on the level of excitation the neuron receives (Figs. 5, 6). During swimming, dINs provide the predominant source of excitation (Li et al., 2006). dINrs receive weak background excitation (Li et al., 2007; Fig. 7A), which is not sufficient to inactivate their I_A. They would require much stronger phasic excitation to fire spikes. In contrast, other non-dINs receive strong background depolarization that inactivates I_A and allows phasic EPSPs to mediate reliable spiking. During struggling, repetitive activation of sensory RB neurons elevates network excitation level globally (Li et al., 2007). ecINs, which have little I_A, are recruited by sensory activation and provide extra excitation. The enhanced excitation in dINrs can then inactivate their I_A, and enable EPSPs to drive intense firing and further increase network excitation. On the other hand, strong phasic and tonic excitation can inactivate I_Na⁺ in dINs, greatly lower their excitability, and prevent them from contributing significantly to struggling by firing multiple times on each cycle. This selective suppression of dIN activity, which is critical for swimming (Li et al., 2006, 2010; Soffe et al., 2009), and the recruitment of dINrs may be critical in switching motor patterns from swimming to struggling. In accord with this, 92% dINrs have delayed firing properties (Fig. 1B), and dIN firing thresholds consistently shift to more positive levels with depolarization (Fig. 3A). About two-thirds of MNs, cINs, and aINs possess delayed firing properties. This may explain the big variance in their thresholds at rest and suggest that some of them are not subject to activity gating mediated by I_A. It is clear that all rhythmic neurons receive similarly patterned synaptic inputs of various amplitudes during swimming and struggling. In the absence of strict, precise synaptic connections, the properties of I_A and I_Na⁺ selectively determine the final spiking of neurons and mediate circuit reconfiguration (Fig. 8).

Figure 8.

Reconfiguration of tadpole motor circuits by intrinsic properties during swimming and struggling. During swimming (left), cINs, MNs, and aINs, but not dINrs, receive sufficient background excitation to inactivate I_A and enable them to fire reliably. During struggling (right), strong excitation inactivates I_A in cINs, MNs, aINs, and dINrs, and allows them to fire vigorously, but dIN activity is suppressed by I_Na⁺ inactivation. Repetitive activation of RB neurons also recruits ecINs during struggling. Synapses on boxes mean all neurons inside receive the inputs. Thick black lines indicate vigorous firing. Gray shows little/weak activity. Only sensory pathways on the left side are shown. dlc, Dorsolateral commissural interneurons; dla, dorsolateral ascending interneurons.

Could other ionic currents explain the discrepancies between synaptic potentials and neuronal activity in swimming and struggling? I_h (hyperpolarization-activated current) and low-voltage-activated Ca²⁺ channels can theoretically facilitate EPSPs in evoking spikes. However, neither has been found in the tadpole neurons (Dale, 1995; Li et al., 2006). Ca²⁺-dependent K⁺ currents have been reported in cultured tadpole spinal neurons (Wall and Dale, 1995), but their activation is very slow (time constant, 437 ms at 0 mV). Their role in limiting dIN firing during struggling would be minimal. All cultured tadpole spinal neurons also possess some Na⁺-dependent K⁺ currents (Dale, 1993), which have kinetics that are similar to those of other delayed rectifier currents. Since non-dINs fire multiple spikes per cycle during struggling, it is reasonable to assume these currents are more strongly activated in non-dINs. The vigorous firing of non-dINs in struggling would thus suggest that Na⁺-dependent K⁺ currents are not important in gating spiking, although we cannot exclude the possibility of the higher density of Na⁺-dependent K⁺ currents in dINs. It would be ideal to link the properties of both I_A and I_Na⁺ to the rhythm-generating capacity of the neuronal circuits using some pharmacological or genetic tools. However, the application of 4-AP and ATX II also changed spike shape, which will directly affect neuronal firing properties and synaptic transmission. Thus, the overall effects of changing I_A or I_Na⁺ properties on network activities would be multifaceted and intricate to interpret (Prinz et al., 2003). The contribution of both currents to activity gating can be explained by interpolating firing thresholds at different membrane potentials (Fig. 3B). In non-dINs with reliable firing in swimming, the sustained depolarization of −41.2 mV could lower their thresholds (−18.6 mV at RMPs) by ∼10 mV, enabling their phasic EPSPs (peaks at −18.8 mV) to trigger reliable spiking. During struggling, the prolonged phasic excitation in dINs (−24.7 mV) could have increased their thresholds (−29.2 mV at RMPs) by ∼10 mV, making it unlikely that dINs will fire multiple spikes on each cycle.

Revealing synaptic connections in neural networks is the critical and challenging first step in decoding how a neural circuit operates. Such tasks are overarched by the fact that functional circuits can be very different from the synaptic connection maps, and they are reconfigurable on millisecond scales. This is because synaptic inputs are computed in a neuron-specific way, depending on the types of ionic currents that neurons express and their distribution on the cellular membrane (Harris-Warrick, 2002; Harnett et al., 2013). The computational outputs, mostly in the form of spiking, still may not guarantee neuronal action in circuit functions. Low release probability (Lisman, 1997) or short-term depression at synapses (Parker and Grillner, 2000) could still gate them out. The same circuit can rarely generate different outputs without reconfiguration (but see Li et al., 2014). Circuit reconfiguration allows activity flow to be routed differently following varied sensory and modulatory inputs (Dickinson et al., 1990; Meyrand et al., 1994; Marder and Calabrese, 1996; Popescu and Frost, 2002; Norris et al., 2006; Marder and Bucher, 2007) or long-term synaptic plasticity (Dan and Poo, 2006). This study presents evidence that intrinsic properties can be instrumental in the fast, dynamic reconfiguration of a multifunctional network.