Abstract
The brain's skill in estimating the 3-D orientation of viewed surfaces supports a range of behaviors, from placing an object on a nearby table, to planning the best route when hill walking. This ability relies on integrating depth signals across extensive regions of space that exceed the receptive fields of early sensory neurons. Although hierarchical selection and pooling is central to understanding of the ventral visual pathway, the successive operations in the dorsal stream are poorly understood. Here we use computational modeling of human fMRI signals to probe the computations that extract 3-D surface orientation from binocular disparity. To understand how representations evolve across the hierarchy, we developed an inference approach using a series of generative models to explain the empirical fMRI data in different cortical areas. Specifically, we simulated the responses of candidate visual processing algorithms and tested how well they explained fMRI responses. Thereby we demonstrate a hierarchical refinement of visual representations moving from the representation of edges and figure–ground segmentation (V1, V2) to spatially extensive disparity gradients in V3A. We show that responses in V3A are little affected by low-level image covariates, and have a partial tolerance to the overall depth position. Finally, we show that responses in V3A parallel perceptual judgments of slant. This reveals a relatively short computational hierarchy that captures key information about the 3-D structure of nearby surfaces, and more generally demonstrates an analysis approach that may be of merit in a diverse range of brain imaging domains.
Keywords: 3-D vision, binocular disparity, fMRI, slant
Introduction
A fundamental challenge in visual neuroscience is to understand how the outputs of neurons responding to local, simple elements are progressively transformed to encode the critical features of spatially extensive objects. While models of the ventral visual stream detail the decoding transformations that support invariance (Riesenhuber and Poggio, 1999; Rust and DiCarlo, 2010), much less is known about the dorsal hierarchy. Here we test the processing of binocular depth signals that strongly engage dorsal visual cortex (Backus et al., 2001; Tsao et al., 2003; Neri et al., 2004; Tyler et al., 2006; Preston et al., 2008, 2009; Goncalves et al., 2015). We set out to test how the brain meets the difficult challenging of inferring the 3-D orientation of a spatially extensive surface from 2-D retinal images. These computations are critical for a range of perceptual judgments and actions, yet there is a notable gap in our understanding between spatially localized disparity extraction (Ohzawa et al., 1990; DeAngelis et al., 1991; Cumming and Parker, 1997; Bredfeldt and Cumming, 2006; Tanabe and Cumming, 2008) versus high-level representations of 3-D structure (Janssen et al., 2000, 2003; Durand et al., 2007).
Previous fMRI studies of binocular disparity have used either simple disparity structures, such as step edges (Backus et al., 2001; Tsao et al., 2003; Neri et al., 2004; Tyler et al., 2006; Preston et al., 2008; Goncalves et al., 2015), or complex 3-D shapes (Nishida et al., 2001; Chandrasekaran et al., 2007; Georgieva et al., 2009; Preston et al., 2009; Minini et al., 2010). For the purpose of understanding how local features are integrated into global surfaces, the former are too simple (i.e., local and global surface properties are perfectly correlated), while the latter are too complex (i.e., the parameters describing surface relief become too numerous) making it difficult to interpret changes in fMRI responses. We therefore targeted surface slant, an intermediate property that relates to the rotation of a plane away from frontoparallel (e.g., the steepness of a hillside path when walking). Empirically, slant provides a low parameter test space (Fig. 1), and by rendering stimuli using random dot stereograms (Fig. 1a), we can test slant from disparity unaccompanied by the monocular features (e.g., texture gradients) that typically covary with it. Thus, we sought to measure fMRI responses when holding constant as many image dimensions as possible and taking account of the low number of parameters associated with slant variation.
Figure 1.
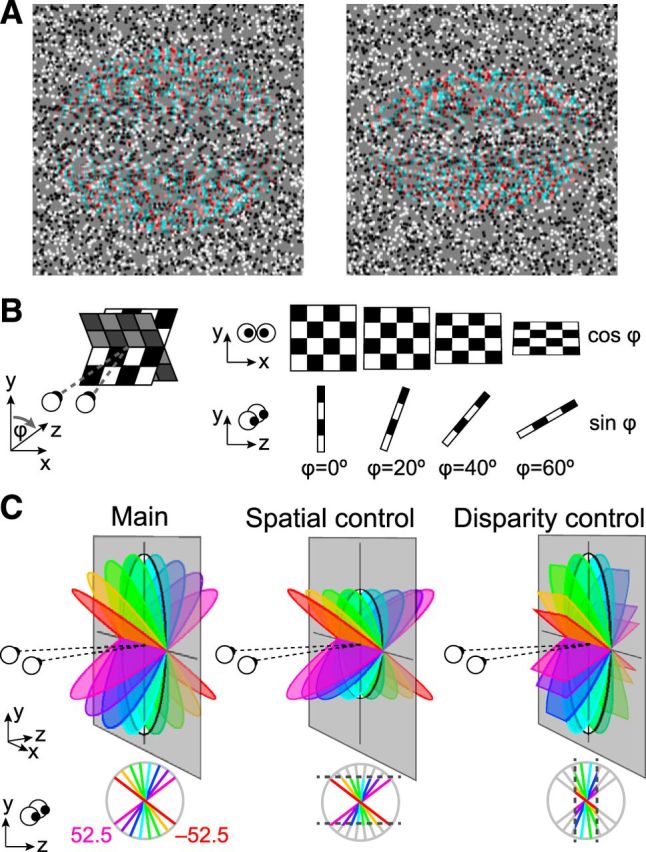
Stimulus illustrations. A, Example random dot stereograms of the slanted discs used in the study rendered as red-cyan anaglyphs. The stimuli depict slants of −37.5° (left) and −52.5° (right) for a participant with an interpupilary spacing of 6.4 cm viewing from a distance of 65 cm. (Note, if viewing without glasses, there might be an apparent blurring of the slanted stimuli that varies with slant angle; this cue was not available when our participants viewed the stimuli in the scanner through spectral comb filters). B, Schematic of the changes that accompany a physical change of slant. C, Diagrams of the parametric slant variations in the three experimental conditions: Main: simulated rotation of a physical disc; Spatial control: projection height in the image plane was constant as slant was manipulated; Disparity control: the mean (unsigned) disparity was constant as slant was varied.
Tracing disparity representations as they are transformed within the dorsal hierarchy using fMRI is challenging because activity within a particular cortical area is likely to reflect a complex mixture of responses to different image features. We therefore developed an approach we refer to as analysis-by-synthesis (Yuille and Kersten, 2006), that seeks to explain activity within a cortical area in terms of plausible computations. In particular, we married a voxel similarity approach (Kriegeskorte et al., 2008a) with synthetic modeling to infer the generative process that results in patterns of brain activity. Thereby, we uncover a processing hierarchy that moves from the representation of edges, and scene segmentation, to the representation of spatially extensive surfaces.
Materials and Methods
Participants.
Eight observers (4 female) from the University of Birmingham participated in the first fMRI experiment, six in the second, and six for psychophysical testing in the laboratory. Participants were screened for MRI contraindications and gave written and verbal informed consent. They had normal or corrected-to-normal vision, and had disparity discrimination thresholds <1 arcmin for briefly presented (500 ms) random dot stimuli. Experiments were approved by the University of Birmingham's STEM ethics committee. An additional participant was recruited for Experiment 1, but they withdrew halfway through the study due to illness.
Stimuli.
Stimuli were random patterns of black and white dots generated using the Psychtoolbox (Kleiner et al., 2007) in MATLAB (Mathworks). A square fixation marker (0.5° length) with horizontal and vertical nonius lines (0.375° length) was presented at the center of a 1° circular hole in the stimulus. The random dot stimulus contained a background region (in the plane of the screen) and a central disc region that depicted a slanted surface. The dots defining the different regions of the stimulus had the same projection size, and we ensured that there were no monocular cues to the surface slant. In particular, there was no foreshortening of the dot size with slant variations, and there were no gaps in the random dot patterns for different disparity magnitudes (unpaired dots were used to fill in gaps that would be caused by dots being shifted in opposite directions in the two eyes). The random dot pattern was surrounded a grid of large black and white squares positioned in the plane of the screen that was designed to provide a background reference.
Stereoscopic presentation was achieved using two projectors containing different spectral interference filters (Infitec, GmbH). The images from the two projectors were superimposed using a beam-splitter cube. Images were projected onto a translucent screen inside the bore of the magnet. Participants viewed the display via a front-surfaced mirror attached to the head coil. Luminance outputs from the two projectors were matched and linearized using photometric measurements. Viewing distance was 68 cm. To control for attention and promote proper fixation, observers performed a subjective assessment of eye vergence task (Popple et al., 1998). Vernier targets were flashed to one eye for 250 ms at either side of the desired fixation position, and a cumulative Gaussian function fit the proportion of “target on the right” responses as a function of vernier displacement.
In the first fMRI experiment, 20 different types of slanted stimuli were depicted in random dot stereograms (RDSs; Fig. 1). In the main condition, RDSs depicted surfaces with slants ranging from ±7.5 to ±52.5° in 15° steps. The projection width was 7.7°, and projection height varied depending on the angle of rotation away from frontoparallel (the plane was circular at zero degrees slant, although participants did not view such stimuli). The maximum binocular disparity was 32.8 arcmin in the most slanted condition. The target plane was surrounded by a background (9 × 9°) of random dots presented in the plane of the screen (thus monocular edge effects were eliminated). For the spatial control condition, the same eight slants were used except that their projection height (4.7°) was limited to that of the most slanted (±52.5°) stimuli from the main condition. This control allowed us to assess the contribution of changes in edge positions in driving the fMRI responses measured in the other two conditions. In the disparity control condition, the eight slanted stimuli had their projection size manipulated so that the disparities they contained fell within a limited range. Specifically, the slant stimuli were cutoff at the mean disparity magnitude of the eight slants used in the main condition. The final stimuli included binocular disparities ranging from −20.6 to 20.6 arcmin. Four of the stimuli were common between conditions: the ±52.5° stimuli in the spatial-control and main conditions; and the ±7.5° stimuli in the disparity-control and main conditions. Thus, a total of 20 unique stimuli were used in the fMRI experiment. Each stimulus presentation was unique for each participant (i.e., we rendered new stimuli that differed in the spatial location of the dots for every presentation).
In Experiment 2, we used two slants (±22.5°). These stimuli were presented at the fixation point (zero) or in a near (−6 arcmin) or far (+6 arcmin) position. In the near condition, the added disparity moved stimuli closer to the observer so that the minimum (unsigned) disparity for the highest slant angle was aligned to the fixation plane. Similarly, in the far condition, the stimuli were moved farther from the observer so that the minimum (unsigned) disparity was aligned to the fixation plane.
Psychophysics.
For psychophysical experiments, stimuli were presented in a lab setting using a stereo setup in which the two eyes viewed separate gamma-corrected CRTs (ViewSonic, FB2100x) through front-silvered mirrors at a distance of 50 cm. Images were displayed at 100 Hz with a screen resolution of 1600 × 1200 pixels. We collected preliminary psychophysical data from all participants who undertook fMRI scanning to ensure that they were able to discriminate slanted stimuli defined by random dot stereograms reliably. We also made detailed measurements of slant discrimination thresholds for six participants. In particular, we used a two-interval forced-choice paradigm (stimulus presentation = 500 ms; ISI = 1000 ms) and participants decided which of the presented stimuli was slanted further away from frontoparallel (i.e., “which stimulus was more slanted?”). We measured thresholds for eight different pedestal slant values (−52.5 to 52.5° in 15° steps). Discrimination thresholds were estimated using interleaved adaptive staircases (60 trials for each slant, repeated on 4 runs). The stimuli had a fixed retinal projection size (as for the spatial control stimuli). We averaged together sensitivities at neighboring positions to yield discrimination sensitivities at seven positions, thus making the data comparable with the fMRI analysis that distinguished between neighboring baseline slant values.
We ran an additional experiment as a sanity check for monocular cues in the stimuli. We presented a single eye's view of the stimuli to both eyes, and asked participants to make judgments with trial-by-trial feedback (affording the potential for learning). Participants judged either: (1) which of two sequentially presented stimuli contained disparity (slanted stimulus vs zero disparity stimulus), or (2) which stimulus was slanted closer at the top (positive vs negatively slanted stimuli). They were not able to perform either task reliably above chance.
fMR imaging.
Imaging data were acquired at the Birmingham University Imaging Centre using a 3T Philips MRI scanner with an 8-channel multi phase-array head coil. BOLD signals were measured with an echoplanar sequence (TE: 35 ms, TR: 2000 ms, flip angle: 79.1°, voxel size: 1.5 × 1.5 × 2 mm, near coronal 28 slices) for both experimental and localizer scans. This sequence meant that we were only able to collect data from the posterior portion of the brain, with the slice prescription enabling us to measure from the occipital cortex, posterior temporal cortex, and the posterior portion of the parietal cortex. A high-resolution T1-weighted anatomical scan (1 mm3) was acquired once for each participant to reconstruct an accurate 3-D cortical surface for each participant. Two separate scans were run for each participant on different days; each had 10 stimuli selected from the three conditions (4 from the main condition, 3 from the spatial-extent control, and 3 from the disparity-extent control) and a fixation baseline condition.
In the main fMRI experiment, stimuli selected from a set of 10 conditions were presented using a blocked-design. Each stimulus block lasted 16 s and repeated three times during an individual run in a randomized order. Each run thus had 30 blocks and two 16 s fixation intervals at the beginning and end of the run (total duration = 512 s). In a block, eight stimuli from a single condition were presented each for 1 s alternating with a 1 s blank. For each 1 s presentation, dots making up stereogram stimuli were randomly placed to exclude any local image feature effects. Eight runs were collected for each observer in a single scanning session and each participant was scanned twice. For Experiment 2, six stimulus types [2 slants (±22.5°) × 3 positions (near, zero, far)] were presented using a blocked design. The presentation procedures were same as Experiment 1. Scans lasted total 320 s. Eight runs were collected for each observer. During scanning participants performed a vernier acuity task at the fixation point (described above).
Regions-of-interest (ROIs) were defined for each participant separately using standard retinotopic mapping procedures (see Fig. 2). V3B/KO, hMT+/V5, and LO were further identified using separate functional localizer scans for each participant (Preston et al., 2008). ROI data for the participants in this study was collected as part of a previous study (Ban et al., 2012). For analysis in which we subdivided the ROIs into a central and peripheral portion, we used the eccentricity mapping localizer to define a boundary at ±2° eccentricity. This ensured we were within the spatial projection of the slanted stimulus in the highest slant condition (height 4.7°).
Figure 2.
Illustrations of the cortical surface with superimposed locations of the ROIs. Sulci are depicted in darker gray than the gyri. Shown on the maps are retinotopic areas, V3B/KO, the human motion complex (hMT+/ V5), and LO area. The activation map shows the results of a random-effects analysis of a searchlight classifier that discriminated between different slanted stimuli. The color code represents the t value of the classification accuracies obtained by moving a spherical aperture throughout the measured volume. This confirmed that our ROIs covered the likely loci of areas encoding stimulus information.
BrainVoyager QX (BrainInnovation B.V.) was used to analyze the fMRI data. For anatomical scans, we first transformed the data into Talairach space, inflated the cortex, and created flattened surfaces of both hemispheres for each subject. Each functional run was preprocessed using 3-D motion correction, slice time correction, linear trend removal, and high-pass filtering (3 cycles per run cutoff). No spatial smoothing was applied. Functional runs were aligned to the subject's corresponding anatomical space and then transformed into Talairach space. Voxel responses acquired on different days were resampled in 1 mm Talairach space using nearest neighbor sampling to avoid spatial distortion of the data. Duplicated voxels in this sampling procedure were excluded before the multivariate analyses.
Statistical analysis.
We used SPSS (IBM) for repeated-measures ANOVAs (with Greenhouse–Geisser correction when appropriate). Statistical tests for fMRI analysis were conducted in BrainVoyager. All other tests were conducted in MATLAB using standard regression functions and general linear models (GLMs), as well as writing custom scripts for bootstrapped resampling analyses (described below). To compare between competing models, we used the Akaike Information Criterion (AIC) with a correction for finite sample sizes.
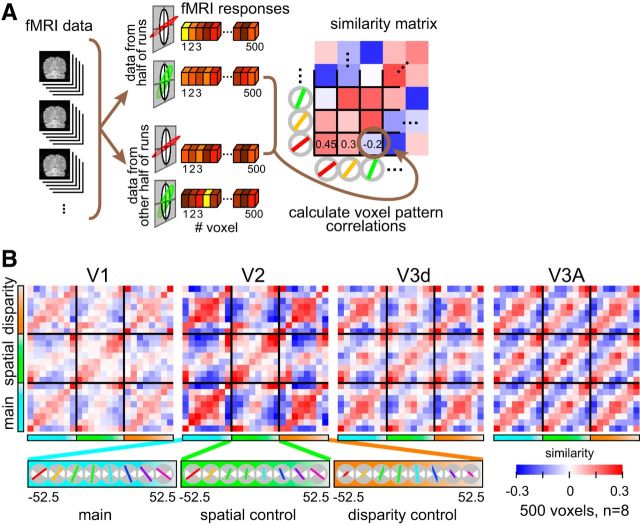
Cross-correlation similarity analysis.
For each ROI, we sorted gray matter voxels according to their response (t statistic) to all stimulus conditions versus fixation baseline, and selected the top ranked 500 voxels. We tested the importance of the number of voxels and their selection, finding that the correlation analysis was robust. Specifically we quantified the repeatability of the fMRI response patterns (mean R along the positive diagonal), as well as statistical significance (p value) as we varied the amount of data available. Repeatability saturated rapidly with the number of voxels, whereas p values were (obviously) dependent on the sample size. We chose to quantify performance at 500 voxels to be consistent with subsequent analysis using multivoxel pattern analysis (MVPA; classifier performance saturated by a pattern size of 500 voxels). In addition, we tested the voxel selection method, quantifying repeatability for: (1) the standard ranking (best), (2) voxels ranked by activity but omitting the top 100 voxels, and (3) voxels ranked in reverse order (worst). Unsurprisingly, reverse ordering led to a considerable drop in repeatability. Interestingly the repeatability remained statistically reliable in V3A once there were >150 voxels, suggesting that V3A voxels were fairly homogenous in their responses to stimuli (i.e., interchangeable) in contrast to V2 where voxel selection was more critical.
Following voxel selection, we normalized (Z-scored) the time course of each voxel separately for each experimental run to minimize baseline differences between runs. The voxel response pattern was generated by shifting the fMRI time series by 4 s (2 TR) to account for the hemodynamic lag. To avoid univariate response differences between acquired volumes, we normalized the mean of each data vector for each volume to zero by subtracting the mean over all voxels for that volume. In this way, the data vectors for each volume had the same mean value across voxels and differed only in the pattern of activity. For each block, we averaged each voxel's time courses to produce a single voxel response for a given block of slanted stimuli. We then calculated the cross-correlation between voxel responses evoked by different stimulus types in each ROI (Fig. 3).
Figure 3.
Illustration of the cross-correlation approach and empirical data. A, A schematic of the data treatment. The fMRI data were split in halves and the vector of voxel responses was then correlated across stimulus conditions. We used a cross-validation procedure, averaging together the results of different splits of the empirical data. The resulting cross-correlation matrix (averaged over cross-validations) is represented using a blue-to-red color code. B, Empirical cross-correlation matrices from areas V1, V2, V3d, and V3A. Slant angle varies in an ordered fashion for the three experimental conditions (main, spatial control, disparity control). The mean regression coefficient across split-halves is represented by the color saturation of each cell in the matrix.
To create the cross-correlation matrices, we calculated all the possible split-halves (i.e., groups of 4) of the data from the eight repetitions we obtained for each condition during one scan session as follows:
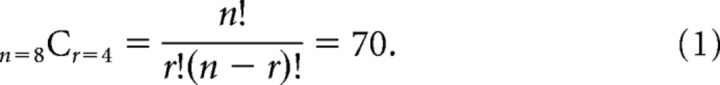 |
As there were two scanning sessions, there were 70 × 70 (4900) ways of combining the independent data samples. We therefore calculated cross-correlation matrices between each condition 4900 times, and then averaged to arrive at the empirical cross-correlation matrices. It should be noted that to create regular (24 × 24) cross-correlation matrices we duplicated the data that was redundant between conditions (i.e., the 4 stimulus conditions that would have been the same between the main, disparity, and spatial control conditions). Moreover, the data in the cross-correlation matrices are duplicated along the positive diagonal [i.e., correlation is commutative: corr(A,B) = corr(B,A)]. However, all of our analysis considered only unique data; i.e., we considered the data as a triangular matrix (including the main diagonal) and omitted the four duplicated cells. The positive diagonal in the similarity matrices represents the repeatability of the response pattern. This value is typically <1 as different (subsamples) of the data were used in each cross-correlation calculation. To establish the statistical reliability of the responses, we use a repeatability statistic calculated as mean Pearson correlation coefficient (R) along the positive diagonal of the matrix. We assessed statistical significance using 10,000 bootstrapped resamples of the whole cross-correlation matrix, and calculated the mean R statistic. We then compared the empirical repeatability with the distribution of random resamples.
Multivoxel pattern analysis.
Following procedures described previously (Preston et al., 2008), we used the libsvm toolbox (Chang and Lin, 2011) to compute prediction accuracies. We used leave-one-run-out cross validation where there were 21 training patterns and three test patterns in each condition. We calculated prediction accuracies for individual participants as the mean accuracy across cross-validations. We quantified performance at the level of 500 voxels, which represented saturated performance of the prediction accuracy as a function pattern size while ensuring that all ROIs could contribute an equal number of voxels in each participant (Preston et al., 2008 provides further quantification of this treatment).
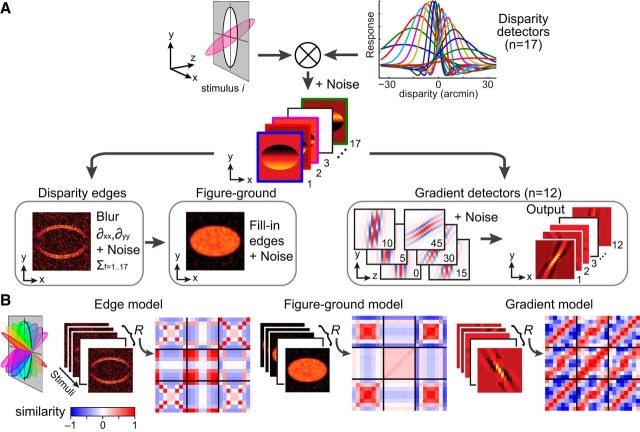
Simulations of cortical slant representations.
To model how local binocular disparities are translated to global 3-D structures, we implemented simulations in MATLAB (Fig. 4 shows a schematic illustration). Our starting point was the bank of 17 binocular disparity filter responses (Lehky and Sejnowski, 1990) in conjunction with a bias for crossed disparities informed by neuroimaging results (Cottereau et al., 2011) and electrophysiological recordings (Tanabe and Cumming, 2008; Tanabe et al., 2011). These filters were implemented as difference of Gaussian functions, whose peaks were centered from −21 to +15 arcmin. The width (sigmas) of the Gaussian functions were varied with the peak disparity (dpeak) based on interpolating the parameters listed in Table 1 of (Lehky and Sejnowski, 1990) by fitting a third-order polynomial using the method of least-squares. The peaks and sigmas (in parenthesis) of the filters were as follows: −21.2 (29.0), −16.7 (21.6), −13.3 (16.0), −11.0 (11.9), −9.2 (8.9), −7.9 (6.6), −6.6 (4.9), −5.0 (3.6), −3.0 (2.7), −1.0 (3.6), 0.6 (4.9), 1.9 (6.6), 3.2 (8.9), 5.0 (11.9), 7.3 (16.0), 10.7 (21.6), and 15.2 (29.0).
Figure 4.
Illustration of the modeling approach. A, The disparity stimulus is fed through a bank of disparity filters with noise. The outputs of these filters are then fed to a disparity edge detection algorithm and a set of disparity gradient filters. The results of the disparity edge detection process are used to generate a figure–ground segmentation map. B, The outputs for the three different models are calculated for all of the stimuli presented to the observers. These model outputs are used to create cross-correlation matrices in the same manner as the empirical data.
Table 1.
Statistical significance of the test–retest reliability of the empirical cross-correlation patterns
| Repeatability | Probability | |
|---|---|---|
| V1 | 0.169 | 0.008 |
| V2 | 0.276 | 0.023 |
| V3v | 0.095 | 0.058 |
| V4 | 0.069 | 0.068 |
| LO | 0.073 | 0.094 |
| V3d | 0.191 | 0.048 |
| V3A | 0.206 | 0.036 |
| V3B/KO | 0.115 | 0.090 |
| V7 | 0.123 | 0.073 |
| hMT+/V5 | 0.020 | 0.260 |
| VIPS | 0.040 | 0.161 |
| POIPS | 0.072 | 0.085 |
The repeatability statistic reflects the mean Pearson correlation coefficient (R) along the positive diagonal of the correlation matrix for each ROI. To assess significance we calculated 10,000 bootstrapped samples of the whole cross-correlation matrix for each area, and calculated the mean repeatability statistic. We then compared the empirical data with the distribution of repeatability statistics based on random resampling of the data. Boldface probability values represent p < 0.05.
“Tuned” (near zero) units had the following form:
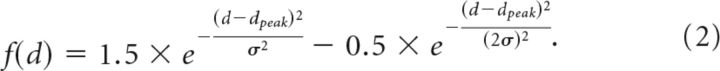 |
Whereas “near” and “far” units had the following form:
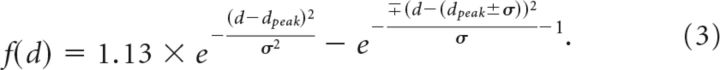 |
To generate the response of the filter bank, we convolved the disparity structure of each stimulus by each detector (i.e., the model did not compute stereo correspondences, but rather took disparity values as its inputs). This produced an x–y response magnitude for each detector in the filter bank. These detector responses were then used as inputs for further stages of processing. (1) To compute disparity edges, we used a simple, first-order edge detection pipeline (Jain et al., 1995). In particular, we first blurred the response of each filter by convolving with a Gaussian to smooth the filter outputs. We then calculated the first-order partial derivatives in the x and y directions to extract gradients:
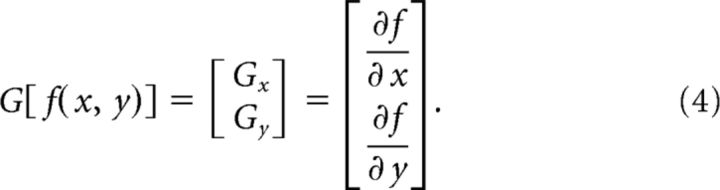 |
The magnitudes of the gradients at each location were then calculated by taking the quadratic sum of the partial derivatives to produce edge maps for each stimulus as follows:
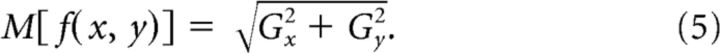 |
Having calculated this quantity for each of the 17 filters, we then calculated the sum across filters to yield an estimate of the edge locations.
(2) The figure–ground model took inputs from the disparity edge detector, and then filled in between the identified contours using MATLAB's imfill function.
(3) To compute disparity gradients, we implemented 12 gradient detectors for disparities defined by slants of [0, ±5, ±10, ±15, ±30, ±45, 90°]. These detectors were Gabor filters orientated in the y–z plane (i.e., vertical position in the screen by depth position relative to the screen). The input space was defined in angular units as follows:
where φ is the slant angle of the filter. The response profile, H, of the filter was defined as follows:
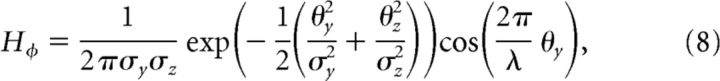 |
where σy and σz are the SDs of the Gabor filter along y- and z-planes, and λ specifies the grating cycles of the Gabor which was set to 1.8. These slant detectors took the outputs of the disparity detectors as their inputs, meaning that the spacing of the inputs and the response variance changed as a function of disparity (explaining the curved appearance of the filters and the variation of images intensity in Fig. 4). To account for differences in the sensitivity of different disparity detectors (Fig. 4A, top-right plot of filters), the disparity detectors were weighted [5, 5, 3, 3, 2, 2, 1] for the [0, ±5, ±10, ±15, ±30, ±45, 90°] gradient detectors.
Having created outputs for three different stages of processing, we created cross-correlation matrices to index the similarity of outputs when different stimuli were presented. These were not deterministic as, at each stage of processing, we added normally distributed zero-mean random noise. As the response magnitudes were different for each stage of the model (and thus responses were not directly comparable), we used an initial parameter search to determine appropriate noise levels. In particular, we selected noise levels by starting from low noise parameter values and then increased the noise until the R2 values of the GLM regressions for all three models fell <0.6 (comparable with the empirical data). This resulted in default model noise parameters of 3% of the peak response output for the disparity detectors, 10% for the edge model, 20% for figure–ground model, and 5% for the gradient detectors. Having obtained these parameters, we then explored how changing these default values affected the fit of the simulations to the empirical data. Specifically, for the edge and figure/ground models, we ran the simulations by adding normally distributed noise whose SDs were ×0.5 (low noise level), ×1.0 (middle), or ×2.0 (high) of the default level. For the gradient model, noise was ×1.0 (low), ×2.0 (middle), or ×3.0 (high) the default. The GLM regressions were repeated 2000 times for each simulation at each combination of noise levels. Noise values below the defaults did not lead to appreciably better fits, suggesting that these noise parameters reflect the maximum bound that our three models could explain the empirical fMRI responses in V1, V2, V3d, and V3A. Values above these noise parameter values degraded the fit, although the pattern of results was fairly robust to increased levels of noise, particularly with respect to responses in areas V2 and V3A.
Simulations of cortical magnification.
To simulate the effects of cortical magnification factors for different regions of interest, we used published estimates (Yamamoto et al., 2008) of the neural receptive field eccentricity for V1, V2, V3, and V3A as a function of cortical distance relative to the midpoint of the eccentricity range tested during eccentricity mapping (this was at 8° eccentricity). In particular, eccentricity mapping data were fit with an exponential function (Daniel and Whitteridge, 1961) to describe the relationship between cortical position, x, and receptive field eccentricity, E:
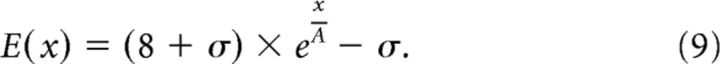 |
Where A and σ are constants (Yamamoto et al., 2008): V1 (A = 22.6, σ = 2.9); V2 (A = 25.6, σ = 3.0); V3 (A = 18.7, σ = 0.9); and V3A (A = 26.0, σ = 1.5). The cortical magnification factor M was estimated by taking derivative of the inverse function of Equation 9:
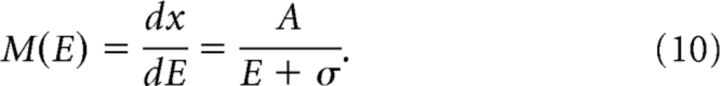 |
By applying M for each visual area on the stimulus inputs, we simulated different representations. Note that there may be individual differences in cortical magnification factor (Dougherty et al., 2003; Harvey and Dumoulin, 2011), that are not accounted for by our approach. However, by fitting between-subjects averaged data with between-subjects averaged cortical magnification factors that align with previous estimates (Dougherty et al., 2003; Harvey and Dumoulin, 2011), the impact of these differences is likely to be minimal.
Results
Participants viewed disparity-defined stimuli depicting a single slanted surface (Fig. 1) in a blocked fMRI design. Across blocks, we presented parametric variations of slant, creating a family of surfaces that were slanted toward or away from the observer. Varying the slant of a surface has obvious consequences (Fig. 1B): as it is rotated away from frontoparallel, the projection size decreases following a cosine function, while the range of depths increases following a sine function. This complicates the interpretation of measures of neural activity, as responses might relate to: (1) changes in projection size, (2) the range of binocular disparities, or (3) the surface slant. To quantify the effects of these covariates, we included stimuli from two control conditions (Fig. 1C) in which either (1) projection size or (2) disparity magnitude was constrained as slant was varied. Thus, we aimed to identify cortical areas that support decoding of surface slant that did not change when low-level changes were made to the stimuli.
We quantified fMRI responses in ROIs in occipital and parietal cortex (Fig. 2) using a voxel pattern similarity approach (Kriegeskorte et al., 2008a). We calculated the mean response vector for a given stimulus by splitting the data into two halves and then calculating the average BOLD response for each of the most responsive voxels (n = 500). We then cross-correlated the vectors evoked by each slant in the three conditions, to generate a 24 × 24 similarity matrix of the Pearson correlation coefficient (R; Fig. 3). The positive diagonal in these plots represents the test-retest reliability of the fMRI responses.
Inspecting the raw cross-correlation matrices suggested that some cortical areas supported the extraction of stimulus information using the cross-correlation technique (Fig. 3), whereas other areas did not. Formally, we calculated mean correlation along the positive diagonal and compared it to the distribution of mean correlation coefficients obtained by bootstrapped resampling the empirical data. On this basis, cross-correlations were reliable in areas V1, V2, V3d, and V3A, but not elsewhere (Table 1).
We obtained strongest patterns of correlation (i.e., highest split-half reliability) in V2 and V3A (Table 1); however, the correlation structure differed (Fig. 3B). In V2, a notable feature of the similarity matrix is that opposing slants in the “main” and “disparity control” conditions gave rise to similar voxel responses (red squares in the corner cells). This can be understood in terms of the stimulus projection size: despite a considerable difference in slant, size was held constant. A similar, although weaker, pattern was observed in area V1. By contrast, the V3A correlation matrix is notable for its regular diagonal structure: stimuli with similar slants produce similar fMRI activity, whether or not the basic low-level features of the stimulus (spatial extent or mean disparity) differ. Further, different slants produce dissimilar fMRI responses. This qualitative comparison of V2 and V3A suggests different representations: edges and segmentation versus responses related to disparity-defined slant.
To assess this formally, we next applied an analysis-by-synthesis approach based on building a disparity slant estimation model (Fig. 4). The front-end comprised a disparity filter bank whose form was determined from previous work (Lehky and Sejnowski, 1990; Cottereau et al., 2011). Thereafter, we implemented three processing stages that were designed to capture key properties of the viewed stimuli, namely, (1) their (disparity-defined) edges, (2) the area of the stimulus comprising the figure versus the background, and (3) the change in disparity across space (i.e., disparity gradients). We computed the response of these models for each of the experimental stimuli, and chose simulation parameters (e.g., number of repetitions, noise levels) to match fMRI measurements. We then generated similarity matrices based on the models' responses (Fig. 4), and used these as regressors for the empirical similarity matrices through a GLM with an information criterion (AIC) on the number of parameters.
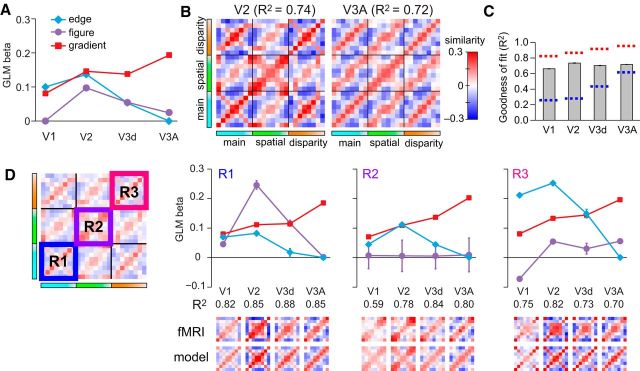
The model-based analysis of the empirical similarity matrices indicated different contributions of edge, figure–ground, and gradient mechanisms in the visual processing hierarchy (Fig. 5A). V2 responses had a significant contribution from mechanisms that represent the spatial extent of the plane, compatible with processes of figure,-ground segmentation (Qiu and von der Heydt, 2005). In contrast, responses in area V3A were explained to a large extent on the basis of responses to the disparity gradients, with responses in V3d intermediate between those in V2 and V3A. As a confirmation of the model fits, we used the model weights to reconstruct the cross-correlation matrices (Fig. 5B); comparison with the empirical data (Fig. 3) suggested that the model captured the principal features of the empirical data. Formally, we computed the noise ceiling range for our fMRI data (Nili et al., 2014) and found that our model was within its bounds, suggesting it performs as well as any possible model given the noise in the fMRI data (Fig. 5C).
Figure 5.
Regression analysis of the empirical cross-correlation matrices. A, The weights of each model are plotted for areas V1, V2, V3d, and V3A. B, Model reconstructions based on the GLM β weights calculated in A with 2000 simulations. This result is confirmatory in allowing visualization of the features captured by the modeling approach. C, Goodness of fit of the GLM model in each region of interest with the associated noise ceiling bounds that estimate the minimum and maximum GLM performance that could be achieved given the noise in the data (Nili et al., 2014). The upper bound (red) is calculated by using the between-subjects mean matrix as a regressor for bootstrapped (10,000 samples) resampled averages of the subjects' data. The lower bound (blue) was calculated using single subjects' matrices as regressors for the bootstrapped resampled averages of the subjects' data. In both cases, the bounds were defined as the median value of the boostrapped R2 samples. D, GLM analyses conducted within subregions of the cross-correlation matrices. Error bars indicate ±SEM.
We also performed a local GLM analysis within cells of the global similarity matrices (Fig. 5D). First, we considered responses in the main condition in which both disparity range and projection size varied (Fig. 5D, R1). We found differential contributions from the three models in each ROI, with most of the variance explained by the figure-,ground model in V2 and the gradient model in V3A. Next we considered the central cell (Fig. 5D, R2) that contrasts fMRI responses when the spatial extent of the stimuli was held constant. Reassuringly, the figure-ground model (purple data series) does not explain the data as the figure–ground relationship was constant across slants. However, contributions from the disparity edge and disparity gradient models across the visual hierarchy are apparent (i.e., nonzero β weights). This suggests that information about the disparity-defined edges is likely to incorporate information about the 3-D structure of the stimuli, rather than being limited to the 2-D retinotopic edge location. Finally, we considered the correlation in the disparity control condition (Fig. 5D, R3). Here the importance of the response to the disparity edges becomes greater in early areas, reflecting the larger changes in stimulus projection size, and demonstrates that low-level stimulus changes play an important role in driving these fMRI responses. Importantly, however, responses in V3A are relatively unaffected by these low-level changes, with the disparity gradient model consistently providing the best explanation for the data (R1, R2, R3).
Further evidence for the role of V3A in representing disparity gradients came from considering the fMRI data retinotopically subdivided into a central portion that was stimulated by every stimulus versus a peripheral portion whose stimulation varied with slant (Fig. 6A). In particular, we identified the central two degree portion of each ROI, corresponding to the region that would be stimulated by each of the presented stimuli, but not include the edges. We reasoned that fMRI responses driven by responses to stimulus edges would be reduced for the central portion of the stimulus, while responses relating to extensive surface properties should be relatively unaffected. We found that similarity matrices computed for the central region were attenuated (i.e., less saturated) in areas V1 and V2 relative to the periphery, but largely unaffected in V3A (Fig. 6B). This again suggests that V3A represents aspects of the stimuli related to spatially extensive properties, and not edges per se.
Figure 6.
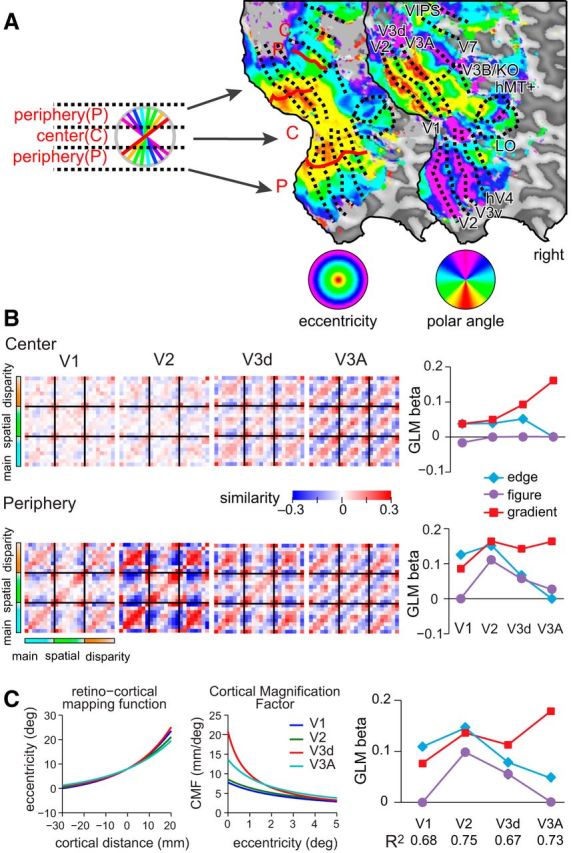
Cross-correlation matrices calculated using fMRI data partitioned into central- and peripheral-regions and taking account of cortical magnification. A, Example flat maps of a hemisphere from one participant showing phase-encoded polar- and eccentricity-based retinotopic maps. We used these maps to partition the cortical regions of interest to localize regions that respond to the central portion of the stimulus and edge locations (shown by the diagram of the partitioned stimulus locations). We then recomputed cross-correlation matrices based on the subdivided regions of interest. B, Model-based GLM analysis of the empirical cross-correlation matrices showing the weights attached to each model in areas V1 to V3A. Error bars (±SEM) lie within plotting symbols. C, Cortical magnification factors (CMFs) were defined separately for each of V1, V2, V3, and V3A using the formulas (Eqs. 4, 5; see Methods and Materials) and parameters estimated from retinotopic mapping data. Visual eccentricity as a function of cortical distance can be approximated by an exponential (left), where we use the 8° eccentricity location as a reference point. CMFs are obtained by computing the derivatives of inverses of these eccentricity representations (middle). The plots were regenerated from Yamamoto et al., (2008). We computed model cross-correlation matrices where the input representations were distorted using cortical magnification factors for each area. We then used these as regressors for the empirical fMRI data, producing the plot of GLM weights (right). Error bars (±SEM) lie within plotting symbols.
In constructing our regressor models, we sought parameters that emulated the noise characteristics of the fMRI data. However, to ensure generality, we systematically varied the level of noise in: (1) the representation of disparities, (2) the extraction of disparity edges, and (3) the representation of the surface extent. Performing simulations at each of these noise levels (Fig. 7), we found that fMRI responses in V3A were consistently best explained by the disparity gradient model. A further consideration for our regression approach is the possibility of multicolinearity between the regressors as they share common stages of processing (Fig. 4). However, the addition of independent noise, and differences in the representations computed at each stage, meant there was little colinearity. Specifically, using the variance inflation factor (VIF) we found low values for disparity edge (VIF = 2.02), figure–ground (VIF = 1.53), and gradient models (VIF = 1.44), indicating little error inflation due to colinearity (Marquardt, 1970). Moreover, the AIC-based model selection procedure used penalized unnecessary models, meaning that redundant models (because of colineaity) would have been excluded.
Figure 7.
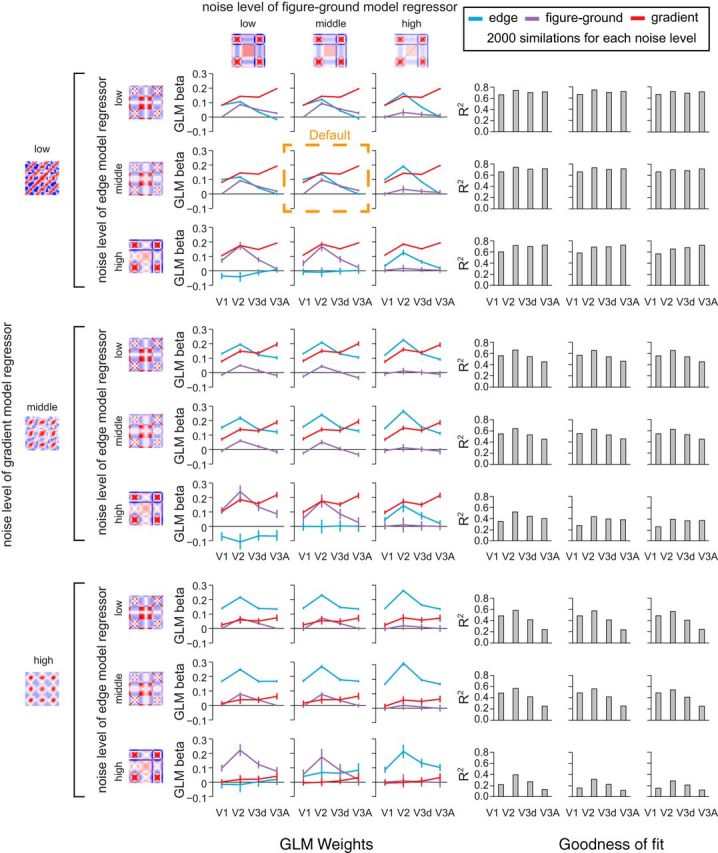
Simulations of the models with different noise parameters. Model-based GLM analysis of the empirical cross-correlation matrices where the three component models (edge, figure-ground and gradient) have their noise levels varied systematically. The default noise parameters used in the main paper are highlighted by the dashed orange box. For the edge and figure-ground models, we ran the simulations by adding normally distributed noise whose SDs were ×0.5 (low noise level), ×1.0 (middle), or ×2.0 (high) of the default level. For the gradient model, noise was ×1.0 (low), ×2.0 (middle), or ×3.0 (high) the default. Bar graphs to the right of the figure plot the R2 value of the model fit; their layout corresponds to the line graphs on the left side of the figure.
A simplification of our modeling approach is our use of a spatially uniform representation. Retinal and cortical sampling is nonuniform, such that there is an over-representation of the central portion of the visual field (Daniel and Whitteridge, 1961). We therefore recomputed model responses after applying a cortical magnification function (Yamamoto et al., 2008). We found that the results were qualitatively unchanged: the amount of variance explained by the model increased marginally for V1, V2, and V3A, and decreased marginally in V3d, and the overall pattern of weights remained consistent (Fig. 6C). This analysis makes unlikely an interpretation of our data premised on differences in receptive field sizes between ROIs. Specifically we see clear differences in the model estimates for individual ROIs with or without accounting for changes in cortical magnification factor. Moreover, although we see disparity gradient responses in area V3A, we find no such effect in area V3v which has similar receptive field sizes (Yamamoto et al., 2008, their Table 2).
Table 2.
Statistical significance slant decoding with respect to the upper 95th centile of the distribution of prediction accuracies obtained with randomly permuted condition labels
| Offset 0 | Offset 1 | Offset 2 | |
|---|---|---|---|
| V1 | <0.0001 | 0.9454 | 1 |
| V2 | <0.0001 | 0.3368 | 1 |
| V3v | 0.0132 | 0.4751 | 1 |
| V4 | 0.0001 | 0.9486 | 1 |
| LO | 0.0022 | 0.3478 | 0.0715 |
| V3d | <0.0001 | 0.0631 | 0.9993 |
| V3A | <0.0001 | 0.0089 | 1 |
| V3B/KO | <0.0001 | 0.0841 | 0.9640 |
| V7 | 0.0017 | 0.3820 | 0.9989 |
| hMT+/V5 | 0.2254 | 0.6269 | 0.9610 |
| VIPS | 0.0135 | 0.1028 | 0.9149 |
| POIPS | 0.1793 | 0.0572 | 0.2754 |
Statistical significance is based on bootstrapping the between-subjects median prediction accuracy (10,000 bootstrap resamples). Boldface probability values represent p < 0.05.
MVPA decoding analyses
To provide additional analyses, we used MVPA to test whether we could predict which of the eight different slanted stimuli was viewed based on fMRI measurements. We could decode stimuli for all three conditions (main, spatial control, disparity control) in areas V1, V2, V3d, V3A, and V7 at levels reliably above randomly permuted data (Fig. 8). Importantly, we found a significant interaction between ROI and condition (F(8,56) = 6.3, p < 0.001). In particular, accuracies differed between conditions in V1 (F(2,14) = 27.0, p < 0.001), V2 (F(2,14) = 13.1, p = 0.001), and V3d (F(2,14) = 5.0, p = 0.022), indicating that low-level stimulus properties played an important role in shaping fMRI responses. By contrast, decoding performance did not differ significantly in V3A (F(2,14) = 1.2, p = 0.344) and V7 (F(2,14)<1, p = 0.427). Consistent with the results from the similarity matrices, this suggests fMRI responses in higher dorsal areas are relatively unaffected by low-level slant covariates.
Figure 8.
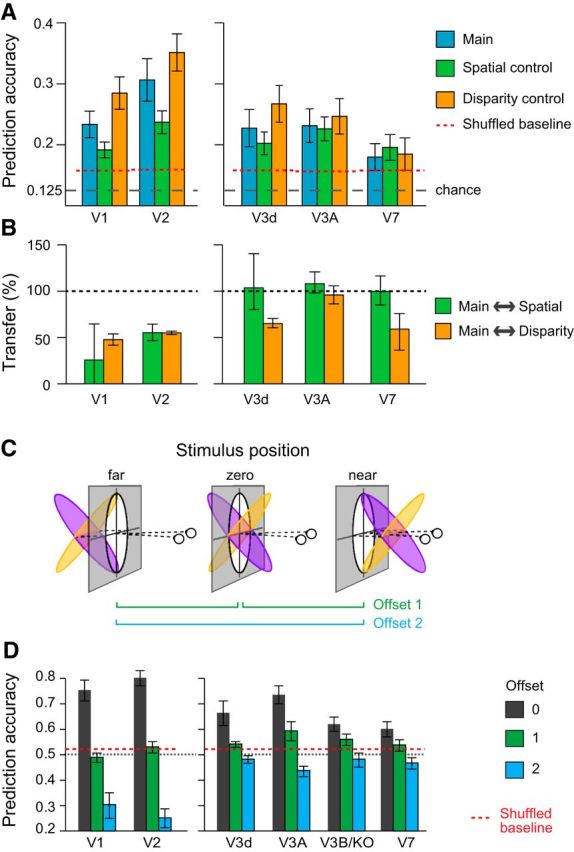
Results of MVPA decoding of surface slant. A, Eight-way classification results across ROIs with above chance prediction accuracy for the three conditions. Error bars show ±SEM. The dotted horizontal line represents the upper 97.5th centile of randomly permuted data. B, Transfer results expressed as a percentage of the within condition prediction accuracy. One-hundred percent would indicate the same accuracy for testing and training between conditions as for testing on the same condition. Error bars show SEM. C, Manipulating the depth positions of the slanted surfaces. Opposing slants were presented centered on the fixation point (zero), or translated away (far) or toward (near) the observer. D, Prediction accuracies for the binary classification of opposing slants. The dashed red line represents the upper 97.5th centile based on randomly permuted data. Error bars show ±SEM.
We then tested whether a decoding algorithm trained with fMRI data from one condition could predict slant in a different condition (e.g., train on the main condition, test on the spatial control condition). Our expectation was that fMRI responses driven by slant covariates (i.e., disparity range, edge location) would show reduced performance, while an area that responded principally to slant would show transfer between conditions. Using an index to express transfer (0%: no transfer; 100%: training and testing within conditions is the same as training and testing between conditions), we found ∼50% transfer in early visual areas (V1, V2), whereas ∼100% in V3A (Fig. 8B). This again suggests that low-level differences between stimuli did not substantially modify the responses of V3A to similarly slanted surfaces.
To provide further tests of slant processing, in Experiment 2 we manipulated the depth position of the surface. In particular, using MVPA decoding, we tested how well opposing slants could be discriminated, and then tested for transfer when the overall disparity of the stimuli was manipulated (Fig. 8C). Logically, we might expect different outcomes depending on the types of representation in an ROI. If an area encoded information about the stimuli purely in terms of changes in the particular disparities across regions of space, we would not expect transfer, as disparities in the stimulus change as it is translated to and fro in depth. By contrast, if an area encoded surface slant regardless of the absolute disparity (i.e., a coordinate frame representing the physical inclination of a surface regardless of the viewing position), we might expect complete tolerance such that surface slant could be decoded in all cases. We would conceptualize such detectors as lying one network stage beyond that modeled by the gradient detectors in Figure 4. In particular, such slant detectors would take inputs from gradient filters centered at the fixation plane (as modeled in Fig. 4) in addition to banks of gradient filters located in front of, and behind, the fixation plane. (Note, in Experiment 1 stimuli were centered on the fixation plane, so we could not have distinguished these alternatives.)
The pattern of decoding accuracies suggested a partial tolerance to depth position in higher dorsal areas in contrast with early visual areas (Fig. 8D). Performance in V1 and V2 dropped to chance when the stimuli were translated one offset in depth, and were significantly below chance for displacements that moved all parts of the stimuli from crossed to uncrossed disparities. This reversal is compatible with responses that reflect the spatial arrangement of the disparity edges in the stimulus: when the stimulus was translated from near to far, opposing slants give rise to a similar pattern of disparity edges with respect to the surround, although with reversed sign. It appears that this spatial configuration is strongly represented in early visual areas, compatible with the results from Experiment 1. Prediction accuracies in V3A showed a somewhat different pattern. Moving the stimuli one offset supported reliable predictions (permutation test p = 0.0089; Table 2). Offsetting the stimuli further in depth led to performance that was slightly below chance, suggesting that there is a limited degree of tolerance to depth position in V3A. Performance in V3d and V3B/KO resembled that of V3A but was statistically weaker.
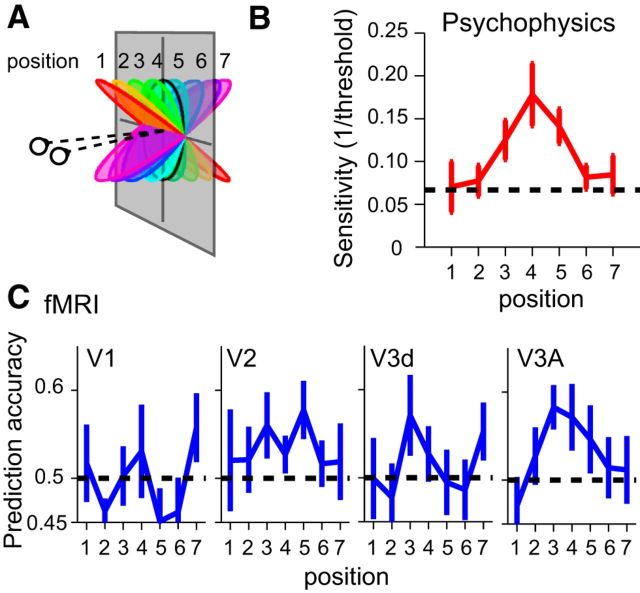
Relation between fMRI measures and slant perception
To test for similarities between fMRI responses and observers' perception of the stimuli, we considered pairwise discriminations of surface slant at the fMRI and psychophysical levels. In particular, participants made slant discrimination judgments in the lab at different baseline slant angles corresponding to the slants tested in the fMRI experiment (Fig. 9). We found that observers' sensitivity was highest for low slant angles and declined as the slant angle increased (Fig. 9B). This is expected as lower slants minimize the discrepancy between the slant signaled by disparity versus texture (the random dots indicated a flat surface; Hillis et al., 2004). We compared psychophysical performance with the results of an MVPA classifier that discriminated neighboring slants based on fMRI data (Fig. 9C). We found a similarity between psychophysical performance and fMRI decoding in area V3A, but not elsewhere. Formally, we used multiple regression with an AIC model selection procedure to explain psychophysical discrimination based on the fMRI results. We found that area V3A yielded the smallest AICc value (indicating it to be the best model) and provided a good fit to the behavioral data (R2 = 0.645, F(1,6) = 9.09, p < 0.0297). The next best model, area V2, did not predict behavioral performance (R2 = 0.281, F(1,6) = 1.95, p = 0.221). This suggests V3A may be a substrate that informs perceptual judgments of slant.
Figure 9.
Testing for similarities between perceptual discriminability and fMRI-decoding. A, An illustration of the stimulus slants used for the psychophysical and fMRI measurements. B, Observers' sensitivity to slight changes in slant at different pedestal slants. Thresholds were measured at each of the eight stimulus slants illustrated in A. To compare with the fMRI results, we averaged neighboring pairs together to yield discrimination thresholds at seven positions. The dashed horizontal line corresponds to a slant discrimination threshold of 15° (i.e., the location at which neighboring pairs of stimuli used in the study would only just be discriminable). Error bar shows ±SEM. C, Two-way prediction accuracies for a classifier trained on fMRI data from neighboring slants. Error bars show ±SEM.
Control measures
We took a number of precautions to avoid experimental artifacts. First, our stimuli depicted slant around a horizontal axis to avoid texture density cues that can emerge in the random dot stimuli for other rotation axes. Second, to ensure equal attentional allocation across conditions, and fixation at the center of the display, we used a vernier target-detection task. This involved determining whether a small line flashed (250 ms) to one eye was left or right of the upper vertical bar of the fixation marker. The brief presentation, small vernier offsets, and irregular timing of presentation (0.5 probability of appearance and variable onset), required that participants maintained vigilance throughout the fMRI scan. Third, the vernier task had a double purpose in that it provided a subjective measure of eye vergence (Popple et al., 1998). We found that participants maintained vergence well: vergence was close to fixation and not systematically different between slant angles (F(7,49)<1, p = 0.917) or conditions (F(2,14) = 2.40, p = 0.127).
Discussion
We used fMRI measurements and a series of generative models to infer the computational hierarchy that supports the estimation of slant, a property important for recognizing 3-D surfaces and planning actions. Using multivoxel analysis approaches (correlation and decoding) we report four main advances. First, area V3A represents information about slanted surfaces by pooling disparity across space and is largely unaffected by low-level stimulus changes. Second, responses in V3A show a degree of tolerance in their responses across different positions in depth. This suggests a stage of representation beyond extracting disparity gradients that may be important for estimating the physical surface of a slant at different viewing distances. Third, the discriminability of fMRI responses in V3A mirrors psychophysical judgments, suggesting a neural population that may contribute to the perception of surface slant. Finally, we show that processes related to gradient estimation in V3A build upon earlier representations of edge processing and figure–ground segmentation in V2.
Previous human functional imaging work (Shikata et al., 2001) suggested responses to planes oriented in depth in the caudal intraparietal area (CIP) and anterior intraparietal area (AIP) of the dorsal stream, consistent with electrophysiological recordings in parietal cortex (Tsutsui et al., 2002). These responses were driven predominantly by the tilt of the surface (i.e., rotation in the image plane, like the changing orientation of a clock's hands over time) rather than slant that requires an explicit estimate of the 3-D structure. Recently, Rosenberg et al. (2013, 2014) uncovered explicit representations of slant in macaque area CIP, suggesting an important cortical locus for the encoding of surface orientation. Our evidence from V3A, which anatomically precedes CIP in the macaque, suggests an earlier locus important for processing disparity signals to slant. Rosenberg et al. (2013, 2014) used surfaces defined by random dots, as well as disparity-rendered checkerboard patterns, which contain surface orientation cues from both disparity and texture. It is possible that information about slant from disparity that we find to be processed in V3A is integrated with other cues to surface orientation in CIP (Tsutsui et al., 2002). However, the homology between humans and macaques may be inexact in that a more lateral locus of area V3B/KO appears important in humans for integrating disparity and texture cues (Murphy et al., 2013), whereas human V7 and/or VIPS are believed to correspond to macaque CIP (Orban et al., 2006).
Our data indicate that disparity gradient representations in V3A are preceded by figure–ground segmentation in V2. Electrophysiological investigations of neurons in macaque area V2 suggested that they play a role in calculating the relative disparity between two surfaces (Thomas et al., 2002) and some cells are selective to disparity-defined edge information in a manner that signals border ownership between figure and ground (Qiu and von der Heydt, 2005). Other work (Bredfeldt and Cumming, 2006) suggested that these edge representations are limited in the extent to which they underlie scene segmentation, providing a relatively simple first step in separating figure from surround. Our fMRI results suggest a significant role for human V2 in representing the enclosed area of a disparity-defined target shape. This activity may result from an aggregated population code of individual neurons with somewhat limited ability to signal figure–ground information, or alternatively may reflect feedback signals that modulate activity based on scene segmentation.
Our fMRI approach enabled us to sample from multiple areas across the visual cortex, however cross-correlation matrices in areas other than V1, V2, V3d, and V3A were not statistically significant (Table 1). Differences in the strength of the cross-correlation matrices may simply reflect our ability to measure fMRI responses in these other areas (V3v, V4, LO, hMT+/V5, VIPS, POIPS). Nevertheless, it is also possible that the representations in these areas reflect a further stage of processing (for instance one that integrates other slant cues), such that the abstracted nature of the random dot stimuli here used make them suboptimal for driving neural responses in these areas. Although random dot stimuli depicting slanted planes do drive neuronal responses in ventral inferior temporal cortex (Liu et al., 2004), these responses were for tilt rather than slant, and it is possible that cue conflicts inherent in random dot stereograms attenuate responses for 3-D shape information. Other work indicates slant responses in area V4 (Hinkle and Connor, 2002), however, monocular cues may underlie these responses. It is also possible that more sophisticated models than we have considered here might be necessary to capture the response characteristics of higher portions of the ventral pathway (e.g., higher order conjunctions of surface features). In preliminary work, we considered an additional model that sought to estimate the physical size of the viewed plane by taking viewing geometry into account; however, it did not account for response profiles in any of the regions of interest we considered. Finally, recordings from macaque MT/V5 suggest it responds to 3-D surface orientation from velocity and disparity gradients (Sanada et al., 2012). However, we did not find reliable responses in human MT+/V5 complex, which likely reflects the absence of motion from our stimuli.
Although our data point strongly to the role played by area V3A, it is difficult to separate the representation of surface slant from disparity gradients. Slant and disparity can be decoupled by changing the overall position of the stimulus in depth so that the disparity content changes, while slant remains constant. In Experiment 2, we made this manipulation, and our decoding results suggest that responses in V3A show a degree of tolerance to changes in depth position. This indicates an intermediate form of surface representation that is beyond gradients, but not completely tolerant to changes in depth position. Such representations that retain information about the current view parameters (Ban et al., 2012) are likely to feed forward to parietal circuits involved in the control of action. This is consistent with recordings from the (more anterior) macaque AIP where neurons retain their selectivity for object configurations when stimuli are translated by up to 30 arcmin of disparity (Srivastava et al., 2009), indicating tolerance over a broad depth range. Nevertheless, neuronal spike rates are strongly modulated by this manipulation, suggesting that neuronal responses are not invariant to changes in overall disparity.
Recent progress has been made in seeking to link fMRI measurements with computations that underlie sensory processing of local features (Kay et al., 2008; Brouwer and Heeger, 2009) and objects (Kriegeskorte et al., 2008b; Huth et al., 2012). Typically, this involves modeling brain activity using a single algorithm per brain area. Here we have taken the approach of using a series of computational models to understand the way in which representations evolve across stages of the visual processing hierarchy. By using parametric stimulus manipulations and models that encode specific image features, we uncover contributions of different processes (edge detection, scene segmentation, and spatially extensive gradients) within the cortical hierarchy. Thus despite the complex nature of the relationship between the BOLD signal and neuronal activity, coupling computational analysis approaches with fMRI responses from large-scale populations has significant potential to help disentangle the complex analysis steps performed by the cortex. As such, the analysis-by-synthesis approach is likely to be highly generalizable beyond the disparity domain, helping to uncover the computations supporting the analysis of form and movement within visual or multisensory cortices. Moreover, it may prove useful in the analysis of other types of complex neuronal recordings (e.g., EEG).
Footnotes
This project was supported by the Wellcome Trust (095183/Z/10/Z) and the Japan Society for the Promotion of Science (H22.290 and KAKENHI 26870911). We thank James Blundell for help with data collection, and N. Kriegeskorte and H. Yamamoto for comments on this study.
The authors declare no competing financial interests.
This is an Open Access article distributed under the terms of the Creative Commons Attribution License Creative Commons Attribution 4.0 International, which permits unrestricted use, distribution and reproduction in any medium provided that the original work is properly attributed.
References
- Backus BT, Fleet DJ, Parker AJ, Heeger DJ. Human cortical activity correlates with stereoscopic depth perception. J Neurophysiol. 2001;86:2054–2068. doi: 10.1152/jn.2001.86.4.2054. [DOI] [PubMed] [Google Scholar]
- Ban H, Preston TJ, Meeson A, Welchman AE. The integration of motion and disparity cues to depth in dorsal visual cortex. Nat Neurosci. 2012;15:636–643. doi: 10.1038/nn.3046. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bredfeldt CE, Cumming BG. A simple account of cyclopean edge responses in macaque V2. J Neurosci. 2006;26:7581–7596. doi: 10.1523/JNEUROSCI.5308-05.2006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Brouwer GJ, Heeger DJ. Decoding and reconstructing color from responses in human visual cortex. J Neurosci. 2009;29:13992–14003. doi: 10.1523/JNEUROSCI.3577-09.2009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chandrasekaran C, Canon V, Dahmen JC, Kourtzi Z, Welchman AE. Neural correlates of disparity-defined shape discrimination in the human brain. J Neurophysiol. 2007;97:1553–1565. doi: 10.1152/jn.01074.2006. [DOI] [PubMed] [Google Scholar]
- Chang CC, Lin CJ. LIBSVM: a library for support vector machines. ACM Trans Intell Syst. 2011;2:1–27. [Google Scholar]
- Cottereau BR, McKee SP, Ales JM, Norcia AM. Disparity-tuned population responses from human visual cortex. J Neurosci. 2011;31:954–965. doi: 10.1523/JNEUROSCI.3795-10.2011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cumming BG, Parker AJ. Responses of primary visual cortical neurons to binocular disparity without depth perception. Nature. 1997;389:280–283. doi: 10.1038/38487. [DOI] [PubMed] [Google Scholar]
- Daniel PM, Whitteridge D. The representation of the visual field on the cerebral cortex in monkeys. J Physiol. 1961;159:203–221. doi: 10.1113/jphysiol.1961.sp006803. [DOI] [PMC free article] [PubMed] [Google Scholar]
- DeAngelis GC, Ohzawa I, Freeman RD. Depth is encoded in the visual cortex by a specialized receptive field structure. Nature. 1991;352:156–159. doi: 10.1038/352156a0. [DOI] [PubMed] [Google Scholar]
- Dougherty RF, Koch VM, Brewer AA, Fischer B, Modersitzki J, Wandell BA. Visual field representations and locations of visual areas V1/2/3 in human visual cortex. J Vis. 2003;3(10):1, 586–598. doi: 10.1167/3.10.1. [DOI] [PubMed] [Google Scholar]
- Durand JB, Nelissen K, Joly O, Wardak C, Todd JT, Norman JF, Janssen P, Vanduffel W, Orban GA. Anterior regions of monkey parietal cortex process visual 3D shape. Neuron. 2007;55:493–505. doi: 10.1016/j.neuron.2007.06.040. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Georgieva S, Peeters R, Kolster H, Todd JT, Orban GA. The processing of three-dimensional shape from disparity in the human brain. J Neurosci. 2009;29:727–742. doi: 10.1523/JNEUROSCI.4753-08.2009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Goncalves NR, Ban H, Sánchez-Panchuelo RM, Francis ST, Schluppeck D, Welchman AE. 7 Tesla fMRI reveals systematic functional organization for binocular disparity in dorsal visual cortex. J Neurosci. 2015;35:3056–3072. doi: 10.1523/JNEUROSCI.3047-14.2015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Harvey BM, Dumoulin SO. The relationship between cortical magnification factor and population receptive field size in human visual cortex: constancies in cortical architecture. J Neurosci. 2011;31:13604–13612. doi: 10.1523/JNEUROSCI.2572-11.2011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hillis JM, Watt SJ, Landy MS, Banks MS. Slant from texture and disparity cues: optimal cue combination. J Vis. 2004;4(12):1, 967–992. doi: 10.1167/4.12.1. [DOI] [PubMed] [Google Scholar]
- Hinkle DA, Connor CE. Three-dimensional orientation tuning in macaque area V4. Nat Neurosci. 2002;5:665–670. doi: 10.1038/nn875. [DOI] [PubMed] [Google Scholar]
- Huth AG, Nishimoto S, Vu AT, Gallant JL. A continuous semantic space describes the representation of thousands of object and action categories across the human brain. Neuron. 2012;76:1210–1224. doi: 10.1016/j.neuron.2012.10.014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jain R, Kasturi R, Schunck BG. Machine vision. New York: McGraw Hill; 1995. [Google Scholar]
- Janssen P, Vogels R, Orban GA. Selectivity for 3D shape that reveals distinct areas within macaque inferior temporal cortex. Science. 2000;288:2054–2056. doi: 10.1126/science.288.5473.2054. [DOI] [PubMed] [Google Scholar]
- Janssen P, Vogels R, Liu Y, Orban GA. At least at the level of inferior temporal cortex, the stereo correspondence problem is solved. Neuron. 2003;37:693–701. doi: 10.1016/S0896-6273(03)00023-0. [DOI] [PubMed] [Google Scholar]
- Kay KN, Naselaris T, Prenger RJ, Gallant JL. Identifying natural images from human brain activity. Nature. 2008;452:352–355. doi: 10.1038/nature06713. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kleiner M, Brainard DH, Pelli DG. What's new in psychtoolbox-3. Perception. 2007;36 Abstr. [Google Scholar]
- Kriegeskorte N, Mur M, Bandettini P. Representational similarity analysis- connecting the branches of systems neuroscience. Front Syst Neurosci. 2008a;2:4. doi: 10.3389/neuro.01.016.2008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kriegeskorte N, Mur M, Ruff DA, Kiani R, Bodurka J, Esteky H, Tanaka K, Bandettini PA. Matching categorical object representations in inferior temporal cortex of man and monkey. Neuron. 2008b;60:1126–1141. doi: 10.1016/j.neuron.2008.10.043. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lehky SR, Sejnowski TJ. Neural model of stereoacuity and depth interpolation based on a distributed representation of stereo disparity. J Neurosci. 1990;10:2281–2299. doi: 10.1523/JNEUROSCI.10-07-02281.1990. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Liu Y, Vogels R, Orban GA. Convergence of depth from texture and depth from disparity in macaque inferior temporal cortex. J Neurosci. 2004;24:3795–3800. doi: 10.1523/JNEUROSCI.0150-04.2004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Marquardt DW. Generalized inverses, ridge regression, biased linear estimation, and nonlinear estimation. Technometrics. 1970;12:591. doi: 10.1080/00401706.1970.10488699. [DOI] [Google Scholar]
- Minini L, Parker AJ, Bridge H. Neural modulation by binocular disparity greatest in human dorsal visual stream. J Neurophysiol. 2010;104:169–178. doi: 10.1152/jn.00790.2009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Murphy AP, Ban H, Welchman AE. Integration of texture and disparity cues to surface slant in dorsal visual cortex. J Neurophysiol. 2013;110:190–203. doi: 10.1152/jn.01055.2012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Neri P, Bridge H, Heeger DJ. Stereoscopic processing of absolute and relative disparity in human visual cortex. J Neurophysiol. 2004;92:1880–1891. doi: 10.1152/jn.01042.2003. [DOI] [PubMed] [Google Scholar]
- Nili H, Wingfield C, Walther A, Su L, Marslen-Wilson W, Kriegeskorte N. A toolbox for representational similarity analysis. PLoS Comput Biol. 2014;10:e1003553. doi: 10.1371/journal.pcbi.1003553. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nishida Y, Hayashi O, Iwami T, Kimura M, Kani K, Ito R, Shiino A, Suzuki M. Stereopsis-processing regions in the human parieto-occipital cortex. Neuroreport. 2001;12:2259–2263. doi: 10.1097/00001756-200107200-00043. [DOI] [PubMed] [Google Scholar]
- Ohzawa I, DeAngelis GC, Freeman RD. Stereoscopic depth discrimination in the visual cortex: neurons ideally suited as disparity detectors. Science. 1990;249:1037–1041. doi: 10.1126/science.2396096. [DOI] [PubMed] [Google Scholar]
- Orban GA, Claeys K, Nelissen K, Smans R, Sunaert S, Todd JT, Wardak C, Durand JB, Vanduffel W. Mapping the parietal cortex of human and non-human primates. Neuropsychologia. 2006;44:2647–2667. doi: 10.1016/j.neuropsychologia.2005.11.001. [DOI] [PubMed] [Google Scholar]
- Popple AV, Smallman HS, Findlay JM. The area of spatial integration for initial horizontal disparity vergence. Vision Res. 1998;38:319–326. doi: 10.1016/S0042-6989(97)00166-1. [DOI] [PubMed] [Google Scholar]
- Preston TJ, Li S, Kourtzi Z, Welchman AE. Multivoxel pattern selectivity for perceptually relevant binocular disparities in the human brain. J Neurosci. 2008;28:11315–11327. doi: 10.1523/JNEUROSCI.2728-08.2008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Preston TJ, Kourtzi Z, Welchman AE. Adaptive estimation of three-dimensional structure in the human brain. J Neurosci. 2009;29:1688–1698. doi: 10.1523/JNEUROSCI.5021-08.2009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Qiu FT, von der Heydt R. Figure and ground in the visual cortex: v2 combines stereoscopic cues with gestalt rules. Neuron. 2005;47:155–166. doi: 10.1016/j.neuron.2005.05.028. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Riesenhuber M, Poggio T. Hierarchical models of object recognition in cortex. Nat Neurosci. 1999;2:1019–1025. doi: 10.1038/14819. [DOI] [PubMed] [Google Scholar]
- Rosenberg A, Angelaki DE. Reliability-dependent contributions of visual orientation cues in parietal cortex. Proc Natl Acad Sci U S A. 2014;111:18043–18048. doi: 10.1073/pnas.1421131111. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rosenberg A, Cowan NJ, Angelaki DE. The visual representation of 3D object orientation in parietal cortex. J Neurosci. 2013;33:19352–19361. doi: 10.1523/JNEUROSCI.3174-13.2013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rust NC, Dicarlo JJ. Selectivity and tolerance (“invariance”) both increase as visual information propagates from cortical area V4 to IT. J Neurosci. 2010;30:12978–12995. doi: 10.1523/JNEUROSCI.0179-10.2010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sanada TM, Nguyenkim JD, Deangelis GC. Representation of 3-D surface orientation by velocity and disparity gradient cues in area MT. J Neurophysiol. 2012;107:2109–2122. doi: 10.1152/jn.00578.2011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shikata E, Hamzei F, Glauche V, Knab R, Dettmers C, Weiller C, Büchel C. Surface orientation discrimination activates caudal and anterior intraparietal sulcus in humans: an event-related fMRI study. J Neurophysiol. 2001;85:1309–1314. doi: 10.1152/jn.2001.85.3.1309. [DOI] [PubMed] [Google Scholar]
- Srivastava S, Orban GA, De Mazière PA, Janssen P. A distinct representation of three-dimensional shape in macaque anterior intraparietal area: fast, metric, and coarse. J Neurosci. 2009;29:10613–10626. doi: 10.1523/JNEUROSCI.6016-08.2009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tanabe S, Cumming BG. Mechanisms underlying the transformation of disparity signals from V1 to V2 in the macaque. J Neurosci. 2008;28:11304–11314. doi: 10.1523/JNEUROSCI.3477-08.2008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tanabe S, Haefner RM, Cumming BG. Suppressive mechanisms in monkey V1 help to solve the stereo correspondence problem. J Neurosci. 2011;31:8295–8305. doi: 10.1523/JNEUROSCI.5000-10.2011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Thomas OM, Cumming BG, Parker AJ. A specialization for relative disparity in V2. Nat Neurosci. 2002;5:472–478. doi: 10.1038/nn837. [DOI] [PubMed] [Google Scholar]
- Tsao DY, Vanduffel W, Sasaki Y, Fize D, Knutsen TA, Mandeville JB, Wald LL, Dale AM, Rosen BR, Van Essen DC, Livingstone MS, Orban GA, Tootell RB. Stereopsis activates V3A and caudal intraparietal areas in macaques and humans. Neuron. 2003;39:555–568. doi: 10.1016/S0896-6273(03)00459-8. [DOI] [PubMed] [Google Scholar]
- Tsutsui KI, Sakata H, Naganuma T, Taira M. Neural correlates for perception of 3D surface orientation from texture gradient. Science. 2002;298:409–412. doi: 10.1126/science.1074128. [DOI] [PubMed] [Google Scholar]
- Tyler CW, Likova LT, Kontsevich LL, Wade AR. The specificity of cortical region KO to depth structure. Neuroimage. 2006;30:228–238. doi: 10.1016/j.neuroimage.2005.09.067. [DOI] [PubMed] [Google Scholar]
- Yamamoto H, Ban H, Fukunaga M, Tanaka C, Ejima Y. Large- and small-scale functional organization of visual field representation in the human visual cortex. In: Portocello TA, Velloti RB, editors. Visual cortex: new research. New York: Nova Science Publishers; 2008. [Google Scholar]
- Yuille A, Kersten D. Vision as Bayesian inference: analysis by synthesis? Trends Cogn Sci. 2006;10:301–308. doi: 10.1016/j.tics.2006.05.002. [DOI] [PubMed] [Google Scholar]