The Chronic Injury Glucose Error Grid

Abstract

Traditional glucose error grids provide error limits for glucose meters. These criteria help to assess the meter’s suitability to prevent acute injury. We present a rationale for an error grid that provides a different set of error limits to help prevent chronic injury in diabetes. For example, glucose values in the no treatment zone of a traditional error grid could be harmful in diabetic retinopathy. The same method comparison data informs both the acute and chronic injury error grids. All of the data are used in an acute injury error grid, whereas only long-term biases populate a chronic injury error grid. These biases can be due to reagent lots and patient specific interferences. An example of a chronic injury glucose error grid is provided using simulated data.

Recently we recommended that error grids should be used to judge acceptability of quantitative assays.¹ To review, an error grid allows one to assess the performance of an assay by analyzing data from a method comparison. In a method comparison, a series of candidate assay results are plotted against reference assay results on a graph which contains lines that demarcate no harm from increasing levels of harm. The best performing assays are ones in which most (or all) results are contained within the lines associated with no patient harm. In this article we propose that different error grids might be needed for the same analyte and how to analyze data from an error grid study. We illustrate these ideas with glucose meters.

Rationale for the Chronic Injury Error Grid for Glucose Meters

A common method to set error grid limits is to survey clinicians. In this process, clinicians are given some scenarios and asked to describe their recommended treatment based on the value of the analyte. The recommended treatment can range from no treatment to emergency treatment. Recently, a new glucose meter error grid used this procedure.²

One can view this procedure as a clinician responding to a patient’s symptoms and recommending treatment as a way to deal with the potential for acute injury. For example, a glucose meter reading of 120 mg/dL when the true value is 100 mg/dL would be in the A zone of a glucose error grid which is the no treatment needed zone. In fact, in the recently published glucose meter error grid, the A zone ranged from 79 to 151 mg/dL. This implies that a glucose meter, which has 100% of it values in the A zone, has acceptable performance. Yet diabetes, similar to other diseases, has both acute and chronic injury components. The chronic component of diabetes involves vascular injury³ which occurs over the duration that glucose is elevated. Diabetic retinopathy is an example of such a vascular injury. In diabetes, the level of hemoglobin A1c provides a measure of a patient’s average glucose level⁴ and the prevalence of diabetic retinopathy has been correlated to the level of A1c with retinopathy starting as low as an A1c of 5.5% which corresponds to an average glucose level of 111 mg/dL.⁵ Within the A zone of a glucose meter error grid, diabetic retinopathy can be a serious problem which implies that the current glucose meter error grid is not appropriate as an acceptance criterion for chronic injury. Thus, for diabetic complications such as diabetic retinopathy, a new error grid must be formulated, which focuses on long-term bias.

Krouwer previously described different types of analytical performance errors.⁶ Examples of long-term bias are interferences in specific patient samples and fixed biases across all samples such as reagent lot-to-lot bias, nonlinearity, and average bias from reference. On the other hand, precision, and other short term errors, such as a 1-time defective reagent strip are unimportant for long-term bias.

The Surveillance Experiment

The surveillance error grid,² as a method to assess the performance of a glucose meter after it has been released in the field, is informed by the surveillance experiment. This experiment is a method comparison (blood glucose meter versus reference) and is suitable for both acute and chronic error grids. To accommodate the analysis for the chronic error grid, triplicates are required for each patient specimen assayed on the glucose meter. Moreover, a minimum of 40 samples⁷ should be run with each reagent lot.

The analysis for the acute error grid is simple. All values are plotted on the error grid. For the chronic error grid, the analysis excludes differences from reference that are random 1-time events but includes long-term biases.

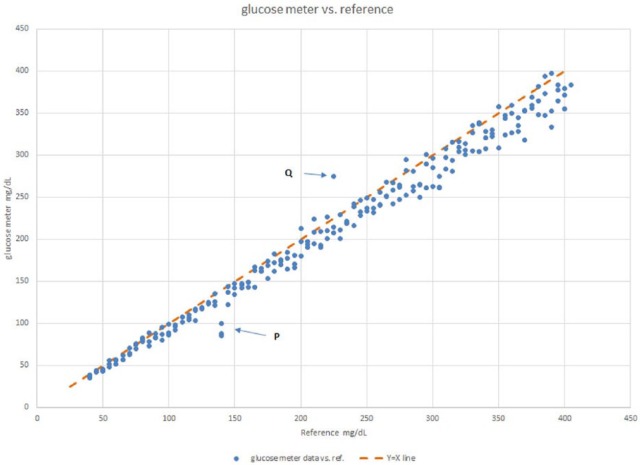
Figure 1 shows an example of the method comparison using simulated data. At point P at X = 140 mg/dL, there are 3 almost identical glucose values that are lower than reference by nearly 50 mg/dL. This trio of points is unlikely to be caused by imprecision (all 3 points at 7 standard deviations from the mean occurring in the same direction). It is much more likely that this sample’s difference from reference is caused by a patient specific interference. This also means that for this patient, the error is likely to persist over time. Moreover, it is likely to be harmful since the patient’s glucose reads normal on the meter when in fact it is hyperglycemic.

Figure 1.

Glucose meter vs reference. Scatterplot of a glucose meter versus reference from a method comparison. The points at location P are likely to be interferences in a patient sample, whereas the deviation at point Q is likely a 1-time event.

On the other hand the 50 mg/dL difference from reference of value Y at X = 225 (Q on graph) is not accompanied by its replicates and would appear to be a random event.

Lawton has provided an approach to model assay error.⁸ Using his approach, each observed meter result can be considered a linear combination of,

$${\mathrm{Y}}_i={\mathrm{b}}_0+{\mathrm{b}}_{1\mathrm{Xi}}+{\mathrm{s}}_{\mathrm{i}}+\mathrm{f}({\mathrm{C}}_{1\mathrm{i}}+{\mathrm{C}}_{2\mathrm{i}}+\mathrm{\dots }{\mathrm{C}}_{\mathrm{ni}})+\mathrm{f}{(\mathrm{unk})}_{\mathrm{i}}$$ (1)

• where Y_i is the observed glucose meter result of the ith sample

• b₀ + b₁x_i is the regression equation for Y vs X at the ith sample for a reagent lot

• s_i is the standard deviation at the ith sample

• f(C_1i + C_2i + . . . C_ni) is the effect of all interferences in the ith sample that affect the meter

• f(unk)_i represents a random error different from the other terms

The term b₀ + b₁x is governed by an algorithm set in the meter during its development as well as any bias in the current reagent lot. Although b₀ + b₁x implies linearity, if the data are nonlinear, a polynomial regression would be used to fit the data. s_i is the imprecision of replicating a sample. f(C_1i + C_2i + . . . C_ni) describes the effect of interfering substances and is dependent on the substances and concentrations in each patient specimen. For example, some glucose meters are affected by hematocrit with biases of 20% at the extremes of hematocrit and zero bias at the average value of hematocrit.⁹ Large patient interferences can be observed visually from a graph. Smaller interference errors may blend into the noise caused by assay imprecision. Where one is uncertain, one could test the difference using a t test. Finally, f(unk)_i represents a large error from a process that is absent from most other results. An example is a defective reagent strip that occurs only for a single result. In a perfect glucose assay, b₀ is 0, b₁ is 1.00, s_i is low, and all other terms are zero. While equation 1 is more complicated than a simple model of error equals average bias plus imprecision, the simple model has been shown to be misleading.¹⁰

The data for Figure 1 were simulated with a regression equation of Y = 0.95x − 1.0 and a CV of 5% using 73 patient samples each replicated 3 times, with points P and Q simulated separately. The observed regression of the data, with points P and Q omitted, yielded the equation Y = 0.951 x − 0.9. This regression equation provides the long-term bias expected for this reagent lot over the range of the assay as shown in Table 1.

Table 1.

Glucose Meter Long-Term Biases.

Reference	Meter	Bias	Percentage Bias
50	46.7	−3.4	−6.7
100	94.2	−5.8	−5.8
150	141.8	−8.3	−5.5
200	189.3	−10.7	−5.4
250	236.9	−13.2	−5.3
300	284.4	−15.6	−5.2
350	332.0	−18.1	−5.2
400	379.5	−20.5	−5.1

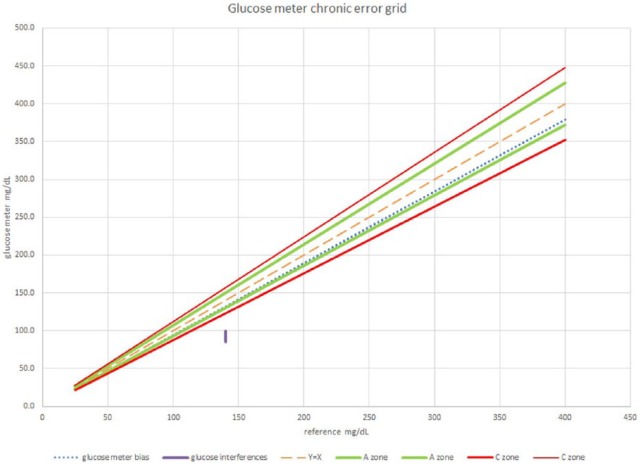
To place the results of an error grid experiment into a chronic glucose error grid requires the average bias of the data. These data are shown in Table 1 and are based on the regression equation Y = 0.951x − 0.9. The setting of the actual zones of a chronic injury error grid is beyond the scope of this article. But for illustration purposes, assume that the values from Table 1 fall within the A zone of a chronic injury error grid as shown in Figure 2. The value at location P on Figure 1 must be treated separately. Since this value falls within the C zone, the percentage of values in the C zone is 1/73 or 1.4% and the results of this experiment are shown in Table 2. The value at location Q from Figure 1 does not appear in the error grid in Figure 2 because it is not a long-term bias.

Figure 2.

Glucose meter chronic error grid. The glucose bias calculated from regression falls within the A zone. The patient who had a large interference is in the C zone.

Table 2.

Percentages in Each Error Grid Zone.

Zone	Percentage
A	98.6
B	0
C	1.4

If multiple reagent lots were assessed, then each lot’s values would be added separately to the surveillance error grid—they would not be averaged—and the percentages for all zones would be adjusted by the larger total sample size.

Note that treating bias as an important component of total error has been considered previously by Klee et al, who showed that biases could affect diagnostic efficacy.¹¹

A1c is used by clinicians to monitor how well glucose is being controlled. The recommended frequency of A1c measurements is 3 months for poorly controlled patients and 6 months for well controlled patients. The purpose of the chronic injury error grid is to assess the performance of glucose meters. If a glucose meter were determined to exhibit moderately negative long-term biases, then use of that meter could potentially cause many patients to have elevated glucose for up to 6 months until revealed by their next A1c result. Clearly, it would be beneficial to both patients and providers to know which glucose meters are free from such biases so that periods of prolonged elevated glucose could be prevented. Moreover, apart from replicating patient samples, the planning and execution of the method comparison needed for the traditional (acute) glucose surveillance error grid is the same that is needed for the chronic injury error grid. Data analysis is the only additional work needed to prepare the chronic injury glucose error grid. The rationale of the surveillance error grid—to assess glucose meter performance after release for sale—is just as valid for the chronic injury error grid as for the acute injury error grid.

Although the limits of a chronic error grid should be decided by clinicians,² it is clear that higher glucose meter accuracy is required to judge acceptability of glucose meters to mitigate complications of diabetes.