Using Filtered Forecasting Techniques to Determine Personalized Monitoring Schedules for Patients with Open-Angle Glaucoma

Abstract

Purpose

To determine whether dynamic and personalized schedules of visual field (VF) testing and intraocular pressure (IOP) measurements result in an improvement in disease progression detection compared with fixed interval schedules for performing these tests when evaluating patients with open-angle glaucoma (OAG).

Design

Secondary analyses using longitudinal data from two randomized controlled trials.

Participants

571 participants from Advanced Glaucoma Intervention Study (AGIS) and Collaborative Initial Glaucoma Treatment Study (CIGTS).

Methods

Perimetric and tonometric data were obtained for AGIS and CIGTS trial participants and used to parameterize and validate a Kalman filter model. The Kalman filter updates knowledge about each participant’s disease dynamics as additional VF tests and IOP measurements are obtained. After incorporating the most recent VF and IOP measurements, the model forecasts each participant’s disease dynamics into the future and characterizes the forecasting error. To determine personalized schedules for future VF tests and IOP measurements, we developed an algorithm by combining the Kalman filter for state estimation with the predictive power of logistic regression to identify OAG progression. The algorithm was compared against 1, 1.5, and 2 year fixed interval schedules of obtaining VF and IOP measurements.

Main Outcome Measures

Length of diagnostic delay in detecting OAG progression, efficiency of detecting progression, number of VF and IOP measurements needed to assess for progression.

Results

Participants were followed in the AGIS and CIGTS trials for a mean (standard deviation) of 6.5 (2.8) years. Our forecasting model achieved a 29% increased efficiency in identifying OAG progression (p<0.0001) and detected OAG progression 57% sooner (reduced diagnostic delay) (p= 0.02) than following a fixed yearly monitoring schedule, without increasing the number of VF tests and IOP measurements required. The model performed well on patients with mild and advanced disease. The model performed significantly more testing on patients who exhibited OAG progression than non-progressing patients (1.3 vs. 1.0 tests per year; p<0.0001).

Conclusion

Use of dynamic and personalized testing schedules can enhance the efficiency of OAG progression detection and reduce diagnostic delay as compared with yearly fixed monitoring intervals. If further validation studies confirm these findings, such algorithms may be able to greatly enhance OAG management.

When evaluating patients with glaucoma to assess for disease progression, clinicians must be able to assimilate past and present information from standard automated perimetry and other functional tests, intraocular pressure (IOP) measurements, and careful assessments of the optic nerve and retinal nerve fiber layer to decide whether patients are stable or whether they exhibit disease progression and require changes in management. Complicating such an assessment is the presence of measurement error and variability in testing performance that is known to exist for many of these testing modalities. Studies have shown that the difficulties associated with evaluating patients with glaucoma to assess for disease progression have led to undertreatment^1,2 and that decision aids, such as risk calculators³, are useful supplements to clinician judgment. In this manuscript we present pilot data from a validation study of a decision aid tool that we hope someday will be able to assist clinicians with management of patients with glaucoma. The tool assimilates data from past and present visual fields (VF) and IOP measurements to determine whether a patient’s disease is stable or not, and helps guide the timing of when the patient should next be examined to assess for disease progression.

At the core of this decision aid is a powerful statistical tool called Kalman filtering, which models the motion of a dynamic system, forecasting the future trajectory and combining multiple measurements for optimal noise reduction.⁴ This technique is useful for accurately extracting state/position estimates from multiple noisy data sources. In the 1960’s, the National Aeronautics and Space Administration (NASA) used Kalman filtering to “optimally” guide Apollo missions to the moon. More recently, there has been an interest in applying it to the management of chronic diseases like monitoring glucose levels in patients with diabetes mellitus⁵ and monitoring prostate specific antigen levels in patients with prostate cancer.⁶ This approach builds a model that optimizes the timing of future tests by integrating a population-based understanding of the natural history of the disease of interest with the individual patient’s disease dynamics. When applied to glaucoma management the model can be used to forecast future perimetric and tonometric measurements for individual patients. Unlike traditional approaches that identify glaucoma progression by comparing test results to a normative database, this approach generates personalized information on the disease state for each patient and forecasts how that state changes over time. Applying this to glaucoma management, it can be used to predict future values of the “positions” and respective velocities and accelerations of VF global indices such as mean deviation (MD), pattern standard deviation (PSD), visual functional index, as well as IOP levels. One would expect these estimates to have increased accuracy over raw observations because the Kalman filter can optimally correct for measurement noise in the forecasts.

The purpose of this study is to determine whether the use of Kalman filtering to obtain personalized monitoring schedules of VF testing and IOP measurements for patients with open-angle glaucoma (OAG) results in an improvement in disease progression detection compared with 1, 1.5, and 2 year fixed interval schedules for performing these tests. Using longitudinal data from two randomized controlled trials of patients with OAG, we developed, parameterized, validated, and tested an algorithm that can determine whether each patient with OAG is stable or experiencing disease progression. The algorithm also dynamically determines the optimal time to perform the next test to monitor for OAG progression based on information from the population that is integrated with past test results from the individual patient.

METHODS

Data Sources

Data from two large multicenter randomized controlled clinical trials, the Collaborative Initial Glaucoma Treatment Study (CIGTS) and Advanced Glaucoma Intervention Study (AGIS), were used for parameterization and validation of a Kalman filter and scheduling algorithm. These clinical trials were chosen because they included multiple measurements of IOP (by Goldmann applanation tonometry) and VF results (using a Humphrey Field Analyzer, Carl Zeiss Meditec, Dublin, CA) for patients with mild to advanced OAG over a period of up to 11 years, and because they had highly structured follow-up examination regimens with perimetry and tonometry performed every six months throughout the trials. In CIGTS, 607 adults with newly-diagnosed, early to moderate OAG were randomized to either trabeculectomy or medical therapy and followed for up to 11 years to assess for disease progression.^7,8 In AGIS, 591 adults with advanced OAG were randomized to treatment with argon laser trabeculoplasty (ALT) or trabeculectomy and followed for at least 5 years to check for OAG progression.⁹ The information contained in both the CIGTS and AGIS datasets was de-identified prior to our accessing it and the University of Michigan Institutional Review Board determined this study was exempt from requiring its approval.

Inclusion / Exclusion Criteria

To be included in our study, individuals from the two trials were required to have ≥4 examinations with VF and IOP readings. From both trials, we only included those participants who were treated with medical therapy or laser trabeculoplasty. Since incisional intraocular surgery can abruptly change glaucoma progression dynamics, we opted in this pilot study not to include data from those who were randomized to initial treatment with trabeculectomy and those who underwent trabeculectomy during the course of either trial were censored at the time of their first trabeculectomy.

Data Elements

For each trial participant we gathered demographic information on their age, sex, and race along with information on the IOP and VF performance at each visit. From every VF test performed on each patient throughout the trial, we extracted the MD and PSD values. By assessing global indices from serial VFs from the same patient over time, we calculated rates of change (i.e. velocity and acceleration) for MD and PSD. Velocity was computed per month, and acceleration was computed as the difference of the velocities from one period to the next period. We also calculated velocity and acceleration for IOP in a similar manner for each participant.

To validate and test our methodology, we divided the study’s CIGTS and AGIS trial data equally into a training set (for parameterizing models) and testing set (for validating and testing the models). We randomly assigned CIGTS/AGIS participants to these sets to assure equal representation of both groups in the training and testing sets. We performed this randomization process 25 times and calibrated the Kalman filter for each randomization. The prediction error of the Kalman filter was consistently unbiased across the randomizations. We present here the numerical results of one of these randomizations.

Probability of Progression

Progression Criterion

We characterized a participant in the dataset as exhibiting progression at a particular visit if he or she experienced a loss of MD of at least 3 decibels (dB) from their baseline MD and this loss was confirmed on a subsequent VF test.⁸ Since there is presently no gold standard for identifying progression on perimetric testing, we compared our progression definition to other progression measures, such as point-wise linear regression¹⁰ and changes in Hodapp-Anderson-Parrish (HAP) classification¹¹ (e.g. change from a HAP classification of moderate to a HAP classification of severe) and found strong similarities in progression identification (data not shown), suggesting robustness of the definition of progression we chose to use. Other progression definitions could easily be incorporated into the algorithm, contingent on the availability of all of the necessary data elements.

Logistic Regression

We developed a probability of progression function using generalized estimating equations with a logit link function and exchangeable correlation structure using the training data as inputs. This binary logistic regression approach accounted for noise in VF and IOP measurements and allowed us to assess the likelihood of a patient experiencing OAG progression at a particular visit given the patient’s specific characteristics (sex, age, race, baseline MD, present MD, MD velocity, MD acceleration, baseline PSD, present PSD, PSD velocity, PSD acceleration, baseline IOP, present IOP, IOP velocity, and IOP acceleration) at the time of that visit. Backward variable selection was used to obtain the final set of predictive covariates for the logistic regression. The variables that were included in the final logistic regression model were age, present MD, MD velocity, MD acceleration, present PSD, and baseline PSD.

The Kalman Filter Approach (Time to Next Test Algorithm)

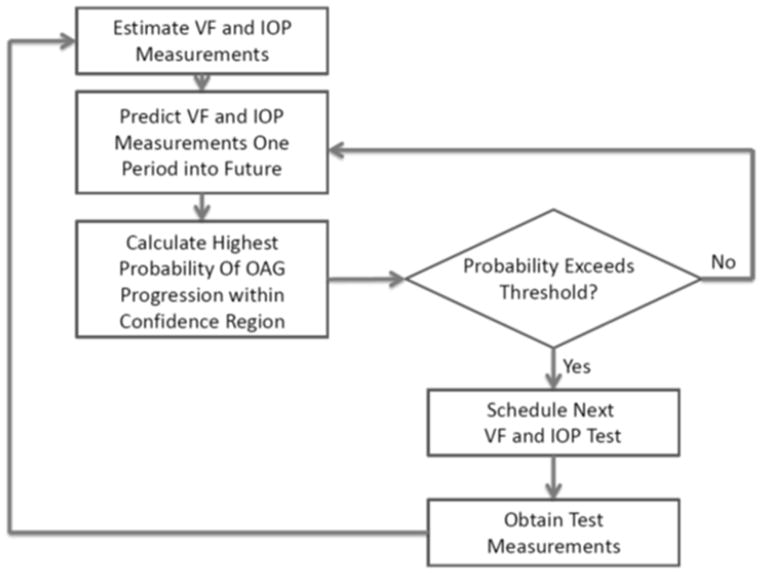
The Time to Next Test (TNT) algorithm steps are illustrated in Figure 1. Key to the Kalman filter approach is its ability to incorporate the new test information with the data from all of the patient’s prior tests and the progression dynamics of the population. The algorithm requires a warm-up period of ≥3 VF/IOP tests in order to calculate velocities and accelerations for MD, PSD, and IOP. Since the data from the AGIS and CIGTS trials were systematically collected every 6 months, it took a total of three 6 month periods (or 18 months) before the glaucoma decision aid could begin forecasting. Had the data from AGIS and CIGTS been collected at shorter time intervals between tests (ex: every 3 months), the tool could begin forecasting sooner than a warm-up period of 18 months.

Figure 1. Time to Next Test Algorithm Flow Diagram.

The Kalman filter estimates the current VF (i.e. MD and PSD) and IOP measurements and predicts their future values while the logistic regression estimates the highest probability of progression for those future values.

VF=visual field; IOP=intraocular pressure; OAG=open angle glaucoma; MD=mean deviation; PSD=pattern standard deviation

Once these are determined, the algorithm uses information about the underlying population and the particular patient’s test results to estimate the patient’s true MD, IOP, PSD and respective velocities and accelerations of these parameters. When the algorithm receives new test measurements, the MD, PSD, IOP and the respective velocities and accelerations are updated using the Kalman filter; which is then used to forecast the patient’s mean values of MD, PSD, IOP and respective velocities and accelerations for future time periods. The Kalman filter also provides an estimate of the variability of the forecasts with designated confidence intervals.

Figure 2 provides a graphical representation of how the progression threshold determines the time of the next test. The progression threshold (illustrated by the plane) separates the Kalman filter space into two regions: “progression” and “non-progression”. This separation is performed by applying the logistic regression function to every point in the space. Those points with a calculated probability of progression less than the progression threshold are situated in the “non-progression” region (to the left of the plane in the figure). Similarly, those points with a calculated probability of progression greater than or equal to the progression threshold are situated in the “progression” region (to the right of the plane in the figure).

Figure 2. Time to Next Test (TNT) Algorithm.

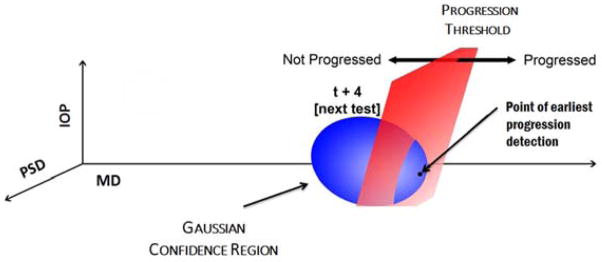
The Kalman filter estimates the mean values of MD, PSD, IOP and their respective velocities and accelerations at future periods, along with estimates of the covariance of these measurements. This generates a confidence region of possible future values which are used as inputs for the logistic regression function to determine the highest probability of progression. Once the highest probability of progression at a future visit exceeds the progression threshold, the TNT algorithm schedules a VF and IOP test.

MD=mean deviation; PSD=pattern standard deviation; IOP=intraocular pressure; TNT=Time to Next Test; VF=visual field; t=time period

In the execution of the TNT algorithm, we use the Kalman filter’s estimation of the mean and covariance of MD, PSD, IOP and the respective velocities and accelerations to generate a confidence region (illustrated by the ellipsoid). For this confidence region, we compute the highest probability of progression using the logistic regression function. Once the highest probability of progression for the confidence region exceeds the progression threshold (i.e. at least one of the points of the confidence region falls into the progression region), the TNT algorithm suggests scheduling a VF and IOP test at that time (in this example, time t+4).The progression threshold and confidence region size can be tailored by the clinician to the needs of the individual patient to more or less aggressively monitor specific patients.

The TNT algorithm was parameterized using an expectation maximization (EM) algorithm. The EM algorithm is an iterative process that uses the training data to find the best estimates for the Kalman filter parameters. Next, using the testing dataset, we compared the performance of our scheduling algorithm against 1 year, 1.5 year and 2 year fixed interval testing schedules for performing VFs and IOPs. To assess how well the algorithm performed relative to the fixed testing intervals, we compared: (i) the average number of examinations (VFs and IOP measurements) performed per patient per year; (ii) efficiency in testing (percent of instances where OAG progression was noted at the time a VF test and IOP measurement was scheduled); and (iii) diagnostic delay (average number of months that a patient's glaucoma progression went undetected between examinations). We used asymptotic values for efficiency (e.g. 50% for 1 year fixed) and diagnostic delay (e.g. 3 months for 1 year fixed) as the performance measures for fixed interval schedules. This algorithm was applied to all trial participants in the testing dataset until a visit was scheduled on or after the date the patient first experienced glaucoma progression.

Analyses were run using MATLAB version 7.7.0 and R version 2.12.2. For all analyses, p<0.05 was considered statistically significant.

RESULTS

A total of 571 participants (571 eyes) with OAG met the study inclusion criteria. Table 1 presents a summary of the participants. Of these, 266 (47%) came from CIGTS and 305 (53%) came from AGIS. The mean (standard deviation) age of the study participants at baseline was 63.2 (10.9) years. The participants included 272 males (48%) and 299 females (52%). There were 263 whites (46%), 288 blacks (50%) and 20 were classified as some other race. Participants were followed in the trials for an average of 6.3 (2.8) years. The training dataset included 286 eyes of 286 patients and the testing dataset included 285 eyes of 285 patients. There was no statistically significant difference in the demographic characteristics, number of visits, or clinical parameters (mean MD, PSD, IOP) between individuals in the training and testing datasets (p > 0.05 for all comparisons) , except there were slightly more blacks in the training set than the testing set (154 vs. 134; p = 0.05).

Table 1.

Description of Study Sample of Patients from the CIGTS/AGIS Trials

		Training		Testing		P- value*
		n	%	n	%
Number of Eyes		286		285		0.48
Number of Participants		286		285		0.48
Number from CIGTS		131	46	135	47	0.64
Number from AGIS		155	54	150	53	0.34
Sex	Male	135	47	137	48	0.57
	Female	151	53	148	52	0.40
Race	White	123	43	140	49	0.93
	Black	154	54	134	47	0.05
	Other	9	3	11	4	0.74
Total Number of Visits		3158		3227		0.89
Number of Instances of Progression		163		166		0.59
Mean ± SD Number of Visits per Patient		11.0 (5.0)		11.3 (5.3)		0.4
Mean ± SD Age		64.2(10.9)		64.3 (11.0)		0.8
Kalman Filter Variables
	Initial MD	−7.55 (3.74)		−7.65 (3.73)		0.91
	Initial PSD	6.49 (3.39)		6.41 (3.83)		0.54
	Initial IOP	17.61 (0.22)		17.7 (0.18)		0.28
	MD	−8.30 (2.04)		−8.27 (1.95)		0.96
	MD Velocity	−0.04 (0.21)		−0.03 (0.20)		0.23
	MD	−0.01 (0.28)		−0.02		0.65
	Acceleration			(0.26)
	PSD	6.58 (1.18)		6.70 (1.13)		0.69
	PSD Velocity	0.01 (0.13)		0.01 (0.12)		0.74
	PSD	0 (0.19)		0.01 (0.17)		0.50
	Acceleration
	IOP	17.43 (2.64)		17.14 (2.63)		0.23
	IOP Velocity	0.00 (0.29)		0 (0.31)		0.67
	IOP	0 (0.42)		0.01 (0.41)		0.62
	Acceleration

SD=standard deviation; MD = mean deviation; PSD = pattern standard deviation; IOP = intraocular pressure; CIGTS=Collaborative Initial Glaucoma Treatment Study; AGIS=Advanced Glaucoma Intervention Study

^*P-value is calculated for the null hypothesis of equal proportion in testing and training set for categorical variables and the null hypothesis of equal means for continuous variables.

Logistic Regression

Table 2 presents the coefficients, standard errors, and p-values of the covariates incorporated into the logistic regression, which we then used to assess the probability of OAG progression for each patient. As expected, patients with more advanced glaucoma as captured on perimetry (a more negative MD or a more positive PSD) had a higher probability of progression compared to those with less advanced disease. In the regression model, each of the covariates in Table 2 was found to be significantly associated with OAG progression (p < 0.04 for each covariate).

Table 2.

Factors in Multivariable Logistic Regression Associated with Open-Angle Glaucoma Progression

Covariate	Coefficient	Standard Error	P Value
Intercept	−6.004	0.723	<0.001
Mean Deviation (dB)	−0.057	0.017	0.001
Mean Deviation Velocity (dB/month)	−4.054	0.666	<0.001
Mean Deviation Acceleration (dB/6 month2)	−1.183	0.326	<0.001
Baseline Pattern Standard Deviation (dB)	−0.162	0.078	0.039
Pattern Standard Deviation (dB)	0.154	0.075	0.039
Age (years)	0.026	0.103	0.013

Validation of Kalman Filter

To validate the fit and predictive ability of the Kalman filter for assessing OAG progression, we calculated the 95% confidence intervals for the mean prediction errors of MD, PSD, and IOP and their respective velocities and accelerations across all study participants in the testing dataset. Errors were calculated at various prediction lengths (6 months, 2 years, and 5 years into the future). Table 3 (available at www.aaojournal.org) shows that the mean differences between the Kalman filter predictions and the observed values from the trials were close to zero across various prediction lengths (alpha=0.05), supporting the accuracy of the Kalman filter predictions.

Table 3.

95% Confidence Intervals for Kalman Filter Error

	95% Confidence Interval
Variable	6 Months	2 Years	5 Years
Present MD	(−0.1493, 0.0329)	(−0.1294, 0.1361)	(−0.2979, 0.3882)
MD Velocity	(−0.0163, −0.0003)	(−0.0175, 0.0024)	(−0.0361, 0.0000)
Present PSD	(0.0163, 0.1227)	(0.1308, 0.2880)	(0.4675, 0.8394)
PSD Velocity	(0.0065, 0.0168)	(0.0039, 0.0166)	(−0.0028, 0.0195)
Present IOP	(−0.2487, 0.0121)	(−0.2751, 0.0792)	(−0.6454, 0.0519)
IOP Velocity	(−0.0033, 0.0194)	(−0.0117, 0.0185)	(−0.0365, 0.0175)

The 95% confidence intervals of the Kalman filter error for each of the variables contain 0 or are close to containing 0 when the Kalman filter is used to predict 6 months, 2 years, and 5 years into the future. This means the values predicted by the Kalman filter are not significantly different from the values observed (alpha=0.05).

MD = mean deviation; PSD = pattern standard deviation; IOP = intraocular pressure

Next, we compared the observed values of MD from each clinical trial participant in the testing dataset against the filtered and predicted values of MD generated by the Kalman filter. The Kalman filter forecasts one period ahead and updates the forecasts with the clinical observation for that period to obtain the filtered estimate of MD at each sequential trial visit. Predicted MD values are those obtained from the Kalman filter without incorporating future clinical observations. To illustrate the Kalman filter’s forecasting ability, we present in Figure 3 four study participants, two of whom exhibited OAG progression and two which experienced no progression during their enrollment in one of the clinical trials. We also estimated 90% confidence intervals for the predicted values toward the end of each participant’s enrollment in the clinical trial. We chose the narrower 90% confidence intervals for the predicted values to demonstrate how strong the predictive power of the Kalman filter actually is. Since all observations fell well within the 90% confidence intervals, the observations would also fall within the wider 95% confidence intervals. We found that at all future time points, the Kalman filter forecasts for MD were close to the observed MD values obtained when the participant took the test during the clinical trial; our confidence intervals for predicted MD fully encompassed the observed MD values, even 3.5 years into the future. Similar analyses were performed on all patients in the testing set for PSD and IOP. Figure 4 (available at www.aaojournal.org) shows an example of how the algorithm forecasts future PSD and IOP measurements.

Figure 3. Kalman Filter Trajectories of Mean Deviation.

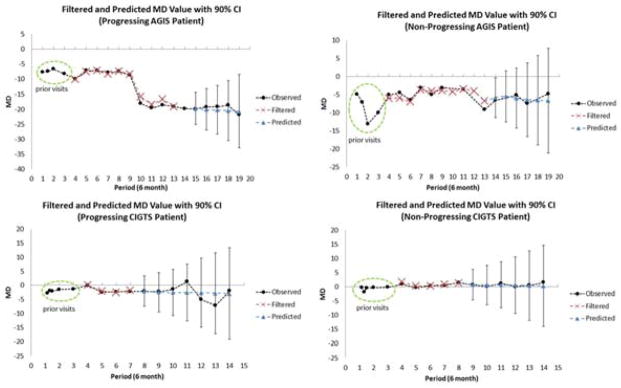
The figures illustrate the Kalman filter’s ability to accurately forecast MD. The Kalman filter requires 3 visits to calculate initial values of velocity and acceleration for MD. Starting in period 4, the Kalman filter is used to calculate filtered estimates of MD. The Kalman filter forecasts one period ahead and updates the forecasts with the clinical observation for that period to obtain the filtered estimate of MD. The figures show the similarity of the observed values and the filtered estimates. For the latter portion of the patients’ enrollment in the trial, we present the 90% confidence intervals for the Kalman filter’s predicted values of MD. Predicted MD values are those obtained from the Kalman filter without incorporating future clinical observations. Every clinical observation is contained within the 90% confidence intervals.

MD=mean deviation; CI=confidence interval; AGIS=Advanced Glaucoma Intervention Study; CIGTS=Collaborative Initial Glaucoma Treatment Study

The Kalman filter assumes the process and measurement noise is normally distributed. We have examined the errors and found that normality holds within two standard deviations of the mean for all of the Kalman filter variables (MD, PSD, IOP and their respective velocities and accelerations) (data not shown).

Kalman Filter Versus Fixed Testing Intervals to Identify OAG Progression

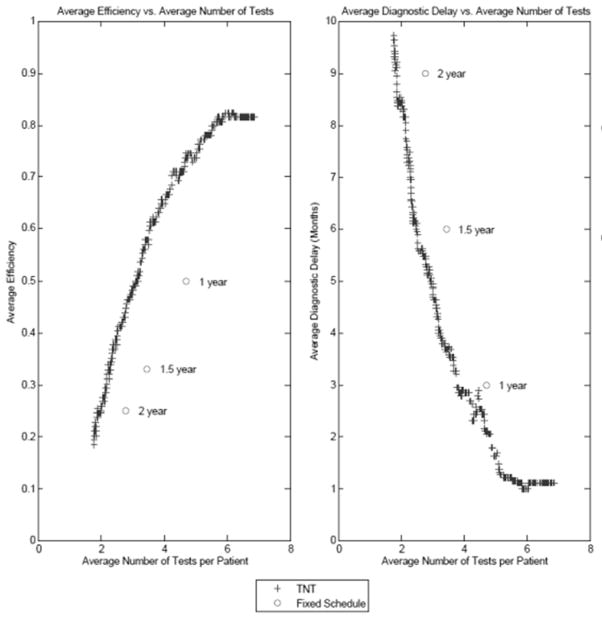
After calibrating the TNT algorithm, we evaluated the algorithm against fixed testing intervals of 1, 1.5, and 2 years. Our evaluation involved assessing the (i) number of tests, (ii) efficiency, and (iii) diagnostic delay. Figure 5 compares the average efficiency and diagnostic delay of the TNT algorithm and 1, 1.5, and 2 year fixed testing intervals. For the same average number of tests as the 1, 1.5, and 2 year fixed testing intervals, the TNT algorithm achieved higher efficiency (p<0.0001 for all comparisons) and reduced diagnostic delay (p= 0.02, <0.0001, and <0.0001 respectively) for detecting OAG progression. For example, when comparing the 1 year fixed testing interval against the TNT algorithm, for the same average number of tests (4.7 tests), the TNT algorithm increased efficiency by 29% and reduced diagnostic delay at OAG progression detection by 1.7 months.

Figure 5. Comparison of Time to Next Test (TNT) Algorithm and Fixed Schedules Performance Measures.

The left graph compares the average efficiency and average number of tests per patient of the TNT algorithm against the 1 year, 1.5 year, and 2 year fixed interval schedules. The graph shows that the TNT algorithm dominates each fixed interval schedule in terms of efficiency. The right graph compares the average diagnostic delay and average number of tests per patient of the TNT algorithm against the 1 year, 1.5 year, and 2 year fixed interval schedules. The graph shows that the TNT algorithm dominates each fixed interval schedule in terms of diagnostic delay

TNT = Time to Next Test

Table 4 shows how the algorithm performed on the subset of participants enrolled in both trials that experienced OAG progression as compared with those who never experienced glaucoma progression. Overall, 116 trial participants in the testing dataset were noted to have OAG progression and 169 did not exhibit progression. Among those in the testing dataset who progressed, the mean (SD) time from study enrollment to first record of OAG progression was 45.7 (23.4) months. Since efficiency and diagnostic delay assess the algorithm’s ability to schedule follow-up tests at times when there was evidence of actual OAG progression, these performance measures were not applicable for the subset of participants who did not exhibit disease progression. The algorithm scheduled more tests per year for patients who were exhibiting OAG progression (1.3 tests per year) than others who were stable (1.0 test per year) (p<0.0001).

Table 4.

Comparison of Algorithm Performance for Progressing vs. Non-Progressing Patients and AGIS vs. CIGTS Patients

Performance Measures	1 Year Fixed Interval Testing	TNT on All Patients	TNT on Progressing Patients	TNT on Non- Progressing Patients	TNT on AGIS Patients	TNT on CIGTS Patients
Average Number of Tests per Year	1.00	1.12	1.28	1.02	1.30	0.92
Average Efficiency (%)	50	79	79	N/A	83	71
Average Diagnostic Delay (months)	3.00	1.29	1.29	N/A	1.02	1.92

Progressing patients are those who met our definition of progression (loss of 3 dB mean deviation from baseline) at least once during their enrollment in the clinical trial. Non-progressing patients are those who never met the definition of progression during their time in AGIS/CIGTS. Efficiency is the percent of instances where OAG progression was noted at the time a test was scheduled. Diagnostic delay is the number of months that a patient's glaucoma progression went undetected between examinations.

AGIS = Advanced Glaucoma Intervention Study; CIGTS = Collaborative Initial Glaucoma Treatment Study; TNT = Time to Next Test algorithm; N/A = not applicable

Table 4 also shows how the TNT algorithm performed on CIGTS patients and AGIS patients in the testing dataset separately. As one might expect, the TNT algorithm scheduled more tests for AGIS patients than CIGTS patients (1.3 average tests per year vs. 0.9 average tests per year; p<0.0001). The TNT algorithm achieved marginally improved efficiency (83% vs. 71%; p= 0.06) for AGIS compared with CIGTS patients, and the efficiency at OAG progression detection for both groups were better than the efficiency achieved using 1 year fixed testing intervals (50%). Diagnostic delay at detecting OAG progression (1.0 months vs. 1.9 months; p= 0.09) was slightly shorter for AGIS patients, though this did not reach statistical significance.

Additional analyses were performed to see how well the TNT algorithm performed on black vs. white patients from the trials. We found that the TNT algorithm performed more tests on average for black patients than white patients (5.31 vs. 4.24; p=0.03). The TNT algorithm performed equally well in terms of efficiency and diagnostic delay (p=0.10 and 0.20, respectively) for black and white patients.

DISCUSSION

Using a forecasting technique called Kalman filtering, we parameterized an algorithm that dynamically updates the timing of future measurements for each individual, based on prior measurements. The Kalman filter starts with information about the population and as patient observations are obtained, the Kalman filter incorporates these data to learn about each individual’s specific progression dynamics. Our algorithm was validated using longitudinal data from two large multicenter clinical trials of patients with mild to advanced OAG. Comparing the output generated from the algorithm with fixed testing intervals of 1, 1.5, and 2 years, we show that the algorithm is capable of detecting OAG progression more efficiently and with reduced diagnostic delay compared with fixed interval schedules, without the need for additional tests. The model appears to work well for those with mild to moderate OAG (participants in CIGTS) as well as for those with more advanced disease (participants in AGIS), and performs well on the subset of trial participants who did and did not exhibit OAG progression, and forecasts well for white and black trial participants.

While we are unaware of other personalized algorithms that use a Kalman filter to determine the frequency of testing of patients with OAG or other ophthalmological diseases, this approach is being applied in other medical specialties to aid clinicians in clinical decision-making for patients with chronic diseases. Examples include estimation of pulmonary blood flow¹² and prediction of arterial blood pressure.¹³ This approach lends itself well to progressive conditions that involve repeated testing using quantitative data.

There are several advantages to using this approach to aid in the evaluating and monitoring of patients with OAG, rather than simply testing all patients at fixed intervals or relying on one’s gestalt of how often to monitor a given patient. By incorporating data from a population of patients with OAG, the Kalman filter is able to identify and filter out systematic noise (e.g. measurement error, variability in test performance) that is known to exist in IOP readings and VF test results. Second, the Kalman filter makes use of data from sequential visits to account for the disease dynamics of each individual patient, and continually updates the model with new test results after each visit to determine the timing of future testing. Third, the algorithm is scalable and can include additional data from structural tests such as optical coherence tomography or confocal scanning laser ophthalmoscopy, as well as other quantifiable data elements. Fourth, since there is presently no consensus on the optimal approach to define OAG progression, the model is flexible enough to be able to make predictions of progression using different definitions. Finally, the algorithm can be tailored by the eye care provider to be more or less aggressive in testing for disease progression. For example, the algorithm can be modified so that a clinician can choose to increase the threshold for detecting OAG progression for an 85 year old patient with early OAG who has multiple medical comorbidities, if she thinks this patient is unlikely to go blind from the disease, so as to not overburden such a patient with frequent tests. Alternatively, for a 40 year old monocular patient with severe OAG, the clinician might opt to lower the threshold so that the algorithm can identify the first hint of possible disease progression. From a societal perspective, the use of Kalman filter forecasting can improve the quality of care offered to patients by aiding in more timely identification of those who are exhibiting OAG progression and require additional treatment while simultaneously limiting patient burden and added costs of performing unnecessary testing.

There are several study limitations that need to be acknowledged. First, the types of parameters we were able to incorporate into the Kalman filter we developed were limited to those that were measured in the CIGTS and AGIS studies. Information that we would have liked to include in the algorithm but was not available from those trials includes pachymetry readings, optical coherence tomography measurements, and other quantifiable measures of the optic nerve or retinal nerve fiber layer. In the future we hope to obtain access to datasets that longitudinally capture information on these parameters so we can refine our algorithm, which should enhance its ability to identify persons who are at increased risk of OAG progression. Second, we have yet to test this algorithm on other groups of patients such as those with ocular hypertension, those with early pre-perimetric glaucoma, those with other forms of glaucoma, and those who underwent incisional glaucoma surgery. Further validation is necessary to determine how well the algorithm predicts disease progression and need for monitoring in these groups. Third, the timing of the follow-up examinations in AGIS and CIGTS restricted our algorithm’s scheduling decisions to no more frequently than every 6 months. If follow-up examination data for smaller time windows, e.g. every 1 month, were available, our algorithm could make scheduling decisions as often as every month. As we shorten the time interval allowed in scheduling (e.g. 6 months to 1 month), we expect the algorithm to achieve higher efficiency and lower diagnostic delay. In particular, this would have large gains in the improvement of our TNT algorithm for diagnostic delay. The exact gains cannot be known until we have tested our TNT algorithm on data collected at the higher frequency of every 1 or 3 months. And lastly, patient adherence to prescribed medications is likely higher for participants in AGIS and CIGTS compared to those routinely care for in clinical practice. When applied to patients seen in clinical practice, the increased IOP variability due to lower medication adherence would likely decrease the predictive capability of the Kalman filter. When we further validate the model on another sample of patients who were not enrolled in a clinical trial we will be able to explore this further.

There are also algorithm limitations to mention. First, the Kalman filter assumes glaucoma evolves linearly over time. To address potential nonlinear evolution, we modeled the velocity and acceleration of MD, PSD, and IOP in the Kalman filter. Second, our approach requires a 3 period warm-up so that we can calculate velocity and acceleration. This warm-up delays when the algorithm can begin predicting the optimal timing of the next time. However, outside a clinical trial setting (in clinical practice) these 3 measurements could be acquired more quickly than every 6 months so the model does not require 18 months before it begins generating forecasts.

In conclusion, we have developed, parameterized, and validated an algorithm that forecasts the probability of OAG progression using a filtered forecasting technique and helps identify the optimal timing to perform additional testing for patients with mild to advanced OAG. With each additional set of measurements obtained, the algorithm updates its predictions so that it generates a personalized assessment of each patient’s risk of progression and the timing of additional testing. The algorithm is scalable, gives clinicians the ability to input how aggressively they wish to manage a given patient, and when tested in a group of patients from the CIGTS and AGIS trials, it performed considerably better than 1, 1.5, and 2 year fixed interval testing schedules. With further refinement of this algorithm and after additional validation studies are performed on patients with other forms of glaucoma, we hope that such an algorithm will soon be accessible in a user-friendly format to enhance the ability of clinicians to effectively care for patients with OAG.