Acoustic and Perceptual Effects of Left–Right Laryngeal Asymmetries Based on Computational Modeling

Abstract

Purpose

Computational modeling was used to examine the consequences of 5 different laryngeal asymmetries on acoustic and perceptual measures of vocal function.

Method

A kinematic vocal fold model was used to impose 5 laryngeal asymmetries: adduction, edge bulging, nodal point ratio, amplitude of vibration, and starting phase. Thirty /a/ and /I/ vowels were generated for each asymmetry and analyzed acoustically using cepstral peak prominence (CPP), harmonics-to-noise ratio (HNR), and 3 measures of spectral slope (H1*-H2*, B0-B1, and B0-B2). Twenty listeners rated voice quality for a subset of the productions.

Results

Increasingly asymmetric adduction, bulging, and nodal point ratio explained significant variance in perceptual rating (R² = .05, p < .001). The same factors resulted in generally decreasing CPP, HNR, and B0-B2 and in increasing B0-B1. Of the acoustic measures, only CPP explained significant variance in perceived quality (R² = .14, p < .001). Increasingly asymmetric amplitude of vibration or starting phase minimally altered vocal function or voice quality.

Conclusion

Asymmetries of adduction, bulging, and nodal point ratio drove acoustic measures and perception in the current study, whereas asymmetric amplitude of vibration and starting phase demonstrated minimal influence on the acoustic signal or voice quality.

It is becoming increasingly recognized that left–right (L-R) asymmetries of laryngeal structure and vocal fold vibration occur in people without and with voice disorders (Bonilha, Deliyski, & Gerlach, 2008; Bonilha, Deliyski, Whiteside, & Gerlach, 2012; Kendall, 2009; Kimura et al., 2010; Krenmayr, Wöllner, Supper, & Zorowka, 2012; Lindestad, Hertegård, & Björck, 2004; Niimi & Miyaji, 2000; Yamauchi et al., 2012). When a patient presents to a voice clinic with concerns about voice quality, asymmetries are often assumed to be part of the presenting disorder (Bonilha, O'Shields, Gerlach, & Deliyski, 2009); yet, L-R and anterior-posterior vibratory asymmetries (Bonilha et al., 2008) and arytenoid adduction asymmetries (Bonilha et al., 2009; Lindestad et al., 2004) occur in most speakers with normal voices. Because vibratory asymmetry is also common in speakers with a variety of laryngeal or voice disorders (Bonilha et al., 2012), it is difficult to determine whether a particular asymmetry is a component of a laryngeal disorder or the cause of a dysphonic voice quality.

Although it is thought that vocal fold vibration asymmetries cause dysphonia, particularly breathy or rough qualities (Niimi & Miyaji, 2000; Verdonck-de Leeuw, Festen, & Mahieu, 2001), the implications and effects of L-R asymmetries are not well understood. Inconsistent terminology and difficulty isolating asymmetries have limited the ability to fully understand the consequences. Terms such as mucosal wave asymmetries, periodic lateral phase asymmetries (Haben, Kost, & Papagiannis, 2003), asymmetry of vibration (amplitude of mucosal wave) (Simpson, May, Green, Eller, & Jackson, 2011), chasing wave (Simpson, Cheung, & Jackson, 2009), asymmetry (Niimi & Miyaji, 2000; Yamauchi et al., 2012), and lateral phase difference (Yamauchi et al., 2012) might refer to similar or very different phenomena and be caused by different underlying factors.

Introduction of vocabulary to specify vibration asymmetries in kymography (Švec, Šram, & Schutte, 2007) and high-speed videoendoscopy, and automation of measures over multiple cycles (Krenmayr et al., 2012; Mehta, Deliyski, Quatieri, & Hillman, 2011; Mehta, Zañartu, Quatieri, Deliyski, & Hillman, 2011) have improved the likelihood of consistency across studies in rating or measuring vibratory symmetry. Human subjects, however, typically present with more than one asymmetry, and the asymmetries often occur in the context of other features of vocal fold vibration such as aperiodicity and incomplete closure, making it difficult to determine which features lead to vocal function changes. Verdonck-de Leeuw et al. (2001), for example, identified phase and amplitude asymmetries as well as incomplete glottal closure, irregular vibration, and other features in kymographic sequences of four patients exhibiting breathiness and roughness in the context of varying vocal fold disorders. Niimi and Miyaji (2000) presented results of 22 patients with a variety of vocal fold lesions, and most of the patients exhibited multiple vibratory differences. Mehta, Deliyski, Zeitels, Quatieri, and Hillman (2010) found that L-R phase asymmetry, amplitude asymmetry, and axis shift might be present following phonosurgical treatment of early glottic cancer. The symmetry measures did not significantly predict acoustic measures of jitter or shimmer, though the standard deviations of L-R phase and amplitude asymmetry were significantly correlated with acoustic jitter, and the standard deviation of open quotient significantly correlated with acoustic shimmer (Mehta et al., 2010).

Computational modeling provides the opportunity to specify asymmetries a priori and measure the effects acoustically or perceptually. Asymmetric mass, stiffness, and tension have been used in computational lumped element models to simulate superior and recurrent laryngeal nerve injuries. Results include spectral bifurcations and chaotic oscillations (Herzel, Berry, Titze, & Steinecke, 1995; Steinecke & Herzel, 1995), closure changes, decreased frequency, and less motion of the immobile side (Smith, Berke, Gerratt, & Kreiman, 1992). Though the results are important to understanding the disease processes and vocal fold physiology, the mechanism of inducing vibration asymmetries (i.e., varying stiffness and mass) generates multiple laryngeal and vibratory asymmetries.

Other types of models have been used to study asymmetry. Khosla, Murugappan, and Gutmark (2008) used excised canine larynges to demonstrate that L-R amplitude asymmetries reduced or eliminated flow separation vortices, leading to reduced rate of flow shut-off (Khosla el al., 2008; Murugappan, Khosla, Casper, Oren, & Gutmark, 2009). In a follow-up study, they unilaterally scarred vocal folds to induce amplitude and phase differences in five canine larynges and compared them 2 months postoperatively to unscarred controls. The scarred vocal folds demonstrated less displacement than the normal vocal folds, particularly during the closing phase, and the scarred larynges produced acoustic signals with flatter spectral slopes and lower harmonics-to-noise ratio (HNR) than the controls (Murugappan et al., 2009). Zhang, Kreiman, Gerratt, and Garellek (2013) used a series of two-layer physical models of the vocal folds to demonstrate that L-R vocal fold body stiffness asymmetries produced perceptually significant voice quality differences only when the asymmetry caused vibratory mode changes that altered multiple vibratory features simultaneously.

It remains unclear whether the type or degree of asymmetry is responsible for changes in voice quality or whether a combination of asymmetries or co-occurrence with another structural or vibratory difference is necessary for asymmetries to become perceptually important. Identifying which asymmetries are perceptually important and cause predictable changes to vocal function measures will improve understanding of normal voice production and the ability to determine when an observed asymmetry is likely contributing to a patient's symptom of dysphonia. Given the difficulty isolating the effects of particular types and degrees of L-R asymmetries on vocal function and voice quality, a conceptually different approach is proposed to determine individual effects of graded L-R asymmetries. The question here is not the effects of physiological changes to the neuromuscular unit of one vocal fold; rather, the question is how asymmetric kinematics (i.e., movement) cause changes in the acoustic signal and voice quality. The current research is part of a series of simulation studies determining which of several structural and vibratory asymmetries caused by vocal fold paralysis are most important to voice quality, and therefore to treatment. The particular asymmetries selected for the study were consistent with those described in subjects with unilateral paresis and paralysis, but might also be generalized to organic pathologies affecting the phonatory mucosa.

The acoustic and perceptual outcomes of fine gradations of symmetric vocal fold structural and vibratory differences have been studied using a computational kinematic model (Samlan & Story, 2011; Samlan, Story, & Bunton, 2013), and the model was adapted for the current study to allow specification of asymmetric characteristics of the vocal folds. The kinematic model was ideal for the current study because it allows specification of individual structural and movement properties without assuming the underlying biomechanical properties and neuromuscular controls. Each asymmetric feature can therefore be studied in a pure form, and underlying etiology does not confound the results by creating changes in other vibration properties.

In the current study, five laryngeal asymmetries consistent with changes occurring in vocal fold paresis and paralysis were imposed on an otherwise symmetric system using a kinematic speech production model. The resulting aerodynamic and acoustic signals were measured and then presented to listeners in a rating experiment.

Method

Speech Production Model

A kinematic vocal fold model (Titze, 1984, 1989, 2006a) was used, consisting of two vocal fold surfaces that have a length (see Figure 1a, distance from Point B to Point C) and thickness (distance from Point A to Point B), and no vocal fold mass. The surfaces are set into simulated vibration, modifying the glottal airspace over time. In contrast to the indirect mechanisms of asymmetry used for self-oscillating models (i.e., asymmetric stiffness and mass), asymmetries are simulated by directly specifying movement properties, and the shape of the vocal fold edges during vibration can be controlled to simulate realistic patterns. The vocal fold model was aerodynamically and acoustically coupled to a wave reflection model of an adult male trachea and vocal tract (Liljencrants, 1985; Story, 1995, 2005; Titze, 2002) configured in /a/ and /I/ vowel shapes, shown in Figure 1b (Story, 2008). The output of the kinematic vocal fold model interacted with supra- and subglottal pressures to create the glottal flow, often referred to as the voice source. A noise component was added to the glottal flow when the Reynolds number (Re) within the glottis exceeded 1,200. The model and characteristics of noise were previously reviewed in detail (Samlan & Story, 2011; Samlan et al., 2013).

Figure 1.

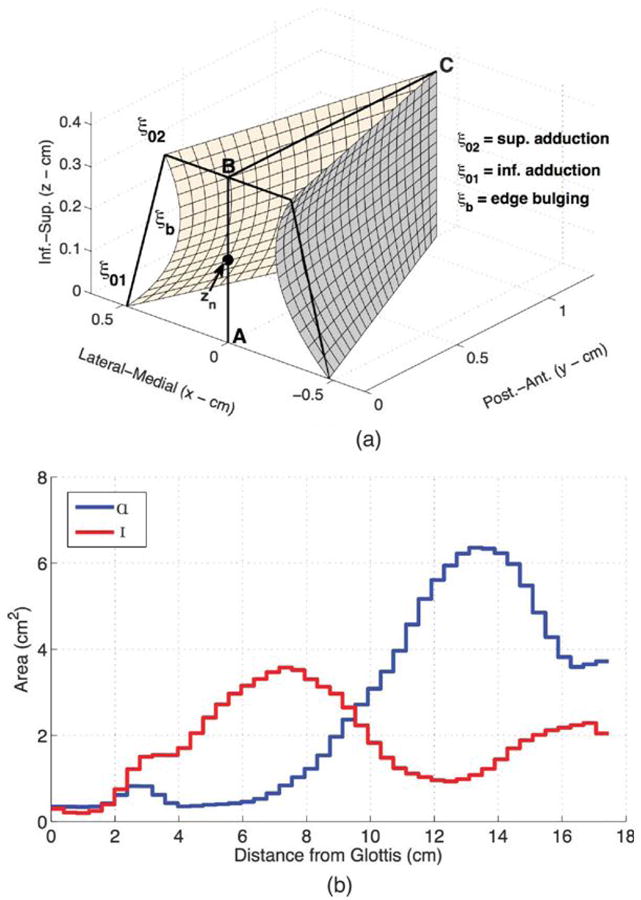
a: Kinematic vocal fold model, with the thickness of the vocal fold surface represented as the distance A–B and the length represented by the distance B–C. b: Vocal tract area functions for /a/ and /I/. Inf. = inferior; Sup. = superior; Post.-Ant. = post-anterior.

For the current study, the vocal fold model was modified to allow for separate specification of the left and right vocal fold surfaces. Five parameters were set independently for the left and right surfaces, with values shown in Table 1. The range of values for each of the parameters was determined on the basis of the results of a sensitivity analysis determining the ranges where voicing occurred. Movie files and audio files of fully symmetric vibration and the most asymmetric value of each of the five parameters are included in the online supplemental materials.

Table 1.

Model parameters and ranges.

Asymmetry	Symbol	Right surface value	Range of left surface values
Adduction	ξ02	0.1 cm	−0.1 to 0.4 cm
Bulging	ξb	0.1 cm	0.1 to −0.1 cm
Nodal point ratio	Rzn	0.8	0.9 to 0.1
Amplitude of vibration	Asym	1.0	1 to 0
Starting phase	φ	0 radians	0 to 2.4

The first model parameter modified was vocal fold adduction (ξ₀₂), the distance, in centimeters, of the superior aspect of the vocal process from midline. Glottal width (2× ξ₀₂) of 0 to 0.1 cm has been recommended for normal phonation (Berry et al., 2001). The right surface ξ₀₂ was set at 0.1 cm, and the left surface was varied in 30 equal steps from −0.1 to 0.4 cm, with larger values reflecting a vocal process positioned further from midline. A negative left ξ₀₂ indicates that the surface crossed the midline, so that the total range of glottal width was 0–0.5 cm.

Edge bulging, ξ_b, is thought to reflect thyroarytenoid muscle contraction (Alipour & Scherer, 2000), and the expected curvature of a healthy vocal fold is 0.02–0.1 cm (Titze, 2006a). The value of 0.1 cm was selected as the symmetric value. Decreased bulging indicates a less curved vocal fold edge, as might occur when there is loss of muscle tone or soft tissue. Increased bulging should assist adduction (Alipour & Scherer, 2000). The range of 0.1 to −0.1 cm, then, indicates the loss of “normal” vocal fold edge convexity and proceeds to slight concavity.

The nodal point, z_n, is the point along the vertical dimension of the vocal fold around which the rotational mode pivots, or changes phase, and is thought to relate to the point of mucosal upheaval (Titze & Story, 2002; Yumoto, Kadota, & Kurokawa, 1993, 1995; Yumoto, Kadota, & Mori, 1996). A high nodal point indicates greater vibratory mass and larger amplitude of the lower portion of the folds, and low nodal point indicates the opposite (Titze & Story, 2002). Though this value is determined by the mechanical properties of the tissue in a self-oscillating vocal fold model, it must be specified in the kinematic model, and “normal” values are not known. The symmetric value (see Table 1) was selected on the basis of findings from previous studies (Samlan & Story, 2011; Samlan el al., 2013), and a large range of left-sided values was selected given the lack of information about anticipated changes with vocal fold paralysis. In the current study, z_n was represented as the ratio of z_n to the thickness of the folds (Z_n/T) and called nodal point ratio, R_zn.

The parameter Asym reflects the amplitude of vibration of the left vocal fold surface relative to the right. An Asym value of 1, for example, indicates equal left and right vibratory amplitude, and 0.5 indicates the vibration of the left surface is 50% of the right. For the current study, the amplitude of the left fold started equal at 1 and was varied in equal steps until there was no amplitude of vibration for the left surface (see Table 1). The amplitude of vibration for the right surface was determined by the rule used for this kinematic model, which is based on vocal fold length, lung pressure, and threshold pressure (Titze, 2006a, p. 206). For the current simulations, all three values were held constant. The amplitude rule was modified so that amplitude of the right surface was based on the vibratory length rather than the resting length.

Starting phase, φ, defines a difference in timing between lateral-medial movements of the two folds, in radians. In the kinematic vocal fold model used, tissue motion is generated by superposition of sinusoidal functions, and starting phase can be set to any given number of radians between 0 and 2π. The right surface φ was always 0 radians, so that left φ = 0 indicates the vocal fold surfaces move as mirror images, reaching midline and maximum amplitude at the same time instants as one another. Higher φ values reflect increased phase difference. If the surfaces are set to be 180° out of phase, an odd result occurs in that there is no variation in glottal area. In order to avoid that condition, the maximum starting phase asymmetry included in this set of experiments was 2.4 radians (137.5°).

The speech production model was programmed to generate vowels at 30 equally spaced left-sided values for ξ₀₂, whereas the right surface and remaining (ξ_b, R_Zn, Asym, φ) left-sided parameters were maintained in the “symmetric” setting (see Table 1). The same process was repeated with 30 left-sided values of ξ_b, whereas the remaining parameters (ξ₀₂, R_Zn, Asym, φ) were maintained in the symmetric setting, and again for each successive parameter (R_Zn, Asym, and φ). The 30 productions of each variable were generated for two vowels, for a total of 150 unique /a/ and 150 unique /I/ vowels. The contact area, glottal area, glottal flow (U_g), and output pressure (P_out) (analogous to the microphone signal) signals were simultaneously collected.

Vocal Function Measurement

Each vowel was analyzed using maximum flow declination rate (MFDR) and five acoustic measures previously shown to be correlated with overall severity judgments of voice quality. MFDR is measured as the valley of the first derivative of glottal flow (Holmberg, Hillman, & Perkell, 1988) and was determined in the current study from the derivative of U_g using the “min” function in MATLAB. The MFDR provides information about how rapidly the airflow decreases in response to closing the glottal airspace and the supraglottal inertance (Titze, 2006b). MFDR is influenced by the degree of lateral vocal fold excursion and the vertical phase difference during vibration as well as vocal tract aerodynamics (Titze, 2006b). As such, it is expected that each of the asymmetries will lead to decreasing MFDR. Smaller MFDR values have been reported for individuals with vocal fold paralysis (Paseman, Casper, Colton, & Kelley, 2004) than for normal voice (Holmberg et al., 1988) and smaller values for quiet voice than for normal or loud voice (Holmberg et al., 1988).

Two measures of relative harmonic energy that have been found to correspond with voice quality were used: HNR and cepstral peak prominence (CPP; de Krom, 1995; Heman-Ackah el al., 2003; Heman-Ackah, Michael, & Goding, 2002). HNR was calculated for a 250-ms stable segment of the P_out spectra using a Praat script (Boersma, 1993; Boersma & Weenink, 2011). The CPP was measured from the cepstrum of P_out using SpeechTool (Hillenbrand. 2008), implemented from within MATLAB.

Spectral slope has also been found to correlate to voice quality (Kreiman, Gerratt, & Antoñanzas-Barroso, 2007), and three measures of spectral slope were selected to characterize different components of the spectrum. The difference between the first and second harmonic amplitudes, H1*-H2*, was measured using a peak-picking algorithm (Titze, Horii, & Scherer, 1987) to identify the amplitude of the first two harmonics from the averaged spectra of the output pressure signal. The harmonic amplitudes were corrected for the amplitude of the first formant (F1) as described by Hanson (1997), and the amplitude of the corrected H2 subtracted from the corrected H1. The frequency of F1 was determined on the basis of analysis of the frequency response of the vocal tract shape generated by the model (Samlan & Story, 2011). The mean root-mean-square energy was calculated from three frequency bands of the P_out, spectra: 60–400 Hz (B0), 400–2000 Hz (B1), and 2000–5000 Hz (B2). The mean intensity level (in dB) of Bl was subtracted from that of B0 for the spectral tilt measure B0-B1 and the level of B2 subtracted from B0 for the measure B0-B2. The bands were selected to be consistent with those used by de Krom (1995) and Hartl, Hans, Vaissière, and Brasnu (2003).

The effects of the five kinematic model parameters on each of the measures of vocal function were assessed through qualitative analysis of a series of figures and quantitative analysis using stepwise regression.

Perception

Twenty naive listeners, 17 men and three women, were recruited from the general population at the University of Arizona and served as participants for the perceptual study. All study procedures were approved by the University of Arizona Institutional Review Board. All listeners were at least 18 years of age; passed a hearing screening in the better ear at 25 dB HL at 0.5, 1, 2, and 4 KHz (American Speech-Language-Hearing Association, 1997); and indicated understanding the directions presented in English. The study was completed in a sound-treated room using the Alvin graphical interface (Hillenbrand & Gayvert, 2005).

The perceptual study was completed using a subset of five audio signals for each parameter (i.e., adduction, bulging, nodal point ratio, amplitude of vibration, and starting phase), equally spaced across the range of asymmetric values listed in Table 1. As previously stated, the current study was an early step in a series of studies simulating vocal fold paralysis and its treatment. The 25 /a/ and 25 /I/ vowels of the current study, simulated using no more than a single asymmetry each, were combined with stimuli from the other studies, where multiple asymmetries were present in each simulation (Samlan, 2012). This allowed testing of a set of 200 stimuli simulated using the same speech production model, rating task, and reference, and encompassing a wide range of severity. A large range of samples is important for minimizing a frequency effect (cf. Eadie & Kapsner-Smith, 2011). The samples were rated twice by every participant. All samples were presented as the second vowel in a paired comparison where listeners were asked to determine whether the second sample was “better” or “worse” than the reference vowel and “by how much.” The reference vowel was generated with the right surface set to the “symmetric value” listed in Table 1 and the left surface with the following parameters: ξ₀₂ = 0.15 cm, ξ_b = 0 cm, R_zn = 0.4, Asym = 1, and φ = 1.8 radians. The following written instructions were provided and reviewed verbally:

You will hear two productions of the vowel “ah” as in “hot.” You need to make two decisions: 1) Is the second “ah” better or worse than the first “ah,” and 2) How much better or worse? Select the center button (labeled “0”) if the two vowels sound equally good (or equally bad). Selecting “0” does not necessarily mean you think they sound the same, just equal. If they do not sound equally good (or equally bad), select a button to the left of center if the second vowel was worse and to the right of center if the second vowel was better. Buttons closer to the center mean the vowels were similar and buttons away from the center mean the second vowel was MUCH worse or MUCH better than the first.

Listeners indicated their rating by selecting one of seven buttons presented in a row. The center button was labeled 0, and buttons on either side of 0 were labeled 1, 2, and 3, with 3 in the most lateral positions. The 3 to the left of 0 was also labeled worse, and the 3 to the right was also labeled better. Button clicks were coded numerically from −3 (best) to +3 (worst) and exported from Alvin to a spreadsheet for analysis. Before rating the experimental samples, all participants completed a training set of 60 samples exposing them to the range of samples and the rating task used in the experiment. They were provided opportunities to ask questions when the instructions were reviewed, after the training set, and between the two experimental sets.

Although the rating task was novel, it was designed to reflect key criteria identified as important to reliable ratings. The rating scale was modified from that used in Samlan et al. (2013) and originally based on a speech clarity rating scale used by Tasko and Greilick (2010). The change from a visual analog to an equal appearing interval scale was based on expert listener feedback during a pilot study. The task is a modification of matching and dissimilarity tasks, which have been shown to improve reliability relative to unanchored tasks (Gerratt, Kreiman, Antoñanzas-Barroso, & Berke, 1993; Kreiman & Gerratt, 1998). Rating each stimulus in comparison to, and following, the reference (i.e., anchor) reduces reliance on internal standards and maintains a consistent context for the stimuli (Awan & Lawson, 2009; Chan & Yiu, 2002, 2006; Eadie & Baylor, 2006; Eadie & Kapsner-Smith, 2011; Gerratt et al., 1993; Kreiman, Gerratt, Kempster, Erman, & Berke, 1993). The simple written anchors are familiar units for the naive listeners, also important to reliability (Patel, Shrivastav, & Eddins, 2010).

Reliability was assessed using the intraclass correlation (ICC). The mean rating of each sample became the outcome variable for stepwise linear regression models determining the order in which kinematic parameters and acoustic measures influenced perceived voice quality for each vowel.

Results

The relation of each individual asymmetry to the vocal function measures is described first, followed by the relation of individual asymmetries to perceptual ratings of severity, and then the relation of the vocal function measures to perceptual ratings.

Vocal Function

The changes in MFDR, H1*-H2*, B0-B1, B0-B2, CPP, and HNR as one parameter at a time became increasingly asymmetric and are shown graphically in the panels of Figure 2. In each panel, /a/ results are in black and /I/ in blue. The setting for the left-sided parameter being modified is on the x-axis, and a light gray vertical line indicates the value of that parameter where the left and right vocal folds are set at the same value (i.e., the symmetric value). The symmetric value is at the far left side of the graph for bulging (ξ_b = 0.1 cm), amplitude asymmetry (Asym = 1), and starting phase (φ = 0 radians). In each of these graphs, movement along the x-axis to the right represents increasing L-R asymmetry of the model parameter and was therefore expected to indicate increasing disorder.

Figure 2.

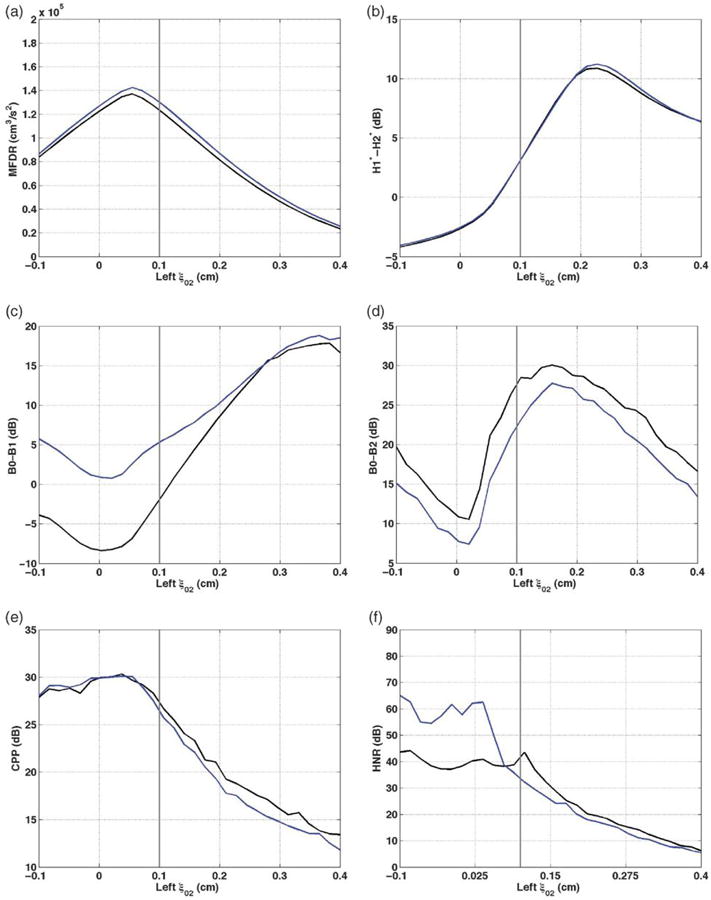
Vocal function with increasing left ξ₀₂. a: maximum flow declination (MFDR). b: H1*-H2*. c: B0-B1. d: B0-B2. e: Cepstral peak prominence (CPP). f: harmonics-to-noise ratio (HNR). /a/ = black; /I/ = blue; vertical gray line = symmetric ξ₀₂ value of 0.1 cm.

Adduction asymmetries (ξ₀₂)

Several changes associated with increasing dysphonia occurred as the left ξ₀₂ value increased from the symmetric value of 0.1 to the most asymmetric value of 0.4 cm, increasing the distance between the vocal processes (see Figure 2). The peak MFDR of 137,260 and 142,050 cm³/s² occurred for /a/ and /I/ at ξ₀₂ = 0.06 cm, which is slightly more adducted than the symmetric case, and MFDR decreased by 113,600 cm³/s² for /a/ and 115,990 cm³/s² for /I/ as vocal process separation increased (see Figure 2a). MFDR also decreased as left ξ₀₂ decreased from 0.06 cm to −0.1 cm, decreasing the distance between the surfaces. H1 *-H2* (see Figure 2b) was negative from ξ₀₂ = −0.1 to ξ₀₂ = 0.06 cm, consistent with pressed and normal voice qualities. It increased by 15.1 dB for /a/ and an additional 0.1 dB for /I/, reaching a maximum when ξ₀₂ = 0.22 cm. HI *-H2* then decreased as ξ₀₂ continued to increase, falling to a value of 6.4 dB by ξ₀₂ = 0.4 cm. B0-B1 increased by 26.2 dB for /a/ and 19.5 dB for /I/ as ξ₀₂ increased from 0.04 cm to 0.4 cm (see Figure 2c), reflecting decreased mean energy in the first two formants relative to the fundamental component. B0-B1 also increased when ξ₀₂ decreased from 0.04 cm toward −0.1 cm. It is noteworthy that, for /a/, B0-B1 shifted from negative to positive around the symmetric value; the energy in the fundamental component was less than that in the first two formants for the low left ξ₀₂ settings and higher than in the first two formants for higher ξ₀₂. B0-B1 was higher for /I/ than /a/ for much of the range, and the difference was most prominent at low ξ₀₂. B0-B2 was positive for all ξ₀₂ values, indicating higher mean B0 than B2 for all adductory manipulations of the symmetric base voice (see Figure 2d). The peak B0-B2 value for /a/ occurred at ξ₀₂ = 0.16 cm, and B0-B2 decreased by 13.4 dB as ξ₀₂ increased to 0.4 cm and by 19.5 dB as ξ₀₂ decreased from 0.16 cm to 0.02 cm. This lowest B0-B2 value occurred at a similar vocal process separation (0.02 cm) as the lowest B0-B1 (see Figure 2c), and the highest MFDR (see Figure 2a), CPP (see Figure 2e), and HNR (see Figure 2f). Values for /a/ were 2.2–5.4 dB higher than for /I/.

CPP decreased by 16.9 dB for /a/ and 18.4 dB for /I/ as ξ₀₂ increased from 0.04 to 0.4 cm (see Figure 2e). As left ξ₀₂ decreased from near 0 toward −0.1 cm, CPP decreased slightly. CPP was quite similar for the vowels /a/ and /I/. HNR decreased by 37.3 (/a/) and 59.8 (/I/) dB as ξ₀₂ increased (see Figure 2f). The highest HNR occurred with negative left ξ₀₂, though most of the decrease in HNR occurred when ξ₀₂ ≤ 0.11 (/a/) or 0.04 cm (/I/). HNR was higher for /I/ until ξ₀₂ = 0.07 cm and then higher for /a/ as ξ₀₂ increased further.

In summary, increasing left ξ₀₂ from the symmetric value (0.1 cm) to 0.4 cm led to changes consistent with increased dysphonia, specifically, increased B0-B1 and decreased MFDR, CPP, B0-B2, and HNR. The increase in B0-B1 is likely reflecting weakening harmonic energy in Bl, the band that includes Fl and F2 for both vowels. H1*-H2* increased over the first portion of that range, also consistent with increased dysphonia, then decreased once again. The range of “overcorrection,” where left ξ₀₂ was less than right ξ₀₂, produced inconsistent vocal function results. For all measures of vocal function, changes in value were similar for /a/ and /I/. yet values for /I/ samples were in the direction of more severely disordered productions than /a/ for CPP and B0-B2 and less severely disordered productions than /a/ for MFDR. The direction was inconsistent for HNR, and the /a/ and /I/ results were very similar for H1 *-H2*.

Bulging asymmetries (ξ_b)

As left bulging decreased from 0.1 to −0.1, creating a concave edge to the left vocal fold surface, measures tended to reflect increased dysphonia (see Figure 3). MFDR decreased by 63,970 cm³/s² for /a/ and 66,150 cm³/s² for /I/, and the decrease was across the full range of bulging values (see Figure 3a). The MFDR values for /I/ were, in general, approximately 6,000 cm³/s² higher than those for /a/. H1*-H2* for /a/ increased by 4.0 dB as bulging decreased from 0.1 to −0.01 cm (see Figure 3b). Creating negative curvature (bowing) led to decrease in H1*-H2* of less than 0.5 dB. H1*-H2* was similar for /a/ and /I/, with values for /a/ no more than 0.1 dB higher than those for /I/ across the bulging range. B0-B1 increased across the range of bulging decrease, by 13.2 dB for /a/ and by 9.2 dB for /I/ (see Figure 3c). B0-B1 was higher for /I/ than /a/, by approximately 2–7 dB. B0-B2 increased by 4.8 dB for /a/ as left bulging decreased from 0.1 to 0.4 dB, then decreased, though not constantly, by 2.9 dB as bulging continued to decrease (see Figure 3d). The pattern was similar for /I/, though B0-B2 was approximately 2.5–4.5 dB higher for /a/ than the matching /I/ production.

Figure 3.

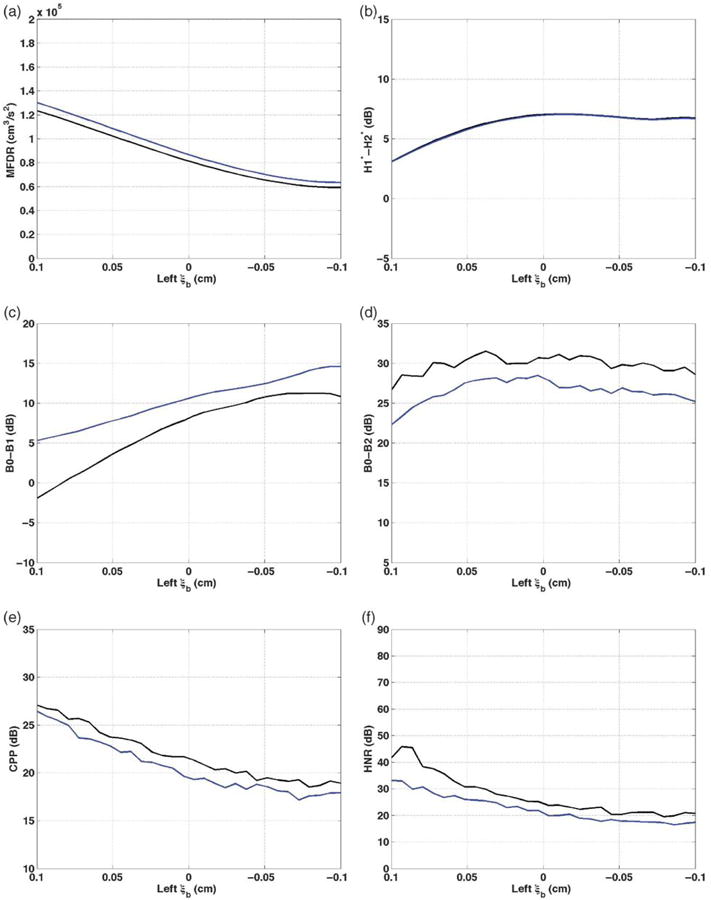
Vocal function with decreasing left ξ_b. a: MFDR. b: H1*-H2*. c: B0-B1. d: B0-B2. e: CPP. f: HNR. /a/ = black; /I/ = blue; symmetric ξ_b = 0.1 cm.

CPP generally decreased across the bulging range, by 8.6 dB for /a/ and by 9.2 dB for /I/, with lowest values at bulging of −0.07 to −0.08 (see Figure 3e). CPP was always higher for /a/ than an equivalent production of /I/, by approximately 0.5–2 dB. HNR decreased by 25.9 dB for /a/ and by 16.7 dB for /I/ as bulging decreased from 0.1 to −0.1 (see Figure 3f). Values were approximately 2–12 dB higher for /a/ than /I/ across the bulging range.

In summary, changing the left surface contour gradually from convex to flat (i.e., left ξ_b from 0.1 to approximately 0 cm) led to changes in every measure that were consistent with increased dysphonia. When bulging decreased further, causing a concave edge, some measures continued to follow the trend of increased dysphonia and others did not. In all cases, the shapes were similar for /a/ and /I/, and in all cases except MFDR and H1*-H2*, the values for /I/ reflected more dysphonic vowels than the corresponding /a/ values.

Nodal point ratio asymmetries (R_zn)

As left nodal point ratio decreased from 0.9 to 0.1, MFDR, H1*-H2*, B0, and CPP values changed in the directions expected for increased dysphonia (see Figure 4). MFDR decreased by 68,200 cm³/s² for /a/ and 70,500 cm³/s² for /I/ (see Figure 4a). MFDR was approximately 4,400–7,500 cm³/s² higher for /I/ than /a/ across the nodal point ratio range. H1*-H2* increased by 16.92 dB for /a/ and by 17.2 dB for /I/ across the full range of left nodal point ratio decrease (see Figure 4b). The values were almost identical for /a/ and /I/, with differences not exceeding 0.5 dB. B0-B1 increased by 18.8 dB for /a/ and by 9.5 dB for /I/ as left nodal point ratio decreased, ending at the same value as one another (see Figure 4c). B0-B1 was most different for /a/ and /I/ at the highest nodal point ratio. B0-B2 increased for /a/ by 9.4 dB as nodal point ratio decreased to 0.4, then decreased by 1.7 dB as nodal point ratio decreased from 0.4 to 0.1 (see Figure 4d). The pattern of B0-B2 for /I/ was similar, though the values were lower by approximately 1.9–4.4 dB.

Figure 4.

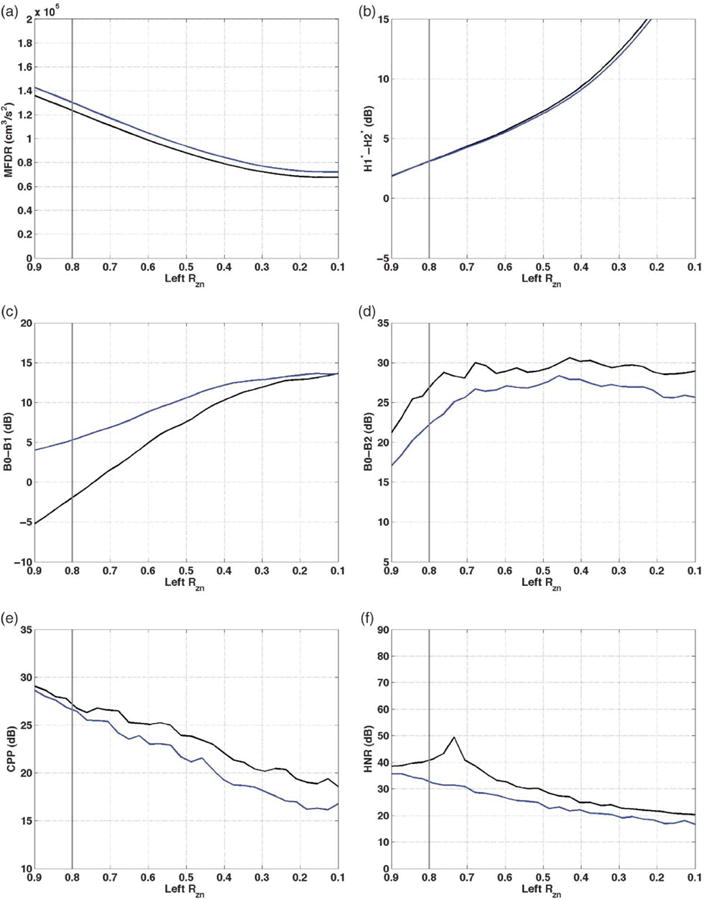
Vocal function with decreasing left R_zn. a: MFDR. b: H1*-H2*. c: B0-B1. d: B0-B2. e: CPP. f: HNR. /a/ = black; /I/ = blue; vertical gray line = symmetric R_zn value of 0.8.

CPP decreased across the range of nodal point ratio values, by 10.5 dB for /a/ and by 12.4 dB for /I/ (see Figure 4e). Values for /a/ were typically higher than the equivalent values for /I/, by approximately 0.5 dB–2.7 dB. The vowel difference was more prominent at low nodal point ratio values than high. HNR was highest for /a/ at nodal point ratio of 0.74 and decreased 29.6 dB as nodal point ratio decreased to 0.1. HNR decreased 19.3 dB across the full nodal point ratio range for /I/ (see Figure 4f). HNR was 3–18 dB higher than the corresponding HNR for /I/ at any given nodal point ratio.

In summary, all measures were consistent with increased impairment as nodal point ratio decreased unilaterally. Patterns were again similar for the vowels /a/ and /I/, with /I/ producing higher H1*-H2*, MFDR, and B0-B1, and lower CPP, B0-B2, and HNR than /a/. H1*-H2* values were quite similar for the two vowels.

Amplitude of vibration asymmetries (Asym)

As vibratory amplitude of the left fold decreased from an Asym value of 1 (i.e., left amplitude of vibration equal to right amplitude) to Asym = 0 (i.e., no left vibratory amplitude), subtle changes occurred and can be observed in Figure 5. MFDR decreased by 46,280 cm³/s² for /a/ and by 50,040 cm³/s² for /I/, consistent with decreased dysphonia (see Figure 5a). The values for /I/ were higher than for /a/, though the difference decreased with amplitude of vibration. H1*-H2* steadily increased by 3.4 dB for both /a/ and /I/ as left vibratory amplitude decreased (see Figure 5b). B0-B1 increased by 7.1 dB for /a/ and by 3.4 dB for /I/ as left amplitude decreased to 0 (see Figure 5c). The values for /I/ were higher than /a/, with the difference decreasing as left amplitude of vibration decreased. Changes in B0-B2 (see Figure 5d) were also subtle, increasing 3.2 dB for /a/ as Asym decreased to 0.4, then decreasing by 1.0 dB as Asym continued to decrease to 0. B0-B2 was 2.5–5.1 dB lower for /I/ than /a/. CPP changed minimally as left amplitude of vibration decreased, increasing by 2.3–3 dB for /a/ and /I/ (see Figure 5e). The HNR increased by 5.8 dB for /a/ and by 43.4 dB as the left amplitude of vibration was reduced to 0 (see Figure 5f). HNR was higher for /a/ than /I/ when Asym ≤ 0.6 and higher for /I/ when Asym ≥ 0.6.

Figure 5.

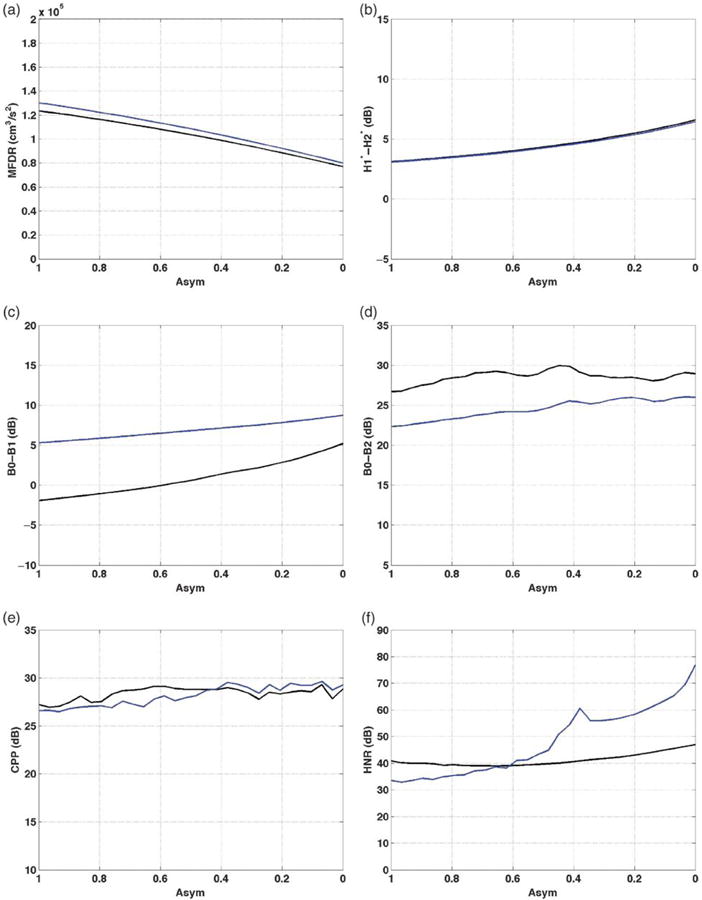
Vocal function with decreasing left amplitude of vibration (Asym). a: MFDR. b: H1*-H2*. c: B0-B1. d: B0-B2. e: CPP. f: HNR. /a/ = black; /I/ = blue; symmetric Asym = 1.

The effect of decreasing the left amplitude of vibration relative to the right was generally subtle. Some of the changes in vocal function were in the direction of increasing dysphonia (i.e., H1*-H2* and B0-B1 increased, and MFDR decreased) and some were not (i.e., CPP, B0-B2, and HNR increased). Patterns across measures were inconsistent for the vowels /a/ and /I/, with MFDR and B0-B1 higher for /I/, and H1*-H2* and B0-B2 higher for /a/. CPP was lower and HNR higher for /a/ when amplitude was symmetric and the pattern reversed as left amplitude of vibration decreased.

Starting phase asymmetries (φ)

The final asymmetry introduced was starting phase (φ). Figure 6 demonstrates the effects on vocal function measures of increasing the starting phase shift from 0 to 2.4 radians. MFDR decreased by 66,760 cm³/s² for /a/ and by 71,000 cm³/s² for /I/ (see Figure 6a). The values were higher for /I/ than /a/, a difference more prominent when vibration was in-phase. H1*-H2* increased by 11.7 dB for /a/ and /I/ as φ increased to 2.4 radians (see Figure 6b). Much of the increase occurred as phase shift increased beyond approximately 1.5 radians. B0-B1 increased by 8.7 dB for /a/ and by 6.6 dB for /I/ as the phase shift increased from 0.6 to 2.4 (see Figure 6c). Consistent with B0-B1 for other parameters, /I/ values were higher than /a/, by 7.2 dB at φ = 0 and the difference narrowed as φ increased. B0-B2 for /a/ decreased by 4.5 dB as φ increased to 0.8, then increased by 8.3 dB as φ continued to increase, demonstrating more rapid change when the phase shift was more substantial (see Figure 6d). The same pattern was present for /I/, with B0-B2 3–4.3 dB less than it was at the same φ for /a/. CPP increased for /a/ by 3.2 dB as φ increased to 1.6 radians, then decreased by 1.8 dB (see Figure 6e). The pattern for /I/ was similar, and CPP was generally within 2 dB of the /a/ value. For /a/, HNR increased by 7.4 dB as φ increased to 2.0 radians, with most of the increase occurring when φ = 1.4 radians (see Figure 6f). For/I/, HNR increased 48.7 dB with φ increase from 1.2 to 1.8 radians and then decreased by 30.8 as φ increased from 1.8 to 2.2 radians.

Figure 6.

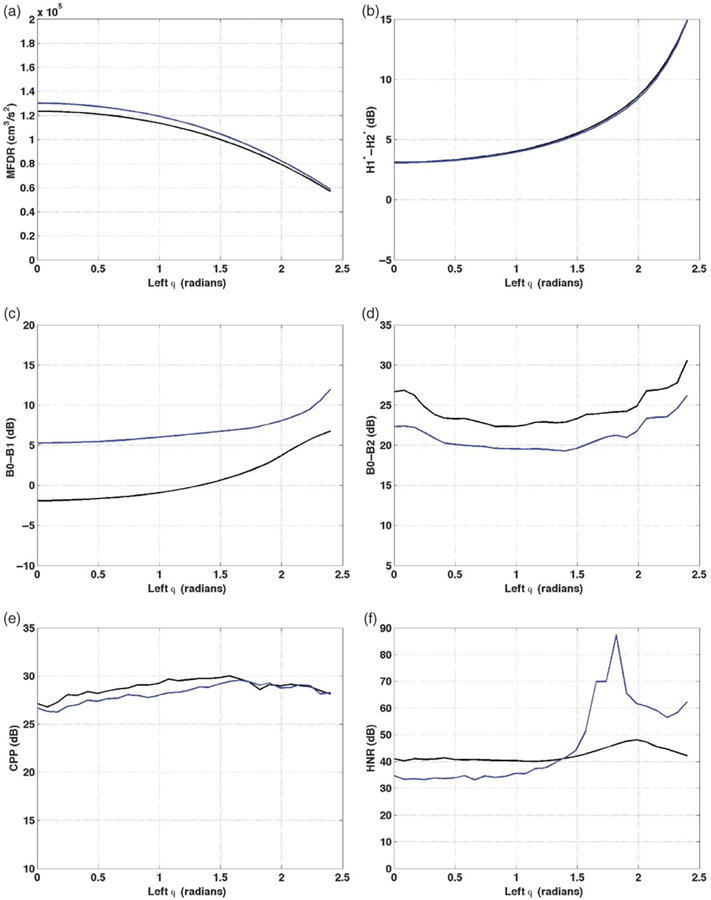
Vocal function with increasing left phase shift (φ). a: MFDR. b: H1*-H2*. c: B0-B1. d: B0-B2. e: CPP. f: HNR. /a/ = black; /I/ = blue; symmetric φ = 0.

In summary, increasing the starting phase difference led to some measures consistent with increased dysphonia (i.e., decreased MFDR, increased H2*-H2*, and increased B0-B1) and other measures consistent with decreased dysphonia (increased CPP, B0-B2, and HNR). Most changes were more evident when φ was high. Patterns were again similar for the vowels /a/ and /I/, with /I/ producing higher MFDR, H1*-H2*, and B0-B1, and lower CPP and B0-B2 than /a/. H1*-H2* was similar for the two vowels.

Perceived Voice Quality

The /a/ and /I/ productions were rated for severity in relation to a reference vowel. Across the 20 listeners, average ICC was .831 (95% CI [.808, .851]), indicating adequate internal consistency in the ratings. As stated, the ratings for this task were part of a larger rating session with a larger severity range. For the full set of samples rated during the task, the average ICC was 0.881 (95% CI [0.873, 0.888]). The overall mean rating for each listener was compared with the mean rating of all 20 raters in order to estimate interrater reliability. The average ICC was 0.87 for the vowels in this study and 0.97 for the full rating session.

The mean ratings of two judgments per sample by 20 listeners (i.e., 40 ratings per sample) were plotted for the vowels /a/ and /I/ for each parameter and can be found in Figure 7. In each plot, the y-axis is mean perceptual rating. A score of “0” represents a severity level that is the same as the reference vowel, a negative value represents a “better” voice, and a positive value represents a “worse” voice so that increasing scores reflect increasing disorder severity. The gray vertical line represents the value where that parameter would be the same as for the right side and is at the left edge of the plot for ξ_b, Asym, and φ. Movement to the right from the left side of the vertical gray line (ξ₀₂ and R_Zn) represents increasing asymmetry.

Figure 7.

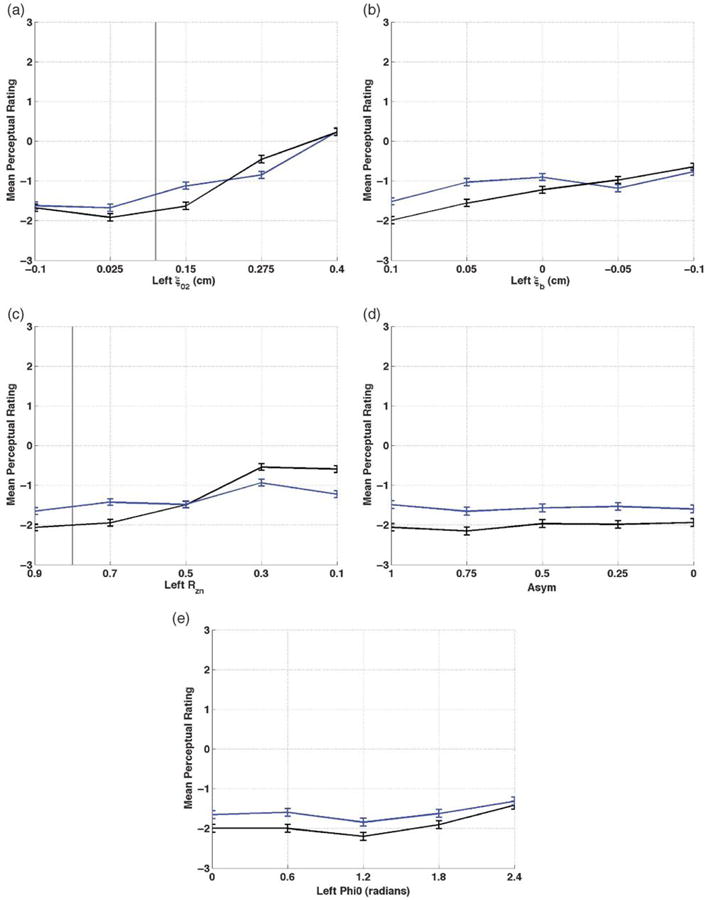
Mean perceptual rating and standard error across a: ξ₀₂; b: ξ_b; c: R_zn; d: Asym; e: φ. /a/ = black; /I/ = blue; the symmetric condition is at the left border of the graph for panels b, d, and e, and at the vertical gray line for panels a and c.

Adduction asymmetries (ξ₀₂)

The perceptual changes resulting from increasing ξ₀₂ can be found in Figure 7a. The production rated least severely impaired, with a mean rating of −1.9 (SD = 2.0), was the /a/ vowel generated with a left ξ₀₂ value of 0.25 cm. As ξ₀₂ increased to 0.4 cm, the mean rating increased by 2.1, and the rating at ξ₀₂ = 0.4 cm was slightly “worse” than the reference comparison (“0”), with a value of 0.2 (SD = 0.4). Decreasing ξ₀₂ to −0.1 (i.e., overadduction of the left fold) also slightly worsened the perceived quality, by 0.4. Ratings for /I/ varied around those for the equivalent /a/, with differences ranging from 0.1 to 0.5.

Bulging asymmetries (ξ_b)

Decreasing bulging led to changes in perceived quality that can be observed in Figure 7b. The smallest degree of impairment was perceived at the symmetric setting (i.e., ξ_b = 0.1 cm), with mean ratings of −2.0 (SD = 1.6) for /a/ and −1.7 for /I/. Perceived severity increased by 1.8 for /a/ and by 0.9 for /I/ as edge bulging decreased unilaterally. Ratings generally indicated less severe impairment for /a/ than /I/, by 0.4–0.6.

Nodal point ratio asymmetries (R_zn)

Ratings for nodal point ratio asymmetry can be found in Figure 7c. The least severe perceptual ratings occurred for the highest nodal point ratio, and severity increased as R_zn decreased. The highest (i.e., most severe) ratings occurred at nodal point ratio of 0.3 and 0.1. Mean ratings for /a/ increased 1.7 scale points, with a mean rating of −0.6 (SD = 1.4) when nodal point ratio was 0.1. The negative value indicates that the vowel with the lowest left nodal point ratio was still perceived as less severely impaired than the reference vowel. The severity increase for /I/ was 0.8, less remarkable than for /a/. The /I/ vowels were perceived as more impaired than /a/ when nodal point ratio was greater than 0.5, and less impaired than /a/ when nodal point ratio was less than 0.5.

Amplitude of vibration asymmetries (Asym)

There was minimal change in perceptual rating as the amplitude of vibration was decreased while all other values remained symmetric (see Figure 7d). For the /a/ vowel, the difference between the minimum and maximum severity ratings was 0.4 scale points. For /I/, this difference was smaller, 0.1. The /a/ vowels were rated as less severely impaired than the /I/.

Starting phase asymmetries (ϕ)

As can be observed in Figure 7e, the least severe ratings occurred at φ = 1.8 radians for /a/ and /I/. Ratings increased by only 0.8 for /a/ and by 0.5 for /I/ as phase asymmetry increased to 2.4 radians. Ratings for /a/ indicated less impairment than for /I/.

Influence of Individual Parameters on Perceived Quality

The relative influence of each of the parameters on perceived overall voice quality was determined separately for /a/ and /I/ using stepwise linear regression. The total variance in mean rating explained by any combination of the five parameters was small: The final model for /a/ included adduction, nodal point, and bulging with adjusted R² = 0.106, F(3, 496) = 20.667, p < .001. The final model for /I/ included adduction and bulging with adjusted R² = 0.051, F(2,497) = 13.319, p < .001.

Relation of Vocal Function Measures to Perceptual Ratings

The relative influence of the information conveyed by each acoustic measure on perceived severity was determined separately for /a/ and /I/ using stepwise linear regression. Note that only the acoustic parameters (H1*-H2*, B0-B1, B0-B2, CPP, and HNR) were entered into the regressions. Only CPP was a significant predictor of mean severity rating for either vowel, and it explained a small percentage of the variance in severity rating. For /a/, adjusted R² = 0.135, F(l, 498) = 78.561, p < .001. For /I/, adjusted R² = 0.057, F(1, 498) = 30.898, p < .001.

Discussion

Five laryngeal asymmetries thought to occur with unilateral vocal fold paralysis were examined individually to determine their characteristic effects on vocal function and voice quality. Increasing the distance of the left vocal process from midline worsened vocal function measures and voice quality more than the other asymmetries examined, consistent with the current practice of vocal fold medialization to improve glottal closure. Unilaterally decreasing the convexity of the vocal fold edge and lowering the vibratory nodal point also worsened acoustic measures and perceived voice quality. Although most treatments for motion impairment increase the convexity of the vocal fold edge through injected or implanted material or increased muscle tone, it is less clear how current treatments alter nodal point ratio, and this requires further study. Decreased or absent amplitude of vibration of the left fold made very little difference to the resultant voice, nor did increasing phase asymmetry. Amplitude of vibration and phase symmetry are commonly altered in vocal fold motion impairment both before and after surgery, and further study of their perceptual importance is necessary. The results must be interpreted with full consideration of the benefits and limitations of the model used and in conjunction with findings from other types of studies. CPP explained a small but significant portion of the variance in mean perceptual severity ratings, whereas the other measures used in the study did not, contributing to the growing body of literature supporting the use of cepstral measures as part of a complete voice assessment. The implications of each of these findings are discussed further in the paragraphs that follow.

Laryngeal Asymmetries

The laryngeal asymmetries selected for the current study are consistent with signs that can be observed clinically during endoscopy and stroboscopy. The exception is R_zn, which can only be inferred during stroboscopy, yet was included given previous evidence of its perceptual importance when modified bilaterally (Samlan et al., 2013). The measured change in vocal function was largest with unilateral increase in vocal process separation, followed by lowered nodal point ratio and decreased surface bulging. Amplitude of vibration and starting phase asymmetries generally produced the least amount of variation in vocal function measures.

General patterns of vocal function change resulting from kinematic model parameter asymmetries are summarized in Table 2. Creating an asymmetry of adduction, bulging, or nodal point ratio while the other parameters remained symmetric led to measures consistent with increasing dysphonia; specifically, MFDR, B0-B2, CPP, and HNR decreased, and H1*-H2* and B0-B1 increased, at least for part of the range of parameter values. There were some points where the pattern did not hold: B0-B2 increased for part of the range before decreasing, the decrease was slight for unilateral nodal point ratio decrease, and H1*-H2* maximum occurred before maximum adduction or bulging asymmetry and then H1*-H2* decreased as the degree of asymmetry continued to increase. The visible effects of increasing ξ₀₂ and decreasing ξ_b are changes to glottal closure, either at the posterior membranous folds (i.e., the result of increasing the distance between the posterior membranous edges through increasing ξ₀₂) or at the midmembranous (i.e., the result of eliminating the convex shape of the one vocal fold edge). These changes are common in patients with vocal fold motion impairment, and the results demonstrate that unilateral change of either feature by itself, as the sole difference in laryngeal structure or function, will produce consistent measurable changes in voice. The inverse is also expected to be the case: Improving glottal closure through increasing the bulge at the medial edge or medializing the vocal process should increase MFDR, the amplitude of energy in bands B1 and B2, and the regularity of the harmonics, while decreasing the noise. The measures might constitute a noninvasive manner to track change during treatment, though they are responsive to many different vocal fold and vocal tract changes, so will not be specific to the stroboscopic finding of interest.

Table 2.

General direction of change in vocal function measure as each left parameter setting varied from the point of symmetry in the direction expected to increase the severity of dysphonia.

Asymmetry	MFDR	CPP	HNR	H1*-H2*	B0-B1	B0-B2
Adduction (ξ02)	↓	↓	↓	—	↑	—
Bulging (ξb)	↓	↓	↓	—	↑	—
Nodal point (Rzn)	↓	↓	↓	↑	↑	↑
Vibratory amplitude (Asym)	↓	↑	↑	↑	↑	↑
Phase (φ)	↓	↑	↑	↑	↑	—

Note. Trends are not included for the trends when ξ₀₂ was decreased or R_zn was increased from symmetry. A dash indicates the direction changed over the course of the parameter range.

Results of perceptual rating tasks were consistent with the vocal function measures: Increased asymmetry of adduction, bulging, and nodal point ratio led to noticeable worsening of the perceived voice quality. The “worst” ratings occurred as vocal process separation increased, followed by low nodal point ratio (for /a/), and then decreased edge bulging. Even though timing and slight asymmetries in arytenoid adduction have been identified in speakers without voice disorders (Bonilha et al., 2009; Lindestad et al., 2004), the findings of the current study support the importance of adductory, bulging, and nodal point symmetry to perceived voice quality.

The importance of vocal process position and edge shape are consistent with current clinical care of people with vocal fold motion impairment. Surgical management to alter vocal process position and edge shape is well established (Fakhry, Flint, & Cummings, 2010), and medical management is emerging (Mattsson et al., 2005). It has yet to be demonstrated that behavioral management alone can effectively change vocal process position or edge contour in a paralyzed fold.

As stated earlier, the nodal point ratio is poorly understood in normal and disordered phonation, yet lowering the nodal point ratios bilaterally has been shown to increase the perception of breathiness (Samlan et al., 2013), and a mismatch of nodal point ratio between the left and the right folds was shown in the current study to worsen vocal function and voice quality in a similar manner to adduction and edge bulging. Nodal point ratio cannot be fully visualized during stroboscopy, because it is an area along the thickness (e.g., vertical dimension) of the edge where minimal vibration occurs, and the edge is not visible throughout the complete vibratory cycle. A low nodal point can, at least partially, be inferred from an observation of the medial surface being visible for most of the closing phase of vibration. Speculation of how to raise a low nodal point through surgical or behavioral intervention must await deeper understanding of the factors that drive nodal point ratio. Possibilities include the stiffness and other vibratory properties of the epithelium and lamina propria and thyroarytenoid muscle activation.

Patterns of vocal function changes were less consistent when the amplitude of vibration (Asym) and starting phase (φ) became increasingly asymmetric, and many of the changes observed here were quite small or shifted direction over the range of parameter settings. Some vocal function measures even changed value in an unexpected direction (i.e., “improved”) as amplitude or phase asymmetry increased. The limited acoustic and perceptual impact of unilaterally decreasing vibratory amplitude was consistent with previous findings that many vibratory and aerodynamic parameters of an excised hemilarynx vibrating against a plexiglass plate were similar to those of a full excised larynx (Jiang & Titze, 1993). Such understanding would naturally lead to targeting treatment of other vibratory features before amplitude. A substantial caveat, however, that the case tested in the current study was one where all other features were normal as amplitude decreased. Most of the time, amplitude decreases occur in conjunction with other vibration changes, complicating this simplistic interpretation. During clinical assessment, a vocal fold with decreased or absent amplitude generally occurs secondary to unilateral stiffness because of a lesion, scarring, or extensive surgical procedure with or without reconstruction. In vocal fold motion impairment, minimal or absent amplitude might occur if the vocal fold is positioned too laterally to be set into vibration during phonation. The importance of vibratory amplitude in assessment is not necessarily its perceptual importance or lack thereof, but that it functions as a marker for other aspects of laryngeal structure and function.

The finding that L-R phase asymmetry did not affect perceptual rating is consistent with the hypothesis that L-R phase asymmetries represent normal variability in healthy speakers (Bonilha et al., 2008; Zhang et al., 2013). During clinical examinations, observed phase asymmetry in an otherwise normal larynx should not be assumed to be the cause of any voice quality concerns. That is not to say that phase asymmetries are not important or have no perceptual consequences. As with amplitude of vibration, asymmetry might be the most obvious sign of a disorder or constellation of symptoms. Even though severe L-R phase asymmetries did not cause increased dysphonia in the otherwise normal and symmetric condition of the current study, the results do not address whether L-R amplitude or phase asymmetries become perceptually important when additional aspects of vibration were also abnormal. Indeed, multiple parameters are often abnormal in disordered productions, and the presence of other asymmetries or abnormalities might change the perceptual importance of phase asymmetries.

The regression analysis did not show a robust prediction of voice quality rating on the basis of the model parameters. This is likely a function of the perceptual experimental design. As indicated, five settings of each parameter (adduction, bulging, nodal point ratio, amplitude of vibration, and starting phase) were used in the perceptual task. One of those settings was at, or close to, the symmetric value, leaving four disordered samples per parameter. It is likely that the limited number of samples was a factor in the low percentage of variance explained, as was variability due to individual differences in rating strategy.

Vowel differences

With the exception of H1*-H2*, which was almost identical for the two vowels, the values of the vocal function measures were different for the /a/ and /I/ vowels, though the patterns were similar. There was no clear pattern of which measures were higher for /a/ than /I/, and vice versa. Perceptual ratings, similarly, were not consistently higher for either vowel.

Relation of acoustic measures to perceived voice quality

In previous studies, CPP has been found to be highly correlated to perceived voice quality (Awan, Roy, & Dromey, 2009; Heman-Ackah et al, 2002, 2003; Hillenbrand, Cleveland, & Erickson, 1994; Hillenbrand & Houde, 1996; Samlan et al., 2013). In the current study, CPP was the only predictor of voice quality in the final regression models for either vowel, though it explained just 5.7%–13.5% of the variance.

Though the other measures did not emerge as significant predictors of perceived quality, there was a general acoustic pattern for the three parameters that influenced perception. When left ξ₀₂, bulging, and nodal point ratio were varied from the symmetric toward the most asymmetric values, MFDR, CPP, and HNR decreased and B0-B1 increased. Note that though MFDR was not entered into the regression model, it decreased as all five manipulated parameters became increasingly asymmetric. The MFDR measured here was based directly on the glottal flow generated using the model and was very responsive to increasing degrees of all asymmetries tested. It is not clear, however, that the same trends would be expected to occur for MFDR measured from the inverse filtered air flow or acoustic pressure measured in natural speech. A comparison of MFDR measured directly from glottal flow versus that from in-versed filtering was beyond the scope of the current study but is a direction for future research.

Limitations

The kinematic model offers precise control over specific parameters that determine the shape of the medial surfaces of the vocal folds and ultimately affect the time-varying glottal area and glottal flow. The limitation, however, is that the coupling of the aerodynamic quantities with tissue motion is not interactive. That is, that the intra-glottal pressure and glottal flow do not affect the characteristics of tissue vibration in the kinematic model. In addition, the glottal jet formed at the point of flow detachment within the glottis is not modeled in such a way that captures the Coanda effect or generation of vortices that impose different pressures on left versus right vocal folds (cf. Drechsel & Thomson, 2008; Erath & Plesniak, 2006; Khosla, Muruguppan, Gutmark, & Scherer, 2007). The complexities of fluid and fluid–structure interactions also affect the characteristics of the turbulence and associated noiselike sound that is generated within the glottis (Zhang, Mongeau, Frankel, Thomson, & Park, 2004). Thus, the simple noise generator based on calculated Re used with the kinematic model may not capture the true character of the noiselike component of the acoustic signal associated with asymmetric vibration. Nonetheless, the computational complexity of true fluid–structure models is daunting when the goal is to generate sound samples on the basis of a large number of parametric variations for use in both acoustic analysis and perceptual experiments.

It must also be noted that these individual asymmetries do not typically occur in humans. The kinematic model was used to assess the individual effects of phenomena that typically occur in combination. Further interpretation of the findings, therefore, will occur only after combinations of these parameters are assessed.

Another benefit of the kinematic model is that effects of laryngeal structure and movement can be studied without reference to the underlying physiology; that is, physiology cannot be inferred from the kinematics. Several different etiological factors can lead to each of the movement patterns studied, and care must be taken not to attribute any particular study parameter to a physiological etiology. There are certainly many asymmetries that are part of voice disorders, and only five were examined in the current study.

The perceptual study shared the limitations inherent to such work. The measurement task was selected to balance listener ease, reliability, and information. A different scale might provide the benefits of a ratio scale or improve exact listener agreement (cf. Kreiman, Gerratt, & Ito, 2007; Kempster, Gerratt, Verdolini Abbott, Barkmeier-Kraemer, & Hillman, 2009; Patel et al., 2010). It is also possible that a new perceptual study with finer gradations of the parameters used for the current set of simulations, and no other stimuli. would yield more robust perceptual results.

Conclusions and Future Directions

Though vocal function measures and perceived voice quality were driven primarily by the distance between the vocal processes during phonation, asymmetries of edge contour (left “bulging” value) and nodal point ratio also caused deterioration of measured and perceived vocal function. In this highly controlled situation in which all other features were fully symmetric, neither eliminating vibratory amplitude unilaterally nor starting phase difference produced substantial changes in vocal function or voice quality. To better understand the relation of these five asymmetries to voice qualities in disordered populations, future work could assess each of the asymmetric parameters in the context of additional asymmetries.