Abstract
Many symptoms of nerve damage arise from ectopic spiking caused by hyperexcitability. Ectopic spiking can originate at the site of axonal damage and elsewhere within affected neurons. This raises the question of whether localized damage elicits cell-wide changes in excitability and/or if localized changes in excitability can drive abnormal spiking at remote locations. Computer modeling revealed an example of the latter involving afterdischarge (AD) – stimulus-evoked spiking that outlasts stimulation. We found that AD originating in a hyperexcitable region of axon could shift to the soma where it was maintained. This repositioning of ectopic spike initiation was independent of distance between the two sites but relied on the rate and number of ectopic spikes originating from the first site. Nonlinear dynamical analysis of a reduced model demonstrated that properties which rendered the axonal site prone to initiating AD discouraged it from maintaining AD, whereas the soma had the inverse properties thus enabling the two sites to interact cooperatively. A first phase of AD originating in the axon could, by providing sufficient drive to trigger somatic AD, give way to a second phase of AD originating in the soma such that spiking continued when axonal AD failed. Ectopic spikes originating from the soma during phase 2 AD propagated successfully through the defunct site of axonal spike initiation. This novel mechanism whereby ectopic spiking at one site facilitates ectopic spiking at another site is likely to contribute to the chronification of hyperexcitability in conditions such as neuropathic pain.
Keywords: Demyelination, Neuropathic pain, Afterdischarge, Chronification, Hyperexcitability, Ectopic spiking
1 Introduction
Axons conduct action potentials, or spikes, from their site of origin to the output synapses of the neuron. Axonal damage, whether by trauma, toxicity, or disease (including demyelination diseases such as multiple sclerosis), can interfere with conduction. This can explain loss of function but, paradoxically, axonal damage also tends to cause hyperexcitability, one manifestation of which is ectopic spike initiation at the site of damage, which we will refer to as the neuroma, and elsewhere in the affected neuron (Amir et al. 2005; Baron 2006; Gold and Flake 2005; Gold and Gebhart 2010; Wall and Gutnick 1974). Increased excitability likely reflects an imperfect compensatory process intended to help restore conduction, but the end result is a mixture of negative and positive symptoms. Adding to the clinical challenge, drugs that reduce positive symptoms tend to exacerbate negative ones (Bowe et al. 1987; Sakurai and Kanazawa 1999). Positive symptoms can be spontaneous or stimulus-evoked, and brief or sustained (Ostermann and Westerberg 1975; Twomey and Espir 1980).
The connection between positive symptoms and cellular hyperexcitability is clearest in the case of peripheral nerve damage where neurons are not synaptically interconnected, thus excluding network contributions. Afterdischarge (AD) – spiking that outlasts the inciting stimulus – may comprise either a brief but intense burst or more prolonged spiking. Brief AD in trigeminal afferents likely underlies paroxysmal symptoms such as the extreme shooting pains experienced by patients with trigeminal neuralgia (Calvin et al. 1977; Devor et al. 2002; Hooge and Redekop 1995). Prolonged AD in somatosensory afferents contributes to other forms of neuropathic pain (Howe et al. 1977); indeed, ectopic spiking maintained in primary afferent somata in the dorsal root ganglia is a leading candidate mechanism for phantom limb pain (Vaso et al. 2014). The distinction between symptoms caused by prolonged AD and spontaneous spiking blurs if the AD trigger is subtle and recurring (Bennett 2012).
Spontaneous and AD spikes are known to originate ectopically in the neuroma and at or near the soma of affected neurons (Amir et al. 2005; Ma and LaMotte 2007; Wall and Devor 1983; Wall and Gutnick 1974), indicating that multiple sites of ectopic spike initiation co-develop after nerve injury. In primary afferents, the soma is spatially remote from the normal site of spike initiation in the peripheral axonal endings. Experiments have shown that additional spikes originating in the soma can be triggered by spikes originating in the axon (Amir et al. 2005), but sites of ectopic spiking have otherwise been assumed to act autonomously. Deciphering the underlying mechanisms and treating the resulting neurological symptoms has proven exceedingly difficult. With the insights and guidance of a computational model, we take aim at elucidating mechanisms that are difficult to observe directly in the clinic or laboratory.
We hypothesized that the two sites of ectopic spiking may interact in a complex manner, competing and/or cooperating with one another to control the output spiking of the affected neuron. Through computational modeling, we found that remote sites of ectopic discharge can interact cooperatively such that AD is initiated at one site (neuroma) but maintained at another site (soma). When both sites can initiate spikes, the faster of the two (i.e. the one with a higher intrinsic spike rate) serves as pacemaker. Spike initiation can shift to the other site if and when spike initiation at the first site stops or slows down. A combination of cooperativity and competition thus explains the transition from brief to prolonged AD and the abrupt repositioning of ectopic spike initiation.
2 Methods
The methodological basis of our work is a tandem of computational models. The first is a multicompartmental Hodgkin-Huxley (HH) model comprised of a soma, axon hillock, initial segment, and a long myelinated axon. The second is a modified Morris-Lecar (ML) model comprised of two compartments that were artificially coupled in different ways in order to test various hypotheses. Because of its simplicity, the ML model is amenable to nonlinear dynamical analysis and also helps establish the minimum necessary and sufficient elements required to explain phenomena observed in the more biologically realistic HH model. Code for all models will be made available through ModelDB and at http://prescottlab.ca.
2.1 Multicompartment HH model
Our HH model (previously described in (Coggan et al. 2010, 2011) included a soma (15 µm), axon hillock (8 µm, with 4:1 mm taper), initial segment (10 µm), and a linear set of 80 pairs of myelinated internodes (200 µm each) and nodes of Ranvier (1 µm each). Results were not qualitatively altered by including a T-junction and central axon branch to the end of the initial segment so as to more accurately capture primary afferent morphology. A hyperexcitable, 10 µm-long unmyelinated region referred to as the “neuroma” was inserted at the midpoint of the axon (Coggan et al. 2010, 2011). Axon diameter throughout was 1 µm unless otherwise stated. Hodgkin-Huxley style voltage-gated Kv3.1 channels (Wang et al. 1998), Nav1.6 channels, persistent sodium conductance gNaP (McIntyre et al. 2002), and leak conductance gL were located in all compartments except the internodes. The internodes nonetheless allowed for the longitudinal spread of both ions and current. Parameter values, ion densities and distributions (soma: gNa = 80, gK = 790, gL = 3, gNaP= 0.19; node or neuroma: gNa = 1500, gK = 1600, gL = 70, gNaP = 1.9, all in mS/cm2) were the same as previously reported (Coggan et al. 2010), except when otherwise indicated.
Intracellular concentrations of Na+ and K+ were updated at every time step based on transmembrane current, intracellular diffusion, and an exponential return to a baseline concentration. The extracellular space was modeled as a Frankenhaueser space in NEURON and extracellular concentrations were similarly updated. Reversal potentials were continuously updated according to the Nernst equation. No pumps or other ion exchange mechanisms were included in the current model. By simplifying the ion handling process (i.e. recovering from activity-dependent ion flux as a simple exponential decay process) we minimized introduction of slow timescales which, while interesting and biologically relevant (N. Yu et al. 2012), would have confounded our analysis. One or more “evoked” spikes were triggered by injecting a square current pulse (10 pA, 0.5 ms) into the soma or axon terminal. All simulations were conducted in NEURON using a 10 µs time step (Carnevale and Hines 2009).
The persistent Na current in our model (adapted from McIntyre et al., . 2002; see Coggan et al. 2010, 2011 for details) is described by the following equations.
| (1) |
| (2) |
| (3) |
| (4) |
Parameters had the following base values: for αP, Aα=0.01, Bα=27 mV and Cα = 10.2 mV; and for βP, Aβ=0.000251, Bβ=34 mV and Cβ = 10 mV. For simulations testing the range of A, B, or C that support cooperative AD, one parameter was varied while all others were held at their base values (see Table 1).
Table 1.
Range of gNaP activation parameters giving AD (see equations 3 and 4). One parameter was varied while all others were held at their base values.
| Coeff. “Aα” | Coeff. “Bα” | Coeff. “Cα” | ||
| αP | Range supporting AD | 0.008 – 0.02 | 25 – 31 | 9 – 11 |
| Base value | .01 | 27 | 10.2 | |
| Coeff. “Aβ” | Coeff. “Bβ” | Coeff. “Cβ” | ||
| βP | Range supporting AD | 0.00017–0.0003 | 28 – 42 | −1 – 18 |
| Base value | 0.00025 | 34 | 10 |
2.2 Two-compartment ML model
The ML model was the same as described by us previously (Coggan et al. 2011; Prescott et al. 2008) except that two compartments, one representing the soma and the other representing a hyperexcitable region of axon, or neuroma, were coupled such that if one compartment spiked, the other was forced to spike via brief (0.01 ms) activation of a strong sodium conductance (120 mS/cm2). This coupling was turned on or off as indicated in the text. Within each compartment, variables evolved according to:
| (5) |
| (6) |
| (7) |
| (8) |
| (9) |
where V is voltage and w and z are variables controlling time- and voltage-dependent activation of gK and gNaP, respectively; gNa activates instantaneously and m was therefore always at steady state. In equations 5 and 6, x corresponds to m, w, or z. The following parameters were used in all simulations: C = 2 µF/cm2, EL = −70 mV, Ek = −100 mV, βm = −1.2 mV, γm = 18 mV, βw = −10 mV, γw = 10 mV, τw = 0.15, βz = −45 mV, γz = 10 mV, τz = 0.05, delayed rectifier potassium conductance gK = 20 mS/cm2 , leak conductance gL = 2 mS/cm2, and fast sodium conductance gNa =20 mS/cm2. The slow-inactivating persistent sodium conductance gNaP was 0.8 mS/cm2 in the soma and 1.1 mS/cm2 in the axon.
Changes in intracellular sodium [Na+]i were calculated independently in each compartment according to
| (10) |
This describes intracellular sodium accumulation on the basis of influx through fast and persistent Na channels and assumes exponential decay towards a steady-state value of 17.5 mM with a time constant τNa = 100 ms. The surface area-to-volume ratio is defined by SAV = s/10r, where s=2 for a cylindrical axon with no ends and s=3 for a spherical soma. The radius r was 0.5 µm for the axon and 7.5 µm for the soma. F is the Faraday constant 96,485 C/mol. ENa was continuously updated according to the Nernst equation, ENa = 25 ln ([Na+]o/[Na+]i) where extracellular sodium concentration [Na+]o was assumed constant at 138 mM.
One or more “evoked” spikes were triggered in one or the other compartment by instantaneously resetting V to 0 mV and then letting the system evolve freely. Equations were numerically integrated in XPP (Gutkin et al. 2003) using the Euler method with a 0.01 ms time step. Bifurcation analysis was conducted in AUTO using the XPP interface. For the analysis, [Na+]i was converted from a variable to a parameter that was systematically varied over a broad range.
3 Results
3.1 Multiple sites of ectopic spike initiation in a multicompartment model
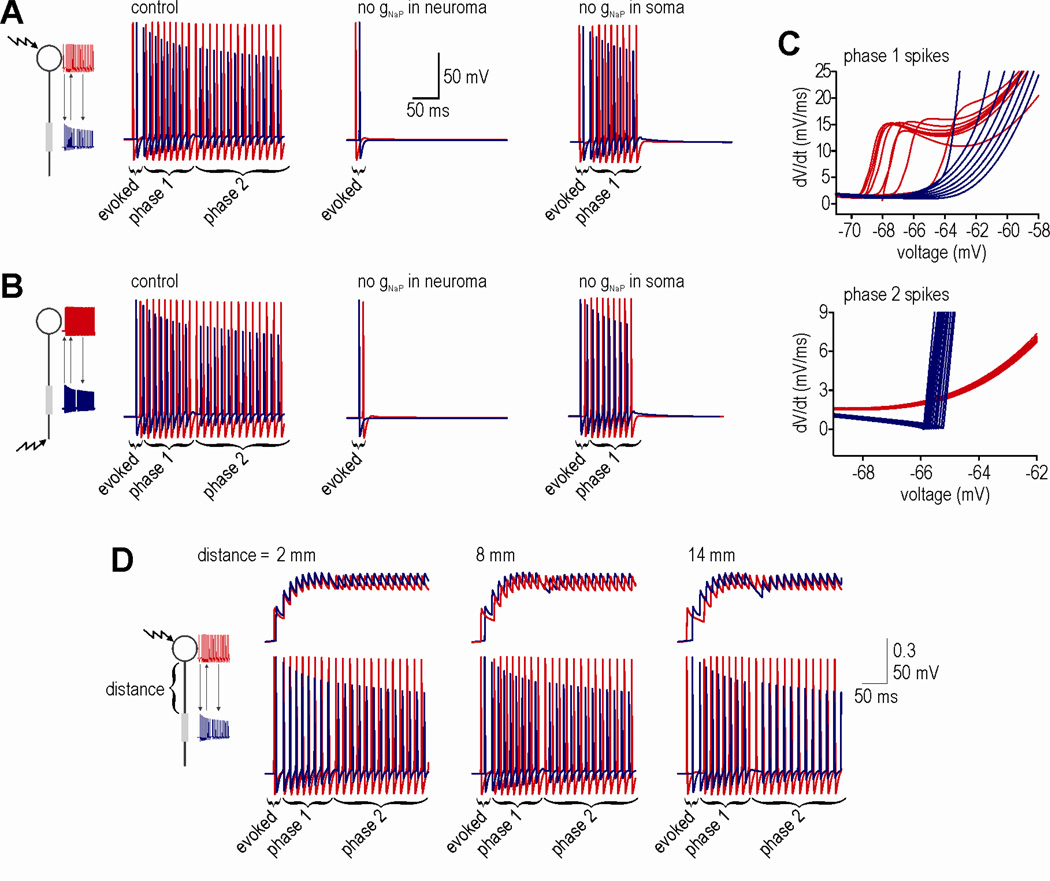
In central neurons, synaptically-evoked spikes originate near the soma; in peripheral sensory neurons, on the other hand, stimulus-evoked spikes originate in the axon terminals. To test both conditions, we evoked a single spike by brief stimulation in the soma (Fig. 1A) or axon terminal (Fig. 1B) of our multicompartment model (see Methods). Evoked spikes originating in either site elicited AD when the ratio of gNa/gL was adjusted to a high enough level in a hyperexcitable region of demyelinated axon (Coggan et al. 2010). That region is henceforth referred to as the “neuroma”. The relative timing of spikes measured from the neuroma and soma suggested that the first few AD spikes originated in the neuroma whereas later ones originated in or near the soma. This was verified by looking, in each location, at the kinkiness of the voltage deflection near spike threshold (Fig. 1C) since locally initiated spikes are associated with smoothly accelerating depolarization whereas spikes propagating from a remote site are associated with abruptly accelerating depolarization (Popovic et al. 2011; Y. Yu et al. 2008). We refer to the first spikes originating at the neuroma as “phase 1 AD” and to later spikes originating at the soma as “phase 2 AD”.
Figure 1.
Multi-phase AD in an HH model. Cartoons depict model with the site of stimulation indicated by a jagged arrow. Direction of spike propagation (indicated by arrow) is inferred from the relative timing of spikes recorded in the soma (red) and neuroma (blue). (A) Somatic stimulation initiated a first phase of AD whose spikes originate in the neuroma and a second phase of AD whose spikes originate in the soma. Removing gNaP from the neuroma (1.9 mS/cm2) prevented both phases of AD whereas removing gNaP from the soma (0.19 mS/cm2) blocked only phase 2 AD. (B) Stimulating the distal end of the axon triggered the same spiking patterns as in A. (C) Phase planes demonstrate the kinkiness of the voltage trajectory near spike threshold: locally initiated spikes exhibit a smoothly accelerating voltage trajectory whereas propagated spikes exhibit a more abruptly accelerating voltage trajectory. This analysis confirms that phase 1 AD spikes originate in the neuroma whereas phase 2 AD spikes originate in the soma. (D) Similar phase 1 and 2 AD patterns were elicited independently of the distance between sites. Top traces show relative activation of gNaP.
Initiation of AD depends on positive feedback activation of an inward current such as that mediated by the persistent sodium conductance gNaP. Hence, we predicted (i) that removing gNaP from the neuroma would prevent phase 1 AD and (ii) that removing gNaP from the soma would prevent phase 2 AD. Our second prediction was correct (Fig 1A and B, right panels) and those data also demonstrate that phase 1 AD is self-limited insofar as it terminates regardless of the onset of phase 2 AD. Our first prediction was only partially correct insofar as removing gNaP from the neuroma prevented both phase 1 and phase 2 AD (Fig. 1A and B, middle panels). This last observation suggests that phase 1 AD is necessary for the initiation of phase 2 AD. To test if this dependency relied on the passive spread of current between the two sites of ectopic spike initiation, we varied the distance between those sites. Absence of an effect of inter-site distance (Fig. 1D) suggests, instead, that active propagation of spikes between the two sites is the basis for their interaction. Indeed, based on responses to hyperpolarization, the length constant of the axon was ~200 µm, which argues that actively propagated spikes (rather than passively spreading current) are the only way remote sites of ectopic spike generation communicate with each other.
3.2 Differential requirement for initiating phase 1 and 2 AD
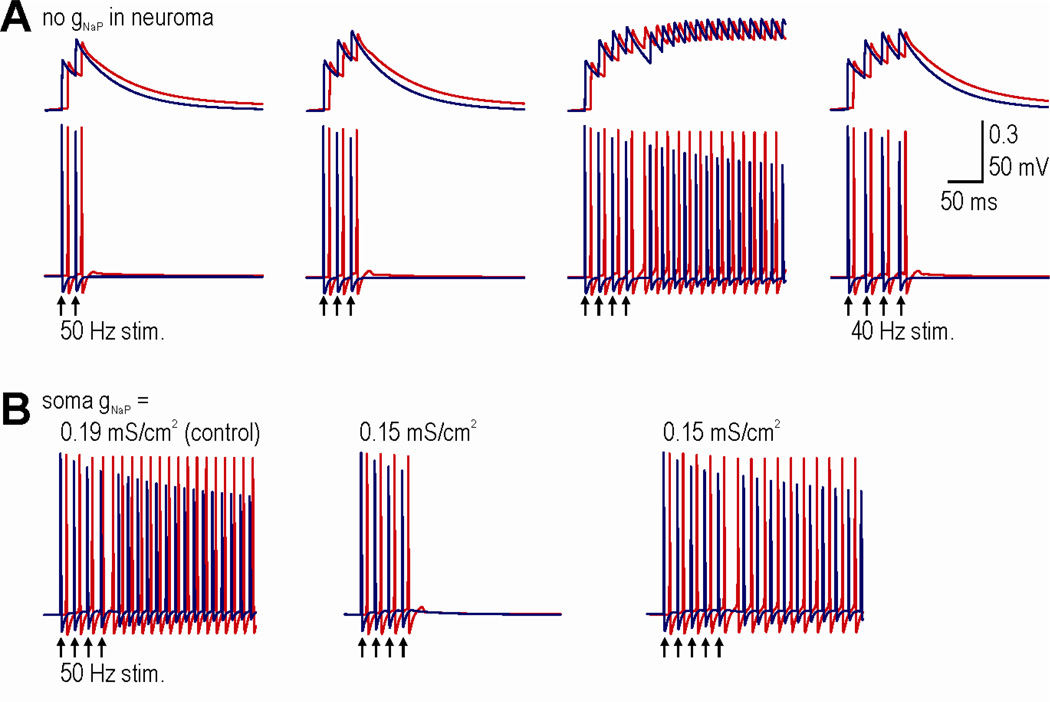
Next, we asked if and how phase 2 AD could be initiated in the absence of phase 1 AD. We hypothesized that phase 2 AD had a higher threshold for initiation (e.g. required greater cumulative activation of gNaP) and, therefore, that it could be initiated by the high-frequency spiking that comprises phase 1 AD whereas it would not be initiated by a single evoked spike. To test this hypothesis, we removed gNaP from the neuroma to prevent phase 1 AD and evoked different numbers of spikes at different frequencies to determine the minimal trigger required to initiate phase 2 AD. As few as four evoked spikes applied at 50 Hz could initiate phase 2 AD, although more spikes were needed as the stimulus frequency was reduced (Fig. 2A). By comparison, phase 1 AD could be initiated by as few as one evoked spike (see Fig. 1). The precise trigger requirements for phase 2 AD depended on the value of gNaP in the soma (Fig. 2B) and indeed the same relationship applies to phase 1 AD trigger requirements and gNaP in the neuroma (Coggan et al. 2010).
Figure 2.
Requirements from triggering phase 2 AD in the absence of phase 1 AD. Bottom traces show voltage recorded from the soma (red) and neuroma (blue) and top traces show corresponding activation of gNaP(A) For stimulation at 50 Hz, a total of four stimuli were needed to trigger AD originating in the soma. The same number of stimuli delivered at 40 Hz was unsuccessful, indicating that both the rate and number of evoked spikes are key. Notably, four spikes at 50 Hz is a weaker trigger than that provided by phase 1 AD spikes (cf. Fig 1). (B) Somatic AD required a more intense trigger when gNaP was reduced.
The above data indicate that phase 1 AD, with its more lenient trigger requirements, can be initiated by fewer evoked spikes than phase 2 AD. A second key observation is that phase 1 AD comprises several spikes at high frequency – eight spikes at ~100 Hz in the example shown in Figure 1 – which is more than enough to trigger phase 2 AD. Putting these observations together, we inferred that phase 1 AD is necessary to trigger phase 2 AD when there are too few evoked spikes because phase 1 AD converts the insufficient number of stimulus-evoked spikes into a barrage of high-frequency spikes that satisfies the stricter phase 2 AD trigger requirements.
3.3 Transition between phase 1 and 2 AD
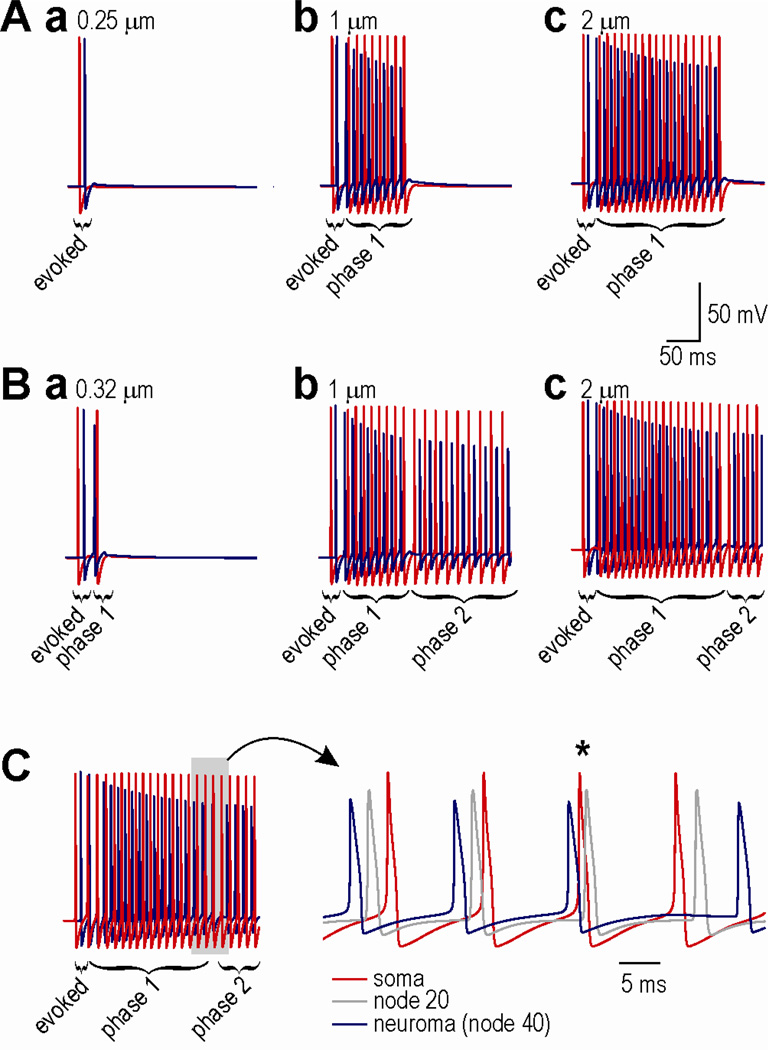
We have shown previously that AD will terminate, despite sustained activation of gNaP, if the driving force associated with that conductance decreases due, for example, to intracellular accumulation of sodium and the consequent shift in sodium reversal potential (Coggan et al. 2011). The rate of intracellular sodium accumulation depends on the surface area-to-volume ratio such that an axon with smaller diameter experiences faster sodium accumulation than one with larger diameter (assuming all other factors are equivalent), which translates into shorter or longer lasting AD, respectively (Fig. 3A). Bearing in mind that one evoked spike is sufficient to initiate phase 1 AD based on the neuroma gNaP value used for these simulations, the results in the left panel of Fig 3A are noteworthy in showing that AD can effectively fail without (before) ever being manifest (i.e. without ever giving rise to an ectopic spike).
Figure 3.
Transition from phase 1 to phase 2 AD. (A) Increased axon diameter results in longer lasting AD. To isolate phase 1 AD, phase 2 AD was prevented by removing gNaP from the soma for these simulations. Note that since a single evoked spike is sufficient to trigger phase 1 AD based on the neuroma gNaP of 1.9 mS/cm2, absence of phase 1 AD in the left panel indicates that AD fails without becoming manifest, which is mechanistically distinct from AD not being triggered. (B) Triggering of Phase 2 AD depends on number of spikes comprising phase 1 AD. For these simulations, gNaP was re-inserted in the soma (0.19 mS/cm2). Panel a shows failure to trigger phase 2 AD. Panels b and c show that phase 1 AD comprises the same number of spikes regardless of whether it is followed by phase 2 AD (cf corresponding panels in A), indicating that phase 2 AD starts only after phase 1 AD ends. (C) When somatic gNaP was increased to 0.28 mS/cm2, a spike (marked by *) originated in the soma before the end of phase 1 AD, as evidenced by the somatic spike preceding the propagated spike recorded at the node midway between the soma and neuroma. This example nicely illustrates how two sites, each capable of initiating spikes, compete to serve as pacemaker for the neuron.
Simulations in Fig. 3A were conducted with gNaP removed from the soma in order to characterize the duration of phase 1 AD in isolation from phase 2 AD. To investigate the transition between phase 1 and 2 AD in Fig. 3B, somatic gNaP was returned to its standard value. According to these data, phase 2 AD failed to be initiated if phase 1 AD comprised too few spikes (Fig. 3Ba). For larger axon diameters (Fig. 3Bb–c), phase 2 AD spiking started after the termination of phase 1 AD as evident from the observation that phase 1 AD comprises the same number of spikes whether or not it is followed by phase 2 AD. Recall that simulations in Fig. 2 demonstrated that phase 2 AD spikes could have started earlier, i.e. after fewer triggering phase 1 AD spikes, which indicates that the soma reaches its AD attractor state earlier than phase 2 AD spiking actually begins. The reason the soma does not start initiating spikes until after the neuroma stops initiating spikes is simply because the intrinsic rate of spike initiation is faster in the neuroma; therefore, when the two sites are coupled, the slower of the two sites receives propagated spikes faster than it can initiate its own spikes. In other words, when two sites are capable of producing AD, the faster of the two eventually serves as the pacemaker. We say that the faster site eventually becomes the pacemaker because, if the intrinsic rate of somatic spike initiation is increased by slightly increasing somatic gNaP, a different transition is observable: as the intrinsic rate of spike initiation in the neuroma slows, the soma can initiate a spike before receiving a propagated spike (Fig. 3C).
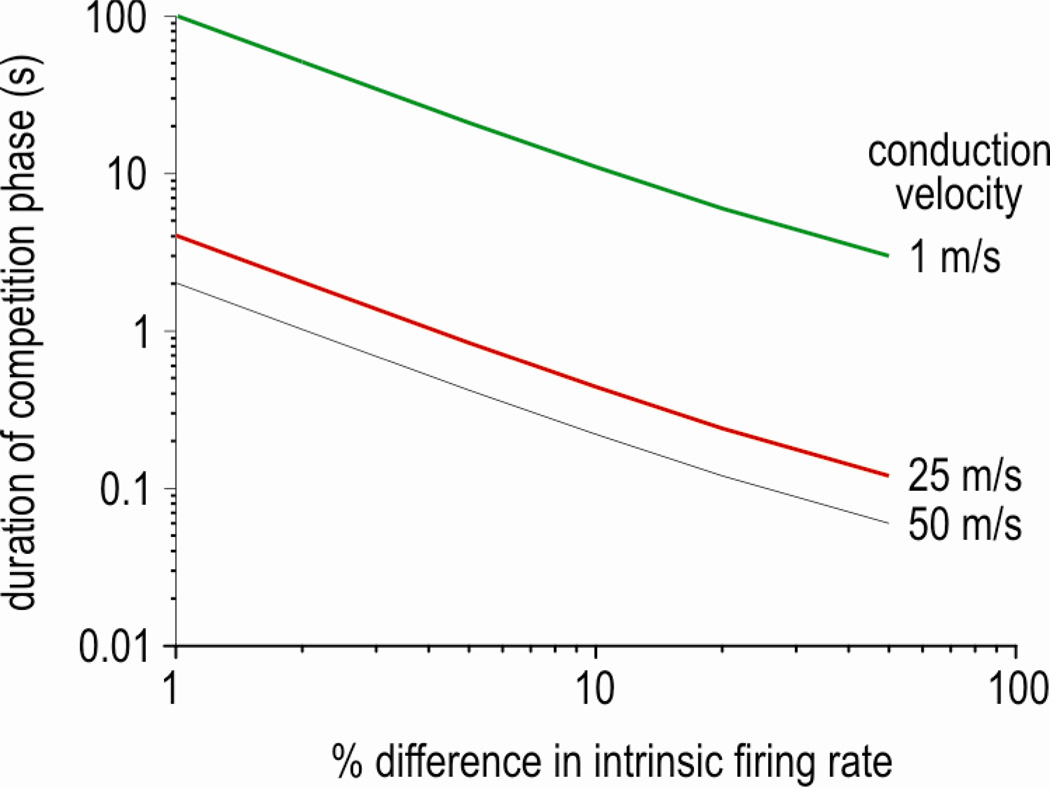
Under these last conditions, spikes initiated at each site collide in the intervening axon. Over time, the point of collision moves closer to the slower spike initiation site until a spike arrives from the faster site before a spike can be initiated at the slower site, meaning the faster site begins to pace the slower site. The longer the distance between the two sites and/or the slower the axonal conduction velocity, the longer it will take (i.e. more spikes will collide) before the faster spike initiation site starts pacing the slower site. Figure 4 shows how long it takes for the collision to shift from the faster ectopic discharge site to the slower site, assuming a separation of 1 m. The required time evidently depends on the conduction velocity and the difference between intrinsic firing rates, and could be quite protracted for slow-conducting C fibers but only if the difference in intrinsic firing rates remains small. If the faster site speeds up and/or the slower site slows down (or altogether stops initiating spikes), the competition will be abbreviated. Furthermore, the closer the two ectopic discharge sites are, the shorter the competition.
Figure 4.
Time required for collision to shift from faster to slower ectopic discharge site (i.e. duration of competition phase). The difference in interspike intervals (ISIs) for spikes originating at each site represents the extra time the spike from the faster site has to travel towards the slower site; the collision shifts by the distance traveled during that extra time. Dividing the total distance by the shift per ISI reveals the number of ISIs needed for the collision to shift the total distance between ectopic discharge sites. Calculations are based on 1 m separation between the ectopic discharge sites and were repeated for conduction velocities typical of C fibers (green), A-δ fibers (red), and A-β fibers (black).
Two observations are critical. First, although spikes are no longer initiated in the neuroma after termination of phase 1 AD, spikes initiated elsewhere can nonetheless propagate through the neuroma. In other words, an inability to continue initiating spikes at a certain site does not equate with an inability to propagate spikes through that site. Second, whereas phase 1 AD eventually fails because of the relatively large surface area-to-volume ratio characteristic of the axonal compartment, phase 2 AD can continue for much longer because of the smaller surface area-to-volume ratio of the somatic compartment. Although active pumping by the Na-K pump was not explicitly modeled here, it is very likely that energy supplies are more limited within the axon than in the soma, especially if/when dysfunction of axonal mitochondria is a contributing pathogenic factor (Flatters and Bennett 2006; Janes et al. 2013), which would exacerbate ion concentration changes. It has been shown that spike-evoked Na influx is similar between soma and axon and that Na clearance from the site of influx is largely due to diffusion rather than pumping (Fleidervish et al. 2010), although pumping presumably becomes more important at longer timescales, especially in the context of sustained, high-frequency spiking. One should also appreciate that even if phase 1 AD never failed, a second site of ectopic spike initiation could exist occultly within the neuron. Although a second discharge site may seem inconsequential, it could make pathological spiking more robust by sustaining AD if ectopic spike initiation at the first site was therapeutically blocked.
We tested the robustness of gNaP mediated cooperative AD by varying the three parameters controlling its activation (see Methods). In this way, we asked whether only a specific and narrow range of gNaP mediated cooperative AD or whether it was a property that was retained over a range of possible gNaP channels. We found that variation of each of the 3 parameters (A, B, and C; see equations 3 and 4 in Methodology) could support AD over a range of 1 to 3 orders of magnitude (Table 1). These results demonstrate that a wide range of gNaP channels would be able to support the cooperative AD we observe in our model.
To summarize, transient phase 1 AD is not strictly necessary to trigger prolonged phase 2 AD, but the former facilitates triggering of the latter by amplifying a small stimulus-evoked trigger. By receiving a strong trigger that would not occur on the basis of stimulation alone, AD can be initiated in a region of the cell that would not manifest ectopic discharge were it not for the other ectopic discharge site. As an aside, the absolute number of required trigger spikes is less important than the relative number: phase 1 AD may require 10 or 100 high-frequency spikes and the mechanism will function so long as phase 2 AD requires >10 or >100 spikes. But in that respect, the properties of the cellular region in which phase 2 AD originates must have properties distinct from those of the cellular region in which phase 1 AD originates; for example, phase 2 AD must not fail at the same rate as phase 1 AD fails otherwise phase 2 AD would not become manifest when phase 1 AD eventually terminates. This explains why phase 2 AD originates in the soma rather than in another part of the axon outside the neuroma, which is consistent with experimental observations implicating the soma (Amir et al. 2005; Ma and LaMotte 2007; Wall and Devor 1983) despite the soma being one of the least excitable cellular regions. The mechanism elucidated here thus represents a form of cooperativity between subcellular compartments that, to the best of our knowledge, has not been previously described.
3.4 Dynamical analysis of coopertivity in a reduced model
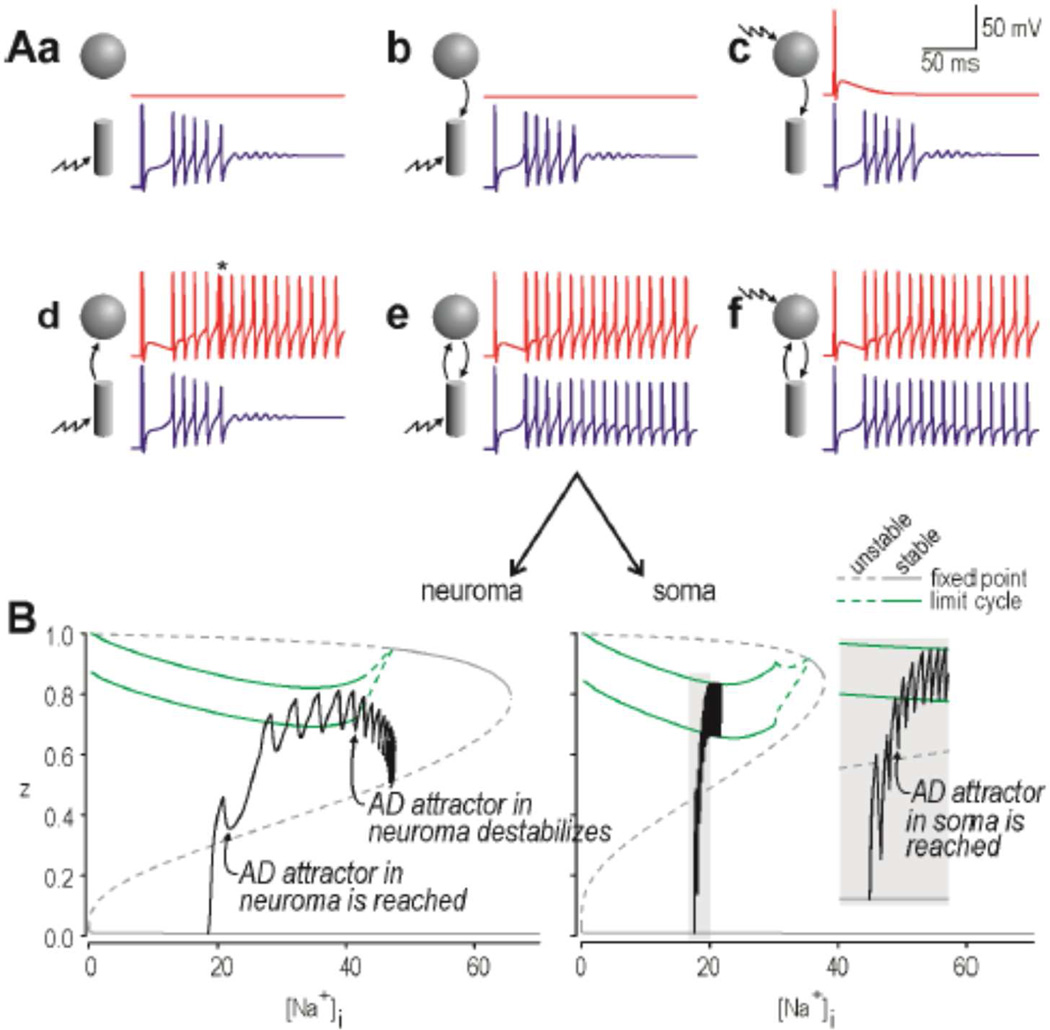
To further investigate subcellular cooperativity, we constructed a Morris-Lecar (ML) model comprising two compartments that were connected such that spikes could pass in one or both directions. Furthermore, the excitability of each compartment was modeled in a manner simple enough that bifurcation analysis could be undertaken. First, we tested whether results from the ML model corroborated those from the HH model. Sample responses following a single spike evoked in either the soma or neuroma confirmed that the ML model behaves similarly to the HH model when different compartment connectivity patterns (curved arrows) and sites of stimulation (jagged arrow) were tested (Figure 5A, panels a–f). A single evoked spike in the axon was sufficient to evoke AD in the neuroma (a, b). A unidirectional soma→neuroma connection allowed a spike evoked in the soma to trigger AD in the neuroma, but that single evoked spike was insufficient to evoke AD in the soma (c). However, a unidirectional neuroma→soma connection allowed phase 1 AD to relay spikes to the soma, eventually triggering phase 2 AD (d). When the connection was made bidirectional, spikes comprising phase 2 AD propagated to the neuroma after phase 1 AD terminated, resulting in continuous spiking in both compartments (e, f). The bidirectional connectivity in e and f most closely approximates real neurons and our multicompartment model.
Figure 5.
Cooperativity in a two-compartment ML model. (A) Panels a-f represent different compartment connectivity patterns (curved arrows) and site of stimulation (jagged arrow). A single evoked spike in the neuroma is sufficient to evoke AD in the neuroma (a, b). A unidirectional soma→neuroma connection allows a spike evoked in the soma to trigger AD in the neuroma, but that single evoked spike is insufficient to evoke AD in the soma (c). However, a unidirectional neuroma→soma connection allows phase 1 AD (originating in the neuroma) to relay spikes to the soma, eventually triggering phase 2 AD in the soma (d). If the connection is bidirectional, phase 2 AD spikes will propagate to the neuroma after phase 1 AD ends (e,f). Spike marked with a star in d is propagated to the soma because the unidirectional connectivity allows one last spike to be initiated in the neuroma; with bidirectional connectivity, the spike initiated earlier in the soma propagates to the neuroma and replaces the locally initiated spike. This illustrates how the sites compete to control spike initiation. (B) Bifurcation diagrams onto which the sample response from panel Ae is projected in order to illustrate the basis for initiation and termination of phase 1 and 2 AD. Bifurcation diagrams for the neuroma (left) and soma (right) were produced by converting intracellular sodium concentration [Na+]i to a parameter whose value was systematically varied. Phase 1 AD starts when the evoked spike causes z, which controls activation of gNaP, to cross and remain above a threshold represented by the central dashed curve. Once threshold is crossed, the system converges on the stable limit cycle that represents the AD attractor state. Unlike phase 1 AD, which is initiated by a single evoked spike, phase 2 AD requires three triggering spike (i.e. the initial evoked spike plus at two spikes from phase 1 AD). In the neuroma, [Na+]i continues to increase, eventually forcing the system beyond the upper border of the stable limit cycle, at which point phase 1 AD stops. In contrast, [Na+]i does not continue to increase in the soma, thus allowing the system to remain within the borders of the stable limit cycle, meaning phase 2 AD can continue indefinitely under these conditions.
Comparison of panels d and e (or f) reveals the competition that occurs when both compartments become capable of initiating spikes. Specifically, in panel d, the sixth spike is initiated in the soma shortly before a sixth spike is initiated independently in the neuroma. The sixth spike is allowed to initiate in the neuroma because of the absence of a soma→neuroma connection. In the presence of such a connection (panels e and f), the somatically initiated spike propagates to the neuroma before a locally initiated spike can occur there, thus preventing local spike initiation.
Bifurcation diagrams illustrate the basis for initiation and termination of phase 1 and 2 AD (Fig. 5B). Bifurcation diagrams for the neuroma (left) and soma (right) were produced by converting [Na+]i to a parameter whose value was systematically varied. The change in [Na+]i (based on the full model shown in Fig. 2A in which [Na+]i is treated as a variable) and the change in z (which controls the activation of gNaP) are plotted relative to one another and overlaid on the bifurcation diagrams. Phase 1 AD starts when the evoked spike causes z to cross and remain above a threshold, represented here by the central dotted lines. Once the threshold is crossed, the system converges onto a stable limit cycle attractor, and thus spikes repetitively. Unlike phase 1 AD, which is initiated by a single evoked spike, phase 2 AD requires three triggering spikes (i.e. the initial evoked spike plus at two spikes from phase 1 AD). In the neuroma, [Na+]i continues to increase, eventually forcing the system beyond the range of the stable limit cycle attractor, at which time phase 1 AD stops. In contrast, [Na+]i does not continue to increase in the soma, thus allowing the system to remain within the bounds of the stable limit cycle attractor, meaning phase 2 AD can continue indefinitely under these conditions.
Results from the ML model thus fully corroborated results from the HH model. By virtue of its simplicity, the ML model demonstrates that exchange of spikes is sufficient to mediate the cooperative interaction; realistic connectivity would involve conduction delays between the two compartments but we did not implement this in our ML model because it and related phenomena like spike collisions are already accounted for in our multicompartment HH model. Analysis of the ML model reveals that each ectopic discharge site has an attractor state that underlies AD, but the threshold for reaching that attractor and the stability of the attractor differs between the sites. Because of those differences, the two sites cooperate in the initiation and maintenance of AD. The site that initiates spikes at a higher rate becomes the pacemaker for the neuron.
4 Discussion
Results of this study suggest that having more than one site of ectopic discharge enables patterns of abnormal spiking that could not occur on the basis of one ectopic discharge site operating alone. Specifically, we have shown that the most hyperexcitable site (i.e. with the lowest threshold for initiating AD) may amplify a stimulus-evoked input such that a less excitable site receives a sufficient trigger. The second site maintains AD if/when the first site fails. In other words, and by analogy to running, a site whose excitability is initially high but rapidly reduced (akin to a sprinter) initiates AD but AD is sustained by a second site whose excitability is lower but more stable (akin to a marathon runner). By having distinct properties that encourage either the initiation or maintenance of AD, the two sites are able to cooperate. This cooperativity could profoundly exacerbate the functional consequences of otherwise modest injury-induced changes in membrane excitability.
The current study is novel insofar as it moves beyond looking at how hyperexcitability develops locally to consider how features of pathological spiking may arise through broader spatial mechanisms. Indeed, past experimental studies have determined that multiple sites of ectopic discharge co-develop in primary afferent neurons after nerve injury (see Introduction) but it has remained unclear if and how those sites interact. The current study demonstrates that sites of ectopic discharge interact nonlinearly, and that they can do so on the basis of spikes, thus enabling remote sites – much further apart than the membrane length constant – to interact. There has been much recent debate about molecular cooperativity, e.g. physical interaction between ion channels (McCormick et al. 2007; Naundorf et al. 2006), and there are other examples of local cooperativity in processes such as transmitter release (Sun et al. 2007), but our example of remote, spike-based cooperativity is distinct. To the best of our knowledge, examples of AD in the central nervous system have not implicated such a mechanism (Egorov et al. 2002; Fransén et al. 2006; Sheffield et al. 2011; Zhang and Séguéla 2010) although some data in peripheral neurons are suggestive (Amir et al. 2005). Spike-based cooperativity has been described at the network level (Selverston et al. 2009) and ephaptic interactions between injured axons have been observed (M. Devor and Wall 1990; Lisney and Devor 1987), but the current study emphasizes remote interactions within a neuron rather than between neurons.
Inter-site interactions can be deconstructed based on the sequence in which the neuroma and soma enter and exit their respective AD attractor states. The site of ectopic discharge with the lowest threshold (i.e. requiring the fewest stimulus-evoked spikes) naturally enters its AD attractor state first. Upon reaching this attractor, it generates a stimulus-independent barrage of spikes that enables the second site of ectopic discharge to reach its attractor. Once both sites have reached their AD attractor states, they compete to determine which one will control neuronal spiking. If a spike propagates to a site before that site can initiate its own spike, local spike initiation is pre-empted by the propagated spike and its refractory period. As a result, the faster ectopic discharge site serves as the pacemaker for the neuron. Indeed, the higher-threshold ectopic discharge site must reach its AD attractor before the lower-threshold site leaves its attractor, implying that competition (on a fast timescale) is an inevitable aspect of cooperativity (on a longer timescale). But one must appreciate that even if spikes originate from only one site, both sites can concurrently be in an AD attractor state, which is to say that two sites can have the capacity to initiate spikes. This is important insofar as AD will continue if either attractor is blocked, since the other attractor can take over in the absence of the other. This redundancy – having >1 ectopic discharge site – will make a pathological spiking pattern more resistant to local interventions.
How does this mechanistic understanding of AD inform our understanding of its biophysical basis? Peripheral nerve injury leads to dozens of different ion channels being up or down regulated in primary afferent neurons (Costigan et al. 2002; Hammer et al. 2010; LaCroix-Fralish et al. 2011; Valder et al. 2003; Xiao et al. 2002). Ion channel function can also be altered by local inflammation (Gold and Flake 2005) or by axonal damage, for example, via altered voltage sensitivity of sodium channels (Boucher et al. 2012). Alterations in ion channel function are liable to be more restricted to the site of damage whereas alterations in gene expression will have a broader impact. Such changes are not mutually exclusive and will, instead, likely compound one another. Indeed, ion channels interact locally to control spiking pattern; in many respects, it is the qualitative alteration of those interactions rather than the alteration of any one ion channel that is key (Ratté et al. 2014; Rho and Prescott 2012). For a recent review of ion channels implicated in primary afferent excitability, see Waxman and Zamponi (2014)
But the generation of AD also has specific requirements that include a slow positive feedback process such as that mediated by the persistent sodium conductance, gNaP (Figure 2; see also (Coggan et al. 2010, 2011)). Nav1.7–1.9 channels have kinetic properties consistent with our model of gNaP and are expressed by primary afferent neurons; TTX-resistant channels (NaV1.8 and 1.9) are mostly expressed by unmyelinated fibers but are present even in some myelinated fibers (Ho and O’leary 2011). Activating gNaP sufficiently to initiate AD in the soma requires a minimum rate and number of spikes either evoked by stimulation or arising spontaneously at a separate location. In this way, gNaP, although lower in density than gNa, leverages its slow gating properties to retain a recent memory of neuronal activity. Consistent with this, gNaP is thought to be involved in ectopic activity in the periphery (Kapoor et al. 1997; Tan et al. 2006; Xie et al. 2011) and centrally (Lampert et al. 2006).
Other candidate processes can be envisaged. For instance, the rate of pumping through the Na-K ATPase can be significantly modulated on the basis of recent spiking activity (N. Yu et al. 2012). As an active process, such pumping depends on energy considerations including mitochondrial function, which can be compromised in certain conditions such as chemotherapy-induced neuropathic pain (Flatters and Bennett 2006; Janes et al. 2013). These changes represent slower processes that would interact with alterations in ion channel expression and function (see above). What is important to recognize is that pathological spiking patterns reflect more than hyperexcitability per se; additional, slow processes include ionic regulation, which in turn implicates energy considerations such as mitochondrial function. In short, a multiplicity of injury-induced changes spanning several spatial and temporal scales leads to complex alterations in excitability as evidenced by abnormal spiking patterns with ectopic origins.
Although there is no direct experimental evidence for the remote, spike-based cooperativity that we describe, the mechanism is entirely plausible given available data. Based on our previous work with this model one would expect the lower threshold region to begin AD earlier, but the eventual spiking complexity that results from the cooperativity and competition between regions provides a non-intuitive and novel insight into single cell dynamics upon disruption of normal physiological or anatomical properties. Our modeling results provide an impetus to experimentally test for cooperative interactions. The functional consequences of remote cooperativity are significant. The origin of AD would, for most instances of nerve damage, shift from a distal locus to a more proximal one in the dorsal root ganglion; consequently, nerve blocks applied near the neuroma would fail to block AD. More generally, if two separate sites are in their AD attractor state, blocking either site will fail to terminate AD. The cooperativity itself would enable smaller local changes in excitability to manifest sustained AD. In our model, the attractor that is more stable (on a long timescale) is also more difficult to reach. It might only be possible to reach that ultra-stable attractor with the help of another transiently stable attractor that may not constitute a major problem on its own. Thus, the phenomenon we describe of dove-tail transitioning from one attractor to another would contribute to the chronification of hyperexcitability within injured afferents and, in turn, by driving central sensitization, to the chronification of neuropathic pain (Gold and Gebhart 2010; Gracely et al. 1992; Louter et al. 2013). Indeed, in phantom limb pain, although the stump can become hypersensitive, recent evidence points to ectopic spikes originating from the dorsal root ganglia as the basis for ongoing pain (Vaso et al. 2014).
5 Conclusion
To summarize, we have identified a novel way in which pathological spiking is shaped by interactions between remote ectopic discharge sites. Because of cooperativity, a small change in local excitability can trigger ectopic spiking that is maintained remotely. Although ectopic spiking only originates from one site at any one time, having two sites capable of initiating ectopic spikes makes the abnormal spiking more resilient to locally directed countermeasures. Our results call for further experiments to work out if and how remote sites of ectopic discharge do indeed interact and how to approach such phenomena therapeutically.
Acknowledgements
This work was supported by NIH grant R21 NS074146, a New Investigator Award from the Canadian Institutes of Health Research and a Mallinckrodt Scholar Award to SAP and the HHMI (TJS).
References
- Amir R, Kocsis JD, Devor M. Multiple interacting sites of ectopic spike electrogenesis in primary sensory neurons. The Journal of Neuroscience: The Official Journal of the Society for Neuroscience. 2005;25(10):2576–2585. doi: 10.1523/JNEUROSCI.4118-04.2005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Baron R. Mechanisms of disease: neuropathic pain--a clinical perspective. Nature Clinical Practice. Neurology. 2006;2(2):95–106. doi: 10.1038/ncpneuro0113. [DOI] [PubMed] [Google Scholar]
- Bennett GJ. What is spontaneous pain and who has it? The Journal of Pain: Official Journal of the American Pain Society. 2012;13(10):921–929. doi: 10.1016/j.jpain.2012.05.008. [DOI] [PubMed] [Google Scholar]
- Boucher P-A, Joós B, Morris CE. Coupled left-shift of Nav channels: modeling the Na+-loading and dysfunctional excitability of damaged axons. Journal of Computational Neuroscience. 2012;33(2):301–319. doi: 10.1007/s10827-012-0387-7. [DOI] [PubMed] [Google Scholar]
- Bowe CM, Kocsis JD, Targ EF, Waxman SG. Physiological effects of 4-aminopyridine on demyelinated mammalian motor and sensory fibers. Annals of Neurology. 1987;22(2):264–268. doi: 10.1002/ana.410220212. [DOI] [PubMed] [Google Scholar]
- Calvin WH, Loeser JD, Howe JF. A neurophysiological theory for the pain mechanism of tic douloureux. Pain. 1977;3(2):147–154. doi: 10.1016/0304-3959(77)90078-1. [DOI] [PubMed] [Google Scholar]
- Carnevale NT, Hines ML. The NEURON book. Cambridge: Cambridge University Press; 2009. [Google Scholar]
- Coggan JS, Ocker GK, Sejnowski TJ, Prescott SA. Explaining pathological changes in axonal excitability through dynamical analysis of conductance-based models. Journal of Neural Engineering. 2011;8(6):065002. doi: 10.1088/1741-2560/8/6/065002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Coggan JS, Prescott SA, Bartol TM, Sejnowski TJ. Imbalance of ionic conductances contributes to diverse symptoms of demyelination. Proceedings of the National Academy of Sciences of the United States of America. 2010;107(48):20602–20609. doi: 10.1073/pnas.1013798107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Costigan M, Befort K, Karchewski L, Griffin RS, D’Urso D, Allchorne A, et al. Replicate high-density rat genome oligonucleotide microarrays reveal hundreds of regulated genes in the dorsal root ganglion after peripheral nerve injury. BMC neuroscience. 2002;3:16. doi: 10.1186/1471-2202-3-16. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Devor M, Amir R, Rappaport ZH. Pathophysiology of trigeminal neuralgia: the ignition hypothesis. The Clinical Journal of Pain. 2002;18(1):4–13. doi: 10.1097/00002508-200201000-00002. [DOI] [PubMed] [Google Scholar]
- Devor M, Wall PD. Cross-excitation in dorsal root ganglia of nerve-injured and intact rats. Journal of Neurophysiology. 1990;64(6):1733–1746. doi: 10.1152/jn.1990.64.6.1733. [DOI] [PubMed] [Google Scholar]
- Egorov AV, Hamam BN, Fransén E, Hasselmo ME, Alonso AA. Graded persistent activity in entorhinal cortex neurons. Nature. 2002;420(6912):173–178. doi: 10.1038/nature01171. [DOI] [PubMed] [Google Scholar]
- Flatters SJL, Bennett GJ. Studies of peripheral sensory nerves in paclitaxel-induced painful peripheral neuropathy: evidence for mitochondrial dysfunction. Pain. 2006;122(3):245–257. doi: 10.1016/j.pain.2006.01.037. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fleidervish IA, Lasser-Ross N, Gutnick MJ, Ross WN. Na+ imaging reveals little difference in action potential-evoked Na+ influx between axon and soma. Nature Neuroscience. 2010;13(7):852–860. doi: 10.1038/nn.2574. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fransén E, Tahvildari B, Egorov AV, Hasselmo ME, Alonso AA. Mechanism of graded persistent cellular activity of entorhinal cortex layer v neurons. Neuron. 2006;49(5):735–746. doi: 10.1016/j.neuron.2006.01.036. [DOI] [PubMed] [Google Scholar]
- Gold MS, Flake NM. Inflammation-mediated hyperexcitability of sensory neurons. Neuro-Signals. 2005;14(4):147–157. doi: 10.1159/000087653. [DOI] [PubMed] [Google Scholar]
- Gold MS, Gebhart GF. Nociceptor sensitization in pain pathogenesis. Nature Medicine. 2010;16(11):1248–1257. doi: 10.1038/nm.2235. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gracely RH, Lynch SA, Bennett GJ. Painful neuropathy: altered central processing maintained dynamically by peripheral input. Pain. 1992;51(2):175–194. doi: 10.1016/0304-3959(92)90259-E. [DOI] [PubMed] [Google Scholar]
- Gutkin B, Pinto D, Ermentrout B. Mathematical neuroscience: from neurons to circuits to systems. Journal of Physiology, Paris. 2003;97(2–3):209–219. doi: 10.1016/j.jphysparis.2003.09.005. [DOI] [PubMed] [Google Scholar]
- Hammer P, Banck MS, Amberg R, Wang C, Petznick G, Luo S, et al. mRNA-seq with agnostic splice site discovery for nervous system transcriptomics tested in chronic pain. Genome Research. 2010;20(6):847–860. doi: 10.1101/gr.101204.109. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ho C, O'Leary ME. Single-cell analysis of sodium channel expression in dorsal root ganglion neurons. Molecular and Cellular Neuroscience. 2011;46(1):159–166. doi: 10.1016/j.mcn.2010.08.017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hooge JP, Redekop WK. Trigeminal neuralgia in multiple sclerosis. Neurology. 1995;45(7):1294–1296. doi: 10.1212/wnl.45.7.1294. [DOI] [PubMed] [Google Scholar]
- Howe JF, Loeser JD, Calvin WH. Mechanosensitivity of dorsal root ganglia and chronically injured axons: a physiological basis for the radicular pain of nerve root compression. Pain. 1977;3(1):25–41. doi: 10.1016/0304-3959(77)90033-1. [DOI] [PubMed] [Google Scholar]
- Janes K, Doyle T, Bryant L, Esposito E, Cuzzocrea S, Ryerse J, et al. Bioenergetic deficits in peripheral nerve sensory axons during chemotherapy-induced neuropathic pain resulting from peroxynitrite-mediated post-translational nitration of mitochondrial superoxide dismutase. Pain. 2013;154(11):2432–2440. doi: 10.1016/j.pain.2013.07.032. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kapoor R, Li YG, Smith KJ. Slow sodium-dependent potential oscillations contribute to ectopic firing in mammalian demyelinated axons. Brain: A Journal of Neurology. 1997;120(Pt 4):647–652. doi: 10.1093/brain/120.4.647. [DOI] [PubMed] [Google Scholar]
- LaCroix-Fralish ML, Austin J-S, Zheng FY, Levitin DJ, Mogil JS. Patterns of pain: meta-analysis of microarray studies of pain. Pain. 2011;152(8):1888–1898. doi: 10.1016/j.pain.2011.04.014. [DOI] [PubMed] [Google Scholar]
- Lampert A, Hains BC, Waxman SG. Upregulation of persistent and ramp sodium current in dorsal horn neurons after spinal cord injury. Experimental Brain Research. 2006;174(4):660–666. doi: 10.1007/s00221-006-0511-x. [DOI] [PubMed] [Google Scholar]
- Lisney SJ, Devor M. Afterdischarge and interactions among fibers in damaged peripheral nerve in the rat. Brain Research. 1987;415(1):122–136. doi: 10.1016/0006-8993(87)90275-7. [DOI] [PubMed] [Google Scholar]
- Louter MA, Bosker JE, van Oosterhout WPJ, van Zwet EW, Zitman FG, Ferrari MD, Terwindt GM. Cutaneous allodynia as a predictor of migraine chronification. Brain: A Journal of Neurology. 2013;136(Pt 11):3489–3496. doi: 10.1093/brain/awt251. [DOI] [PubMed] [Google Scholar]
- Ma C, LaMotte RH. Multiple sites for generation of ectopic spontaneous activity in neurons of the chronically compressed dorsal root ganglion. The Journal of Neuroscience: The Official Journal of the Society for Neuroscience. 2007;27(51):14059–14068. doi: 10.1523/JNEUROSCI.3699-07.2007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- McCormick DA, Shu Y, Yu Y. Neurophysiology: Hodgkin and Huxley model--still standing? Nature. 2007;445(7123):E1–E2. doi: 10.1038/nature05523. discussion E2-3. [DOI] [PubMed] [Google Scholar]
- McIntyre CC, Richardson AG, Grill WM. Modeling the excitability of mammalian nerve fibers: influence of afterpotentials on the recovery cycle. Journal of Neurophysiology. 2002;87(2):995–1006. doi: 10.1152/jn.00353.2001. [DOI] [PubMed] [Google Scholar]
- Naundorf B, Wolf F, Volgushev M. Unique features of action potential initiation in cortical neurons. Nature. 2006;440(7087):1060–1063. doi: 10.1038/nature04610. [DOI] [PubMed] [Google Scholar]
- Ostermann PO, Westerberg CE. Paroxysmal attacks in multiple sclerosis. Brain: A Journal of Neurology. 1975;98(2):189–202. doi: 10.1093/brain/98.2.189. [DOI] [PubMed] [Google Scholar]
- Popovic MA, Foust AJ, McCormick DA, Zecevic D. The spatio-temporal characteristics of action potential initiation in layer 5 pyramidal neurons: a voltage imaging study. The Journal of Physiology. 2011;589(Pt 17):4167–4187. doi: 10.1113/jphysiol.2011.209015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Prescott SA, De Koninck Y, Sejnowski TJ. Biophysical basis for three distinct dynamical mechanisms of action potential initiation. PLoS computational biology. 2008;4(10):e1000198. doi: 10.1371/journal.pcbi.1000198. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ratté S, Zhu Y, Lee KY, Prescott SA. Criticality and degeneracy in injury-induced changes in primary afferent excitability and the implications for neuropathic pain. eLife. 2014;3:e02370. doi: 10.7554/eLife.02370. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rho Y-A, Prescott SA. Identification of molecular pathologies sufficient to cause neuropathic excitability in primary somatosensory afferents using dynamical systems theory. PLoS computational biology. 2012;8(5):e1002524. doi: 10.1371/journal.pcbi.1002524. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sakurai M, Kanazawa I. Positive symptoms in multiple sclerosis: their treatment with sodium channel blockers, lidocaine and mexiletine. Journal of the Neurological Sciences. 1999;162(2):162–168. doi: 10.1016/s0022-510x(98)00322-0. [DOI] [PubMed] [Google Scholar]
- Selverston AI, Szücs A, Huerta R, Pinto R, Reyes M. Neural mechanisms underlying the generation of the lobster gastric mill motor pattern. Frontiers in Neural Circuits. 2009;3:12. doi: 10.3389/neuro.04.012.2009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sheffield MEJ, Best TK, Mensh BD, Kath WL, Spruston N. Slow integration leads to persistent action potential firing in distal axons of coupled interneurons. Nature Neuroscience. 2011;14(2):200–207. doi: 10.1038/nn.2728. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sun J, Pang ZP, Qin D, Fahim AT, Adachi R, Südhof TC. A dual-Ca2+-sensor model for neurotransmitter release in a central synapse. Nature. 2007;450(7170):676–682. doi: 10.1038/nature06308. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tan ZY, Donnelly DF, LaMotte RH. Effects of a chronic compression of the dorsal root ganglion on voltage-gated Na+ and K+ currents in cutaneous afferent neurons. Journal of Neurophysiology. 2006;95(2):1115–1123. doi: 10.1152/jn.00830.2005. [DOI] [PubMed] [Google Scholar]
- Twomey JA, Espir ML. Paroxysmal symptoms as the first manifestations of multiple sclerosis. Journal of Neurology, Neurosurgery, and Psychiatry. 1980;43(4):296–304. doi: 10.1136/jnnp.43.4.296. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Valder CR, Liu J-J, Song Y-H, Luo ZD. Coupling gene chip analyses and rat genetic variances in identifying potential target genes that may contribute to neuropathic allodynia development. Journal of Neurochemistry. 2003;87(3):560–573. doi: 10.1046/j.1471-4159.2003.02016.x. [DOI] [PubMed] [Google Scholar]
- Vaso A, Adahan H-M, Gjika A, Zahaj S, Zhurda T, Vyshka G, Devor M. Peripheral nervous system origin of phantom limb pain. Pain. 2014;155(7):1384–1391. doi: 10.1016/j.pain.2014.04.018. [DOI] [PubMed] [Google Scholar]
- Wall PD, Devor M. Sensory afferent impulses originate from dorsal root ganglia as well as from the periphery in normal and nerve injured rats. Pain. 1983;17(4):321–339. doi: 10.1016/0304-3959(83)90164-1. [DOI] [PubMed] [Google Scholar]
- Wall PD, Gutnick M. Properties of afferent nerve impulses originating from a neuroma. Nature. 1974;248(5451):740–743. doi: 10.1038/248740a0. [DOI] [PubMed] [Google Scholar]
- Waxman SG, Zamponi GW. Regulating excitability of peripheral afferents: emerging ion channel targets. Nature Neuroscience. 2014;17:153–163. doi: 10.1038/nn.3602. [DOI] [PubMed] [Google Scholar]
- Wang LY, Gan L, Forsythe ID, Kaczmarek LK. Contribution of the Kv3.1 potassium channel to high-frequency firing in mouse auditory neurones. The Journal of Physiology. 1998;509(Pt 1):183–194. doi: 10.1111/j.1469-7793.1998.183bo.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Xiao H-S, Huang Q-H, Zhang F-X, Bao L, Lu Y-J, Guo C, et al. Identification of gene expression profile of dorsal root ganglion in the rat peripheral axotomy model of neuropathic pain. Proceedings of the National Academy of Sciences of the United States of America. 2002;99(12):8360–8365. doi: 10.1073/pnas.122231899. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Xie R-G, Zheng D-W, Xing J-L, Zhang X-J, Song Y, Xie Y-B, et al. Blockade of persistent sodium currents contributes to the riluzole-induced inhibition of spontaneous activity and oscillations in injured DRG neurons. PloS One. 2011;6(4):e18681. doi: 10.1371/journal.pone.0018681. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yu N, Morris CE, Joós B, Longtin A. Spontaneous excitation patterns computed for axons with injury-like impairments of sodium channels and Na/K pumps. PLoS computational biology. 2012;8(9):e1002664. doi: 10.1371/journal.pcbi.1002664. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yu Y, Shu Y, McCormick DA. Cortical action potential backpropagation explains spike threshold variability and rapid-onset kinetics. The Journal of Neuroscience: The Official Journal of the Society for Neuroscience. 2008;28(29):7260–7272. doi: 10.1523/JNEUROSCI.1613-08.2008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhang Z, Séguéla P. Metabotropic induction of persistent activity in layers II/III of anterior cingulate cortex. Cerebral Cortex (New York, N.Y.: 1991. 2010;20(12):2948–2957. doi: 10.1093/cercor/bhq043. [DOI] [PubMed] [Google Scholar]