The mobility of single-file water molecules is governed by the number of H-bonds they may form with channel-lining residues

Mobility of single-file water molecules determined by H-bonds.

Abstract

Channel geometry governs the unitary osmotic water channel permeability, p_f, according to classical hydrodynamics. Yet, p_f varies by several orders of magnitude for membrane channels with a constriction zone that is one water molecule in width and four to eight molecules in length. We show that both the p_f of those channels and the diffusion coefficient of the single-file waters within them are determined by the number N_H of residues in the channel wall that may form a hydrogen bond with the single-file waters. The logarithmic dependence of water diffusivity on N_H is in line with the multiplicity of binding options at higher N_H densities. We obtained high-precision p_f values by (i) having measured the abundance of the reconstituted aquaporins in the vesicular membrane via fluorescence correlation spectroscopy and via high-speed atomic force microscopy, and (ii) having acquired the vesicular water efflux from scattered light intensities via our new adaptation of the Rayleigh-Gans-Debye equation.

Movement of water through very narrow membrane channels is different from Poiseuillian flow through macroscopic tubes (1). The diffusive nature of single-file transport (2) and the unaltered fluidity of confined water (3) suggest that the unitary osmotic water channel permeability p_f may only vary within the narrow limits that are set by the small length deviations of the single-file region. This is in sharp contrast to the experimental observation that p_f alterations stretch over three orders of magnitude (4).

Part of the p_f scatter is likely to be caused by technical difficulties: reported p_f values for correspondent aquaporins can vary by more than an order of magnitude. For example, p_f for human aquaporin-1 (AQP1) ranges from 1 × 10⁻¹⁴ to 16 × 10⁻¹⁴ cm³ s⁻¹ (5). The problem of obtaining correct p_f values is also underscored by the differences in the in vitro and in silico order in which p_f decreases among the members of the protein family. Three experimental groups reported that p_f in AQPZ, the orthodox water channel of Escherichia coli, exceeds p_f of the glycerol facilitator from E. coli, GlpF (6–8), whereas three other theoretical groups observed the exact opposite (table S1) (9–11).

Single-file water movement may be governed by interactions with the channel wall or limited by water dehydration at the channel entrance. The dehydration energy penalty arises because the single-file waters only have two of the four usual hydrogen bonds available when entering a channel, which does not provide a surrogate for the waters of hydration. In the presence of pore-lining residues that donate or accept hydrogen bonds, water movement should be limited by the time required for breaking H-bonds, reorientation of the molecules, and reforming H-bonds while traversing the channel. If so, the fastest flow should occur when the interaction between single-file waters and the channel wall is restricted to van der Waals interactions, and no hydrogen bonds are formed as is the case in carbon nanotubes (12).

Water mobility in these tubes and in membrane water channels is best compared to bulk water mobility by means of the diffusion constant D_W of the single-file water molecules. D_W can be calculated according to the Einstein relation (13, 14):

$${\mathit{D}}_{\mathrm{W}}=\frac{{\mathit{k}}_0{\mathit{z}}^2}{2}=\frac{{\mathit{z}}^2{\mathit{p}}_{\mathrm{f}}}{2{\mathit{v}}_{\mathrm{w}}}$$ 1

where z, k₀, and v_w indicate the average distance between two water molecules in the single-file region, the transport rate, and the molecular volume of one water molecule, respectively.

By inserting p_f = 5.43 × 10⁻¹⁴ cm³ s⁻¹ (15) of AQP1 and assuming z = 2.8 Å, we found that D_w ≈ 4 × 10⁻⁷ cm² s⁻¹. This result does not agree with previous estimates of D_w ≈ 4 × 10⁻⁶ to 8 × 10⁻⁶ cm² s⁻¹ (5, 16) in aquaporins. They have been derived using the equation D_w = l_c/A_C × p_f, where A_C is the cross-sectional area of the channel (5, 17). Assuming that channel length l_c = z × N_W, where N_W is the number of single-file waters and that l_c × A_C = N_W × v_w, we find that D_w was exaggerated by a factor of 2N_W. Thus, the uncertainty in the experimental p_f was amplified by the ambiguity in extracting D_w from it.

We now set out to obtain molecular insight into what determines D_w. To obtain precise p_f values, we had to overcome the uncertainty in the number of channels per unit membrane area. Otherwise, osmotic channel water permeability P_f,c cannot be dissected from lipid water permeability P_f,l. P_f,l and P_f,c add up to osmotic membrane water permeability (18):

$${\mathit{P}}_{\mathrm{f}}={\mathit{P}}_{\mathrm{f},1}+{\mathit{P}}_{\mathrm{f},\mathrm{c}}={\mathit{P}}_{\mathrm{f},1}+\mathit{n}{\mathit{p}}_{\mathrm{f}}{\mathit{d}}_{\mathrm{v}}^{-2}{\mathrm{\pi }}^{-1}$$ 2

where n is the number of aquaporins per vesicle and d_V is vesicle diameter. Previously, the uncertainty in n arose chiefly from the poor repeatability and the limited accuracy of channel abundance determination by Coomassie and silver staining of SDS–polyacrylamide gel electrophoresis (19). Instead, we used both atomic force microscopy (AFM) and fluorescence correlation spectroscopy (FCS) to accurately measure membrane channel abundance. Therefore, the yellow fluorescent protein (YFP) was anchored to the N terminus of AQP1. AQPZ and GlpF were modified by site-directed mutagenesis to contain only one N-terminal or two C-terminal cysteine residues, respectively, thereby enabling covalent labeling with the fluorescent dye Atto 488 maleimide. We also had to render unstirred layer effects negligibly small. This was mainly achieved by reconstituting the purified aquaporins into vesicles that were only d_V = 120 nm in diameter (7, 20, 21). Assuming that the width of the unstirred (stagnant water) layer w_UL is comparable to vesicle size, and that the diffusion coefficient of bulk water D_B is equal to 2.3 × 10^–5 cm² s^–1, we find an unstirred layer water permeability P_UL = D_B/w_UL ≈ 2 cm/s. Thus, even if P_f,c is 10 times larger than P_f,l = 20 μm/s, P_UL exceeds P_f hundredfold. Because 1/P_a = 1/P_UL + 1/P_f, the apparent (measured) water permeability P_a does not differ from P_f by more than 1%.

In the immediate membrane vicinity of bigger objects, w_UL is so large in size that osmotic flow through them results in osmolyte dilution. If unaccounted for, the result is a severe underestimation of both P_f and p_f (Eq. 2).

The small vesicle size led to the third problem: the assessment of changes in vesicle volume V from measurements of scattered light intensity I. Empirical approximations thus far used ranged from double logarithmic (22), over quadratic (23), to simple linear dependencies (24) of V from I. Here, we adopted the Rayleigh-Gans-Debye approximation and analytically solved the differential equation to calculate p_f from the water efflux rate.

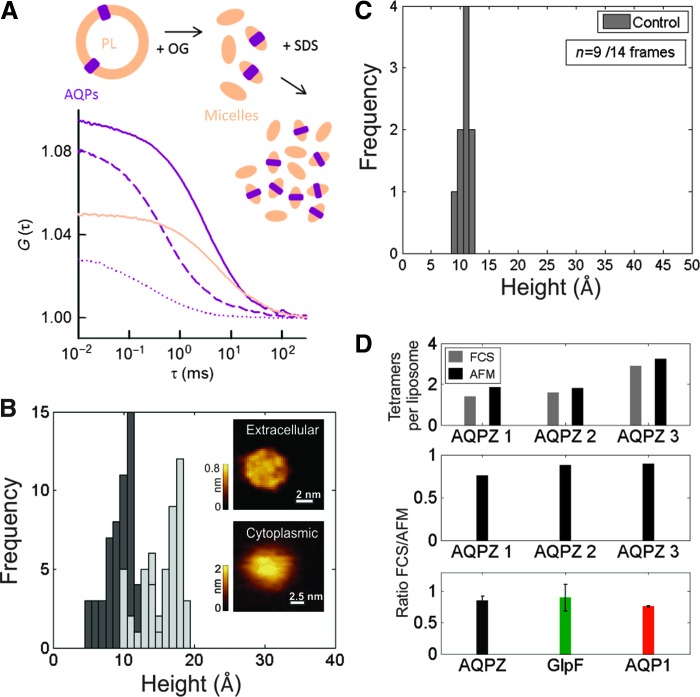
We determined the number n of aquaporin monomers per proteoliposome by FCS as previously described (25) and as exemplified in Fig. 1A (see also fig. S5). Depending on the preparation, n varied between 1 and 30. The reconstitution efficiency varied between 10 and 50% (fig. S6). At very low concentrations, AQP1 and GlpF reconstituted as functional monomers, dimers, or trimers. To enable comparison with AFM measurements, we calculated the expected number N_O,FCS of oligomers per proteoliposome by assuming (i) a Poisson distribution of functional units among the proteoliposomes and (ii) that all units within one vesicle assembled into the smallest number of oligomers possible.

Fig. 1. Determination of reconstitution efficiency.

(A) FCS autocorrelation curves allowed us to obtain the number of (i) vesicles labeled with 0.004% (w/w) N-(lissamine-rhodamine-sulfonyl)phosphatidylethanolamine (sandy brown), (ii) AQP1-YFP–containing vesicles (purple), (iii) AQP1-YFP oligomers containing micelles that formed upon vesicle dissolution in mild detergent (dashed purple), and (iv) AQP1-YFP monomer containing micelles that formed upon further dissolution in harsh detergent (dotted purple) per confocal volume. The buffer (pH 7.4) contained 100 mM NaCl, 20 mM Mops, and a protease inhibitor. (B and C) AFM imaging of solid-supported lipid bilayers that were prepared from AQPZ proteoliposomes (B) or empty vesicles (investigated area: 14 × 400 × 400nm²) (C) resulted in histograms of height values (n = 50). (B) Inset: The high-resolution raw data allowed differentiation of the extracellular and cytoplasmic AQPZ surfaces. (C) The density of unspecified features (0.218 per vesicle) served to correct the protein count (see also fig. S1). (D) Comparison of both the absolute AFM and FCS counts of AQPZ tetramers per liposome (at three different concentrations) (upper panel) and their ratio (middle panel). Average ratio of AFM and FCS counts per liposome for AQPZ, GlpF, and AQP1 oligomers (lower panel: compare also eqs. S9 and S10).

To confirm the FCS count, we performed additional measurements using high-speed AFM (HS-AFM) (26). In brief, we spread the vesicles on mica and imaged the resulting supported bilayers (Fig. 1, B to D). Initially, high-magnification raw data images were recorded and compared to the topography of the extracellular and cytoplasmic aquaporin surfaces known from previous studies of aquaporins reconstituted into two-dimensional crystals (27, 28). This enabled us to identify the extracellular and cytoplasmic surfaces of single aquaporins (Fig. 1B, inset) and to conclude that the aquaporins were reconstituted with random orientation (29). We generated a height histogram of the membrane-protruding parts with respect to the surrounding lipids by randomly taking 50 cross-sections of the protein surface. Subsequently, protein-free bilayers were spread on mica, and a second histogram of maximum height values (investigated area: 13 × 400 × 400 nm²) was constructed from the observed unspecified membrane-protruding features (Fig. 1C). Protein abundances per vesicle were determined for AQPZ, AQP1, and GlpF as exemplified for AQPZ in fig. S7. The comparison to N_O,FCS was quite satisfactory. When repeating the procedure for at least three different protein concentrations of each of the aquaporins, HS-AFM always counted f_c ≈ 1.2 times more particles than FCS (Fig. 1D).

Subsequently, we subjected the reconstituted vesicles to osmotic stress. V was determined by the vesicular water permeability P_f = P_f,l + P_f,c, which reflects the permeabilities P_f,c and P_f,l of all channels and the lipid bilayer, respectively:

$$\mathit{V}(\mathit{t})={\mathit{V}}_0\frac{{\mathit{c}}_0^{\mathrm{i}}}{{\mathit{c}}_0^{\mathrm{i}}+{\mathit{c}}_{\mathrm{s}}}\left\{1+\mathit{L}\left(\frac{{\mathit{c}}_{\mathrm{s}}}{{\mathit{c}}_{\mathrm{i}}^0}\text{exp}\left(\frac{{\mathit{c}}_{\mathrm{s}}}{{\mathit{c}}_0^{\mathrm{i}}}-\frac{\mathit{A}{\mathit{P}}_{\mathrm{f}}{\mathit{V}}_{\mathrm{w}}{({\mathit{c}}_0^{\mathrm{i}}+{\mathit{c}}_{\mathrm{s}})}^2}{{\mathit{V}}_0{\mathit{c}}_0^{\mathrm{i}}}\mathit{t}\right)\right)\right\}$$ 3

where V_w, V₀, A, ${\mathit{c}}_0^{\mathit{i}}$, c_s, and L are the molar volume of water, vesicle volume at time zero, surface area of the vesicle, the initial osmolyte concentration inside the vesicles, the incremental osmolyte concentration in the external solution due to sucrose addition, and the Lambert function L(x)e^L(x) = x, respectively. V(t) is experimentally accessible by measuring I(t). To derive the corresponding expression, we exploited the Rayleigh-Gans-Debye relation (see the Supplementary Materials). We then substituted the dependence of the scattered light intensity on V for its Taylor series (figs. S1 and S2) and took into account the fraction α of bare vesicles, which does not contain any protein:

$$\mathit{I}(\mathit{t})=\mathit{a}+\mathit{b}[\mathrm{\alpha }{\mathit{V}}_{\text{bare}}(\mathit{t})+(1-\mathrm{\alpha }){\mathit{V}}_{\text{AQP}}(\mathit{t})]+\mathit{d}{[\mathrm{\alpha }{\mathit{V}}_{\text{bare}}(\mathit{t})+(1-\mathrm{\alpha }){\mathit{V}}_{\text{AQP}}(\mathit{t})]}^2$$ 4

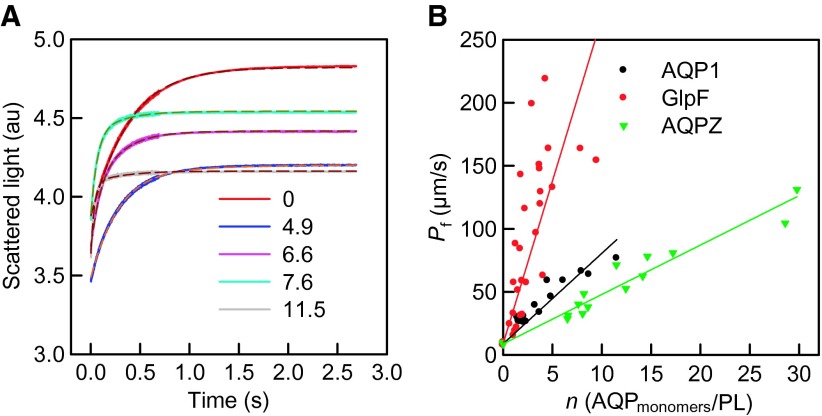
where V_AQP(t) and V_bare(t) are the volumes of proteoliposomes and bare vesicles, respectively. The parameter a is calculated as follows: $\mathit{a}=\mathit{I}(\infty )-\mathit{b}{\mathit{V}}_{\mathrm{f}}-\mathit{d}{\mathit{V}}_{\mathrm{f}}^2$, where ${\mathit{V}}_{\mathrm{f}}={\mathit{V}}_0{\mathit{c}}_0^{\mathrm{i}}/({\mathit{c}}_0^{\mathrm{i}}+{\mathit{c}}_{\mathrm{s}})$. The fitting parameters b and d can be found analytically (see the Supplementary Materials) so that P_f may remain as the sole fitting parameter. However, this rather laborious procedure returned the same P_f value as the simpler fitting approach, which simultaneously determined b, d, and P_f for all test cases. When fitting Eq. 4 to the stopped-flow data (Fig. 2A), we fixed P_f,l to its value in pure lipid vesicles.

Fig. 2. The osmotic shrinkage of proteoliposomes.

(A) Representative stopped-flow raw data (spline lines) for AQPZ and the fit (dashed lines) according to Eq. 4. Equal volumes of vesicle suspension and hyperosmotic solution (300 mM sucrose) were mixed (5°C, same buffer as in Fig. 1). The number of reconstituted AQP monomers per proteoliposome is indicated. (B) P_f of reconstituted vesicles was calculated as shown in (A) for at least three independently purified and reconstituted batches for each protein and plotted as a function of the channel number per proteoliposome.

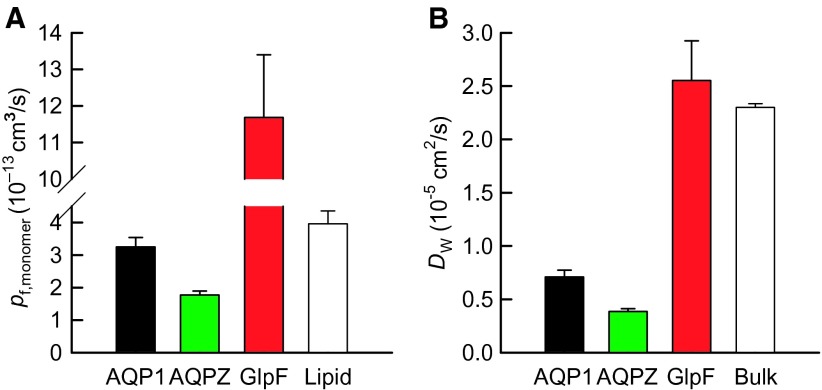
We performed the stopped-flow experiments for different numbers n of functional AQP units per vesicle (Fig. 2 and fig. S4) to determine p_f (Fig. 3A) from the linear regression of Eq. 2. Because the measurements were made at 5°C, we used the known activation energy of ~4 kcal/mol (21, 30) to estimate p_f at room temperature. D_W (Eq. 1) decreased while N_W increased from 4 in GlpF (10) to 7 in AQP1 and AQPZ (Fig. 3B). Our p_f values exceeded previously reported ones, confirming that p_f estimations from larger objects were subject to unstirred layer effects (15, 31) (see the Supplementary Materials). Our p_f exceeds the in silico p_f for AQPZ by a factor of 2 (11), that of AQP1 by a factor of 5 (32), and that of GlpF by a factor of 12 (9, 11).

Fig. 3. Water movement in aquaporins.

(A) p_f (at 5°C) for AQPZ, GlpF, and AQP1 was taken from the slopes in Fig. 2B. The background water permeability of a single lipid vesicle was calculated by multiplying P_f,l by the surface area of the vesicle. (B) The diffusion coefficient D_W (25°C) of water molecules inside the channel was calculated (Eq. 1). The bulk water diffusion coefficient is shown for comparison.

We took the 0.88-Å resolution structure of yeast AQP1 (33) as a template and used PyMol (34) to construct homology models for AQP1, AQPZ, and GlpF (fig. S8). We count N_H = 12 possible hydrogen bonds between the single-file waters and pore-lining residues in the plot that shows the water-filled cavity (Fig. 4). The twofold lower p_f of AQPZ may be caused by closings of AQPZ (35). To allow for the passage of the comparatively large glycerol molecules, the constriction site of GlpF is wider and shorter than that of the pure water channels AQP1 and AQPZ. In contrast to the glycerol-free crystal structure and its molecular dynamics simulation (16), more recent simulations found the length of the single-file region to be halved in GlpF (10, 11). In agreement with the more recent simulations, we find N_H = 6 from the homology model (Fig. 4). Because the single-file region contains only a small number of binding places, it is not surprising that GlpF has the highest p_f among the three aquaporins investigated.

Fig. 4. Number N_H of pore-lining residues (in yellow circles) that may form hydrogen bonds (dotted lines) with single-file water molecules.

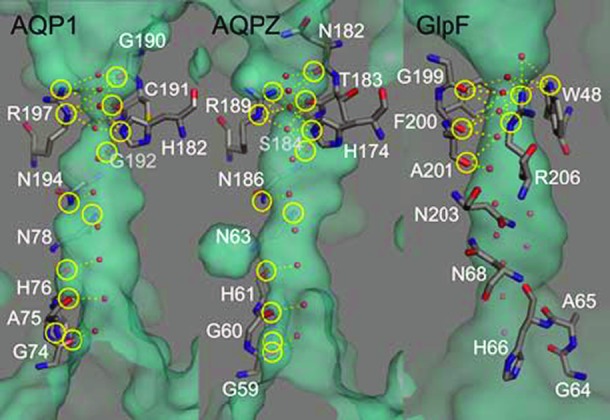
The 0.88-Å resolution structure of yeast AQP1 (33) [Protein Data Bank (PDB) #3Z0J] served as a template to find a model for the AQP1 (PDB #1J4N), AQPZ (PDB #1RC2), and GlpF (PDB #1FX8) structures via the PyMol’s “align” routine (34). The position of the water molecules (red spheres) is from the yeast AQP1 structure. The two water molecules below R206 have been added in the GlpF model to indicate that this region is wide enough to let the water molecules bypass each other within the pore.

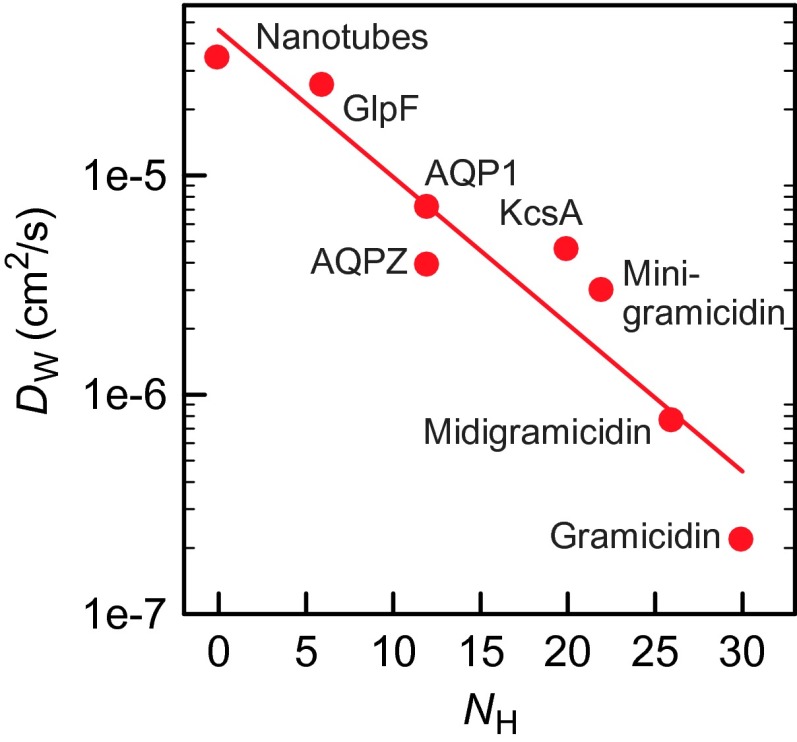
Plotting N_H against D_W reveals a logarithmic dependence (Fig. 5). This observation is reminiscent of the logarithmic length dependence described for gramicidin derivatives (17). Because gramicidin conducts the single-file waters within the helix, we assume that all 30 backbone carbonyls may form hydrogen bonds. Midigramicidin and minigramicidin are four and eight residues shorter, respectively, which reduce N_H. Their D_W (Eq. 1) fits into the logarithmic dependence (Fig. 4). Finally, we recalculated p_f for the bacterial potassium channel KcsA by applying Eq. 4 to our previously published stopped-flow curves (18). The corresponding D_W (Eq. 1) is in line with the assumption that all 20 filter carbonyls are capable of contributing to N_H (Fig. 4).

Fig. 5. D_W depends on the number N_H of hydrogen bonds that single-file water molecules may form with pore-lining residues.

D_W in nanotubes assumes z = 2.6 Å and k₀ = 0.1 p s⁻¹ (13). p_f for the bacterial potassium channel KcsA was calculated by applying Eq. 4 to our previously published stopped-flow curves (18). Equation 1 served to compute D_W from the p_f values of gramicidin, midigramicidin, minigramicidin (17), and KcsA.

The logarithmic dependence reflects that the number of binding sites increases out of proportion to N_H. A binding site in this sense represents a unique combination of the hydrogen bonds that any of the single-file water may form with pore-lining residues. If these residues are sparse, the binding sites are well-separated and their number coincides with N_H. With increasing N_H, there will be a spatial overlap between the binding sites. As a result, only a fraction of the available binding sites may be occupied simultaneously. This phenomenon has already been described for the yeast aquaporin: N_H of its selectivity filter amounts to six. However, sterical hindrance prevents that the four resulting binding sites may accommodate more than two water molecules. Thus, the water molecules move pairwise through the filter (33), first occupying the first and third binding sites and then the second and fourth. In consequence, every water molecule must be released from a succession of two binding sites to traverse the distance that corresponds to its thickness.

Other single-file channels may have an even denser packing of binding sites. For example, gramicidin may accommodate only seven water molecules but its N_H of 30 translates into a multitude of that number in terms of binding options. If all of them are satisfied with the same probability, and if each of the seven water molecules dwells at all binding sites for roughly the same time, a logarithmic increase of D_W with N_H is expected.

N_H sets the limits for the maximal p_f value of an open single-file pore. Thus, the functional relationship between p_f and N_H does not hold for channels that are capable of gating. For example, N_H of AQP0 amounts to 16 (compare fig. S9) and not to 60, as may have been derived from its low p_f ≈ 2.8 × 10⁻¹⁶ cm³ s⁻¹ (36). The low p_f may be due to the considerable amount of time that the AQP0 channel spends in its closed state: two Tyr residues (Y²³ and Y¹⁴⁹) may plug the channel [compare (37, 38) and fig. S9]. In addition, p_f of AQP0 was reported to be increased by acidic pH (39, 40).

We conclude that in single-file transport, D_W is not governed by channel geometry. Rather, the capability of the single-file waters to form hydrogen bonds to channel wall-lining residues causes the observed variability of two orders of magnitude. Other factors (for example, an increased penalty for entering the channel) may further reduce p_f.

Supplementary Materials

Supplementary material for this article is available at http://advances.sciencemag.org/cgi/content/full/1/2/e1400083/DC1

Fig. S1. The intensity I of scattered light for osmotically challenged vesicles as a function of vesicle radius R (A) and vesicle volume V (B).

Fig. S2. Comparison of the exact dependencies for I (red) with the approximate representations by their Taylor series (green) for R: I(t) = a + bR(t) + dR₂(t) (A) or for V: I(t) = a + bV(t) + dV₂(t) (B).

Fig. S3. Osmotically induced vesicle shrinkage was accompanied by an increase in I.

Fig. S4. Osmotic shrinkage of proteoliposomes.

Fig. S5. A typical FCS counting experiment of an AQP1-YFP reconstitution series.

Fig. S6. Reconstitution efficiency varied between 10 and 50%.

Fig. S7. Membrane protein detection by AFM.

Fig. S8. Alignments of aquaporin structures.

Fig. S9. Water-filled cavities in the open and closed structures of AQP0.

Table S1. Overview of published in vitro and in silico single-channel permeability values p_f for AQP1, GlpF, and AQPZ as discussed in the main text.