Improved protein structure selection using decoy-dependent discriminatory functions

Abstract

Background

A key component in protein structure prediction is a scoring or discriminatory function that can distinguish near-native conformations from misfolded ones. Various types of scoring functions have been developed to accomplish this goal, but their performance is not adequate to solve the structure selection problem. In addition, there is poor correlation between the scores and the accuracy of the generated conformations.

Results

We present a simple and nonparametric formula to estimate the accuracy of predicted conformations (or decoys). This scoring function, called the density score function, evaluates decoy conformations by performing an all-against-all C_α RMSD (Root Mean Square Deviation) calculation in a given decoy set. We tested the density score function on 83 decoy sets grouped by their generation methods (4state_reduced, fisa, fisa_casp3, lmds, lattice_ssfit, semfold and Rosetta). The density scores have correlations as high as 0.9 with the C_α RMSDs of the decoy conformations, measured relative to the experimental conformation for each decoy.

We previously developed a residue-specific all-atom probability discriminatory function (RAPDF), which compiles statistics from a database of experimentally determined conformations, to aid in structure selection. Here, we present a decoy-dependent discriminatory function called self-RAPDF, where we compiled the atom-atom contact probabilities from all the conformations in a decoy set instead of using an ensemble of native conformations, with a weighting scheme based on the density scores. The self-RAPDF has a higher correlation with C_α RMSD than RAPDF for 76/83 decoy sets, and selects better near-native conformations for 62/83 decoy sets. Self-RAPDF may be useful not only for selecting near-native conformations from decoy sets, but also for fold simulations and protein structure refinement.

Conclusions

Both the density score and the self-RAPDF functions are decoy-dependent scoring functions for improved protein structure selection. Their success indicates that information from the ensemble of decoy conformations can be used to derive statistical probabilities and facilitate the identification of near-native structures.

Background

A scoring or discriminatory function that can reliably distinguish near-native conformations from misfolded ones is a necessity to solve the structure prediction problem. Various types of scoring functions have been developed to accomplish this goal, and can be grouped into two categories: physics-based functions that take into account electrostatic, Van der Waals, hydrogen bonding, solvation and covalent interactions [1-4], and knowledge-based functions that compile statistics on the preferences of amino acid residues/atoms (such as pairwise distances or solvent accessibility) from experimentally solved structures [5-10]. In particular, knowledge-based scoring functions, especially detailed all-atom ones, have been applied in all areas of structure prediction: comparative or homology modeling, fold recognition or threading, and de novo prediction.

The knowledge-based scoring functions have been very successful in discriminating the native conformation from misfolded ones [10-13]. However, even the best conformations generated by the structure prediction protocols, particularly de novo ones, are usually still quite distant from the native conformation [14-18]. Therefore, it is more important to assess how well a given scoring function can distinguish the best predicted conformations in a given decoy set generated by structure prediction methods. In this regard, none of these functions can consistently select the most near-native conformations from non-native ones, and there is poor correlation between the scores and measures of similarity between the predicted conformations (or "decoys") and the native conformation, such as the C_α root mean square deviation (RMSD) of the decoys relative to the native conformation.

There are problems with the theoretical justification of both the physics-based [19] and knowledge-based [20-23] approaches, which in part explains the ineffectiveness of these scoring functions [19-23]. Specifically in the case of knowledge-based scoring functions, which are "trained" using experimentally determined structures, the intrinsic structural properties of native conformations may be captured, but these functions may not contain the information necessary to evaluate the quality of near-native and misfolded conformations. However, borrowing information from all the conformations in a decoy set may be helpful to evaluate the proximity of any given near-native or misfolded conformation to the corresponding native structure. This is supported by recent findings that prediction of native contacts was improved when using the frequency of occurrence of contacts in decoy conformations from a decoy set [24,25].

A new variety of scoring functions that attempt to use all the information in the ensemble of conformations generated by a structure prediction protocol have been used as a final filtering step in de novo structure prediction. This strategy for predicting protein structure is based on the assumption that there are a greater number of low-energy conformations surrounding the correct fold than there are surrounding incorrect folds in a decoy set. These functions compute a score for a given conformation based on its distance in Cartesian space relative to its neighbors. Initially used successfully at CASP3, one approach was implemented simply by adding the number of neighbors within a particular C_α RMSD cutoff to a given conformation [26,27]. In these cases, the conformation with the greatest number of neighbors was closer to the experimentally determined conformation than were the majority of conformations in the ensemble. The method was refined further at CASP4 to simultaneously cluster decoy conformations and pick the centers of these largest clusters [28].

Here we describe a similar and simple formula, called the density score function, to pick the near-native conformations from a large ensemble of conformations in a decoy set. The logic underlying such a nonparametric function is that a significant fraction of conformations in the decoy set resemble the native conformation from different directions in the space. These decoy conformations form a single cluster, and the density of the cluster gradually increases from the periphery to the center of the cluster. When near-native conformations are sampled adequately, the center of the cluster is where the most near-native conformations should reside. Therefore, by calculating the density around a given conformation, we can estimate the similarity between this conformation and the corresponding native one. To calculate the densities, we first perform an all-against-all C_α RMSD calculation, and the density score for each conformation is then calculated as the sum of RMSDs between it and all other decoy conformations.

Publicly available decoy sets provide a means to evaluate performance of scoring functions, and permit comparisons between different structure discrimination methods [29,30]. Many of these decoy sets contain a large number (>100) of decoy conformations, with varying degrees of similarity to the native conformation. The goal of any scoring function is to pick the conformations that are most similar to the native one. We tested the density score function on 83 decoy sets grouped by their generation methods (4state_reduced, fisa, fisa_casp3, lmds, lattice_ssfit, semfold and Rosetta). Since these sets contain conformations generated by different conformational search algorithms, the performance of a scoring function depends on each set, and success in one set does not guarantee success in another [31]. Therefore, the goal of testing on a wide variety and large number of decoy sets is to provide a rigorous evaluation of how well a scoring function works. In general, the density scores have relatively high correlation with the C_α RMSD relative to the experimentally determined structure in the decoy sets we evaluated. However, because the calculation of the density score function depends on an existing decoy set, this scoring function cannot be easily used in a fold simulation.

The success of the density score function led us to believe that using information in the decoy set itself can be helpful in selecting the best conformations using knowledge-based scoring functions. These functions usually compile statistics on the preferences of amino acid residue or atomic contacts in a large ensemble of experimentally determined structures [5-10]. In previous efforts we derived a residue-specific all-atom probability discriminatory function (RAPDF) to compute the probability of a conformation being native-like, given a set of pairwise atom-atom distances [7]. Here, we hypothesize that such a knowledge-based function may be used to derive statistics from all the decoy conformations in a large decoy set. We can use all the included decoy conformations to derive the parameters for the all-atom function and then use the parameters to select the most near-native conformations in the same set.

For a given decoy set, the C_α RMSDs relative to the experimentally determined structures usually follow a Gaussian-like distribution, which means that only a small fraction of conformations have relatively low C_α RMSD. When compiling the atom-atom contact probabilities from such a set, an appropriate weighting method is necessary to inflate the contribution of the low-RMSD conformations to the statistics. Given the strong correlation between C_α RMSDs and the density scores, the latter can be used as a parameter in the weighting scheme.

We therefore derived a statistical probability function, called self-RAPDF, from the decoy conformations using an exponential weighting scheme based on the density scores. We tested the performance of self-RAPDF on 83 publicly available decoy sets. In almost all cases, this method produced a higher correlation with C_α RMSD than the RAPDF, whose parameters were derived from a large ensemble of experimentally determined structures. It also performed better than RAPDF at selecting near-native conformations for most of the decoy sets. Unlike the density score function, self-RAPDF can also be used in a fold simulation and for structure refinement.

Results

Performance of the density score function

The performance of the density score function on the 4state_reduced decoy sets, as evaluated by correlation coefficients between scores and C_α RMSDs of decoys relative to experimentally determined conformations, is summarized in Table 1. For comparison purposes, we also list the results generated by the self-RAPDF and other published scoring functions on the same set, including the empirical free energy function with an atomic solvation model [32], the atomic knowledge-based potential [8], and the Shell function [33]. For all the 4state_reduced decoy sets, the density scores and self-RAPDF produce a significantly higher correlation between scores and C_α RMSDs than the other functions. The 4state_reduced sets contain decoys for seven small proteins, and were generated by exhaustively enumerating the backbone rotamer states of 10 selected residues in each protein, using an off-lattice model with four discrete dihedral angle states per residue [12]. Compact structures were further filtered to produce these sets, and various scoring functions have a satisfactory performance on it. We used the 4state_reduced sets since they allowed us to compare our function to others that have used the same sets. However, it is also important to examine the performance on other decoy sets since the performance of scoring functions may be highly set dependent.

Table 1.

Correlation coefficients between C_α RMSDs of decoys relative to the experimentally determined conformations and scores generated by the density score function, the self-RAPDF and other published scoring functions applied to the 4state_reduced decoy sets.

Protein (PDB code)	Number of conformations	Empirical function [32]	Atomic KBP [8]	Shell [33]	RAPDF [7]	Density score	Self-RAPDF
1ctf	630	0.68	0.6	0.65	0.73	0.98	0.89
1r69	675	0.66	0.5	0.52	0.70	0.96	0.88
1sn3	660	0.53	0.5	0.42	0.47	0.96	0.89
2cro	674	0.58	0.7	0.58	0.76	0.96	0.92
3icb	653	0.77	0.8	0.74	0.85	0.98	0.92
4pti	687	0.46	0.5	0.34	0.49	0.95	0.89
4rxn	677	0.61	0.6	0.57	0.57	0.98	0.88

The density scores and the self-RAPDF scores have the best correlation coefficient with C_α RMSDs of decoys relative to experimentally determined conformations for all seven sets.

Besides correlation coefficient (C.C.), the performance of scoring functions can be evaluated by other measures that emphasize particular features. For structure prediction applications, where near-native conformations are rarely, if ever, sampled, it is more important to know how the decoys are ranked relative to each other and whether it is possible to identify conformations that are closest to the experimentally determined conformation. Three other kinds of measurements are provided in Table 2 for the evaluation of the density score function on 83 decoy sets from seven sources: these are the log probability of selecting the best scoring conformation (log P_B1), log probability of selecting the lowest RMSD conformation among the top 10 best scoring conformations (log P_B10), and the fraction enrichment (F.E.) of the 10% lowest RMSD conformations in the top 10% best scoring conformations (see Methods). For comparison purposes, the correlation coefficients based on the original formulation by Simons et al. are also listed [27]. In their formula, they counted the number of structural neighbors within a 7 Å threshold and used it as the score for a given conformation.

Table 2.

Performance of the density score function on 83 decoy sets grouped by their generation methods.

Protein (PDB code)	N	RMSD range (Å)	RB1	log PB1	log PB10	F.E.(%)	C.C.	R.C.	Rexp	C.C.orig
4state_reduced
1ctf	630	1.32 – 9.07	7	-1.95	-2.8	88.9	0.98	0.99	1	0.95
1r69	675	0.88 – 8.31	7	-1.98	-2.83	87.4	0.96	0.98	1	0.88
1sn3	660	1.31 – 9.13	11	-1.78	-2.82	86.4	0.96	0.97	1	0.95
2cro	674	0.81 – 8.31	1	-2.82	-2.83	84.6	0.96	0.98	1	0.82
3icb	653	0.95 – 9.39	2	-2.51	-2.81	84.2	0.98	0.99	4	0.95
4pti	687	1.41 – 9.27	11	-1.8	-2.84	91.7	0.95	0.96	3	0.91
4rxn	677	1.36 – 8.14	3	-2.35	-2.83	84.2	0.98	0.98	1	0.95
Average	665	1.15 – 8.80		-2.17	-2.82	86.8	0.97	0.98		0.92
fisa
1fc2	500	3.11 – 10.58	115	-0.64	-0.98	6	0.95	0.67	399	0.91
1hdd-C	500	2.77 – 12.92	18	-1.44	-1.62	28	0.95	0.88	248	0.93
2cro	500	4.29 – 12.60	109	-0.66	-1.7	26	0.74	0.75	98	0.62
4icb	500	4.75 – 14.13	81	-0.79	-1.68	24	0.69	0.69	138	0.60
Average	500	3.73 – 12.56		-0.89	-1.5	21	0.83	0.75		0.77
fisa_casp3
1bg8-A	1,200	6.03 – 15.80	177	-0.83	-1.16	13.3	0.39	0.39	721	0.2
1bl0	971	3.63 – 18.17	44	-1.34	-2.03	57.7	0.74	0.73	129	0.7
1eh2	2,413	4.00 – 15.29	196	-1.09	-2.68	52.6	0.8	0.81	300	0.75
1jwe	1,407	7.79 – 20.87	345	-0.61	-0.72	4.2	-0.24	-0.23	1298	-0.23
l30	1,400	6.47 – 24.62	474	-0.47	-0.91	0	0.28	0.25	N/A	0.21
smd3	1,200	8.54 – 17.00	74	-1.21	-1.21	17.5	0.65	0.6	993	0.45
Average	1,432	6.08 – 18.63		-0.93	-1.45	24.2	0.43	0.42		0.35
lattice_ssfit
1beo	2,000	7.00 – 15.61	6	-2.52	-2.52	30.5	0.46	0.45	1069	0.07
1ctf	2,000	5.45 – 12.81	174	-1.06	-1.74	40	0.71	0.72	882	0.55
1dkt-A	2,000	6.69 – 14.05	74	-1.43	-2	34	0.42	0.4	1987	0.18
1fca	2,000	5.14 – 11.39	224	-0.95	-1.81	43	0.55	0.54	1287	0.35
1nkl	2,000	5.27 – 13.64	264	-0.88	-2.19	20	0.54	0.56	1103	0.33
1pgb	2,000	5.81 – 12.91	796	-0.4	-1.04	10	0.39	0.35	1840	0.27
1trl-A	2,000	5.38 – 12.52	480	-0.62	-1.63	14.5	0.41	0.39	1458	0.3
4icb	2,000	4.74 – 12.92	16	-2.1	-2.3	41	0.69	0.69	318	0.61
Average	2,000	5.68 – 13.23		-1.24	-1.9	29.1	0.52	0.51		0.33
lmds
1b0n-B	497	2.45 – 6.03	70	-0.85	-0.85	2	0.14	0.16	468	0.15
1bba	500	2.78 – 8.91	162	-0.49	-0.72	0	0.39	0.24	300	0.5
1ctf	497	3.59 – 12.53	185	-0.43	-0.58	0	0.41	0.49	367	0.1
1dtk	215	4.32 – 12.58	90	-0.38	-0.93	14	0.63	0.55	121	0.53
1fc2	500	3.99 – 8.45	245	-0.31	-0.7	4	0.46	0.22	488	0.25
1igd	500	3.11 – 12.55	135	-0.57	-1.7	38	0.81	0.79	113	0.84
1shf-A	437	4.39 – 12.35	19	-1.36	-1.36	13.7	0.15	0.16	211	0.18
2cro	500	3.87 – 13.48	208	-0.38	-0.8	0	0.36	0.36	362	0.16
2ovo	347	4.38 – 13.38	15	-1.36	-1.5	23.1	0.56	0.59	162	0.45
4pti	343	4.94 – 13.18	119	-0.46	-1.28	14.6	0.67	0.52	250	0.63
unk	500	6.68 – 13.94	190	-0.42	-0.46	0	0.25	0.07	N/A	0.07
Average	440	4.05 – 11.58		-0.64	-0.99	9.9	0.44	0.38		0.35
semfold
1ctf	11,400	4.44 – 12.98	1,936	-0.77	-0.87	9.7	0.13	0.17	10252	0.05
1e68	11,360	2.98 – 12.53	6,388	-0.25	-0.27	14.5	0.19	0.13	2951	0.31
1eh2	11,440	5.32 – 15.07	1,068	-1.03	-1.41	21.9	0.24	0.21	3998	0.22
1khm	21,080	3.84 – 14.77	8,992	-0.37	-0.67	5.9	0.1	0.1	13444	0.07
1nkl	11,660	3.84 – 14.22	2,862	-0.61	-0.73	14.4	0.32	0.32	3992	0.32
1pgb	11,280	4.67 – 13.01	3,650	-0.49	-0.59	7.4	0.09	0.11	11274	0.06
Average	13,037	4.18 – 13.76		-0.59	-0.76	12.3	0.18	0.17		0.17
Rosetta
1a32	1,610	0.92 – 16.89	352	-0.66	-1.02	19.3	0.89	0.93	290	0.87
1aa3	1,865	3.02 – 12.77	390	-0.68	-0.77	3.8	0.57	0.6	1	0.66
1afi	1,824	2.24 – 15.14	26	-1.85	-2.22	42.8	0.92	0.94	201	0.95
1ail	1,807	1.97 – 14.69	95	-1.28	-1.77	59.8	0.92	0.93	49	0.91
1am3	1,898	1.36 – 11.63	245	-0.89	-1.92	39	0.69	0.75	1	0.81
1bq9	1,825	2.59 – 15.73	303	-0.78	-1.88	30.1	0.41	0.47	1	0.68
1bw6	1,900	1.89 – 12.30	11	-2.22	-2.5	27.9	0.75	0.74	1	0.84
1cc5	1,892	6.41 – 26.78	280	-0.83	-1.06	30.7	0.46	0.46	1891	0.36
1cei	1,897	4.57 – 16.34	185	-1.01	-2.8	51.1	0.82	0.84	255	0.75
1csp	1,809	3.89 – 17.92	361	-0.7	-1.03	7.7	0.49	0.47	1	0.58
1ctf	1,922	5.07 – 15.81	305	-0.8	-2.44	31.2	0.75	0.7	1	0.67
1dol	1,871	3.77 – 14.87	100	-1.27	-1.27	17.1	0.37	0.4	1	0.6
1gab	1,898	2.75 – 11.81	345	-0.74	-0.74	0.5	0.29	0.29	1	0.38
1hyp	1,893	4.64 – 15.63	337	-0.75	-1.62	20.6	0.19	0.26	55	0.42
1kjs	1,893	3.37 – 13.68	77	-1.39	-1.68	30.1	0.79	0.76	1	0.78
1lfb	1,893	2.47 – 14.93	198	-0.98	-1.65	27.5	0.73	0.74	1	0.81
1msi	1,894	5.84 – 14.52	107	-1.25	-1.58	32.7	0.47	0.49	1	0.59
1mzm	1,934	3.68 – 15.08	443	-0.64	-0.66	1	0.05	0.1	191	0.19
1nkl	1,898	2.73 – 12.74	208	-0.96	-1.41	24.2	0.58	0.54	1	0.58
1nre	1,893	1.80 – 17.11	300	-0.8	-1.5	37	0.7	0.75	1	0.82
1orc	1,883	2.88 – 15.08	343	-0.74	-1.09	20.2	0.57	0.57	2	0.65
1pgx	1,851	5.03 – 16.75	465	-0.6	-0.6	0	-0.19	-0.17	1261	-0.2
1pou	1,898	2.28 – 17.68	322	-0.77	-2.13	46.9	0.59	0.64	1	0.77
1ptq	1,885	5.42 – 12.23	368	-0.71	-1.29	11.7	0.12	0.09	1	0.41
1r69	1,733	2.26 – 12.58	218	-0.9	-1.03	30	0.73	0.76	1	0.74
1res	1,723	1.89 – 9.15	475	-0.56	-0.57	0	-0.13	0	334	-0.17
1sro	1,881	3.39 – 15.36	462	-0.61	-0.83	4.8	0.77	0.75	1	0.68
1tif	1,849	2.61 – 11.56	464	-0.6	-1.46	15.1	0.59	0.53	1	0.61
1tuc	1,894	4.49 – 16.85	37	-1.71	-2.16	35.9	0.66	0.66	1	0.69
1uba	1,899	4.07 – 11.62	346	-0.74	-1.22	31.6	0.39	0.41	1	0.51
1utg	1,897	3.36 – 16.50	535	-0.55	-0.73	18.5	0.51	0.5	1	0.65
1uxd	1,896	1.12 – 10.13	181	-1.02	-1.21	25.8	0.61	0.58	1	0.68
1vcc	1,857	3.85 – 16.90	64	-1.46	-3.27	41.5	0.76	0.78	1	0.6
1vif	1,896	4.78 – 15.18	233	-0.91	-1.03	6.9	0.76	0.76	1	0.76
2ezh	1,893	2.34 – 18.26	510	-0.57	-2.24	28.5	0.56	0.57	1	0.68
2fow	1,834	4.03 – 13.89	59	-1.49	-2.22	39.3	0.46	0.54	1	0.64
2fxb	1,800	7.46 – 19.02	58	-1.49	-2.3	47.8	0.75	0.75	1	0.48
2pdd	1,740	2.33 – 10.02	934	-0.27	-1.09	17.8	0.21	0.23	1	0.53
2ptl	1,835	2.21 – 15.45	16	-2.06	-2.22	38.2	0.86	0.86	1	0.78
5icb	1,870	2.98 – 13.68	527	-0.55	-2.49	30	0.59	0.62	1	0.7
5pti	1,853	4.88 – 15.31	586	-0.5	-1.28	8.6	0.24	0.2	1	0.6
Average	1,858	3.38 – 14.87		-0.96	-1.56	25.2	0.54	0.56		0.61

The PDB code, the number of decoy conformations (N), the RMSD range of the decoys relative to the experimentally determined conformation, the RMSD ranking of the best-scoring conformation, the log probability of selecting the best-scoring conformation (log P_B1), the log probability of selecting the lowest RMSD conformation in the top 10 best scoring conformations (log P_B10), the fraction enrichment of the 10% lowest RMSD conformations in the top 10% best scoring conformations (F.E.), the correlation coefficient between scores and RMSDs (C.C.), the Spearman's rank correlation coefficient between scores and RMSDs (R.C.), the ranking of the experimentally determined conformation relative to the decoy conformations based on density scores (R_exp), and the correlation coefficient calculated by the original formula used by Simons et. al. [27] (C.C._orig) are shown. In general, the density score function performs very well, with dependence on the properties of the decoy sets.

Table 2 shows that the performance of the density score function is strongly dependent on the intrinsic properties of decoy generation methods and the quality of the decoy sets, with the best performance achieved in the 4state_reduced sets and the worst in the semfold sets. Although in general the density scores have relatively high correlation with C_α RMSDs, they have negative correlations in a small number of cases, indicating a failure of the function on these decoy sets. These include one protein (1jwe) in the fisa_casp3 sets and two proteins (1pgx and 1res) in the most recent Rosetta 10-14-01 sets.

Mechanism of the density score function

The 83 decoy sets used in our study were produced using several different simulation methods, which may explain why the same scoring function performs very differently on sets generated by different methods [31]. To further investigate how the density score function works, we plotted four pairwise RMSD matrices using the decoy conformations for the 1ctf protein (Figure 1). 1ctf represents the carboxy-terminal domain of L7/L12 50s ribosomal protein from Escherichia coli and was chosen for this analysis since it is present in four groups of decoy sets that we used (4state_reduced, lattice_ssfit, lmds and semfold). The correlation coefficients between the density scores and C_α RMSDs for 1ctf in these four decoy sets are 0.98, 0.71, 0.41 and 0.13, respectively (Table 2). Only the 1000 lowest RMSD conformations were used for lattice_ssfit and semfold sets because of their large size. For all the four matrices, the upper left corner tends to be black, which means that low RMSD decoy conformations tend to be more similar with each other. The density score formula calculates the overall distance between a given conformation and all other conformations, so ideally it has a perfect negative correlation with the density around the decoy conformations. When conformations in a region tend to have lower pairwise RMSD with each other, the density of such a region will be higher, which explains the high correlation between density scores and C_α RMSDs of decoys relative to the experimentally determined structure.

Figure 1.

Pairwise RMSD matrix plot for 1ctf in the 4state_reduced, lattice_ssfit, lmds and semfold decoy sets. Each column or row represents one decoy conformation, and each cell represents the pairwise RMSD between the two conformations that correspond to the row and the column. Both columns and rows are ordered by the C_α RMSD between the corresponding decoy conformation and the experimentally determined conformation. The color of the cells reflects the value of the pairwise RMSD between two decoys: the darker the cell, the lower the pairwise RMSD. The dimension of the four matrices are 630 × 630 (a), 1000 × 1000 (b), 497 × 497 (c) and 1000 × 1000 (d), respectively. Low-RMSD decoy conformations tend to have lower pairwise RMSD with each other.

Based on the above observations, we propose a theory on how the density score function works. During each step of a simulation process, a scoring function is used to judge whether a newly simulated conformation is energetically more favorable than the previous one. This step is iterated for certain times, and at the end of the simulation one or a few low scoring conformations are kept, achieving a local minima in terms of the scoring function. We call such minima "scoring basins". The scoring basins may or may not resemble the energy basin in conformational space. Usually structure predictors repeat the simulation process many times and save all the output conformations which comprise the decoy sets. These decoys tend to accumulate around such scoring basins so that the bottom of the basin has a higher density relative to the upper part of the basin. For exhaustive methods where the conformational space is evenly sampled, conformations near each other in space are more likely to have similar structures; once the non-native conformations are filtered out, similar structures tend to cluster together and scoring basins are formed by the filtering criteria, as is the case for the 4state_reduced sets. When a scoring basin is in close proximity to the energy basin, conformations around the bottom of the basin are near-native ones. In this case, there is a strong correlation between C_α RMSDs and the density of the space around these conformations. In our formula, we use the sum of RMSDs between a given conformation and with all other conformations in the decoy set to approximate the density.

For the four ensembles of decoy conformations depicted in Figure 1, the conformations represented in the upper left corner of the matrices have lower C_α RMSD, so they tend to reside near the bottom of the scoring basin. The density is higher near the bottom, so decoys in that region have lower pairwise RMSDs between each other, making the cells darker than others. Interestingly, for the lmds set, three obvious "black blocks" are seen in the corresponding matrix. By examining the C_α RMSD histogram of this protein (Figure 2), we found that there are actually three peaks, which account for the three "black blocks". This means that the pathological tendencies of simulation methods used in lmds sets may produce decoys that are far from the native conformation but tend to cluster together. In other words, three distinct scoring basins are encountered during the fold simulation process around which decoys tend to accumulate, yet only one of the basins can approximate the real energy basin. Because of that, high-density conformations in this set may not be near-native conformations if they reside in a wrong scoring basin, and the correlation coefficients between density scores and C_α RMSDs of decoys relative to native conformations cannot be very high. In the case of the 4state_reduced set, although there are two peaks in the C_α RMSD histogram, only one scoring basin is formed because conformations are sampled evenly by this simulation method. Here, the density scores have high correlation with the C_α RMSD of decoys relative to experimentally determined conformations.

Figure 2.

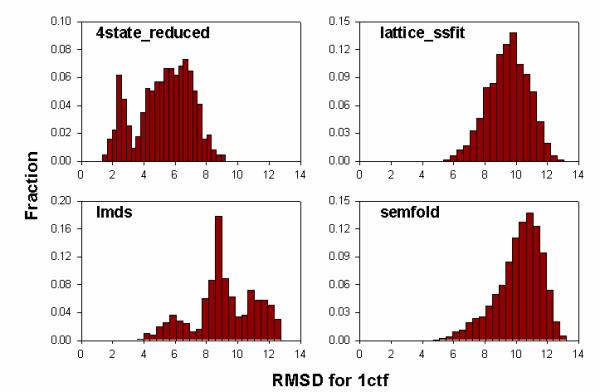
Histogram of C_α RMSDs relative to experimentally determined conformation for the 1ctf protein in the 4state_reduced, lattice_ssfit, lmds and semfold sets. There are two peaks for the 4state_reduced set though only one scoring basin was found in Figure 1. There are three peaks for lmds set, which happen to represent three scoring basins where decoy conformations tend to accumulate.

Based on our theory, when near-native conformations are not sufficiently sampled, native conformations will not necessarily have the highest density. This explains why for most proteins, the density score ranking of the native conformation is not very high (Table 2, Column 10) in spite of the high correlation between C_α RMSDs and density scores. Our goal for developing these scoring functions is to select the most near-native conformations from a decoy set, when the experimental structure is unknown. The ranking of native conformation per se is not important for structure prediction since it may not be an indicator of how well a function can select near-native ones. In other words, it is relatively easy to design functions that discriminate the native conformation from a set of decoys, but hard to design functions that can discriminate near-native decoys from other decoys. The density score function (as well as self-RAPDF) is highly dependent on the search function used in the fold simulation process, and does not contain explicit information about native conformations (i.e., they are trained on decoys, not native conformations). Therefore, a complementary and good search method must be used with density scores (or self-RAPDF) at least for the initial decoy generation to minimize bias to erroneous conformations, which is the case for the methods used to generate our decoy sets. Finally, a scoring function that scores native conformation well is dependent on the particular types of native conformations that it is derived from. In our case, for 57 out of 83 decoy sets, the native conformation (or its slightly refined version; C_α RMSD < 0.2 Å) scores as the top best conformation by the original RAPDF. Of the remaining 26 decoy sets, the native conformation for 11 of them are derived by NMR spectroscopy which usually do not score well with RAPDF since the function is parameterized on structures derived from X-ray crystallography (Liu and Samudrala, manuscript in preparation).

Performance of self-RAPDF

For every decoy set, we generated a separate set of atom-atom contact probabilities using a formulation similar to the residue-specific all-atom scoring function (RAPDF) [7]. Using this function, called self-RAPDF, we scored all the decoy conformations used to compile the function, and evaluated the performance of the function with the four measures described before. Table 3 compares the performance of the RAPDF and the self-RAPDF on individual decoy sets, and Figure 3 compares the performance on the decoy sets grouped by their generation methods. The self-RAPDF has better performance than RAPDF in terms of log P_B1 (62/83 decoy sets), log P_B10 (56/83 decoy sets), F.E. (63/83 decoy sets) or C.C. (76/83 decoy sets). We noticed that the performance of self-RAPDF is highly dependent on the performance of the density score function, which specifies the weighting scheme in generating the self-RAPDF. Because of the high correlation between C_α RMSDs and the density scores, the self-RAPDF generated higher correlation with C_α RMSDs than RAPDF in all decoy groups. However, for some proteins in the fisa and semfold sets, self-RAPDF did not tend to pick lower RMSD conformations over RAPDF, as judged by the mean of log P_B1 for these groups of sets. This suggests that when performing structure selection, we can choose RAPDF or self-RAPDF based on the decoy generation methods to achieve the best results. However, since self-RAPDF almost always has better performance than RAPDF in terms of correlation with RMSD, this means self-RAPDF may be a better scoring function than RAPDF to be used in fold simulation during the structure refinement process.

Table 3.

Comparison of performance of the RAPDF and self-RAPDF on 83 decoy sets grouped by their generation methods.

Protein (PDB code)	RAPDF				Self-RAPDF
	log PB1	log PB10	F.E.(%)	C.C.	log PB1	log PB10	F.E.(%)	C.C.
4state_reduced
1ctf	-2.50	-2.80	57.14	0.73	-2.32	-2.80	79.37	0.89
1r69	-1.93	-2.83	42.96	0.70	-2.83	-2.83	72.59	0.88
1sn3	-1.44	-1.97	40.91	0.47	-2.82	-2.82	84.85	0.89
2cro	-2.05	-2.23	45.99	0.76	-2.83	-2.83	78.64	0.92
3icb	-1.40	-2.34	68.91	0.85	-2.21	-2.51	81.16	0.92
4pti	-0.64	-2.54	23.29	0.49	-1.80	-2.84	87.34	0.89
4rxn	-0.43	-2.35	53.18	0.57	-2.53	-2.83	78.29	0.88
fisa
1fc2	-0.86	-0.86	4.00	0.52	-0.39	-0.98	6.00	0.77
1hdd-C	-2.40	-2.40	44.00	0.55	-0.52	-1.80	30.00	0.74
2cro	-2.40	-2.40	26.00	0.19	-0.66	-1.70	24.00	0.29
4icb	-0.71	-1.30	20.00	0.20	-0.67	-1.12	26.00	0.46
fisa_casp3
1bg8-A	-0.94	-1.90	15.00	0.16	-0.80	-1.25	9.17	0.09
1bl0	-0.28	-2.69	12.36	0.18	-0.17	-0.20	47.37	0.59
1eh2	-1.11	-1.80	18.65	0.25	-0.65	-2.91	43.93	0.53
1jwe	-0.42	-1.19	2.84	-0.14	-0.12	-0.38	1.42	-0.23
l30	-0.27	-1.65	12.14	-0.12	-0.58	-0.86	0.00	0.18
smd3	0.00	-0.57	4.17	-0.20	-0.59	-1.48	15.83	0.28
lattice_ssfit
1beo	-0.86	-1.49	7.00	-0.02	-2.52	-2.52	12.00	0.09
1ctf	-0.15	-1.55	10.00	-0.06	-1.40	-1.48	23.50	0.15
1dkt-A	-0.31	-3.00	10.50	-0.04	-1.43	-2.00	25.00	0.15
1fca	-0.07	-1.19	8.00	0.00	-1.32	-1.33	23.00	0.13
1nkl	-0.05	-0.96	5.00	-0.19	-0.88	-1.54	7.50	-0.01
1pgb	-0.16	-0.67	10.00	-0.07	-0.40	-0.40	8.50	0.04
1trl-A	-0.45	-1.10	7.50	-0.07	-0.62	-1.63	12.00	0.09
4icb	-1.82	-1.82	21.50	-0.01	-1.76	-2.70	27.00	0.20
lmds
1b0n-B	-0.06	-1.44	6.04	-0.21	-0.85	-2.00	16.10	0.10
1bba	-0.38	-1.85	16.00	0.23	-0.41	-0.49	0.00	0.15
1ctf	-0.32	-2.40	10.06	0.26	-0.38	-0.60	0.00	0.39
1dtk	-0.14	-0.97	4.65	0.04	-0.38	-1.05	9.30	0.41
1fc2	-0.62	-2.10	8.00	0.02	-0.20	-0.62	6.00	0.27
1igd	-1.18	-2.70	22.00	0.08	-0.57	-1.52	28.00	0.68
1shf-A	-0.10	-0.85	11.44	-0.03	-1.36	-1.36	13.73	0.14
2cro	-0.10	-0.36	6.00	-0.22	-0.27	-0.39	0.00	-0.19
2ovo	-0.58	-0.68	14.41	0.18	-1.50	-1.50	23.05	0.51
4pti	-0.05	-1.93	23.32	0.09	-0.46	-1.28	29.15	0.53
unk	-0.70	-1.27	16.00	0.17	-0.46	-0.85	6.00	0.10
semfold
1ctf	-0.39	-0.48	11.05	0.07	-0.34	-0.40	8.86	0.10
1e68	-2.62	-2.68	25.17	0.13	-0.17	-2.68	27.29	0.13
1eh2	-0.08	-0.29	14.51	0.07	-0.47	-0.55	19.84	0.10
1khm	-0.09	-0.36	12.48	0.01	-0.34	-0.38	9.01	-0.03
1nkl	-3.11	-3.11	17.67	0.10	-2.55	-2.77	20.07	0.21
1pgb	-0.05	-0.59	15.07	0.05	-0.53	-0.76	15.51	0.10
Rosetta
1a32	-0.09	-0.31	0.00	-0.22	-0.97	-1.41	44.10	0.89
1aa3	-0.14	-0.69	9.65	-0.06	-0.52	-0.70	6.97	0.44
1afi	-0.54	-2.22	27.96	0.45	-2.18	-2.78	52.08	0.91
1ail	-0.07	-0.33	5.53	0.01	-1.77	-3.26	57.55	0.71
1am3	-0.08	-0.27	9.48	0.06	-2.38	-2.38	44.26	0.85
1bq9	-0.38	-1.11	14.80	0.04	-1.88	-1.90	25.75	0.23
1bw6	-0.14	-0.89	18.42	0.49	-1.04	-2.22	44.21	0.75
1cc5	-0.42	-2.37	8.99	0.02	-0.20	-2.37	24.31	0.24
1cei	-0.27	-0.30	13.71	0.02	-1.18	-2.38	45.86	0.49
1csp	-0.53	-1.30	11.06	0.04	-0.58	-1.47	16.58	0.31
1ctf	-0.04	-0.56	8.85	-0.06	-0.27	-1.64	21.33	0.31
1dol	-0.57	-1.58	20.31	0.08	-0.69	-1.58	24.59	0.27
1gab	-0.11	-1.49	14.75	-0.04	-0.64	-0.70	0.53	0.16
1hyp	-0.34	-0.34	3.17	-0.29	-0.89	-1.09	8.98	-0.24
1kjs	-0.91	-1.56	20.07	0.44	-1.39	-2.16	36.45	0.74
1lfb	-0.17	-0.55	5.28	-0.02	-1.86	-2.02	43.85	0.64
1msi	-1.35	-1.35	16.90	0.11	-0.83	-1.50	25.87	0.19
1mzm	-0.81	-0.81	4.65	-0.19	-0.32	-0.85	0.52	-0.13
1nkl	-1.07	-1.35	20.55	0.10	-0.96	-1.03	17.39	0.53
1nre	-0.30	-0.37	3.17	0.05	-0.94	-2.68	50.71	0.74
1orc	-0.03	-0.43	0.00	-0.35	-0.74	-1.03	21.24	0.43
1pgx	-0.07	-0.38	1.08	-0.55	-0.37	-0.47	1.08	-0.39
1pou	-0.29	-1.65	11.06	0.05	-2.13	-2.80	54.27	0.49
1ptq	-0.12	-1.39	16.98	0.07	-0.87	-1.31	9.55	0.01
1r69	-0.51	-1.20	19.04	0.14	-1.82	-1.82	53.09	0.61
1res	-0.95	-1.50	13.35	0.00	-0.41	-0.57	0.00	0.01
1sro	-0.55	-1.11	15.95	0.15	-0.66	-0.84	18.08	0.68
1tif	-0.53	-1.93	15.68	0.11	-1.17	-1.93	42.19	0.61
1tuc	-0.55	-0.78	11.09	0.18	-1.11	-1.90	33.79	0.71
1uba	-0.56	-0.74	4.74	-0.10	-0.63	-2.05	22.12	0.19
1utg	-0.16	-1.42	7.38	0.02	-0.73	-0.80	26.36	0.56
1uxd	-0.29	-0.58	13.19	0.07	-1.20	-2.43	29.54	0.79
1vcc	-0.05	-0.80	13.46	0.17	-1.46	-2.42	29.08	0.47
1vif	-0.24	-3.28	37.45	0.39	-0.97	-0.97	11.08	0.74
2ezh	-0.53	-1.13	26.41	0.40	-0.86	-1.06	36.98	0.78
2fow	-0.52	-0.57	9.27	0.13	-1.25	-1.39	25.63	0.51
2fxb	-0.43	-2.65	11.67	0.05	-0.87	-2.65	29.44	0.40
2pdd	-0.01	-2.01	16.09	-0.04	-1.01	-1.56	38.51	0.45
2ptl	-0.35	-2.06	20.71	0.17	-1.65	-2.06	39.78	0.72
5icb	-0.57	-0.99	21.93	0.40	-1.02	-2.57	32.62	0.66
5pti	-0.12	-0.34	1.08	-0.15	-0.50	-1.28	9.17	0.09

For legends please refer to Table 2. The self-RAPDF has better performance than RAPDF in terms of log P_B1 (62/83 decoy sets), log P_B10 (56/83 decoy sets), F.E. (63/83 decoy sets) and C.C. (76/83 decoy sets).

Figure 3.

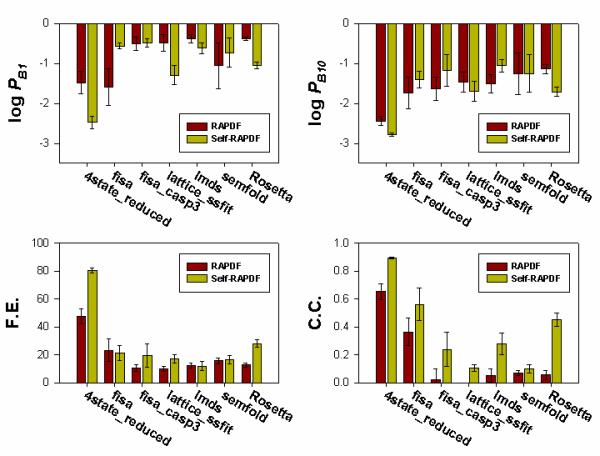
Comparison of the performance of RAPDF and self-RAPDF on 83 decoy sets grouped by their generation methods. The average value and standard error of log P_B1, log P_B10, fraction enrichment (F.E.) and correlation coefficient (C.C.) for each group of sets are shown. In most cases, self-RAPDF performs better than RAPDF.

More recent decoy sets such as those generated by the semfold method [34] or the Rosetta method [35] provide particularly challenging tests for scoring functions, because the decoys were assembled from fragments of experimentally determined structures. These sets contain a subset of misfolded conformations with similar local interactions, but are globally distant from the native fold. As a consequence, discriminating near-native conformations from the semfold [29] and the most recent Rosetta 10-14-01[30] sets is expected to be more challenging for any scoring function [36], and few results have been published on the performance of scoring functions using these decoy sets.

Unlike the density score function, the self-RAPDF can be used for not only structure selection, but also fold simulation. Therefore, it is especially important for self-RAPDF to have high correlation with the RMSD of decoy conformations. We compared the performance of RAPDF and self-RAPDF on the Rosetta sets in terms of log P_B1 and correlation coefficients (Figure 4). RAPDF generally performed poorly on these decoy sets, while self-RAPDF was superior at discriminating low RMSD structures for these decoy sets for 37/41 proteins, in terms of the C_α RMSD of the best scoring conformation.

Figure 4.

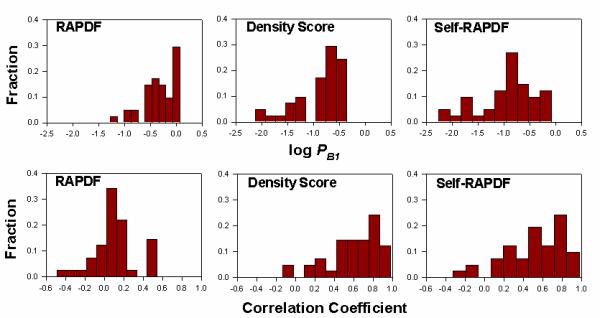
Histogram of log P_B1 (upper panel) and correlation coefficient between RMSD relative to experimentally determined conformation and scores (lower panel) generated by the RAPDF, the density score function and the self-RAPDF for the 41 decoy sets generated by the Rosetta method. Both the density score function and self-RAPDF perform much better than RAPDF for these sets.

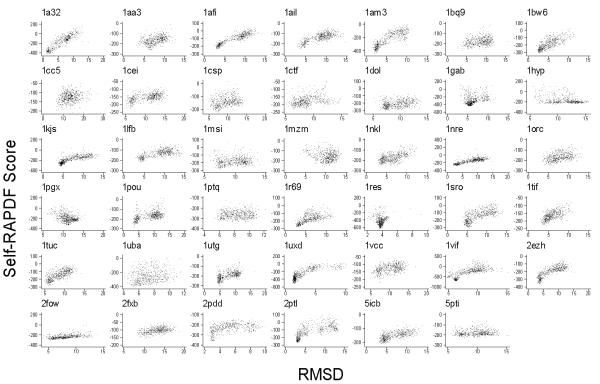
Figure 5 shows the scatter plot of the self-RAPDF scores versus C_α RMSDs of decoys relative to experimentally determined conformations for all 41 proteins in the Rosetta sets. A large fraction of near-native conformations were sampled in these sets [30]. Scores for most of the proteins have very good correlation with C_α RMSDs except 1hyp, 1mzm and 1pgx. The density score function for these 3 proteins had either negative or near-zero correlation with C_α RMSDs (Table 2), which explains the poor performance of the self-RAPDF on them.

Figure 5.

Self-RAPDF score versus C_α RMSD for 41 most recent Rosetta 10-14-01 decoy sets [30]. For most sets, self-RAPDF scores tend to have high correlation with C_α RMSDs between decoys and experimentally determined conformations.

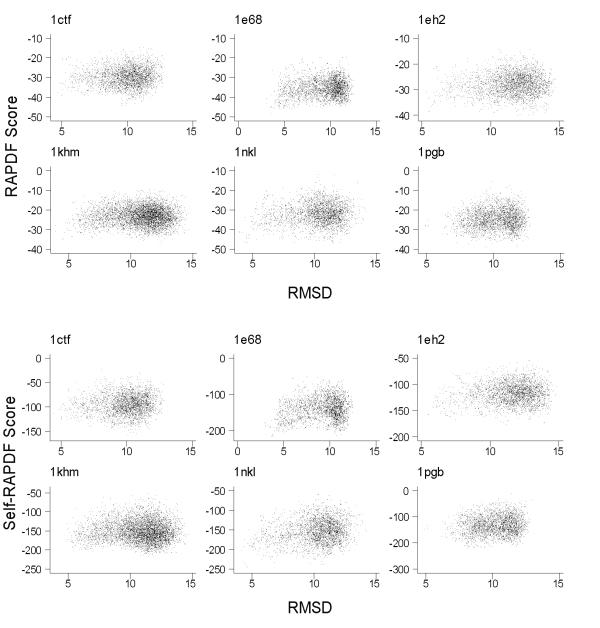
We also observed that neither RAPDF nor self-RAPDF has satisfactory performance on the semfold decoy sets (Figure 6). From our previous experience, these sets are difficult. None of the scoring functions we used before had good correlation with C_α RMSD on these decoy sets. Some possible reasons to explain the poor performance are detailed in the Discussion section.

Figure 6.

Scatter plot of RAPDF score or self-RAPDF score versus C_α RMSD for six semfold decoy sets. Both RAPDF score and self-RAPDF score do not discriminate decoys well on these sets.

Discussion

Current scoring functions generally try to maximize the Z score to discriminate native conformations from near-native ones, but perform poorly in the real problem that we are facing with in structure prediction: selecting the most near-native conformations from an ensemble of decoys. Here, we introduce two decoy-dependent scoring functions, the density score function and self-RAPDF, which can be used to aid structure selection. They work better at selecting the most near-native conformations compared to previously published results.

It has been hypothesized that the behavior of the density score function represents a feature of the protein energetic surface [26], i.e., that the lowest energy conformation is the most populated one. A simpler explanation is that what we are observing is purely a statistical phenomenon: traditional scoring functions are not perfect, and if they are partially correct, then it is likely that two conformations that are close to each other are also likely to be close to the native conformation. In effect, the conformation with the best score is the median, i.e., the one with the smallest total distance to every conformation in the entire decoy set. By taking into account the ensemble of conformations generated by the scoring function, we maximize the amount of information used. In other words, conformations that score poorly by a discriminatory function also have information content that can be used to achieve better discrimination.

We therefore argue that the resulting ensemble of conformations after a structure prediction process will not be an unbiased sampling of the real energy basin. Instead, we propose that since any scoring function used in structure simulation cannot be perfect, it will form one or more scoring basins that may or may not resemble the real energy basin. These decoys then accumulate around the scoring basins, instead of the energy basin. When a scoring basin is near the energy basin, i.e., when a lot of near-native conformations are sampled in the decoy sets, we expect good performance from density-based approaches. Otherwise, we do not expect high correlation between the density around a given decoy conformation and the spatial distance between this conformation and the bottom of the energy basin, where the native conformation resides.

The key to the success of such decoy-dependent scoring functions is that near-native conformations are adequately sampled in the conformational space, which is not true in some cases. This in part accounts for the failure of both functions on some proteins in the fisa_casp3, semfold and Rosetta decoy sets. On the other hand, the intrinsic properties of the simulation process itself may dictate whether these functions will work well or not. This explains why decoy sets generated by the same simulation methods tend to have similar performance with a particular scoring function, but the performance is divergent across those sets from different sources. The 4state_reduced sets always yield the best performance for most scoring functions, since they are generated by sampling conformational space around native conformations evenly, using knowledge of the experimental structures. In such cases, the scoring basin should largely overlap with the energy basin of the proteins. The semfold and Rosetta sets are similar in that both of them are generated by assembling small pieces (3–9 amino acid residues) of local conformations from experimentally determined structures, and thus both sets provide a challenge. The density score function and self-RAPDF perform reasonably well on the Rosetta decoy sets with a few exceptions, but perform unsatisfactorily on the semfold sets. One reason is that the semfold sets does not contain as many near-native conformations as the Rosetta sets (Table 2). It is also worth noting that RAPDF itself was a component of the scoring function used in the semfold structure simulation process. We therefore expect that the scoring basin itself be biased toward correct RAPDF atom-atom contacts. So decoy conformations in semfold sets are already minimized in terms of the normal range of atom-atom contacts, and would not be easily discriminated by another atom-atom contact probability scoring function such as self-RAPDF.

It is not very surprising that self-RAPDF works better than RAPDF when near-native conformations are sampled adequately in the decoy sets. The RAPDF scoring function was compiled from an ensemble of native structures in certain structure databases, such as the Protein Data Bank (PDB), which contains very diverse conformations with bias to certain types of folds. The statistics may not work well for certain protein targets if their folds are not represented in the experimentally determined structure database. Self-RAPDF is compiled from an ensemble of decoy conformations, some of which resemble the native fold. So if a large fraction of near-native conformations are present in the decoy set, appropriate residue-specific atom-atom contacts for the particular sequence are more likely to be present in these decoys. Compiling this contact information can help in determining whether a given decoy conformation conforms to the majority of near-native conformations.

Besides RAPDF, other knowledge-based scoring functions have been developed in recent years with varying degrees of success [8-10]. These functions usually compile some statistics from databases that contain experimentally determined structures, and use such statistics to test the probability of a given conformation to be native-like. The results in this paper also have implications on the performance of other knowledge-based scoring functions.

Other structure clustering algorithms similar to our scoring functions have been applied in previous CASP experiments for structure selection. Simons et al. used the number of structural neighbors within a certain RMSD threshold as the basis of the clustering during the CASP3 experiment [27], and Bonneau et al. used simultaneously clustering of conformations using an iteratively reduced RMSD cutoff [28]. The original clustering algorithm fixed the RMSD cutoff to generate clusters of different sizes, but the simultaneous clustering algorithm fixed the size of each cluster to contain ~100 conformations. They worked well for the decoy sets generated by Rosetta method, but their performance was not reported for other decoy sets. Compared to these clustering algorithms, both the density score function and the self-RAPDF function give quantitative scores for every decoy conformation. In addition, the self-RAPDF function can be used in structure refinement and fold simulation, after an initial decoy set has been generated.

The weighting scheme in our work was chosen somewhat arbitrarily. Only a small fraction of conformations have low C_α RMSDs for any given decoy set, which are the ones that we are most interested in. We seek to derive weights to inflate the contribution of these low-RMSD conformations to the self-RAPDF function. However, the low-RMSD conformations cannot be identified without knowledge of the experimentally determined structures. Since the density score function usually has high correlation with C_α RMSDs, we can use it as a surrogate of how similar a given decoy conformation is to the experimentally determined conformation, and derive weights based on the density scores. An exponential weighting scheme based on the density scores is shown to work quite well. Other weighting scheme parameterized on other scoring functions need to be explored.

During a fold simulation, we need a scoring method to evaluate the quality of newly simulated conformations relative to those already generated. This method should be reasonably fast, and have a relatively high correlation to the accuracy of predicted conformations. Currently we are using the RAPDF as one such component in our de novo structure prediction protocol [34]. Based on the high correlation of self-RAPDF scores and RMSDs relative to experimentally determined conformations, it is also possible to use self-RAPDF for further refinement of predicted protein conformations. Further work is needed to test this hypothesis.

Conclusions

In conclusion, both the density score and the self-RAPDF functions are decoy-dependent scoring functions for improved protein structure selection. The implementation of both methods is simple, and the execution is very fast, so they can be applied to very large decoy sets. Both scoring functions compile information from the ensemble of decoy conformations, based on the assumption that a large fraction of near-native conformations are sampled in the decoy set, and these decoys can provide information about the native conformation. Unlike other knowledge-based scoring functions, both functions used here do not use any knowledge of experimentally determined structures. Besides structure selection, the self-RAPDF may also aid in fold simulation, the effectiveness of which is currently being evaluated. Based on our work, it is reasonable to assume that other knowledge-based scoring functions can also compile statistics from decoy conformations, for use in both structure selection and simulation.

Methods

Formulation of the density score function

Suppose a decoy set contains n decoys x₁, x₂, ..., x_n. For any given decoy x_i (1 ≤ i ≤ n), the density score is calculated using the formula:

where S_i is the density score of decoy x_i, r_ij is the pairwise C_α RMSD between decoy x_i and decoy x_j (1 ≤ i,j ≤ n).

Formulation of the self-RAPDF function

For a given decoy set, we first normalize the density scores to be between -1 and 1 using the following formula:

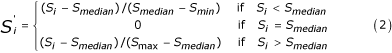
where is the normalized density score for decoy x_i, and S_median is the median density score for the set.

Each decoy conformation is weighted according to its normalized density score:

where W_i represents the weight of decoy x_i and k is a constant. In this paper we choose k to be 5. The contribution of each decoy conformation is multiplied by its own weight during the compilation process of the self-RAPDF statistics.

The all-atom scoring function, RAPDF, was used to calculate the probability of a conformation being native-like, given a set of inter-atomic distances. A full description can be found in the original paper [7]. The compilation of self-RAPDF library uses a modified version of RAPDF and incorporates the weighting scheme described above. Briefly, the required probabilities are compiled by counting frequencies of distances between pairs of atom types in a decoy set. The counts for each conformation are multiplied by its weight, and are summed together to generate an overall probability. All non-hydrogen atoms are considered, and the description of the atoms is residue specific, which results in a total of 167 atom types. We divide the observed distances into 1.0 Å bins ranging from 3.0 Å to 20.0 Å. Contacts between atom types in the 0.0–3.0 Å range are placed in a separate bin, resulting in a total of 18 distance bins.

We compile tables of scores s proportional to the negative log conditional probability that we are observing a native conformation given an inter-atomic distance d for all possible pairs of the 167 atom types, a and b, for the 18 distance ranges, P(C | d_ab):

where P(d_ab|C) is the probability of observing a distance d between atom types a and b in a correct structure, and P(d_ab) is the probability of observing such a distance in any structure. The required ratios P(d_ab|C)/P(d_ab) can be obtained by:

where 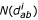is the number of observations of atom types a and b in a particular distance bin d in decoy x_i, and W_i is the weight for decoy x_i from equation (3). No intra-residue distances are included in the summation.

Source of decoy sets

The decoy sets used for the evaluation of these scoring functions were obtained from the Decoys 'R' Us database http://dd.compbio.washington.edu and the most recent Rosetta 10-14-01 decoy set http://www.bakerlab.org. We used only those decoy sets that contained a reasonably large number (>100) of decoy conformations, resulting in 83 decoy sets from seven different sources (4state_reduce, fisa, fisa_casp3, lattice_ssfit, lmds, semfold and Rosetta). The 4state_reduced sets were generated by exhaustively enumerating 10 selectively chosen residues in each protein using a 4-state off-lattice model, and filtering the conformations with a variety of criteria [12]. The fisa, fisa_casp3, semfold and Rosetta sets were generated using a fragment insertion simulated annealing procedure to assemble near-native structures from fragments of unrelated protein structures with similar local sequences [30,34,35]. The lattice_ssfit sets were generated by exhaustively enumerating sequence on a tetrahedral lattice and filtering the conformations by a combination of all-atom functions [37]. The lmds sets were generated using a scoring function which is based on a united and soft atom version of the "classic" ENCAD forcefield that ensures that local minima are chemically valid with reasonable geometry and without clashes [29]. More detailed description of these sets is available in the corresponding websites.

Methods used to evaluate scoring functions

Four different methods were used in this study to evaluate the performance of scoring functions, emphasizing their different aspects. These include:

(1) log P_B1: The log probability of selecting the best scoring conformation. Suppose the best scoring conformation x_i has the C_α RMSD rank of R_i in n decoy conformations, this probability can be calculated as

log P_B1 = log₁₀ (R_i/n)     (6)

(2) log P_B10: The log probability of selecting the lowest RMSD conformation among the top 10 best scoring conformations. Suppose x_i has the lowest RMSD among the 10 best scoring conformations, with the RMSD rank of R_i in all the N decoy conformations, this probability is calculated using the above formula. Since the number of conformations varies a lot for different types of decoy sets, dividing the rank by n in the formulation of both logP_B1 and logP_B10 ensures a fair comparison between different decoy sets.

(3) F.E.: Fraction enrichment of the top 10% lowest RMSD conformations in the top 10% best scoring conformations.

(4) C.C.: The correlation coefficient between C_α RMSDs and the scores generated by the scoring function.

Score calculation and data analysis

The structure preparation and score calculation were performed using the RAMP program suite, available at http://software.compbio.washington.edu. Additional data analysis was done using the statistics software STATA (College Station, TX, USA).

Authors' contributions

KW carried out the computational experiments and drafted the manuscript. BF and RS developed the idea and evaluated the results. ML and RS provided intellectual guidance and mentorship. RS coordinated the whole study.