Projection-Based Volume Alignment

Abstract

When heterogeneous samples of macromolecular assemblies are being examined by 3D electron microscopy (3DEM), often multiple reconstructions are obtained. For example, subtomograms of individual particles can be acquired from tomography, or volumes of multiple 2D classes can be obtained by random conical tilt reconstruction. Of these, similar volumes can be averaged to achieve higher resolution. Volume alignment is an essential step before 3D classification and averaging. Here we present a projection-based volume alignment (PBVA) algorithm. We select a set of projections to represent the reference volume and align them to a second volume. Projection alignment is achieved by maximizing the cross-correlation function with respect to rotation and translation parameters. If data are missing, the cross-correlation functions are normalized accordingly. Accurate alignments are obtained by averaging and quadratic interpolation of the cross-correlation maximum. Comparisons of the computation time between PBVA and traditional 3D cross-correlation methods demonstrate that PBVA outperforms the traditional methods. Performance tests were carried out with different signal-to-noise ratios using modeled noise and with different percentages of missing data using a cryo-EM dataset. All tests show that the algorithm is robust and highly accurate. PBVA was applied to align the reconstructions of a subcomplex of the NADH: ubiquinone oxidoreductase (Complex I) from the yeast Yarrowia lipolytica, followed by classification and averaging.

1. Introduction

High resolution in 3D electron microscopy (3DEM) requires averaging data from multiple images and/or multiple volumes. Techniques ideally suited for analyzing single particles that show conformational variations, especially when these variations are not localized, are the random conical tilt reconstruction (RCT) (Radermacher et al., 1986; Radermacher et al., 1987) and the orthogonal tilt reconstruction techniques (OTR) (Leschziner and Nogales, 2006). In both techniques, pattern recognition methods are required to separate the projection images into different groups containing only similar particles before carrying out individual 3D reconstructions for each group. Since pattern recognition of 2D images cannot differentiate between variations of particle orientation and particle shape, a second alignment and classification step must be applied to the set of 3D reconstructions to find the source of the variations. Projection data belonging to similar volumes in different orientations can then be merged to obtain a higher resolution structure. An alternative technique for studying structures in different conformations and/or orientations is electron tomography (Hoppe et al., 1976a; 1976b; 1976c). Using either single axis, dual axis or conical tilting tomography methods, each object is reconstructed individually. The volumes are aligned, classified, using one of the methods suitable for 3D classification of volumes with missing data, and the projection data of volumes that are similar after alignment are merged into a single reconstruction. Missing data, however, limits the selection of classification methods. For example visual classification alone may be misleading, since missing data create artifacts that can easily be interpreted as conformational differences (eg. Frank, 1992).

Most of the alignment algorithms of 3D density maps with missing data are based on a normalized distance measurement using only the overlapping data. The constrained cross-correlation (Förster et al., 2008; Frangakis et al., 2002), implemented in real space, was used as the similarity measure for obtaining class averages of subtomograms of the envelope glycoproteins on the surface of SIV and HIV virions (Winkler, 2007; Winkler et al., 2009). A renormalized cross-correlation, implemented in Fourier space and normalized to the region of the commonly existing data was used and tested with GroEL particles (Schmid and Booth, 2008). A more general normalized distance measure was implemented by (Bartesaghi et al., 2008). Simultaneously searching shift and rotation parameters by either finding the maximum of a cross-correlation or the minimum of a distance is an onerous task. Hence, all the methods mentioned above perform separate searches for shifts and rotations. Recently, a maximum likelihood based algorithm was developed to optimize all parameters in the model (shifts, rotations, classification parameters, and the missing data) at the same time (Stölken et al., 2011). However, this algorithm is computationally expensive, especially when alignment parameters need to be determined with high accuracy.

We present here a new algorithm for aligning 3D density maps with missing data, that we have named projection-based volume alignment (PBVA). This algorithm searches 3D shift and rotation parameters simultaneously by multiple projection alignment. It is computationally faster than an exhaustive search using 3D cross-correlation and provides an accurate determination of the parameters. The algorithm is an extension of the earlier alignment techniques where 0° projections were used to align volumes to a reference (Radermacher et al., 2001; Ruiz et al., 2001). While we previously expanded this approach to sets of orthogonal projections (unpublished), here we present the generalization of the method, using multiple projections of a reference at arbitrary angles for the alignment of volumes. The angles of the reference projections can be chosen such that the projections show the most rotation sensitive features, thus further increasing the robustness of the algorithm. The alignment method has been tested with different signal-to-noise ratios and varying amounts of missing data. Tests have been carried out with model data and with cryo-EM data that represent single axis tilt series. Finally, the complete method, including multivariate statistical analysis by PPCA-EM (Yu et al., 2010) has been applied to a small RCT data set of a subcomplex of the NADH: ubiquinone oxidoreductase (Complex I) from the yeast Yarrowia lipolytica (Dröse et al., 2011).

2. Methods

3D alignment methods are used to bring two 3D density maps to the same orientation and position. Below we will present a detailed description of the projection based volume alignment method (PBVA) which uses a projection matching algorithm based on Radon transforms (Radermacher, 1994; 1997). Two volumes are aligned by aligning several projections of a reference volume to a second volume whose orientation is unknown. The alignment parameters of the projections are then combined to obtain the 3D alignment parameters of the second volume. Figure 1 illustrates the basic principle of the method for three projections. In practice, a larger number of projections are used to achieve a good balance between accuracy of the results and computational speed of the procedure. Missing data in the second volume do not influence the alignment, since the cross-correlation method used in the Radon transform based projection matching algorithm excludes known missing regions and adjusts the normalization of the cross-correlation accordingly. In addition, a method is presented to find the regions of missing data if they are not known a priori.

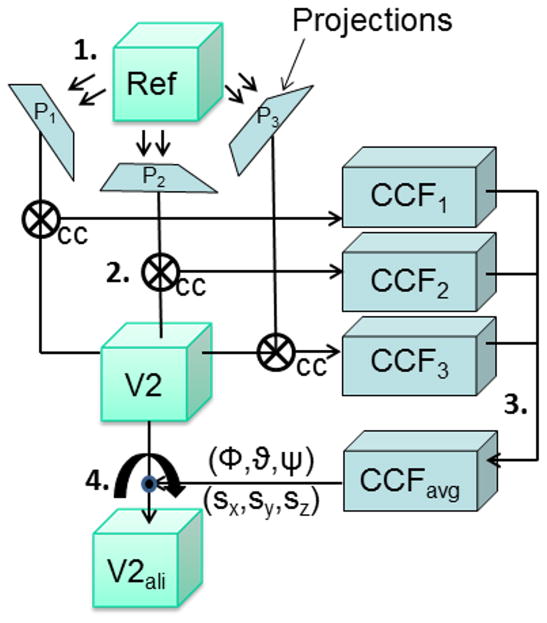
Figure 1.

Alignment of two volumes by projection matching, shown here for only three projections. The main steps are numbered. (1) The reference volume is projected along three directions, onto the projections, P1, P2 and P3. (2) Each projection then is matched to the second volume (V2) by a cross-correlation algorithm (cc). (3) The cross-correlation functions (CCF_i) are averaged, and the maximum of the averaged cross-correlation indicates the rotation of the second volume. The 2D translation vectors from all projections are combined into a 3D vector that describes the translational difference between the two volumes. (4) Rotation and translation parameters are applied to (V2) to obtain the aligned volume (V2_ali).

Projection matching is carried out by cross-correlation of the 2D Radon transform of a projection with the 3D Radon transform of a volume. In two dimensions, a discrete Radon transform is the set of all one-dimensional projections (line integrals) over a 180° angular range. In three dimensions, the Radon transform is the set of all lines obtained by integrating over all possible planes whose directions can be described by two angles, each sampled over a 180° range. When a one-dimensional Fourier transform is applied to the lines of either a 2D or 3D Radon transform, a Fourier transform in polar coordinates is obtained. Like for Fourier transforms, the central section theorem holds also for Radon transforms. The 2D Radon transform of a projection is a central cross-section through the 3D Radon transform of the corresponding volume. For computational purposes, both, polar Fourier transforms and Radon transforms can be used interchangeably, the main difference being that Fourier transforms are complex valued while Radon transforms are real valued which simplifies certain interpolation processes. The reconstruction algorithm frequently used in our laboratory averages 2D Radon transforms into a 3D Radon transform. In our implementation, every line in the 3D Radon transform contains an index that counts how many projection transform lines have been averaged into each line in the 3D transform (Radermacher, 1994). Thus, this index also provides information regarding the location of missing data; lines where no data have contributed show 0 as the index value. For projection matching, the 2D Radon or polar Fourier transform of a projection is cross-correlated line by line with all the lines in the central sections of the 3D Radon or Fourier transform, essentially comparing the projection with all possible projections of the volume. Lines with no contributions (missing data) are excluded from these calculations.

2.1 The geometric relation between two volumes

The geometric relation between two density maps can be described by a rotation matrix and a translation vector. If f(r) is the reference volume and g(r) is the volume that is shifted and rotated relative to the reference, then the relation between the two volumes can be written as

$$g(\mathbf{r})=f(\mathbf{Rr}+\mathbf{t}),$$ (1)

or

$$f(\mathbf{r})=g\left({\mathbf{R}}^{\text{T}}(\mathbf{r}-\mathbf{t})\right),$$

where $\mathbf{r}={\left(\begin{array}{ccc}x& y& z\end{array}\right)}^{\text{T}}$ are Cartesian coordinates, R ∈ ℝ^3×3 is a rotation matrix and $\mathbf{t}={\left(\begin{array}{ccc}{t}_x& t_y& t_z\end{array}\right)}^{\text{T}}$ is the translation between the two density maps. The rotation matrix R defines the rotation by a set of Euler angles (α, β,γ). Here we follow the same Euler angle convention as used in the EM system (Hegerl and Altbauer, 1982) and SPIDER (Frank, 2006; Frank et al., 1981), i.e., in a right handed coordinate system, the object is first rotated by an angle γ clockwise around the Z-axis, then by angle β counterclockwise around the new Y-axis and finally by angle α clockwise around the new Z-axis. The rotation matrices for rotations by an arbitrary angle η around the Z and Y-axis are defined as

$${\mathbf{R}}_z(\eta )=\left(\begin{array}{ccc}cos\eta & sin\eta & 0\\ -sin\eta & cos\eta & 0\\ 0& 0& 1\end{array}\right)\text{and}{\mathbf{R}}_y(\eta )=\left(\begin{array}{ccc}cos\eta & 0& -sin\eta \\ 0& 1& 0\\ sin\eta & 0& cos\eta \end{array}\right).$$

The Euler rotation matrix R is calculated as the product of the three corresponding rotation matrices R = R_Z (α)R_Y (β)R_Z (γ). The same convention is also used in other EM software packages such as IMAGIC, MRC, FREALIGN, EMAN2 and SPARX, see Penczek (2010) for a review. Even with this definition the values of the Euler angles that describe a specific 3D rotation are in general not unique without restricting the range of the three angles. In Appendix A, we present an algorithm for obtaining a unique set of angles for any given rotation that is used in our alignment.

2.2. Projection angles and translations

A projection p (x, y) of f (r) at the projection angles (α_f, β_f,γ_f) is defined as,

$$p\left(x_1,y_1\right)=\int f(\mathbf{r}){dz}_1=\int g\left({\mathbf{R}}^{\text{T}}(\mathbf{r}-\mathbf{t})\right){dz}_1,$$ (2)

where f (r) and g(r) are two volumes rotated and shifted relative to each other as defined in (1), z₁is the Z-direction of the coordinate system of f (r) rotated by (α_f, β_f, γ_f) and (x₁, y₁) are the corresponding x-y coordinates in the projection plane

$${\left(\begin{array}{ccc}{x}_1& y_1& z_1\end{array}\right)}^{\text{T}}={\mathbf{Q}}_f\mathbf{r}\text{and}{\mathbf{Q}}_f={\mathbf{R}}_Z\left({\alpha }_f\right){\mathbf{R}}_Y\left({\beta }_f\right){\mathbf{R}}_Z\left({\gamma }_f\right).$$

Likewise, the projection q (x, y) of g(r) at the projection angles (α_g, β_g, γ_g) is,

$$q\left(x_2,y_2\right)=\int g(\mathbf{r}){dz}_2,$$ (3)

where z₂ is the Z-direction of the coordinate system of g(r) rotated by (α_g, β_g, γ_g) and (x₂, y₂) are the corresponding x-y coordinates in the projection plane

$${\left(\begin{array}{ccc}{x}_2& y_2& z_2\end{array}\right)}^{\text{T}}={\mathbf{Q}}_g\mathbf{r}\text{and}{\mathbf{Q}}_g={\mathbf{R}}_Z\left({\alpha }_g\right){\mathbf{R}}_Y\left({\beta }_g\right){\mathbf{R}}_Z\left({\gamma }_g\right).$$

Let r′= R^Tr and r″ = R^T(r − t). Then Equation 3 becomes,

$$q\left(x_2^{″},y_2^{″}\right)=\int g\left({\mathbf{r}}^{″}\right){dz}_2^{″}=q\left(x_2^{\prime }-s_x,y_2^{\prime }-s_y\right),$$ (4)

where ${\left(\begin{array}{ccc}{x}_2^{\prime }& y_2^{\prime }& z_2^{\prime }\end{array}\right)}^{\text{T}}={\mathbf{Q}}_g{\mathbf{R}}^{\text{T}}\mathbf{r},{\left(\begin{array}{ccc}{x}_2^{″}& y_2^{″}& z_2^{″}\end{array}\right)}^{\text{T}}={\mathbf{Q}}_g{\mathbf{R}}^{\text{T}}(\mathbf{r}-\mathbf{t})$, and

$$\left(\begin{array}{c}{s}_x\\ s_y\end{array}\right)=\left(\begin{array}{ccc}1& 0& 0\\ 0& 1& 0\end{array}\right){\mathbf{Q}}_g{\mathbf{R}}^{\text{T}}\mathbf{t},$$ (5)

In the following context, we let M denote the matrix $\left(\begin{array}{ccc}1& 0& 0\\ 0& 1& 0\end{array}\right)$.

Equations 4 and 2 are identical when

$$\mathbf{R}={\mathbf{Q}}_f^{\text{T}}{\mathbf{Q}}_g.$$ (6)

Using Equation 6, Equation 5 can be simplified to

$${\left(\begin{array}{cc}{s}_x& s_y\end{array}\right)}^{\text{T}}={\mathbf{MQ}}_f\mathbf{t}.$$ (7)

In summary, if the projection p of the reference f(r) and the projection q of g(r) are the same except for the translation (s_x, s_y), then the rotation R between the volumes can be computed using the two projection matrices Q_f and Q_g; and the translation (s_x, s_y) in the plane of the projection q is related to the 3D translation t through Q_g providing two dimensions of the 3D shift vector needed for translational 3D alignment.

2.3. Rotational alignment using a single projection

The rotational alignment R between two volumes can be found by finding two matched projections: the projection p of the reference f(r) and the matching projection q of the volume g(r), whose alignment is to be determined. The projection p is projected at angles (α_f, β_f,γ_f), the subscript f again indicating the angles relative to the coordinate system of f(r). The matching projection q is found by cross-correlating p to all possible projections of the volume g(r), which results in a five-dimensional cross-correlation function, c_{αf, βf,γf} (α_g, β_g, γ_g, s_x, s_y), where the subscript g indicates angles relative to the coordinate system of g(r) and (s_x, s_y)^T is a translation vector in the plane of the projection. The algorithm for acquiring the five-dimensional cross-correlation function is described in detail in Radermacher (1994) and is reiterated in Appendix B.

The rotational alignment of a projection results in a 3D rotation cross-correlation function, which is the five-dimensional cross-correlation function maximized over all possible in-plane shifts, i.e.,

$${\text{cc}}_{{\alpha }_f,{\beta }_f,{\gamma }_f}\left({\alpha }_g,{\beta }_g,{\gamma }_g\right)={max}_{s_x,s_y}{\text{c}}_{{\alpha }_f,{\beta }_f,{\gamma }_f}\left({\alpha }_g,{\beta }_g,{\gamma }_g,s_x,s_y\right).$$ (8)

The best matching projection is found at angles $\left({\alpha }_g^o,{\beta }_g^o,{\gamma }_g^o\right)$, where the maximum of the rotation cross-correlation function is found, i.e., $\left({\alpha }_g^o,{\beta }_g^o,{\gamma }_g^o\right)=argmax{\text{cc}}_{{\alpha }_f,{\beta }_f,{\gamma }_f}\left({\alpha }_g,{\beta }_g,{\gamma }_g\right)$. The rotation alignment R using only a single projection is then computed as $\mathbf{R}={\mathbf{Q}}_f^{\text{T}}{\mathbf{Q}}_g^o$ (Eq. 6), where the rotation matrices are

$${\mathbf{Q}}_f={\mathbf{R}}_Z\left({\alpha }_f\right){\mathbf{R}}_Y\left({\beta }_f\right){\mathbf{R}}_Z\left({\gamma }_f\right)\text{and}{\mathbf{Q}}_g^o={\mathbf{R}}_Z\left({\alpha }_g^o\right){\mathbf{R}}_Y\left({\beta }_g^o\right){\mathbf{R}}_Z\left({\gamma }_g^o\right).$$

A single projection would be sufficient to carry out a 3D rotational alignment. However, the cross-correlation is strongly affected by noise, which cannot be neglected in EM images and density maps. Hence, multiple projections are introduced to make the rotational alignment more robust.

2.4. Rotational alignment using multiple projections

Multiple projections p_i,i =1, 2,…, N, (N is the number of projections used for the alignment) of the reference volume f(r), generate multiple rotation cross-correlation functions cc_{αf,i, βf,i,γf,i} (α_g, β_g, γ_g), i =1, 2,…, N. The rotational alignment R is computed by determining the maximum of the combined cross-correlation (ccc) function, which is computed as

$$\text{ccc}(\alpha ,\beta ,\gamma )=\frac{{\displaystyle \sum _{i=1}^N}\left({\text{cc}}_{{\alpha }_{f,i},{\beta }_{f,i},{\gamma }_{f,i}}\left({\alpha }_g,{\beta }_g,{\gamma }_g\right)\right)}{N}.$$ (9)

(See Appendix C for technical details.)

Three sets of angles and their corresponding rotation matrices are involved in the combined cross-correlation function: Q_f,i = R_Z(α_f,i)R_Y (β_f,i)R_Z (γ_f,i) defining the orientation of the i-th projection of the reference f(r), Q_g = R_Z (α_g)R_Y (β_g)R_Z (γ_g) defining the orientation of a projection of the volume g(r), and R = R _Z (α)R_Y (β) R_Z (γ) defining the rotation between the two density maps. The relation between the three rotation matrices is $\mathbf{R}={\mathbf{Q}}_{f,i}^{\text{T}}{\mathbf{Q}}_g$ (Eq. 6).

The values in combined cross-correlation function ccc(α, β,γ) (Eq. 9) indicate the degree of matching between the volume and a set of projections p_i,i =1,…, N, rotating simultaneously as a group. Essentially, the set of Radon or Fourier transforms of the reference projections represent a subsampled version of the 3D Radon transform or Fourier transform of the reference. The best match occurs when ccc(α, β,γ) reaches the maximum value, i.e. (α^o, β^o,γ^o) = arg max ccc (α, β,γ). Hence, R = R_Z (α^o)R_Y (β^o)R_Z (γ^o) is the 3D rotational alignment between the two density maps.

2.5. Translational alignment using multiple projections

The 3D translational alignment t can also be computed from sets of 2D in-plane shifts found by the projection matching algorithm by essentially back-projecting each of the 2D translation vectors found for multiple projections. This process leads to an equation system that can be solved by linear least squares minimization

A set of in-plane shifts as well as the angles that best match the projections to the volume g(r) can be found by maximizing the five-dimensional cross-correlation, i.e. $\left({\alpha }_g^o,{\beta }_g^o,{\gamma }_g^o,s_x^o,s_y^o\right)=argmax{\text{c}}_{{\alpha }_f,{\beta }_f,{\gamma }_f}\left({\alpha }_g,{\beta }_g,{\gamma }_g,s_x,s_y\right)$. However, the shift vector for a single projection is insufficient to calculate the 3D translational alignment since the information of one dimension is lost during the projection process.

A set of projections of the reference volume, p_i,i =1, 2,…, N, aligned to the volume g(r), results in a set of shifts in the corresponding projection planes,

$$\left({\alpha }_{g,i}^o,{\beta }_{g,i}^o,{\gamma }_{g,i}^o,s_{x,i}^o,s_{y,i}^o\right)=argmax{\text{c}}_{{\alpha }_{f,i},{\beta }_{f,i},{\gamma }_{f,i}}\left({\alpha }_g,{\beta }_g,{\gamma }_g,s_x,s_y\right)$$ (10)

As shown in Equation 7, ${\left(\begin{array}{cc}{s}_{x,i}^o& s_{y,i}^o\end{array}\right)}^{\text{T}}={\mathbf{MQ}}_{f,i}\mathbf{t}$, is a system of linear equations. We reformulate the linear equations as follows: let $\mathbf{s}={\left(\begin{array}{ccccc}{s}_{x,1}^o& s_{y,1}^o& \dots & s_{x,N}^o& s_{y,N}^o\end{array}\right)}^{\text{T}}$ and a matrix Q̃_f ∈ ℝ^{2 N×3} containing the selected rows of Q_f,i,

$${\stackrel{\sim }{\mathbf{Q}}}_f={\left({\left({\mathbf{Q}}_{f,1}\right)}_{1•},{\left({\mathbf{Q}}_{f,1}\right)}_{2•},\cdots ,{\left({\mathbf{Q}}_{f,i}\right)}_{1•},{\left({\mathbf{Q}}_{f,i}\right)}_{2•},\cdots ,{\left({\mathbf{Q}}_{f,N}\right)}_{1•},{\left({\mathbf{Q}}_{f,N}\right)}_{2•}\right)}^{\text{T}}$$

where (Q_f,i)_1• and (Q_f,i)_2• are the first and second rows of the matrix Q_f,i. We obtain a concise form of the linear system: $\mathbf{s}={\stackrel{\sim }{\mathbf{Q}}}_f\mathbf{t}.$ This set of equations can be easily solved by a least squares regression, and results in

$$\mathbf{t}={\left({\stackrel{\sim }{\mathbf{Q}}}_f^{\text{T}}{\stackrel{\sim }{\mathbf{Q}}}_f\right)}^{-1}{\stackrel{\sim }{\mathbf{Q}}}_f^{\text{T}}\mathbf{s}.$$ (11)

A minimum of two projections are needed for calculating the 3D translational alignment. More projections are recommended for robustness of the algorithm.

2.6. Translational alignment using a 3D cross-correlation

An alternative method to compute the 3D translational alignment is to perform a straightforward cross-correlation once the two volumes have been rotationally aligned. A translation cross-correlation is calculated as,

$${\text{cc}}_t(\stackrel{\sim }{\mathbf{t}})=\int f(\mathbf{r}+\stackrel{\sim }{\mathbf{t}})g(\mathbf{Rr})d\mathbf{r},$$

Where $\stackrel{\sim }{\mathbf{t}}$ is the cross-correlation variable representing all possible translations between f(r) and g(Rr). The shifts between the density maps are the parameters that maximize this cross-correlation, i.e., t = arg max cc_t ($\stackrel{\sim }{\mathbf{t}}$) is the 3D translation between the rotationally aligned volumes. The method can also be used to confirm the results obtained by the method presented in section 2.5.

2.7. Missing data

Missing data occur in 3D reconstructions calculated from tomography, RCT datasets, or OTR datasets if sampling is sparse. Radon transforms are used to compute the five-dimensional cross-correlation between a projection of the reference and the volume being aligned. Since Radon transforms are represented in polar coordinates, all data that lie on a common radial line are either entirely present or missing. This property allows us to calculate the cross-correlation only in the areas where data are commonly present and to normalize it accordingly. Details are shown in Appendix B.

When 3D density maps are reconstructed by averaging the projections either into 3D Radon transforms or 3D polar Fourier transforms, the presence of each radial line can easily be recognized. A radial line is either 0, except at the origin, or it contains data. In addition, the index maintained in each radial line of the Radon transform in our implementation of the 3D reconstruction algorithm is 0 when no data are present. 3D density maps that are reconstructed using other algorithms, such as weighted back-projection, lack this information. One possible solution is to carefully keep track of the reconstruction geometry and build an index from this information. This may become complicated, especially when multiple alignment steps are involved. In cases where the 3D Radon transforms or polar Fourier transforms are computed from 3D reconstructions in real space, for example from a boxed out 3D sub-tomogram, none of the radial lines may be truly 0. However, the variances of radial lines in regions of missing data are substantially lower than in regions where data are present (Fig. 2). Given the reconstruction geometry, percentages of missing data can be calculated and a threshold for the line variances or standard deviations can be determined, below which a radial line is considered missing. This represents only an estimate, and is obviously less accurate than acquiring the information directly as part of the reconstruction process, since reconstruction algorithms smooth the boundaries between regions of present and missing data. The variances are best determined in the high-pass filtered 3D Radon transform, filtered with $\sqrt{{\rho }^{\ast }}$, ρ* being the Fourier radius. This filter is applied as part of the 3D Radon/Fourier cross-correlation procedure (Radermacher, 1997) to obtain a sharp cross-correlation maximum.

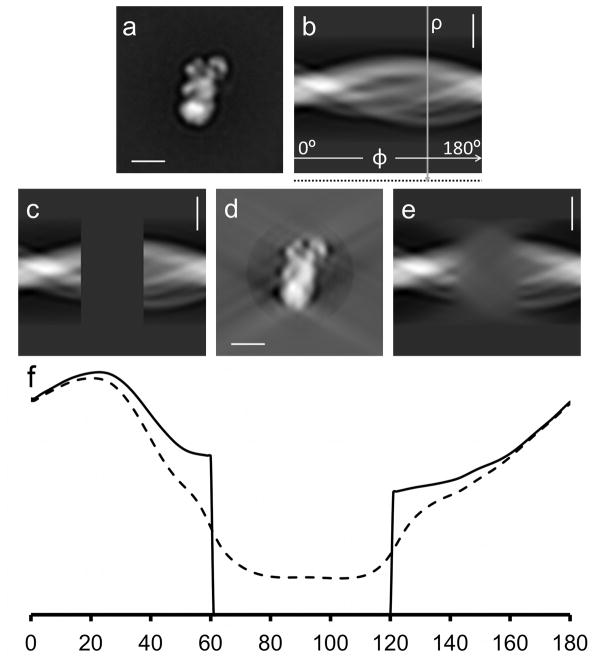
Figure 2.

Localization of missing data regions using the line variance of the Radon transform. a) Average image of a subcomplex of complex I from Y. lipolytica also used in section 4. b) Radon transform of the image. Angular coordinate Φ from 0° to 180°, radial coordinate ρ. The vertical arrow indicates a line along which the standard deviation is calculated. Standard deviation values are stored at the end of each line of the transform indicated by the dotted line in the margin below (b). c) The same Radon transform with 1/3 of the data set to 0 (33% missing data). d) r*-weighted back-projection calculated from the Radon transform with missing data. e) Radon transform calculated from the reconstructed image in (d). Note that the missing data are not 0 anymore but instead the transform shows data with a blurred appearance in the corresponding area. f) Plot of the standard deviations of the values in the radial lines of a Radon transform versus angle, calculated from a $\sqrt{{\rho }^{\ast }}$ high-pass filtered version of the 2D Radon transforms shown in (c), solid line and (e) dashed line, ρ* being the radial coordinate in the Fourier transform. The missing data area can be detected from the standard deviation values that fall below a certain threshold. Scale bars 100Å.

Currently, missing data are indicated only in the 3D Radon transform and not in the 2D transform of the reference projections (this will be implemented in the near future). Therefore, reference projections are carefully chosen to avoid including areas of missing data. However, if missing data in the projections are allowed, it will result in a reduction of the area contributing to the cross-correlation and increase the sensitivity to noise.

2.8. Alignment procedure

The alignment procedure consists of two major steps: aligning each projection p_i of the reference to another 3D volume, and combining the projection alignments to determine the final 3D rotational and translational alignments for the volume.

Five-dimensional searches are performed to align each of the reference projections to the 3D volume of unknown orientation. The alignment results in three Euler angles α_g, β_g, γ_g and two in-plane shifts s_x, s_y. The rotation cross-correlation function, cc_{αf,i, βf,i,γf,i} (α_g, β_g,γ_g) (Eq. 8), as well as the in-plane shifts $\left({\alpha }_{g,i}^o,{\beta }_{g,i}^o,{\gamma }_{g,i}^o,s_{x,i}^o,s_{y,i}^o\right)$ (Eq. 10), are computed and saved. The alignment of projections is carried out in two steps: first, a global search within an asymmetric unit with a coarse step size is carried out, followed by a local search, with a finer step size, around the correlation maximum found in the global search. Low-pass filtration in both steps is critical to prevent the algorithm from getting trapped in local maxima. The required low-pass filter radius is estimated using Crowther’s formula (Crowther et al., 1970) with the largest angular search increment Δα being the angular increment in:

$$d=\frac{\pi }{N}·D=\mathrm{\Delta }\alpha ·D,$$

where D is the effective diameter of the volume and d is the resolution that determines the low-pass filter radius (1/d). The use of a mild high-pass filter may be advantageous to sharpen the correlation maximum, for example with a radius corresponding to one divided by two to three times the image size.

The second part of the alignment procedure integrates the alignments of multiple projections. For the rotational alignment, the combined cross-correlation function ccc (α, β, γ) is computed from individual rotation cross-correlation functions (Eq. 9). It should be noted that because of the multi-step search scheme, the fine search is limited to a rather small region. These regions might not entirely overlap, thus the denominator N in Equation 9 is replaced with Ñ, the number of actual cross-correlation values being averaged. The final parameters for the 3D rotational alignment are calculated by finding the maximum of the combined cross-correlation function. A peak-fitting algorithm is used to obtain sub-pixel accuracy. Of the possible fitting algorithms, we chose to fit the adjacent sampling points of the maximum to a 4-elliptic paraboloid function using a least square fitting technique (second order 3D fit). For the translational alignment, a linear system is formed and solved (Eq. 11). Note that the computations of rotational and translational alignments are carried out simultaneously.

3. Tests

We have tested the performance of PBVA for accuracy using different signal-to-noise ratios and different percentages of missing data. Time efficiency was tested in comparison to other existing cross-correlation and normalized cross-correlation methods.

3.1. Signal-to-noise ratio tests

The algorithm was applied to volumes, artificially rotated, shifted and reconstructed with synthetic noise. The initial volume used was a 3D binary model of the envelope structure of complex I from Y. lipolytica (Clason et al., 2007; Radermacher et al., 2006). The 3D model has a pixel size of 3.6Å and was smoothed by low-pass filtration to 14.4Å, (see Fig. 3a–b). This 3D model was subsequently shifted and rotated to create a second model.

Figure 3.

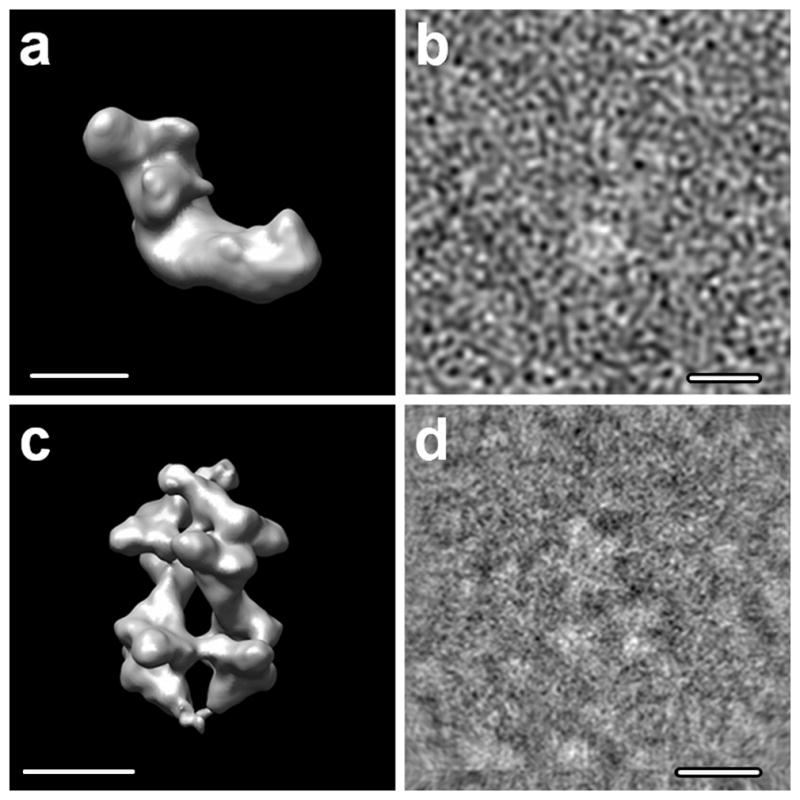
Test data sets: a) complex I of Y. lipolytica; b) an example image at SNR=0.33; c) S. cerevisiae PFK in the presence of ATP; d) an example cryo-EM image. Scale bars 100Å.

Volumes with different signal-to-noise ratios (SNR) were reconstructed by adding noise to the projections. First, single axis tilt series of both models with a 2° angular increment were created and low-pass filtered to 18Å, to remove any numerical artifacts that may have been created in the projection step. Second, Gaussian noise images were generated and scaled to obtain the desired signal-to-noise ratio (SNR), shown in Table 1. The SNR here is defined as the ratio between the variance of the signal and the variance of the noise. Note that the SNR values referred to later were measured at 30Å resolution in a square of 160×160 pixels². During the Radon transform calculation, a circular mask of 50 pixels radius was applied. Thus, the SNRs measured within this circular mask, which comprised 7845 pixels, of which between 1380 to 2000 pixels contained signal, is also included in Table 1. Since the structure is L-shaped, the signal occupied different areas in projections, depending on the projection angles. Finally, 3D volumes were reconstructed from the sets of noisy projections. Since the purpose of this first test was to investigate how the algorithm behaves under difference SNRs, none of the reconstructions had missing data.

Table 1.

Signal-to-noise ratios at different resolutions. The Signal-to-noise ratio is defined as ratio between the variances of the signal and the noise.

Resolution (Å)	7.2	30	30
Measurement Area (Pixels)	25,600	25,600	7,825
SNR=∞	∞	∞	∞
SNR=1	0.035	1	8.821
SNR=0.25	0.009	0.25	0.551
SNR=0.1	0.004	0.1	0.088

First column: With Pixel size of 3.6Å and the full resolution of 7.2Å (Nyquist-Shannon), using the full image (160×160). Second column: the SNR after low-pass filter to 30Å, Third column: at 30Å resolution with the image area restricted closer to the signal area (mask radius 50). Since the noise covers all frequencies, low-pass filtering to 30Å results in a higher signal-to-noise ratio.

Alignments of the reconstructed volumes were carried out using the PBVA algorithm. The first volume was chosen as reference and a set of projections were calculated. Fifteen projections were selected randomly at a resolution of 30Å. All these projections were aligned to the second volume using the projection matching algorithm via Radon transforms (Radermacher, 1994). The procedures were carried out in SPIDER (Version 5.0 with extensions). The results from each projection were combined to calculate the final 3D rotational translational parameters of the second volume.

The results of the alignment were compared to the known shifts and rotations applied to create the models. We carried out 36 tests for each signal-to-noise ratio condition. In each test the volumes were created as described above, using independently generated Gaussian distributed white noise. The standard deviations of the errors are shown in Table. 2. The translational errors are measured in pixels. Let $\mathrm{\Delta }{t}_x=|t_x-t_x^{\prime }|$ be the error in the X direction, where t_x is the original shift along the X-axis and $t_x^{\prime }$ be the shift found, and Δt_y and Δt_z the corresponding errors in Y, Z directions. The error in pixels is then calculated as $\mathrm{\Delta }r=\sqrt{\mathrm{\Delta }{t_x}^2+\mathrm{\Delta }{t_y}^2+\mathrm{\Delta }{t_z}^2}$. The rotational errors are measured and expressed as the angle around Euler pole, which represents the difference between the rotation matrix R originally applied, and the rotation matrix R′ determined in the alignment. The difference between the two rotation matrices is ΔR = R^TR′. As the Euler’s rotation theorem states (Euler, 1776), any rigid rotation in 3D can be represented as a single rotation around one axis (Euler pole), a unit vector which is not changed by the rotation. Let Δε be the rotation angle of ΔR then the influence of the angular error on the resolution of the reconstruction can be estimated by calculating the equivalent error in pixels at the periphery of the structure, which for small Δε is rΔε, where r is the distance between the center and the periphery and Δε is measured in radians. In general, the errors increase as the signal-to-noise ratio increases, but the method is still robust and accurate under the condition that SNR=0.1.

Table 2.

The standard deviations of the alignment errors for different signal-to-noise ratios, when applied to model data with Gaussian additive noise.

Errors	Translations	Rotations
	σΔr (pixels)	σΔλ (radians)
SNR=∞	0.2147	0.0127
SNR=1	0.4113	0.0190
SNR=0.25	0.9126	0.0354
SNR=0.1	1.3898	0.0603

3.2. Percentage of missing data tests

The algorithm was applied to volumes with different missing data, which were rotated and shifted artificially. We used a data set of cryo-EM images of Saccharomyces cerevisiae phosphofructokinase (PFK, EC 2.7.1.11, 835 kDa, 21S) in the ATP bound state. The set of cryo images, with a pixel size of 2.4Å, were extracted from 0°-micrograph and had been aligned previously to obtain a 3D reconstruction with 13Å resolution (Bárcena et al., 2007). Since PFK is elongated and the longer axis tends to sit parallel to the supporting surface, the data sets represent approximately a single axis tilt series with random tilt angles. We chose a single axis tilt geometry in this test because of its simplicity and because it constitutes a worst case scenario. Only in a single axis tilt series is it possible that an entire cross-section through the polar Fourier transform of a volume is empty, while in 3D reconstructions from conical or dual axis tilt data all cross-sections are at least partially occupied.

The data set contains more than 11000 images. The projections were separated into 121 groups, each containing approximately 90 images sufficient to cover the Fourier space sampling to a resolution of 30 Å (Fig. 3c–d). We created 121 volumes with the structure in the same position and in the same orientation. One volume was chosen as reference, and the remaining 120 volumes were shifted and rotated.

Missing data were simulated by randomly deleting slices in the polar Fourier transforms of the 120 shifted and rotated volumes. The number of slices was adjusted to create different percentages of missing data in the 3D volumes; 0%, 10%, 20%, and 30%.

The alignment procedure was applied as follows: First, a set of projections of the reference was computed and low-pass filtered to 30Å. The projections were randomly selected exclusively in the region where there was no missing data, ensuring that the projections were all complete. Second, all projections were aligned to the 3D volumes with missing data. Finally, the results of all the individual projections were combined. The final alignments obtained were compared to the shifts and rotations applied in the tests. The standard deviations of the errors are shown in Table 3. The translational and the rotational errors are determined the same as it was described for Table 2. The errors increase only slightly as the percentage of missing data increases, showing that the algorithm is robust to the missing data.

Table 3.

The standard deviations of the alignment errors for different amount of missing data, when applied to cryo-EM PFK data set.

Errors	Translations	Rotations
	σΔr (pixels)	σΔλ (radians)
0% missing	0.6765	0.0451
10% missing	1.1010	0.0454
20% missing	1.1248	0.0775
30% missing	1.7063	0.0317

3.3. Time efficiency tests

The algorithm was tested and compared to other existing six-dimensional cross-correlation search algorithms to estimate time efficiency. All the tests were carried out on the same machine (Alpha server ES40, using a single processor EV6.8AL at 833 MHz) and the results are shown in Table 4. The PBVA procedure was applied using 15 projections. The rough and fine search for the alignment parameters of the 15 projections, together with the integration of the results of individual projection to obtain the translation and rotation parameters for the second volume, were completed after 10 minutes of computation.

Table 4.

Time efficiency tests for aligning two volumes on a single processor of Alpha server ES40, processor EV6.8AL, 833 Mhz. PBVA with 15 projections was used in the test. The search ranges are specified in columns 1 and 2. The translational range for the full 6D cross-correlation differs slightly between direct volume alignment and PBVA, since PBVA searches on a polar grid, while the other algorithms use a Cartesian grid. Column CC: Direct volume alignment without missing data correction, Column “Normalized CC”: Direct volume alignment with correction for missing data. PBVA is a factor of 220 to 160 times faster than a full 3D volume alignment. Even after optimization of the full alignment algorithm the factor should still be substantial.

	Rotational Search	Translational Search	CC	Normalized CC	PBVA
Rough search	25×13×25	7×7×7	11:06:42	15:21:49
	25×13×25	Radius 10			0:04:06
Fine search	23×23×23	7×7×7	16:39:09	22:47:47
	23×23×23	Radius 10			0:04:53
Rotation alignment			x	x	0:01:22
Translation alignment			x	x	0:00:01
Total time			27:45:51	38:09:36	0:10:22

A six-dimensional exhaustive search was carried out between two 3D volumes, which included rotating the second volume, calculating the translation cross-correlation, and searching the maximum of the cross-correlation. Volume rotations can be performed either in real space or Fourier space. We elected to compute volume rotations in real space to avoid interpolation problems observed when performing Fourier space rotations (Welling et al., 2006). Cross-correlations can also be computed in either real space or Fourier space. In real space, calculations using a traditional method have a time complexity of O(n²), where n denotes the number of voxels in the volume. In Fourier space, calculations have a complexity of O(nlogn), which are faster, so we calculated the cross-correlation in Fourier space. While searching the maximum of the cross-correlation, the search range was limited to a range comparable to the one used in PBVA. There are fast local cross-correlation algorithms (Rath and Frank, 2004; Rath et al., 2003; Yoo and Han, 2009) that can be used to accelerate the process, however, these were not implemented here. For these tests, the algorithm was implemented as a procedure in Spider without any special optimization. The non-normalized cross-correlation takes 1165 minutes to search a comparable amount of the rotations and translations as in the test above, using our PBVA procedure.

In a second test, we used a normalized cross-correlation as described in Schmidt and Booth (Schmid and Booth, 2008), normalized to the ratio of overlapping areas. The search takes as long as 2289 minutes when implemented as a procedure in Spider. The constrained cross-correlation (Förster et al., 2008; Frangakis et al., 2002) that is normalized with the variance of the volumes limited to the commonly present areas was not tested. However, since this procedure is more complex it should require more computation time.

4. Application

The PBVA method was applied to the 3D reconstructions of the ΔNB8M subcomplex of complex I from Y. lipolytica (Dröse et al., 2011). Deletion of the accessory subunit NB8M of complex I results in a subcomplex that exhibits an incompletely assembled membrane arm, lacking several essential subunits. In addition, this subcomplex exhibits a reduced proton pumping activity. 3D structure determination was carried out using a single particle 3D reconstruction method on images of an RCT data set (Radermacher et al., 1986) recorded of a NanoW (Nanoprobes, Yaphank, NY) deep stain embedded sample with a tilt angle of 55°. The data set contained a total of 10897 image pairs digitized with a calibrated pixel size of 3.136Å at the specimen scale. The study resulted in the separation of the untilted images into 10 classes. A 3D reconstruction for each of the classes was obtained from the corresponding tilt images (Fig. 4a). The number of images, percentage of missing data and the resolutions are listed in Table 5a.

Figure 4.

10 reconstructions of subcomplex Δ NB8M of complex I from Y. lipolytica reconstructed using RCT. Row numbers indicate volume number, used in the text and in Figure 5. Column a: Reconstructions of the 10 classes originally obtained after classification of the 0° data. Column b: The reconstructions after alignment by PBVA using volume 1 as reference. Column c: The reconstructions after estimation of the missing data as part of the PPCA-EM algorithm. Scale bar 100 Å.

Table 5.

a) Some facts of the original 10 subcomplex reconstructions. b) Rotations (α, β,γ) and shifts (t_x, t_y, t_z) found in the alignment of the 10 volumes.

a)
Vol #	# of projections	Percentage of missing data	Resolution at FSC=0.3
1	1270	8%	28.77
2	918	8%	32.67
3	2235	8%	25.09
4	681	13%	29.31
5	947	8%	28.51
6	1024	9%	33.01
7	509	11%	36.89
8	703	12%	29.87
9	778	12%	31.05
10	1521	7%	28.77

b)
Vol #	tx	ty	tz	α	β	γ
1	0	0	0	0	0	0
2	−0.260	−0.202	1.328	77.209	18.269	−80.670
3	−0.215	−0.014	0.954	28.704	16.620	−31.492
4	0	0	0	45.074	6.916	−46.230
5	−0.069	0.008	0.585	40.464	13.621	−41.111
6	−0.169	−0.026	0.554	25.091	20.524	−27.342
7	0.236	0.190	0.934	17.286	6.385	−17.101
8	−0.517	−0.165	−0.822	−154.546	19.189	153.692
9	−0.016	0.006	−0.607	−155.537	10.832	156.063
10	−0.174	−0.128	0.679	−158.358	65.185	158.605

Four types of differences in the data set may be present: First, apparently the reconstructions appear to be in different orientations; second, several conformations may be present; third, the missing data are different in these reconstructions, hence creating different artifacts; and fourth, the volumes have different signal-to-noise ratios and different resolutions. Additional artifacts may be introduced in the surface rendering presentation that may interfere with a visual evaluation of the differences, since a single threshold is used to represent the structure as a solid model.

The PBVA algorithm was applied to re-orient the 10 final reconstructions of the Δ NB8M subcomplex. Volume 1 (Fig. 4) was selected as the reference for the alignment procedure. 16 reference projections were selected and the projection angles were chosen such that there were no missing data in the projections. The projections were matched to all the other 9 volumes using the projection matching algorithm with Radon transforms. The alignment results from each set of projections were combined (Tab. 5b) and applied to the rest of the volumes (Fig. 4b). The translations, t_x, t_y and t_z are less than one voxel, with only one exception, demonstrating that the original reconstructions were well-centered. After alignment, there are still noticeable differences among the reconstructions, which may be caused by conformational changes, and the missing data. Again apparent differences may be caused by the surface representations.

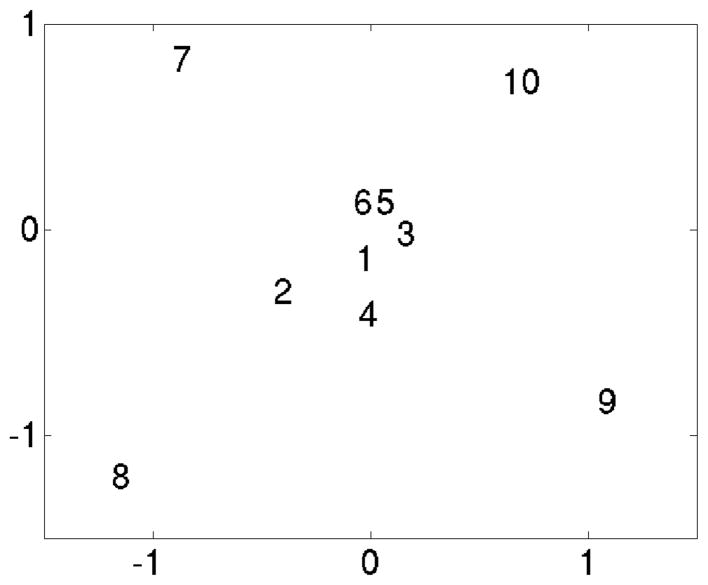
The Probabilistic principal component analysis using expectation maximization (PPCA-EM) algorithm was applied to the dataset (Yu et al., 2010) to examine the conformational features in the dataset and at the same time estimate the missing data. Pairwise distances between the ten volumes in the subspace of the first three eigenvectors, which covers more than 50% of the total variance (Tab. 6) were measured and used to determine if the volumes represent the same conformation and can be averaged (Tab. 7). To better represent the scattering of the volumes in this subspace, we applied nonlinear mapping (Radermacher and Frank, 1985). When mapping the distances in a 3D space to a 2D space, Sammon’s formula for non-linear mapping was used (Sammon, 1969), such that the shorter distances are emphasized in the scatter plots. The results show that volumes 1 to 6 form a group at the center of the map, while volumes 7 to 10 are outside (Fig. 5).

Figure 5.

Scatter plot of the 10 volumes. PPCA-EM was applied to the aligned volumes, shown is the non-linear map obtained from the coordinates in the first 3 eigenvectors. The numbers corresponds to the volumes numbers in Figure 4. Distances scaled by 10⁻⁴.

The PPCA-EM algorithm estimates the missing data in an eight-dimensional eigenspace. The reconstructions with missing data estimated are shown in Figure 4c. With the missing data estimated the surface presentations now provide us with visual evidence why the volumes 7, 8, 9 and 10 are different from the rest, and why volume 2 slightly deviates from the major group.

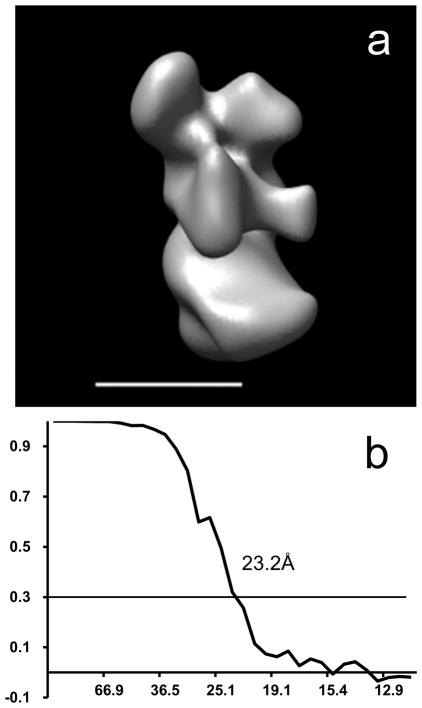
Based on the scatter plots (Fig. 5) and the visual examination of the volumes with filled-in data in the missing data area (Fig. 4c), volumes 1 to 6 are similar, thus an average of these volumes was computed. The average structure was calculated from the original projections with updated projection angles combining both the original projection angles and the 3D rotation angles, shifted with the in-plane translation derived from the 3D shifts. The average structure was used as a reference for a further refinement. A final structure was obtained from all the projections of classes 1 to 6 matched to the reference (Fig. 6a). The resulting structure has a resolution of 23.2Å, determined using the Fourier Shell Correlation with a cutoff of 0.3 (Fig. 6b) (Rosenthal and Henderson, 2003).

Figure 6.

Final 3D reconstruction of subcomplex Δ NB8M of complex I from Y. lipolytica a) Average structure of volumes 1 to 6; b) FSC of the average structure showing resolutions of 23.2Å at a cutoff of 0.3 (~24.4Å at a cutoff of 0.5).

5. Conclusion

We present here a new method, projection based volume alignment (PBVA) for aligning 3D density maps based on a projection matching algorithm, which simultaneously and exhaustively searches the five orientational and translational alignment parameters (3 angles and 2 translations per projection). Thus, after combining the results from individual projections, the PBVA procedure finds simultaneously the six orientational and translational alignment parameters between a reference and a second volume.

The PBVA procedure divides the alignment problem between two volumes into an alignment between reference projections and the second volume. The core of the PBVA procedure is a projection matching algorithm. Projections can either be created from the reference and matched to all other volumes, or from all other volumes and matched to the reference volume. The presented scheme is the former since it presents several advantages. When aligning more than two volumes, one volume can be chosen as the reference and studied comprehensively. Projections can be deliberately chosen to best represent the volume. The projection directions are selected to create projections without missing data, thus maximizing the areas used in the cross-correlation, using the information of the reconstruction geometry. In addition, the projections are chosen to show the most rotation sensitive features of the structure, which improves the accuracy of the projection matching results.

The projection set, in essence, represents a subsampled volume and the number of projections represents how fine the volume is sampled. The larger the number of projections used, the finer is the sampling, and the more robust is the volume alignment. However, the alignment becomes lengthier since the computing time increases with O(n) where n is the number of projections. In our test experiments and application, we have used 15 to 16 projections, which is an empirical number that works well for this type of studies. This sampling, however, may not be evenly spaced given the selection rules described above. We have observed anisotropic accuracies in the Z-direction when the reference projections are all taken at low tilts. Reference projections without missing data can only be taken at tilts less than the maximum tilt angle used during data collection. Hence we will expand the algorithm to allow missing data also in the reference projection, which provide more flexibility and in some cases more accuracy, however, fewer pixels will contribute to the calculation of the cross-correlation function.

The PBVA procedure is a relatively fast algorithm. The algorithm subsamples the reference into a set of projections, thus the calculation of the cross-correlation is faster. The exhaustive search of the projection matching is 5-dimensional and faster than a comparable 6-dimensional exhaustive search for two 3D volumes. Moreover, it avoids rotating the volume by extracting the projections that belong to different orientations from the polar sampled 3D Fourier or Radon transform, which is much faster than rotating the real 3D volume.

PBVA is an accurate algorithm, which determines the translational parameters within sub-pixel accuracy and the rotational parameters with accuracy finer than the angular search step size. The rotational alignments are found by estimating where the maximum of the combined cross-correlation (ccc) occurs (Sec. 2.). Accuracy better than the search step size is achieved by quadratic fitting. The translational parameters are found by solving a linear system using a least square fit (Sec. 2.5). Thus, the translational parameters are also determined with sub-pixel accuracy.

We have demonstrated that under different conditions, different signal-to-noise ratios and different percentages of missing data, the PBVA procedure is a fast, accurate and robust algorithm for finding translational and rotational alignment parameters. Combined with multivariate statistical analysis designed for 3D volumes with missing data like PPCA-EM, the algorithm can be used to combine multiple 3D reconstructions and achieve high resolution structures.

Software

The projection alignment programs are part of SPIDER version 5.0 with extensions running under HP-OSF. Standalone FORTRAN code, for compilation with PGI (The Portland Group, Lake Oswego, OR) or Lahey (Lahey Computer Systems, Incline Village, NV) compilers, for the calculation of Radon transforms and Radon transform based projection alignment are under development and will be made available upon request. Programs newly developed for this work, written in C, are available upon request. A download link for all programs is planned for the near future.

Table 6.

Results of PPCA-EM: Eigenvalues and the percentage of the total variance represented by each eigenvector.

No	Eigenvalues	Percentage
1	3.53E+07	21.14%
2	2.97E+07	17.74%
3	2.40E+07	14.34%
4	2.18E+07	13.04%
5	1.71E+07	10.22%
6	1.39E+07	8.34%
7	1.19E+07	7.10%
8	1.07E+07	6.41%
>8	2.79E+06	1.67%

Table 7.

Results of PPCA-EM: Pairwise distance between the 10 volumes in an 3-dimensional subspace (using the first 3 eigenvectors). The distances are scaled by 10⁻⁴.

Vol #	1	2	3	4	5	6	7	8	9	10
1	0	0.53	0.32	0.32	0.29	0.28	1.34	1.54	1.26	1.10
2		0	0.58	0.40	0.64	0.72	1.18	1.71	1.46	1.54
3			0	0.44	0.23	0.25	1.17	1.63	1.45	0.98
4				0	0.54	0.54	1.39	1.64	1.22	1.34
5					0	0.14	1.19	1.61	1.43	0.92
6						0	1.29	1.58	1.38	0.84
7							0	2.32	2.31	1.70
8								0	2.49	1.98
9									0	1.74
10										0

Appendix A: Euler angles and rotation matrix

Any rigid body rotation can be described with a set of three angles (Euler, 1776). Following a specific convention, they can be mapped to a unique rotation matrix. The conversion from Euler angles to rotation matrices in a right-handed coordinate system rotating around Z-Y-Z axes sequentially is

$$\begin{array}{l}\mathbf{R}={\mathbf{R}}_Z(\alpha ){\mathbf{R}}_Y(\beta ){\mathbf{R}}_Z(\gamma )=\left(\begin{array}{ccc}{r}_{11}& r_{12}& r_{13}\\ r_{21}& r_{22}& r_{23}\\ r_{31}& r_{32}& r_{33}\end{array}\right)\\ =\left(\begin{array}{ccc}cos\alpha cos\beta cos\gamma -sin\alpha sin\gamma & cos\alpha cos\beta sin\gamma +sin\alpha cos\gamma & -cos\alpha sin\beta \\ -sin\alpha cos\beta cos\gamma -cos\alpha sin\gamma & -sin\alpha cos\beta sin\gamma +cos\alpha cos\gamma & sin\alpha sin\beta \\ sin\beta cos\gamma & sin\beta sin\gamma & cos\beta \end{array}\right).\end{array}$$ (A1)

with

$${\mathbf{R}}_z(\eta )=\left(\begin{array}{ccc}cos\eta & sin\eta & 0\\ -sin\eta & cos\eta & 0\\ 0& 0& 1\end{array}\right)\text{and}{\mathbf{R}}_y(\eta )=\left(\begin{array}{ccc}cos\eta & 0& -sin\eta \\ 0& 1& 0\\ sin\eta & 0& cos\eta \end{array}\right)$$

However, a rotation matrix can be mapped to multiple combinations of Euler angles. We impose some restriction so that a rotation matrix can be converted to a unique set of Euler angles ($\dot{\alpha }$, $\dot{\beta }$, $\dot{\gamma }$). First, when the Gimbal lock occurs, i.e. $\dot{\beta }$ = 0 or π, we let $\dot{\gamma }$ = 0 and $\dot{\alpha }$ =α+ γ if $\dot{\beta }$ = 0 or $\dot{\alpha }$ =α − γ if $\dot{\beta }$ = π. Second, we force the ranges of the angles to be: $\dot{\alpha }$ ∈ [0, 2π), $\dot{\beta }$ ∈ [0,π] and $\dot{\gamma }$ ∈ [0, 2π). Any 3D rotation can be expressed by this unique set of angles. Given the restrictions, the following formulas can be used to compute the corresponding Euler angles,

$$\begin{array}{l}\stackrel{.}{\beta }=\text{acos}\left(r_{33}\right)\hfill \\ \stackrel{.}{\alpha }=\{\begin{array}{ll}\text{atan}2\left(r_{12},r_{11}\right),\hfill & \text{when}\beta =0\text{or}\pi \hfill \\ \text{atan}2\left(r_{23},-r_{13}\right),\hfill & \text{otherwise}\hfill \end{array}\hfill \\ \stackrel{.}{\gamma }=\{\begin{array}{ll}0,\hfill & \text{when}\beta =0\text{or}\pi \hfill \\ \text{atan}2\left(r_{32},r_{31}\right),\hfill & \text{otherwise}\hfill \end{array}\hfill \end{array},$$ (A2)

where the function acos and atan 2 are defined as in the FORTRAN, C standard library (math.h), Java math library, Python math module and etc. Note that there are three different methods to compute ($\stackrel{.}{\mathit{\alpha }}$, $\stackrel{.}{\mathit{\beta }}$, $\stackrel{.}{\mathit{\gamma }}$) from a rotation matrix R, as derived in Radermacher (1994). Here we list one as an example. While implementing, a combination of the three is recommended such that numerical errors are minimized.

An arbitrary set of Euler angles (α, β,γ) can be converted to the unique set of Euler angles ( $\stackrel{.}{\mathit{\alpha }}$, $\stackrel{.}{\mathit{\beta }}$, $\stackrel{.}{\mathit{\gamma }}$) defined above using the rules in Table 1. In the procedure for combining rotation cross-correlation functions and in the quadratic interpolation using values surrounding the main maximum, required values may fall outside the sampling range (wrap-around). The procedure to find an equivalent set of Euler angles finds the values of rotation cross-correlation (cc_{αf,j, βf,j,γf,j}) outside of our sampling range according to Table A1.

Table A1.

The table used to convert an arbitrary set of Euler angles (α, β,γ) to a unique set ($\stackrel{.}{\mathit{\alpha }}$, $\stackrel{.}{\mathit{\beta }}$, $\stackrel{.}{\mathit{\gamma }}$) in the region of $\dot{\alpha }$ ∈ [0, 2π), $\dot{\beta }$ ∈ [0,π] and $\dot{\gamma }$ ∈ [0, 2π). *The conversion is made based on the relation:

$${\mathbf{R}}_Z(\mathbf{a}){\mathbf{R}}_Y(\beta ){\mathbf{R}}_Z(\gamma )={\mathbf{R}}_Z(\alpha -\pi ){\mathbf{R}}_Y(2\pi -\beta ){\mathbf{R}}_Z(\gamma -\pi ).$$

	β mod 2π
	0	(0, π)	π	(π, 2π)
$\stackrel{.}{\mathit{\alpha }}$,	(α + γ) mod 2 π	α mod 2π	(α − γ) mod 2π	(α − π) mod 2π
$\stackrel{.}{\mathit{\beta }}$,	0	β mod 2π	π	2π − (β mod 2π)
$\stackrel{.}{\mathit{\gamma }}$,	0	γ mod 2π	0	(γ − π) mod 2π

Appendix B: Projection matching using Radon transforms

The algorithm was introduced in Radermacher (1994). However, even though implemented from the beginning, the handling of the missing data has not been published in detail. Hence we reiterate and emphasize how the cross-correlation between a 2D projection and a 3D volume is normalized with respect to missing data. More details about Radon transforms can be found in Deans (Deans, 1983).

Let p be a projection of the reference f(r). The Radon transform $\widehat{p}$ of p is calculated as

$$\widehat{p}(\rho ,\zeta )=\iint p(x,y)\delta (\rho -xsin\zeta -ycos\zeta )dxdy,$$

where ρ is the radial coordinate in the Radon transform and ζ is the angular coordinate. The integral over the δ - function selects all line integrals along lines at angle ζ for each point on the perpendicular line at radius ρ. If p (x, y) is shifted by (s_x, s_y) then, according to the shifting theorem, the Radon transform of the shifted projection is

$$\begin{array}{l}\text{R}\left(p(x-sx,y-sy)\right)=\iint p(x-sx,y-sy)\delta (p-xsin\zeta -ycos\zeta )dxdy\\ =\iint p(\stackrel{\sim }{x},\stackrel{\sim }{y})\delta (p-s_{x}sin\zeta -s_{y}cos\zeta -\stackrel{\sim }{x}sin\zeta -\stackrel{\sim }{y}cos\zeta )d\stackrel{\sim }{x}d\stackrel{\sim }{y}\\ =\widehat{p}(p-s_{x}sin\zeta -s_{y}cos\zeta ,\zeta )\end{array}$$

where the symbol R stands for Radon transform.

The 2D Radon transform of q, a projection of the volume g(r), is extracted from the 3D Radon transform $\widehat{g}$(ρ,θ,φ) of g(r).

$$\widehat{g}(\rho ,\theta ,\phi )=\iiint g(x,y,z)\delta (\rho -xcos\theta sin\phi -ycos\phi -zsin\theta sin\phi )\mathit{dxdydz}$$

The Radon transform of q extracted from g at angles (α_g, β_g,γ_g) is $\widehat{q}$ _{αg, βg,γg} (ρ,ζ), where (ρ, ζ) are the polar coordinates in the plane of the extracted projection transform. The last rotation angle α_g is a rotation within the projection plane and can be merged with the angular coordinate of the 2D Radon transform, thus ${\widehat{q}}_{{\alpha }_g,{\beta }_g,{\gamma }_g}(\rho ,\zeta )={\widehat{q}}_{{\beta }_g,{\gamma }_g}(\rho ,\zeta +{\alpha }_g)$. The relation between (θ,φ) and (ζ + α_g, β_g,γ_g) and the implementation of the extraction is discussed in detail in Radermacher (1994) and is not presented here since the equations are lengthy. It is a fast algorithm to acquire the 2D Radon transform of an arbitrary projection from a 3D Radon transform. Here we focus on the variance calculations for normalizing the cross-correlation when data are missing.

Discrete Radon transforms are calculated by replacing the integrals by summations over sampling points along the lines or planes defined by the δ -functions in the above equations. The values of the sampling points are obtained by interpolation. The resulting Radon transforms are discrete with an angular sampling of Δζ in 2D and Δθ and Δφ in 3D, and a radial sampling of Δρ. Using the shifting property of Radon transform, the normalized cross-correlation between a projection $\widehat{p}$ and a cross-section $\widehat{q}$ , extracted from the 3D transform, is

$${c^{\prime }}_{{\alpha }_f,{\beta }_f,{\gamma }_f}({\alpha }_g,{\beta }_g,{\gamma }_g,s_x,s_y)=\sum _i\sum _k\frac{({\widehat{q}}_{{\beta }_g,{\gamma }_g}({\rho }_k,{\zeta }_i)-{{\mu }^{\prime }}_{\widehat{q}})(\widehat{p}({\rho }_k-s_{x}sin{\zeta }_i-s_{y}cos{\zeta }_i,{\zeta }_i+{\alpha }_g)-{{\mu }^{\prime }}_{\widehat{p}})}{{{\sigma }^{\prime }}_{\widehat{q}}{{\sigma }^{\prime }}_{\widehat{p}}}$$ (B1)

with ζ_i = i·Δζ, i_max = 2π/Δζ and ρ_k = k·Δρ, k ≥ 0

The means ${\mu }_{\widehat{q}}^{\prime }$ and ${\mu }_{\widehat{p}}^{\prime }$ of a complete data set are computed as

$$\begin{array}{l}{\mu }_{\widehat{q}}^{\prime }={\sum }_i{\sum }_k{\widehat{q}}_{{\beta }_g,{\gamma }_g}\left({\rho }_k,{\zeta }_i\right)/n,\\ {\mu }_{\widehat{p}}^{\prime }={\sum }_i{\sum }_k\widehat{p}\left({\rho }_k,{\xi }_i\right)/n,\end{array}$$

where n is the number of sampling points. In the denominators of Equation B1, the standard deviations ${\sigma }_{\widehat{q}}^{\prime }$ and ${\sigma }_{\widehat{p}}^{\prime }$ of the complete Radon transforms $\widehat{q}$ and $\widehat{p}$ are

$$\begin{array}{l}{\sigma }_{\widehat{q}}^{\prime }=\sqrt{\sum _i\sum _k{\left({\widehat{q}}_{{\beta }_g,{\gamma }_g}\left({\rho }_k,{\zeta }_i\right)-{\mu }_{\widehat{q}}^{\prime }\right)}^2/(n-1)},\\ {\sigma }_{\widehat{p}}^{\prime }=\sqrt{\sum _i\sum _k{\left(\widehat{p}\left({\rho }_k-s_{x}sin{\zeta }_i-s_{y}cos{\zeta }_i,{\zeta }_i+{\alpha }_g\right)-{\mu }_{\widehat{p}}^{\prime }\right)}^2/(n-1)}.\end{array}$$

The standard deviations are constants for a given projection/cross-section pair when there are no missing data. However, the variances need to be limited to the commonly present region when there are missing data.

The cross-correlation is carried out line by line in polar coordinates where a radial line is either present or missing completely. Only a subset of the radial lines is present in both Radon transforms when data are missing. We can define subsets of all sampled radial lines. The subset of lines present in $\widehat{p}$ is: $W_{\widehat{p}}$ = {ζ + α_g| p̂(ρ,ζ+α_g) is present} and the subset of lines present in $\widehat{q}$ is: $W_{\widehat{q}}$ = {ζ | q̂_βg,γg (ρ,ζ) is present}, and the intersection of the two subsets is $W=W_{\widehat{p}}\cap W_{\widehat{q}}$, which varies when (α_g, β_g,γ_g) vary. In order to properly normalize the cross-correlation function, we use the radial lines in W only, and the cross-correlation (Eq. B1) is adjusted as

$${\text{c}}_{{\alpha }_f,{\beta }_f,{\gamma }_f}\left({\alpha }_g,{\beta }_g,{\gamma }_g,s_x,s_y\right)=\sum _{{\zeta }_i\in W}\sum _k\frac{\left({\widehat{q}}_{{\beta }_g,{\gamma }_g}\left({\rho }_k,{\zeta }_i\right)-{\mu }_{\widehat{q}}\right)\left(\widehat{p}\left({\rho }_k-s_{x}sin{\zeta }_i-s_{y}cos{\zeta }_i,{\zeta }_i+{\alpha }_g\right)-{\mu }_{\widehat{p}}\right)}{{\sigma }_{\widehat{q}}{\sigma }_{\widehat{p}}}$$ (B2)

The means are calculated also only within the common present region, i.e.,

$$\begin{array}{l}{\mu }_{\widehat{q}}={\sum }_{{\zeta }_i\in W}{\sum }_{{\rho }_k}{\widehat{q}}_{{\beta }_g,{\gamma }_g}\left({\rho }_k,{\zeta }_i\right)/\left(n_{\zeta }\mid W\mid \right),\\ {\mu }_{\widehat{p}}={\sum }_{{\zeta }_i\in W}{\sum }_{{\rho }_k}\widehat{p}\left({\rho }_k,{\zeta }_i\right)/\left(n_{\zeta }\mid W\mid \right),\end{array}$$

where |W| is the number of lines in W and n_ζ is the number of sampling points along each radial line. Likewise the standard deviations are calculated as

$$\begin{array}{l}{\sigma }_{\widehat{q}}=\sqrt{\sum _{{\zeta }_i\in W}\sum _k{\left({\widehat{q}}_{{\beta }_g,{\gamma }_g}\left({\rho }_k,{\zeta }_i\right)-{\mu }_{\widehat{q}}\right)}^2/\left(n_{\zeta }\mid W\mid -1\right)},\\ {\sigma }_{\widehat{p}}=\sqrt{\sum _{{\zeta }_i\in W}\sum _k{\left(\widehat{p}\left({\rho }_k-s_{x}sin{\zeta }_i-s_{y}cos{\zeta }_i,{\zeta }_i+{\alpha }_g\right)-{\mu }_{\widehat{p}}\right)}^2/\left(n_{\zeta }\mid W\mid -1\right)}.\end{array}$$

When the cross-correlation is implemented as a Fourier multiplication, simplifications can be made that also lead to greater efficiency.

The Fourier transform of a line in $\widehat{p}$ is:

$${\widehat{P}}_{{\zeta }_i}=P_0^{{\zeta }_i}+\sum _{k=1}^{n_{\zeta }}{P}_k^{{\zeta }_i},$$

where $\widehat{P}$ is the Fourier transform of $\widehat{p}$ and $P_k^{{\zeta }_i}$ are the Fourier coefficients of line ζ_i in $\widehat{P}$ . Since $P_0^{{\zeta }_i}$ contains the average value of the line, using Parseval’s theorem the line variances can be calculated as:

$${\sigma }_{{\zeta }_i}^2=\frac{1}{n_{\zeta }-1}\sum _{k=1}^{n_{\zeta }}{\left|P_k^{{\zeta }_i}\right|}^2.$$

and can be precalculated for the complete projection or volume. The combined variances in the denominator of the cross-correlation can then be determined from the line variances using the equation (e.g. (Sachs, 1984)):

$${\sigma }_{\mathit{comb}}^2=\frac{1}{n-1}\left[\sum _i(n_i-1)s_i^2+\sum _i{n}_i{({\overline{x}}_i-\overline{x})}^2\right]$$

where n are the total number of points in the combined variance, which for equation B2 is n = n_ζ · |W|; n_i is the number of points in the individual samples, here n_i = n_ζ; x̄_i are the averages of the individual samples ${\overline{x}}_i=P_0^{{\zeta }_i}$

and $\overline{x}$ is the average of the combined data or

$$\overline{x}=\frac{1}{\mid W\mid }\sum _{i=1}^{\mid W\mid }{P}_0^{{\zeta }_i}.$$

The calculations for q̂ are analogous.

Appendix C: Combined cross-correlation

When projections at different angles are matched by rotation cross-correlation to a volume, each 3D cross-correlation function is in the (polar) coordinate system of the projection. To calculate the average, interpolations are required from the polar coordinate system of each projection cross-correlation function to the coordinate system of the average cross-correlation function. There are two schemes to calculate the combined cross-correlation, ccc(α, β,γ), (Eq. 9). The first is called “forward scheme”: from a sampling point of each rotation cross-correlation, cc_{αf,i, βf,i,γf,i} (α_g, β_g, γ_g), 1, 2, …, N, where (α_f,i, β_f,i,γ_f,i) are the coordinates in the rotation cross-correlation function that belongs to the i-th projection of the reference volume f, to the combined cross-correlation. Given a sampling point k at coordinates $\left({\alpha }_g^k,{\beta }_g^k,{\gamma }_g^k\right)$ in cc_{αf,i, βf,i,γf,i} (α_g, β_g,γ_g), the corresponding point (α̃^k, β̃^k,γ̃^k) in the combined function ccc(α, β,γ) can be found using Equation 6, i.e., $\mathbf{R}={\mathbf{Q}}_{f,i}^{\text{T}}{\mathbf{Q}}_g={\mathbf{Q}}_{f,i}^{\text{T}}{\mathbf{R}}_Z\left({\alpha }_g^k\right){\mathbf{R}}_Y\left({\beta }_g^k\right){\mathbf{R}}_Z\left({\gamma }_g^k\right)$ and solving for the rotation angles in R. The problem of the “forward” scheme is that the corresponding point does not necessarily fall on the sampling grid. Hence a forward interpolation is needed. However, forward interpolation which assigns values to points in the neighborhood of a single point is an ill-posed problem.

In our implementation we used the second scheme, “backward scheme” starting from a sampling point of the combined cross-correlation and calculating back to the rotation cross-correlation of each projection. Given a sampling point (α^k, β^k,γ^k) of the combined cross-correlation ccc(α, β, γ), the corresponding point $\left({\stackrel{\sim }{\alpha }}_g^k,{\stackrel{\sim }{\beta }}_g^k,{\stackrel{\sim }{\gamma }}_g^k\right)$ in each single cross-correlation function cc_{αf,i, βf,i,γf,i} (α_g, β_g,γ_g), can be found using

$$\begin{array}{l}{\mathbf{Q}}_g={\mathbf{Q}}_{f,i}\mathbf{R}={\mathbf{Q}}_{f,i}{\mathbf{R}}_Z\left({\alpha }^k\right){\mathbf{R}}_Y\left({\beta }^k\right){\mathbf{R}}_Z\left({\gamma }^k\right)\\ ={\mathbf{R}}_Z\left({\alpha }_g^k\right){\mathbf{R}}_Y\left({\beta }_g^k\right){\mathbf{R}}_Z\left({\gamma }_g^k\right)\end{array}$$

and solving for the Euler angles in Q_g.

The same as previously, the resulting values may not fall on the sampling grids; however, the value can be easily acquired by a proper interpolation using the values of surrounding points. We used a straightforward trilinear interpolation. The “backward scheme” iterates all possible combinations of (α, β,γ), which sometimes can get slow. We used the following relations to reduce the number of matrix multiplications in the calculation and speed up the process:

$$\begin{array}{l}{\mathbf{R}}_Z\left({\alpha }_g^k\right){\mathbf{R}}_Y\left({\beta }_g^k\right){\mathbf{R}}_Z\left({\gamma }_g^k+\mathrm{\Delta }\gamma \right)={\mathbf{R}}_Z\left({\alpha }_g^k\right){\mathbf{R}}_Y\left({\beta }_g^k\right){\mathbf{R}}_Z\left({\gamma }_g^k\right){\mathbf{R}}_Z\left(\mathrm{\Delta }\gamma \right)\\ ={\mathbf{Q}}_{f,i}{\mathbf{R}}_Z\left({\alpha }^k\right){\mathbf{R}}_Y\left({\beta }^k\right){\mathbf{R}}_Z\left({\gamma }^k\right){\mathbf{R}}_Z\left(\mathrm{\Delta }\gamma \right),\\ ={\mathbf{Q}}_{f,i}{\mathbf{R}}_Z\left({\alpha }^k\right){\mathbf{R}}_Y\left({\beta }^k\right){\mathbf{R}}_Z\left({\gamma }^k+\mathrm{\Delta }\gamma \right)\end{array}$$

where Δγ is the increment in the angle γ. Let (α^k, β^k,γ^k) be the corresponding point of $\left({\alpha }_g^k,{\beta }_g^k,{\gamma }_g^k\right)$ in the “backward scheme”. When the angle γ^k is incremented by Δγ, ${\gamma }_g^k$ will also be incremented by the same amount Δγ. This only applies to the angle γ when the other two angles, α and β, remain unchanged.