Dynamic weakening of serpentinite gouges and bare surfaces at seismic slip rates

Abstract

To investigate differences in the frictional behavior between initially bare rock surfaces of serpentinite and powdered serpentinite (“gouge”) at subseismic to seismic slip rates, we conducted single-velocity step and multiple-velocity step friction experiments on an antigorite-rich and lizardite-rich serpentinite at slip rates (V) from 0.003 m/s to 6.5 m/s, sliding displacements up to 1.6 m, and normal stresses (σ_n) up to 22 MPa for gouge and 97 MPa for bare surfaces. Nominal steady state friction values (μ_nss) in gouge at V = 1 m/s are larger than in bare surfaces for all σ_n tested and demonstrate a strong σ_n dependence; μ_nss decreased from 0.51 at 4.0 MPa to 0.39 at 22.4 MPa. Conversely, μ_nss values for bare surfaces remained ∼0.1 with increasing σ_n and V. Additionally, the velocity at the onset of frictional weakening and the amount of slip prior to weakening were orders of magnitude larger in gouge than in bare surfaces. Extrapolation of the normal stress dependence for μ_nss suggests that the behavior of antigorite gouge approaches that of bare surfaces at σ_n ≥ 60 MPa. X-ray diffraction revealed dehydration reaction products in samples that frictionally weakened. Microstructural analysis revealed highly localized slip zones with melt-like textures in some cases gouge experiments and in all bare surfaces experiments for V ≥ 1 m/s. One-dimensional thermal modeling indicates that flash heating causes frictional weakening in both bare surfaces and gouge. Friction values for gouge decrease at higher velocities and after longer displacements than bare surfaces because strain is more distributed.

Key Points

• Gouge friction approaches that of bare surfaces at high normal stress

• Dehydration reactions and bulk melting in serpentinite in < 1 m of slip

• Flash heating causes dynamic frictional weakening in gouge and bare surfaces

1. Introduction

Our understanding of the frictional behavior of faults at seismic slip velocities (>0.1 m/s) has significantly improved over the last 15 years with experiments performed on initially bare rock surfaces [e.g., Di Toro et al., ²⁰⁰⁴; Goldsby and Tullis, ²⁰¹¹; Han et al., ²⁰⁰⁷; Hirose and Shimamoto, ²⁰⁰³; Tsutsumi and Shimamoto, ¹⁹⁹⁷] and gouges [e.g., Brantut et al., ²⁰⁰⁸; Han et al., ²⁰¹⁰; Kitajima et al., ²⁰¹⁰; Mizoguchi et al., ²⁰⁰⁹; Reches and Lockner, ²⁰¹⁰]. In general, these studies of high-velocity friction (HVF) demonstrate that rock friction coefficients decrease dramatically from ∼0.7 to as low as 0.1 as slip velocities approach seismic rates and (in most cases) increase rapidly as velocities decelerate; this general behavior is nominally independent of rock composition [Di Toro et al., ²⁰¹¹; Goldsby and Tullis, ²⁰¹¹]. Such dynamic fault-weakening behavior revealed in laboratory experiments is consistent with several earthquake-related observations retrieved from the following: (1) seismology, e.g., the large stress drops constrained from analysis of seismic radiation patterns of some earthquakes [Imanishi and Ellsworth, ²⁰⁰⁶; Malagnini et al., ²⁰¹⁰; Viegas et al., ²⁰¹⁰] or the (debated) breakdown of the scaling between radiated energy and seismic moment [Abercrombie, ¹⁹⁹⁵; Kanamori and Heaton, ²⁰⁰⁰], (2) geophysics, e.g., the lack of a pronounced heat flow anomaly along major fault zones [Lachenbruch and Sass, ¹⁹⁹²; Fulton et al., ²⁰¹³] or the large seismic slip accommodated in fault patches in the Sumatra 2004 of moment magnitude (M_w) 9.3 (15 m of max slip [Stein and Okal, ²⁰⁰⁵]) and the Tohoku 2011 M_w 9.0 (50 m of max slip [Fujiwara et al., ²⁰¹¹]) events, and (3) geology, e.g., estimates of coseismic frictional strength obtained from ancient exhumed faults [e.g., Di Toro et al., ²⁰⁰⁶; Griffith et al., ²⁰⁰⁹] or active deep-drilled seismic faults [Chester et al., ²⁰¹³; Hirono et al., ²⁰⁰⁷].

A number of physical mechanisms have been proposed to explain the dynamic weakening behavior observed in experiments and postulated to occur on faults (see Di Toro et al. [2011], Niemeijer et al. [2012], and Rice and Cocco [2007] for a summary). In particular, mechanical data and microstructural investigations of experimentally deformed bare rocks are consistent with flash heating of asperities [Goldsby and Tullis, ²⁰¹¹; Violay et al., ²⁰¹⁴], frictional melting [Di Toro et al., ²⁰⁰⁶; Hirose and Shimamoto, ²⁰⁰⁵; Niemeijer et al., ²⁰¹¹; Spray, ²⁰⁰⁵], silica gel weakening [Di Toro et al., ²⁰⁰⁴; Goldsby and Tullis, ²⁰⁰²], and superplasticity (grain boundary sliding accommodated by dislocation motion or diffusion) [Green et al., ²⁰¹⁰; Holdsworth et al., ²⁰¹³; Schubnel et al., ²⁰¹³]. However, all faults generate a millimeter to centimeter thick layer of gouge during rupture and seismic slip [Reches and Dewers, ²⁰⁰⁵], even within their deeper roots (6–15 km [e.g., Sibson, ¹⁹⁷⁷; Snoke et al., ¹⁹⁹⁹]). This raises the following questions: Which dynamic-weakening mechanisms occur in gouge-bearing faults? How might the presence of gouge modify the occurrence and/or efficacy of these weakening processes at seismic slip rates? Lubrication due to the presence of powders (i.e., powder lubrication) [Han et al., ²⁰¹⁰; Reches and Lockner, ²⁰¹⁰; Tisato et al., ²⁰¹²] is inconsistent with the rapid recovery of frictional strength at the end of sliding. Moreover, in exposed fault zones it is commonly observed that slip tends to be localized along very thin surfaces within gouge [e.g., Chester and Chester, ¹⁹⁹⁸; Fondriest et al., ²⁰¹³; Sibson, ²⁰⁰³], leading some workers to suggest that once strain is localized within gouge the system will emulate bare surface slip behavior [e.g., Smith et al., ²⁰¹²; T. Tullis, personal communication, 2013]. But is it appropriate to extrapolate rock friction behavior obtained in rock-on-rock friction experiments to natural gouge-bearing faults? Furthermore, how does the effective normal stress affect this behavior? Interestingly, the results from Smith et al. [2013b] on calcite gouge and Han et al. [2007] on (cohesive) calcite-bearing marble suggest that the shear stress or strength of calcite gouge is a factor of 2 or greater than marble bare surfaces at seismic slip velocities despite having localized strain.

Serpentinite is a common rock type in the oceanic lithosphere, and earthquakes may propagate into serpentinized mantle along mid-oceanic ridges, transform faults, and subduction zones; the latter alone release about 85–90% of the global seismic moment [Scholz, ²⁰⁰²]. For this reason, the frictional behavior of serpentinite has been studied over a wide range of slip rates from plate rates to seismic slip rates [e.g., Hirose and Bystricky, ²⁰⁰⁷; Kohli et al., ²⁰¹¹; Reinen et al., ¹⁹⁹²]. Moreover, serpentine group minerals are expected to react to talc, olivine, and enstatite due to frictional heating during rapid slip. These minerals are thought to be stable in the geologic record and could therefore provide evidence for seismic slip [e.g., Kohli et al., ²⁰¹¹]. Currently, the only widely accepted evidence for ancient seismic faulting is the presence of pseudotachylytes [Sibson, ¹⁹⁷⁵]. Other proposed geologic evidence for seismic slip includes thermally altered biomarkers in sedimentary rocks [Polissar et al., ²⁰¹¹], peculiar crystal-plastic features [Bestmann et al., ²⁰¹²; Smith et al., ^{2013a, 2013b}], injection of fluidized gouge [Fondriest et al., ²⁰¹²; Lin, ²⁰¹¹; Rowe, ²⁰¹³], and the combination of mirror-like surfaces with truncated and exploded grains [Fondriest et al., ²⁰¹³; Siman-Tov et al., ²⁰¹³]. As a consequence, the occurrence of serpentine breakdown minerals in slipping zones could be indicative of ancient seismicity in faults exhumed from seismogenic depths, outlining the importance for further field studies of exhumed fault zones hosted in oceanic rocks.

Employing a rotary-shear apparatus, we extend the study of the frictional behavior of serpentinite rocks to higher normal stresses (up to 96.6 MPa for bare surfaces and 22.4 MPa for gouges) and slip velocities (up to 4.3 m/s for bare surfaces and 6.5 m/s for gouges) than investigated previously. We also explore differences in dynamic frictional-weakening behavior observed on serpentine gouge and during tests on initially bare surfaces of serpentine by conducting relatively short-displacement, high-velocity experiments while varying the normal stress between tests. Following each experiment, the slip surfaces and wear material were analyzed with X-ray powder diffraction (XRPD) and several microstructural analysis techniques. These analyses, coupled with 1-D thermal modeling, allow us to constrain the effects of velocity, normal stress, shear heating, strain localization, and dehydration reactions on dynamic frictional weakening of serpentine and, by extension, other materials.

2. Experimental Procedures

2.1. Sample Preparation and Data Acquisition

Twenty-seven frictional sliding experiments on initially bare surfaces and powdered rock samples were performed with SHIVA (slow- to high-velocity rotary-shear friction apparatus) at the Istituto Nazionale di Geofisica e Vulcanologia in Rome, Italy (for a description of SHIVA, see Di Toro et al. [2010] and Niemeijer et al. [2011]). Two materials were tested: an antigorite-rich serpentinite (ATG) and a lizardite-rich serpentinite (LIZ). ATG samples contain ∼90% antigorite with minor magnesite and magnetite; LIZ samples contain ∼80% lizardite, ∼14% clinochlore (chlorite), and minor magnetite and trace amounts of olivine and enstatite, as determined by petrographic and XRPD analyses (Table 1).

Table 1.

Experimental Conditions and Mechanical Data From 27 High-Velocity Friction Experiments^a

Experiment #	Material	Experiment Conditions	Total Displacement (m)	Peak Velocity (m s−1)	Peak Acceleration, Deceleration (m s−2)	Peak τ (MPa)	Average σn (MPa)	Slow μnss	Fast μnss; *μmin	Dw(mm)	Dth (mm)	δ (mm)	Vf (m s−1)	XRPD
736a	ATG_BS	SS_1	1.01	NA	41, 31	NA	5.4	NA	0.14	NA	NA	NA	NA	Atg, En, Ol
736b	ATG_BS	SS_1	1.01	1.09	49, 30	5	12.4	NA	0.14	27	4.6	0.4	0.2	Atg, En, Ol
736c	ATG_BS	SS_1	1.01	1.09	50, 30	8.1	20	NA	0.12	82	4.8	0.4	0.2	Atg, En, Ol
736d	ATG_BS	SS_1	1.01	1.09	48, 29	11.4	32.1	NA	0.11	15	2.3	0.4	0.2	Atg, En, Ol
736e	ATG_BS	SS_1	1.01	1.09	47, 30	16	49.8	NA	0.11	21	1.9	0.4	0.2	Atg, En, Ol
736f	ATG_BS	SS_1	1.01	1.09	45, 29	26.2	65.1	NA	0.11	24	1.6	0.4	0.2	Atg, En, Ol
736 g	ATG_BS	SS_1	1.01	1.09	49, 30	31.1	75.7	NA	0.11	22	1.6	0.3	0.2	Atg, En, Ol
736 h	ATG_BS	SS_1	1.01	1.09	50, 29	35.2	96.6	NA	0.11	9.3	1.5	0.3	0.22	Atg, En, Ol
820	ATG_G	SS_1	0.92	1	47, 49	2.5	4.0 (0.2)	NA	0.51 (0.03)	200	130	NA	NA	Atg, Mgs, Mt
745	ATG_G	SS_1	0.92	1.2	60, 60	5.5	8.3 (0.03)	NA	0.48 (0.02)	240	120	55	1	Atg, En, Mt, Ol
821	ATG_G	SS_1	0.91	1	41, 50	9	11.8 (0.04)	NA	0.52 (0.01)	280	200	60	1	Atg, Mgs, Ol
822	ATG_G	SS_1	0.9	1	35, 46	12.4	17.8 (0.08)	NA	0.4 (0.02)	175	67	40	0.85	Atg, Mgs, Ol
823	ATG_G	SS_1	0.9	1.1	24, 49	16.1	22.4 (0.07)	NA	0.39 (0.02)	162	57	30	0.76	Atg, Mgs, Ol
747	LIZ_G	SS_1	0.92	1.2	65, 63	NA	3.8 (0.06)	NA	*0.50	NW	NW	NW	NW	Chl, En, Liz, Mt, Ol
746	LIZ_G	SS_1	0.92	1.2	60, 62	5.45	8.5 (0.09)	NA	*0.46	NA	NA	150	1	Chl, En, Liz, Mt, Ol
748	LIZ_G	SS_1	0.92	1.2	51, 60	8.3	11.5 (0.6)	NA	*0.52	NA	NA	100	1	Chl, En, Liz, Mt, Ol
825	LIZ_G	SS_1	0.9	1	40, 52	11.7	17.8 (0.3)	NA	*0.34	NA	NA	90	0.92	Aug, Chl, En, Liz, Mt, Ol
826	LIZ_G	SS_1	0.9	1.1	29, 48	14.3	18.7 (0.4)	NA	*0.31	NA	NA	70	0.87	Aug, Chl, En, Liz, Mt, Ol
834	ATG_G	SS_6.5	1.65	6.5	59, 30	8.9	10.9 (0.08)	NA	0.31 (0.02)	180	70	20	1.4	Ol, Pyx
835	ATG_G	SS_0.1	0.89	0.14	4, 9	NA	13.3 (0.07)	NA	0.65 (0.02)	NW	NW	NW	NW	Atg, Mgs, Mt
734	ATG_BS	MS_0.003_4.5	0.46	4.3	60, 70	4.4	4.9 (0.04)	0.83 (0.06)	0.12 (0.03)	25	2.5	1	0.3	Atg, En, Mgs, Mt, Ol
727	ATG_BS	MS_0.003_4.5	0.46	4.3	NA	6.6	8.8 (0.01)	0.67 (0.01)	0.09 (0.02)	NA	NA	NA	NA	Atg, En, Mgs, Mt, Ol
735	ATG_BS	MS_0.003_4.5	0.46	4.3	62, 70	10	14.9 (0.4)	0.66 (0.005)	0.09 (0.01)	38	5.9	0.5	0.3	Atg, En, Mgs, Mt, Ol
733	ATG_BS	MS_0.003_4.5	0.46	4.3	NA	16	19.5 (0.3)	0.68 (0.05)	0.09 (0.02)	NA	NA	NA	NA	Atg, En, Mgs, Mt, Ol
824b	ATG_G	MS_0.003_4.5	0.51	4	65, 50	6.9	8.5 (0.2)	0.72 (0.002)	0.35 (0.03)	68	44	33	2	Atg, Mgs, Ol
818	ATG_G	MS_0.003_4.5	0.51	4	63, 49	7.1	7 (0.2)	0.73 (0.002)	0.38 (0.05)	197	183	70	2.6	NA
705	LIZ_G	MS_0.003_5	0.51	4.8	65, 75	5.9	8.5 (0.2)	0.65 (0.003)	0.38 (0.02)	163	131	20	1.6	NA
Composition	LIZ													Chl, Liz, Mt (±Ol, En)
Composition	ATG													Atg, Mgs, Mt

^aMaterials: ATG, antigorite-rich serpentinite; LIZ, lizardite-rich serpentinite; bare surface (BS) and gouge (G). Experimental conditions: SS_X, single-velocity step test at X m/s; MS_X_Y, multiple-velocity step test with initial velocity X m/s and stepped velocity Y m/s. NA, not applicable, indicates that data were not recorded or measured. NW, experiment had no frictional weakening. Parentheses indicate standard deviation. X-ray powder diffraction (XRPD) data are reported in alphabetical order for observed mineral phases, antigorite (Atg), augite (Aug), clinochlore (chlorite, Chl), enstatite (En), lizardite (Liz), magnesite (Mgs), magnetite (Mt), and olivine (Ol).

Bare surface samples were first cored into two ∼50 mm long solid cylinders. The cylinders were pressed inside precut aluminum rings with an inner and outer diameter of 50 mm and 55 mm, respectively, and cemented within the rings with epoxy. Next, using a lathe, a depression was machined into the end face of each cylinder to yield an annulus with 50 and 30 mm outer and inner diameters, respectively. The sliding surface was ground with 320 grit sandpaper, and samples were loaded into SHIVA using holders described in Niemeijer et al. [2011] (Figures 1a and 1b). Powdered (“gouge”) samples were crushed and sieved between 37 and 105 µm, although some finer-grained material was also present in the starting material. The powder was evenly packed into a steel gouge holder (55 and 35 mm outer and inner diameters) and sheared between two roughened steel discs (Figures 1c– 1e) (for a description of the steel gouge holder and its calibration, see Smith et al. [2013b]). Normal stress was applied from the nonrotary end with an air-actuated pneumatic piston cylinder and servo controlled via an electrovalve in parallel with a digital pneumatic regulator. The regulator has a resolution of 0.02 bars and a response time of 0.2 s for a step of 50% of full scale [Di Toro et al., ²⁰¹⁰].

Figure 1.

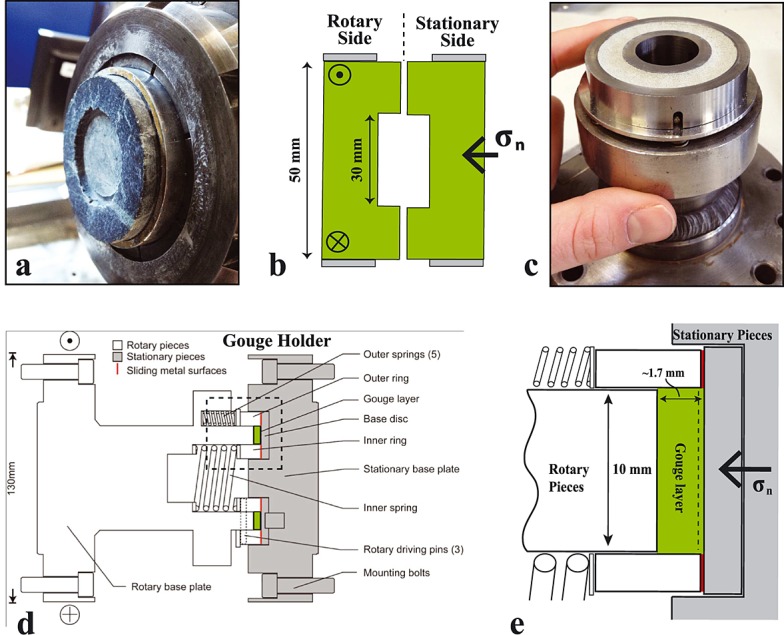
Sample assembly for bare surface and gouge experiments. (a) Photograph of rotary side of bare surface sample holder with serpentinite sample prior to deformation. (b) Schematic of bare surface experimental assembly. (c) Photograph of gouge holder (rotary side) loaded with serpentinite powder. (d) Schematic of gouge holder (modified after Smith et al. [2013b]). (e) Enlargement of Figure 1d showing gouge sample compartment (green) and lubricated metal-metal rotary contacts (red). Dashed line indicates typical location of strain localization within the gouge.

In all gouge experiments, 4 g of powder was used, yielding an ∼1.7 mm thick layer of compacted gouge. Slight variations in thickness occurred after initial loading of the gouge. This produced small fluctuations in the shear stress data with a wavelength of ∼150 mm, consistent with the average circumference of the gouge holder (outer and inner circumferences of 173 and 111 mm). The normal stress also fluctuated in response to variations in thickness. These fluctuations were in some cases accentuated by the delayed servo response of the regulator such that the stress was either overcorrected or undercorrected causing variations as high as 5%; we report the average imposed normal stress during deformation in Table 1. In most experiments, the sample holder prevented extrusion of the gouge, but in Runs 705, 818, 825, and 826, as much as ∼0.2 g (∼85 µm of thickness) of the gouge leaked from the holder during deformation. In Runs 727 and 733, sliding displacement was not recorded; however, we still report mechanical data assuming that the imposed velocity profile was similar to that in other experiments with identical experimental parameters. Mechanical data (axial load, torque, axial displacement, and angular rotation) were acquired at a frequency of 25 Hz for samples deformed at velocities less than 0.1 m/s and 25 kHz for higher slip velocities. The total slip, slip rate, and shear stress were determined following methods discussed in Di Toro et al. [2010]. High-frequency noise in the data was reduced with a fast Fourier transform (FFT) smoothing filter (Appendix A).

Following each gouge experiment, a portion of the slip surface was collected for XRPD analysis. Similarly, following each bare surface experiment, a portion of the wear material was collected for XRPD analysis. All but one XRPD analyses were conducted at Geosciences Department, Padua, Italy (see Appendix B for XRPD analysis details).

Microimaging was conducted with an Olympus SZX16 optical microscope fit with a digital camera, a JEOL 6500 and LEO 1500VP field-emission scanning electron microscope (SEM) with an accelerating voltage of 10–20 kV and a Cameca SX100 electron microprobe.

2.2. Multiple-Velocity Step Experiments

In each multiple-velocity step experiments, we imposed the identical preset velocity function. Samples were first deformed at a sliding velocity of ∼3 mm/s to a displacement of 60 mm; then the velocity was stepped to ∼4.5 m/s then decelerated back to rest, resulting in a total displacement of ∼0.5 m. We imposed an acceleration and deceleration of ∼40 m/s²; however, the servo-controlled response of the motor tends to overshoot this value, and we observe initial peaks as high as 65 m/s² during acceleration and 70 m/s² during deceleration (see Table 1). In these experiments a constant normal stress (σ_n) was imposed, ranging from 4.9 to 19.5 MPa in bare surface experiments (Runs 734, 727, 735, and 733), 7 to 8.5 MPa in ATG gouge experiments (Runs 824b and 818), and 8.5 MPa in one LIZ gouge experiment (Run 705).

2.3. Single-Velocity Step Experiments

In single-velocity step experiments, samples were accelerated from rest to a set velocity then decelerated back to rest after a preset amount of displacement. In one suite of experiments the samples were slid at 1 m/s for ∼1 m of displacement with an imposed acceleration and deceleration of ∼20 m/s²; actual accelerations and decelerations peaked as high as 65 m/s² (Table 1). In bare surface experiments (Run 736), a constant σ_n was imposed, ranging from 5 to ∼97 MPa, which is the highest normal stress ever applied in high-velocity friction experiments on natural rocks: 4 times higher than in the study of Hirose and Bystricky [2007] (see Appendix C for normal stress calculation of these runs). In ATG gouge experiments (Runs 820, 745, 821, 822, and 823), a constant σ_n was imposed, ranging from 4 to 22.4 MPa and in LIZ gouge experiments (Runs 747, 746, 748, 825, and 826) from 3.8 to 18.7 MPa. We were not able to deform gouge at higher normal stresses due to the torque limit of SHIVA. We also deformed ATG gouge at 0.1 m/s and 13.3 MPa for 1 m of slip (Run 835) and ∼6.5 m/s and 10.9 MPa for 1.6 m of displacement (Run 834), respectively.

3. Results

3.1. Multiple-Velocity Step Tests

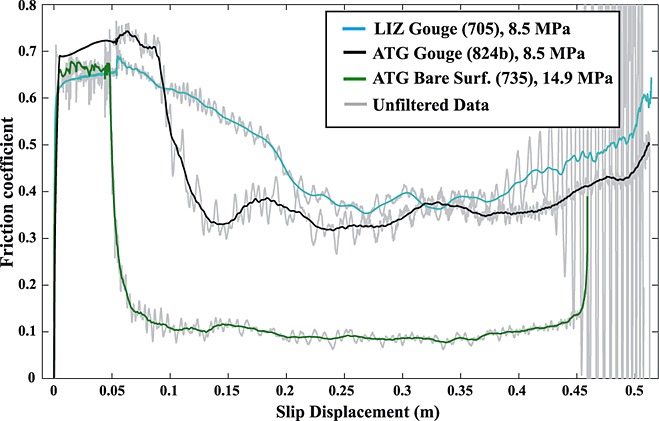
Results from all multiple-velocity step tests are reported in Table 1. Three representative experiments (Runs 705, 824b, and 735) are shown in Figure 2a. These tests illustrate differences between the frictional behavior of serpentine bare surfaces and serpentine gouge at subseismic and seismic slip velocities.

Figure 2.

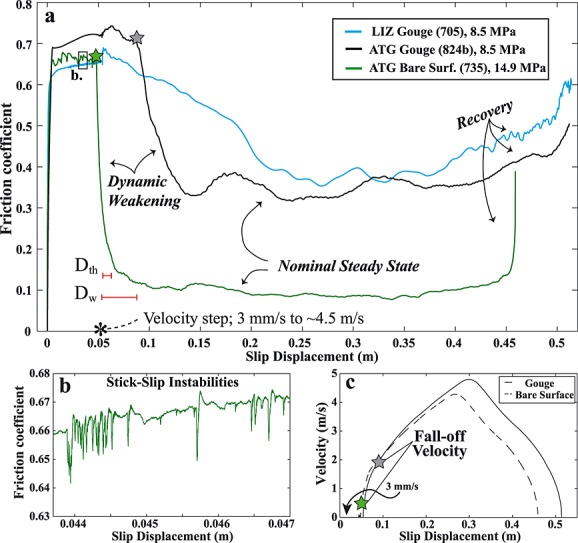
(a) Results from three multiple-velocity step experiments: 3 mm/s for ∼6 cm of displacement, acceleration to ∼4.5 m/s, and deceleration to rest. The approximate thermal-weakening distance (D_th) and slip-weakening distance (D_w) are indicated for Run 735 (see text for details). Stars indicate the displacement at which the friction rapidly decreases; the corresponding velocity (falloff velocity) is shown in Figure 2b. (b) Frictional stick-slip instabilities observed in Run 735 at 3 mm/s. (c) The imposed velocity profiles for experiments shown in Figure 2a. Note that the acceleration is very similar in both gouge and bare surface experiments.

During slip at 3 mm/s, ATG bare surfaces and LIZ and ATG gouge had similar nominal steady state values of the friction coefficient (μ_nss) but differed in their frictional stability; μ_nss is the average of the relatively constant friction values generated during slip at these velocities. We use the term “nominal” to acknowledge that friction may evolve with continued displacement due to changes in the shear zone microstructure and/or thermal structure. Values of μ_nss for ATG were ∼0.67 for bare surfaces (although slightly higher at lower normal stresses), ∼0.7 for ATG gouge and ∼0.65 for LIZ gouge (Table 1, labeled “Slow μ_nss”). Both LIZ and ATG gouge displayed stable sliding and slight strain hardening. Conversely, stick-slip instabilities occurred in all bare surface experiments at 3 mm/s. These events were audible and produced 0.1–0.25 MPa stress drops, as reflected in the friction record (Figure 2b).

After the velocity increased, friction of both bare surface and gouge samples first decreased (dynamically weakened) over a finite sliding displacement, reaching a minimum value. During deceleration, friction increased (recovered), resulting in a U-shaped friction versus displacement profile (e.g., Figure 2a). In all runs there were sustained flat regions defining the minimum of the U-shaped profiles in which friction was relatively constant with changes in velocity. Similar to sliding at lower velocities, we define the average friction over these flat regions as μ_nss (labeled as “Fast μ_nss” in Table 1). The μ_nss values for ATG bare surfaces were ∼0.1 while those for ATG and LIZ gouge ranged from 0.35 to 0.38 (Table 1).

To characterize the dynamic weakening, we report the amount of slip required to reach the new nominal steady state friction value after the velocity step. Previous studies have defined this length-scale as either the slip-weakening distance (D_w), the distance over which the shear stress (or friction) drops by 95% of the total stress drop [Hirose and Shimamoto, ²⁰⁰⁵; Mizoguchi et al., ²⁰⁰⁹], or the thermal-weakening distance (D_th), the distance over which stress falls to 1/e of the total stress drop [Di Toro et al., ²⁰¹¹]. We report both distances in Table 1 for comparison with previous studies; however, we discuss only D_th in this study. Values of D_th in bare surface experiments on ATG ranged from 3 to 8 mm. In contrast, for the same acceleration and normal stresses, D_th values in both the ATG and LIZ gouge experiments were over an order of magnitude larger, ranging from 40 to 180 mm.

To further quantify dynamic weakening, we report the velocity at the onset of frictional weakening, which we refer to as the falloff velocity (V_f). Values of V_f were determined by first noting the displacement at which friction rapidly decreases (green and gray star in Figure 2a), then finding the corresponding velocity for the given displacement (Figure 2c). Values of V_f thus determined are simply a first-order observation dependent upon the imposed experimental conditions. For otherwise equivalent experimental conditions, V_f in gouge was as much as an order of magnitude larger than that in bare surface experiments (Table 1).

3.2. Single-Velocity Step Tests at 1 m/s

The results of all single-velocity step experiments are reported in Table 1 and illustrated in Figure 3. In general, these experiments demonstrated similar differences between the behavior of bare surfaces and gouge observed in the multiple-velocity step experiments. In addition, because the velocity was held constant and normal stress was varied, we were able to explore the normal stress dependence on μ_nss, D_th, and V_f (compiled in Figure 4).

Figure 3.

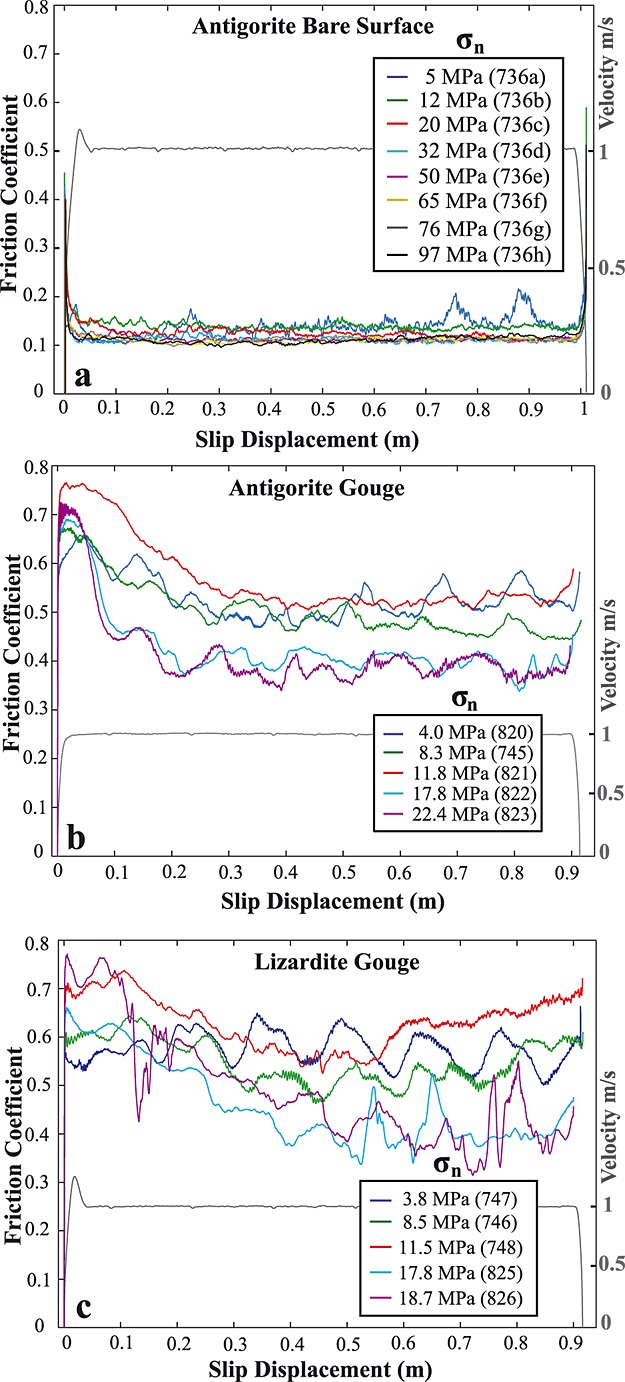
Results from single-velocity step experiments with peak velocities of 1 m/s on (a) antigorite bare surfaces, (b) antigorite gouge, and (c) lizardite gouge. A representative velocity profile is shown for each suite of experiments (gray line). Large wavelength oscillations in gouge friction are caused by inconsistencies in gouge thickness (see section 2.1).

Figure 4.

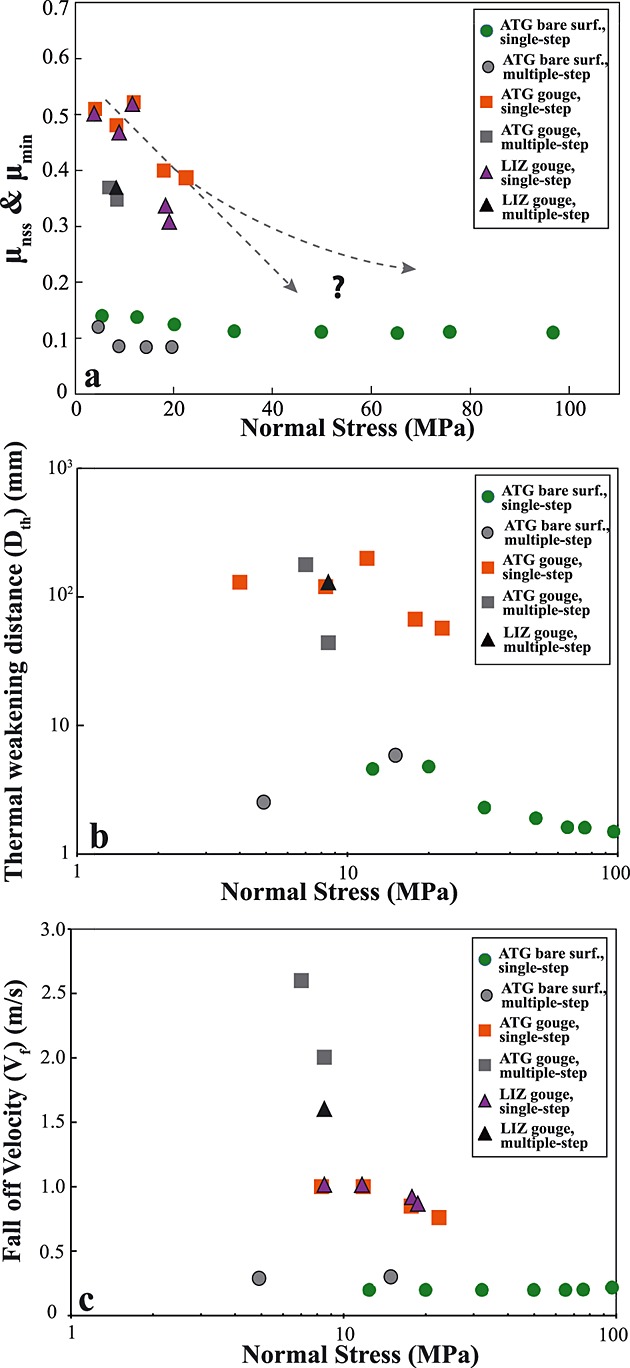
Normal stress dependence on (a) nominal steady state and minimum friction values (LIZ gouge), (b) thermal weakening distance, and (c) the falloff velocity for multiple-velocity step and single-velocity step experiments. Run numbers are indicated in parentheses.

Values of μ_nss decreased with increasing normal stress in both gouge and bare surface experiments (Figures 3a– 3c); the normal stress dependence is larger for gouge than for bare surfaces (Figure 4a). Values of μ_nss for bare surfaces decreased from 0.14 to 0.11 with an increase in σ_n from 5 to ∼30 MPa and remained at a value of ∼0.11 with additional increase in σ_n from 30 to ∼97 MPa (Figure 4a). The friction data for gouge are more scattered than for bare surfaces. Interpretation of these experiments is complicated by (1) variations in sample thickness which caused sinusoidal oscillations in shear and normal stress and (2) sample leaks, which caused spikes in the data. As such, the reported μ_nss values have larger standard deviations (Table 1). Values of μ_nss for ATG gouge decreased from 0.51 to 0.39 with an increase in σ_n from 4 to 22.4 MPa (Figure 4a). Friction for LIZ gouge did not appear to reach a steady state value in any single-velocity experiment (Figure 4a); for these experiments we report only a minimum friction value (μ_min). Values of μ_min for LIZ gouge decreased from 0.50 to 0.31 with an increase in σ_n from 3.8 to 18.7 MPa. The ATG and LIZ gouge samples deformed at σ_n ∼12 MPa (Runs 821 and 748) deviate somewhat from this general trend. Values for μ_nss from multiple-velocity step experiments (with maximum slip rates of ∼4.5 m/s) are generally consistent with single-velocity step results (with maximum slip rates of ∼1 m/s) (Figure 4a).

Values of D_th for both ATG bare surfaces and gouge decreased with increasing normal stress, though there is scatter for the gouge samples (Figure 4b). We did not calculate D_th values for LIZ gouge because steady state friction was not reached. Values of D_th for ATG bare surfaces decreased from 0.46 to 0.15 mm with an increase in σ_n from ∼11 to 97 MPa. Values of D_th for ATG gouge are more than an order of magnitude greater than for ATG bare surfaces and decreased from 130 to 57 mm with an increase in σ_n from 4 to 22.4 MPa. Values of D_th from multiple-velocity step experiments are similar to those observed from single-velocity step experiments on both bare surface and gouge samples (Figure 4b).

Values of V_f are independent of normal stress in bare surface experiments and decrease modestly with increasing normal stress in gouge experiments; V_f is much smaller for bare surface samples than gouge samples deformed at the same conditions. Figure 4c shows that values of V_f for all ATG bare surface experiments were ∼0.2 m/s. In contrast, for approximately the same velocity profile, V_f decreased from 1 to 0.76 m/s for LIZ gouge and from 1 to 0.87 m/s for ATG gouge with increasing normal stress. These trends in V_f for gouge also reflect a decrease in the amount of slip that occurred prior to frictional weakening with increasing normal stress; at low σ_n, the gouge experiments reached the peak velocity (1 m/s) and continued to slip for tens of millimeters before frictional weakening occurred, while at higher σ_n, the gouge weakened during acceleration before the peak velocity was attained. For bare surfaces, values of V_f in multiple-velocity step experiments are similar to those observed from single-velocity step experiments (Figure 4c). In contrast, for gouge samples, values for V_f are significantly higher in the multiple-velocity step experiments (Figure 4c).

3.3. Additional Single-Velocity Step Tests

To better constrain the velocity and displacement dependence of friction for the ATG gouge samples, we conducted two single-velocity step experiments at 0.1 m/s and ∼6.5 m/s (Runs 835 and 834, Figure 5). These experiments were conducted at normal stresses of 13.3 and 10.9 MPa, respectively. No frictional weakening was observed at 0.1 m/s (Run 835, blue trace in Figure 5); the value of μ_nss remained ∼0.65 throughout the duration of the 0.9 m slip cycle. In contrast, the sample deformed at a peak velocity of 6.5 m/s (Run 834, red trace in Figure 5) yielded a value of the friction coefficient of 0.31. This sample was also deformed to a larger amount of slip, ∼1.6 m, than in the other single-velocity tests (slip ∼1 m) and velocity-stepping tests (slip ∼0.45 m). As is shown in Figure 5, the friction coefficient was independent of velocity and achieved a steady value (∼0.3) during the acceleration stage for V > 4 m/s (after 0.2 m of slip) and began to increase during the deceleration stage for V < 2.5 m/s (after 1.5 m of slip).

Figure 5.

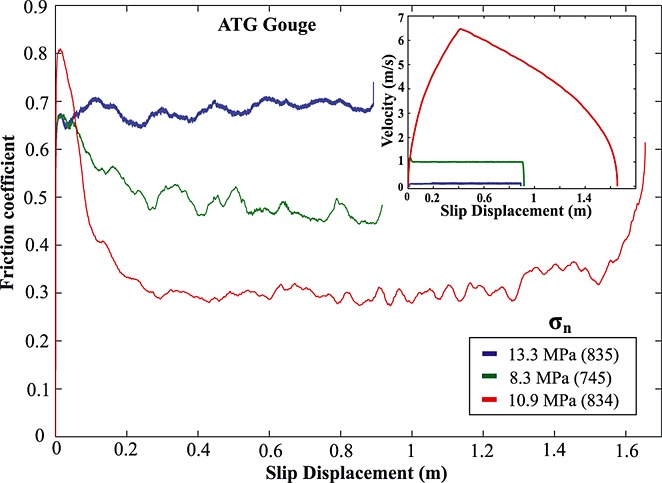
Velocity dependence of antigorite gouge; inset shows velocity profile for corresponding experiments. Run numbers are indicated in parentheses.

3.4. Velocity Dependence and Frictional Hysteresis

In all of the high-velocity experiments, we observe hysteresis in plots of friction versus velocity, with greater velocity dependence and higher friction values during acceleration than deceleration (e.g., Figures 2a, 3a, 3b, 3c, and 5). In Figure 6a we plot unfiltered data for two multiple-velocity step experiments on ATG bare surfaces (Runs 734 and 735; blue and green traces). In this figure the value of friction traces a clockwise “path” in log velocity space. During acceleration from 3 mm/s to ∼0.1 m/s, the friction remains nominally constant; friction then begins to decrease at a velocity of ∼0.1 m/s and decreases more rapidly at velocities above ∼0.3 m/s. In Figure 6b we plot the friction data for ATG gouge during one single-velocity step experiment (Run 834, red trace in Figure 6b). In this run, there was no initial period of slow slip at 3 mm/s; the sample was accelerated from rest to the target slip rate of 6.5 m/s. We also plot the data from a multiple-velocity step gouge experiment (Run 824b, black trace in Figure 6b); in this test, the sample was slid for 60 mm at 3 mm/s and then accelerated to 4.5 m/s.

Figure 6.

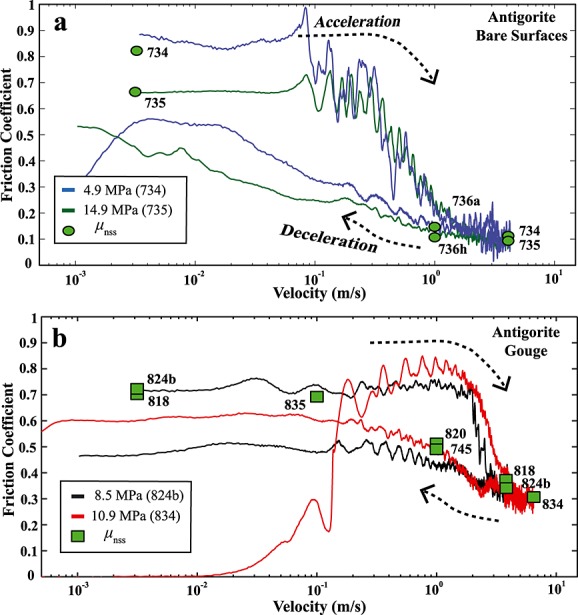
Hysteresis and velocity dependence of (a) ATG bare surfaces and (b) ATG gouge. Lines trace the evolution of friction from the onset of acceleration to the completion of deceleration. Run numbers are indicated in parentheses. In Runs 734, 735, and 824b, the velocity was accelerated from 3 mm/s from which they were sheared for 6 cm. Experiment 834 was accelerated from rest with no prior deformation. Symbols indicate nominal steady state values (μ_nss); corresponding run number is noted in black.

During acceleration, the gouge experiments show behavior similar to that for the bare surface experiments; except that for the gouge, the onset of weakening is shifted to higher velocities (∼1 m/s) producing a larger hysteresis (Figure 6b). During deceleration, friction during both ATG bare surface and ATG gouge experiments increases to values somewhat lower than those determined during the initial low-velocity portion of the experiments; friction for the gouge recovers at a higher velocity (∼0.2 m/s) than for the bare surfaces (<0.02 m/s) (Figures 6a and 6b).

In Figure 6 we superimpose μ_nss data on the friction path data for experiments on bare surfaces (green circles) and gouge (green squares). In both diagrams, black numbers correspond to the run number. For velocities below ∼0.1 m/s, values of μ_nss are similar to the transient values observed during acceleration. In contrast, at higher velocities, values of μ_nss are similar to the transient values observed during deceleration.

3.5. Microstructural and Mineralogical Analysis

3.5.1. Bare Surface Experiments

All bare surface samples deformed at velocities of 1 m/s and higher developed grooved striations and exhibit glass-like material on the slip surface. The glass-like material was observed in two textural forms. The first was a dark green veneer with glassy sheen that occurred in bands along topographically higher ridges on the slip surface (Figure 7a). This material was observed in all bare surface experiments. An SEM micrograph of one of these surfaces shows finger-like tendrils and bulbous structures (Figure 7b), similar to glass fibers described in Friedman et al. [1974]. The second textural form of glass-like material was 10–20 µm thick glassy patches of light green and translucent material observed on the slip surface (Figures 7c and 7d) of samples deformed at σ_n > 20 MPa. The glassy material is composed of a nominally homogenous ultra-fine-grained matrix (i.e., the matrix grain size is either too small to resolve with an SEM (<10 nm) or amorphous) with larger magnetite inclusions as suggested by backscattered electron SEM micrographs (Figures 7e and 7f) and exploratory microchemical analyses. These glassy patches occurred as bands oriented parallel to striations on the slip surface (similar to the “melt welts” described by Brown and Fialko [2012]) and are more numerous in samples that deformed higher normal stresses. At the highest normal stress the entire slip surface appeared to be covered with the glass-like material.

Figure 7.

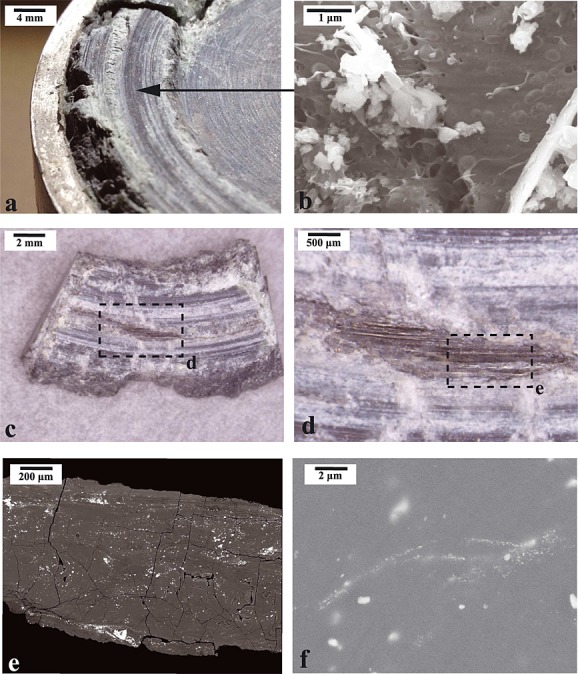
Microstructures of antigorite bare surfaces. (a) Photomicrograph showing dark striations on slip surface at low normal stress: Run 727, σ_n = 8.8 MPa. (b) SEM micrograph of dark band from sample from Run 727 showing melt-like tendrils and bulbous features on the slip surface. (c) Photomicrograph showing glass-like band on cut section of the slip surface at higher normal stress: Run 733, σ_n = 19.5 MPa. (d) Magnified region from Figure 6c showing glassy luster and transparent nature of the material. (e) SEM micrograph from polished glassy surface shown in Figure 7d. (f) Enlargement from Figure 7e showing gray ultra-fine-grained matrix with bands of nanometer-scale iron-rich minerals that are too fine-grained to resolve.

X-ray powder diffraction analysis of wear material collected after bare surface experiments showed evidence of serpentine dehydration products, olivine and enstatite (Table 1), in all samples tested (all of which were deformed at high enough slip velocity to cause frictional weakening). In several ATG bare surface experiments (e.g., Runs 733, 734, and 735), magnesite was detected but never in the LIZ experiments where carbonates were not present in the starting material. A comparison of XRPD profiles shows a systematic increase in the peak heights of olivine with increasing applied normal stress (Figure 8), suggesting a relative increase in the mass of the reaction products. None of the bare surface samples showed XRPD evidence for talc.

Figure 8.

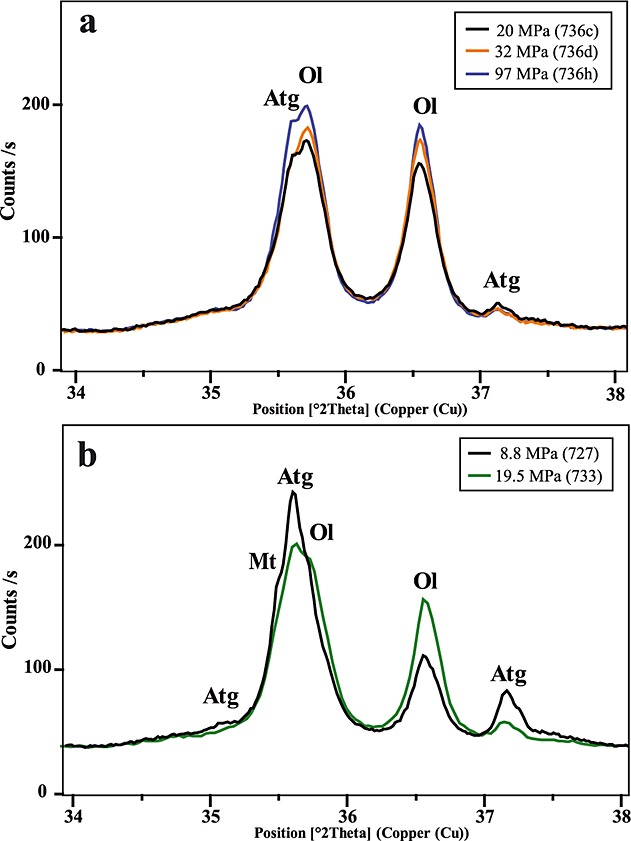
Comparison of XRPD results from (a) three single-velocity step experiments and (b) two multiple-velocity step experiments; the applied normal stress for each experiment and run number is noted in the key.

3.5.2. Gouge Experiments

In all gouge samples, some degree of strain localization and grain size reduction was observed. The ATG gouge sample tested at V = 0.1 m/s was poorly consolidated after deformation and developed a 400–500 µm thick zone of reduced grain size where strain was apparently localized (Figure 9a). The localized zone was composed of a matrix of 50–500 nm rounded antigorite grains (Figure 9b). This sample did not develop a well-defined slip surface or slickenlines.

Figure 9.

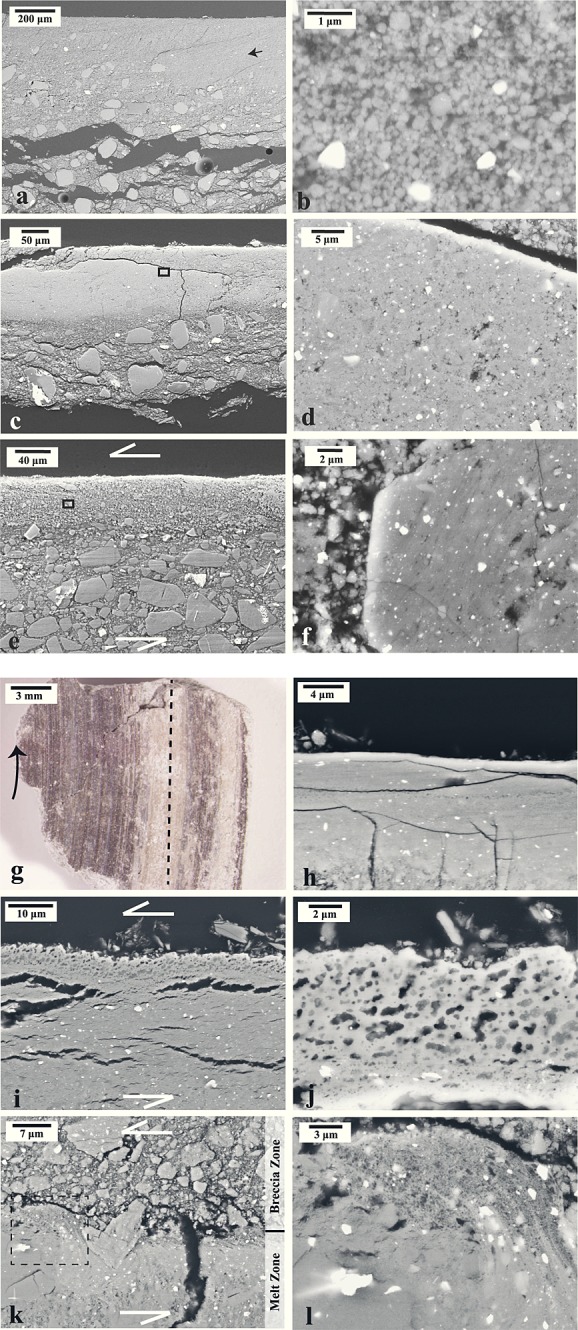
Microstructures of antigorite and lizardite gouges (all BSE-SEM micrographs with exception of Figure 9g). The SEM micrographs show cross-sectional profiles; samples are oriented such that top surface was adjacent to nonrotary disk; however, in all cases the section of the gouge zone closest to the stationary side was not recovered. (a) Run 835 (ATG) deformed at 0.1 m/s; orientation of shearing is not known, σ_n = 13.3 MPa. (b) Enlargement of granular fine-grained material within localized zone from Figure 9a (black arrow). (c) Run 821 (ATG) deformed at 1 m/s; sample is cut perpendicular to shearing direction, σ_n = 11.8 MPa. (d) Enlargement of ultra-fine-grained material in Figure 9c (black frame box). (e) Run 746 (LIZ) deformed at 1 m/s; sample is cut parallel to shearing direction, σ_n = 8.5 MPa. (f) Enlargement of brecciated clast within localized zone in Figure 9e. (g) Photomicrograph of slip surface from Run 823 deformed at 1 m/s showing vitreous and striated dark material and whitish streaks; rotary direction is indicated with black arrow, σ_n = 22.4 MPa. (h) Enlargement of dark glassy material shown in Figure 9g; sample is cut perpendicular to shearing direction. (i) Enlargement of whitish streak in Figure 9g showing vesicular ultra-fine-grained material along the slip surface; sample is cut along black dashed line. (j) Enlargement of Figure 9i showing irregular-shaped vesicles. (k) Run 826 deformed at 1 m/s showing an ultra-fine-grained zone “flowing” into the brecciated zone; sample is cut parallel to shearing direction, σ_n = 19 MPa. (l) Enlargement of Figure 9k (dashed box) showing flow structure.

ATG and LIZ gouge samples deformed at V ≥ 1 m/s developed 100–200 µm thick fine-grained localized zones consisting of an ultra-fine-grained matrix hosting clasts ranging from < 1 to 20 µm in diameter (Figures 9c and 9e). The fine-grained zones tend to be welded in all samples (e.g., Figures 9d and 9f). In some cases, microstructures indicate that the welded zones were brecciated after welding. The inspection of the localized zone from Run 746 (LIZ) illustrates clasts that are welded aggregates of fine-grained material (Figure 9f), suggesting a welded zone formed first then became brecciated and comminuted. In instances where the localized slip surface was exposed during sample recovery, we observed dark glassy striated patches (Figure 9g). These thin zones appeared translucent and became more abundant in samples deformed at higher normal stresses. An SEM image shows the cross-sectional profile of the dark glassy material (Figure 9h). At higher normal stresses and at the highest slip velocities (Run 834), we observed whitish (e.g., Figure 9g) and brownish streaks along the slip surface in addition to the dark glassy material. Brownish streaks are composed of micron to submicron in size granular clasts; spot XRPD analysis of one of these streaks revealed strong peaks for olivine and weak peaks for enstatite (Run 834, Table 1). A cross section through a whitish streak in an ATG sample (Run 823, Figures 9i and 9j) shows an ultra-fine-grained matrix with amoeboid-shaped vesicles. The vesicles are dispersed in a glass-like matrix probably resulting from quenching of the friction melt. The vesicles become smaller with increasing distance from the slip surface; next to the latter, they become interconnected defining a shear-parallel fabric (Figure 9j). Similar glass-like material and degassing-related textures were observed in LIZ samples. Figures 9k and 9l show an ultra-fine-grained zone that appears to have been injected into the brecciated zone. In this sample we note a high density of vesicles near the top of this apparently once-molten layer.

In both LIZ and ATG gouge samples, strain localized within the gouge layer near the interface between the gouge holder and the stationary side of the shearing rotary disk (dashed line, Figure 1e). In all ATG samples deformed at V ≥ 1 m/s we observed little textural evidence for deformation outside of the 100–200 µm thick localized zone. This is also true of LIZ gouge samples at lower normal stresses (<10 MPa); however, in samples from Runs 825 and 826 deformed at a normal stress of 18 and 19 MPa, respectively, we observed localized zones containing ultra-fine-grained (glassy) material adjacent to both the stationary and rotary side of the sheared layer. Further microstructural inspection of these samples revealed a varying degree of deformation throughout the shearing gouge layer.

X-ray powder diffraction revealed a general trend that gouge samples that underwent frictional weakening showed evidence for serpentine dehydration products (Table 1). In contrast, Run 835 (which was conducted at 0.1 m/s and showed no frictional weakening) did not show XRPD peaks for olivine or enstatite (Table 1). Two samples did not fit this trend. One LIZ sample (Run 747) did not demonstrate frictional weakening yet contained trace amounts of olivine and enstatite; we suspect that these phases were inherited from the starting material. One ATG sample (Run 820) demonstrated frictional weakening yet contained no XRPD evidence for dehydration; since this sample was deformed at 4 MPa, we suspect that the amount of reaction products may have been too small to resolve with XRPD. Diffraction peaks for talc were not found in any samples.

4. Discussion

Our experiments show that serpentine bare surfaces and gouge undergo frictional weakening during high-velocity shear experiments. However, friction evolves differently in each material with changes in slip displacement, velocity, and normal stress. These differences can be reconciled by exploring the underlying processes that promote dynamic weakening: strain localization and shear heating. In the following discussion, we first compare our bare surface data to previous high-velocity friction studies on similar materials. This comparison allows us to develop a conceptual model to better understand experimental observations on serpentine bare surfaces. We then use 1-D thermal models to explore how measured friction values are affected by frictional heating at the surface-scale (mm) and asperity-scale (µm) in both bare surface and gouge experiments.

4.1. Displacement- and Velocity-Dependent Hysteresis of Friction on Bare Surfaces

Values of macroscopic friction for a given sliding surface are a manifestation of frictional heating and temperature evolution on both the macroscale (slip surface) and the asperity scale (µm). These relationships are qualitatively demonstrated via variations in hysteresis loops between short- and long-displacement experiments shown in Figure 10a. In Figure 10a we plot results from our ATG bare surface experiments together with results of 50 experiments from Kohli et al. [2011] on ATG bare surfaces conducted at a normal stress of 5 MPa, a maximum velocity of 0.3 m/s, and a maximum acceleration of 10 m/s². This data set can be subdivided into two friction paths shown schematically in Figure 10b. Path 1 is modeled after the friction data from small displacement experiments (<0.05 m) from Kohli et al. [2011] shown in Figure 10a. Kohli et al. [2011] concluded that weakening occurred via flash heating of asperities above a critical weakening velocity (V_w) of ∼0.1 m/s for samples deformed at room temperature, based on the coincidence of the steady state friction data (gray diamonds in Figure 10a) with the deceleration path data, the observation of talc in XRPD analyses from the wear material of high-velocity samples, and the general agreement between the data and theoretical descriptions for flash weakening [Beeler et al., ²⁰⁰⁸; Rice, ²⁰⁰⁶].

Figure 10.

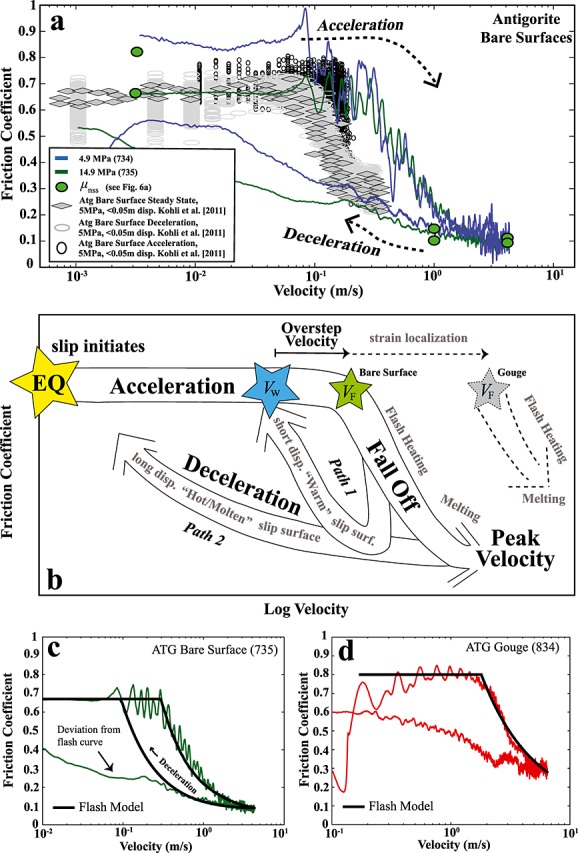
Interpretation of friction hysteresis in high-speed experiments on serpentinites. (a) Comparison of ATG bare surface friction data from this study with results from short displacement experiments from Kohli et al. [2011] (see text for discussion). Parentheses indicate the run number. (b) Schematic model illustrating friction hysteresis during an earthquake slip event (EQ) for serpentinite bar surfaces (solid lines) and dry gouge (dashed lines) (see text for discussion). (c) Predicted friction profile (black curve) using flash-weakening model [Rice, ²⁰⁰⁶] for bare surface sample (Run 735); equation (1) is used to model surface temperature increase during slip, which is then inserted into the formula for V_w from Rice [2006]. Model shows that the deceleration friction path will be offset to lower velocities, and the measured friction data (green trace) only partially fits the model during deceleration. (d) Predicted friction profile (black curve) during acceleration using flash-weakening model [Rice, ²⁰⁰⁶] for gouge sample (Run 834); the temperature of the deforming zone is assumed constant.

Flash-weakening theory predicts that values of friction should decrease when the asperity velocity exceeds the weakening velocity V_w [Rice, ²⁰⁰⁶]. However, in all experiments in which the slip rate was accelerated above V_w, friction remained transiently high before decreasing to steady state values (black ovals, Figure 10a), resulting in a modest hysteresis. This velocity overstepping represents a deviation from theoretical predictions and is characterized using the difference between the falloff velocity (V_f) and the critical weakening velocity (V_w), defining an overstep velocity (V_f-V_w) (Figure 10b). Following Kohli et al. [2011] and Goldsby and Tullis [2011], we posit that the overstepping results from the displacement required for strain localization and subsequent shear heating to occur within the thin gouge layer generated by wear between the bare surfaces. The displacement that occurs during acceleration between V_f and V_w is defined as an overstep displacement (δ) following Kohli et al. [2011] (labeled δ_w therein). All δ values are reported in Table 1, assuming V_w = 0.1 m/s. In this study δ was ∼0.4 mm for single-step velocity step tests and ranged from 0.5 to 1 mm in multiple-velocity step tests, consistent with δ values observed by Kohli et al. [2011].

Path 2 is defined by experiments conducted in this study (green and blue traces in Figure 10a) that have higher total displacement, peak velocities, and normal stresses than the Kohli et al. [2011] experiments. In our experiments, the friction during acceleration is similar to that observed in the short displacement (Path 1) experiments of Kohli et al. [2011]; the somewhat higher value for V_f in the Path 2 experiments arises from greater acceleration (50 m/s² compared to 10 m/s²). Nonetheless, δ remains approximately the same (Table 1), indicating that the initial weakening results from flash heating in both suites of experiments. At peak velocities, the Path 2 steady state friction values are lower than the Path 1 values but are consistent with the overall weakening trend and the results of Hirose and Bystricky [2007] on serpentine bare surfaces slid at 1 m/s. During deceleration, frictional recovery is delayed to lower velocities than observed in Path 1 experiments, resulting in a larger hysteresis loop (Figure 10b). We suggest that the difference between Paths 1 and 2 experiments is in part due to the sensitive dependence of V_w on the fault surface temperature (T_surf), where V_w ∝ (T_w − T_surf)²; if the difference between the surface temperature and the weakening temperature (T_w) is reduced by a factor of 2, a typical value seen in our thermal models, then V_w decreases by a factor of 4 [Rice, ²⁰⁰⁶]. The higher displacements, slip rates, and normal stresses used in Path 2 experiments generate higher surface temperatures, leading to lower values of V_w during deceleration than seen in Path 1 experiments. This is consistent with the observation that in Run 734 performed at 4.9 MPa normal stress, the recovery of the friction coefficient occurs at a higher velocity than in Run 735 performed at 14.9 MPa (Figure 10a). Small patches of melt produced on the slip surface may further delay Path 2 recovery. Conversely, in Path 1 experiments, there is not enough time for the surface temperature to significantly increase; thus, V_w remains constant, resulting in rapid friction recovery at velocities higher than in Path 2 experiments. In the following section, we use 1-D thermal modeling to further explore this hypothesis.

4.2. One-Dimensional Thermal Modeling: Bare Surfaces

To quantitatively explore differences in temperature evolution between the slip surface and asperity contacts in bare surface experiments, we employ 1-D thermal models. These models do not consider the latent heat of reaction; nonetheless, they allow for a first-order exploration of the processes governing dynamic weakening and frictional recovery. For the bare surface experiments, we calculate the surface temperature using the following model (see Appendix D for derivation):

(1)

where T₀ is the initial temperature (21°C), τ (t′) is time-dependent shear stress, V (t′) is time-dependent velocity, ρc is the effective heat capacity per unit volume, and α_th is the thermal diffusivity. The heat capacity and thermal diffusivity for antigorite are 2700 kJ (K m³)⁻¹ and 0.90 mm² s⁻¹, respectively [Osako et al., ²⁰¹⁰]. For a given experiment the integral is evaluated numerically using measured values for τ and V. In Figure 11a we plot T_surf for three single-velocity step tests and one multiple-velocity step test together with a projection of the MgO-SiO₂-H₂O phase diagram [Perrillat et al., ²⁰⁰⁵] and the wet solidus for ultramafic rocks [Till et al., ²⁰¹²] (see discussion below). Figure 1a shows that peak surface temperatures increase with increasing normal stress from ∼200°C at 5 MPa to > 1600°C at 97 MPa which is generally consistent with the microstructural observation of glassy material on samples deformed at the highest normal stresses. However, recall that olivine and enstatite were observed in the wear material in all bare surface experiments (Table 1), even those at the lowest normal stress (e.g., Run 734). The presence of these dehydration products is inconsistent with the 1-D thermal model for the surface temperature. To reconcile this observation with the thermal model, we consider the temperature evolution at the asperity contacts (T_asp) with the following flash-heating model (see Appendix D):

Figure 11.

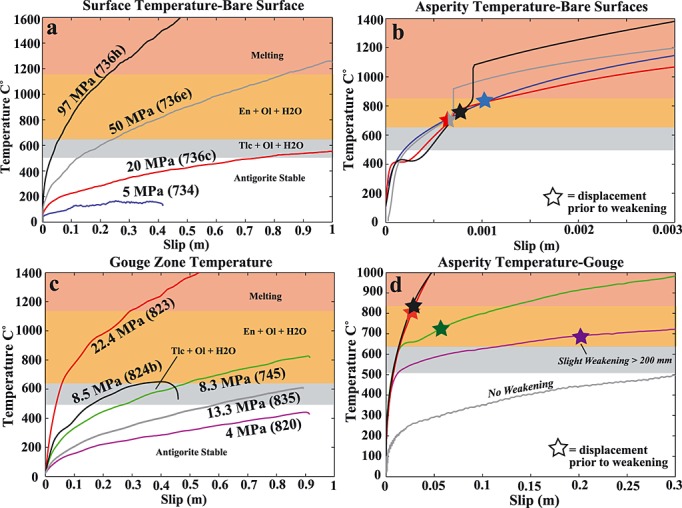
Results from 1-D thermal modeling with projected antigorite phase diagram (see text details). (a) Sliding surface temperatures in four ATG bare surface experiments; the applied normal stress and run number are noted by the corresponding temperature profile. (b) Asperity contact temperatures for bare surface samples modeled in Figure 1a; line colors correspond with Figure 1a. (c) Shear zone temperatures in five ATG gouge experiments assuming a 150 µm wide shear zones. (d) Asperity contact temperatures within deforming gouge; line colors correspond with Figure 1c.

(2)

where τ_c is the contact shear stress and d is the contact diameter. Here we have assumed that a contact ceases to exist after it has slipped a distance equal to the contact diameter, and thus, the contact lifetime is equal to d/V. Following Kohli et al. [2011], τ_c is approximated as 3 GPa (based on indentation hardness measurements [Goldsby and Hirth, ²⁰⁰⁶] and plasticity data for antigorite [Hilairet et al., ²⁰⁰⁶]) and d is estimated to be 5 µm (based on the critical slip distance observed during velocity changes at low slip velocities on identical samples of similar roughness [Reinen et al., ¹⁹⁹¹]). Figure 1b shows that T_asp in all experiments quickly increased above antigorite thermal stability over slip displacements < 1 mm. The total displacements at which the onset of weakening was observed (stars in Figure 1b) is coincident with predicted antigorite dehydration reactions and generally consistent with the flash-weakening temperature inferred by Kohli et al. [2011] (∼600°C). Recall that δ is the displacement that occurs during acceleration between V_f and V_w, where V_w is 0.1 m/s. So the total displacement prior to weakening is simply δ + slip that occurs from the onset of acceleration to 0.1 m/s which is on the order of 200 to 300 µm. Furthermore, using experimental parameters from Kohli et al. [2011], equation (2) predicts temperatures consistent with their observation of talc in the wear material. In contrast, our experiments have over an order of magnitude larger velocity, which promotes asperity temperatures significantly above the talc stability field, into the olivine and enstatite field, and eventually above the wet solidus, consistent with the observation of olivine and enstatite in the wear material and the glass-like textures and materials on the slip surface (e.g., Figure 7b). The modeled asperity temperature is only valid before the onset of weakening, since we have neglected changes to the contact shear stress and possible latent heat effects that accompany the onset of weakening.

These models also suggest that flash heating is likely causing the initial weakening observed in Path 2 experiments, similar to the Path 1 (Figure 10b); moreover, the fact that both samples from Runs 734 and 735 (performed at normal stresses of 4.9 MPa and 14.9 MPa, respectively), weaken at about the same slip rate of 0.1 m/s (Figure 6a), suggest that the initial weakening is independent of normal stress, consistent with the flash-heating mechanism [Rice, ²⁰⁰⁶]. However, with increasing displacement/deformation time, the T_surf increases at a rate dependent on the shear stress and velocity. For high enough slip and velocity, weakening due to flash heating will be associated with asperity melting, which will lead to the generation of melt patches with increasing power dissipation and eventually lead to bulk melting of the entire fault surface [Tsutsumi and Shimamoto, ¹⁹⁹⁷; Hirose and Shimamoto, ²⁰⁰⁵]. A first-order fit of the friction data from Run 735 (ATG) with the flash-weakening model given in Rice [2006], such that T_surf is allowed to increase using equation (1) (Figure 10c), demonstrates that an increase in surface temperature alone cannot explain the delayed recovery during deceleration. We therefore conclude that the delayed frictional recovery shown in Path 2 is in part a manifestation of this transition from flash weakening to bulk melting.

4.3. One-Dimensional Thermal Modeling: Gouge

To quantitatively explore differences in temperature evolution between a uniformly shearing gouge zone and asperity contacts between clasts within the zone, we modify the 1-D thermal modeling to account for the thickness of the deforming zone. Similar to bare surface models, we do not consider the latent heat of reaction; nonetheless, these models allow for a first-order exploration of the processes governing dynamic weakening in gouge. To calculate the temperature within the gouge samples (T_goug), we set y = 0 in equation (D5) to find

(3)

where W is the half width of the deforming zone. T_goug is the maximum temperature in the deforming zone (at y = 0), where shearing is most intense; repeating the analysis using the average temperature in the deforming zone did not significantly alter our results. Figure 1c shows the predicted temperatures for three single-velocity step experiments with a peak velocity of 1 m/s (Runs 820, 745, and 823), one single-velocity step experiment with a peak velocity of 0.1 m/s (Run 835), and one multiple-velocity step experiment with a peak velocity of 4 m/s (Run 824b). We use a deforming zone thickness of 150 µm (i.e., W = 75 µm), based on our microstructural observations (see Figure 9). Repeating the analysis for thicknesses ranging from 50 to 500 µm resulted in negligible differences (∼25°C). The model predicts that gouge temperatures may become high enough to dehydrate serpentine for all experiments at σ_n > 5 MPa, which is consistent with XRPD data, except for Run 835 that did not contain dehydration products. Additionally, the model predicts temperatures high enough to produce melt in Run 823, consistent with the melt textures along the slip surface. However, if dynamic weakening occurs for T > 600°C, the model is inconsistent with the observed total weakening distances in the all experiments. For example, Runs 820 and 745 dynamically weakened after ∼200 mm and 5 mm of slip, respectively, whereas the model predicts that the temperatures in both runs should be ∼200°C for the given slip, far below the critical temperature.

To reconcile this inconsistency, we explore the role of flash heating within the gouge zone using the relationship suggested by Beeler et al. [2008], which accounts for the width of the deforming zone. In this case, the flash-heating model (D7) is modified to

(4)

where g is the grain size and w is the thickness of the deforming gouge layer. Again, we assume that the deforming gouge layer thickness is ∼150 µm (i.e., w = 2W = 150 µm) based on the width of ultra-fine-grained zones in our experiments. The initial grain size (g) within this deforming zone is less obvious. The grain size prior to deformation (i.e., the grain size of the starting material) will undoubtedly be somewhat comminuted during initial slip as strain becomes more concentrated into the ∼150 µm shear zone. As demonstrated by Di Toro et al. [2013], once strain becomes highly localized, very little additional deformation occurs outside the localized zone, and thus, the material adjacent to the localized zone should preserve the grain size at the onset of localization. In our experiments the grain size of the material adjacent to the ultra-fine-grained zones was ∼15 µm suggesting a g/w ratio of ∼0.1. In equation (4) we assume (g/w) = 0.1 while all other physical constants remain the same as previously assumed in equation (2). Figure 1d shows that the asperity-scale temperature increase varies dramatically with varying normal stress and velocity and that the magnitude of the temperature rise for a given displacement is significantly lower than in equivalent bare surface experiments (Figure 1b). Similar to bare surface experiments, there is a strong correlation between the onset of dynamic weakening (stars, Figure 1b) and model temperatures >600°C, suggesting that dynamic weakening is caused by flash heating in gouge. However, the dynamic weakening in gouge occurs after larger displacements and at higher velocities than bare surfaces because strain is more distributed. Remarkably, the gouge flash heating model predicts that Run 824b and 823 should have similar asperity-scale temperatures with slip despite having different imposed normal stresses and velocity profiles, consistent with the total weakening distances observed in both runs (Figure 1d). Our conclusion that dynamic weakening in the gouge is promoted by flash heating is also supported by comparison of the friction data (during acceleration) with the model illustrated in Figure 10d.

Flash heating has also been observed in HVF experiments on carbonate gouge. In experiments conducted at ≤ 2 MPa, De Paola et al. [2011] and more recently Mitchell et al. [2013] showed CO₂ degassing after only a few hundred microns of slip suggesting that flash heating was occurring. In higher normal-stress experiments (8.5 MPa), Smith et al. [2013a] demonstrate that dynamic weakening in carbonate gouge initiates at sliding displacements of (100–150 mm), similar to the behavior seen in our experiments.

The application of phase equilibria to high-velocity frictional processes remains a challenge due to short reaction times, high-energy input rates, and dynamic nature of the physical parameters under which reactions occur. Based on the identification of crystalline reaction products in wear material, in conjunction with the thermal models, we conclude that reaction kinetics must be rapid enough for phase transformations to occur within the lifetime of an asperity (few milliseconds). In the short-displacement experiments of Kohli et al. [2011], the consistency between the modeled asperity temperatures, XRPD observation of talc and the predicted reaction temperature suggests near-equilibrium phase relationships at pressures similar to the asperity normal stress are applicable in HVF systems. For material not in contact at asperities, the reaction pressure will be set by the pore fluid pressure (which is lower than the asperity pressure), thus generally reducing the reaction temperature in these zones. Following this logic, in Figure 1 we projected phase boundaries through ambient pressures for T_surf and T_goug plots and through 5–6 GPa for asperity temperature plots (based on our assumption that the contact shear stress is 3 GPa and friction is ∼0.6 prior to weakening). Nonetheless, we acknowledge that considerable uncertainty remains regarding the magnitude, spatiotemporal variability of pressure at the asperity scale.

Other textural observations suggest that the application of equilibrium phase boundaries is more complicated in HVF systems. Recall that in antigorite bare surface and gouge experiments, we observed melt-like textures directly on the slip surfaces (e.g., Figures 7b, 7d, and 9j). These textures suggest the reaction Atg → melt + H₂O, which is not consistent with equilibrium thermodynamics. Thus, rapid heating apparently promotes reaction overstepping.

4.4. Comparisons of Gouge and Bare Surfaces at Higher Normal Stress

With increasing normal stress, the high-velocity friction behavior of gouge approaches that of bare surfaces. This trend is demonstrated by both δ and μ_nss values. As discussed above, values of δ characterize the onset of dynamic weakening. In gouge, values of δ decrease with increasing normal stress while values for bare surfaces remain approximately constant (e.g., Figure 1d and Table 1). Similarly, values of μ_nss for gouge decrease with increasing normal stress while values for bare surfaces remain approximately constant (e.g., Figure 4a). A linear approximation to the μ_nss data for gouge predicts that both gouge and bare surfaces would have the same values of μ_nss at normal stresses ∼60 MPa or larger (as shown by dashed line in Figure 4a), and data for both would be nominally independent of normal stress. A normal stress of 60 MPa corresponds to a depth of ∼5 km along an Andersonian normal fault at hydrostatic conditions [e.g., Cowie et al., ¹⁹⁹³]. It remains unclear if bare surface samples would actually strengthen if wear material was allowed to accumulate during slip; in our experimental assembly, wear products are flung out of the assembly, leaving a minimal thickness of wear debris.

4.5. Geophysical Implications

The results of this study have potential implication for earthquakes in geologic locations that contain serpentine, such as within oceanic transform faults [e.g., Francis, ¹⁹⁸¹], oceanic detachment faults [e.g., MacLeod et al., ²⁰⁰²], and some locations along the San Andreas Fault [e.g., Moore and Rymer, ²⁰⁰⁷]. However, all natural faults contain a layer of gouge material produced during a seismic rupture propagation even in initially cohesive fault rocks [Reches and Dewers, ²⁰⁰⁵]. Thus, some of the first-order observations found in this study may be applicable for all nominally dry faults as those reproduced in our experiments (room humidity).

For serpentine-rich fault zones at low normal stresses (<60 MPa) under nominally dry conditions, dynamic frictional weakening will be delayed to longer slip by the presence of unconsolidated material possibly resulting in smaller slips during earthquakes. For ruptures that propagate into shallow unconsolidated fault patches, less seismic energy will be emitted due to smaller static and dynamic stress drops. These interpretations complement hypotheses derived from slow-velocity experiments on gouge, which have been interpreted to promote the lack of shallow seismicity in some fault zones [e.g., Marone and Scholz, ¹⁹⁸⁸]. For large slip events (>5 m) gouge likely has no ability to subdue radiated seismic energy; previous studies have demonstrated that for long displacements (5–25 m) under room humidity conditions, friction values will decay to ∼0.1 for phyllosilicate-rich gouges [e.g., Kitajima et al., ²⁰¹⁰; Mizoguchi et al., ²⁰⁰⁷]. We suspect that these friction trends are also applicable in highly permeable fluid-saturated faults, with the added complication that water cools the asperity contacts rendering the flash-heating weakening mechanism less efficient than in room humidity [Violay et al., ²⁰¹⁴]. In water saturated faults with low permeability, thermal pressurization may occur adding further complication [e.g., Noda et al., ²⁰⁰⁹]. In such cases it is not clear how the presence of gouge may affect dynamic weakening during seismic slip; no machine to date can simulate these conditions. At normal stresses > 60 MPa the presence of unconsolidated serpentine within the fault may have no direct effect on the onset of dynamic weakening or steady state friction values.

5. Conclusions

Our work finds significant frictional differences between the serpentinite bare surfaces and gouge at low normal stresses (<22 MPa). We demonstrate that the frictional behavior is strongly normal stress dependent in gouge while relatively normal stress invariant in bare surfaces. Extrapolation of our data suggests that the behavior of antigorite gouge will approach that of bare surfaces at normal stresses ≥60 MPa (∼5 km depth). We thus infer that the presence of gouge will alter the weakening properties of shallow sections of serpentine-rich faults but have little effect at greater depths. Using 1-D thermal modeling, X-ray diffraction, and microstructural analysis, we constrain the effects of velocity, normal stress, shear heating, strain localization, and dehydration reactions on frictional weakening. We show that the evolution of friction for a given slip event on either bare surfaces or gouge zones is dependent on the evolution of temperature at both the asperity-scale and surface-scale, and we show that both scales need to be modeled in order to reconcile experimental data. We conclude that flash heating is the primary process causing initial weakening in bare surfaces. Flash heating also occurs in gouge; however, because strain is more distributed, dynamic weakening occurs at higher velocities and after larger displacements than in bare surfaces experiments. We find that values of friction in LIZ gouge have longer weakening distances than ATG gouge but generally have similar dynamic weakening trends. Finally, we observe slip-generated dehydration products and melt textures in both bare surface and gouge samples. These mineral and textural signatures likely form in natural serpentine-rich faults, the presence of which would indicate seismic slip.

Appendix A: Smoothing Data

High-frequency noise was removed from all data using a fast Fourier transform (FFT) smoothing filter. Figure A1 shows filtered or smoothed friction data from three representative experiments (black, green, and blue lines) and corresponding unsmoothed (raw) data (gray lines).

Figure A1.

Results from high-frequency noise filtering in three characteristic friction experiments. Parentheses indicate experimental run number.

Appendix B: X-Ray Powder Diffraction Methods

Twenty-six X-ray powder diffraction analyses that were conducted at the Geosciences Department at the University of Padua used a Panalytical θ-θ diffractometer (Cu radiation) equipped with a long, fine-focus Cu X-ray tube (operating at 40 kV and 40 mA), sample spinner, Ni filter, and a solid-state detector (X'Celerator). The system optics consist of a fixed 0.5° divergent slit and 1° antiscatter slit on the incident beam path and soller slits (0.04 rad) on incident and diffracted beam paths. The powders were mounted on a 32 mm (internal diameter) circular sample holder. Scans were performed over the 2θ range 3–80° with a virtual step size of 0.017° in 2θ and a counting time of 100 s/step. Phase identification and semiquantitative analysis were performed using the software package X'Pert HighScore Plus; the phase identification was confirmed by comparison with the reference pattern database Panalytical-Inorganic Crystal Structure Database. One additional XRPD analysis was conducted at Brown University on sample 834 using a Bruker D-8 Advance diffractometer with DaVinci system, a Cu X-ray tube operating at 40 kV and 40 mA, and a Bruker Vantec-500 (Xe-CO₂ gas filled) detector with a 13.5 cm diameter window set at 20 cm from the goniometer center and Ni filter. The scans were performed over the 2θ range 25–80° with a virtual step size of 0.25° in 2θ and a counting time of 60 s/step. The phase identification was performed using the software package Diffrac.Eva by Bruker and confirmed by comparison with the International Centre for Diffraction Data.

Appendix C: Area Correction for Single-Velocity Step Bare Surface Experiments

In the suite of 1 m/s experiments on ATG bare surfaces (Runs 736a to 736h), one sample was used for eight consecutive slip cycles, with 1 m of slip per cycle. The applied normal force was increased after each cycle from 6.2 kN during the first cycle up to 53 kN during the last cycle. This force correlates with an increase in nominal normal stress from ∼5 to 40 MPa assuming that the initial nominal area of the slip surface (∼12.5 cm²) remained constant. However, during each slip cycle the area progressively decreased because the sample on the stationary side became progressively wedge shaped due to wear during sliding (Figure C1a). Wear of the sample on the opposing rotary side resulted in significant loss of material normal to the fault, but the surface area remained approximately constant. The final slip surface area (dashed orange region in Figure C1c) was determined via imaging software to be 5.38 cm², indicating that the actual normal stress was 96.6 MPa during the last cycle.

Figure C1.

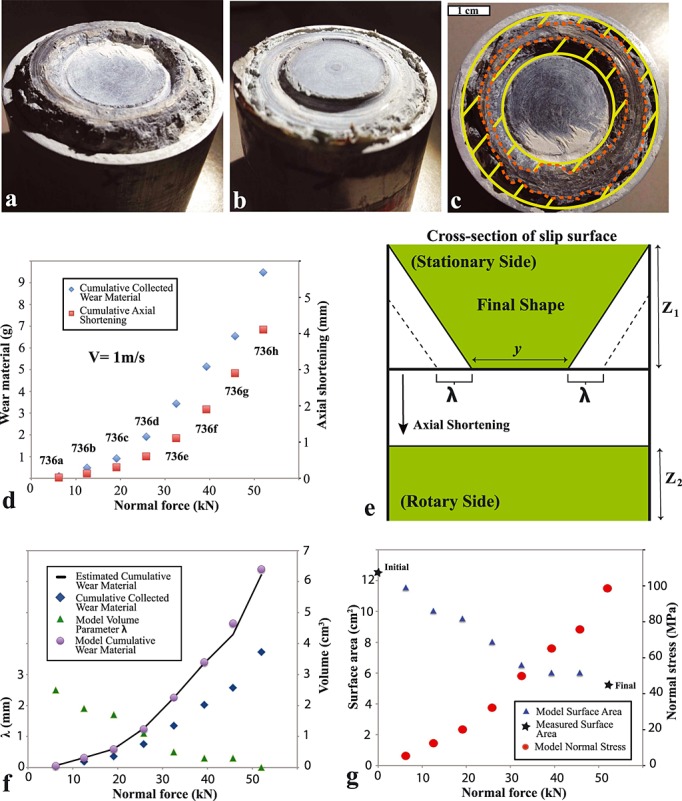
Photographs of deformed bare surface sample (Run 736) after eight consecutive deformation cycles: (a) the stationary surface and (b) rotary surface. (c) Sequential mechanical erosion reduced the surface area of the nonrotary side by ∼57%; yellow lines indicate initial surface area and orange dashed lines outline final slip surface area. (d) Mass of wear material collected after each deformation cycle with the corresponding applied normal force and axial shortening for the given slip cycle. (e) Cross-sectional diagram modeling the final sample shape (green) and material lost to erosion (white). The initial shape is indicated with bold black lines (see text for description of model). (f) Cumulative collected wear (blue diamonds) and the estimated total mass of wear material (black line), assuming 60% of wear material was captured. The modeled volume of wear material (purple circles) was fit to the estimated wear and the corresponding surface area parameter (lambda, green triangles). (g) Modeled surface area after each deformation cycle (Runs 736a to 736h) and the calculated normal stress (applied normal force/surface area). The measured initial and final surface areas are indicated with black stars.

We constructed a simple model to estimate the area of the slip surface after each slip cycle. The model is constrained by the final slip surface outline in plane view, the initial and final area of the slip surface, the mass of wear material collected after each slip cycle, and the axial shortening. The axial shortening was monitored with a linear variable differential transformer (LVDT), and the wear material was collected in a foil tray located under the sample. In Figure C1d the cumulative mass of collected wear material and cumulative axial shortening are plotted for all eight slip cycles; both data sets show a similar nonlinear increase with increasing normal force. The final shape of the slip surface is modeled as a wedge-shaped quadrilateral (in cross section) on one side (Figure C1e) and as a migrating flat surface on the other side (Figure C1e). The effective annular width of the slip surface (y) is calculated from the final measured surface area (Figure C1c). The thickness of the stationary sample (Z₁) remained approximately constant, while the thickness of the rotary sample (Z₂) decreased in accord with axial shortening. The evolution of the cross-sectional area of the top sample is calculated using mass balance and the change in the annular width (λ); values of λ are estimated by assuming that the eroded angle remains constant. The total volume of wear calculated from this model is ∼ 6.5 cm³ (purple circle in Figure C1f). The total volume of collected wear (collected mass/density of antigorite) was somewhat less than the value determined by mass balance (blue diamond in Figure C1f), indicating that ∼ 60% of the total wear material was recovered. We ignore changes in mass due to frictional-heating-induced metamorphism. The black line in Figure C1f shows cumulative wear by assuming that 60% of the total wear material was collected after each slip pulse. This assumption is reasonable because the collection tray did not capture all particles expelled from the sample. We then use the cumulative collected wear in conjunction with the LVDT displacement to calculate the value of λ that is consistent with the estimated volume of wear material produced after each slip cycle (green triangles in Figure C1f). Finally, we use λ to calculate the surface area. The modeled surface area values were used to correct the recorded normal stress and shear stress values for each slip cycle (Figure C1g).

Appendix D: Thermal Model

To model the temperature evolution within the deforming zone, we use the one-dimensional heat equation

(D1)

where t is the time since slip began, y is the distance from the center of the deforming zone, τ is the shear stress, 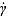is the strain rate, α_th is the thermal diffusivity, and ρc is the effective heat capacity per unit volume. The initial conditions are T = T₀ at t = 0, which models the ambient laboratory conditions before deformation begins. For the boundary conditions we choose T → T₀ as y → ±∞. These boundary conditions ignore the presence of the metal gouge holder, which will have a higher thermal diffusivity than the gouge. However, for the typical experiment durations of about 1 s it is likely that thermal diffusion through the gouge holder has a small effect, justifying our choice of boundary conditions.

The frictional heating in the deforming zone is controlled by the shear stress and strain rate. Rice [2006] argued that unrealistically high accelerations are required to make inertial effects important within the gouge layer, and thus, the shear stress should be constant throughout the deforming zone. Platt et al. [2014] used numerical simulations to show that this assumption is valid for the normal stresses considered here. We assume that the deforming zone has a gaussian shape

(D2)

where W is the half width of the deforming zone. A better approach would be to model the physical processes driving strain localization within the gouge, but this is beyond the scope of this paper.

For the shear stress and strain rate profiles justified in the previous paragraph, we can solve equation (D1) using a Green's function approach, leading to the solution

(D3)

where the Green's function is

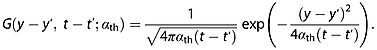(D4)

The integral over y′ can be done exactly leading to

(D5)

This expression was previously derived in Andrews [2002] and was used to model thermal pressurization during seismic shear.

To find the temperature evolution of the sliding surface for the bare surface experiments, we set the deforming zone thickness equal to zero in equation (D5). This is equivalent to solving using a Green's function for a half-space heated by a flux at the boundary and leads to the solution for the surface temperature

(D6)

Equation (D6) can be repurposed to calculate the asperity temperature using the typical flash-heating model by setting the shear stress equal to the contact shear stress τ_c, the slip velocity equal to the current value from the experiment, and the initial temperature T₀ equal to the current temperature on the sliding surface. The assumptions of constant velocity and shear stress allow us to evaluate the integral in equation (D6) to find the maximum asperity temperature

(D7)

where d is the contact (i.e., asperity) diameter.