Skip to main content
PMC home page
Wiley Open Access Collection logoLink to Wiley Open Access Collection
. 2015 Feb 10;120(2):904–914. doi: 10.1002/2014JA020857

Electron densities inferred from plasma wave spectra obtained by the Waves instrument on Van Allen Probes

W S Kurth 1,✉, S De Pascuale 1, J B Faden 1, C A Kletzing 1, G B Hospodarsky 1, S Thaller 2, J R Wygant 2
PMCID: PMC4497465  PMID: 26167442

Abstract

The twin Van Allen Probe spacecraft, launched in August 2012, carry identical scientific payloads. The Electric and Magnetic Field Instrument Suite and Integrated Science suite includes a plasma wave instrument (Waves) that measures three magnetic and three electric components of plasma waves in the frequency range of 10 Hz to 12 kHz using triaxial search coils and the Electric Fields and Waves triaxial electric field sensors. The Waves instrument also measures a single electric field component of waves in the frequency range of 10 to 500 kHz. A primary objective of the higher-frequency measurements is the determination of the electron density ne at the spacecraft, primarily inferred from the upper hybrid resonance frequency fuh. Considerable work has gone into developing a process and tools for identifying and digitizing the upper hybrid resonance frequency in order to infer the electron density as an essential parameter for interpreting not only the plasma wave data from the mission but also as input to various magnetospheric models. Good progress has been made in developing algorithms to identify fuh and create a data set of electron densities. However, it is often difficult to interpret the plasma wave spectra during active times to identify fuh and accurately determine ne. In some cases, there is no clear signature of the upper hybrid band, and the low-frequency cutoff of the continuum radiation is used. We describe the expected accuracy of ne and issues in the interpretation of the electrostatic wave spectrum.

1. Introduction

The plasma density, herein specifically the electron number density ne, is a fundamental parameter of a plasma and is often a key to understanding the propagation of waves in a plasma, estimating the growth rates for instabilities, mapping regions of the magnetosphere such as the plasmasphere, and building models of the magnetosphere, such as magnetohydrodynamic, kinetic, or others. For example, in a recent simulation of electron acceleration by chorus emissions, Thorne et al. [2013] achieved a much better replication of the observed electron spectrum as a function of time when the actual electron density derived from the Van Allen Probe Waves instrument was used, instead of a model magnetospheric density [Sheeley et al., 2001].

It has always been a challenge to measure the plasma density, whether ne or the ion density, accurately. Direct particle counting techniques with various types of plasma instruments, whether Faraday cups or electrostatic analyzers, always have to deal with the nonzero potential of the spacecraft and the fact that the bulk of the plasma population is often cold, of the order of the potential of the spacecraft, in many cases. In addition, the acceptance angle of such instruments is seldom a full 4π sr. Plasma wave measurements avoid such issues and use the detection of commonly observed characteristic frequencies of the plasma to determine ne. These modes typically have wavelengths that are large compared to the spacecraft, hence are not seriously affected by the presence of the spacecraft. For example, electron plasma oscillations commonly found in the solar wind are a basic mode of a plasma that in the absence of nonlinear effects, directly provide ne through the determination of the frequency of the waves, ωpe. This frequency is given by ωpe2 = 4πnee2/me, where e is the electron charge and me is the electron mass. Electron plasma oscillations exist in a nonmagnetized plasma and, in the presence of a magnetic field, are polarized parallel to the magnetic field B. Since the underlying motion of the electrons is also parallel to B, the magnetic field does not affect the frequency of this mode.

Quasi-thermal noise spectroscopy is another method of determining the electron density (as well as multicomponent temperatures and even bulk velocity), which results from the interaction of a plasma with an antenna. The analysis is well developed in Meyer-Vernet and Perche [1989] and is most often used with long-dipole antennas under the condition that the length of the antenna L ≫ λD, the Debye length.

The spacecraft potential has also been used as a proxy for the electron density [cf., Escoubet et al., 1997]. However, this technique requires an independent source of ne in order to develop an empirical relation between the potential and density. The spacecraft potential depends on the plasma temperature as well as the density, so variations in the temperature can lead to potential changes that are not related to changes in the density. Also, it is possible that this relation will require updating as various aspects of the probes change with time or conditions.

In planetary magnetospheres, electron plasma oscillations are found less frequently than a band of emission at the upper hybrid resonance fuh. In the plasmasphere, this emission has been reported by a number of authors [cf., Mosier et al., 1973; Taylor and Shawhan, 1974] and was observed to reside between the upper hybrid resonance frequency and the electron plasma frequency. Beyond the plasmapause, there are a large number of banded emissions. Sentman [1982] discusses the diffuse electrostatic emissions between the harmonics of the electron cyclotron frequency from fce up to fuh. At similar frequencies, more intense electrostatic waves can be found that are the result of an instability. These emissions are sometimes referred to as electron cyclotron harmonic emissions or (n + 1/2)fce bands. These bands are thought to be driven by anisotropic electron distributions as from a loss cone or a temperature anisotropy [Ashour-Abdalla and Kennel, 1978a, 1978b; Christiansen et al., 1978; Hubbard and Birmingham, 1978; Hubbard et al., 1979]. Kurth et al. [1979] showed that the (n + 1/2)fce band including fuh was often the most intense band above the 3fce/2 band. Finally, the fq resonances occur at frequencies above fuh [Canu et al., 2001; Benson et al., 2003]. In some cases, the first fq resonance above fuh can be more intense than the upper hybrid band [Canu et al., 2001]. However, without an active sounder, it is not possible to unambiguously distinguish between these two bands.

The upper hybrid resonance frequency is defined as ωuh2 = ωce2 + ωpe2. Converting now to real frequency using fpe = ωpe/2π, since the remainder of this work is involved with measuring the frequencies of these spectral features, we can relate fpe and fuh to ne. In the following fce = 28|B|, where fce is measured in hertz and |B| is well determined in nanotesla by the magnetometer, it is straightforward to determine ne from fuh. From the above and substituting appropriate values for the electron charge and mass, we get

graphic file with name jgra0120-0904-m1.jpg 1

or

graphic file with name jgra0120-0904-m2.jpg 2

Throughout, frequencies are expressed in hertz and density in cubic centimeter. We note that Benson et al. [2004] describe measurements of magnetospheric plasma densities with the Radio Plasma Imager instrument on the IMAGE satellite using the same principles we employ here, with the exception that they have the ability to compare passive plasma wave spectra with active magnetospheric sounding to determine with much more confidence the identification of spectral features. And, Trotignon et al. [2010] present the methodology for determining electron densities from the Waves of High frequency and Sounder for Probing of Electron density by Relaxation investigation on the four Cluster satellites, again using both passive and active techniques.

Earth's magnetosphere is also filled with nonthermal continuum radiation [Gurnett, 1975]. The emission is thought to be generated in the left-hand, ordinary (L-O) mode, hence has a low-frequency limit at fpe. The continuum radiation has been observed to also exhibit a right-hand, extraordinary (R-X) mode cutoff [Shaw and Gurnett, 1980]. In the absence of a clear identification of the upper hybrid resonance frequency, the continuum cutoff provides an alternative manner to determine ne. It is important to stress, however, that the low-frequency limit of continuum radiation is necessarily an upper limit to the local electron density for a couple of reasons. First, it can sometimes be difficult to determine if the apparent cutoff is due to a cutoff at the plasma frequency, or simply a source effect, that is, the waves are simply not generated at lower frequencies. Second, even if the low-frequency limit is caused by a cutoff, it is possible that the cutoff occurs somewhere between the source and the observer; hence, the electron density at the observer can be substantially lower than that indicated by the cutoff.

This paper describes the technique used for determining the electron density using the Van Allen Probe Waves instrument, which is part of the Electric and Magnetic Field Instrument Suite and Integrated Science (EMFISIS) instrument suite [Kletzing et al., 2013]. Waves comprises a six-channel waveform receiver (WFR), which allows for the simultaneous detection of all three electric and all three magnetic components of waves in the frequency range of ∽10 Hz to 12 kHz, a single channel high-frequency receiver (HFR) for electric fields covering the frequency range of 10 to 500 kHz, and a triaxial search coil magnetometer. The search coils consist of 40 cm mu-metal cores wound with 10,000 turns of fine copper wire. The electric field signals are obtained from the triaxial electric field booms of the Electric Fields and Waves (EFW) instrument [Wygant et al., 2013]. The electric field booms are parallel to the three search coil axes with two of the booms in the spacecraft spin plane having lengths of 100 m tip to tip and the axial boom perpendicular to the spin plane having a tip-to-tip length of ∽14 m. The WFR simultaneously samples all six channels with a 35 kHz sampling rate and 16 bits of digitization. The HFR has a selectable input but is usually connected to one of the spin plane booms and samples the electric field at a rate of 1.25 million samples per second with 14-bit digitization. EMFISIS also includes a fluxgate magnetometer, which provides measurements of |B| used in this paper, specifically to determine fce.

While there are a number of burst modes that provide continuous waveforms or very high temporal resolution spectral matrices (30 ms resolution), the data used for the density determination are obtained in a survey mode, which collects spectral densities from all seven channels (WFR plus HFR) every 6 s. In survey mode, all digital waveforms are Fourier transformed using a floating point fast Fourier transform (FFT) on board. A Hanning function is used to minimize artifacts from a simple square sampling window. However, since all except the lowest-frequency spectral matrices are computed by binning over a number of FFT components, the window function should have little or no effect on the resolution. Spectral matrices are produced from the WFR measurements with 20 log-spaced spectral bins per decade of frequency, and the electric spectral density is returned for the HFR in 48 log-spaced bins per decade of frequency. This spacing provides about 5% spectral resolution (Δf/f) and sets the ultimate resolution for determining the electron density. Since ne is proportional to fpe2, the density resolution is ultimately 10%, but see the discussion below on other sources of uncertainty. The upper frequency limit of the HFR limits the highest density that can be determined to about 2000 cm−3. It is possible that the upper hybrid resonance frequency can drop below the 10 kHz low-frequency limit of the HFR. In principle, the analysis described herein can be extended into the WFR frequency range. However, there are some practical limitations in doing this. Primarily, the spectral resolution of the WFR is not optimum for obtaining the electron density, and differences in the noise levels in the two receivers make it difficult to follow spectral features across the frequency boundary between the two receivers.

It should be noted that the HFR is sometimes operated at a higher cadence of one spectrum every 0.5 s and that waveform measurements can be recorded for short intervals. In principle, these higher-resolution measurements can be analyzed for electron density. However, we do not anticipate using anything other than the 6 s survey measurements for the standard density data set except for special studies limited to highly localized time intervals.

2. Using Van Allen Probe Plasma Wave Observations to Determine ne

The Waves HFR is used to identify fuh or other spectral features useful in determining the electron density. Figure1 shows an example of observations from Van Allen Probe A from orbit 684 beginning late on 12 May 2013 and continuing into 13 May. In Figure1a, the electric field spectral densities are plotted as a function of frequency and time using the color bar at the right to assign color to spectral density. In Figure1b, the spectrogram is repeated but with the upper hybrid resonance frequency as determined using the process described below, highlighted in white. Also overplotted in both panels is the electron cyclotron frequency in red. As can be seen, the density fluctuates between values that might be considered plasmapause and plasma trough values both outbound and inbound on this orbit. Figure2 shows an expanded time view of the outbound plasmapause crossing to show the complexity of the density structure at this boundary. Note that there are a number of ways to define the location of the plasmapause, including densities falling below a specified value [e.g., Goldstein et al., 2014] or at a steep gradient in the density [e.g., Moldwin et al., 2002]. By the latter definition, one might conclude that there are numerous plasmapause crossings in Figure2 or that there is simply a lot of structure in the plasmapause at this location and time. Note, however, that it is not the point of this process to identify the plasmapause but to provide the electron density so that users may use that to define their own boundaries. Also note in Figure1 that there are two types of radio emissions well above fuh. The broad drifting features are solar type III bursts. A pair of these are seen starting in rapid succession around 02:30 UT, and a third begins near 04:00. The other somewhat more bursty emissions are auroral kilometric radiation. Figure3 shows the electron density derived from fuh in Figure1. This paper describes the process by which densities like those in Figure3 are determined.

Figure 1.

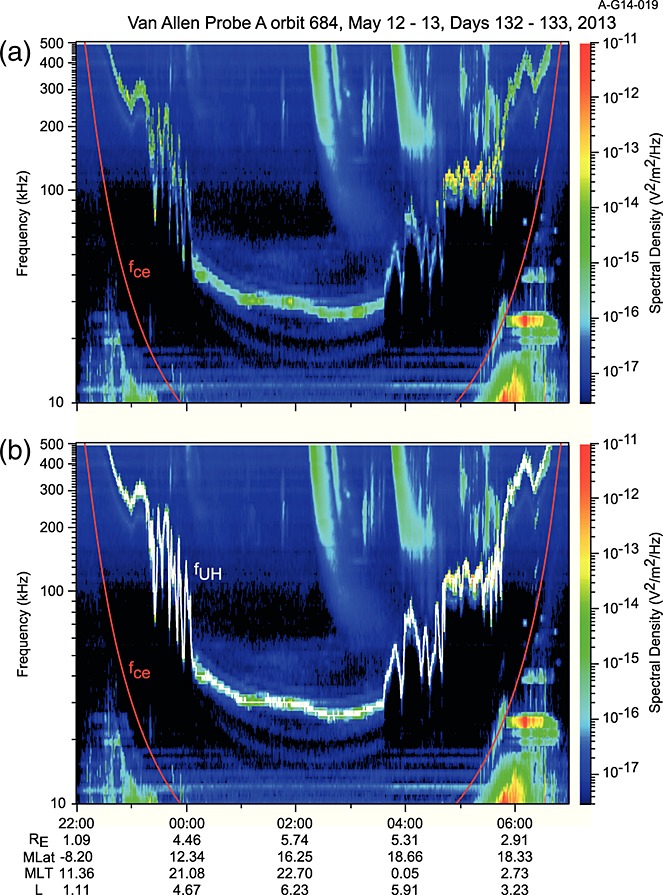
Figure 1

Open in a new tab

(a) An example spectrogram of Waves HFR data showing the upper hybrid resonance band. (b) In this panel, fuh is highlighted in white. The electron cyclotron frequency is indicated with a red trace.

Figure 2.

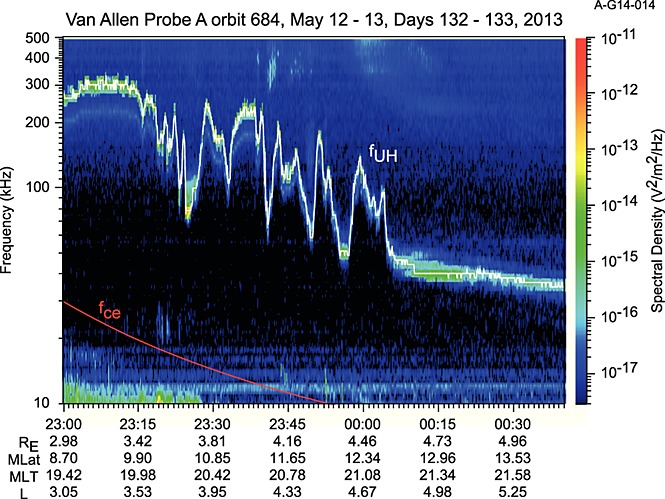
Figure 2

Open in a new tab

An expanded view of the spectrogram shown in Figure1 to show the structure of the plasmapause crossing.

Figure 3.

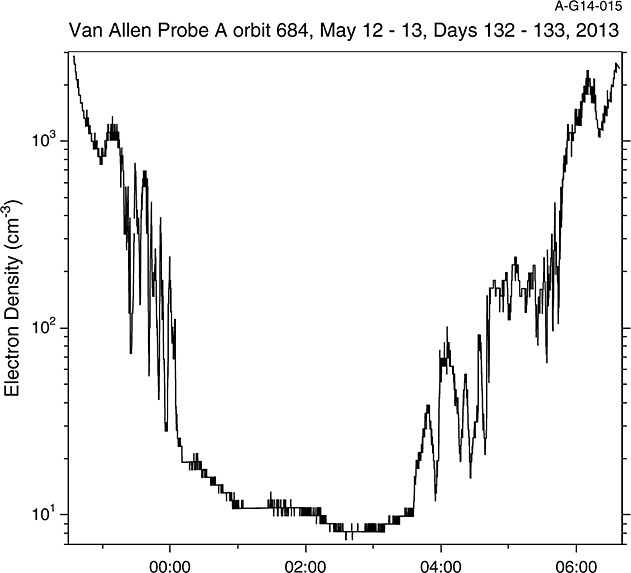
Figure 3

Open in a new tab

The resulting electron density for the identified fuh profile in Figure1.

There are three regions of interest in Figure1. Prior to about 23:15 UT, the spacecraft is clearly in the plasmasphere, and the upper hybrid band is in the frequency range above a few hundred kilohertz. After the highly structured plasmapause region, which ends around 00:10 UT, there is a relatively quiet region with bands of thermal emission between the harmonics of the electron cyclotron frequency [Sentman, 1982]. (Other examples of these are found in Figures7b and 7c, to be discussed below.) Deep in the plasmasphere, the Van Allen Probe Waves instrument typically finds two bands of emission. We have identified the upper hybrid band as the one that is brighter and at higher frequencies. Often, though, there is a lower “shadow” band which tracks the brighter band at lower amplitudes and frequencies.

Figure 7.

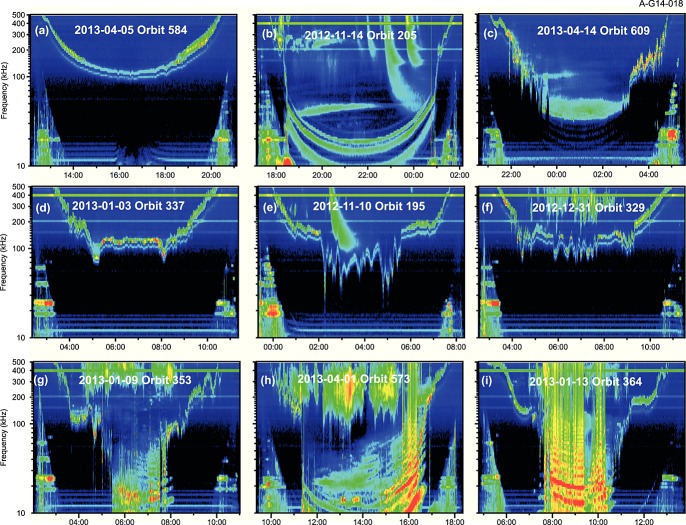
Figure 7

Open in a new tab

A selection of Van Allen Probe A orbits showing the wide range of appearance of the spectrum and the challenges this presents to the identification of the upper hybrid resonance band in order to derive the electron density. Each of these plots is for an entire orbit and runs between consecutive periapses.

Figure4 is taken from Kurth [1982] and is a schematic of the Z-mode emissions found near the plasmapause obtained from high-resolution ISEE 1 wideband measurements. As described in that paper, the electron density can vary such that the upper hybrid frequency moves between the (n +1/2)fce bands and, as described by Kurth et al. [1979], the (n + 1/2)fce band including fuh is often the brightest of the electron cyclotron harmonic bands other than perhaps the first band at ∽3fce/2. In Figure4, one can also note the relation between characteristic frequencies in the Z-mode band with fuh being the upper frequency limit and fL = 0 the lower frequency limit. The L = 0 cutoff fL = 0 is defined as

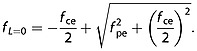graphic file with name jgra0120-0904-m3.jpg 3

Figure 4.

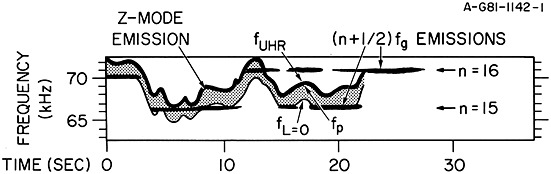
Figure 4

Open in a new tab

A schematic of the variation of fuh at the plasmapause as observed by ISEE 1. The detail also shows the relation between fuh, fpe, and fL = 0 encompassing the Z-mode emission from Kurth [1982].

The ISEE 1 data showed that the band between fpe and fuh was often more intense than the Z-mode emission between fpe and fL = 0. Figure5 is an expanded view of Van Allen Probe A Waves HFR data from 27 February 2014 showing the plasma wave spectrum at the 5% spectral resolution afforded by the instrument. The white trace is fuh. For context, we have shown the ninth and tenth harmonics of fce in red. Among other things, these two bands provide a guide for the magnitude of fce relative to fuh. At the time of the vertical white arrow, 13:01 UT, we have used the relations in the previous section to compute various characteristic frequencies of the plasma based on the assumption that our identification of fuh is correct and is 302 kHz at this time. Based on the magnetic field strength, fce = 27.6 kHz, hence, fpe = 301 kHz. The left-hand ordinary cutoff fL = 0 = 287 kHz at this time. Note that the 5% spectral resolution at 300 kHz is approximately 15 kHz, hence, fuh and fpe are certainly unresolved. We suggest that the lower bound of the bright band we have identified as fuh is actually defined by fL = 0. For completeness, we also note that the right-hand cutoff fR = 0, defined as

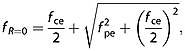graphic file with name jgra0120-0904-m4.jpg 4

is 315 kHz. Notice that a type III radio burst occurs just above the upper hybrid band and, in fact, is cutoff at the band. Type III bursts are unpolarized, hence, can propagate down to the local electron plasma frequency. Hence, the fact that there is no evidence of the radio emission below what we have identified as the upper hybrid band assures that this is the correct identification. The lower frequency “shadow” band at about 228 kHz is clearly too low in frequency to be confused with the plasma frequency and the cutoff of the type III emission. This shadow band has been observed by other plasma wave instruments, and its origin is unknown (P. Canu, personal communications, 2014).

Figure 5.

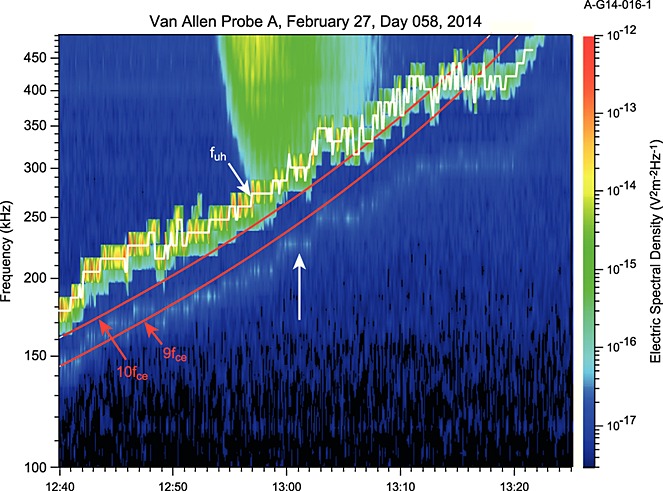
Figure 5

Open in a new tab

Detail of the upper hybrid band and the apparent cutoff of a type III radio emission. This example shows that the more intense higher frequency of these two bands includes fpe and not the weaker shadow band at lower frequencies.

2.1 Process Used to Infer the Electron Density From Van Allen Probe Plasma Wave Spectra

The identification of fuh, as demonstrated in the previous section, ranges from being quite straightforward to a highly nontrivial interpretation of the plasma wave spectrum. In any case, identifying fuh is a tedious and demanding task.

An automated tool to digitize the fuh, the Automated Upper-hybrid Resonance detection Algorithm (AURA) has been developed to speed the processing of HFR data and remove some of the tedium. AURA employs a restricted searching approach to detect the frequency of a relative peak embedded in a spectrum. Optimized parameters and a bootstrapping method using the EFW-determined spacecraft potential as in Escoubet et al. [1997] and Wygant et al. [2013] guide the determined spectral peaks to more likely correspond to fuh.

AURA relies on a rule of hysteresis that assumes that each successive spectrum contains a peak frequency associated with fuh near the previously identified peak (i.e., there is not a large change in frequency of the binned signal within a 6 s sampling time step). The routine operates in a two-dimensional array of frequency rows and temporal columns. AURA's peak tracking behavior then most nearly matches the prominence of visually apparent emission in the traditional manner of considering the dynamic spectra of the EMFISIS Waves instrument.

AURA begins at the periapses at each end of an orbit and terminates at apogee (forward or backward in time for outbound/inbound passes, respectively) when processing a frequency-time array. After selecting as a starting point the highest frequency fuh peak near periapsis, the algorithm works toward apoapsis in an attempt to follow the band to lower frequencies. The starting point for AURA is determined to be the occurrence of a signal 1 order of magnitude above the minimum (background) spectral density in the highest frequency spectral bin at 480 kHz nearest perigee. Since the upper hybrid band is more easily discerned in the plasmasphere, it is more likely that the algorithm can work outward into the plasma trough without being attracted to confusing high-frequency radio emissions, if present. Further, as will be discussed below, there are a number of interpretational issues in the plasma trough, and it is less likely that the automated algorithm will succeed near apoapsis.

Once a starting fuh coordinate (frequency bin, spectral time) or initial seed frequency bin is determined, AURA proceeds to each successive spectrum to search for a peak in a limited range of bins centered at the seed frequency bin. The logarithm of the amplitudes in this range is normalized by the minimum value and weighted by a central Gaussian profile given by

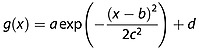graphic file with name jgra0120-0904-m5.jpg 5

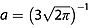where Inline graphic, b is the seed bin number, c = 3, and d = 0. Figure6 shows how this is applied. The Gaussian function, g(x), is used as a probability profile when its values are normalized by the central peak. The values of parameters a, b, c, and d are an ad hoc selection such that the power in frequency bins at least 3 away from the seed frequency within individual spectra are weighted by no lower than a factor of 0.5 (Figure6, bottom).

Figure 6.

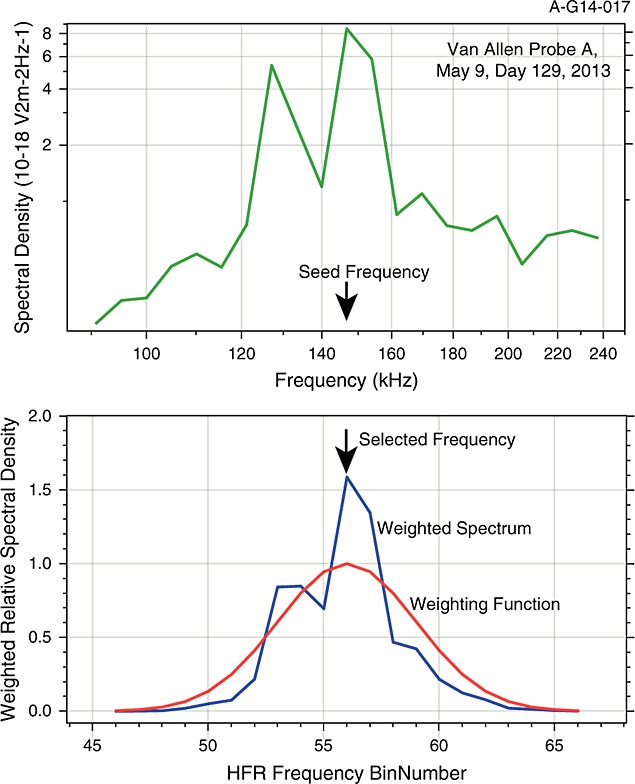
Figure 6

Open in a new tab

A schematic showing how the AURA rule of hysteresis is employed using a Gaussian probability distribution to weight spectral points closer to the seed frequency more than those farther from the seed.

The bootstrapping method is triggered at a sharp gradient; that is, the overall displacement in successive frequency bins for the previous 10 spectral samples total 8 bins or more. Bootstrapping consists of using EFW potential measurements for those last 10 records to calculate the corresponding fuh frequencies to use as seed values in AURA, guiding the routine through the gradient.

Guidance from EFW is excluded during conditions that compromise EFW potential measurements such as changes to probe bias, eclipse, spacecraft charging events, or the presence of instrumental interference such as thruster events. In such cases, AURA will move to the next nominal spectral time when EFW data are valid. Hence, the routine can track fuh without being confused by anomalous potential measurements.

Clearly, the use of EFW potential measurements represent a circular approach to the problem. The relation between electron density and spacecraft potential is through an empirical relation between the electron density derived from the fuh band and the potential. Hence, it may seem inappropriate to use this proxy as a means of “seeding” within AURA. However, there are times when identifying fuh in the Waves spectrogram is confused by a number of factors described below, and using the proxy as a guide is often helpful for both AURA and more manual interpretation used when AURA fails.

AURA does an excellent job of automatically finding fuh with little or no manual intervention when the spectrum is simple. Typically, such orbits are those for which the spacecraft never leaves the plasmasphere as in the example in Figure7a or when geomagnetic conditions are very quiet. However, there are many orbits which require manual attention, and there is no way to ensure that the algorithm has run successfully without inspection. This has spawned a processing and inspection process which leads to a final density data file for a given orbit.

The first step in the process is to run AURA on the HFR data for an orbit. Second, an operator inspects the resulting fuh profile overplotted on the spectrogram. This inspection is carried out with a version of AURA that allows the operator to selectively reprocess intervals where the operator has found that the algorithm has clearly deviated from the upper hybrid band. The rule of hysteresis, for example, may cause the algorithm to fail to accurately follow an abrupt change in the upper hybrid frequency at the plasmapause; such issues are usually easily identified and corrected. Through this inspection and correction process, a type of triage is carried out. In effect, the result of the inspection/correction process is to classify a given orbit into one of three levels of success. The highest level of success, class A, requires less than 25% of the data points to be corrected for a given orbit. Approximately 70% of orbits from the first year and one-half of the mission were classified in this category. About 20% of the orbits were classified as class B, requiring 25 to 50% of the data points to be corrected. The remaining 10% of the orbits, class C, represent challenges, typically occurring during high geomagnetic activity in which a large portion of the outer part of the orbit presents interpretational difficulties in finding the upper hybrid band for a number of reasons. Typically, these orbits exhibit very low densities in the plasma trough.

The final step in the process is for an operator well versed in the interpretation of the plasma wave spectrum to inspect the output of the preceding steps. This operator has access to both the main AURA algorithm as well as other options. First, a box digitizer can be used. When AURA has failed, the operator can define a frequency-time box within which the algorithm is confined to search for a peak. The operator has full control over the time and spectral resolution used to focus on the upper hybrid band when it is visually apparent. The operator may, at this point, decide that there simply is no reliable upper hybrid band to identify. However, there may be continuum radiation present with a low-frequency cutoff. The tool allows this cutoff to be identified as the electron plasma frequency, and the electron density is determined using equation 1. As explained above, this density is necessarily an upper limit to the local electron density. Gaps may appear in the density data set for intervals where no reliable spectral feature is available.

When the final inspection step is completed, the resulting data file is staged for conversion into a standard common data format (CDF) file and added to the EMFISIS level 4 data store.

2.2 Uncertainty and Accuracy of Derived Electron Densities

There are two sources of error in the determination of ne from the plasma wave spectrum. The first of these is the spectral resolution of the instrument which, as described above, translates to a density resolution of about 10%, Δn/n. In most cases, the digitization results in a density profile that appears to toggle between two and three values, corresponding to two or three spectral bins in the spectrum. This can happen, for example, due to spin modulation effects. The spin rate is about 5 rpm, about a factor of 2 slower than the spectral sampling rate. It would be prudent to treat these fluctuations as a measure of the uncertainty in the density determination. Goldstein et al. [2014] carried out a validation of two methods of determining the electron number density in the plasmasphere utilizing nine Van Allen Probe A orbits. For the Goldstein study, the lower bound of the upper hybrid band was assumed to be fpe. They determined densities using a manual inspection of spectrograms with a tool that allowed the lower frequency bound to be digitized to obtain fpe. They compared their values of ne to those from the semiautomated process described in this paper. They found a mean percentage difference between the manual process and the semiautomatic process described here to be 8.7%, which is less than the ∽10% resolution available for an individual measurement, given the 5% spectral resolution. A small percentage of individual points showed differences of a few tens of percent, and a small number of outliers had differences of up to 100%. Since the identification of the upper hybrid band in the plasmasphere is straightforward, this analysis is a good, independent assessment of the typical uncertainty in the determination of ne given a confident interpretation of the spectrum.

The second source of error lies in the interpretation of the plasma wave spectrum. Under many situations, such as in the plasmasphere just discussed, the upper hybrid resonance frequency is easily identified and the above-described techniques for digitizing fuh do a good job of picking out this peak. However, there are many situations where the spectrum becomes complex and the identification of the upper hybrid band is subject to incorrect interpretation.

Figure7 presents a collection of spectrograms from Van Allen Probe A that exhibit the variety of spectral forms that need to be interpreted in order to determine the electron density. Figure7a is an example of an orbit for which the spacecraft remained in the plasmasphere for the entire orbit. Other than selecting the brighter, higher frequency band for the upper hybrid band (see the discussion of this double band above), this type of orbit is among the simplest for AURA to handle, and there are seldom any manual corrections required by an operator. Figure7b shows an orbit for which the plasmapause is just beyond the periapses but for which there are three very smooth thermal emissions of the nature described by Sentman [1982]. Just above the top of these is a weaker emission, which is likely an fq resonance [Canu et al., 2001]. The fq resonances are above fuh but can confuse the identification of fuh. In fact, it is sometimes not possible to distinguish between the upper hybrid band and an fq resonance; hence, this is a source of error in our process. We assume that the brighter of the top two diffuse bands is the (n + 1/2)fce band that includes fuh. Notice the band of continuum radiation slowly drifting upward starting at about 19:00 near 40 kHz and the auroral kilometric radiation and type III solar bursts at higher frequencies. Figure7c presents an orbit with considerable structure on the outbound plasmapause and in the inbound plasmasphere. At apoapsis, however, there is no clear evidence of the upper hybrid band, but there is a clear low-frequency cutoff of the continuum radiation between about 23:30 and 03:00. Since Shaw and Gurnett [1980] found that continuum radiation propagates in a mix of left-hand ordinary (L-O) and right-hand extraordinary (R-X) modes, the low-frequency cutoff is at the ordinary mode cutoff, fpe. Hence, for the apoapsis period in Figure7c, the continuum cutoff would be identified as fpe for use in determining ne. But since this may not be a local cutoff, the resulting ne is an upper limit.

Figure7d is similar in many respects to Figure7a except that there is considerably more structure. The AURA algorithm is quite successful for this type of orbit as long as the frequency steps are not too great. Figure7e shows considerable structure in the plasma trough density. Some of the abrupt variations may be difficult for AURA to track, but these are easily identified and corrected in the inspection process. Note the prominent type III burst near the middle of this orbit. Figure7f is another example with considerable density structure and also has intense auroral kilometric radiation which may cause trouble for the algorithm. This spectrum is, however, relatively simple to correct in the inspection stage.

Figures7g–7i represent orbits with sharp plasmapause gradients, some with considerable structure and with strong electron-cyclotron harmonic instabilities in the plasma trough. In Figures7h and 7i, these are strong enough to clip the signal and cause spectral distortion in the form of large numbers of harmonic tones. All three have intense auroral kilometric radiation at high frequencies. And all three have varying degrees of banded or less-structured continuum radiation. These orbits not only challenge the AURA algorithm but also the operator who is expected to identify the upper hybrid band throughout these orbits.

The primary interpretational issues occur in the plasma trough in geomagnetically active times when the electron densities are low. These issues arise for a number of reasons. First, there are a number of banded emissions possible in this region, including electron-cyclotron harmonic emissions, diffuse electrostatic bands, and the fq resonances. It is even possible for the nonthermal continuum radiation to occur in bands that can confuse the spectrum. We use the fact that Kurth et al. [1979] and Hubbard et al. [1979] both remark that the highest electron cyclotron band near fuh is often the most intense electron cyclotron band above the 3fce/2 band as a method of selecting the upper hybrid band. While Canu et al. [2001] suggest that the first fq resonance can sometimes be more intense than the upper hybrid band, we have no way to distinguish between this and the upper hybrid band and use the brightest line as our guide. Hence, when there are multiple electron-cyclotron harmonic bands such as those in Figures7g–7i, we use the most intense band above 3fce/2 as fuh. Since the 3fce/2 band is often intense, if there are no additional electron cyclotron bands above this, we hesitate to identify this band as the upper hybrid band.

We also hesitate to follow the upper hybrid band below 10 kHz into the WFR receiver's domain. As mentioned above, the spectral resolution in this receiver is not optimized to identify fuh, and the background level is often different as an attenuator is commonly set to avoid saturating the receiver with strong chorus emissions. Furthermore, at such low frequencies, the selection of the incorrect electron cyclotron harmonic band for fuh leads to large errors in ne, as discussed below. Hence, in these cases, we simply fail to identify any spectral feature for fuh and leave a gap in the data set for such times. If there is continuum radiation present, we will use the low-frequency extent of that emission as an indicator of fpe. But as noted above, this low-frequency extent may be a source effect or may be a cutoff at some distant high-density structure; hence, the local plasma frequency may be significantly lower; the resulting value for ne is an upper limit.

Another issue affecting the accuracy of ne in low-density regions is the fact that we are identifying a (n + 1/2)fce band as fuh in a frequency regime where the upper hybrid band is a small harmonic of fce. This means that if we have misidentified the correct band, then we are off in frequency by a factor of fce or possibly more. At low harmonics of fce, this can translate into a very large error in ne. Even if we have selected the correct band, Figure4 illustrates that the actual fuh can be anywhere within one of the (n + 1/2)fce bands; hence, the determination of fuh is uncertain by an order of fce.

The upper hybrid band is polarized with its electric field approximately perpendicular to B [Kurth et al., 1979]. Hence, the emission can be spin modulated when using one of the spin plane booms for the HFR, which is normally the case. Such a modulation can cause the AURA-detected frequency to toggle across two or three spectral bins. Hence, the resulting electron density may show a few tens of percent fluctuations. We suggest that such fluctuations be taken as an indication of the uncertainty in the measurement.

3. The Van Allen Probe Electron Density Data Set

The results of the above analysis of the plasma wave spectrum deriving the electron density are collected into a series of day-long files using the common data format (CDF). Since the CDF is self-describing, we will not burden the reader with the details of the format here. However, it is important to indicate that the file contains a number of different parameters of interest. There is a date and time tag for each entry in the table. The frequency, which was digitized, is indicated with a later column, indicating whether the digitized frequency was identified as fuh or fpe (in the case of a continuum radiation cutoff). There is also a value for |B| used for the determination of fce and a time tag for that value (which may be slightly different from the time of the digitized frequency). There are also columns for computed values of fce, fpe, and fuh as well as the ratio of fpe/fce, which is of importance for some wave growth computations. Of course, ne is also given.

4. Summary and Conclusions

We have presented a description of the process used to derive the local electron density from the analysis of the Van Allen Probe plasma wave spectrum observed by the Waves high-frequency receiver. In order to develop a useful and reliable electron density data set, a rather elaborate tool and process has been developed to ensure both the accuracy to the extent possible and to automate the process as much is feasible. As well as the AURA algorithm works to identify the spectral peak at fuh, it is not possible to know that the algorithm has worked properly without inspection, and a fair fraction of the observations has to be reworked with a human operator of the tools.

The ultimate accuracy of the resulting electron density is close to 10%; however, there are a number of interpretational issues that can lead to much larger errors, especially in the plasma trough where the densities are low as a result of recent geomagnetic activity.

Acknowledgments

The authors thank P. Canu and P. Decreau for their insightful discussions. Data used in this paper are available from http://emfisis.physics.uiowa.edu/data/index. The research at University of Iowa was supported by JHU/APL contract 921647 under NASA prime contract NAS5-01072.

Michael Liemohn thanks Patrick Canu and another reviewer for their assistance in evaluating this paper.

Key Points

  • We use the upper hybrid resonance band to determine the electron density

  • A semi-automated process is used to find the upper hybrid resonance

  • We provide expected uncertainties for the density and some caveats for use

References

  1. Ashour-Abdalla M. Kennel CF. Nonconvective and convective electron cyclotron harmonic instabilities. J. Geophys. Res. 1978a;83:1531–1543. doi: 10.1029/JA083iA04p01531. [Google Scholar]
  2. Ashour-Abdalla M. Kennel CF. Multi-harmonic electron cyclotron instabilities. Geophys. Res. Lett. 1978b;5:711–714. doi: 10.1029/GL005i008p00711. [Google Scholar]
  3. Benson RF, Osherovich VA, Fainberg J. Reinisch BW. Classification of IMAGE/RPI-stimulated plasma resonances for the accurate determination of magnetospheric electron density and magnetic field values. J. Geophys. Res. 2003;108(A5):1207. doi: 10.1029/2002JA009589. [Google Scholar]
  4. Benson RF, Webb PA, Green JL, Garcia L. Reinisch BW. Magnetospheric electron densities inferred from upper-hybrid band emissions. Geophys. Res. Lett. 2004;31 L20803, doi: 10.1029/2004GL020847. [Google Scholar]
  5. Canu P. Identification of natural plasma emissions observed close to the plasmapause by the Cluster-WHISPER relaxation sounder. Ann. Geophys. 2001;19:1697–1709. , et al. ( [Google Scholar]
  6. Christiansen P, Gough P, Martelli G, Block J-J, Cornilleau N, Etcheto J, Gendrin R, Jones D, Béghin C. Décréau P. GEOS I: Identification of natural magnetospheric emissions. Nature. 1978;272:682–686. [Google Scholar]
  7. Escoubet CP, Pedersen A, Schmidt R. Lindqvist PA. Density in the magnetosphere inferred from ISEE 1 spacecraft potential. J. Geophys. Res. 1997;102:17,595–17,609. doi: 10.1029/97JA00290. [Google Scholar]
  8. Goldstein J. Simulation of Van Allen Probes plasmapause encounters. J. Geophys. Res. Space Physics. 2014;119:7464–7484. , et al. (, doi: 10.1002/2014JA020252. [Google Scholar]
  9. Gurnett DA. The Earth as a radio source: The non-thermal continuum. J. Geophys. Res. 1975;80:2751–2763. , doi: 10.1029/JA080i019p02751. [Google Scholar]
  10. Hubbard RF. Birmingham TJ. Electrostatic emissions between electron gyroharmonics in the outer magnetosphere. J. Geophys. Res. 1978;83:4837–4850. doi: 10.1029/JA083iA10p04837. [Google Scholar]
  11. Hubbard RF, Birmingham TJ. Hones EW. Magnetospheric electrostatic emissions and cold plasma densities. J. Geophys. Res. 1979;84:5828–5838. doi: 10.1029/JA084iA10p05828. [Google Scholar]
  12. Kletzing CA. The electric and magnetic field instrument suite and integrated science (EMFISIS) on RBSP. Space Sci. Rev. 2013;179:127–181. doi: 10.1007/s11214-023-00973-z. , et al. (, doi: 10.1007/s11214-013-9993-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
  13. Kurth WS. Detailed observations of the source of terrestrial narrowband electromagnetic radiation. Geophys. Res. Lett. 1982;9:1341–1344. , doi: 10.1029/GL009i012p01341. [Google Scholar]
  14. Kurth WS, Craven JD, Frank LA. Gurnett DA. Intense electrostatic waves near the upper hybrid resonance frequency. J. Geophys. Res. 1979;84(A8):4145–4164. doi: 10.1029/JA084iA08p04145. [Google Scholar]
  15. Meyer-Vernet N. Perche C. Tool kit for antennae and thermal noise near the plasma frequency. J. Geophys. Res. 1989;94:2405–2415. doi: 10.1029/JA094iA03p02405. [Google Scholar]
  16. Moldwin MB, Downward L, Rassoul HK, Amin R. Anderson RR. A new model of the location of the plasmapause: CRRES results. J. Geophys. Res. 2002;107(A11):1339. doi: 10.1029/2001JA009211. [Google Scholar]
  17. Mosier SR, Kaiser ML. Brown LW. Observations of noise bands associated with the upper hybrid resonance by the Imp 6 radio astronomy experiment. J. Geophys. Res. 1973;78:1673–1679. doi: 10.1029/JA078i010p01673. [Google Scholar]
  18. Sentman DD. Thermal fluctuations and the diffuse electrostatic emissions. J. Geophys. Res. 1982;87:1455–1472. , doi: 10.1029/JA087iA03p01455. [Google Scholar]
  19. Shaw RR. Gurnett DA. A test of two theories for the low frequency cutoffs of nonthermal continuum radiation. J. Geophys. Res. 1980;85:4571–4576. doi: 10.1029/JA085iA09p04571. [Google Scholar]
  20. Sheeley BW, Moldwin MB, Rassoul HK. Anderson RR. An empirical plasmasphere and trough density model: CRRES observations. J. Geophys. Res. 2001;106:25,631–25,641. doi: 10.1029/2000JA000286. [Google Scholar]
  21. Taylor WWL. Shawhan SD. A test of incoherent Cerenkov radiation for VLF hiss and other magnetospheric emissions. J. Geophys. Res. 1974;79:105–117. doi: 10.1029/JA079i001p00105. [Google Scholar]
  22. Thorne RM. Rapid local acceleration of relativistic radiation-belt electrons by magnetospheric chorus. Nature. 2013;504:411–414. doi: 10.1038/nature12889. , et al. (, doi: 10.1038/nature12889. [DOI] [PubMed] [Google Scholar]
  23. Trotignon JG. The WHISPER relaxation sounder and the CLUSTER active archive. In: Escoubet CP, editor; Laakso H, Taylor M, editors. The Cluster Active Archive, Studying the Earth's Space Plasma Environment. Berlin: Springer; 2010. pp. 185–208. Astrophysics and Space Science Proceedings et al. (,, edited by, doi: 10.1007/978-90-481-3499-1_12. [Google Scholar]
  24. Wygant JR. The electric field and waves instruments on the Radiation Belt Storm Probes Mission. Space Sci. Rev. 2013;179:183–220. , et al. ( [Google Scholar]

Articles from Journal of Geophysical Research. Space Physics are provided here courtesy of Wiley

RESOURCES