A simple and fast physics-based analytical method to calculate therapeutic and stray doses from external beam, megavoltage x-ray therapy

Abstract

State-of-the-art radiotherapy treatment planning systems provide reliable estimates of the therapeutic radiation but are known to underestimate or neglect the stray radiation exposures. Most commonly, stray radiation exposures are reconstructed using empirical formulas or lookup tables. The purpose of this study was to develop the basic physics of a model capable of calculating the total absorbed dose both inside and outside of the therapeutic radiation beam for external beam photon therapy. The model was developed using measurements of total absorbed dose in a water-box phantom from a 6 MV medical linear accelerator to calculate dose profiles in both the in-plane and cross-plane direction for a variety of square field sizes and depths in water. The water-box phantom facilitated development of the basic physical aspects of the model. RMS discrepancies between measured and calculated total absorbed dose values in water were less than 9.3% for all fields studied. Computation times for 10 million dose points within a homogeneous phantom were approximately 4 minutes. These results suggest that the basic physics of the model are sufficiently simple, fast, and accurate to serve as a foundation for a variety of clinical and research applications, some of which may require that the model be extended or simplified based on the needs of the user. A potentially important advantage of a physics-based approach is that the model is more readily adaptable to a wide variety of treatment units and treatment techniques than with empirical models.

1. Introduction

Modern radiotherapy practices seek to eradicate local disease while minimizing acute and late side effects of radiation exposure. In delivering the therapeutic radiation beam to the malignancy, smaller levels of unwanted stray radiation are also incident upon the whole body (Newhauser and Durante, 2011). With megavoltage photon therapy there are three main sources of stray radiation: photon leakage through the treatment head, photon scatter from the beam spreading and collimation systems, and photon scatter within the patient. Additionally, photoneutrons are generated, mainly in the treatment head, at electron energies greater than approximately 8 MeV (Awotwi-Pratt and Spyrou, 2007; NCRP, 2005). The dose deposited by stray radiation can cause numerous late effects, including second malignancies (NCRP, 2009). When one considers that second cancers comprise approximately 15% of all cancers (Howlader et al., 2013) and that it is projected that by the year 2020, there will be almost 20 million cancer survivors in the United States (de Moor et al., 2013), the need for accurate knowledge of radiation dose to all tissues and organs becomes apparent.

Many investigators have studied the use of analytical models to predict absorbed dose. However, the majority of these studies focused on the absorbed dose inside of the treatment field (Johns and Cunningham, 1953; Mackie et al., 1985; Mohan et al., 1986; Ahnesjo, 1989; Han et al., 2011). Comparatively fewer works reported on the analytical modeling of absorbed dose outside of this region (NCRP, 2009). To our knowledge, no contemporary commercial treatment planning system (TPS) includes the capability to accurately predict stray dose far from the treatment field. Thus, there is a large and systematic underestimation of stray radiation exposures by commonly used clinical TPSs (Howell et al., 2010; Schneider et al., 2014; Joosten et al., 2013a) and as a result, these doses and their effects are not accurately considered during treatment.

The objective of this work was to develop a simple and fast, physics-based analytical model to calculate the total absorbed dose in a simple water-box phantom from 6 MV photon radiotherapy treatment fields. To accomplish this objective, the analytical model was first developed to calculate absorbed dose in air and then generalized to include the effects of scatter and attenuation in a water phantom. This was accomplished using measured total absorbed dose profiles both in air and in a water-tank phantom from a 6 MV medical linear accelerator.

2. Methods

2.1 General Modeling Approach

The framework of our model is the basic physics of linac radiation therapy. To build this framework we explicitly model photon production, transmission, and scatter in the treatment head as well as scatter and transmission through the phantom. We did this using widely available and well established equations and physical principles. We then continued to develop the model by layering in additional refinements with the goal of achieving greater accuracy at minimal added complexity. Finally, we included empirical parameters and verified that the parameter values were physically meaningful.

We chose this approach in order to develop a model that is both transparent and physically meaningful. Depending on the needs on the user, this model could be utilized in a number of different ways. The model as developed below could be directly applied to other, similar treatment machines with expected additional uncertainty, or this framework could easily be further refined, extended, or even simplified, and the fitting process repeated, in order to be adapted to other treatment machines and the specific needs of the user.

2.2 Analytical Model of Absorbed Dose

According to the proposed model, the total absorbed dose, D_T, at a point in a water phantom is,

$$D_{\mathrm{T}}=D_{\mathrm{P}}+D_{\mathrm{L}}+D_{\mathrm{S}},$$ (2.1)

where D_P, D_L, and D_S denote the absorbed dose deposited by primary, leakage, and scattered photons, respectively. These terms are described in detail in the following sections.

2.2.1 Un-collimated Primary Photon Fluence

The un-collimated primary photon fluence, ϕ, is related to S, the number of photons emitted by the electron target in the treatment head, as shown in Figure 1. This includes photons that will deposit absorbed dose as primary and leakage radiation, but not as scatter radiation, which is modeled as originating elsewhere in the treatment head and phantom. The value S is proportional to the charge of electrons incident on the target, Q, or

$$S=\kappa \times Q,$$ (2.2)

where the constant of proportionality, κ, is given by,

$$\kappa =\frac{Y(T_0)\times T_0}{{Ē}_{T_0}}\times \frac{1}{e},$$ (2.3)

where the radiation yield, Y(T₀), is defined as the fraction of electron kinetic energy emitted as electromagnetic radiation (Attix, 1986), T₀ is the nominal electron beam energy, and therefore, Y(T₀) × T₀ gives the total energy radiated per electron, e is the electron charge, and Ē_T0 is the average photon beam energy. For simplicity, we assumed a triangular shape for the primary photon spectral fluence and an average photon energy equal to one-third of the peak energy (Attix, 1986). Thus, for the 6 MV photon beams studied in this paper, the average photon energy was estimated at 2 MeV. Simplifications such as this have little effect on the dosimetric results because in this range, the Compton cross section depends weakly on photon energy (Attix, 1986).

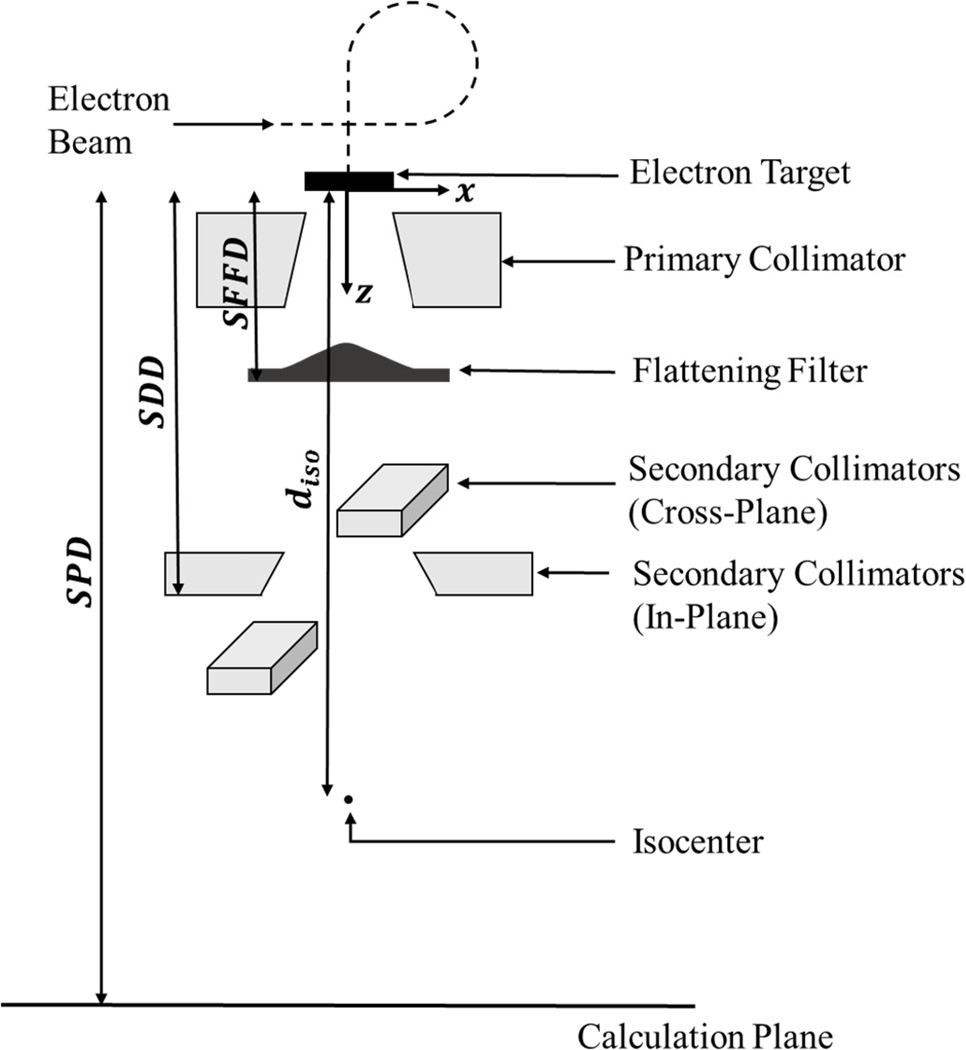
Figure 1.

Schematic diagram of the linac head where the secondary collimators represent the final field-defining aperture. The distances involved in modeling the various absorbed dose components are also indicated. (Not to scale)

The size of the effective photon source is small but non negligible (Svensson and Brahme, 1996). In this work, the finite lateral source size was modeled according to

$$S(x)=S\times G(x,\overline{x},\sigma ),$$ (2.4)

where S is from equation 2.2, G(x, x̄, σ) is a normalized Gaussian distribution, x is the off-axis distance, and x̄ and σ are the mean and standard deviation of that normalized Gaussian, respectively.

In addition to being spatially distributed, the resulting photon beam is known to exhibit horns at depths shallower than 10 cm in water due to the effects of the flattening filter (Khan, 2010). In order to model these horns, the un-collimated primary photon fluence was treated as a composite of three Gaussians. One Gaussian, G₁, was located on the central axis (CAX) and the other two, denoted by G₂ and G₃, were identical to one another but located symmetrically on either side of the CAX,

$$S(x)=S_1\times G_1(x,{\overline{x}}_1,{\sigma }_1)+S_2\times G_2(x,-{\overline{x}}_2,{\sigma }_2)+S_2\times G_3(x,{\overline{x}}_2,{\sigma }_2).$$ (2.5)

In addition, empirical adjustment factors were introduced for each of these parameters to facilitate fine tuning the model to measurements, yielding

$$S(x)=\sum _{i=1}^n{S}_i\times {\alpha }_{\mathrm{Q}i}\times G_i(x,{\overline{x}}_i\times {\alpha }_{{\overline{x}}_i},{\sigma }_i\times {\alpha }_{{\sigma }_i}),$$ (2.6)

where n is the number of Gaussians needed to model the source, in this case 3, α_Qi; is an empirical adjustment factor to the electron charge on target, α_x̄i, and α_σi are adjustment factors to the mean and width parameter of each source Gaussian, respectively, and the magnitude of S is equal to ${\sum }_{i=1}^n{S}_i$.

S_i is similar to S as described in equation 2.2 and is given by,

$$S_i=\kappa \times Q_i,$$ (2.7)

where κ is as was defined in Equation 2.3 and Q_i is the charge of electrons incident on the target that contribute photons to G_i such that Q, the total charge of electrons incident on the target, is equal to ${\sum }_{i=1}^n{Q}_i$.

The un-collimated primary photon fluence due to each source Gaussian, ϕ_i(x, z), was calculated according to,

$${\varphi }_i(x,z)=S_i\times \frac{1}{4\pi {[r_i(x,z)]}^p},$$ (2.8)

where r_i is the distance (Euclidean-norm) from the centroid of the i^th source Gaussian to the point of calculation. The exponent p governs the fall off of fluence with distance from the source and was empirically found.

The distance r_i was calculated according to,

$$r_i=\sqrt{{(x-{\overline{x}}_i)}^2+{(z-{\overline{z}}_i)}^2},$$ (2.9)

where x̄_i, the x-coordinate of the centroid of the i^th source Gaussian, was empirically found and z̄_i, the position of the centroid of the i^th source Gaussian on the z-axis, corresponds to the plane from which the photons appear to originate and is the same for all i source Gaussians. This is known as the virtual photon source position and corresponds to the location of the target in the treatment head (Svensson and Brahme, 1996). The virtual photon source position defined the origin of the coordinate system used in this study (see Figure 1).

2.2.2 Collimated Primary Photon Fluence

The collimated primary photon fluence was calculated using the un-collimated primary photon fluence and a function that describes the field shape. The collimated primary photon fluence represents only those photons which contribute to primary dose, or

$${\varphi }_{\mathrm{P}}(x,z)=\sum _{i=1}^n[{\varphi }_i\times G_{\mathrm{P},i}(x,{\overline{x}}_{\mathrm{P},i}(z),{\sigma }_{\mathrm{P},i}(z)\left)\right]\times C(x,z),$$ (2.10)

where n=3, ϕ_i is from Equation 2.8, G_P,i (x, x̄_P,i(z), σ_P,i(z)) is a normalized Gaussian characterized by a mean of x̄_P,i(z) and a width parameter of σ_P,i(z), and C(x, z) represents the off-axis shape caused by the black body collimation of the final field-defining aperture, which is depicted in Figure 2.

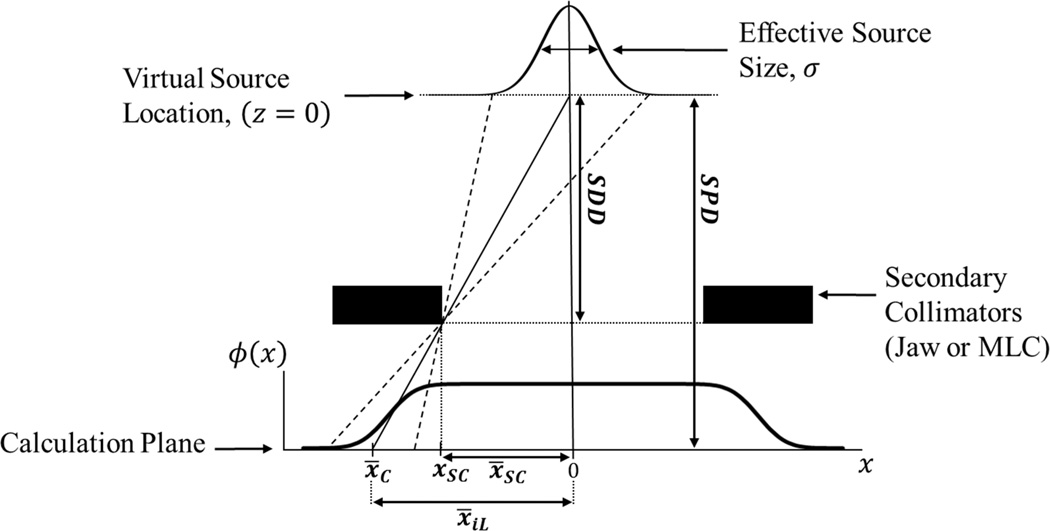
Figure 2.

Illustration of the black body collimation of primary photon fluence. Schematic diagram showing the effect of black body absorption by the secondary collimator on the primary photon fluence as well as the distances involved in determining the mean location and width parameter of the cumulative normal corresponding to the Gaussian located on the CAX by way of similar triangles. (Not to scale)

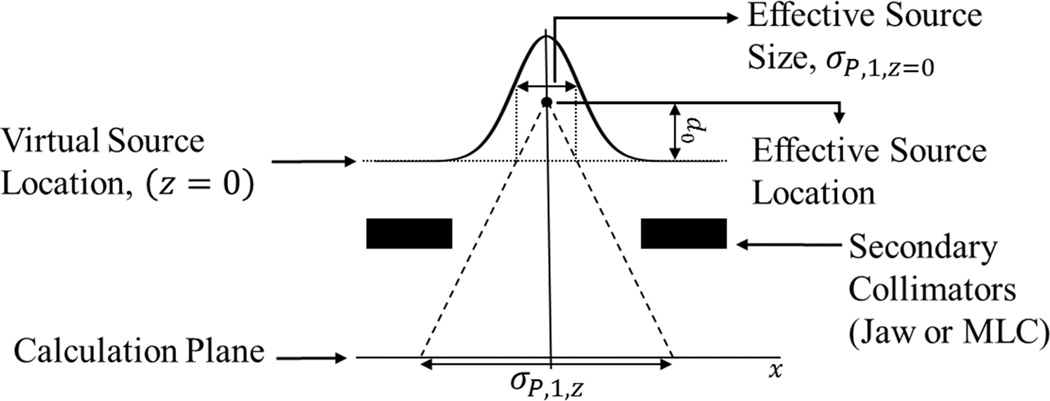
G_P,i (x, x̄_P,i(z), σ_P,i(z)) is the normally distributed un-collimated fluence from equation 2.8 projected to the calculation plane. This was accomplished by projecting the spatial distribution given by G_i(x, x̄_i × α_x̄i, σ_i × α_σi) in equation 2.6 using the effective source location as shown in Figure 3. The effective source location represents the empirically found position from which the source width appears to project (Svensson and Brahme, 1996). It should be noted that while the effective source location and the virtual source positions are conceptually distinct, they may be numerically similar.

Figure 3.

Diagram showing the projection of the effective source size to the calculation plane using the empirically found effective source location. (Not to scale)

C(x, z) models the black body absorption of primary photons by secondary collimators as shown in Figure 2 and is mathematically represented by

$$C(x,z)=\mathrm{c}\text{norm}(x,-{\overline{x}}_{\mathrm{C}}(z),{\sigma }_{\mathrm{S}\mathrm{R}\mathrm{C}}(z))\times (1-\mathrm{c}\text{norm}(x,{\overline{x}}_{\mathrm{C}}(z),{\sigma }_{\mathrm{S}\mathrm{R}\mathrm{C}}(z))),$$ (2.11)

where cnorm(x, −x̄_C(z), σ_SRC(z)) and cnorm(x, x̄_C(z), σ_SRC(z)) are cumulative normal functions or cnorm

$$\mathrm{c}\text{norm}(x,\overline{x},\sigma )=\frac{1}{\sqrt{2\pi }\sigma }{\int }_{-\infty }^x{\mathrm{e}}^{-\left(\frac{{(x-\overline{x})}^2}{2{\sigma }^2}\right)}\mathrm{d}x,$$ (2.12)

where x̄ and σ are the mean and width parameters of the cumulative normal, respectively. The mean of this cumulative normal function, x̄_C(z), is equal to the projected location of the collimator edge at the calculation plane. The width parameter of this cumulative normal corresponds to the size of the Gaussian source at the effective source location, σ_SRC. For simplicity it was estimated as the electron-charge-weighted average of the width parameters of the three un-collimated primary photon sources, or

$${\sigma }_{\mathrm{S}\mathrm{R}\mathrm{C}}(z=0)=\frac{{\sum }_{i=1}^n\left[\right({\sigma }_i\times {\alpha }_{{\sigma }_i}+{\overline{x}}_i\times {\alpha }_{{\overline{x}}_i})\times Q_i\times {\alpha }_{{\mathrm{Q}}_i}]}{{\sum }_{i=1}^n{Q}_i\times {\alpha }_{{\mathrm{Q}}_i}},$$ (2.13)

where σ_i, α_σi, x̄_i, α_x̄i, Q_i, and α_Qi are as previously defined in equations 2.6 and 2.7. This width parameter was then projected to the plane of calculation by similar triangles (see Figure 2).

2.2.3 Absorbed Dose from Collimated Primary Photon Fluence

In air, the component of the total absorbed dose deposited by the collimated primary photon fluence was modeled as

$$D_{\mathrm{P},\text{air}}^{\mathrm{C}\mathrm{P}\mathrm{E}}(x,z)={\varphi }_{\mathrm{P}}(x,z)\times {\left(\frac{{\mu }_{\mathrm{e}\mathrm{n}}}{\rho }\right)}_{{Ē}_{T_0},\text{air}}\times {Ē}_{T_0},$$ (2.14)

where ϕ_P(x, z) is the collimated primary photon fluence (equation 2.10), ${\left(\frac{{\mu }_{\mathrm{e}\mathrm{n}}}{\rho }\right)}_{{Ē}_{T_0},Z}$ is the mean mass energy absorption coefficient from the NIST database (Hubbell and Seltzer, 2011), Z is the atomic number of the medium in which the dose is being deposited, and Ē_T0 is the average photon beam energy.

To model the absorbed dose to water, we generalized Equation 2.14 to additionally take into account attenuation in water, or

$$D_{\mathrm{P},\mathrm{w}}^{\mathrm{C}\mathrm{P}\mathrm{E}}(x,z)=\sum _{i=1}^n[{\varphi }_i\times G_{\mathrm{P},i}(x,z)\times T{F}_{i,\mathrm{w}}(x,d)]\times C(x,z)\times {\left(\frac{{\mu }_{\mathrm{e}\mathrm{n}}}{\rho }\right)}_{Ē,\mathrm{w}}\times {Ē}_{T_0},$$ (2.15)

where TF_i,w(x, d) is the photon transmission factor in water.

TF_i,w(x, d) represents the fraction of the primary fluence incident on the water phantom that was transmitted through water to the calculation plane. This was modeled as simple exponential attenuation of the primary photon fluence in water to the point of calculation, or

$$T{F}_{i,\mathrm{w}}(x,d)=\text{exp}[-{\mu }_{\mathrm{w}}·d_i(x,z)·{\alpha }_{\mathrm{w}}],$$ (2.16)

where μ_w is the linear attenuation coefficient of water for the estimated mean photon energy of Ē = 2 MeV taken from data tables from the National Institute of Standards and Technology (NIST) (Hubbell and Seltzer, 2011), d_i(x, z) is the oblique depth in water, and α_w is an empirical adjustment parameter included to reduce systematic uncertainties in the estimated mean linear attenuation coefficient for photons. Implicit in Equation 2.16 is the simplifying assumption of charged particle equilibrium at shallow depths (e.g., d ≤ d_max = 16 mm for 6 MV photons). In fact, the dose in the buildup region is less than that estimated by Equation 2.15 by up to 80% (Klein et al., 2003). For simplicity, we have neglected the buildup effect in this work, although it could be taken into account with an asymptotic exponential function.

2.2.4 Un-Attenuated Leakage Photon Fluence

The absorbed dose from photons that leak through the collimators will be modeled in two steps. First we calculate the fluence in air that would leak through an infinitesimally thin secondary collimator, i.e., as described in this section. In the second step, we take into account attenuation of photon fluence in the actual (i.e., thick) collimators and convert photon fluence to absorbed dose in air and water (see Section 2.1.5).

The fluence of photons leaking through infinitesimally thin secondary collimators was modeled as

$${\varphi }_{\mathrm{L}}(x,z)=\sum _{i=1}^n[{\varphi }_i\times G_{\mathrm{P},i}(x,{\overline{x}}_{\mathrm{P},i}(z),{\sigma }_{\mathrm{P},i}(z)\left)\right]\times A(x,z),$$ (2.17)

where n was defined in Equation 2.6, ϕ_i and G_P,i (x, x̄_P,i(z), σ_P,i(z)) are the same as in equation 2.10, and A(x, z) represents the percentage of photons that are transmitted through an infinitesimally thin secondary collimator as a function of x, as depicted in Figure 4. For simplicity, in our leakage model we replaced three source Gaussians with three point sources located at the mean locations of the original source Gaussians and represented by

$${\varphi }_{\mathrm{L}}(x,z)\approx \sum _{i=1}^n[{\varphi }_i]\times A(x,z),$$ (2.18)

where A(x, z) is as above.

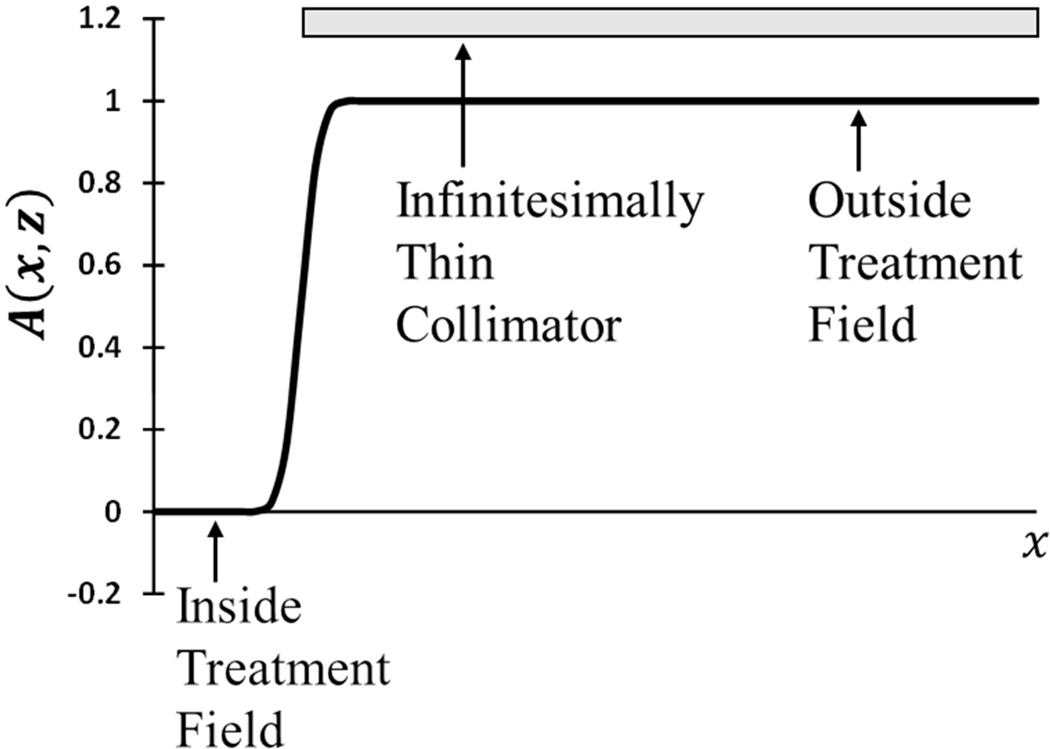
Figure 4.

Diagram depicting the shape, A(x, z), of the un-attenuated leakage photon fluence as resulting from an infinitesimally thin collimator as a function of off-axis position x.

In essence, A(x, z) simply suppresses the photon fluence that passes through the aperture of a secondary collimator. By definition, A(x, z) has a magnitude of 0 inside the treatment field where no collimation occurs, 1 outside of the treatment field where photons reaching that calculation point from the source must traverse collimation, and of intermediate value in the penumbral region. A(x, z) was modeled with a combination of cumulative normal functions (see equation 2.12). Thus, the model for the off-axis shape of the leakage photon fluence was given by

$$A(x,z)=(1-\mathrm{c}\text{norm}(x,-{\overline{x}}_{\mathrm{C}}(z),{\sigma }_{\mathrm{S}\mathrm{R}\mathrm{C}}(z)\left)\right)+\mathrm{c}\text{norm}(x,{\overline{x}}_{\mathrm{C}}(z),{\sigma }_{\mathrm{S}\mathrm{R}\mathrm{C}}(z)),$$ (2.19)

where x̄_C(z) and σ_SRC(z) are as in equation 2.11.

2.2.5 Absorbed Dose from Leakage Photon Fluence

The absorbed dose deposited by the leakage photon fluence is known as the leakage absorbed dose. This was modeled in air as

$$D_{\mathrm{L},\text{air}}^{\mathrm{C}\mathrm{P}\mathrm{E}}(x,z)=\sum _{i=1}^n[\frac{S_i}{4\pi {[r_i(x,z)]}^q}\times \prod _{k=1}^{m}T{F}_{i,k}(x,z)]\times A(x,z)\times {\left(\frac{{\mu }_{\mathrm{e}\mathrm{n}}}{\rho }\right)}_{{Ē}_{T_0},\text{air}}\times {Ē}_{T_0},$$ (2.20)

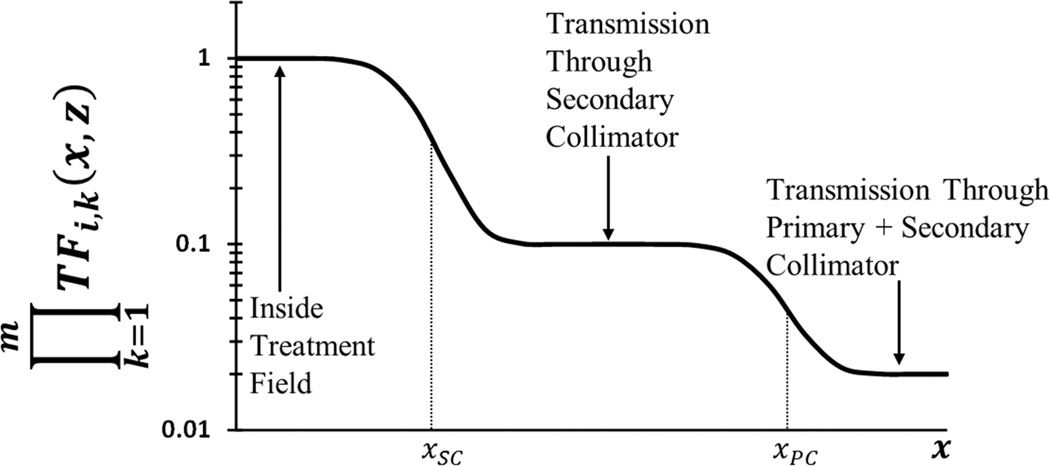
where n, S_i, r_i(x, z), ${\left(\frac{{\mu }_{\mathrm{e}\mathrm{n}}}{\rho }\right)}_{{Ē}_{T_0},\text{air}}$, and Ē_T0 are defined in earlier sections, and the exponent q governs the divergence of the leakage photons. The product over k=1 to m represents the attenuation through all m attenuating layers (e.g., jaw, MLC, primary collimator), and TF_i,k(x, z) is the transmission factor through each layer (equation 2.16). The effects of the primary and secondary collimators on the transmitted fluence is depicted in Figure 5.

Figure 5.

Schematic illustration of the effect of two laterally staggered attenuating layers. Plot of TF_i,k(x, z) after two laterally staggered attenuating layers where x_sc. is the projected location of the secondary collimator in the plane of calculation and x_pc is that of the primary collimator.

Equation 2.20 was modified to take into account the effect of attenuation in a water phantom to become

$$D_{\mathrm{L},\mathrm{w}}^{\mathrm{C}\mathrm{P}\mathrm{E}}(x,z)=\sum _{i=1}^n[\frac{S_i}{4\pi {[r_i(x,z)]}^q}\times \prod _{k=1}^{m\prime }T{F}_{i,k}(x,z)]\times A(x,z)\times {\left(\frac{{\mu }_{\mathrm{e}\mathrm{n}}}{\rho }\right)}_{{Ē}_{T_0},\mathrm{w}}\times {Ē}_{T_0},$$ (2.21)

where ${\left(\frac{{\mu }_{\mathrm{e}\mathrm{n}}}{\rho }\right)}_{{Ē}_{T_0},\mathrm{W}}$ was previously defined and m′ = m + 1 to allow for the transmission factor of an additional attenuating layer, i.e., water, given by TF_i,w(x, d). The additional transmission factor, TF_i,w(x, d), represents the fraction of incident leakage radiation that was transmitted to the depth of the calculation point in water and is as was given by equation 2.16.

2.2.6 Dose from Head Scatter and Phantom Scatter

The absorbed dose due to scattered radiation is

$$D_{\mathrm{S}}=D_{\mathrm{H}\mathrm{S}}+D_{\mathrm{P}\mathrm{S}},$$ (2.22)

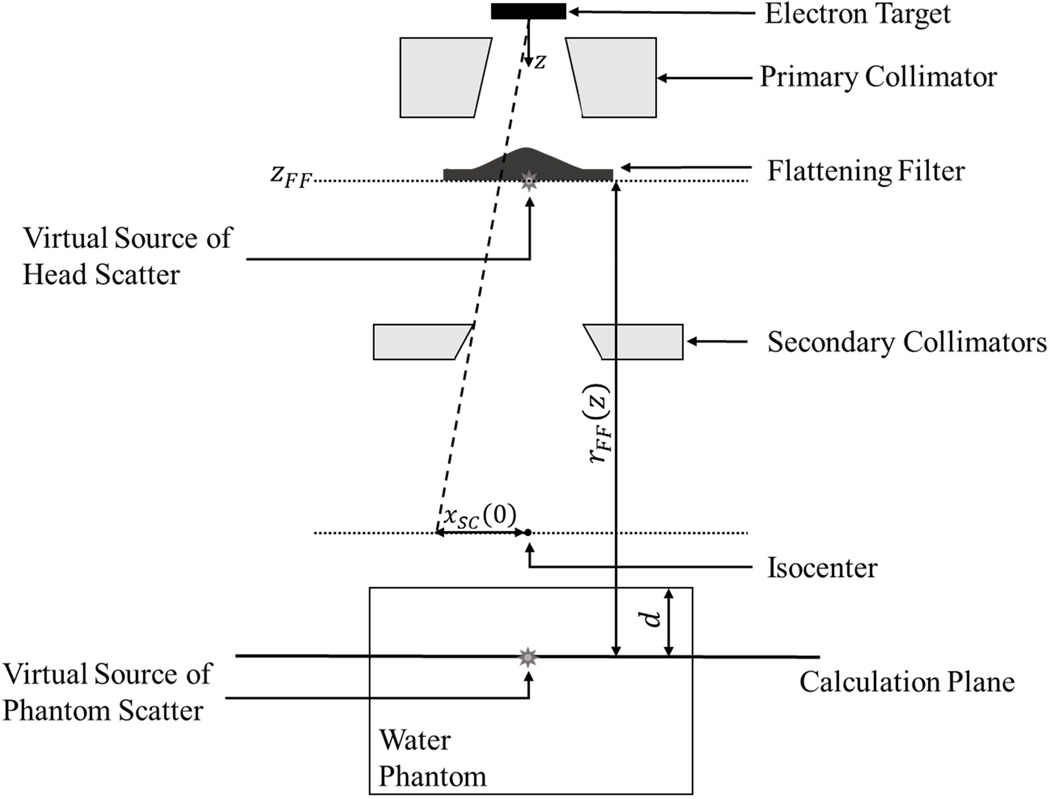
where D_HS is the absorbed dose from photons scattered in the treatment head, and D_PS is the absorbed dose from radiation scattered in the phantom. We modeled scatter radiation as emanating from a pair of virtual point sources, as shown in Figure 6.

Figure 6.

Schematic illustration of the various virtual sources in the scattered dose portion of the model as well as the distances involved in the calculation of dose due to scattered radiation. (Not to scale)

2.2.7 Absorbed Dose from the Virtual Source of Head-Scattered Radiation

The virtual source of head-scattered radiation is located at the downstream edge of the flattening filter and on the CAX (McKenzie and Stevens, 1993), as shown in Figure 6. The absorbed dose in air from this virtual source was modeled as

$$D_{\mathrm{H}\mathrm{S},\text{air}}^{\mathrm{C}\mathrm{P}\mathrm{E}}(x,z)=D_{\mathrm{H}\mathrm{S}}(Z_{\mathrm{F}\mathrm{F}})\times \frac{1}{{[r_{\mathrm{F}\mathrm{F}}(z)]}^s}\times {\tilde{G}}_{\mathrm{H}\mathrm{S}}(x,z),$$ (2.23)

where D_HS(z_FF) is the empirically found head scatter reference absorbed dose defined at the CAX at the flattening filter, r_FF(z) is the Euclidean norm between this virtual photon source position and a point in the calculation plane, the exponent s governs the divergence of head-scattered radiation, and G̃_HS(x, z) is an un-normalized Gaussian representing the lateral shape of the dose distribution.

D_HS(z_FF) is related to the size of the primary field incident on the phantom. As the effective field area increases, more of the head-scattered radiation reaches the phantom. As such, this dependence was modeled as a power law, or,

$$D_{\mathrm{H}\mathrm{S}}(z_{\mathrm{F}\mathrm{F}})={\kappa }_{\mathrm{H}\mathrm{S},\mathrm{F}\mathrm{A}}\times F{A_{\text{eff}}}^{1/u},$$ (2.24)

where FA_eff denotes the effective field area defined at the depth of calculation, the exponent u governs how strongly this amplitude varies with changes in field area, and κ_HS,FA is an empirically determined constant of proportionality. Eventually, the effective field size will reach a point where the entire head-scatter source is visible, and D_HS(z_FF), the reference absorbed dose, will no longer increase with the field size. Thus, the effective field area was approximated as

$$F{A}_{\text{eff}}=\{\begin{array}{cc}FA\hfill & \text{if}FA\le F{A}_{\text{max}}\hfill \\ F{A}_{\text{max}}\hfill & \text{if}FA>F{A}_{\text{max}}\hfill \end{array}$$ (2.25)

where FA is the field area at the plane of calculation and FA_max is the empirical cut-off field area defined at the plane of calculation.

G̃_HS(x, z) denotes the un-normalized lateral shape of the head scatter dose. This Gaussian is characterized by a mean located on the CAX and a width parameter at the depth of calculation of σ_HS(z). This width parameter at depth is the empirically found head-scatter effective source size, σ_HS(0), projected to the depth of calculation using similar triangles.

The width parameter of the head-scatter effective source size is related to the location of the secondary collimator and was modeled as a power law, or

$${\sigma }_{\mathrm{H}\mathrm{S}}(0)={\kappa }_{\mathrm{H}\mathrm{S},\sigma }\times {[x_{\mathrm{S}\mathrm{C}}(0)]}^{1/\nu },$$ (2.26)

where x_SC(0) is the off-axis location of the secondary collimator (SC) projected to the isocentric plane as shown in Figure 6, the exponent ν governs how strongly the width parameter varies with lateral secondary collimator position, and κ_HS,σ is an empirical constant of proportionality.

The absorbed dose to water due to head-scattered radiation was calculated according to

$$D_{\mathrm{H}\mathrm{S},\text{water}}^{\mathrm{C}\mathrm{P}\mathrm{E}}(x,z)=D_{\mathrm{H}\mathrm{S},\text{air}}(x,z)\times T{F}_{\mathrm{H}\mathrm{S},\mathrm{w}},$$ (2.27)

where D_HS,air(x, z) is from equation 2.23 and TF_HS,w is the transmission factor for head-scattered photons through water modeled in the same form as equation 2.16.

2.2.8 Absorbed Dose to Water from Phantom-Scattered Radiation

A virtual source of phantom-scatter radiation is shown schematically in Figure 6. The dose due to phantom-scattered radiation was calculated as

$$D_{\mathrm{P}\mathrm{S},\text{water}}^{\mathrm{C}\mathrm{P}\mathrm{E}}(x,d)=D_{\mathrm{P}\mathrm{S}}(d)[C(d)\times {\tilde{G}}_{\mathrm{P}\mathrm{S},1}(x)\times T{F}_{\mathrm{P}\mathrm{S},1}(x)+(1-C(d))\times {\tilde{G}}_{\mathrm{P}\mathrm{S},2}(x)\times T{F}_{\mathrm{P}\mathrm{S},2}(x)],$$ (2.28)

where D_PS(d) is the integral absorbed phantom scatter dose, C(d) is a partitioning factor to apportion the two component Gaussians, G̃_PS,1(x) and G̃_PS,2(x) are each un-normalized Gaussians centered on the CAX, and TF_PS,1(x) and TF_PS,2(x) are the corresponding transmission factors in water. The method in equation 2.28 was previously described in Zhang et al. (2011) and Taddei et al. (2013).

In our model, D_PS(d) depends on the field area that was incident upon the phantom as well as the depth of the calculation in water. This was modeled as a power law relationship, or

$$D_{\mathrm{P}\mathrm{S}}(d)={\kappa }_{\mathrm{P}\mathrm{S},\mathrm{F}\mathrm{A}}\times FA{(0)}^{1/W}\times d^{1/b},$$ (2.29)

where κ_PS,FA is an empirical constant of proportionality, FA(0) is the area of the treatment field defined at the isocentric plane, the exponent w governs the dependence on FA, d is the perpendicular depth of the calculation plane (see Figure 6), and the exponent b governs the dependence on depth.

G̃_PS,1(x) is the narrower of the two Gaussians. The width parameter, σ_PS,1, was modeled as proportional to the secondary collimator position as in

$${\sigma }_{\mathrm{P}\mathrm{S},1}={\kappa }_{\mathrm{P}\mathrm{S},\sigma ,1}\times {[x_{\mathrm{S}\mathrm{C}}(0)]}^{1/f},$$ (2.30)

where κ_PS,σ,1 is an empirical constant of proportionality, x_SC(0) is the secondary collimator position as was defined in equation 2.26, and the exponent f governs the dependence on field edge location.

G̃_PS,2(x) represents the wider of the two Gaussians. The width parameter, σ_PS,2, was modeled as a function of the primary field area as in

$${\sigma }_{\mathrm{P}\mathrm{S},2}={\kappa }_{\mathrm{P}\mathrm{S},\sigma ,2}\times F{A}^{1/h},$$ (2.31)

where κ_PS,σ,2 is an empirical constant of proportionality, FA is the area of the treatment field projected to the depth of calculation, and the exponent h governs the dependence on field area.

TF_PS,i(x) models attenuation of the phantom scattered radiation according to

$$T{F}_{\mathrm{P}\mathrm{S},i}(x)=\text{exp}[-{\mu }_{\mathrm{W}}·x·{\alpha }_{\mathrm{P}\mathrm{S},i}],$$ (2.32)

where μ_w is the same as in previous sections, x is the off-axis distance of the calculation point, and α_PS,i is an empirical adjustment parameter to correct for systematic errors in the estimation of average energy of the phantom-scattered radiation.

2.2.9 Training Data

The analytic model was trained using measured profiles of photon doses. The measurement conditions for all training data are listed in Table 1. Water-tank measurements used to train this model were taken from a study by Kaderka et al. (2012) that were performed on an electron linac (Elekta SL25, Stockholm) at Universitätsklinikum (KGU) in Frankfurt, Germany operated at 6 MV. Kaderka et al. measured photon doses using a diamond detector (60003 PTW, Freiburg) in a water tank (PTW, Freiburg). We selected this data set because of its completeness in providing a clinically meaningful range of irradiation parameters as well as the favorable diamond detector properties of high sensitivity in the low-dose range and low energy dependence (Laub et al., 1999). We measured in-air photon doses with a farmer-type ion chamber (PTW, TN30013, S/N:0579, Freiburg) for fields produced by an electron linear accelerator (Elekta Synergy, S/N:151892, Stockholm) at Mary Bird Perkins Cancer Center in Baton Rouge, Louisiana.

Table 1.

The measurement conditions for the profiles used to train the dose model are listed below including the field size, source-to-surface distance (SSD), depth, source-to-measurement-plane distance (SPD), and scan direction.

Water-Phantom
Field Size (cm2)	SSD (cm)	Depth (cm)	Profile	Source
5×5	100	1.5	In-Plane	(Kaderka et al., 2012)
			Cross-Plane	“
		10	In-Plane	“
			Cross-Plane	This Worka
10×10*	100*	1.5*	In-Plane*	(Kaderka et al., 2012)
			Cross-Plane	“
In-Air
Field Size (cm2)	SPD (cm)		Profile	Source
5×5	101.5		In-Plane	This Work
			Cross-Plane	“
	110		In-Plane	“
			Cross-Plane	“
10×10*	101.5*		In-Plane*	“
			Cross-Plane	“
40×40	85		In-Plane	“
			Cross-Plane	“
	100		In-Plane	“
			Cross-Plane	“
	115		In-Plane	“
			Cross-Plane	“
	130		In-Plane	“
			Cross-Plane	“

The measurement conditions indicated by * represent the reference conditions selected for this study.

^aChauvenet’s Criterion was used to exclude the results of the water-phantom profile measured in this work due to the significantly lower dose resolution than those from Kaderka et al.

2.2.10 Model Parameters

In previous sections, model parameters were discussed in terms of their placement in the model. However, in order to facilitate qualitative understanding of the physical and phenomenological aspects of the model, we digress to discuss model parameters in terms of slightly different classifications. In this, model parameters were grouped into four categories.

First are geometrical parameters. These are parameters which describe the dimensions of the machine and phantom, the location of the phantom and various machine components, as well as material characteristics of the phantom and machine components. These parameters were taken from published literature and unpublished proprietary information that was obtained from the linac manufacturer.

Second are radiation source parameters. These parameters describe the location, size, and divergence of the source of primary and leakage photons and include things such as the charge of electrons incident on the target and photon yield. These parameters were estimated based on widely accepted generalizations and simplifications to more complex phenomena.

Third are radiation interaction parameters. These parameters describe the attenuation of photons in both the phantom as well as various treatment head components and include narrow-beam attenuation ceofficients in water and tungsten.

Fourth are empirical parameters, of which there are two classes, completely empirical parameters and adjustment factors. Completely empirical parameters were used to model effects for which we lacked a physics-based model, e.g., phantom-scatter and head-scatter photons. Empirical adjustment factors were used for two purposes. First, they were used when knowledge of geometric and source parameters was either incomplete or inaccurate, such as incomplete material information for linac head components. Second, adjustment parameters were used to compensate for approximations in the physical modeling approach, such as using narrow-beam-geometry attenuation factors and assumed photon source locations.

2.2.11 Parameter Selection

Empirical model parameters were determined with the use of the generalized reduced gradient method (Lasdon et al., 1973). This algorithm minimized the local relative dose differences for groups of profiles simultaneously so that fitted parameters are applicable to multiple irradiation conditions. Once optimizations were complete, it was verified that all parameter values were physically meaningful and the root mean square (RMS) local relative dose difference, δ_Dr, for each profile was ≤ 10%.

The empirical parameters of relevance to the un-collimated primary photon fluence were found by fitting to measured training data for the in-air, open field (40×40 cm²). The mean of the central source Gaussian was assigned to be located on the CAX while all other empirical parameters were allowed to vary independently in the in-plane and cross-plane directions, allowing for the possibility of a nonradially symmetric source. Additionally, we constrained the fit so that the magnitude of the source on the CAX was identical in the in-plane and cross-plane directions.

The empirical adjustment parameters of relevance to absorbed dose from the collimated photon fluence and the absorbed dose from the un-attenuated leakage fluence were found by simultaneously fitting to all training data that were measured in water. These empirical adjustment parameters were found separately for the in-plane and cross-plane directions.

In order to better isolate the parameters for head-scatter from those for phantom-scatter, the empirical adjustment parameters of relevance to the model for absorbed dose from head-scattered radiation were found by simultaneously fitting all profiles measured in air only. In this way, the potentially confounding effects from phantom scatter were avoided in the determination of head-scatter parameters. The empirical adjustment parameter to the linear attenuation coefficient of water, α_HS, was found by simultaneously fitting all water-phantom training data and allowing only this parameter to vary. Values were fitted separately for the in-plane and cross-plane directions.

The empirical parameters describing dose due to phantom-scattered photons were found by simultaneously fitting all profiles that were measured in water. The dose due to phantom-scattered photons was most affected by the size and shape of the radiation field incident on the phantom rather than the specific shape and location of linac head characteristics. Thus, with the exception of the partitioning factor, C, parameter values fitted simultaneously to data in both the in-plane and cross-plane directions and at all depths. The partitioning factor for phantom scatter, C, was fitted independently for each depth of calculation but simultaneously in the in-plane and cross-plane directions at each depth.

3. Results

Empirical model parameters found to best fit the measured training data in air and water are presented in tables 2 through 6. One way to gauge the physical realism of the model was by how much empirical adjustment parameters deviated from unity. In tables 2 through 6 it can be seen that these parameters remained close to 1. The largest adjustments were needed for those parameters associated with the primary collimator. This was expected because the primary collimator was the component about which the least amount of information was available. The small adjustments to other parameters indicate that the physical basis of the model is sound.

Table 2.

Parameters to model the un-collimated primary photon fluence.

Symbol	Description	In-Plane	Cross-Plane	Source
Q1	Charge of electrons incident on the target contributing photons to the central Gaussian (C)	0.146	0.121	This Worka
Q2	Charge of electrons incident on the target contributing photons to each peripheral Gaussian (C)	0.080	0.101	“
σ1	Width parameter of the central Gaussian (mm)	2.51	2.75	“
σ2	Width parameter of each peripheral Gaussian (mm)	0.85	0.97	“
x̄1	Mean location of the central Gaussian (mm)	0		“
x̄2	Off-axis mean location of each peripheral Gaussian (mm)	1.13	1.24	“
p	Exponent governing the divergence of the un-collimated photon fluence	0.97		“
Y(T0)	Photon yield for 6 MeV electrons in tungsten	0.216		(Attix, 1986)

^aFrom iterative fitting procedure

Table 6.

Parameters to model the absorbed dose from the phantom-scattered photons. All parameters are from an iterative fitting procedure from this work.

Symbol	Description	d=1.5 cm	d=10 cm
κFA	Constant of proportionality for the double-Gaussian amplitude $(\mathrm{m}\mathrm{G}\mathrm{y}·\mathrm{G}{\mathrm{y}}^{-1}·\mathrm{m}{\mathrm{m}}^{-2·\frac{1}{\mathrm{w}}·\frac{1}{\mathrm{b}}})$	3.8×10−2
w	Exponent defining power law relationship between the amplitude and field area	1.7
b	Exponent defining power law relationship between amplitude and depth	1.9
κPS,σ,1	Constant of proportionality for the width parameter of Gaussian 1 $(\mathrm{m}\mathrm{m}·\mathrm{m}{\mathrm{m}}^{\frac{-1}{\mathrm{f}}})$	12
f	Exponent defining power law relationship between width parameter of Gaussian 1 and field size	3.0
κPS,σ,2	Constant of proportionality for the width parameter of Gaussian 2 $(\mathrm{m}\mathrm{m}·\mathrm{m}{\mathrm{m}}^{\frac{-1}{\mathrm{h}}})$	1.1
h	Exponent defining power law relationship between width parameter of Gaussian 2 and field area	1.6
C	Partitioning factor for the two Gaussians making up the phantom-scatter double-Gaussian	0.59	0.80
αPS,1	Adjustment parameter to the μd of the phantom-scattered photons in Gaussian 1	1.7
αPS,2	Adjustment parameter to the μd of the phantom-scattered photons in Gaussian 2	2.5

Also in tables 2 through 6 it can be seen that model parameters differed, sometimes significantly, in the in-plane and cross-plane directions. These differences were attributed to differing treatment head characteristics in the in-plane and cross-plane directions. For example, both the design (i.e., MLC versus block) and position (see Table 3) of the secondary collimators are different between the in-plane and cross-plane directions.

Table 3.

Parameters to model the absorbed dose from primary photon fluence in water.

Symbol	Description	In-Plane	Cross-Plane	Source
αQ1	Incident electron charge empirical adjustment parameter for Gaussian 1	1.24	1.20	This Worka
αQ2	Incident electron charge empirical adjustment parameter for Gaussian 2	0.62	1.00	“
ασ1	Width parameter adjustment factor for Gaussian 1	0.79	0.52	“
ασ2	Width parameter adjustment factor for Gaussian 2	0.51	0.74	“
αx̄2	Adjustment parameter for the mean of Gaussian 2	0.82	1.51	“
αw	Adjustment parameter to the μt of water	0.77		“
d0	Upstream distance from the effective photon source to the virtual photon source (mm)	6.03		“
μw	Linear attenuation coefficient of water for 2 MeV photons (1/cm)	4.942 × 10−2		(Hubbell and Seltzer, 2011)
SSD	Source-to-surface-distance (cm)	100	100	(Kaderka, 2012)
SDD	Source-to-diaphragm-distance (cm)	47	37.7	(Elekta, 2007)

^aFrom iterative fitting procedure

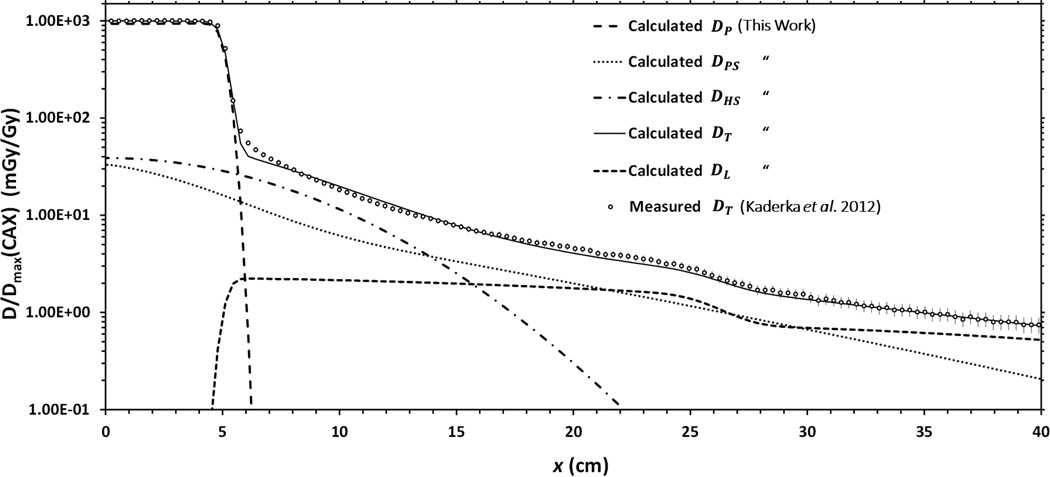
The total absorbed dose in both air and water was calculated using equation 2.1. Figure 7 shows each of the calculated dose components, D_P, D_L, D_HS, and D_PS, the calculated total absorbed dose, D_T, and the measured total absorbed dose profile for a representative case. In this figure, it can be seen that the absorbed dose due to the primary photon fluence accounts for nearly all of the dose deposited inside of the treatment field while the leakage fluence deposits the majority of the dose in the far-from-field region. Both head-scattered photons and phantom-scattered photons contribute substantially to the total absorbed dose in the near-field region. In a water phantom, the discrepancies between measured and calculated total absorbed dose values were 7.8% mean RMS and 9.3% maximum RMS for all fields studied.

Figure 7.

Plot of each of the components of the calculated total absorbed dose along with their sum and measured total absorbed dose. Doses were measured in the cross-plane direction for a 10×10 cm² field with an SSD of 100 cm and at a depth of 1.5 cm in water. Measured data include error bars representing one standard deviation, as reported by Kaderka et al. (2012).

In order to estimate the speed of dose calculations, the proposed model was timed while calculating 50,000 dose points for a 5×5 cm² treatment field. This time was then scaled to determine the amount of time that would be needed to calculate 10 million dose points, e.g., for a whole body dose calculation. By these methods it was found that the model needed approximately 4 minutes to calculate 10 million dose points.

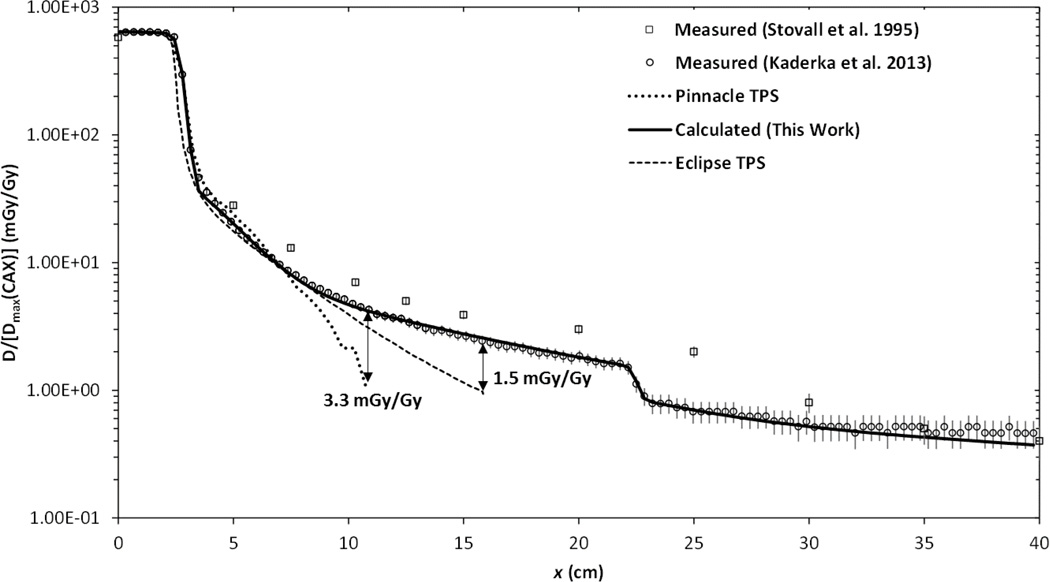
These results suggest that it is feasible to improve dosimetric accuracy in near-field and out-of-field regions using a simple and computationally fast physics-based analytical algorithm. The potential benefit is illustrated in Figure 8 were it can be seen that two treatment planning systems underestimate absorbed dose outside a distance of approximately 7.5 cm from the CAX. Importantly, the degree to which commercial treatment planning systems underestimate out-of-field dose varies strongly with position and the TPS dose algorithm used. These findings are similar to that which have recently been reported for a number of different TPSs and treatment modalities (Howell et al., 2010; Joosten et al., 2013b; Schneider et al., 2013). The analytical model proposed in this work, on the other hand, continues to predict measured doses at greater accuracy out to a distance of 40 cm from the CAX.

Figure 8.

Plot of the total absorbed dose for a 5×5 cm² treatment field at a depth of 10 cm normalized to 1 mGy/Gy on the CAX at a depth of maximum dose measured with a diamond detector in the in-plane direction a water-box phantom (Kaderka, 2012), measured with TLDs in a water-equivalent phantom (Stovall et al., 1995), calculated by two different commercial treatment planning systems (Pinnacle, Philips Healthcare, Andover, MA and Eclipse, Varian Medical Systems, Inc., Palo Alto, CA), and calculated by the analytical model proposed in this work.

4. Discussion and Conclusion

We developed a physics-based analytical model to calculate the total absorbed dose deposited both inside and outside of the treatment field for 6 MV radiotherapy. The model includes separate terms for absorbed dose from primary, leakage, and scattered photons and was developed to reproduce measured total absorbed dose profiles in a water-box phantom from 6 MV conventional photon radiotherapy. The major finding of this study is that it is possible to accurately model the total absorbed dose from a 6 MV photon field with 10% RMS or better agreement with measured dose values using a simple and fast, physics-based model.

Current treatment planning systems do not include the capability to accurately predict the absorbed dose beyond a few centimeters outside of the treatment field (Taylor and Kron, 2011). Previous to this work, relatively few out-of-field dose reconstruction algorithms have been reported in the literature. Of those, some only attempted to model certain components of the stray dose rather than the total absorbed dose (Benadjaoud et al., 2012; Chofor et al., 2012), others were based on measurements made using linacs from previous decades (Francois et al., 1988; Stovall et al., 1995), and many authors omitted key aspects of their proposed models (Stovall et al., 2006; Van der Giessen, 1996; Diallo et al., 1996) which would allow their results to be reproduced.

Our model could prove useful in a number of different applications. The accurate knowledge of absorbed dose deposited outside of the treatment field is especially important for predicting radiation late effects such as second cancer (Newhauser and Durante, 2011), fertility complications (Perez-Andujar et al., 2013), cardiac toxicity (Zhang et al., 2011), and other endpoints in utero exposures. When treating patients with implanted electronic devices, such as defibrillators and pacemakers, the dose to the device must be carefully tracked and kept below 2 Gy for pacemakers and only 1 Gy for defibrillators (Marbach et al., 1994) in order to avoid device malfunction. Additionally, this model could find applicability in large-scale radiation epidemiology studies where calculation speed and dosimetric accuracy are both important considerations.

For dose and risk reconstructions, knowledge of uncertainties is of paramount importance (Travis et al., 2011). With this in mind, it should be noted that use of the model for specific applications should be accompanied by an appropriate validation to ensure that the uncertainties in the model predictions meet the requirements of the application. For example, higher accuracy might be required for a prospective dose estimation to inform clinical decision making, such as for a pregnant radiotherapy patient or a patient with an implanted electronic device, than for a retrospective analysis of thousands of patients to develop or refine risk models for radiation late effects. The purposes of this study were simply to develop and demonstrate the potential of such a physics-based model.

Our findings are in good agreement with previous out-of-field dose studies in the literature. In the most directly comparable studies Zhang et al. (2011) and Taddei et al. (2013) fit measured total absorbed dose with a double-Gaussian function. This double Gaussian was used to calculate the total absorbed dose near to and outside of the treatment field, while in this work the double-Gaussian term represents only the dose deposited by phantom-scattered photons. However, the qualitative finding of both Zhang et al. and Taddei et al., that the out-of-field absorbed dose could be accurately modeled by a simple analytic model consisting of a combination of Gaussians, is in good agreement with this work. Additionally, Taddei et al. reported absolute RMS deviations between model calculated and measured dose values of 0.91 cGy/Gy and 1.67 cGy/Gy in the two clinics studied which is comparable to the 1.04 cGy/Gy absolute RMS deviation found in this study. While the accuracy is comparable, the model proposed by this work is physics-based and mathematically represents specific treatment head components which provides the framework to be more readily adapted to different treatment machines than that proposed by both Taddei et al. and Zhang et al.

Chofor et al. (2012) used a double exponential to model the internal scatter, or “phantom-scatter,” component of dose. Comparison of the model proposed by Chofor et al. to the model for absorbed dose from the phantom-scatter virtual source in this work, both calculated for a 5×5 cm² treatment field in water, revealed an average dose difference of only 0.15 mGy/Gy. In this same publication, Chofor et al. also estimated a constant combined head-scatter and leakage magnitude of 0.3% for a 5×5 cm² field. In our work, the average combined magnitude of calculated absorbed dose from head-scatter and leakage radiation for a 5×5 cm² field was 0.5%, which is in good agreement. Qualitatively, both models used simple analytical formulas to predict absorbed dose outside of the treatment field. However, our results suggest that the double-Gaussian function approach for internal scatter is physically more realistic as the double-exponential has a singularity at zero distance.

In 1995, the American Association of Physicists in Medicine (AAPM) published the report of Task Group 36 on techniques to estimate and reduce fetal dose from radiotherapy (Stovall et al.). This report included an appendix presenting out-of-field dose measurements for a range of photon beam energies and depths in the phantom. Figure 8 plots data from Stovall et al. along with measured and calculated dose values for the same field size from this work. Error bars for measured data from Kaderka et al. (2012) represent one standard deviation as reported in their study. Error bars for Stovall et al. (1995) represent one standard deviation estimated based on subsequently published uncertainty in out-of-field TLD measurements for a 6 MV photon beam (Kry et al., 2007). From this figure it can be seen that all of the profiles are in reasonably good agreement. However, in the near-field region, doses reported by Stovall et al. were consistently larger than ours, possibly due to changes in linac designs over the last two decades.

In a directly comparable study, Craig et al. (2008) compared computation times for multiple Monte Carlo dose calculation methods on a water equivalent phantom for a 5×5 cm², 6 MV treatment field. Of available methods, Monte Carlo dose models provide the most comparable physical realism and dosimetric accuracy to the model proposed in this work. However, Monte Carlo computation times reported for 10 million dose points were ≥12.3 minutes, or approximately three times slower. In our study, no attempt was made to optimize the code for execution speed and calculations were done in a spreadsheet using a 1.8 GHz processor. This provides promising evidence of the potential timing advantages of using a model like the one proposed in this work.

This study had several notable strengths. First, it is the first to report a complete, physics-based analytical model to calculate the total dose both inside and outside of the treatment field from external beam photon radiation treatments. Second, due to the physics-based approach, the model is inherently more readily adaptable to a wide variety of treatment units and treatment techniques than models based on empirical formulae or machine specific lookup-tables. We do not know at this time the minimum amount of training data that will ultimately be required to commission this model for use with different treatment units. Given the good level of agreement achieved in this work, we believe that the minimum amount of training data is probably significantly less than used here, however, we have not yet performed this test. Third, this model was trained using absorbed dose measurements for contemporary radiotherapy treatment units. The majority of previously available models were developed for equipment that is obsolete and the validity of the application of such models to modern linacs is unclear. Finally, this work provides promising evidence that it will be feasible to accurately and quickly reconstruct whole body dose distributions from 6 MV photon therapy. The methods appear well suited for integration into clinical TPSs.

One limitation of our study is that training data measured at our facility was measured using a farmer-type ion chamber. The large volume of this chamber leads to dose averaging in regions of steep dose gradient. This affects the locations of the mean and magnitude of the width parameter for the Gaussian functions used to model the un-collimated source of photon fluence. This was not a serious limitation because of the inclusion of empirical adjustment parameters determined in the later stages of model development from small-volume chamber measurements. Additionally, there was one profile that was measured in water using the farmer-type ion chamber. In addition to the farmer chamber’s larger dimensions and lower spatial resolution, Chauvenet’s criterion revealed that the model agreement with this field was an outlier compared to the agreement to all other fields studied and justified its exclusion from the final analysis.

Another minor limitation was that individual dose components were optimized independently using only total dose measurements. This made it difficult to differentiate between the different components of the total absorbed dose, especially in the near field region where multiple sources of stray dose are important. While this limitation introduced uncertainty in each independently calculated component of dose, empirically found adjustment parameters remained small and the summation of all components reasonably predicts total absorbed dose in water. Thus, the accuracy of this partitioning did not significantly hinder the accuracy of the total absorbed dose model. Furthermore, the use of separate measurements made in air and water aided in minimizing these issues.

Additionally, only calculation of dose to a homogeneous water phantom was explored here. This was done in order to develop and calibrate the basic physics of the model before applying it to human anatomy. We believe the application of the model to calculate dose in irregular and inhomogeneous tissues would be straightforward when integrated into an existing TPS or similar stand-alone program.

Finally, the model, as currently developed, does not apply to IMRT, which is a widely used treatment modality today. However, we believe that the model can be extended using methods similar to those employed by monitor unit and shielding calculations for IMRT [see for example (NCRP, 2005) and (Gibbons et al., 2014)]. Such an approach would only require knowledge of IMRT fluence factors, monitor unit ratios, and/or other treatment delivery data that are readily available.

This work demonstrated that it is possible to calculate the absorbed dose, both inside and outside of a conventional treatment field of 6 MV photons, using a physics-based analytical model. This work provided specific results which suggest the use of models, such as the one developed in this project, can predict dose values with better accuracy in the out-of-field region than current TPS methods. This was demonstrated by an average RMS local percent deviation of 7.8% which is significantly lower than is achievable with the use of contemporary treatment planning systems. Thus, we conclude that, with additional development, analytical modeling of the total absorbed dose is a viable method of routinely determining the dose delivered to the whole body from photon radiotherapy.

Table 4.

Parameters to model the absorbed dose from un-attenuated leakage photon fluence.

Symbol	Description	In-Plane	Cross-Plane	Source
αPC,σ	Adjustment parameter for source width for the leakage fluence attenuated by the primary collimator	0.87	4.13	This Worka
q	Divergence factor for the leakage photon fluence	1.58	1.11	“
αSC	Adjustment factor to the μt of the secondary collimator	1.46	1.85	“
αPC	Adjustment factor to the μt of the primary collimator	0.32	0.28	“
SIDPC	Distance from the focus of the primary collimator cone to isocenter (cm)	112		“
αSID	Adjustment factor for the SIDPC in each plane	1.09	0.87	“
μSC	Linear attenuation coefficient of the secondary collimator (1/cm)	0.77	0.58	(NCRP, 2005)
tSC	Secondary collimator thickness (cm)	7.8	11.2	Personal Communication, Elekta, Stockholm, Sweden
μwSC	Effective attenuation of the primary collimator	0.64		(NCRP, 2005), Personal Communication, Elekta, Stockholm, Sweden
x̄PC	Projected location of the primary collimator in the isocentric plane (cm)	25		Personal Communication, Elekta, Stockholm, Sweden

^aFrom iterative fitting procedure

Table 5.

Parameters to model the absorbed dose from head-scattered photons.

Symbol	Description	In-Plane	Cross-Plane	Source
κHS, FA	Constant of proportionality for the head-scatter Gaussian (mGy · Gy−1 · mm−2·1/u)	4.66 × 106	4.15 × 107	This Worka
u	Exponent defining power law relationship between the amplitude and field area	3.59	2.62	“
s	Divergence factor for head-scattered absorbed dose	2.07	2.55	“
κHS, σ	Constant of proportionality for the head-scatter Gaussian width parameter (mm · mm−1/ν)	0.72	1.2	“
αHS	Adjustment parameter for the μt of water for head-scattered absorbed dose	1.12	2.79	“
FAmax	Cut-off field area defined in the isocentric plane (cm2)	301		“
SFFD	Effective-source-to-flattening-filter-distance (cm)	17		(Elekta, 2007)

^aFrom iterative fitting procedure