An Implantable RF Solenoid for Magnetic Resonance Microscopy and Microspectroscopy

Abstract

Miniature solenoids routinely enhance small volume nuclear magnetic resonance imaging and spectroscopy; however, no such techniques exist for patients. We present an implantable microcoil for diverse clinical applications, with a microliter coil volume. The design is loosely based on implantable depth electrodes, in which a flexible tube serves as the substrate, and a metal stylet is inserted into the tube during implantation. The goal is to provide enhanced signal-to-noise ratio (SNR) of structures that are not easily accessed by surface coils. The first-generation prototype was designed for implantation up to 2 cm, and provided initial proof-of-concept for microscopy. Subsequently, we optimized the design to minimize the influence of lead inductances, and to thereby double the length of the implantable depth (4 cm). The second-generation design represents an estimated SNR improvement of over 30% as compared to the original design when extended to 4 cm. Impedance measurements indicate that the device is stable for up to 24 h in body temperature saline. We evaluated the SNR and MR-related heating of the device at 3T. The implantable microcoil can differentiate fat and water peaks, and resolve submillimeter features.

I. Introduction

SMALL volume spectroscopy and single-cell imaging have been achieved through the use of microcoils in nuclear magnetic resonance (NMR) [1]–[6]. The NMR microcoils are typically wound around glass capillaries mounted on silicon substrates and, therefore, cannot be implanted in patients. The sensitivity of microcoils increases as the solenoid diameter is reduced [4], making the microcoil especially suitable for small bioimaging probes. However, miniature solenoids intended for implantation have been limited to glass substrates [7].

Our development of the MR microcoil was motivated by an opportunity for enhancing signal-to-noise ratio (SNR) for MR techniques by designing an MR coil for future integration with intracranial depth electrodes for temporal lobe epilepsy (Fig. 1). Those suffering from epilepsy often have only subtle structural abnormalities in their brains, while the changes seen in the available animal models are typically severe [8]. Histopathology of resected tissue correlates highly with surgical outcome [9]–[12], in particular cell loss in the hippocampal subregion CA1 [13]. The difficulty of acquiring submillimeter resolution data in vivo has limited the extent to which these findings have been used for treatment planning.

Fig. 1.

Target applications of MR microcoils include integration with neural depth electrodes, and intraductal use for breast oncology.

A future device that combines the single- and multiunit neural recordings of microwires with similar spatial scale MRI and microliter magnetic resonance spectroscopy (MRS) may contribute to an increased understanding of the underlying mechanisms of recurrent-seizure disorders. By correlating epileptogenic and ictal waveforms with morphological and metabolic changes on the submillimeter scale, our device may ultimately prove useful for treatment development and planning. The targeted hippocampus is a well-studied brain region dominated by unidirectional, closed-loop networks. As such, the hippocampus is an attractive model for exploring neural processes and networks through submillimeter resolution funtional MRI data correlated with the microwire electrical recordings.

The enhanced SNR per-unit-volume of an implantable micro-coil may also provide a means of exploiting MRS techniques for early detection of breast cancer. MRS can distinguish between benign and malignant breast tissue with both specificity and sensitivity exceeding 80% [14]. However, the clinical utility of MRS is limited by the general need for large voxel sizes [15]. More than 95% of breast cancers originate in the mammary ducts [16]. Therefore, a miniaturized coil inserted into the ducts may prove useful for evaluating early-stage lesions on the order of a cubic millimeter (Fig. 1). As core biopsies confound dynamic contrast enhanced (DCE) MRI, an implantable microcoil may provide a novel method to assess malignancy that is more compatible with continued DCE-MRI.

Several factors must be considered in adapting the NMR microcoil design to an implantable catheter. Foremost is the challenge of creating a nontoxic device that is stable in the harsh environment of the body. The lead length for an implantable coil may easily exceed those of the ex vivo NMR counterpart by two orders of magnitude. In order to minimize tissue damage, the outer diameter and rigidity of the probe must be constrained. Consequently, low resistance leads and the use of capacitors inside the probe become less feasible. Combining an MR microcoil with other devices, such as mammary ductoscopes, may facilitate identification of target tissue samples. Similarly, integration of a microcoil with a neural depth electrode will allow increased information to be obtained without increasing the invasiveness of the procedure. MR compatibility and MR-related heating of the probe and supplementary devices must also be evaluated.

Our catheter coil is a small solenoid at the tip of a flexible catheter. The probe is optimized for implantation perpendicular to the axis of the body, which is the optimal orientation for targeting the hippocampus as well as lesions within mammary ducts (see Fig. 1). We have limited the outer diameter of the probe to less than 2 mm, and set a desired implantation depth of 4 cm based on likely clinical targets. Thus far we have fabricated and tested two generations of implantable microcoils for use with 3-T MR systems. Our goal for the first-generation prototype was to fabricate a device within the diameter constraints, and to provide proof-of-concept for microscopic imaging, which we did in collaboration with a group experienced with small-volume coils. For the second-generation device, we redesigned the coil and leads to meet the target total length of 4.5 cm. We assessed stability of the second-generation device in body temperature saline, and evaluated the MR-related heating. We compared estimated SNR to experimental values, demonstrated the proof-of-concept for microspectroscopy, and tested the ability of the probe to resolve features just beyond the tip of the solenoid.

II. Theory

Grover provide a semiempirical method for calculating the inductance of a single-layer solenoid [17]. The inductance of an equivalent uniform current sheet with diameter d_coil and length l_coil is adapted to the finite turns by correction factors (J and K):

$$L_{\text{coil}}=\frac{9850·n^2·d_{\text{coil}}}{4.5+10(l_{\text{coil}}/d_{\text{coil}})}-628·d_{\text{coil}}·n(J+K)[nH].$$ (1)

The correction factors are derived experimentally. For a coil with two to ten turns, the correction factor K can be estimated as 0.2 (or for more precise values see [18]). The value of J is a function of wire diameter d_wire and turn spacing s:

$$J=2.33·log\left(\frac{d_{\text{wire}}}{s}\right)+\mathrm{0.515.}$$ (2)

The resistance of a straight wire R_s with length equal to that of the coil can be derived from the dc resistance and the skin depth. A proportionality constant relating the coil resistance R_coil to R_s can be estimated from the work of Butterworth [19], and tailored to solenoids with few turns by the work of Medhurst [20]. Please see [18] for a complete table, and summary of proximity factors before and after the Medhurst correction.

The straight wire model commonly used to estimate the impedance of NMR microcoil leads does not apply to our microcoil because the lead lengths are no longer two orders of magnitude less than the wavelength. Therefore, we estimated lead impedances from a two-wire transmission line model. For the twisted-pair leads, the diameter of the insulated wire defines the conductor spacing.

The signal is proportional to the induced transverse magnetic flux density for a unit of current B_xy, while the noise is proportional to the square root of the system resistance [21]. Therefore, $B_{xy}/\sqrt{R_{\text{coil}}}\text{mT}·A^{-1}·{\mathrm{\Omega }}^{-0.5}$ is a useful metric for comparing coil designs. For a microcoil, the coil resistance dominates whether or not the sample is conductive [22]. The estimate of B_xy inside a coil with many turns provides an upper bound and has been used frequently for solenoids [21], [23]–[25]:

$$B_{xy}=\frac{n·{\mu }_0}{\sqrt{d_{\text{coil}}^2+l_{\text{coil}}^2}}.$$ (3)

We calculated the SNR in the center of the solenoid after a 90° pulse [21]. Given our interest in the SNR per voxel in the imaging domain, we set the bandwidth to that of a voxel, and did not transform the calculation to fit the Lorentzian of the spectrum (final step by Hoult and Richards). We account for the system preamplifier noise in the calculation by converting the noise figure into an equivalent temperature [26], and adding this to the coil temperature (289 K) [25].

For the second-generation coil, we estimated the transverse magnetic flux density as a function of position by integrating the off-axis fields for a given loop [27], over the number of loops (see the Appendix).

III. Prototypes

We wound all coils by hand on 1-mm-diameter medical-grade silicone tubing (806400 A-M Systems, Inc. Carlsborg, WA). A key component of the fabrication process is a metal stylet (800-μm diameter) set in an alligator clip stand. The stylet maintains the tubing diameter and allows rotation of the tubing during winding. The stylet also provides sufficient rigidity during future implantation. Turn spacing was defined by the wire insulation. Winding was done under magnification to ensure coil uniformity and turn proximity.

The first-generation coils were wound in accordance with Hoult and Richards [21], with three wire radii between the centers of adjacent turns (see Fig. 2), and a wire diameter (100 μm) corresponding to a tenth of the coil diameter (1mm) [28]. We coated 38-gauge copper wire (8085 Belden, Richmond, IN) with 25 μm of Parylene C (plasma deposition). The number of turns (4.5) was empirically determined such that the self-resonant frequency of the coil was three times that of the operating frequency, to ensure that the inductive current exceeded the capacitive current by an order of magnitude. We limited the lead length to 2.5 cm to minimize influence of the lead impedance. One of the leads was threaded through the lumen of the silicone tube before winding, and the other was glued to the outside of the tube with cyanoacrylate. The spacing between the leads was approximately 0.5 mm.

Fig. 2.

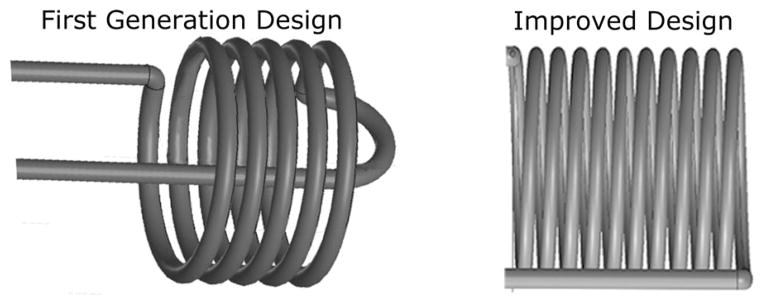
Solenoids of the two designs. First-generation device optimizes solenoid, while the solenoid for second generation aims at minimizing influence of leads. Insulators and leads are not shown.

We modified the second-generation microcoil in order to reach the target probe length of 4.5 cm (see Fig. 2). With an estimated lead inductance of 20 nH, we selected a 9.5 turn coil with 40-nH inductance. We explored several different twisted-lead configurations. Although characterization of leads alone confirmed the reduced resistance of Litz wire, the results for leads with a microcoil favored single-stranded wire configurations. We increased the wire diameter from 38 to 36 AWG to reduce the contribution of lead resistance. We did not add any additional insulation to the wire (8058 Belden, Richmond, IN), resulting in a turn spacing of 2.3 wire radii. To minimize dielectric losses, we explored numerous biocompatible materials [e.g., polyurethane, epoxy, cyanoacrylate, silicone, and polydimethyl-siloxane (PDMS)]. We achieved a stable resistance by insulating the probe with heat shrink tubing, and further improved performance by sealing the interface between the concentric tubing layers with PDMS. Twisted leads were wound by securing the leads in a pin vise and rolling the vise on a flat surface. The twisted portion accounts for 39.7 mm, and 2 × 5 mm straight leads connect the twisted leads to the tuning and matching circuit.

The tuning and matching circuit was connected to the solenoid via the microcoil leads. Capacitors were soldered directly to the microcoil probes, because we found that the use of circuit boards for component mounting resulted in too much added capacitance. Through bench top measurements, we concluded that balanced matching schemes and baluns were not critical in this implementation.

For the first-generation device, we used parallel-tuning and series-matching capacitors (ATC100B, American Technical Ceramics, Huntington Station, NY), and a nonmagnetic variable capacitor (5241, Johanson RF Division, Boonton, NJ) parallel to the tuning capacitor C_V. As small changes in either capacitor affect both tuning and matching, we switched to a series capacitor for tuning (9402-6, Johanson Manufacturing, Boonton, NJ) and a parallel inductance for matching the second-generation coil (see Fig. 3). The inductive matching was accomplished with a looped strip of brass foil (≈18 nH). Brass was chosen over copper in order to facilitate soldering. We configured the microcoil as a transceiver, using a simple duplexer with crossed hot-carrier diodes (see Fig. 4). We used 20-dB transmit attenuation, and an amplifier with 28-dB gain and a noise factor of less than 0.3dB (123GNST, Angle Linear, Lomita, CA).

Fig. 3.

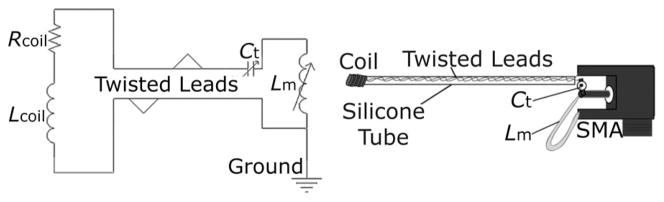
Mechanical drawing and schematic of second-generation microcoil, with series tuning capacitor Ct and parallel matching inductor Lm integrated on a small connector (SMA).

Fig. 4.

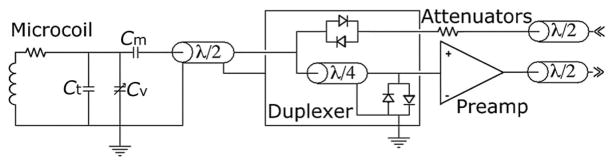
Transciever microcoil schematic as used in the first-generation tuning and matching circuit.

We characterized coils with a network analyzer (calibrated for open, short, load, and port extension). The Q of the tuned and matched coil was evaluated from the −7-dB bandwidth Q₇ dB of the reflection scattering parameter S₁₁ [26].

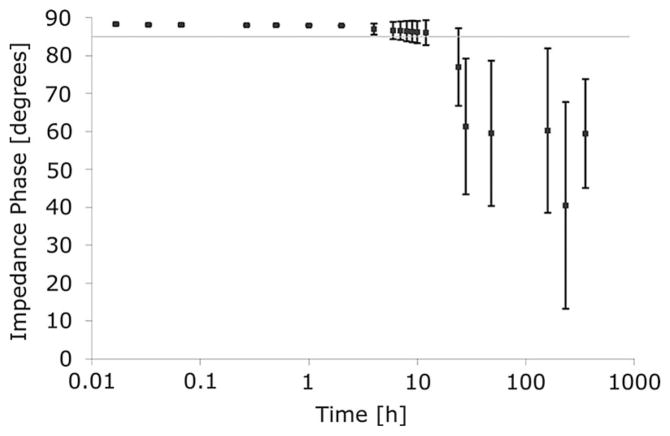
The second-generation microcoils underwent a 2-week-long heated (37 °C) soak test. Five microcoils were immersed in vials containing 0.9% saline solution by weight (see Fig. 5). We define the end of the usable time period as the last time point in which the phase is within 5% of 90° (85.5%).

Fig. 5.

Second-generation devices prepared for soak testing. Additional heat-shrink, and teflon tape protect components from condensation.

IV. Magnetic Resonance Experiments

A. MR-Related Heating

As no heating was observed when the microcoil was used as a transceiver, we investigated the risk of MR-related heating of the microcoil using the body coil for excitation. Temperature measurements were taken with a fluroptic temperature probe (Lumasense, Santa Clarita, CA). The temperature probe was lined up along the length of the microcoil and held in place with two small bands. The microcoil and temperature probe complex were inserted into a vial containing 40 mL of poly-acrylic acid (5.85 g/L). Baseline temperature values were averaged from 20 s of data prior to each scan. A steady-state free precession sequence (TR/TE: 3.37/1.69 ms) with a flip angle of 40° and with a calculated SAR of 1.9 W/kg, was run for 60 s. We conducted two trials with the microcoil alone, and one with the microcoil connected to a half-wave coaxial cable.

B. First Generation

As a proof of principle, we performed MR microscopy, collecting proton images at 3 T (Magnetom Allegra, Siemens AG, Erlangen) of butcher-grade neural tissue (Ovis aries). Covering the tissue with plastic-wrap prevented desiccation of the sample. The duplexer, attenuators, and preamplifier contained components with nickel adhesion layers, all were anchored λ/2 away from the magnet isocenter. Transverse images were obtained using a turbo spin-echo imaging sequence: 256 × 256 image matrix; 100-μm in-plane resolution; 0.4-mm slice thickness; TR/TE of 3000/22 ms; 7 echos; an acquisition time of 0:05:29 (h:min:s); 3 averages; 15 slices; fat saturation; and a pixel bandwidth of 130 Hz. We also collected images with a GRE sequence: 1024 × 640 image matrix; 22-μm in-plane resolution; 170-μm slice thickness; TR/TE of 123/48 ms; an acquisition time of 3:56:10; 6 averages; 1 slab with 30 slices; fat saturation; and a pixel bandwidth of 19 Hz.

C. Second Generation

For the second-generation microcoil, we characterized the SNR, obtained spectra, and imaged submillimeter diameter features. We used a different scanner for the second-generation device, a 2.89 T (123.2MHz) scanner (Tim Trio, Siemens AG, Berlin, Germany).

We assessed the SNR in a uniform spin-density phantom (5 mM CuSO₄ and 15.4 mM NaCl, T2 = 0.350 s) with a spin-echo pulse sequence (TR/TE: 500/30 ms), 90° flip angle, 130-Hz/pixel bandwidth, 31-mm field of view, 256 × 256 matrix, 9 slices each 0.8 mm thick, resulting in a total scan time of 132 s. We collected a pair of identical images and calculated the SNR according to method 1 described in [29]. The same phantom was used to assess the field of view, using a T1-weighted 3-D MPRAGE pulse sequence (TR/TE/TI: 1520/4.7/1100 ms), 15° flip angle, 210-Hz/pixel bandwidth, 51 ×75 mm field of view, 176 ×256 image matrix, 32 slices of 0.6 mm thickness, with an acquisition time of 5 min. Spectra of the copper(II)sulfate phantom and of mayonnaise (15% moisture) were acquired from the manual frequency adjustment window of the scanner. The microcoil obtained spectra from a 1.5-μL sample with a single acquisition using a 10-Hz STEAM 25-V transmit pulse.

We created a phantom to test the ability of a microcoil to resolve submillimeter features located at its tip. Three glass capillary tubes (400-μm outer diameter) were bundled together with heat shrink tubing that extended beyond the capillary tubes. The microcoil fit snugly inside the tubing, such that the capillary bundle was held in place at the tip of the microcoil. Two of the three silica tubes were filled with an Mn²⁺ solution, and a small amount of the solution was contained by the outer tubing in between the probe and the capillary tubes. The phantom was imaged with a spin echo pulse sequence (TR/TE: 300/50 ms), 130-Hz/pixel bandwidth, 31 ×31 mm field of view, 256 ×256 image matrix, 9 slices of 0.8 mm thickness, 3 averages, and an acquisition time of 132 s.

V. Results

Impedance calculations for the designs appear in Table I. We limited the length of the first-generation device to 2.5 cm, such that the lead inductance was approximately equal to that of the coil. For the second-generation design, we were able to reach the target probe length of 4.5 cm by increasing the coil inductance and twisting the leads. Despite the increased length, the lead inductance of the improved design was less than half that of the solenoid inductance.

TABLE I.

Estimates of Coil and Total Probe Impedances for the First and Second Generation Designs. For Better Comparison Between Designs, Estimates also Included for First Generation Design Extended 4.5 cm

Design	Lcoil	Lleads	Lleads/Ltotal	Rcoil	Rtotal
1st 2.5 cm	18.6 nH	22.7 nH	0.55	0.28 Ω	0.74 Ω
1st 4.5 cm	18.6 nH	48.6 nH	0.72	0.28 Ω	1.14 Ω
2nd 4.5 cm	51.6 nH	20.0 nH	0.28	0.79 Ω	1.6 Ω

The second-generation design meets our target length criteria, and its estimated performance exceeds that of the original design. The $B_{xy}/\sqrt{R_{\text{total}}}$ gives an estimated SNR improvement of 10% over that of the original 2.5-cm design (5.7 mT·A⁻¹ · Ω ^−0.5 versus 5.2 mT·A⁻¹ · Ω ^−0.5 in the center of the solenoid). However, as compared to the original design extended to 4.5 cm, the second-generation design provides a 34% SNR improvement.

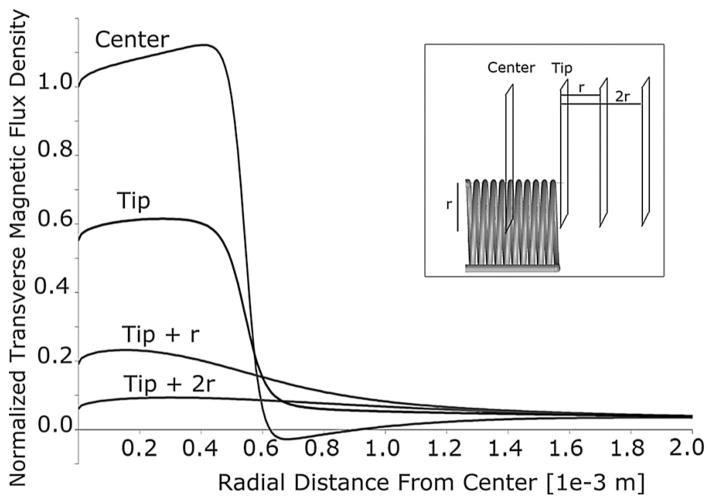
The performance of the second-generation coil as a function of position can be inferred from plots of the transverse magnetic flux density (see Fig. 6). At the tip of the probe (0.8 mm from the center of the solenoid), the magnetic flux density is homogeneous across the width of the solenoid and over 50% of that in the central region.

Fig. 6.

Transverse magnetic flux density of the second-generation coil with respect to distance from the coil axis, including traces from different positions along the axis (center, tip, one radius beyond the tip, and two radii beyond the tip). All values are normalized by the transverse magnetic flux density at the center of the coil (on-axis).

Based on the measured coil impedance, we selected a 28-pF capacitor for tuning the first-generation coils. However, an additional 3.7 pF was required for tuning, indicating 7 nH of stray inductance. For the second-generation device, we estimated 24.2 pF for tuning in air based on the theoretical and measured inductance values. The measured value of 21.7 pF gives an estimated stray capacitance of 2.5 pF.

Table II provides theoretical and measured Q values, including the ratio of unloaded to loaded Q (QRatio). The Q values of the first-generation devices are in agreement with the Q estimated from the total reactance, regardless of the measurement method. For the second-generation devices, the Q derived from measured impedance is in agreement with that of the total reactance, while that for the tuned and matched coil (Q_{7 dB} ) corresponds to the Q estimated from the solenoid reactance. This suggests that the twisting serves the intended purpose of canceling the magnetic-flux contribution of the leads. The loaded to unloaded Q values exceed the typical 10% degradation of loaded Q expected for microcoils, because the entire probe is immersed in a conductive solution.

TABLE II.

Theoretical Q Values From Estimated Impedances Agree with Experimental Ratios of Reactance to Resistance. Measured Q for First Generation Design Matches Estimate Q That Includes Lead Inductance, Whereas for the Second Design, Measured Q is not Dominated by Lead Inductances. Ratio of Unloaded to Loaded Q Appears in Last Column

Design	Theoretical		Experimental
	wLcoil/R	wLtotal/R	wL/R	Q−7dB	Q Ratio
1st	18.9	44.7	43	43	1.16
2nd	25	34.5	33.5	25	1.14

The second-generation microcoil (with twisted-pair leads) is sufficiently stable for in vivo use. Drift of the resistance, as characterized by the sample mean, begins after approximately 4 h of soaking in body temperature saline. Of the five probes tested, four remained stable for 12 h, while two of those four were stable for 24 h. After 2 days, one of the five probes still had a resistance less than 6 Ω. Impedance phases of microcoils during soak tests indicate feasible use within 4 h of implantation for each probe tested, and a mean of 20 h (see Fig. 7).

Fig. 7.

Phase of the impedance during the soak test averaged for five probes. Error bars ± 1 standard deviation. Feasible period of use defined by a phase within 5% of ideal inductor phase, indicated by gray line.

The observed temperature changes for a tuned and matched microcoil were within the standard error of the fluoroptic temperature probes (0.1 °C). Heating of the microcoil due to coupling with the transmit pulse of the microcoil is, therefore, in-significant. However, connecting a half-wave length coaxial cable to the microcoil led to an excess of 10 °C in 30 s. The mean temperature change of the microcoil alone was 0.02 °C, with a standard deviation of 0.04 °C.

We provide two images from the first-generation microcoil with different resolutions and imaging parameters, including dramatically different imaging times. The ultrahigh spatial resolution of Fig. 8(a) (22-μm in-plane, 140-μm -thick slices) was acquired with a 4-h scan. In Fig. 8(a), the bright central signal corresponds to tissue inside the microcoil solenoid, with a diffuse cloud of signal suggesting the boundary of the sensitive region of the probe. The region of sensitivity is more apparent in Fig. 8(b), extending beyond the microcoil and approximating an ellipsoid with major and minor axes equal to 4 and 3 mm, respectively. Images with 100-μm in-plane resolution and 400-μm slice thickness were obtained in only 5min. When the microcoil was not inserted into the tissue sample, no signal was observed.

Fig. 8.

Image obtained of ex vivo neural tissue with the first-generation microcoil. (a) Turbo spin echo with 20-μm in-plane resolution in a 170-μm slice, acquired in 4h. (b) Gradient echo acquired in 5min, with 100-μm in-plane resolution and 400-μm-thick slices.

The maximum SNR of 215 is within 10% of the value calculated (232) from the measured resistance of the coil immersed in saline for 30 min. The field of view of the microcoil is an ellipsoid with a cross-sectional diameter of 3 mm and a length of 5 mm. Signal is visible inside the tube as well as outside of the coil, and a dark region corresponds to the dimensions of the tubing layers (see Fig. 10). Manipulation of the transmit voltage changes the region of dominant signal. The spectrum of the copper(II)sulfate phantom has only one peak, and is fairly symmetric (see Fig. 9). Spectra of 1.5 μL of mayonnaise contain fat and water peaks separated by 3.55 ppm (see Fig. 9). The microcoil resolved the submillimeter features at the tip of the solenoid (see Fig. 11).

Fig. 10.

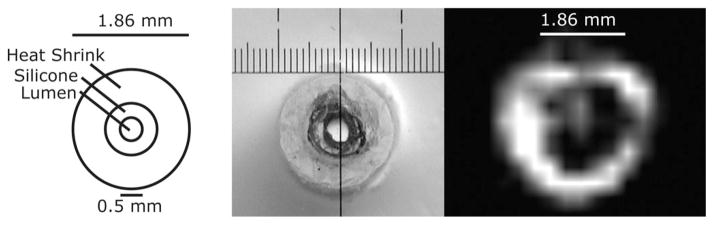
Dark void in the MRI (right) corresponds to the dimensions of the silicone and heat shrink tubing (seen in diagram and photograph).

Fig. 9.

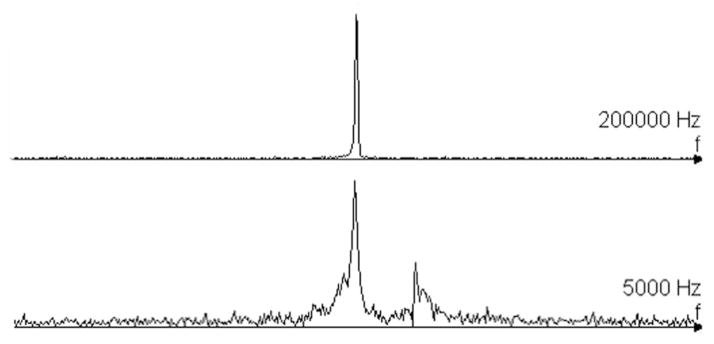
Unfiltered spectra from Copper(II)sulfate saline phantom, and micro-liter sample of mayonnise. Water and fat peak separated by 438 Hz.

Fig. 11.

Microcoil resolves two capillary tubes filled with manganese salt solution at the tip of the probe (0.8-mm along axis from center of solenoid). Two of the three capillary tubes are filled with the contrast agent. Presented image windowing allows visualization of small amounts of contrast solution contained by the heat shrink tubing. Spin echo (TR/TE: 300/50 ms), 0.8 mm thickness, 3 averages, and acquisition time of 132 s.

VI. Discussion

We presented a catheter-based small solenoid MR probe capable of resolving submillimeter features and the fat and water peaks of a microliter sample. The flexible device is implantable up to 4 cm, and stable in conductive liquids at body temperature.

Berry et al. present a solenoid (164-μm diameter) for implantation up to 1 cm [7]. Their device is wrapped on a brittle substrate of fused silica, and the interior of the solenoid is filled with cyanoacrylate. The device is capable of resolving fat and water peaks from a sample outside of the coil. The authors present spectra from nonconductive samples, and therefore, stability of the device in conductive samples is unknown. Baxan et al. have microfabricated planar coils for implantation up to 1 cm [30]. The presented design has a multiturn coil (500-μm diameter) at the end of 1-cm leads, and an estimated $B_{xy}/\sqrt{R_{\text{total}}}$ of less than 2 mT·A⁻¹ · Ω ^−0.5 at 4.7 T. The evaluated limits of detection approach those of ¹ H brain metabolites in rodents. The silicon substrate needles, thus, far remain fragile, and the lead resistances are dependent on the sample material.

Needle coils remain a current area of research. Syms et al. created single- and double-loop coils implantable up to 1.2 cm [31]. The coil is 1.2 cm long and 1 mm wide. The impedance of the device is close to that of our first-generation microcoil. The authors demonstrate robustness of the design, and present spectra from a small tomato with spectral SNR of 3.5 per acquisition at 1.5 T. In an improved design, a flexible photoresist material (SU-8) serves as substrate, encasing gold-plated copper traces [32]. The authors demonstrate ³¹ P spectra from the rat muscle at 4.7 T (implanting less than 1 cm), and speculate that the concentrations are similar to the relevant moieties for proton spectroscopy at 1.5 T for evaluating tumors. The coil loaded and unloaded Q values were identical, suggesting that the SU-8 block (cross section 1 × 1.5 mm² ) prevented proper sample loading. The large SU-8 block also caused considerable line broadening. In a related paper, Ahmad et al. present a multiloop planar coil made of SU-8 for integration with a bile duct endoscope [33]. The planar coils have a 2.8-mm width, which is appropriate for the 3.2-mm working channel of the endoscope. The device is capable of resolving 1-mm features at 1.5 T; however, no spectra are presented.

All of the materials used in our device are within 2 ppm of the magnetic susceptibility of water. The dark ring visible in Fig. 10 corresponds to the dimensions of the tubing, and we, therefore, attributed the lack of signal to a short T2 rather than a magnetic susceptibility artifact. However, we can improve the MRS performance by reducing the thickness of the silicone tube and the saline barrier layer. The spectral linewidth of NMR microcoils was reduced by Oslon et al. by surrounding the probe with a magnetic susceptibility matching fluid [3]. The microcoil is intended for use fully submerged in a sample. However, we collected images of the submillimeter features and the mayonnaise spectra with air in the coil field of view, which may have degraded the quality.

The soak tests of this study indicate that the microcoil is sufficiently stable for use. After roughly 12h the PDMS becomes saturated with water. The differences in probe stability may be caused by varying amounts of oils on the tubing prior to coating with PDMS. By using a primer to enhance adhesion, we may be able to improve on probe stability. Alternatively, we can reduce the outer diameter, and potentially lengthen the window of possible use with a silicone rubber known for providing a good moisture barrier (RTV 3140, Dow Corning, Midland, MI) encased in a biocompatible rubber [34].

The presented safety study indicates that there is a potential risk of the body coil coupling with the coaxial cable connected to the microcoil. In this first implementation, we were interested in the worst possible heating scenario. We will investigate possible safety features such as cable traps, with the intention of ensuring patient safety without dramatically decreasing the SNR performance of the device.

Fortunately, the inductance of single-layer solenoids was painstakingly studied in the early 20th century. We combine the resultant semiempirical methods with a two-wire transmission line model, to accurately bridge the diverse scales of the MR microcoil features accurately. Finite element modeling of the microcoil was attempted using commercially available software (HFSS, ANSYS, Canonsburg, PA). However, due to the large ranges of scale the computations exceeded available resources and capabilities of the software. A lack of radial symmetry prevents simplification.

The MR microcoil was devised to fill a technology gap in epilepsy research. The use of surgically implanted electrodes has led to great interest in two classes of electrophysiological waveforms, termed ripples (80 to 200 Hz) and fast ripples (250 to 500 Hz). Evidence suggests that epileptogenicity is correlated with an increase in the ratio of fast ripples to ripples [35]. Fast ripples are thought to originate from volumes on the order of cubic millimeters. Anatomical and metabolic changes associated with fast ripples have been identified in animal models [36], and recently in subregions of human hippocampus in a histological specimen [37]. Staba et al. use MRI to quantify changes in overall hippocampal volume because the technologies do not yet exist to examine structural changes in the subregions of interest [37].

We have investigated MR-related heating of microwire arrays, and modified them for reduced risk [38]. Preliminary tests suggest that the SNR of the microcoils was not detrimentally degraded by the presence of microwires in the lumen. The micro-coil could also be used to scout the target region before insertion of the microwires, as well as to examine damage done to tissue after implantation. The challenges of avoiding cross contamination of EEG and MR signals have been solved by those in the field [39]. Concurrent MR and depth electrode measurements have been conducted recently in patients [40]. Despite increasing evidence that depth electrodes can be combined safely with MR [41]–[43], there is a lack of commercially available MR-compatible electrodes for patients made of materials within the −7 to −11ppm range of tissue magnetic susceptibilities.

Although 25% of breast cancers are now diagnosed as ductal carcinoma in situ (DCIS), less than 1% are thought to progress into invasive cancers [44]. Mammography is more likely to identify DCIS associated with calcifications; however, evidence correlates a lack of calcification with less favorable prognosis [44]. Existing imaging methods for diagnosing DCIS suffer from poor sensitivity, including DCE MRI (40–89%), mammography (37–60%), and ultrasound (47%) [45]–[47]. Core needle biopsies erroneously diagnose invasive cancers as DCIS in approximately 15% of patients [44].

We aim to improve the sensitivity of MR techniques for small lesions, and thereby reduce the risk associated with breast conservation surgeries and treatments. Prior to use in humans, we will collaborate with a device manufacturer of MR compatible ductoscopes, and assess the risk of MR-related heating and performance of the combined device in saline and in ex vivo tissue. We are currently designing a noninvasive coil that can be used as a transceiver or in combination with the microcoil.

While we present research on a 1-mm-diameter microcoil for use at 3 T, the possible use of microcoils extend over a wide range of designs and field strengths. The enhanced SNR of microcoils may prove useful at any field strength. Microcoil diameter can be increased to provide larger fields of view, or decreased to interrogate smaller spectroscopic volumes. We are in the process of adapting the second-generation microcoil for use at 7 T. The presented circuit without any modifications had a tuning range of up to 210 MHz. If the microcoil does not require major modifications, ex vivo studies of human neural tissue will follow shortly thereafter.

Appendix

MATLAB code for generating off-axis values for the transverse magnetic flux density:

r = 6e-4 % coil radius [m]y = 0:1e-5:3e-3 % distance from axis [m]u0 = 4*pi*1e-7;N = 10; % number of turnsL = 1.31e-3; % coil length [m]x = 7e-4+r % axial distance from center [m]for i=1:1:N;d(i)=-L/2+L/(N-1)*(i-1) %; distance to loopa = (y./r);b = (x-d)(i))/r;Q = ((1+a). ^ 2+b^2);k = (4.*a./Q). ^ (.5)[K,E] = ellipke (k);B(i,:) = u0/(2*r).*(pi.*Q. ^.5). ^-1.*...(E.*(1-a. ^2-b^2)./(Q-4.*a)+KendB = sum(B (i))

For a, b, Q, k, and the formula for B see [27].