Emerging brain morphologies from axonal elongation

Abstract

Understanding the characteristic morphology of our brain remains a challenging, yet important task in human evolution, developmental biology, and neurosciences. Mathematical modeling shapes our understanding of cortical folding and provides functional relations between cortical wavelength, thickness, and stiffness. Yet, current mathematical models are phenomenologically isotropic and typically predict non-physiological, periodic folding patterns. Here we establish a mechanistic model for cortical folding, in which macroscopic changes in white matter volume are a natural consequence of microscopic axonal growth. To calibrate our model, we consult axon elongation experiments in chick sensory neurons. We demonstrate that a single parameter, the axonal growth rate, explains a wide variety of in vitro conditions including immediate axonal thinning and gradual thickness restoration. We embed our axonal growth model into a continuum model for brain development using axonal orientation distributions motivated by diffusion spectrum imaging. Our simulations suggest that white matter anisotropy - as an emergent property from directional axonal growth - intrinsically induces symmetry breaking, and predicts more physiological, less regular morphologies with regionally varying gyral wavelengths and sulcal depths. Mechanistic modeling of brain development could establish valuable relationships between brain connectivity, brain anatomy, and brain function.

1 Motivation

During the third trimester of gestation, our brain grows rapidly in surface area and begins to take on the characteristic wrinkled appearance of the adult human brain [29]. While the benefits of this folding, the increase in information processing capacity [27], are widely appreciated, the mechanism of how it arises is still under investigation [49]. Also unknown is the exact role that cortical folding plays in the function of the brain, although research has indicated that abnormal folding can be associated with mental and psychological problems including autism [34] and schizophrenia [45]. A deeper understanding of the process of cortical folding and its relationship to the workings of the healthy brain could lead to improved diagnostics, treatments, and interventions for folding abnormalities in the diseased brain.

While some folds, known as the primary gyri and sulci, are located fairly consistently across individuals of the same species, secondary and tertiary folds exhibit a more varied pattern [6]. The consistency of primary folding has been attributed to specific heterogeneities including spatial or temporal variations in growth [58]. The variation of secondary and tertiary folding is thought to be an instability phenomenon triggered by some form of stress in the developing brain [6]. During the later stages of development, when primary folds are already in place [23], the formation and loss of cortico-cortical connections may alter the cortical thickness and reshape existing folds, particularly in certain pathologies including autism [25] and schizophrenia [45].

One of the earliest theories of cortical folding posited the spatial constraint of the skull as the origin of this stress. Removing parts of the skull from fetal sheep disproved this idea [4]. The first purely mechanical theories of convolutional development attributed this stress to differential growth, either between the six cortical layers [42] or between the cortex and the underlying substrate [52]. While mechanically sound, this theory crucially relied on an unrealistically large stiffness contrast between gray and white matter and was therefore largely ignored by neurophysiologists. The second prominent theory suggested that axons, the main component in white matter tissue, cause stress and create folding by pulling functionally connected regions topologically closer together [55]. Yet, this concept failed to accurately predict residual stress patterns in the developing brain [58]. Despite these inconsistencies, the hypotheses of differential growth and axonal tension remain the most popular theories for cortical folding among biophysicists. Neurobiologists, however, consider almost exclusively gyrogenetic theories, which attribute folding to a regional variation in genetic control [41, 47, 56].

A recent improvement to the differential growth theory replaced substrate elasticity by isotropic, stress-driven subcortical growth and achieved more realistic residual stress patterns [5]. Isotropic growth, however, is only capable of producing regular sinusoidal folds, unlike the intricate and diverse folding patterns seen in the human brain [9]. In fact, white matter has a natural source of anisotropy, the axon, which suggests a transversely isotropic constitutive model with a pronounced response along the preferred axonal orientation [57].

Axons are neural processes that connect neuronal cell bodies and transmit information between them [44]. Surrounded by a thick dielectric layer, the myelin sheath, axons make up the majority of the white matter tissue in our brain. During early development, axons grow in length to form connections between different regions of the brain [29]. As those regions move closer together or further apart, axons experience what has been termed “towed growth”, growth or retraction to maintain a desired level of axonal tension [8, 14]. At this time, the axons are still unmyelinated - their myelin sheaths form later, after primary folding is completed.

Figure 1 illustrates the stretch and intercalation model of axonal growth [50]. Axons are made up of densely packed microtubules and neurofilaments surrounded by an actin cortex. Cross-linking proteins stabilize these microtubules and generate a homeostatic equilibrium state of axonal tension [20]. Chronic perturbations away from this equilibrium state activate mechanotransduction pathways including stretch-activated calcium channels to increase protein synthesis and transport along the axon [50]. Within a few hours, stretched axons add new material along their length to recover their initial thickness. The axonal growth rate, a critical parameter in white matter growth, is therefore limited by intracellular mass production and transport [36].

Fig. 1.

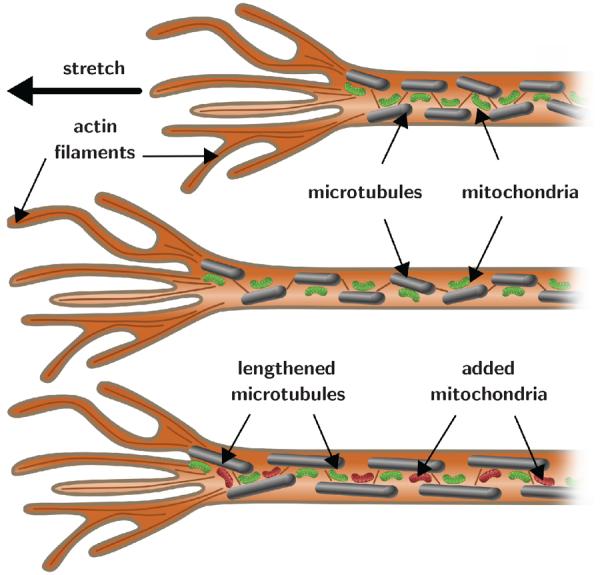
Stretch and intercalation model of axonal growth. Axons respond to overstretch through immediate lengthening and thinning. Overstretch and thinning activate mechanotransduction pathways, which trigger the creation of new material along the axon, and the axon gradually recovers its initial thickness. Intracellular mass production and transport are the rate limiting factors of axonal growth.

Here we hypothesize axonal growth plays a central role in modulating brain surface morphology. We test this hypothesis using a multiscale computational model of differential growth in which stretch-induced changes in axonal length on the microscopic scale translate into anisotropic white matter growth on the macroscopic scale. The axonal orientation, which varies throughout our brain, is an important feature of this model: it naturally induces symmetry breaking and creates physiological, irregular surface morphologies. Understanding the importance of axonal growth will shed light on the two competing theories of cortical folding, axonal tension and differential growth, and combine both mechanisms in a unified theory for gyrogenesis in the developing brain.

2 Methods

2.1 Continuum model of the growing brain

We model cortical folding using the nonlinear field theories of mechanics supplemented by the theory of finite growth [2]. To represent large deformations during brain development, we introduce the deformation map φ. At any given time t during brain development, φ maps physical particles X in the ungrown configuration onto particles x = φ (X, t) in the grown configuration. We adopt the concept of fictitious, incompatible configurations, and decompose the gradient of this mapping, F = $#x2207;_Xφ, into an elastic part F^e and a growth part F^g [43],

$$\mathit{F}={\nabla }_{\mathit{X}}\phi ={\mathit{F}}^{\mathrm{e}}\cdot {\mathit{F}}^{\mathrm{g}}.$$ (1)

The total change in tissue volume is defined by the Jacobian of the deformation gradient,

$$J=\text{det}\left(\mathit{F}\right)=J^{\mathrm{e}}{J}^{\mathrm{g}},$$ (2)

which we again decompose into an elastic volume change J^e = det (F^e) and volume growth J^g = det (F^g). For J^g ≠ 1, the growing brain acts like a thermodynamically open system with a non-constant mass, and the associated enhancements of the continuum equations apply [30]. Unlike the deformation gradient itself, neither the elastic tensor nor the growth tensor are gradients of a vector field. Instead, we prescribe the growth tensor constitutively and then determine the elastic tensor, F^e = F · F^g–1, accordingly. On the time scales of seconds, minutes, or hours, brain is a poroviscoelastic material [18]. On the time scales of days, weeks, or months relevant for brain development, we can approximate brain tissue as a growing elastic material [11]. We adopt a Neo-Hookean free energy function for both gray and white matter tissue,

$$\psi =\frac{1}{2}L{\ln }^2\left(J^{\mathrm{e}}\right)+\frac{1}{2}G\left[\mathrm{tr}\right(b^{\mathrm{e}})-3-2\ln (J^{\mathrm{e}}\left)\right],$$ (3)

with the Lamé constants L and G. We parameterize the free energy function exclusively in terms of the elastic left Cauchy Green tensor, b^e = F^e · F^et, and the elastic Jacobian J^e, assuming that only the elastic deformation generates stress. We obtain the Kirchhoff stress τ from the standard Coleman-Noll evaluation of the dissipation inequality in open system thermodynamics [33],

$$\tau =2\frac{\partial \psi }{\partial b^{\mathrm{e}}}\cdot b^{\mathrm{e}}=\left[L\ln \right(J^{\mathrm{e}})-G]I+G{b}^{\mathrm{e}},$$ (4)

where I denotes the second order unit tensor. It remains to specify the growth kinematics and growth kinetics for gray and white matter tissue.

Gray matter grows via neural progenitor division

The gray matter tissue of the cerebral cortex is mainly made up of neurons, which migrate to the surface of the brain along radial glial cells [56]. Unlike the cortical surface area, the cortical thickness is remarkably preserved across all mammals [27]. While the cortical thickness changes during the early stages of neurodevelopment [47], during the later stages, it is primarily the change in surface area that triggers cortical folding. We thus model gray matter growth as in-plane area growth and assume that the response normal to the cortical surface is purely elastic. The resulting gray matter growth tensor is transversely isotropic with a preferred direction n₀ normal to the cortical surface [60],

$${\mathit{F}}^{\mathrm{g}}=\sqrt{{\vartheta }^{\mathrm{g}}}I+[1-\sqrt{{\vartheta }^{\mathrm{g}}}]n_0\otimes n_0.$$ (5)

The gray matter growth parameter ϑ^g represents the increase in cortical surface area,

$${\vartheta }^{\mathrm{g}}=\Vert J^{\mathrm{g}}{\mathit{F}}^{g-t}\cdot n_0\Vert =\text{det}\left({\mathit{F}}^{\mathrm{g}}\right)=J^{\mathrm{g}},$$ (6)

which is identical to the increase in gray matter volume J^g. In gray matter, the multiplicative decomposition of the deformation gradient (1) translates into the multiplicative decomposition of the total cortical area change ϑ into an elastic area change ϑ^e and area growth ϑ^g,

$$\vartheta =\Vert J{\mathit{F}}^{-t}\cdot n_0\Vert ={\vartheta }^{\mathrm{e}}{\vartheta }^{\mathrm{g}}.$$ (7)

Because of its simple rank-one update structure, we can invert the growth tensor using the Sherman-Morrison formula,

$${\mathit{F}}^{\mathrm{g}-1}=\frac{1}{\sqrt{{\vartheta }^{\mathrm{g}}}}\mathit{I}+\frac{\sqrt{{\vartheta }^{\mathrm{g}}}-1}{\sqrt{{\vartheta }^{\mathrm{g}}}}{n}_0\otimes n_0.$$ (8)

We can then explicitly calculate the gray matter elastic tensor,

$${\mathit{F}}^{\mathrm{e}}=\frac{1}{\sqrt{{\vartheta }^{\mathrm{g}}}}\mathit{F}+\frac{\sqrt{{\vartheta }^{\mathrm{g}}}-1}{\sqrt{{\vartheta }^{\mathrm{g}}}}n\otimes n_0,$$ (9)

and its elastic left Cauchy Green deformation tensor,

$$b^{\mathrm{e}}=\frac{1}{{\vartheta }^{\mathrm{g}}}b+\left[1-\frac{1}{{\vartheta }^{\mathrm{g}}}\right]n\otimes n,$$ (10)

in terms of the grown cortical normal, n = F · n₀, and the total left Cauchy Green deformation tensor, b = F · F^t. We suggest a linear kinetic model for gray matter growth,

$${\stackrel{.}{\vartheta }}^{\mathrm{g}}=G^{\text{ctx}},$$ (11)

where G^ctx the cortical growth rate, which we can eventually correlate to several corticogenetic events: During the early stages of development, the increase of cortical volume is associated with the division of neural progenitor cells. Symmetric division is correlated to an increase in cortical surface area [49]; asymmetric division is correlated to an increase in cortical thickness [39]. During the later stages of development, tangential expansion is associated with the maturation of the neo-cortex caused by an increase of neurons in size, the formation of cortico-cortical connections, and the addition of intracortical glia cells [56].

White matter grows via chronic axonal elongation

The white matter tissue underneath the cerebral cortex consists largely of myelinated axons. Axons are capable of growing in length when exposed to chronic overstretch [8, 14]. We thus model white matter growth as fiber growth and assume that the response normal to the fiber direction is purely elastic. The resulting white matter growth tensor is transversely isotropic with a preferred direction a₀ along the axonal direction [59],

$${\mathit{F}}^{\mathrm{g}}=\mathit{I}+[{\lambda }^{\mathrm{g}}-1]a_0\otimes a_0.$$ (12)

The white matter growth parameter λ^g represents the increase in length of the axonal vector a^g = F^g · a₀,

$${\lambda }^{\mathrm{g}}=\Vert a^{\mathrm{g}}\Vert =\sqrt{a_0\cdot F^{\mathrm{gt}}\cdot F^{\mathrm{g}}\cdot a_0}=\text{det}\left(F^{\mathrm{g}}\right)=J^{\mathrm{g}},$$ (13)

which is identical to the increase in white matter volume J^g and thus directly correlated to the cumulative length of all axons in the white matter tissue. In white matter, the multiplicative decomposition of the deformation gradient (1) translates into the multiplicative decomposition of the total stretch along the axon λ into an elastic part λ^e and a growth part λ^g,

$$\lambda =\Vert a\Vert =\sqrt{a_0\cdot F^{\mathrm{t}}\cdot F\cdot a_0}={\lambda }^{\mathrm{e}}{\lambda }^g.$$ (14)

Again, we invert the growth tensor using the Sherman-Morrison formula,

$${\mathit{F}}^{\mathrm{g}-1}=\mathit{I}+\frac{1-{\lambda }^{\mathrm{g}}}{{\lambda }^{\mathrm{g}}}{\mathit{a}}_0\otimes {\mathit{a}}_0,$$ (15)

to explicitly calculate the white matter elastic tensor,

$${\mathit{F}}^{\mathrm{e}}=\mathit{F}+\frac{1-{\lambda }^{\mathrm{g}}}{{\lambda }^{\mathrm{g}}}\mathit{a}\otimes {\mathit{a}}_0,$$ (16)

and its elastic left Cauchy Green deformation tensor,

$${\mathit{b}}^{\mathrm{e}}=\mathit{b}+\frac{1-{\lambda }^{\mathrm{g}2}}{{\lambda }^{\mathrm{g}2}}\mathit{a}\otimes \mathit{a},$$ (17)

in terms of the current axonal vector, a = F · a₀. White matter growth is primarily a result of chronic axonal elongation upon prolonged overstretch [8]. This suggests the following ansatz,

$${\stackrel{.}{\lambda }}^{\mathrm{g}}=G^{\text{axn}}[{\lambda }^e-{\lambda }^0],$$ (18)

where G^axn is the rate of axonal growth. This implies that the increase in white matter volume is an emergent property from chronic axonal lengthening: when elastically stretched beyond the homeostatic baseline value of λ⁰, axons lengthen, when unstretched they shorten [14].

Figure 2 illustrates directional axonal elongation as a mechanism for anisotropic white matter growth. Table 1 summarizes the individual mechanisms and mathematical models for gray and white matter growth.

Fig. 2.

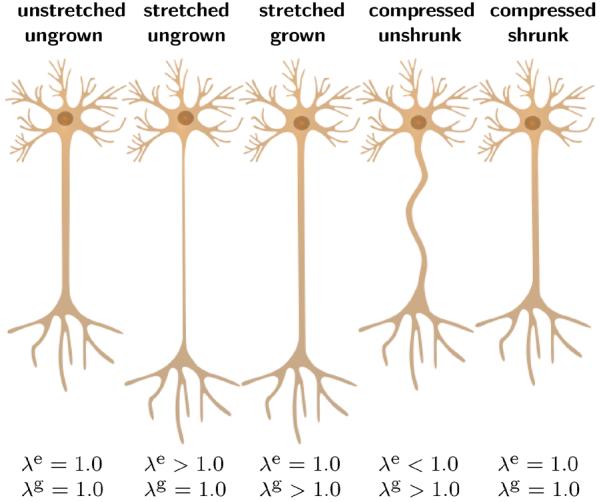
Axon at its unstretched, ungrown state of homeostatic equilibrium; at its stretched, ungrown state of acute thinning upon stretching; at its stretched, grown state having recovered its original diameter after growth; at its compressed, unshrunk state exhibiting slackening upon stretch release; and at its compressed, shrunk state having recovered its original diameter after negative growth; from left to right.

Table 1.

Gray and white matter growth. Underlying mechanisms and mathematical models.

	gray matter	white matter
microstructural mechanisms	cell division, cell growth, formation of connections	stretch-induced axonal growth
macrostructural effect	increase in surface area	increase in volume
kinematics	area growth ${\mathit{F}}^{\mathrm{g}}=\sqrt{{\vartheta }^{\mathrm{g}}}\mathit{I}+[1-\sqrt{{\vartheta }^{\mathrm{g}}}]{\mathit{n}}_0\otimes {\mathit{n}}_0$	fiber growth ${\mathit{F}}^{\mathrm{g}}=\mathit{I}+[{\lambda }^{\mathrm{g}}-1]{\mathit{a}}_0\otimes {\mathit{a}}_0$
kinetics	cortical area ${\stackrel{.}{\vartheta }}^{\mathrm{g}}=G^{\text{ctx}}$	axonal length ${\stackrel{.}{\lambda }}^{\mathrm{g}}=G^{\text{axn}}[{\lambda }^{\mathrm{e}}-{\lambda }^0]$
parameters	Gctx cortical growth rate n0 cortical normal	Gaxn axonal growth rate a0 axon orientation

2.2 Computational model of growth

To solve the governing equations of brain development, we implement the gray and white matter growth models as user-defined material subroutines in the nonlinear finite element program Abaqus/Standard [1]. To characterize brain development at each instant in time t, we introduce the number of cortical neurons ϑ^g and the axonal growth λ^g as internal variables in the gray and white matter regions. We solve their evolution equations (11) and (18) locally on the integration point level using a finite di erence approximation in terms of the current time increment Δt = t – t_n,

$${\stackrel{.}{\vartheta }}^{\mathrm{g}}=[{\vartheta }^{\mathrm{g}}-{\vartheta }_{\mathrm{n}}^{\mathrm{g}}]∕\Delta t\text{and}{\stackrel{.}{\lambda }}^{\mathrm{g}}=[{\lambda }^{\mathrm{g}}-{\lambda }_{\mathrm{n}}^{\mathrm{g}}]∕\Delta t.$$ (19)

Gray matter growth is linear in time. We update the cortical surface area using a simple single-step modification,

$${\vartheta }^{\mathrm{g}}\leftarrow {\vartheta }^{\mathrm{g}}+G^{\text{ctx}}t.$$ (20)

White matter growth depends nonlinearly on the axonal growth itself. We update axonal growth using an incremental iterative Newton Raphson scheme,

$${\lambda }^{\mathrm{g}}\leftarrow {\lambda }^{\mathrm{g}}-{\mathrm{R}}^{\lambda }∕{\mathrm{K}}^{\lambda },$$ (21)

where R^λ is the local residual,

$${\mathrm{R}}^{\lambda }={\lambda }^{\mathrm{g}}-{\lambda }_{\mathrm{n}}^{\mathrm{g}}-G^{\text{axn}}\left[\frac{\lambda }{{\lambda }^{\mathrm{g}}}-{\lambda }^0\right]\Delta t,$$ (22)

and K^λ is its linearization with respect to the axonal growth λ^g,

$${\mathrm{K}}^{\lambda }=\frac{{\mathrm{dR}}^{\lambda }}{\mathrm{d}{\lambda }^{\mathrm{g}}}=1+G^{\text{axn}}\frac{\lambda }{{\left({\lambda }^{\mathrm{g}}\right)}^2}\Delta t.$$ (23)

We iteratively update axonal growth (21) until we achieve convergence and the residual (22) falls below a user-defined threshold value. Once we have determined the current number of cortical neurons ϑ^g and axonal growth λ^g, we can successively calculate the growth tensors in gray and white matter F^g using equations (5) and (12), the elastic tensors F^e using equations (9) and (16), the left Cauchy Green deformation tensors b^e using equations (10) and (17), and the Kirchho stresses τ using equation (4).

For the global righthand side vector, the user-defined subroutine in Abaqus/Standard utilizes the Cauchy or true stress, σ = τ / J, for which we simply divide the Kirchho stress (4) by the Jacobian,

$${\sigma }^{\text{abaqus}}=\left[\right[L\text{ln}\left(J^{\mathrm{e}}\right)-G]\mathit{I}+G{\mathit{b}}^{\mathrm{e}}]∕J.$$ (24)

For the global iteration matrix, the user-defined subroutine in Abaqus/Standard utilizes the Jauman rate of the Kirchho stress divided by the Jacobian [60],

$${\mathbf{c}}^{\text{abaqus}}=[{\mathbf{c}}^{\mathrm{e}}+{\mathbf{c}}^{\mathrm{g}}+{\mathbf{c}}^{\tau }]∕J.$$ (25)

The first term, c^e = 4 b^e · [∂²ψ/∂b^e ⊗ ∂b^e] · b^e|_Fg, the elastic tangent, is the Hessian of the free energy function (3) at constant growth F^g,

$${\mathbf{c}}^{\mathrm{e}}=L\mathit{I}\otimes \mathit{I}+[G-L\text{ln}(J^{\mathrm{e}}\left)\right][\mathit{I}\overline{\otimes }\mathit{I}+[\mathit{I}\underset{¯}{\otimes }\mathit{I}].$$ (26)

The second term, c^g = 4 b^e · [∂²ψ/∂b^e ⊗ ∂b^e] · b^e|_F, the growth tangent, is the Hessian of the free energy function (3) at constant deformation F. Gray matter growth does not depend on deformation and its growth tangent vanishes identically, c^g = 0. White matter growth depends on deformation, and its tangent takes the following format [59],

$${\mathbf{c}}^{\mathrm{g}}=\frac{G^{\text{axn}}}{\lambda {\lambda }^{\mathrm{g}}{\mathrm{K}}^{\lambda }}[L\mathit{I}+\frac{2G}{{\left({\lambda }^{\mathrm{g}}\right)}^2}\mathit{a}\otimes \mathit{a}]\otimes [\mathit{a}\otimes \mathit{a}]\Delta t.$$ (27)

The third term contains the correction term for the Jauman rate [60],

$${\mathbf{c}}^{\tau }=\frac{1}{2}[\tau \overline{\otimes }\mathit{I}+\mathit{I}\overline{\otimes }\tau +\tau \underset{¯}{\otimes }\mathit{I}+\mathit{I}\underset{¯}{\otimes }\tau ].$$ (28)

The local stress σ^abaqus of equation (24) and the local tangent moduli c^abaqus of equation (25) enter the righthand side vector and the iteration matrix of the global Newton iteration. Upon its convergence, we store the current number of cortical neurons ϑ^g and the current axonal length λ^g locally at the integration point level.

3 Results

3.1 Growth of single axons

To calibrate the axonal growth rate G^axn, the rate by which axons grow in length when exposed to chronic overstretch, we consult in vitro experiments of axonal growth in response to displacement-controlled elongation [31]. Figure 3, top, summarizes the applied stretch versus time for n = 23 individual chick sensory neurons. All neurons were stretched to λ = 1.3–7.0 times their original length over a period of 1–10 hours, and allowed to recover at that new length for 1–20 hours. Figure 3, middle, shows a representative neuron before stretching, immediately after rapid stretching of 3 hours, and after a period of recovery of 18 hours. Figure 3, bottom, summarizes the resulting diameter versus time for all 23 axons in response to the loading-holding experiments. The black dots indicate the experimental measurements at discrete points in time.

Fig. 3.

Growth of single axons. Stretch-time curves for 23 axons summarize the individual applied loading-holding histories, top. Images display a representative axon before stretching, immediately after stretching, and after recovery, middle. Normalized diameter-time curves for 23 axons summarize the individual growth response to loading-holding experiments, bottom. Black dots indicate experimental measurements; solid lines represent computational predictions for an axonal growth rate of G^axn=0.08/hour.

For the simulation, we represent the growing axon as a three-dimensional cylinder with one end fixed and one end stretched. We elongate each axon according to the stretch history in Figure 3, top, allow it to gradually recover using our sub-cortical growth model of Section 2.1, and predict the corresponding diameter in Figure 3, bottom. To calibrate the axonal growth rate G^axn, we vary G^axn between 0.0/hour and 0.5/hour in increments of 0.01/hour. For each simulation, we calculate the error between all experimentally measured and computationally predicted axonal diameters as the distance between all dots and curves in Figure 3. Figure 4 illustrates the error function, which is convex within the analyzed interval and takes a minimum at G^axn=0.08/hour. The solid lines in Figure 3 represent the computational simulations for this calibration with G^axn=0.08/hour.

Fig. 4.

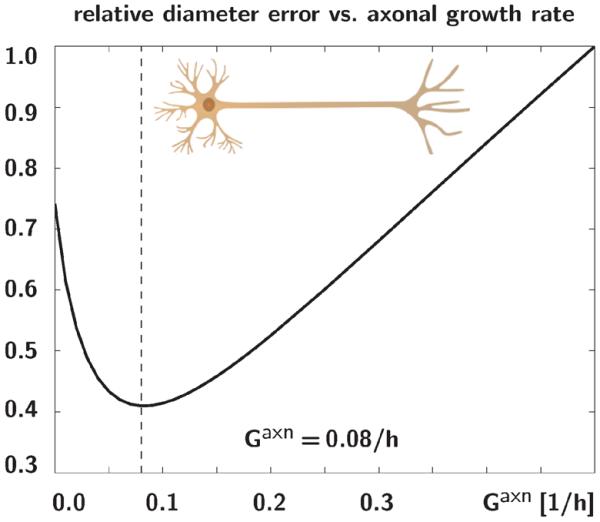
Relative diameter error for varying axonal growth rates. The error between all experimentally measured and computationally predicted axonal diameters is a convex function with a minimum at G^axn=0.08/hour.

3.2 Growth of brain slices

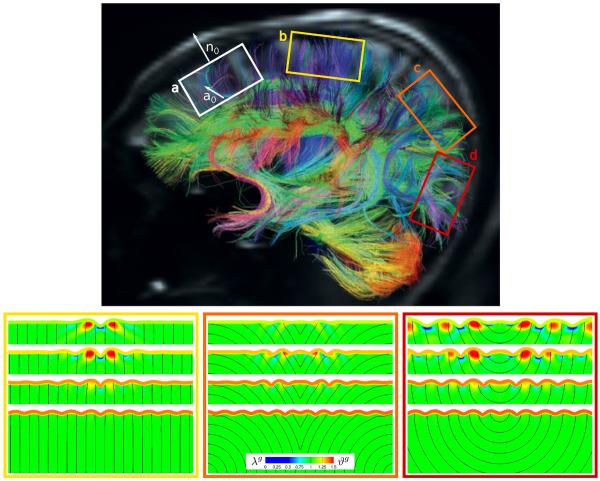
To explore the impact of the axonal orientation on brain growth, we perform finite-element simulations of rectangular brain slices using Abaqus/Standard [1] with our own user material subroutines for gray and white matter introduced in Section 2.2. We follow established protocols [5, 10, 13] and discretize a 3cm×1cm domain with an initial cortical thickness of 0.05cm by 200×30 quadrilateral linear brick elements. We use 26 elements across the white and 4 across the gray matter domain, assume a plane strain state, and allow the boundary nodes to slide freely along the domain edges. We model the gray and white matter tissue as Neo-Hookean elastic and choose the sti ness contrast, the ratio between gray and white matter stiffness, as E^gray / E^white = 3.0, which results in Lamé-constant ratios of three. To trigger the formation of instabilities, we apply a small sinusoidal perturbation with an amplitude of 1/50 times the cortical thickness in the center region. We assume that axons grow if they sense a stretch above λ^e > λ⁰ and retract for a stretch below λ^e < λ⁰, where λ⁰ = 1.0. We fix the axonal growth and retraction rate to G^axn = 0.08/hour according to Section 3.1 and vary the growth contrast, the ratio between gray and white matter growth, as G^ctx / G^axn = 10^−2.5, 10⁻², 10^−1.5, 10⁻¹. Motivated by the di usion spectrum image in Figure 7, we focus on four di erent axonal orientations a₀: randomly isotropic, radially straight I-shaped, radially curved V-shaped, and radially curved U-shaped. We compare the randomly isotropic growth model against a plain isotropic growth model with F^g = J^gI, for which we drive the evolution of the growth parameter, J^g = G^axn[J^e – J⁰], by the volumetric elastic overstretch, [J^e – J⁰] [9].

Fig. 7.

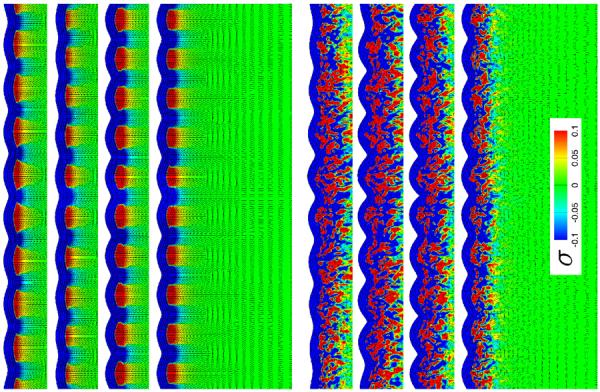
Stress in brain slices for isotropic white matter growth, top, and anisotropic white matter growth with randomly isotropic axonal orientation, bottom, at varying growth contrasts. For each set, the growth contrast between gray and white matter varies between 10^−2.5, 10⁻², 10^−1.5, 10⁻¹, from top to bottom. The black lines illustrate the directions of maximum principal stress; the color contours indicate the maximum principal stress along this direction.

3.2.1 Sensitivity with respect to growth contrast

Figures 5 and 6, bottom, illustrate the evolving brain surface morphology for varying growth contrasts G^ctx / G^axn. As the growth ratio between gray and white matter increases, from top to bottom, the gray matter layer grows faster relative to the white matter core. The top rows of Figures 5 and 6 display the largest amount of axonal growth and axonal retraction, indicated by the red gyri and blue sulci. The bottom rows show almost no axonal growth and retraction, indicated by the homogeneous green growth profiles. With increasing growth ratio, from top to bottom, the influence of white matter growth, and with it the degree of anisotropy, becomes less pronounced, and the surface morphology becomes more regular. The side-by-side comparison with the plain isotropic growth model in Figure 5, top, confirms this trend: With increasing growth ratio, the randomly isotropic model, bottom, becomes more homogeneous; its growth values and surface morphologies become more regular and resemble the plain isotropic model, top.

Fig. 5.

Growth in brain slices for isotropic white matter growth, top, and anisotropic white matter growth with randomly isotropic axonal orientation, bottom, at varying growth contrasts. For each set, the growth contrast between gray and white matter varies between 10^−2.5, 10⁻², 10^−1.5, 10⁻¹, from top to bottom. The black streamtraces illustrate the local axonal orientation a₀ of the anisotropic growth model; the color contours indicate the local isotropic growth Jg, top, and local axonal growth λg, bottom, and number of cortical neurons ϑg.

Fig. 6.

Growth in brain slices for anisotropic axonal orientation at varying growth contrasts. Diffusion spectrum imaging of the adult human brain reveals regionally varying cortical normals n₀ and axonal orientations a₀, which induce anisotropic gray and white matter growth (a), modified with permission from [3]. Axons display radially straight I-shaped (b), radially curved V-shaped (c), and radially curved U-shaped (d) orientations. The growth contrast between gray and white matter varies between 10^−2.5, 10⁻², 10^−1.5, 10⁻¹, from top to bottom. The black streamtraces illustrate the local axonal orientation a₀; the color contours indicate the local axonal growth λg and number of cortical neurons ϑg.

Figures 7 and 8 illustrate the stress profiles for varying growth contrasts G^ctx/G^axn. The maximum principal stresses for the plain and randomly isotropic models in Figure 7 seem relatively insensitive to the growth contrast, both in direction and in magnitude. The maximum principal stresses for the anisotropic models in Figure 8, however, vary largely with varying growth contrast: With increasing growth ratio, from top to bottom, the stress profiles of the I-, V-, and U-shaped axonal orientations become more homogeneous and resemble the plain isotropic model in Figure 7, top.

Fig. 8.

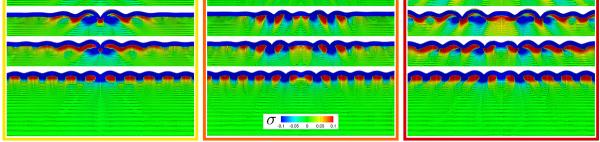
Stress in brain slices for anisotropic axonal orientation at varying growth contrasts. The axonal orientation varies between I-shaped, radially curved V-shaped, and radially curved U-shaped, from left to right. The growth contrast between gray and white matter varies between 10^−2.5, 10⁻², 10^−1.5, 10⁻¹, from top to bottom. The black lines illustrate the directions of maximum principal stress; the color contours indicate the maximum principal stress along this direction.

3.2.2 Sensitivity with respect to axonal orientation

Figures 5 and 6, bottom, illustrate the evolving brain surface morphology for varying axonal orientations a₀. The axonal orientation clearly impacts the folding pattern, the gyral wavelength, and the sulcal depth: While the isotropic axonal orientation in Figure 5 creates a regular sinusoidal surface morphology with short gyral wavelengths and moderate sulcal depths, the anisotropic axonal orientations in Figures 6 generate irregular surface morphologies with long gyral wavelengths and pronounced sulcal depth.

Figures 7 and 8 illustrate the stress profiles for varying axonal orientations a₀. The top rows of Figure 8, with the smallest growth ratio, display the largest effect of white matter growth, and with it the largest degree of anisotropy. Their maximum principal stress directions and magnitudes vary significantly between the I-, V-, and U-shaped axonal orientations. As the growth ratio increases, from top to bottom, the stress profiles become more regular and resemble the plain isotropic model in Figure 7, top.

3.3 Growth of brain morphologies

To explore the impact of the axonal orientation on evolving brain morphologies, we perform finite-element simulations of ellipsoidal brain geometries using our model for gray and white matter introduced in Section 2.2. We discretize the ellipsoid with 27,216 tri-linear brick elements, 23,328 for the white matter core and 3,888 for the two-element thick gray matter layer. The ellipticity of the ellipsoid is 1.2 with a long axis diameter of 16.8 cm and short axis diameters of 14 cm. We assume symmetry in the three axial planes. Unlike the previous example, the ellipsoid possesses a natural heterogeneity induced by its non-homogeneous curvature. This implies that it folds naturally upon growth without requiring additional perturbations [5]. Similar to the previous example, we model the gray and white matter tissue as Neo-Hookean elastic with a stiffness contrast of E^gray/E^white = 3.0 resulting in Lamé-constant ratios of three. We assume that axons grow if they sense a stretch above λ^e > λ⁰ and retract for a stretch below λ^e < λ⁰, where λ⁰ = 1.0. The axonal growth and retraction rate is G^axn = 0.08/hour and we assume a growth contrast of G^ctx/G^axn = 10^−1.5. We simulate four different axonal orientations a₀: unidirectionally one-dimensional, planar radially outward-pointing two-dimensional, radially outward-pointing three dimensional, and isotropic with no pronounced axonal direction [10].

Figure 9 illustrates the brain surface morphology for the four different axonal orientations. As the degree of white matter isotropy increases, from left to right, the cortex becomes more regularly folded. The axonal orientation clearly impacts the folding pattern, the gyral wavelength, and the sulcal depth: in regions where axons are oriented perpendicular to the surface, the cortex becomes locally gyrencephalic with gyri of maximum axonal growth and sulci of maximum axonal shortening; in regions where axons are oriented parallel to the surface, the cortex remains locally lissencephalic.

Fig. 9.

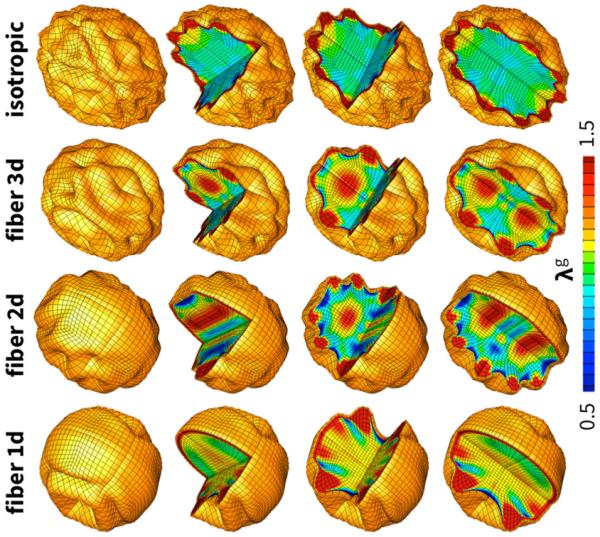
Surface morphology for varying axonal orientation. The degree of anisotropy varies between unidirectionally one-dimensional, planar radially outward-pointing two-dimensional, radially outward-pointing three dimensional, and isotropic, from left to right. As the degree of white matter isotropy increases the cortex becomes more regularly folded. In regions where axons are oriented perpendicular to the surface, the cortex becomes locally gyrencephalic with gyri of maximum axonal growth and sulci of maximum axonal shortening; in regions where axons are oriented parallel to the surface, the cortex remains locally lissencephalic. The color contours indicate the local axonal growth λg.

4 Discussion

Motivated by the hypothesis that axonal growth in the human brain plays a central role in modulating surface morphology, we have established a mechanistic model for brain development using the continuum theory of finite growth.

On the macroscopic scale, cortical folding is tightly regulated by the interplay between the area increase of the gray matter surface and the volume increase of the white matter core. To characterize these phenomena, we have adopted the multiplicative decomposition of the deformation gradient into an elastic and a growth part. Key to the success of this concept is the appropriate definition of the growth part, a second order tensor, for which we need to postulate appropriate kinematics, i.e., equations that tell us how this tensor is populated, and appropriate kinetics, i.e., equations that define how it evolves in time. Here we derive these equations as emergent properties from cellular and molecular events.

On the microscopic scale, the gray matter surface area is closely correlated to the number of cortical neurons, and an increase in surface area is modulated by neural progenitor division. Since neurons stack radially to form cortical columns, we propose to populate the gray matter growth tensor transversely isotropically with the brain surface normal as the pronounced microstructural direction. White matter volume, on the contrary, does not scale with cell number but rather with cell size, or, more specifically, with the length of the neuronal axons. Axons grow in length when their two ends are pulled apart, and an increase in volume is modulated by mechanical stretch. Since axons are arranged in bundles that connect different regions of the brain, we propose to populate the white matter growth tensor transversely isotropically with the regionally varying axonal orientation as the pronounced microsturctural direction.

4.1 Axonal growth is rate limited by mass production

In close agreement with in vitro experiments of chronic axon elongation, our model predicts an immediate axonal thinning in response to stretch, followed by a gradual axonal thickening as the axon recovers. Initially, there is no axonal growth, λ^g = 1.0, and the applied stretch is entirely elastic, λ = λ^e. Over time, the applied stretch is gradually accumulated by growth, λ = λ^g, the elastic stretch returns to its baseline value, λ^e = λ⁰, and the axonal tension decreases. Our simulations demonstrate that a single model parameter, the axonal growth rate, explains axonal elongation experiments for a wide range of loading conditions, including stretches ranging from less than 50% to more than 700% and recovery times from one to twenty hours [31]. Our calibrated axonal growth rate of G^axn = 0.08 / hour indicates that axons actively respond to environmental stimuli within the order of hours [35]. In vivo experiments have shown that axonal elongation activates mechanotransduction pathways which converge in the cellular production of mitochondria to maintain a constant mitochondrial density along the axon [50]. This suggests that mass production and transport, intracellular phenomena associated with time scales of minutes to hours, are the rate limiting factors of axonal growth [36].

4.2 Axonal elongation regulates white matter growth

The ability of neurons to change their length in response to environmental cues has been documented for more than three decades [8]. Various studies have shown that axons respond to mechanical stretch through active growth rather than passive elongation [14]; they try to achieve and maintain an optimal density along their length [35]; they grow in the direction of applied tension [19]; and they retract if the tension is relieved [32]. The ability to dynamically adjust their length is an important feature of axons during growth and development: neurons are forced to maintain connection between different parts of the body as they grow apart, which, in the case of the giraffe's neck, occurs at rates of up to 0.08cm/hour [38]. Here we propose a multiscale approach to naturally correlate growth of individual axons on the microstructural scale with a volume increase of white matter tissue on the macrostructural scale. Rather than introducing the material parameters of white matter growth on a phenomenological level [10], multiscale modeling allows us to introduce material parameters with a clear physiological interpretation. As Figure 3 documents, our axonal growth rate G^axn follows naturally from length-diameter measurements during controlled axonal elongation.

4.3 Axonal orientation introduces symmetry breaking

Previous attempts to understand cortical folding are based on phenomenological, isotropic models for white matter tissue [5]. While these models provide valuable functional relations between cortical wavelength, thickness, and stiffness, they typically predict irregular folding patterns on regular, homogeneous geometries [9]. On irregular geometries, for example on three-dimensional ellipsoids with regionally varying curvature, even isotropic models are capable of reproducing complex folding patterns [51,53]. In addition to local variations in geometry [6], local variations in thickness [51], stiffness [54], and growth [52] are other potential sources to trigger inhomgeneous folding. In the post-buckling regime, the initial sinusoidal folding pattern typically becomes even more complex and transitions into cusped sulci [48, 51] or undergoes period doubling and tripling [12]. In reality, however, white matter tissue is highly anisotropic with well-defined, regionally varying microstructural orientations [15]. Recent advancements in neuroradiology now provide precise mappings of the brain's axonal network from diffusion spectrum imaging [3]. The concept of structural tensors allows us to seamlessly integrate this microstructural information and embed our directional axonal growth model into realistic brain geometries. Rather than using an axisymmetric ellipsoidal model [5], we adapt a fully three-dimensional ellipsoidal model, to explore a wide range of axonal orientations. Our results demonstrate that axonal growth naturally generates structural anisotropy, intrinsically induces symmetry breaking, and predicts more physiological, less regular folding patterns with varying gyral wavelengths and sulcal depths.

4.4 Axons do not pull on the brain - the brain pulls on the axons

Axonal tension has long been believed to be a regulator of cortical folding [55]. The human cortex experiences a period of maximum growth during weeks 23 and 37 of gestation, where it turns from a flat surface into a wrinkled structure and approximately triples its area [46]. For our model with ${\stackrel{.}{\vartheta }}^{\mathrm{g}}=G^{\text{ctx}}$, this suggests an upper limit of cortical growth with G^ctx = 10^−2.5/hr. Axons, on the contrary, respond quickly to mechanical loading and can double their length within the order of hours [35]. For our model with ${\stackrel{.}{\lambda }}^{\mathrm{g}}=G^{\text{axn}}$, our experiments reveal an average axonal growth rate of G^axn = 10⁻¹/hr. These estimates suggests a growth contrast on the order of G^ctx/G^axn = 10^−1.5. Recent studies have shown that the growth contrast is an important regulator of cortical complexity, and that smaller growth contrasts trigger larger wavelengths [5]. In the limit of G^ctx/G^axn → 0, we would recover the extreme case of a growing gray matter layer on a perfectly viscous, fluid-like white matter substrate resulting in infinite wavelengths [7, 28]. On the time scale of human development with G^ctx/G^axn = 10^−1.5, white matter behaves like a highly viscous solid that can respond almost instantly to mechanical stretch [10,58]. In our case, we model white matter viscosity as anisotropic with a pronounced microstructural direction, the axonal orientation a₀ [15]. When sensing mechanical stretch, axons quickly resume their new resting length and the stretch-induced axonal tension rapidly returns to its physiological baseline value. This suggests that - rather than axons pulling on the brain to induce cortical folding [55] - the folding cortex pulls on the axons to trigger axonal elongation and white matter growth [58].

4.5 White matter growth stabilizes morphogenesis

Our simulations suggest that an overall increase in white matter volume is an important contributor to shape brain morphogenesis. Pioneering models of brain development suggested an interpretation of cortical folding as the buckling of a growing surface on a non-growing, elastic foundation [42]. To simulate folding instabilities, however, these models required a non-physiological stiffness contrast of up to three orders of magnitude. Recent indentation tests have shown that gray and white matter display rather similar stiffnesses, both of the order of 1kPa [11]. These values agree with recent in vivo measurements using magnetic resonance elastography [16]. Introducing white matter growth makes cortical folding possible, even for small stiffness contrasts [5]. Models with white matter growth also display a better agreement with microdissection experiments than models without growth [58]. Specifically, microdissection assays have revealed significant radial tension in the developing gyri, but no tension across the gyri [6], as initially postulated by the axonal tension hypothesis [55]. This is in excellent agreement with our maximum principal stress directions in Figure 8, which display a pronounced radial orientation in the individual gyri, but virtually no tension across the gyri. This suggests that white matter growth, ideally of anisotropic nature, is critical to stabilize morphogenesis and accurately capture the mechanophysiology of cortical folding.

4.6 Limitations and potential improvements

While our model shows potential to further our understanding of cortical folding, this is only a preliminary study. We suggest to address the following limitations as this research continues: (i) In this study, we have focused on the role of anisotropy in white matter growth. Axonal orientation might also affect the elastic response of white matter; in fact, recent research suggests that white matter tissue is indeed anisotropic [54]. In our model, incorporating anisotropy would imply supplementing the free energy function (3) with a term in the fourth invariant, to captures anisotropic effects through the elastic axonal stretch λ^e. (ii) In our current model, throughout the entire time interval of interest, all axons maintain their predefined stiffness and orientation. The axonal stiffness depends critically on the degree of myelination may change substantially during development. Experiments have shown that axons grow in the direction away from the tension they experience [20]. This suggests that the axonal orientation might change during development or disease progression, especially as new connections form. Incorporating axonal reorientation could improve the current model and make it more realistic [26]. This would be critical to capture the differences between the connectivity in the developing cortex and the adult cortex in Figure 6. (iii) While axons are highly aligned in some regions of the brain, for example in the corpus callosum [37], they exhibit higher levels of dispersion elsewhere. Currently, our model only captures a single axonal orientation a₀, but future work could include a dispersion parameter to allow for different levels of anisotropy [21]. Additionally, the theory of axonal tension relies on regionally varying axonal densities to draw strongly interconnected areas closer together, while weakly connected areas drift further apart [55]. Here we assign each integration point its own axonal orientation, but do not distinguish different axonal densities, which we could easily incorporate through an additional order parameter. (iv) One of the most obvious areas for improvement is the need for more realistic modeling, both in terms of model geometry and model parameters. On the axonal level, our growth model is calibrated by experiments with cultured chick sensory neurons, which may behave very differently from growing axons in an in vivo setting, where growth is also guided by wiring among different cortical regions. On the whole brain level, our current model is limited to idealized geometries and idealized axonal orientations. Once we have gained a better understanding of the model as a whole, we will test it in realistic brain geometries based on magnetic resonance images with axonal orientations from diffusion tensor imaging. We are also working in close collaboration with neuroradiologists [9] to confirm that our microscopically motivated model indeed predicts a macroscopically realistic response in terms of gray matter surface area and white matter volume.

5 Conclusion

We have established the first three-dimensional finite element model of the developing brain to incorporate white matter anisotropy. This addition lends a multiscale approach to the modeling of brain development, connecting the mechanical behavior at the tissue and organ level with the response of axons on the cellular level. Axons, the major components of white matter tissue, have long been known to grow under mechanical stimuli and retract upon their removal. Here we calibrated the rate at which axons growth by simulating a variety of loading scenarios and comparing their long-term length-diameter response. We then utilized this growth rate in simulations of growing brain slices to explore the role of axonal orientation in gyrogenesis and pattern formation. Our simulations suggest that axonal growth is an important regulator of brain surface morphology: increasing axonal growth along specific axonal directions induces symmetry breaking and increases surface irregularity, gyral wavelengths, and sulcal depths.

Understanding the mechanisms of gyrogenesis is an important medical problem as more and more studies are finding relationships between folding abnormalities and psychological or mental disorders [17]. Some of these disorders appear to be associated with atypical connectivity, irregular folding patterns, and abnormal wavelengths or sulcal depths [25]. This suggests that there is some functional correlation between the connectivity of the brain, its folding, and its function or dysfunction. By interpreting anisotropic white matter growth as an emergent property from directional axonal elongation, our model may shed light on the interplay between connectivity and folding, and, ultimately, on its relevance in neurological disorders including epilepsy, schizophrenia, and autism.