Abstract
The aim of this work was to develop a framework for modeling organ effects within TOPAS (TOol for PArticle Simulation), a wrapper of the Geant4 Monte Carlo toolkit that facilitates particle therapy simulation. The DICOM interface for TOPAS was extended to permit contour input, used to assign voxels to organs. The following dose response models were implemented: The Lyman-Kutcher-Burman model, the critical element model, the population based critical volume model, the parallel-serial model, a sigmoid-based model of Niemierko for Normal Tissue Complication Probability (NTCP) and Tumor Control Probability (TCP), and a Poisson-based model for TCP. The framework allows easy manipulation of the parameters of these models and the implementation of other models.
As part of the verification, results for the parallel-serial and Poisson model for x-ray irradiation of a water phantom were compared to data from the AAPM Task Group 166. When using the task group dose-volume histograms (DVHs), results were found to be sensitive to the number of points in the DVH, with differences up to 2.4%, some of which are attributable to differences between the implemented models. New results are given with the point spacing specified. When using Monte Carlo calculations with TOPAS, despite the relatively good match to the published DVH’s, differences up to 9% were found for the parallel-serial model (for a maximum DVH difference of 2%) and up to 0.5% for the Poisson model (for a maximum DVH difference of 0.5%). However, differences of 74.5% (in Rectangle1), 34.8% (in PTV) and 52.1% (in Triangle) for the critical element, critical volume and the sigmoid-based models were found respectively.
We propose a new benchmark for verification of organ effect models in proton therapy. The benchmark consists of customized structures in the spread out Bragg peak (SOBP) plateau, normal tissue, tumor, penumbra and in the distal region. The DVH’s, DVH point spacing, and results of the organ effect models are provided. The models were used to calculate dose response for a Head and Neck patient to demonstrate functionality of the new framework and indicate the degree of variability between the models in proton therapy.
Introduction
The superior accuracy of Monte Carlo simulations over analytical methods for dose calculation in radiotherapy is advantageous in proton therapy [Paganetti2012], perhaps more important than in x-ray therapy [TG105]. In either case, dose differences of 5% in radiotherapy can result in differences up to 10–20% in tumor control probability (TCP) or up to 20–30% in normal tissue complication probability (NTCP) [TG105]. The determination of the best treatment plan is aided through dose-effect modeling by evaluating the dose-volume histograms (DVH) for the target and nearby critical structures or organs. Commercial planning systems generally provide DVHs. If Monte Carlo simulation is not available in the planning system, the simulation may be performed separately. The subsequent step in organ effect modeling is to evaluate the therapeutic ratio using TCP and NTCP calculated from the DVHs or full dose distributions to determine the best plan [Armstrong2005]. Most often, the analysis of DVHs or the calculation of NTCP and TCP is performed using separate software for organ effect modeling such as DRESS [ElNaqa2006], CERR [Deasy2003], BIOPLAN [SanchezNieto2000], BIOSUITE [Uzan2009], HART [Pyakuryal2010] and others. None of these incorporate calculation of the dose distribution.
The TOPAS software was introduced in 2012 as an accurate, easy to use Monte Carlo tool for proton therapy simulation ([Perl2012] [Shin2012] [Schuemann2012]). The accuracy of TOPAS has been demonstrated using various experimental data [Testa2013]. Along with the accuracy, the availability of TOPAS to simulate time dependent calculations [Shin2012] makes it a powerful and easy to use Monte Carlo tool. The implementation of biological modeling in TOPAS is a step towards a full toolkit for patient specific dose and effect calculation in proton therapy.
The AAPM Task Group 166 [TG166] provides a benchmark for verification of the implementation of TCP/NTCP methods. A benchmark phantom configuration for TCP/NTCP calculation for photon therapy is described and reference data is supplied. However, due to the differences in dose distributions between photons and protons, this phantom configuration is not suitable for proton therapy and a new benchmark configuration is needed.
This work describes the addition of TCP/NTCP models to the TOPAS toolkit. A framework for adding dose response models to Monte Carlo simulation systems is described. A number of organ effect models were added to TOPAS using this framework, including many commonly used models. Models were validated against the TG-166 benchmark data for photon therapy and new information to improve the accuracy of the verification along with new data for models that were not benchmarked in TG-166 is supplied. A new benchmark based on the TG-166 photon benchmark is devised with data to support verification of organ models implemented by others. In order to show the new features of TOPAS for TCP/NTCP calculation, results of the various TCP/NTCP models implemented in TOPAS are compared for a head and neck patient with a realistic treatment plan using accurately commissioned proton fields.
2 Methods
2.1 TOPAS framework for dose response modeling
TOPAS has the ability to read 3D information including CT data from DICOM files by means of the Grassroots DICOM Library (GDCM)[GDCM]. The DICOM reading functionality has been extended to read structure information. The dose distribution for each structure can be delineated and the corresponding DVH calculated. The dose at each organ is classified as follows. At initialization of TOPAS, for each organ, the coordinates that compose their corresponding contours are read from the DICOM-RT file, a winding number algorithm is used to determine whether a voxel (of the score grid) is enclosed by the polygon created with the coordinates of that contour. If it is enclosed, its location is storage in a Boolean grid with value set to True. At finalization, the corresponding DVH is calculated from the full dose distribution by assigning each voxel to a dose bin, to which it contributes with a count of the DVH [Sempau2000] and by using the Boolean grid as a filter for each organ considered.
The TOPAS modeling extension provides the capability to add dose response models to calculate the TCP and NTCP values using the full dose distribution calculated with TOPAS or DVHs (differential or cumulative) input separately. The values for the parameters of the TCP/NTCP models are defined by the user within the framework of the TOPAS parameter system [Perl2012]. Default values are provided. The user can override these values for any of the parameters using their own parameter files. The user defines the model and associate parameters in the input parameter file and TOPAS can calculate the TCP or NTCP from two scenarios. Scenario 1: If the dose calculation in an organ of interest is requested, the dose is calculated and TOPAS classifies those voxels contained in the organ. If the user does not request DVHs, TOPAS calculates the TCP or NTCP from the full dose distribution in the selected organ. In this case there is no re-binning in the dose axis of the DVH, with the number of bins in the DVH equal to the number of voxels in the corresponding organ with dose values larger than zero, while the voxel volume is set to unity. Otherwise, TOPAS uses the differential DVHs. Scenario 2: TOPAS reads external DVHs (in comma separated values format) or dose distributions for each organ of interest and calculates the NTCP or TCP values. If cumulative DVHs are imported they are converted to differential DVHs prior the dose response calculation. Summarizing, Scenario 1 uses the data produced by TOPAS at the end of a simulation (particle tracking plus TCP or NTCP calculation) whereas Scenario 2 uses input data to calculate TCP or NTCP (no particle tracking).
In addition to models that have been implemented in TOPAS, users may implement other models and may also include their own databases for the prebuilt models. The Figure 1 shows a sample of the code to implement a new model. TOPAS takes care of most of the underlying work so that the user who writes a new outcome modeling class just has to implement that which is unique about their own model.
Figure 1.
TOPAS takes care of most of the underlying work so that the user who writes a new NTCP/TCP modeling class just has to implement that which is unique about their own model.
2.2 Analytical methods for radiobiological modeling in TOPAS
In this section, we provide the equations of the main models we tested in order to avoid conflict with variations that even mathematically equivalent, computationally present certain differences. Several analytical methods are implemented in TOPAS to calculate NTCP or TCP, i.e. for NTCP, the Lyman-Kutcher-Burman [Burman1991], the parallel-serial or s-model [Kallman1992], the Critical Volume (population based) [Stavrev2001], the critical element [Niemierko1992] and the Niemierko model [Gay2007], and for TCP, a Poisson-based model [Warkentin2004] and the Niemierko model [Gay2007].
2.2.1 LKB model
The Lyman-Kutcher-Burman (LKB) model [Burman1991] is used to calculate NTCP. The model is implemented as written by [Mohan1992]:
| [1] |
where
| [2] |
and
| [3] |
TD50 is the position of the 50% probability dose point, m is a parameter to control the slope of the dose response and gEUDa is the generalized uniform equivalent dose with a value a. vi is the fractional organ volume receiving a dose Di. To account for differences in dose per fraction, the dose Di can be substituted with the equivalent dose delivered in N fractions of 2 Gy [TG166] given by:
| [4] |
where α and β are the coefficients of the linear quadratic model.
In this work, we calculated the LKB model with equation [1] only and with equation [1] in conjunction with equation [4].
2.2.2 Critical Element, Critical Volume, and S-Model
The Critical Element model (CE) [Niemierko1991], the Critical Volume model [Niemierko1992] (a population-based variation is included in TOPAS and fully described in [Stavrev2001]), and the parallel-serial or S-model [Kallman1992] are included. These models are based on the idea that organs are composed of functional subunits. The CE model considers that these subunits are arranged in a serial way, while the CV model considers a parallel arrangement. The S-model is a generalization of the idea of functional subunits. Basically this model merges the CV and CE models into one single model. A value s determines the ‘degree’ of relatively seriality of the subunits. For s equal to 0, this model is equivalent to the CV model, while for s equal to unity it is equivalent to the CE model. Nevertheless, values outside of the range 0 and 1 are often found [Savreva2002]. The NTCP [Kallman1992] is then given by:
| [5] |
where P(Di) is calculate by means of the Poisson model written as [Kallman1992]
| [6] |
where γ is the normalized dose-response gradient at the dose, where the absolute dose-response gradient is the steepest.
2.2.3 Niemierko model
Another NTCP model included is the proposal of Niemierko for parameterization of dose response using the logistic function for NTCP or TCP [Gay2007]. The model depends on the gEUDa value described in equation 3. The value for the tolerance of dose determines the kind of calculation that is performed [Gay2007]. The NTCP and TCP are given by:
| [7] |
and
| [8] |
where TCD50 states for tumor control dose at 50%.
2.2.4 Poisson probability
This TCP model is based on the Poisson probability distribution as described in [Kallman1992]. In the TOPAS implementation, the probability per voxel is calculated with equation 10 [Warkentin2004], and the TCP is calculated as the product over all voxels as:
| [9] |
with
| [10] |
2.2.5 Predefined parameter files
For LKB, CV and Poisson models, predefined databases with parameters corresponding to certain organs or tumor sites are implemented in TOPAS. The data were obtained from references [Burman1991] [Stavrev2001] [Okunieff1995] for LKB, CV and Poisson models, respectively. In addition, users may revise these model parameters by including customized TOPAS parameter values in their own parameter files, which will override the predefined values of the databases.
2.3 Verification of TOPAS calculated TCP/NTCP values with benchmark data
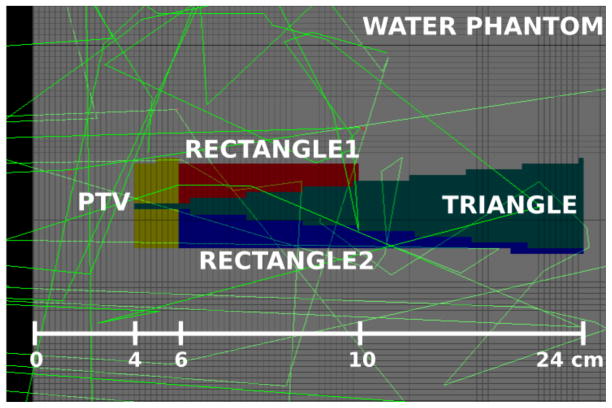
To verify the implementation of the models in TOPAS, the NTCP and TCP values calculated with TOPAS were compared to the corresponding values calculated with Pinnacle system version 9.2 (Philips Medical Systems, Andover, MA) for the benchmark water phantom and structures configuration for photon beams in the AAPM TG-166 task group report [TG166]. For this work a water phantom was created consisting of 100 × 100 × 100 voxels of 5 × 5 × 2.5 mm3 dimension with 4 basic structures (Table VI in TG-166). The phantom was created using Pinnacle and exported to a DICOM-RT file read by TOPAS for dose calculation and subsequent TCP/NTCP calculation. The geometry with structures is shown in Figure 2. The beam source consisted of accurate phase space files from a Siemens 6 MV x-ray beam modeled with the BEAMnrc software [Rogers1995] using accurately determined source and geometry details [Sawkey2009]. This is the same beam commissioned at UCSF in Pinnacle on the 4 UCSF Siemens Primus linacs, matched to within 1% out to the penumbra. The field was set to 20 × 20 cm2 at the 100 cm source to surface distance. The dose calculation was performed with TOPAS up to a statistical uncertainty (calculated using the method recommended in [Rogers2000]) lower than 0.7% for voxels with dose exceeding 50% of the maximum. The production cut of secondary particles was set to 0.05 mm with a max step length of 0.5 mm. The source phase space was recycled 10 times. The final dose distribution was normalized to a dose of 72 Gy in the 20 × 20 × 0.5 cm3 region located at 6 cm depth along the central axis of the water phantom. The dose normalization region encompassed several voxels to minimize statistical fluctuation in this region.
Figure 2.
Geant4 viewer display of the central slice of the DICOM phantom as read into TOPAS, showing the 4 structures and a few particle tracks. The photon beam was incident from the left side of the phantom.
The TCP or NTCP values for the 4 structures (for organs listed in the Table VI in [TG-166]) were calculated as follows:
By using the S-model available in the treatment planning system (TPS) of Pinnacle v9.2 (named Biological Response Panel), with the input parameters in Table VII of reference [TG166]. On other hand, by using the LKB model available in the TPS of Pinnacle (named NTCP/TCP Editor) with the parameters from Burman [Burman1991]. Results of Pinnacle, using the 6 MV Siemens Primus beam, and TOPAS using the DVH from Pinnacle, were compared to each other and to results of TG-166.
For the 5 models implemented in TOPAS using the full dose calculation starting with validated, pre-calculated phase-space data for the 6 MV Siemens Primus beam the dependence of the NTCP results on the increment in the dose points of the DVH was determined.
For the 5 models implemented in TOPAS, the Pinnacle results calculated using the 6 MV Siemens Primus beam were compared to TOPAS results calculated using the Pinnacle DVH with 200 points in the DVHs.
Summarizing, item 2 was used to estimate the variations in NTCP values when different number of bins in the DVH is used. Item 3 was used to compare the NTCP TOPAS calculations by using the same DVH as Pinnacle.
2.4 Geometrical configuration for proton therapy TCP/NTCP calculations
The previous section described a benchmark configuration for TCP/NTCP suggested by the TG166. This setup was defined for photon radiotherapy. Because of differences between dose conformality between photon therapy and proton therapy this benchmarking (mainly the particle source) of dose response models using the phantom from report [TG166] is not suitable for proton therapy. To our knowledge, a setup to benchmark dose response models for proton therapy is currently not available. In this section we propose a benchmark phantom for proton therapy.
As in [TG166] the phantom implemented in TOPAS consist of a water phantom but with different structures configuration. Four structures were considered to account for the dose at proximal, target, distal, and penumbra regions. The parameters of the structures to be used in the models were chosen to avoid 0 % and 100% values in NTCP or TCP calculations. The detailed configuration is given in the Figure 3 and Table 1. The water phantom has 20 × 20 × 20 cm3 dimension with voxel resolution of 0.5 × 0.5 × 2 mm3. A squared proton field of 10 cm in x and y, 10 cm of range and 5 cm of modulation impinges on the surface of the phantom from the negative z-axis. The source model was calculated based on the Francis H Burr Proton Therapy treatment head [Paganetti2004]. To reduce the computation time at the treatment head, a geometrical particle split was used [Ramos2012]. Phase space files were scored at the end of the treatment head and subsequently used for the dose calculation. In total, 72 million source protons were simulated to achieve a statistical uncertainty below 1% at the flat region of the spread-out Bragg peak (SOBP).
Figure 3.
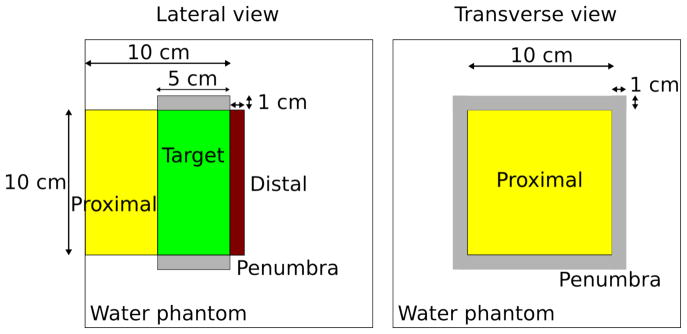
Structure configuration for benchmark NTCP and TCP models for proton beams.
Table 1.
Structures configuration for a phantom suitable for proton therapy. The parameters for the S-Model are provided, whereas the organs name can be used to find the corresponding parameters of the LKB, CV, CE and Niemierko model.
| Structure | PTV | Proximal | PTV | Proximal | Penumbra | Distal |
|---|---|---|---|---|---|---|
| Organ | Glottic | Nasopharynx | Brachial plexus | Brain | Colon | Spinal cord |
| Seriality | Not applicable | Not applicable | 8.4 | 0.64 | 0.69 | 4 |
| α/β | 10 | 10 | 3 | 3 | 3 | 3 |
| γ | 1.6 | 1 | 2.8 | 2.6 | 3.1 | 1.9 |
| TCD50 or TD50 (Gy) | 44.2 | 40.9 | 75.1 | 60 | 55.3 | 68.6 |
The final dose distribution was re-scaled to obtain a dose of 78 Gy in 39 fractions at the center of the SOBP (7.5 cm from the entrance beam in the water phantom on the central z-axis).
3 Results and Discussion
3.1 Comparison of DVHs between TOPAS and Pinnacle
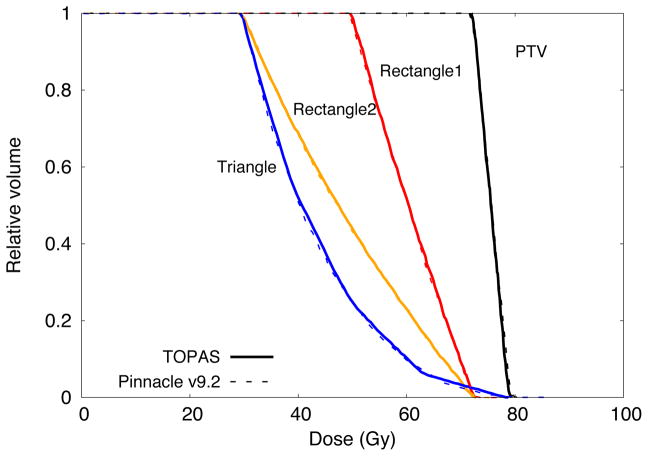
Figure 4 shows the cumulative DVHs calculated with TOPAS and Pinnacle, the latter calculated with the adaptive convolution option. The DVHs of the four structures considered were included. Differences of about 0.5% between both systems were found for the structures PTV, Rectangle1 and Rectangle2 and up to 2% for the structure Triangle. These differences were mainly due to the algorithms used for dose calculation. For Monte Carlo calculations the statistical uncertainties in dose distributions were below the 0.7% for voxels with values larger than the 50% of the maximum dose. Further, a maximum difference of 1% was found between the DVHs from [TG166] and those calculated in this work with Pinnacle for the structures PTV, Rectangle1, Rectangle2 and Triangle.
Figure 4.
Cumulative DVH calculated with Pinnacle and TOPAS for the structures described in [TG166]
3.2 TCP and NTCP values verification
The TCP and NTCP values are shown in the Table 2. The TCP values were calculated for the structures PTV and Rectangle1 only, as in TG-166. Further, the gEUDa value for a=1 is included in the table. ‘LKB with Eq. 4’ denotes the dose fractionation correction prior to evaluating the dose response; ‘LKB without Eq. 4’ denotes that dose fractionation was not considered in the dose response evaluation.
Table 2.
TCP and NTCP values for the TG-166 water phantom irradiated with the UCSF 6 MV Primus beam calculated with TOPAS and Pinnacle. Statistical uncertainties are shown in the parenthesis and are due to the Monte Carlo calculation only. The adaptive convolution algorithm was used to calculate the dose in Pinnacle. S-Model results from TG-166 are shown in the first row.
| Model | Function | PTV | RECTANGLE1 | RECTANGLE2 | TRIANGLE | |||||
|---|---|---|---|---|---|---|---|---|---|---|
| TOPAS | Pinnacle | TOPAS | Pinnacle | TOPAS | Pinnacle | TOPAS | Pinnacle | |||
| S-Model TG-166 | NTCP | 26.6 | 18.1 | 23.5 | 29.5 | |||||
|
| ||||||||||
| S-Model | NTCP | 27.5 (0.4) | 26.9 | 19.6 (1.1) | 18.4 | 24.6 (1.8) | 23.9 | 33.7 (0.2) | 31.0 | |
| LKB with Eq. 4 | NTCP | 24.4 (1.6) | 11.2 (0.8) | 23.0 (1.6) | 14.1 (0.7) | |||||
| LKB without Eq. 4 | NTCP | 30.7 (1.4) | 30.0 | 19.4 (0.9) | 18.0 | 51.0 (1.8) | 48.0 | 41.2 (1.2) | 36.6 | |
| Poisson | TCP | 94.48 (0.03) | 94.0 | 81.31 (0.02) | 80.6 | NA | NA | |||
| gEUDa=1 (Gy) with Eq. 4 | NTCP | 75.52 (0.02) | 75.63 | 60.56 (0.01) | 60.2 | 48.58 (0.01) | 48.2 | 43.57(0.01) | 42.8 | |
| gEUDa=1 (Gy) without Eq. 4 | NTCP | 73.86 (0.03) | 54.89 (0.01) | 41.71 (0.01) | 36.26 (0.01) | |||||
The NTCP of the dose distributions calculated with the adaptive convolution algorithm in Pinnacle was within 0.5% of the TG-166 result, in agreement with the TG-166 comparison to values calculated with their spreadsheet. The LKB without Eq. 4 matched better with the Pinnacle LKB model, suggesting the model in Pinnacle is incomplete, lacking the correction. This underscores the importance of verification testing as discussed in TG-166.
There is a wide range of values from the different dose response models. For the LKB model, a difference of up to 50% between the NTCP values calculated with S-model and LKB has been observed [TG166], consistent with the results for Rectangle2.
The TCP/NTCP results for the PTV and rectangular structures calculated with the models implemented in TOPAS and Pinnacle agree within 2 standard deviations of the statistical precision of the TOPAS calculation or 1% of the TCP/NTCP result. However, for the triangle, there are significant differences between TOPAS and Pinnacle for the LKB without Eq. 4 (a 9% difference) and S-Model (13%) outside of the statistical precision of the TOPAS dose calculation. These differences are attributed to the (unknown) point spacing in the DVH used in Pinnacle and to the difference in the dose distributions calculated with TOPAS and Pinnacle. For example, differences up to 4% in NTCP with respect to the TG166 data were found for the three algorithms (adaptive convolution, fast convolution and collapse cone convolution) available in the Pinnacle
Results from TOPAS in Table 2 used dose distributions calculated with TOPAS. To eliminate the dependence of the verification testing on the Monte Carlo calculation, further TCP/NTCP calculations were done with the DVHs from Pinnacle imported directly into TOPAS.
We used an arbitrary dose point spacing of 29.7 cGy (corresponding to 200 points) for comparison purposes, which was not necessarily the spacing used internally by Pinnacle. Table 3 shows the differences in percent between Pinnacle and TOPAS in this case. For this particular study, the difference could be mainly due to a difference in the number of points in the DVH. Cozzi et al [Cozzi2000] have shown that a refinement as small as 2% in the DVH point spacing leads to a difference up to 10% in TCP/NTCP values. For the TCP model, our implementation of the Poisson model agreed within 0.5% with the reference given in [TG166]. For the S-Model in Table 3, the maximum difference of 3% between the Pinnacle and TOPAS results (5.4% corresponding to 100 points) was obtained for the structure Rectangle2. This difference was also in part due to the Poisson distribution P(Di) in Equation 6, which differs mathematically from the distribution implemented in Pinnacle [TG166]. On the other hand, the Niemierko, CE and CV models were compared against the S-Model from Pinnacle, and differences up to 74.5% (Critical Element model in Rectangle1) were found. The differences are largely attributable to the sensitivity of the model results to DVH point spacing. This shows that the benchmark results in [TG166] should specify the DVH point spacing, or preferably not use rebinning (see section 2.1).
Table 3.
Differences in TCP and NTCP between Pinnacle and TOPAS. The DVHs from Pinnacle calculations with 29.7 cGy spacing were used to calculate the TOPAS results. The differences increase when points are dropped from the DVHs (data not shown). The error due to using 100 dose points compared to using the full dose distribution is shown in brackets.
| Model in TOPAS | PTV (%) | Rectangle1 (%) | Rectangle2 (%) | Triangle (%) |
|---|---|---|---|---|
| S-Model | 0.79 (1.9) | 1.1 (4.7) | −3.0 (5.4) | 1.7 (6.1) |
| LKB | 1.4 (0.6) | −2.4 (7.4) | 0.7 (1.6) | −0.10 (2.2) |
| Niemierko | −2.2 (0.2) | 26.1 (30.8) | 4.8 (9.0) | 52.1 (55.6) |
| Critical element | −4.2 (−1.4) | 74.5 (76.7) | −24.9 (−22.2) | 1.7 (6.1) |
| Critical volume | −34.8(−32.6) | −17.4 (−12.4) | 10.5 (14.4) | Not Applicable |
| Poisson (TCP) | 0.3 (−0.15) | −0.43 (0.66) | Not Applicable | Not Applicable |
| gEUDa=1 | −0.2 (0.4) | −0.34 (0.63) | −0.34 (0.6) | 0.3 (1.2) |
3.3 Benchmark NTCP and TCP for proton therapy beams
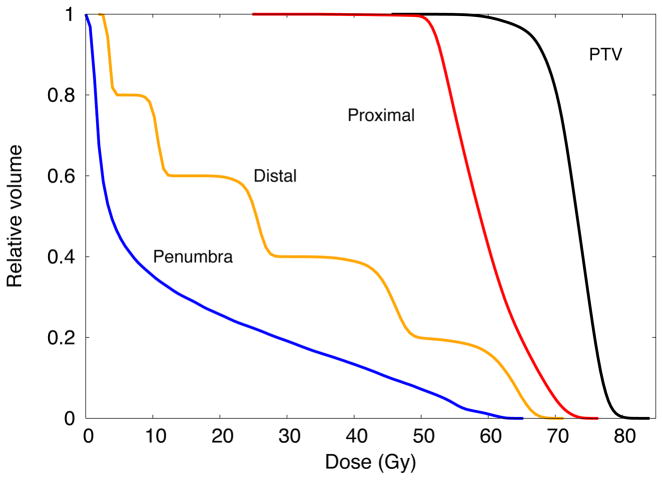
The cumulative DVHs (bin width of 0.01 Gy) for the proposed benchmark phantom are shown in Figure 5. The corresponding statistical uncertainties were below 0.8% for those voxels with dose values larger than the 10% of the maximum dose. In Table 4, the NTCP, TCP and gEUDa=1 values are shown. The statistical uncertainties are only due to Monte Carlo. The values for the LKB without Eq 4 and gEUDa=1 without Eq. 4 are included for completeness. The S-model was taken as reference to validate the LKB model with Eq. 4, the CV model, the CE model, and the Niemierko model. This is a convenient reference as the S-model is used in TG-166 to validate biological modeling implemented in commercial planning systems. Interestingly, the differences largely fall within the statistical precision of the TOPAS calculation. The largest differences were 2.0%±4.6% for LKB with Eq. 4, 1.6%±4.9% for Niemierko model, 3.7%±1.6% for CV model and 12.05%±0.38% for CE Model. Although the models evaluated in this work have been generally restricted to photon therapy, with limited development of proton specific models, they should be useful for protons. The validation for photons in this study applies equally to protons as there is no distinction between protons and photons for these models, other than the model parameters, listed in the Table 1 and in references [Burman1991] and [Stavrev2001]. Thus the results for the proposed benchmark geometry serve as validation data.
Figure 5.
Cumulative dose volume histograms for the four structures used as benchmark for NTCP and TCP models for proton therapy.
Table 4.
NTCP, TCP and gEUD (a=n=1) values per structure for proton therapy calculations. A dose of 78 Gy in 39 fractions at the center of the SOBP. Statistical uncertainties in the parenthesis are only for the Monte Carlo calculation.
| Model | PTV | Proximal | Penumbra | Distal |
|---|---|---|---|---|
| S-Model | 46.88 (0.02) | 29.39 (0.01) | 1.15 (1.09) | 16.83 (0.28) |
| LKB with Eq. 4 | 44.91 (4.62) | 29.83 (2.36) | 0.04 (0.01) | 15.66 (2.20) |
| LKB without Eq. 4 | 47.72 (3.32) | 51.01 (2.19) | 0.48 (0.11) | 25.21 (2.32) |
| Niemierko | 45.31 (4.95) | 29.72 (3.02) | 0.32 (0.07) | 15.29 (2.40) |
| Critical volume | 50.62 (1.60) | 29.76 (0.78) | 0.12 (0.04) | 15.85 (1.99) |
| Critical element | 36.26 (0.01) | 32.23 (0.01) | 2.97 (1.09) | 4.78 (0.27) |
| Poisson (TCP) | 95.85 (0.01) | 78.73 (0.01) | Not applicable | Not applicable |
| gEUDa=1(Gy) with Eq. 4 | 70.69 (1.21) | 53.95 (0.74) | 11.86 (0.30) | 24.46 (0.73) |
| gEUDa=1 (Gy) without Eq. 4 | 72.63 (0.91) | 59.45 (0.61) | 14.92 (0.34) | 29.32 (0.74) |
3.4 Application to a head and neck patient
This section shows a short example of how to use the TCP/NTCP extension implemented in TOPAS. In this example, the LKB model is calculated for the organ Brain stem. The user inputs the DICOM and dose scoring information along with the parameters of the model as shown in Figure 6. The figure also shows the cumulative DVHs for selected organs of a Head and Neck patient treated with protons as calculated with TOPAS. The corresponding parameters for the LKB and CV models can be found in [Burman1991] and [Stavrev2001], respectively. Table 5 shows the parameters for the S-Model, CE, and Niemierko models. The prescribed dose was 60 Gy at the target delivered in 30 fractions. Table 6 shows the NTCP and TCP values (corrected for fractionation assuming 2 Gy per fraction and α/β of 3 Gy) for the corresponding organs. The TCP values were calculated only for GTV and CTV regions. As shown, the critical element and the S-Model agreed for the brain stem NTCP value, because the seriality of the organ is equal to 1. The missing values in the cells are because the parameter values for the Critical Volume model for optical nerve are not defined in the literature.
Figure 6.
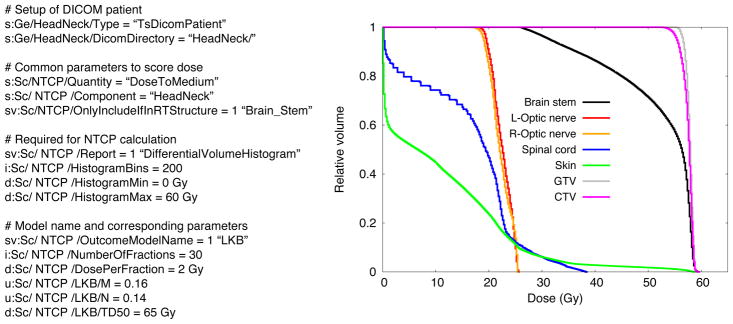
Left: Sample of TOPAS parameters to calculate NTCP with LKB model for the organ Brain. Right: Cumulative DVH for selected organs of a Head and Neck patient treated with protons as calculated with TOPAS.
Table 5.
Relevant parameters for the S-Model, CE and Niemerko models used in the Head and Neck example.
| Model parameter | CTV/GTV | Brain stem | Skin | Spinal cord |
|---|---|---|---|---|
| Seriality | Not applicable | 1 | 0.86 | 4 |
| α/β | 10 | 3 | 3 | 3 |
| γ | 1.6 | 2.4 | 2.5 | 1.9 |
| TCD50 or TD50 (Gy) | 44.2 | 65.1 | 70.0 | 68.6 |
Table 6.
NTCP, TCP values (in percent) and gEUD (for a = 1) for selected organs of the head and neck patient (NA is “Not Applicable”). The prescribed dose was 60 Gy at the target delivered in 30 fractions
| Brain stem | Optical nerve (left) | Optical nerve (right) | Spinal cord | Skin | CTV | GTV | |
|---|---|---|---|---|---|---|---|
| S-Model | 12.30 | 1.0×10−6 | 1.0×10−6 | 0.0 | 0.048 | NA | NA |
| LKB with Eq. 4 | 9.27 | 7.17×10−6 | 6.18×10−6 | 0.02 | 0.004 | NA | NA |
| Niemierko | 12.10 | 5.0×10−4 | 4.0×10−4 | 0.06 | 0.159 | NA | NA |
| Critical Volume | 6.92 | -- | -- | 0.17 | 0.015 | NA | NA |
| Critical Element | 12.30 | 1.0×10−6 | 1.0×10−6 | 0.0 | 0.093 | NA | NA |
| gEUDa=1 (Gy) | 49.30 | 16.88 | 16.58 | 12.31 | 8.211 | 57.41 | 57.74 |
| Poisson (TCP) | NA | NA | NA | NA | NA | 69.72 | 71.08 |
4 Summary and conclusions
In this work, commonly used NTCP and TCP models were implemented in TOPAS. The framework developed for this purpose is suitable for implementation of other models.
In [TG166] the dose distribution was calculated with analytical algorithms available in several systems (Pinnacle system included). We compared TOPAS results to the Pinnacle system. NTCP results for the LKB model, S-model and a Poisson-based model agreed with the benchmark data provided in [TG166] for x-ray therapy. The largest differences are due to differences in the dose calculation algorithm and the number of points in the DVHs. The Pinnacle result reported in TG-166 was likely calculated with the adaptive convolution algorithm, although this was not stated in the publication, and the LKB model implemented in Pinnacle version 9.2 appears to lack a correction for fractionation. When comparing the Critical Element, Critical Volume and Niemierko models, maximum differences of 74.5% (in Rectangle1), 34.8% (in PTV) and 52.1% (in Triangle) were found respectively. This is attributed to differences in the DVH point spacing, which was not given in [TG166]. The point spacing is explicit in our results.
We provided a benchmark configuration suitable for reporting validation data for proton beams for NTCP and TCP calculation. The structure was configured to account for 4 regions of interest in proton therapy: at plateau, at maximum, at penumbra and at range straggling region of a spread out Bragg peak. We provided new reference NTCP/TCP values for all 6 models implemented in TOPAS. Interestingly, the differences between the S-Model and either the LKB model, Critical Volume and Niemierko models, largely fall within the statistical precision of the TOPAS calculation. The largest differences were 1.97%±4.6% for LKB with Eq. 4, 1.57%±4.9% for Niemierko model, 3.74%±1.6% for CV model and 12.05%±0.38% for CE Model.
Finally, for the head and neck patient, the framework implemented in TOPAS allows the simultaneous comparison of all implemented models in a practical scenario, with different criteria for evaluating the TCP/NTCP. In this particular example, the Critical Element, Niemierko and S-Model showed similar results for the Brain stem organ (7–12%).
Acknowledgments
We would like to thank Dr. Josephine Chen at the University of California San Francisco for help with the Pinnacle treatment planning system. This work was supported by National Cancer Institute Grant R01CA140735
References
- [Armstrong2005].Armstrong K, Weber B, Ubel PA, Peters N, Holmes J, Schwartz JS. Individualized survival curves improve satisfaction with cancer risk management decisions in women with BRCA1/2 mutations. J Clin Oncol. 2005;23:9319–9328. doi: 10.1200/JCO.2005.06.119. [DOI] [PubMed] [Google Scholar]
- [Burman1991].Burman C, Kijtcher GJ, Emami B, Goitein M. Fitting of normal tissue tolerance data to an analytical function. Int J Radiation Oncology Biol Phys. 1991;21:123–135. doi: 10.1016/0360-3016(91)90172-z. [DOI] [PubMed] [Google Scholar]
- [Cozzi2000].Cozzi L, Buffa FM, Fogliata A. Comparative analysis of Dose Volume Histogram reduction algorithms for Normal Tissue Complication Probability Calculations. Acta Oncol. 2000;39(2):165–171. doi: 10.1080/028418600430725. [DOI] [PubMed] [Google Scholar]
- [Deasy2003].Deasy JO, Blanco Angel I, Clark Vanessa H. CERR: A computational environment for radiotherapy research. Med Phys. 2003;30(5):979–985. doi: 10.1118/1.1568978. [DOI] [PubMed] [Google Scholar]
- [ElNaqa2006].El Naqa I, Suneja G, Lindsay PE, Hope AJ, Alaly JR, Vicic M, Bradley JD, Apte A, Deasy JO. Dose response explorer: an integrated open-source tool for exploring and modelling radiotherapy dose–volume outcome relationships. Phys Med Biol. 2006;51:5719–5735. doi: 10.1088/0031-9155/51/22/001. [DOI] [PubMed] [Google Scholar]
- [Gay2007]**.Gay HA, Niemierko A. A free program for calculating EUD-based NTCP and TCP in external beam radiotherapy. Phys Med. 2007;23(3–4):115–125. doi: 10.1016/j.ejmp.2007.07.001. The model needs to be traced from here. [DOI] [PubMed] [Google Scholar]
- [GDCM].http://gdcm.sourceforge.net/wiki/index.php/Main_Page.
- [Kallman1992].Källman P, Lind BK, Löf J. Tumor and normal tissue responses to fractionated non-uniform dose delivery” Int. J Radiat Biol. 1992;62(2):249–262. doi: 10.1080/09553009214552071. [DOI] [PubMed] [Google Scholar]
- [Mohan1992].Mohan R, Mageras GS, Baldwin B, Brewster LJ, Kutcher GJ, Leibel S, Burman CM, Ling CC, Fulks Z. Clinically relevant optimization of 3D conformal treatments. Med Phys. 1992;19(4):933–944. doi: 10.1118/1.596781. [DOI] [PubMed] [Google Scholar]
- [Niemierko1991].Niemierko A, Goitein M. Calculation of normal tissue complication probability and dose-volume histogram reduction schemes for tissues with a critical element structure. Radiotherapy and Oncology. 1991;20:166–176. doi: 10.1016/0167-8140(91)90093-v. [DOI] [PubMed] [Google Scholar]
- [Niemierko1992].Niemierko A, Goitein M. Modeling of normal tissue response to radiation: the critical volume model. Int J Radiation Oncology Biol Phys. 1992;25:135–145. doi: 10.1016/0360-3016(93)90156-p. [DOI] [PubMed] [Google Scholar]
- [Okinieff1995].Okunieff P, Morgan D, Niemierko A, Suit H. Radiation dose-response of human tumors. Int J Radiation Oncology Biol Phys. 1995;32(4):1227–1237. doi: 10.1016/0360-3016(94)00475-z. [DOI] [PubMed] [Google Scholar]
- [Paganetti2004].Paganetti H, Jiang H, Lee SY, Kooy HM. Accurate Monte Carlo simulations for nozzle design, commissioning and quality assurance for a proton therapy facility. Med Phys. 2004;31(7):2107–2118. doi: 10.1118/1.1762792. [DOI] [PubMed] [Google Scholar]
- [Paganetti2012].Paganetti H. Range uncertainties in proton therapy and the role of Monte Carlo simulations. Phys Med Biol. 2012;57:R99–R117. doi: 10.1088/0031-9155/57/11/R99. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [Perl2012].Perl J, Shin J, Schumann J, Faddegon B, Paganetti H. TOPAS: an innovative proton Monte Carlo platform for research and clinical applications. Med Phys. 2012;39(11):6818–6837. doi: 10.1118/1.4758060. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [Ramos2012].Ramos-Méndez J, Perl J, Faddegon B, Schümann J, Paganetti H. Geometrical splitting technique to improve the computational efficiency in Monte Carlo calculations for proton therapy. Med Phys. 2012;40(4):041718. doi: 10.1118/1.4795343. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [Rogers1995].Rogers DW, Faddegon BA, Ding GX, Ma CM, We J, Mackie TR. BEAM: a Monte Carlo code to simulate radiotherapy treatment units. Med Phys. 1995;22(5):503–524. doi: 10.1118/1.597552. [DOI] [PubMed] [Google Scholar]
- [Rogers2000].Rogers DW, Mohan R. Questions for comparison of clinical Monte Carlo codes. In: Bortfeld T, Schlegel W, editors. Proceedings of the 31th ICCR. Springer-Verlag; Heidelberg: 2000. pp. 120–122. [Google Scholar]
- [SanchezNieto2000].Sanchez-Nieto B, Nahum AE. Bioplan: software for the biological evaluation of radiotherapy treatment plans. Med Dosim. 2000;25(2):71–76. doi: 10.1016/s0958-3947(00)00031-5. [DOI] [PubMed] [Google Scholar]
- 2009. [Sawkey2009].Sawkey D, Faddegon BA. Simulation of large x-ray fields using independently measured source and geometry details. Med Phys. 2009;36(12):5622–5632. doi: 10.1118/1.3259729. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [Sempau2000].Sempau J, Bielajew AF. Towards the elimination of Monte Carlo statistical fluctuation from dose volume histograms for radiotherapy treatment planning. Phys Med Biol. 2000;45:131–157. doi: 10.1088/0031-9155/45/1/310. [DOI] [PubMed] [Google Scholar]
- [Shin2012].Shin J, Perl J, Schümann J, Paganetti H, Faddegon BA. A modular method to handle multiple time-dependent quantities in Monte Carlo simulations. Phys Med Biol. 2012;57:3295–3308. doi: 10.1088/0031-9155/57/11/3295. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [Shuemann2012].Schümann J, Perl J, Shin J, Faddegon BA, Pagenetti H. Efficient voxel navigation for proton therapy dose calculation in TOPAS and Geant4. Phys Med Biol. 2012;57:3281–3293. doi: 10.1088/0031-9155/57/11/3281. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [Stavrev2001].Stavrev P, Niemierko A, Stavreva N, Goitein M. The application of biological models to clinical data. Physica Medica. 2001;17(2):1–12. [Google Scholar]
- [Stavreva2002].Stavreva NA, Stavrev PV. Some limitations of the application of the NTCP model describing the response of organs with relatively serial structure. Int J Radiat Biol. 2002;78(10):948–950. [PubMed] [Google Scholar]
- [Testa2013].Testa M, Schumann J, Lu J, Shin J, Faddegon B, Paganetti H. Experimental validation of the TOPAS Monte Carlo system for passive scattering proton therapy. Med Phys. 2013;40(12):121719. doi: 10.1118/1.4828781. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [TG105].Chetty IJ, Curran B, DeMarco JJ, Ezzell G, Faddegon BA, Kawrakow I, Keall PJ, Liu H, Ma CM, Rogers DWO, Seuntjens J, Sheikh-Bagheri D, Siebers JV. Report of the AAPM Task Group No. 105, Issues associated with clinical implementation of Monte Carlo-based photon and electron external beam treatment planning. Med Phys. 2007;34(12):4818–4853. doi: 10.1118/1.2795842. [DOI] [PubMed] [Google Scholar]
- [TG166].Li XA, Alber M, Deasy JO, Jackson A, Jee K-WK, Marks LB, Martel MK, Mayo C, Moiseenko V, Nahum AE, Niemierko A, Semenenko VA, Yorke ED. The use and QA of biologically related models for treatment planning. Report of AAPM Task Group 166 of the therapy physics committee. 2012 Mar; doi: 10.1118/1.3685447. [DOI] [PubMed] [Google Scholar]
- [Uzan2009].Uzan J, Nahum AE. BioSuite, new software for radiobiological customization of dose and fraction size in external-beam radiotherapy. 10th Biennial ESTRO meeting.2009. [Google Scholar]
- [Warkentin2004].Warkentin B, Stavrev P, Stavreva N, Field C, Fallone BG. A TCP-NTCP estimation module using DVHs and known radiobiological models and parameter sets. J Applied Clinical Med Phys. 2004;5(1):50–63. doi: 10.1120/jacmp.v5i1.1970. [DOI] [PMC free article] [PubMed] [Google Scholar]