Model selection for degree-corrected block models

Abstract

The proliferation of models for networks raises challenging problems of model selection: the data are sparse and globally dependent, and models are typically high-dimensional and have large numbers of latent variables. Together, these issues mean that the usual model-selection criteria do not work properly for networks. We illustrate these challenges, and show one way to resolve them, by considering the key network-analysis problem of dividing a graph into communities or blocks of nodes with homogeneous patterns of links to the rest of the network. The standard tool for undertaking this is the stochastic block model, under which the probability of a link between two nodes is a function solely of the blocks to which they belong. This imposes a homogeneous degree distribution within each block; this can be unrealistic, so degree-corrected block models add a parameter for each node, modulating its overall degree. The choice between ordinary and degree-corrected block models matters because they make very different inferences about communities. We present the first principled and tractable approach to model selection between standard and degree-corrected block models, based on new large-graph asymptotics for the distribution of log-likelihood ratios under the stochastic block model, finding substantial departures from classical results for sparse graphs. We also develop linear-time approximations for log-likelihoods under both the stochastic block model and the degree-corrected model, using belief propagation. Applications to simulated and real networks show excellent agreement with our approximations. Our results thus both solve the practical problem of deciding on degree correction and point to a general approach to model selection in network analysis.

1. Introduction

In many networks, nodes divide naturally into modules or communities, where nodes in the same group connect to the rest of the network in similar ways. Discovering such communities is an important part of modeling networks [31], as community structure offers clues to the processes which generated the graph, on scales ranging from face-to-face social interaction [39] through social-media communications [1] to the organization of food webs [3, 24].

The stochastic block model [2, 5, 15, 19, 35] has, deservedly, become one of the most popular generative models for community detection. It splits nodes into communities or blocks, within which all nodes are stochastically equivalent [36]. That is, the probability of an edge between any two nodes depends only on which blocks they belong to, and all edges are independent given the nodes’ block memberships. Block models are highly flexible, representing assortative, disassortative and satellite community structures, as well as combinations thereof, in a single generative framework [5, 28, 29]. Their asymptotic properties, including phase transitions in the detectability of communities, can be determined exactly using tools from statistical physics [10, 11] and random graph theory [26].

Despite this flexibility, stochastic block models impose real restrictions on networks; notably in large graphs, within each block, vertex degrees asymptotically follow identical Poisson distributions. This makes the stochastic block model implausible for many networks, where the degrees within each community are highly inhomogeneous. Fitting stochastic block models to such networks tends to split the high- and low- degree nodes in the same community into distinct blocks; for instance, dividing both liberal and conservative political blogs into high-degree ‘leaders’ and low-degree ‘followers’ [1, 23]. To avoid this pathology, and to allow degree inhomogeneity within blocks, there is a long history of generative models where the probability of an edge depends on node attributes as well as their group memberships (e.g., [25, 32]). Here we use a natural generalization of the stochastic block model due to [23], called the degree-corrected block model⁸.

We often lack the domain knowledge to choose between the ordinary and the degree-corrected block model, and so face a model-selection problem. The standard methods of model selection are largely based on likelihood ratios (possibly penalized), and we follow that approach here. Since both the ordinary and the degree-corrected block models have many latent variables, calculating likelihood ratios is itself non-trivial; the likelihood must be summed over all partitions of nodes into blocks, so (in statistical physics terms) the log-likelihood is a free energy. We extend the belief-propagation framework for estimating the free energy [10, 11] to the degree-corrected block model.

Our algorithm is particularly scalable when dealing with sparse networks, which come naturally in the real world from various preferences and limits in the underlying generating processes [13, 18, 22]. However, even with the likelihoods in hand, it turns out that the usual χ² theory for likelihood ratios is invalid in our setting, because of a combination of the sparsity of the data and the high-dimensional nature of the degree-corrected model. To address these situations, which are so prevalent in practice, we derive the correct asymptotics, under regularity assumptions, recovering the classic results in the limit of large, dense graphs. We find that substantial corrections are needed for sparse graphs, corrections that grow with graph size. Simulations confirm the validity of our theory, and we apply our method to both real and synthetic networks.

2. Poisson stochastic block models

Let us set the problem on an observed, stochastic graph with n nodes and m edges; we assume edges are undirected, though the directed case is only notationally more cumbersome. The graph is represented by its symmetric adjacency matrix A. We want to split the nodes into k communities, taking k to be a fixed constant that is the same for both models. (Choosing k is a difficult model-selection problem of its own, and we shall address it elsewhere.)

Traditionally, stochastic block models are applied to simple graphs, where each entry A_uv of the adjacency matrix follows a Bernoulli distribution. Following, e.g., [23], we use a multigraph version of the block model, where the A_uv are independent and Poisson-distributed. (For simplicity, we ignore self-loops.) In the sparse network regime we are most interested in, this Poisson model differs only negligibly from the original Bernoulli model [30], but the former is statistically easier to analyze, especially when compared with its degree-corrected generalization.

In this paper, we shall follow the notion of sparseness as it is defined in [10, 11], that is, when m = O(n), i.e. the number of edges scales (sub)linearly as the network grows; in denser graphs, the average degree diverges as n → ∞.

2.1. The ordinary stochastic block model

In all stochastic block models, each node u has a latent variable G_u ∈ {1, …, k} indicating which of the k blocks it belongs to. The block assignment is then G = {G_u}. The G_u are independent draws from a multinomial distribution parameterized by γ, so γ_r = P(G_u = r) is the prior probability that a node is in block r. Thus G_u ~ Multi(γ). After it assigns nodes to blocks, a block model generates the number of edges A_uv between the nodes u and v by making an independent Poisson draw for each pair. In the ordinary stochastic block model, the means of these Poisson draws are specified by the k × k block affinity matrix ω, so

$$A_{uv}\mid G=g~\text{Poi}({\omega }_{g_u{g}_v}).$$

The complete-data likelihood (involving G as well as A) is

$$\begin{array}{l}{P}_{\text{complete}}(A=a,G=g\mid \gamma ,\omega )=\prod _u{\gamma }_{g_u}\prod _{u<v}\frac{{\omega }_{g_u{g}_v}^{a_{uv}}{\mathrm{e}}^{-{\omega }_{g_u{g}_v}}}{a_{uv}!}\\ =\prod _r{\gamma }_r^{n_r}\prod _{rs}{\omega }_{rs}^{m_{rs}/2}{\mathrm{e}}^{-(1/2)n_r{n}_s{\omega }_{rs}}\prod _{u<v}\frac{1}{a_{uv}!}.\end{array}$$ (1)

Here n_r is the number of nodes in block r, and m_rs the number of edges connecting block r to block s, or twice that number if r = s. The last product in (1) over u and v is constant in the parameters, and 1 for simple graphs. We shall refer to the following equation as the log-likelihood for the rest of the paper:

$$logP(A=a,G=g\mid \gamma ,\omega )=\sum _r{n}_{r}log{\gamma }_r+\frac{1}{2}\left(\sum _{rs}{m}_{rs}log{\omega }_{rs}-n_r{n}_s{\omega }_{rs}\right).$$ (2)

Maximizing (2) over γ and ω gives

$${\widehat{\gamma }}_r=\frac{n_r}{n},{\widehat{\omega }}_{rs}=\frac{m_{rs}}{n_r{n}_s}.$$ (3)

Of course, the block assignments G are not observed, but rather are what we want to infer. We could try to find G by maximizing (2) over γ, ω and g jointly; in terms borrowed from statistical physics, this amounts to finding the ground state ĝ that minimizes the energy −log P (a, g|γ, ω). When this ĝ can be found, it recovers the correct g exactly if the graph is dense enough (denser than) [5]. But if we wish to infer the parameters γ, ω, or to perform model selection, we are interested in the total likelihood of generating the graph a at hand. This is

$$P(A=a\mid \gamma ,\omega )=\sum _{g}P(A=a,G=g\mid \gamma ,\omega ),$$

summing over all kⁿ possible block assignments. Again following the physics lexicon, this is the partition function of the Gibbs distribution of G, and its logarithm is (minus) the free energy.

As is usual with latent variable models, we can infer γ and ω using an EM algorithm [12], where the E step approximates the average likelihood over G with respect to the Gibbs distribution, and the M step estimates γ and ω in order to maximize that average [27]. One approach to the E step would use a Monte Carlo Markov chain algorithm to sample G from the Gibbs distribution. However, as we review below, in order to determine γ and ω it suffices to estimate the marginal distributions of G_u of each u, and joint distributions of (G_u, G_v) for each pair of nodes u, v [4]. As we show in section 3, belief propagation efficiently approximates both the log-likelihood −log P(A = a|γ, ω) and these marginals, and for typical networks it converges very rapidly. Other methods of approximating the E step are certainly possible, and could be used with our model-selection analysis.

2.2. The degree-corrected block model

As discussed above, in the Poisson version of the stochastic block model, all nodes in the same block have the same degree distribution. Moreover, their degrees are sums of independent Poisson variables, so this distribution is Poisson. As a consequence, the stochastic block model resists putting nodes with very different degrees in the same block. This leads to problems with networks where the degree distributions within blocks are highly skewed.

The degree-corrected model allows for heterogeneity of degree within blocks. Nodes are assigned to blocks as before, but each node also gets an additional parameter θ_u, which scales the expected number of edges connecting it to other nodes. Thus

$$A_{uv}\mid G=g~\text{Poi}({\theta }_u{\theta }_v{\omega }_{g_u{g}_v}).$$

Varying the θ_u gives any desired expected degree sequence. Setting θ_u = 1 for all u recovers the stochastic block model, making the latter a special case of the former. In statistical terms, the two form a pair of nested models. This is crucial for our theoretical analysis.

The likelihood stays the same if we increase θ_u by some factor c for all nodes in block r, provided we also decrease ω_rs for all s by the same factor, and decrease ω_rr by c². Thus identification demands a constraint, and here we use the one that forces θ_u to sum to the total number of nodes within each block,

$$\sum _{u:g_u=r}{\theta }_u=n_r.$$ (4)

This constraint allows us to write the complete-data likelihood of the degree-corrected model in a similar mathematical form to that of the ordinary stochastic block model,

$$\begin{array}{l}{P}_{\text{complete}}(A=a,G=g\mid \gamma ,\omega ,\theta )=\prod _u{\gamma }_{g_u}\prod _{u<v}\frac{{({\theta }_u{\theta }_v{\omega }_{g_u{g}_v})}^{a_{uv}}}{a_{uv}!}{e}^{-{\theta }_u{\theta }_v{\omega }_{g_u{g}_v}}\\ =\prod _r{\gamma }_r^{n_r}\prod _u{\theta }_u^{d_u}\prod _{rs}{\omega }_{rs}^{m_{rs}/2}{\mathrm{e}}^{-(1/2)n_r{n}_s{\omega }_{rs}}\prod _{u<v}\frac{1}{a_{uv}!},\end{array}$$ (5)

where n_r and m_rs are as in (1). Again dropping constants, the log-likelihood is

$$logP(A=a,G=g\mid \gamma ,\omega ,\theta )=\sum _r{n}_{r}log{\gamma }_r+\sum _u{d}_{u}log{\theta }_u+\frac{1}{2}\left(\sum _{rs}{m}_{rs}log{\omega }_{rs}-n_r{n}_s{\omega }_{rs}\right).$$ (6)

Maximizing (6) yields

$${\widehat{\theta }}_u=\frac{d_u}{d_{g_u}},{\widehat{\gamma }}_r=\frac{n_r}{n},{\widehat{\omega }}_{rs}=\frac{m_{rs}}{n_r{n}_s},$$ (7)

where

$$d_r=\frac{1}{n_r}\sum _{u:g_u=r}{d}_u$$

is the average degree of the nodes in block r. Notice how (7) agrees with (3) under the same assignment g, with the only difference being the additional parameter θ_u.

However, as with the ordinary stochastic block model, we will estimate θ, γ and ω not just for a ground state ĝ, but using belief propagation to find the marginal distributions of G_u and (G_u, G_v).

3. Belief propagation

We referred above to the use of belief propagation for computing log-likelihoods and marginal distributions of block assignments; for our purposes, belief propagation is essentially a way of performing the expectation step of the expectation-maximization algorithm. Here we describe how belief propagation works for the degree-corrected block model, extending the treatment of the ordinary stochastic block model in [10, 11].

The key idea [37] is that each node u sends a ‘message’ to every other node v, indicating the marginal distribution of G_u if v were absent. We write ${\mu }_r^{u\to v}$ for the probability that u would be of type r in the absence of v. Then μ^u→v gets updated in light of the messages u gets from the other nodes as follows. Let

$$h({\theta }_u,{\theta }_v,{\omega }_{rs},a_{uv})=\frac{{({\theta }_u{\theta }_v{\omega }_{rs})}^{a_{uv}}}{a_{uv}!}{\mathrm{e}}^{-{\theta }_u{\theta }_v{\omega }_{rs}}$$ (8)

be the probability that a_uv takes its observed value if G_u = r and G_v = s. Then

$${\mu }_r^{u\to v}=\frac{1}{Z^{u\to v}}{\gamma }_r\prod _{w\ne u,v}\sum _{s=1}^k{\mu }_s^{w\to u}h({\theta }_{\omega },{\theta }_u,{\omega }_{rs},a_{wu}),$$ (9)

where Z^u→v ensures that ${\sum }_r{\mu }_r^{u\to v}=1$. Here, as usual in belief propagation, we treat the block assignments G_w of the other nodes as independent, conditioned on G_u.

Each node sends messages to every other node, not just to its neighbors, since non-edges (where a_uv = 0) are also informative about G_u and G_v. Thus we have a Markov random field on a weighted complete graph, as opposed to just on the network a itself. However, keeping track of n² messages is cumbersome. For sparse networks, we can restore scalability by noticing that, up to O(1/n) terms, each node u sends the same message to all of its non-neighbors. That is, for any v such that a_uv = 0, we have ${\mu }_r^{u\to v}={\mu }_r^u$ where

$${\mu }_r^u=\frac{1}{Z^u}{\gamma }_r\prod _{w\ne u}\sum _{s=1}^k{\mu }_s^{w\to u}h({\theta }_{\omega },{\theta }_u,{\omega }_{rs},a_{wu}).$$

This simplification reduces the number of messages to O(n + m) where m is the number of edges. We can then write

$${\mu }_r^{u\to v}=\frac{1}{Z^{u\to v}}{\gamma }_r\prod _w\sum _{s=1}^k{\mu }_s^{w}h({\theta }_{\omega },{\theta }_u,{\omega }_{rs},0)\prod _{w\ne v,a_{uw\ne 0}}\frac{{\sum }_{s=1}^k{\mu }_s^{w\to u}h({\theta }_{\omega },{\theta }_u,{\omega }_{rs},a_{wu})}{{\sum }_{s=1}^k{\mu }_s^{w}h({\theta }_{\omega },{\theta }_u,{\omega }_{rs},0)}.$$

Since the second product depends only on θ_u, we can compute it once for each distinct degree in the network, and then update the messages for each u in O(k²d_u) time. Thus, for fixed k, the total time needed to update all the messages is O(m + ℓn), where ℓ is the number of distinct degrees. For many families of networks the number of updates necessary to reach a fixed point is only a constant or O(log n), making the entire algorithm quite scalable (see [10, 11] for details).

The belief-propagation estimate of the joint distribution of G_u, G_v is

$$b_{rs}^{uv}\propto h({\theta }_u,{\theta }_v,{\omega }_{rs},A_{uv}){\mu }_r^{u\to v}{\mu }_s^{v\to u},$$

normalized so that ${\sum }_{rs}{b}_{rs}^{uv}=1$. The maximization step of the expectation-maximization algorithm sets θ, γ and ω

$${\widehat{\theta }}_u=\frac{d_u}{{\overline{d}}_{g_u}},{\widehat{\gamma }}_r=\frac{{\overline{n}}_r}{n}=\frac{{\sum }_u{\mu }_r^u}{n},{\widehat{\omega }}_{rs}=\frac{{\overline{m}}_{rs}}{{\overline{n}}_r{\overline{n}}_s}=\frac{{\sum }_{u\ne v:a_{uv}\ne 0}{a}_{uv}{b}_{rs}^{uv}}{{\sum }_u{\mu }_r^u{\sum }_u{\mu }_s^u},$$ (10)

where n̄_r is the average size of block r, and d̄_r is the average degree of block r, with respect to the belief-propagation estimates. These are very similar to the most likely estimates in (7), and they again share exactly the same formulation as those for the ordinary stochastic block model, with θ_u = 1.

Finally, belief propagation also lets us approximate the total log-likelihood, summed over G but holding the observed graph a fixed. The Bethe free energy is the following approximation to the log-likelihood [38]:

$$logP(A=a\mid \gamma ,\omega ,\theta )\approx \sum _{u}log{Z}^u+\frac{1}{2}\sum _{rs}{\omega }_{rs}{\overline{d}}_r{\overline{d}}_s-\sum _{u\ne v,a_{uv}\ne 0}log\left[\sum _{rs}h({\theta }_u,{\theta }_v,{\omega }_{rs},a_{uv}){\mu }_r^{u\to v}{\mu }_s^{v\to u}\right].$$ (11)

An alternative to belief propagation would be the use of Markov chain Monte Carlo maximum likelihood, which is often advocated for network modeling [21]. However, the computational complexity of Monte Carlo maximum likelihood is typically much worse than that of belief propagation; it does not seem to be practical for graphs beyond a few hundred nodes. We reiterate that while we use belief propagation in our numerical work, our results on model selection in the next section are quite indifferent as to how the likelihood is computed.

4. Model selection

When the degree distribution is relatively homogeneous within each block (e.g., [15, 19]), the ordinary stochastic block model is better than the degree-corrected model, since the extra parameters θ_u simply lead to over-fitting. On the other hand, when degree distributions within blocks are highly heterogeneous, the degree-corrected model is better. However, without prior knowledge about the communities, and thus the block degree distributions, we need to use the data to pick a model, i.e., to do model selection.

It is natural to approach the problem as one of hypothesis testing⁹. Since the ordinary stochastic block model is nested within the degree-corrected model given an assignment g, any given graph a is at least as likely under the latter as under the former. Moreover, if the ordinary block model really is the ground truth, the degree-corrected model should converge to the same ground state, at least in the limit of large networks¹⁰. However, we have averaged our models over the latent variables g, thus using the free energy instead of the most likely ground state energy. Extra precautions are required when applying classical statistical techniques.

Our null model H₀ is the stochastic block model, and the larger, nesting alternative H₁ is the degree-corrected model. The test statistic we are interested in is the total log- likelihood ratio,

$$\mathrm{\Lambda }(a)=log\frac{{sup}_{H_1}{\sum }_{g}P(a,g\mid \gamma ,\omega ,\theta )}{{sup}_{H_0}{\sum }_{g}P(a,g\mid \gamma ,\omega )},$$ (12)

with the P functions defined in (1) and (5).

As usual, we reject the null model in favor of the more elaborate alternative when Λ exceeds some threshold. This threshold, in turn, is fixed by our desired error rate, and by the distribution of Λ when A is generated from the null model. When n is small, the null-model distribution of Λ can be found through parametric bootstrapping [9, section 4.2.3]: fitting H₀, generating new graphs à from it, and evaluating Λ(Ã). When n is large, however, it is helpful to replace bootstrapping with analytical calculations.

Classically [34, Theorem 7.125, p 459], the large-n null distribution of such log-likelihood ratios approaches $\frac{1}{2}{\chi }_{\ell }^2$, where ℓ is the number of constraints that must be imposed on H₁ to recover H₀. In this case we have ℓ = n − k, as we must set all n of the θ_u to 1, while our identifiability convention (4) already imposed k constraints.

However, the χ² distribution rests on the assumption that the log-likelihood of both models is well-approximated by a quadratic function in the vicinity of its maximum, so that the parameter estimates have Gaussian distributions around the true model [16]. The most common grounds for this assumption are central limit theorems for the data, together with a smooth functional dependence of each parameter estimate on a growing number of samples, i.e., being in a ‘large data limit’. This assumption fails in the present case. The degree-corrected model has n node-specific θ_u parameters. Dense graphs have an effective sample size of O(n²), so even with a growing parameter space the degree-corrected model can pass to the large data limit. But in sparse networks, the effective sample size is only O(n), and so we never get the usual asymptotics no matter how large n grows.

Nevertheless, with some work we are able to compute the mean and variance of Λs null distribution. While we recover the classical χ² distribution in the limit of dense graphs, there are important corrections when the graph is sparse, even as n → ∞. As we will show, this has drastic consequences for the appropriate threshold in likelihood ratio tests.

4.1. Analysis of the log-likelihood ratio

To characterize and simplify the null distribution of Λ, we assume that the two models based on the free energy also form a nested pair. That is, if the underlying data is generated by the null model, both models converge to the same joint distributions of G_u. Under this assumption, Λ gives the form of a Kullback–Leibler divergence,

$$\begin{array}{l}\mathrm{\Lambda }=log\frac{{sup}_{H_1}{\sum }_g{\prod }_u{\theta }_u^{d_u}{\prod }_r{\gamma }_r^{n_r}{\prod }_{rs}{\omega }_{rs}^{m_{rs}/2}{\mathrm{e}}^{-(1/2)n_r{n}_s{\omega }_{rs}}}{{sup}_{H_0}{\sum }_g{\prod }_r{\gamma }_r^{n_r}{\prod }_{rs}{\omega }_{rs}^{m_{rs}/2}{\mathrm{e}}^{-(1/2)n_r{n}_s{\omega }_{rs}}}\\ \approx log\frac{{\sum }_g{\prod }_u{\widehat{\theta }}_u^{d_u}{\prod }_r{\widehat{\gamma }}_r^{n_r}{\prod }_{rs}{\widehat{\omega }}_{rs}^{m_{rs}/2}{\mathrm{e}}^{-(1/2)n_r{n}_s{\widehat{\omega }}_{rs}}}{{\sum }_g{\prod }_r{\widehat{\gamma }}_r^{n_r}{\prod }_{rs}{\widehat{\omega }}_{rs}^{m_{rs}/2}{\mathrm{e}}^{-(1/2)n_r{n}_s{\widehat{\omega }}_{rs}}}\\ =log\prod _u{\widehat{\theta }}_u^{d_u}=log\prod _u{\left(\frac{d_u}{{\overline{d}}_{g_u}}\right)}^{d_u}=\sum _u{d}_{u}log\frac{d_u}{{\overline{d}}_{g_u}}\end{array}$$ (13)

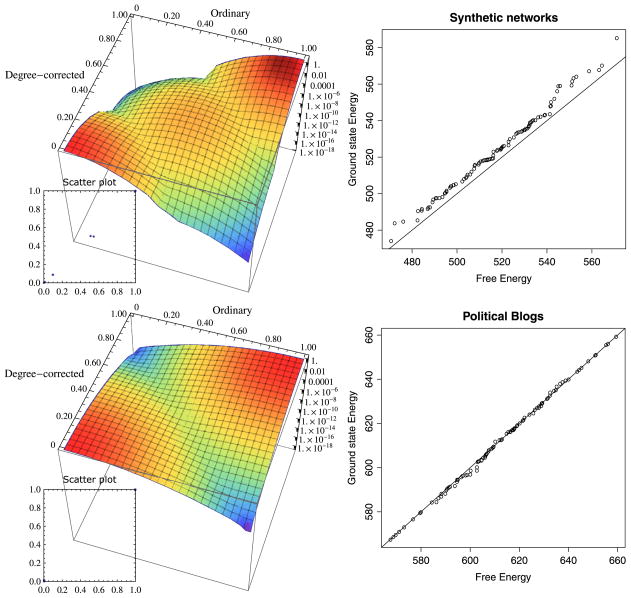
where we substitute in (10). Notice that under this assumption, most likely estimates of the parameters under H₀ and H₁ agree, and each term in the sums in the numerator and denominator cancels to the exact same ratio ${\prod }_u{\widehat{\theta }}_u^{d_u}$. Keep in mind that d̄_r is the empirical mean degree of block r, not the expected degree μ_r =Σ_s γ_sω_rs of the stochastic block model. Using our belief-propagation algorithm, we can verify the above assumption based on the marginal distributions of G_u and (G_u, G_v) (figure 1, left column).

Figure 1.

Left column: 3D heat maps with top-view scatter plots of posterior probabilities over block assignments, according to our belief-propagation algorithm on one of the sample networks. It shows that the ordinary and the degree-corrected block models converge to the same marginal distributions of G_u (first assumption). Furthermore, the concentration of the marginals suggests the strong dominance of the ground state (second assumption). The x- and y-axes in both parts are the marginal probabilities of being in block 1 according to ordinary and degree-corrected models, respectively. The Z-axes are logarithmic. Right column: QQ plots (100 samples) for comparing the distributions of the ground state energy difference to those of free energy difference under the null model. A point in a QQ plot corresponds to one of the quantiles of the first distribution (x-coordinate) plotted against the same quantile of the second distribution (y-coordinate). Observe that here the points approximately lie on the line y = x, which means that the two distributions are very similar. Top row: synthetic network with n = 10³, k = 2 equally-sized blocks (γ₁ = γ₂ = 1/2), average degree μ_r = 11, and associative structure with ω₁₂/ω₁₁ = ω₂₁/ω₂₂ = 1/11. Bottom row: bootstrapped networks with the assignments and parameters of the political blog network.

For further confirmation, we can justify (13) with an alternative assumption. If the posterior distributions P(G = g | A = a, γ, ω) and P(G = g | A = a, γ, ω, θ) concentrate on the same block assignment g, the maximum-likelihood estimates for H₀ and H₁ are then (3) and (7) respectively. Substituting these into (12), most terms cancel and we recover (13)

$$\begin{array}{l}\mathrm{\Lambda }\approx log\frac{{sup}_{H_1}{\prod }_u{\theta }_u^{d_u}{\prod }_r{\gamma }_r^{n_r}{\prod }_{rs}{\omega }_{rs}^{m_{rs}/2}{\mathrm{e}}^{-(1/2)n_r{n}_s{\omega }_{rs}}}{{sup}_{H_0}{\prod }_r{\gamma }_r^{n_r}{\prod }_{rs}{\omega }_{rs}^{m_{rs}/2}{\mathrm{e}}^{-(1/2)n_r{n}_s{\omega }_{rs}}}\\ =log\underset{H_1}{sup}\prod _u{\theta }_u^{d_u}=log\prod _u{\left(\frac{d_u}{d_{g_u}}\right)}^{d_u}=\sum _u{d}_{u}log\frac{d_u}{d_{g_u}}.\end{array}$$

Either justification is a major approximation. Fortunately for us, while the free energy differs from the ground state energy, the free energy difference between the two models follows a very similar distribution to the ground state energy difference. According to our simulations (figures 1 and 2(c)), both assumptions tend to hold on synthetic networks with prescribed blocks as well as on bootstrapped networks with real world assignments and parameters. For small average degree, which is the focus of our work, we will see that the obtained analytical formulas agree well with the actual log-likelihood ratio evaluated from simulations.

Figure 2.

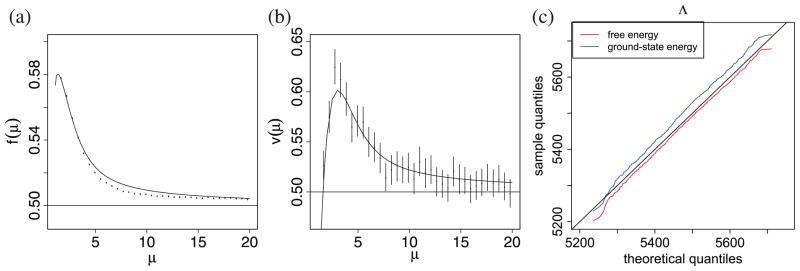
Comparison of asymptotic theory to finite-n simulations. We generated networks from the stochastic block model with varying average degree μ (n = 10⁴, k = 2, γ₁ = γ₂ = 1/2, ω₁₁ = ω₂₂, and ω₁₂/ω₁₁ = ω₂₁/ω₂₂ = 0.15) and computed Λ (the log-likelihood ratio) for each graph. Parts (a) and (b) show n⁻¹E(Λ) and n⁻¹var(Λ), comparing 95% bootstrap confidence intervals (over 10³ replicates) to the asymptotic formulas (respectively f(μ) from (15) and v(μ) from (17)). Part (c) compares the distribution of Λ from 10⁴ replicates, all with μ = 3, to a Gaussian with the theoretical mean and variance.

Given (13), the distribution of Λ follows from the distributions of the nodes’ degrees; under the null model, all the D_u in block r are independent ~Poi(μ_r). (This assumption is sound in the limit n → ∞, since the correlations between node degrees are O(1/n).) Using this, we can compute the expectation and variance of Λ analytically (see appendix), showing that Λ departs from classical χ² asymptotics, as well as revealing the limits where those results apply. Specifically,

$$E(\mathrm{\Lambda })=\sum _r{n}_{r}f({\mu }_r)-f(n_r{\mu }_r)$$ (14)

where, if D ~ Poi(μ),

$$f(\mu )=E(\mathit{D}logD)-\mu log\mu .$$ (15)

For dense graphs, where μ → ∞, both f(μ) and f(nμ) approach 1/2, and (14) gives E(Λ) = (n − k)/2 just as in the standard χ² analysis. However, when μ is small, f(μ) differs noticeably from 1/2.

The variance of Λ is somewhat more complicated. The limiting variance per node is

$$\underset{n\to \infty }{lim}\frac{1}{n}var(\mathrm{\Lambda })=\sum _r{\gamma }_{r}v({\mu }_r),$$ (16)

where, again taking D ~ Poi(μ),

$$v(\mu )=\mu {(1+log\mu )}^2+var(\mathit{D}logD)-2(1+log\mu )cov(D,\mathit{D}logD).$$ (17)

Since the variance of ${\chi }_{\ell }^2$ is 2ℓ, χ² asymptotics would predict (1/n)var(Λ) = 1/2. Indeed v(μ) approaches 1/2 as μ → ∞, but like f(μ) it differs substantially from 1/2 for small μ. Figure 2 plots f(μ) and v(μ) for 1 ≤ μ ≤ 10.

Figure 2 shows that, for networks simulated from the stochastic block model, the mean and variance of Λ are very well fitted by our formulas. We have not attempted to compute higher moments of Λ. However, if we assume that D_u are independent, then the simplest form of the central limit theorem applies, and n⁻¹Λ will approach a Gaussian distribution as n → ∞. Quantile plots from the same simulations (figure 2(c)) show that a Gaussian with mean and variance from (14) and (16) is indeed a good fit. Moreover, the free energy difference and the ground state energy difference have similar distributions, as implied by either of our assumptions when deriving equation (13). Interestingly, in figure 2(c), the degree is low enough that this concentration must be imperfect, but our theory still holds remarkably well. For ease of illustration, we assume that γ_r = 1/k and μ_r are the same for all r.

Fundamentally, Λ does not follow the usual χ² distribution because the θ parameters are in a high-dimensional regime. For each θ_u, we really have only one relevant observation, the node degree D_u. If θ_u is large, then the Poisson distribution of D_u is well-approximated by a Gaussian, as is the sampling distribution of the most likely estimate of θ_u, so that the usual χ² analysis applies. In a sparse graph, however, all the Poisson distributions have small expected values and are highly non-Gaussian, as are the maximum-likelihood estimates [40]. Stated differently, the degree-corrected model has O(n) more parameters than the null model. In the dense-graph case, there are O(n²) observations, at least O(n) of which are informative about each of these extra parameters. For sparse graphs, however, there are really only O(n) observations, and only O(1) of them are informative about each θ_u, so the ordinary large-n asymptotics cannot apply to them. As we have seen, the expected increase in likelihood from adding the θ parameters is larger than χ² theory predicts, as are the fluctuations in this increase in likelihood.

This reasoning elaborates on a point made long ago by [14] regarding hypothesis testing in the p₁ model, where each node has two node-specific parameters (for in- and out-degree); our calculations of f(μ) and v(μ) above, and in particular of how and why they differ from 1/2, go some way towards meeting Fienberg and Wasserman’s call for appropriate asymptotics for large-but-sparse graphs.

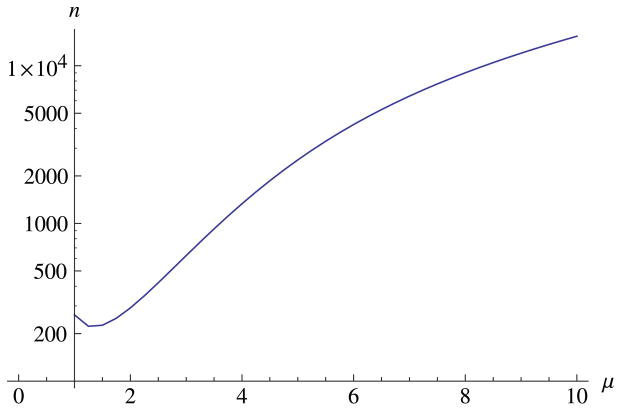
Ignoring these phenomena and using a χ² test inflates the type I error rate (α), eventually rejecting the stochastic block model for almost all graphs which it generates. Indeed, since the χ² distribution is tightly peaked around 0.5n, this inflation of α gets worse as n gets bigger. For instance, if we use the standard rejecting criteria of p-value < 0.05, when μ = 5, a χ² test commits a type I error with 95% confidence at roughly n = 3000, while for μ = 3, this happens once n ≈ 700 (figure 3). In essence, the χ² test underestimates the amount of degree inhomogeneity we would get simply from noise, incorrectly concluding that the inhomogeneity must come from underlying properties of the nodes.

Figure 3.

The size n, as a function of the average degree μ, above which a naive χ² test commits a type I error with 95% confidence. Type I error means incorrectly rejecting the ordinary stochastic block model for graphs that are actually generated by it. Here we assume the asymptotic analysis of (14)–(17) for the mean and variance of the likelihood ratio.

5. Results on real networks

We have derived the theoretical null distribution of Λ, and backed up our calculations with simulations. We now apply our theory to two examples, considering networks studied in [23].

The first is a social network consisting of 34 members of a karate club, where undirected edges represent friendships [39]. The network is made up of two assortative blocks, each with one high-degree hub (respectively the instructor and the club president) and many low-degree peripheral nodes. Karrer and Newman [23] compared the performance of the ordinary and the degree-corrected block models on this network, and heavily favored degree correction, because the latter leads to division into communities agreeing with ethnographic observations.

While a classic data set for network modeling, the karate club has both low degree and very small n. If we nonetheless use parametric bootstrapping to find the null distribution of Λ, we see that it fits a Gaussian with our predicted mean and variance reasonably well (figure 4(a)). The observed Λ = 20.7 has a p-value of 0.187 according to the bootstrap, and 0.186 according to our Gaussian asymptotics. Thus a prudent analyst would think twice before embracing the n additional degree-correction parameters. Indeed, using active learning, [24] found that the stochastic block model labels most of the nodes correctly if the instructor and the president are forced into different blocks (red nodes in 4(b)). This implies that the degree inhomogeneity is mild, and that only a handful of nodes are responsible for the better performance of the degree-corrected model.

Figure 4.

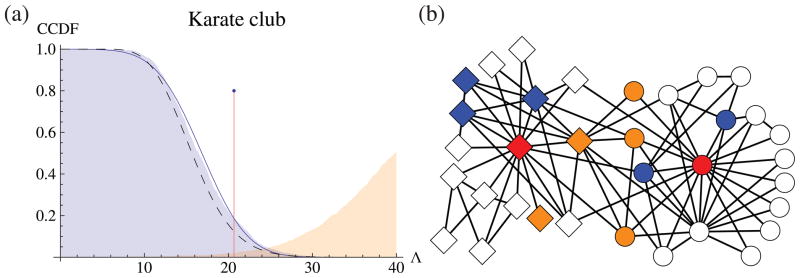
(a) Complementary cumulative distribution function of the log-likelihood ratio Λ for testing for degree correction. The distribution found by parametric bootstrapping (blue shaded) fits reasonably well to a Gaussian (curve) with our theoretical mean and variance. The observed Λ = 20.7 (marked with the red line) has p-values of 0.186 and 0.187 according to the bootstrap and theoretical distributions respectively, whereas the χ² test (dashed) has a p-value of 0.125. If we bootstrap the karate club using the degree-corrected block model (orange shaded, CDF), the observed Λ = 20.7 has an even smaller p-value (0.02) for being at most that much. (b) Query order chosen by the active learning algorithm by [24]. Red nodes are the top priorities, followed by orange nodes. Blue nodes are the last to query. Once the red nodes are placed into separate blocks, the ordinary stochastic block model can find the correct block (indicated by shape) for most of the nodes.

Note that if we apply standard χ² testing to the karate club, we obtain a lower p-value of 0.125. As in figure 3, χ² testing underestimates the extent to which an inhomogeneous degree distribution can result simply from noise, causing it to reject the null model more confidently than it should. This is further confirmed by the bootstrapping results under the alternative model (Orange shade in figure 4(a)). With an even lower p-value of 0.02, the karate club network is very unlikely to be generated by the degree-corrected block model.

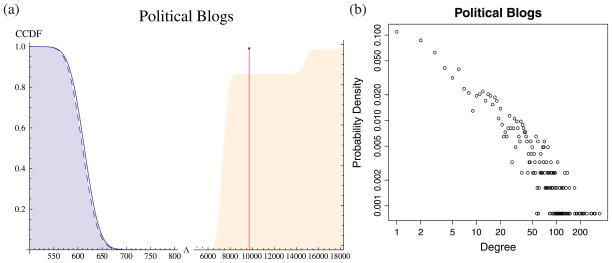
The second example is a network of political blogs in the US assembled by [1]. As in [23], we focus on the giant component, which contains 1222 blogs with 19 087 links between them. The blogs have known political leanings, and were labeled as either liberal or conservative. The network is politically assortative, with a heavy-tailed degree distribution (see figure 5(b)) within each block, so degree correction greatly assists in recovering political divisions, as observed by [23]. This time around, our hypothesis testing procedure completely agrees with their choice of model. As shown in figure 5(a), the bootstrap distribution of Λ is very well fit by a Gaussian with our theoretical prediction of the mean and variance. The observed log-likelihood ratio Λ = 8883 is 330 standard deviations above the mean. It is essentially impossible to produce such extreme results through mere fluctuations under the null model. Thus, for this network, introducing n extra parameters to capture the degree heterogeneity is fully justified. This is again confirmed by the bootstrapping results under the alternative model (Orange shade in figure 5(a)). With a respectable p-value of 0.876, the political blog network is very likely to be generated by the degree-corrected block model.

Figure 5.

(a) Complementary cumulative distribution function of the log-likelihood ratio Λ for testing for degree correction. The bootstrap distribution (shaded) is very well fitted by our theoretical Gaussian (curve) as well as the χ² test (blue dashed). The actual log-likelihood ratio is so far in the tail (marked with the red line) that its p-value is effectively zero (notice the break and indices of the x-axis). If we bootstrap the political blogs using the degree-corrected block model (orange shaded, CDF), the observed Λ = 8883 has a p-value of 0.876 for being at most that much. (b) Degree distribution of political blogs. Both the x-axis and the y-axis are logarithmic. This empirical distribution has a heavy tail and is very different from the Poisson distribution predicted by the ordinary stochastic block model.

The blog network shows the advantage of theoretical approaches over bootstrapping. As with many other real networks, n is too large for efficient bootstrapping. However, since this is a relatively dense network, the naive χ² test does just as well as our theoretical approximation for Λ.

6. Conclusion

Deciding between ordinary and degree-corrected stochastic block models for sparse graphs presents a difficult hypothesis testing problem. The distribution of the log-likelihood ratio Λ does not follow the classic χ² theory, because the nuisance parameter θ, only present in the alternative, is in a high-dimensional regime. We have nonetheless derived unbiased estimations of Λ’s mean and variance in the limit of large, sparse graphs, where node degrees become independent and Poisson. Simulations confirm the accuracy of our theory for moderate n, and we applied it to two real networks.

Beyond hypothesis testing, two standard approaches to model selection are information criteria and cross-validation. While we have not directly dealt with the former, the derivations of such popular criteria as the Akaike information criterion or deviance information criterion use exactly the same asymptotics as the χ² test [7, chapter 2]; these tools will break down for the same reasons χ² theory fails. As for cross-validation, standard practice in machine learning suggests using multi-fold cross-validation, but the global dependence of network data means there is (as yet) no good way to split a graph into training and testing sets. Predicting missing links or tagging false positives are popular forms of leave-k-out cross-validation in the network literature [8, 17], but leave-k-out does not converge on the true model even for independent and identically-distributed data [7, section 2.9]. Thus, while our results apply directly only to the specific problem of testing the need for degree correction, they open the way to more general approaches to model selection and hypothesis testing in a wide range of network problems.

Appendix. Behavior of Λ under the null hypothesis

For simplicity we focus on one block with expected degree μ. Independence between blocks will then recover the expressions (14) and (16) where the mean and variance of Λ is a weighted sum over blocks. We have

$$\begin{array}{l}\mathrm{\Lambda }=\sum _{i=1}^n{D}_{i}log\frac{D_i}{\overline{D}}\\ =\sum _i{D}_{i}log{D}_i-\left(\sum _i{D}_i\right)log\left(\sum _i{D}_i\right)+\left(\sum _i{D}_i\right)logn,\end{array}$$ (A.1)

where D̄ = (1/n) Σ_i D_i is the empirical mean degree. We wish to compute the mean and expectation of Λ if the data are generated by the null model.

If D ~ Poi(μ), let f(μ) denote the difference between the expectation of D log D and its most probable value μ log μ,

$$f(\mu )=\left(\sum _{d=1}^{\infty }\frac{{\mathrm{e}}^{-\mu }{\mu }^d}{d!}\mathit{d}logd\right)-\mu log\mu .$$ (A.2)

Assume that the D_i are independent and ~Poi(μ); this is reasonable in a large sparse graph, since the correlation between degrees of different nodes is O(1/n). Then nD̄ ~ Poi(nμ), and (A.1) gives

$$E(\mathrm{\Lambda })=nf(\mu )-f(n\mu ).$$ (A.3)

To grasp what this implies, begin by observing that f(μ) converges to 1/2 when μ → ∞. Thus in the limit of large n, $E(\mathrm{\Lambda })=nf(\mu )-\frac{1}{2}$. When μ is large, this gives E(Λ) = (n − 1)/2, just as χ² theory suggests. However, as figure A.1 shows, f(μ) deviates noticeably from 1/2 for finite μ. We can obtain the leading corrections as a power series in 1/μ by approximating (A.2) with the Taylor series of d log d around d = μ, giving

$$f(\mu )=\frac{1}{2}+\frac{1}{12\mu }+\frac{1}{12{\mu }^2}+O(1/{\mu }^3).$$

Figure A.1.

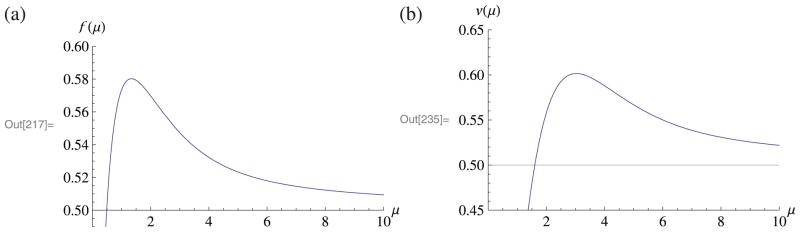
(a) Asymptotic limit of n⁻¹E(Λ), the f(μ) of (A.2). (b) Asymptotic limit of n⁻¹var(Λ), from (A.8). Here μ is the average degree, and Λ is the log-likelihood ratio. Figure 2 compares these to simulations.

Computing the variance is harder. It will be convenient to define several functions. If D ~ Poi(μ), let ϕ(μ) denote the variance of D log D,

$$\varphi (\mu )=var(\mathit{D}logD)=\sum _{d=0}^{\infty }\frac{e^{-\mu }{\mu }^d}{d!}{(\mathit{d}logd)}^2-{(f(\mu )+\mu log\mu )}^2.$$ (A.4)

We will also use

$$c(\mu )=cov(D,\mathit{D}logD)=\sum _{d=1}^{\infty }\frac{e^{-\mu }{\mu }^d}{d!}{d}^{2}logd-\mu (f(\mu )+\mu log\mu ).$$ (A.5)

Finally, let ψ ≥ μ, and let D and U be independent and Poisson with mean μ and ψ − μ respectively. Then let

$$\begin{array}{l}r(\mu ,\psi )=cov(\mathit{D}logD,(D+U)log(D+U))\\ =E((\mathit{D}logD)((D+U)log(D+U)))-E(\mathit{D}logD)E((D+U)log(D+U))\\ =E((\mathit{D}logD)((D+U)log(D+U)))-(f(\mu )+\mu log\mu )(f(\psi )+\psi log\psi ),\end{array}$$ (A.6)

where we use the fact that D + U ~ Poi(ψ).

Again assuming that the D_i are independent, we have the following terms and cross-terms for the variance of (A.1):

$$\begin{array}{ll}\hfill var\left(\sum _i{D}_{i}log{D}_i\right)& =n\varphi (\mu )\hfill \\ \hfill var((n\overline{D})log(n\overline{D}))& =\varphi (n\mu )\hfill \\ \hfill var(n\overline{D})& =n\mu \hfill \\ \hfill cov\left(\sum _i{D}_{i}log{D}_i,(n\overline{D})log(n\overline{D})\right)& =nr(\mu ,n\mu )\hfill \\ \hfill cov\left(\sum _i{D}_{i}log{D}_i,n\overline{D}\right)& =nc(\mu )\hfill \\ \hfill cov((n\overline{D})logn\overline{D},n\overline{D})& =c(n\mu ).\hfill \end{array}$$

Putting this all together, we have

$$var(\mathrm{\Lambda })=n\varphi (\mu )+\varphi (n\mu )+n\mu {log}^{2}n-2nr(\mu ,n\mu )+2(nc(\mu )-c(n\mu ))logn.$$ (A.7)

For large μ, Taylor-expanding the summands of (A.4) and (A.5) yields

$$\begin{array}{ll}\hfill \varphi (\mu )& =\mu {log}^2\mu +2\mu log\mu +\mu +\frac{1}{2}+O\left(\frac{log\mu }{\mu }\right)\\ \hfill c(\mu )& =\mu log\mu +\mu +O(1/\mu ).\end{array}$$

Also, when ψ ≫ μ and μ = O(1), using log (D + U) ≈ log U + D/U lets us simplify (A.6), giving

$$r(\mu ,\lambda )=E(D^{2}logD)(1+log\lambda )+E(\mathit{D}logD)E(\mathit{U}logU)-E(\mathit{D}logD)E((D+U)logD+U))+O(1/\lambda ).$$

In particular, setting ψ = nμ gives

$$r(\mu ,n\mu )=c(\mu )(1+logn\mu )+O(1/n).$$

Finally, keeping O(n) terms in (A.7) and defining v(μ) as in (16) gives

$$v(\mu )=\underset{n\to \infty }{lim}\frac{1}{n}var(\mathrm{\Lambda })=\varphi (\mu )+\mu {(1+log\mu )}^2-2c(\mu )(1+log\mu ).$$ (A.8)

Using the definitions of ϕ and c, we can write this more explicitly as

$$v(\mu )=\mu {(1+log\mu )}^2+var(\mathit{D}logD)-2(1+log\mu )cov(D,\mathit{D}logD),$$ (A.9)

where D ~ Poi(μ). We plot this function in figure A.1(b). It converges to 1/2 in the limit of large μ, but it is significantly larger for finite μ.