Therapist recognition of impaired muscle groups in simulated multi-joint hypertonia

Abstract

It is common in today’s clinical practice for a therapist to physically manipulate patients’ limbs to assess hypertonic conditions (e.g. spasticity, rigidity, dystonia, among others). We present a study that evaluates the capabilities of expert therapists to correctly identify the location of a hypertonic impairment of an arm through standard manipulation. Therapists interacted with a hypertonic virtual arms rendered on a robotic device. Our results show that testing joints independently can cause misjudgment of the mechanical contributions of pluri-articular muscles to multi-joint impairment.

I. Introduction

A frequent condition that contribute to poor voluntary motor performance or involuntary muscle contractions after neuro-muscular disorders (e.g. cerebral palsy, Parkinson’s disease or after stroke) is hypertonia [3, 4]. Hypertonia is a collective manifestation of symptoms that induce an abnormal increase in resistance to an externally imposed movement [5]. Depending on the pathophysiology it can be categorized as spasticity, dystonic hypertonia, rigidity, to name few. Current clinical assessments of hypertonia (e.g. modified Ashworth scale, Tardieu scale, Hypertonia Assessment Tool) [6–9] are based on physical manipulation of the patient by the therapist and are restricted to single joints. Yet, hypertonia can encompass alteration of inter-muscular (heteronymous) reflexes [10] or abnormal multi-joint couplings due to increased rigidity [11, 12]. Hence, it is essential to extend the manual assessment of hypertonia to more than one joint so as to capture the effect of multi-joint coupling.

A first step to achieve this goal is to understand the human capabilities to distinguish different haptic stimuli during physical patient-therapist interaction. To this end, we propose the use of a physical simulator, in which a model of an impaired arm is rendered on a robotic device and therapists can physically interact with it. We conceived a simple representation of the human arm (two joints, six muscle groups) in which the force produced by muscles is a linear combination of non-linear passive and active components. This simple, yet representative, model allows us to simulate different normal and hypertonic-like forces at the point of interaction by increasing both the intrinsic rigidity and the active reflexes in the model.

In this paper, we investigated how different hypertonic-like conditions are haptically recognized by therapists. In particular, we present a study that evaluates the capabilities of expert therapists in discriminating between different hypertonic virtual arms with diverse muscle groups affected. Three different muscles groups were tested – i) hypertonic shoulder muscles, ii) hypertonic elbow muscles and iii) hypertonic bi-articular muscles – at four levels of severity – i) very mild, ii) mild, iii) moderate and iv) severe. We identified the manipulation strategies and quantified the therapists’ capability to correctly identify the location of impairment. Our results indicate that the mechanical contributions of pluri-articular muscles to multi-joint impairment can cause expert therapists to make an incorrect diagnosis.

II. Materials and Methods

Six right-handed licensed therapists (5 females, 1 male, between 30 and 35 years-old), qualified to diagnose hypertonia and administer the Ashworth scale for the assessment of spasticity participated in the study. Subjects gave informed consent prior to participation. Experiments were approved by the Northwestern University’s Institutional Review Board.

A. Apparatus

Therapists were seated in front of a two degrees of-freedom robotic manipulandum and interacted with a physical model of an arm (virtual arm) by holding the robot’s end effector (Figure 1) [13]. The model was implemented in Simulink and was executed in real-time using xPC Target at a rate of 1 kHz.

Figure 1.

A therapist interacting with a simulated hypertonic arm.

Therapists held the handle with the end-effector positioned at the center of the robot’s workspace. The arm model was rendered as if the virtual patient were seated opposite to the therapist. Both the therapists’ hand and the robotic arm were covered by an opaque horizontal screen, on which the image of the rendered virtual arm was projected. The image of a 35 cm diameter circle was shown centered at the virtual arm endpoint and represented most of the virtual arm workspace. Before the beginning of each trial, subjects saw the static image of the arm while a white dot moved synchronously with the position of the subject hand. In order to activate the physical therapists-model physical interaction, therapists needed to bring the white dot to the depicted virtual hand (a virtual “hand shake”).

B. Experimental protocol

The experiment was divided in two consecutive phases: a) familiarization and b) assessment. During familiarization, participants interacted with four different virtual arms: i) unimpaired arm, ii) maximally impaired shoulder, iii) maximally impaired elbow and iv) maximally impaired bi-articular muscles. Subjects interacted sequentially with each condition in blocks of 30s for eight trials (8 trials x 4 conditions = 32 trials). During this phase, a legend appeared on the top right corner of the screen indicating the condition that the therapist was experiencing. Therapists were free to interact with those four conditions as they wished in order to familiarize with the different haptic sensations produced by the hypertonic muscle groups.

During assessment, therapists were randomly presented with different abnormal virtual arms of varied hypertonic severity. Their task was to identify which group of muscles was impaired. Therapists were presented each condition nine times in trials of 15s (3 hypertonic conditions x 4 levels of severity x 9 trials = 108 trials). The only information available to the therapist during this phase was the configuration of the arm and the rendered force at the end effector. After physical manipulation of the virtual arm, therapists were required to select one of the three options presented on the screen – shoulder, elbow, or both. Participants could take as much time as they wanted to give their assessments and start a new trial. The whole experiment lasted for about 45 minutes.

C. Neuro-mechanical model of the human arm

The dynamics of the virtual arm moving in a horizontal plane while interacting with the environment were modeled as:

$$H(q)\ddot{q}+C\left(q,\stackrel{.}{q}\right)\stackrel{.}{q}=J_q{(q)}^T·F_{\text{external}}-J_{\lambda }^T·\left(\mathrm{\Phi }\left(\lambda ,u(\stackrel{.}{\lambda })\right)+\mathrm{\Psi }(\lambda )\right)$$ (1)

H(q) is the arm inertia matrix of a double pendulum, q denote the vector of shoulder and elbow joint angles [rad], C(q,q̇)q̇ is the term corresponding to Coriolis and centripetal forces, J_q(q) is the Jacobian matrix transforming endpoint force into joint torque.

We assumed the Jacobian matrix [m] transforming muscle tension into joint torque, J_λ independent of the joint angles [2]. This term essentially contains the muscle moment arms ρ [m] at any particular position which for simplicity can be considered constant with values falling on reported anthropometric data in the literature [2], thus:

$$J_{\lambda }(\lambda )={\left(\begin{array}{cccccc}-{\rho }_{sf}& {\rho }_{se}& 0& 0& -{\rho }_{{bf}_1}& {\rho }_{{be}_1}\\ 0& 0& -{\rho }_{ef}& {\rho }_{ee}& -{\rho }_{{bf}_2}& {\rho }_{{be}_2}\end{array}\right)}^T$$ (2)

The sub-indexes correspond to sf, shoulder adductors (Deltoid anterior, Coracobrachialis, Pectoralis major clav.); se, the shoulder abductors (Deltoid posterior); ef, elbow flexors (Biceps long, Brachialis, Brachioradialis); ee, elbow extensors (Triceps lateral, Anconeus); bf, bi-articular flexors (Biceps short); and be, bi-articular extensors (Triceps long) muscle groups. Simulation-specific parameters are reported in Table II.

Table II.

Joint and Cartesian Stiffness when all Muscle groups are impaired

Level of severity	υ	κ	Kq | λ = 0 [N · m/rad]	Kx | λ = 0 [N/m]
Normal	0.0	3	$\left(\begin{array}{cc}2.03& 0.47\\ 0.47& 1.18\end{array}\right)$	$\left(\begin{array}{cc}23.48& -10.65\\ -10.65& 17.72\end{array}\right)$
Very mild	0.25	5	$\left(\begin{array}{cc}3.39& 0.78\\ 0.78& 1.96\end{array}\right)$	$\left(\begin{array}{cc}39.14& -17.76\\ -17.76& 29.54\end{array}\right)$
Mild	0.5	8	$\left(\begin{array}{cc}5.43& 1.26\\ 1.26& 3.15\end{array}\right)$	$\left(\begin{array}{cc}62.62& -28.42\\ -28.42& 47.27\end{array}\right)$
Moderate	0.75	13	$\left(\begin{array}{cc}8.83& 2.05\\ 2.05& 5.15\end{array}\right)$	$\left(\begin{array}{cc}101.76& -46.18\\ -46.18& 76.82\end{array}\right)$
Severe	1.0	21	$\left(\begin{array}{cc}14.27& 3.31\\ 3.31& 8.27\end{array}\right)$	$\left(\begin{array}{cc}164.39& -74.60\\ -74.60& 124.10\end{array}\right)$

The force of each muscle group is modeled as a linear combination of active (i.e. produced by a motor command u) and passive (i.e. produced by intrinsic rigidity of the muscles and connective tissue) components [14, 15]. The force produced on each muscle by the motor command u is:

$$\begin{array}{l}\mathrm{\Phi }(\lambda ,u(\stackrel{.}{\lambda }))={(\begin{array}{cccccc}{\phi }_{sf}& {\phi }_{se}& {\phi }_{ef}& {\phi }_{ee}& {\phi }_{bf}& {\phi }_{be}\end{array})}^T\\ {\phi }_i=max\left(\begin{array}{l}0,\hfill \\ {\alpha }_{i}u({\stackrel{.}{\lambda }}_i)·\mathrm{\Gamma }·e^{-{(\mathrm{\Gamma })}^2}\hfill \end{array}\right);\mathrm{\Gamma }=\left(\frac{{\lambda }_i}{{\lambda }_{max,i}}-\left(1-u({\stackrel{.}{\lambda }}_i)\right)\right)\end{array}$$ (3)

The term τ corresponds to the muscle stiffness, and u(λ̇) to an active motor command that depends on the muscle stretch velocity and is defined as:

$$u({\stackrel{.}{\lambda }}_i)={\beta }_{i}min\left(1,max\left(0,\frac{{\stackrel{.}{\lambda }}_i}{{\stackrel{.}{\lambda }}_{max,i}}\right)\right)\mid {\beta }_i\in [0,1]$$ (4)

where β corresponds to a “stretch reflex gain”. The variables λ_max,i, and λ̇_max,i correspond to the maximum length and rate of length change of the i^th muscle group. The maximum rate of length change was calculated as the one obtained by moving the end point of virtual arm along the circle of 35cm in diameter at a frequency of 3Hz.

The force produced by the intrinsic rigidity of the muscles and connective tissue is function of the muscle length and is defined as:

$$\begin{array}{l}\mathrm{\Psi }(\lambda )={(\begin{array}{llllll}{\psi }_{sf}\hfill & {\psi }_{se}\hfill & {\psi }_{ef}\hfill & {\psi }_{ee}\hfill & {\psi }_{bf}\hfill & {\psi }_{be}\hfill \end{array})}^T\\ {\psi }_i=max\left(\begin{array}{l}0,\hfill \\ K_{m,i}\left({\lambda }_i-{\lambda }_{\mathit{rest},i}\right)e^{-{\left({\lambda }_i-{\lambda }_{\mathit{rest},i}\right)}^2}\hfill \end{array}\right)\end{array}$$ (5)

The term λ_i and K_m,i, represent the length and rigidity of the i^th muscle group. The variable λ_rest,i, corresponds to the length at rest in the equilibrium position. The term Ψ(λ) can be multiplied by a generalized logistic function to avoid sharp discontinuities when adding both passive and active components in eq. (1).

D. Selection of Rigidity boundary parameters

Measurements of joints’ rigidity during passive movements are available in the literature for both stroke survivors and unimpaired individuals [16, 17]. Based on such data, we assumed the average joint passive stiffness of unimpaired individuals as the lower boundary of joint rigidity, namely: $K_q=\left(\begin{array}{cc}2& 0.5\\ 0.5& 1\end{array}\right)[N·m/\mathit{rad}]$. The upper boundary of joint rigidity was set as $K_q=\left(\begin{array}{cc}14& 3\\ 3& 8\end{array}\right)[N·m/\mathit{rad}]$, this value corresponds to the passive stiffness recorded on stroke survivors with Modified Ashworth Score (MAS) equal to 4 [11, 18].

E. Simulating hypertonic-like forces

Among the numerous factors that characterize hypertonia we are interested in verifying the participants’ ability to discriminate forces produced by increased muscle rigidity and the nonlinear phenomena associated with velocity dependent stiffness. To this end, we assumed that hypertonic-like forces could be achieved by increasing both the stiffness term α and rigidity term K_m eqs. (3) and (5) respectively.

Given the upper and the lower boundaries of joint rigidity, our goal was to simulate several degrees of hypertonia that could be recognized by the therapists via proprioceptive feedback. In the haptic literature, the just noticeable difference (JND), or Weber fraction, is an important index representing the sensitivity of the subject to stiffness stimuli. Stiffness JND is defined as the ratio between the perceived difference in stiffness about a specific stiffness level and the stiffness level itself normalized to 100 (i.e. JND = ΔK/K ·100). In general ΔK is the stimulus difference between the first and the third quartile of a stiffness distribution. Different stiffness JND have been obtained empirically, depending on the experimental protocol used. For palpation with a fixed displacement, the value of stiffness JND is around 8% [19]. For free exploration, the JND is much higher and can be up to 67% [20]. Since the rigidity discrimination in the clinical setting is performed with a free movement we imposed as a first approximation a stiffness JND=60% which correspond to a Weber fraction of 0.6. Knowing the Weber fraction of stiffness allowed us to set adjacent stiffness levels thus, segmenting the whole range of rigidity between the two aforementioned boundary conditions using five possible levels. The ratio between the stiffness at different levels for the specific muscle group i was set so that:

$$\frac{K_{m,i}^{\mathit{level}}}{K_{m,i}^{\mathit{level}+1}}\in \left[\frac{3}{5},\frac{5}{8},\frac{8}{13},\frac{13}{21}\right]\mid \mathit{level}=\mathrm{0..4}\Rightarrow K_{m,i}^{\mathit{level}}={\kappa }_{\text{level}}{K}_{\text{nominal},i}\mid \kappa =\{3,5,8,13,21\}$$ (6)

thus following a Fibonacci succession that approximate a 0.6 Weber fraction. Notice that also the MAS encompasses five ordinal levels (i.e. 0,1,2,3,4) analogous to our five levels of severity – normal, very mild, mild, moderate and severe. A score of 0 represents a “normal” joint stiffness and a score of 4 corresponds to a very rigid joint (i.e. very hard to move). In addition, it is important to notice that given the linearity of the Jacobian transformation between muscles’, joints’ and Cartesian space, multiplying the muscle stiffness matrix by κ will increase rigidity in all the other three spaces by the same proportion. The values for the nominal muscle stiffness were chosen as:

$$K_{\text{nominal}}=(\begin{array}{cccccc}{k}_{sf}& k_{se}& k_{ef}& k_{ee}& k_{bf}& k_{be}\end{array})=(\begin{array}{cccccc}540& 540& 600& 600& 100& 100\end{array})[N/m]$$ (7)

According to our parameters, the intrinsic muscle stiffness τ was assumed to be 1/4 of $K_m^{\mathit{level}}$. The ratio between muscle stiffness and rigidity of the connective tissue has been reported to vary between 1:1 and 1:10 [21–24].

Hence, by varying $K_m^{\mathit{level}}$ according to eq. (6) would automatically produce an increase in the active force Φ following a Weber law.

We imposed a concurrent linear variation of υ from 0 to 1 in eq. (4) in intervals so to obtain five equally spaced levels of reflex gains which can be associated to the five levels of severity of our task.

To render the different hypertonic conditions in our experiment, the hypertonic gains (i.e. υ and ϱ in eqs. (4) and (6)) were selected according to the muscle group of interest. For the hypertonic shoulder hypertonic gains were imposed for the sf and se, while for the rest of the muscle groups (ef, ee, bf and be) these gains were set to normal; for the hypertonic elbow, only ef and ee were modified; and for the hypertonic bi-articular, only bf and be were changed.

III. Results

Even though no specific instructions on how to manipulate the virtual arm were given to the therapists, they were all very consistent in performing probing motions that isolated individual joints or that looked like circular movements (Figure 2). The isolated joint motions were characterized by fast motions of the impaired arm in directions that were orthogonal to the different limb segments. For example, to examine the elbow joint, therapists produced a movement orthogonal to the virtual patient’s forearm so that the movement did not perturb the shoulder joint; to examine the shoulder joint, therapists tried to maintain the impaired limb with a 90° elbow flexion and to produce a movement orthogonal to the Humerus. Forces produced by these movements were not sufficiently different to allow discrimination between conditions. As seen in Figure 2, forces produced by the motion to examine the shoulder joint are very similar when interacting with an arm with hypertonic shoulder or bi-articular muscle groups.

Figure 2.

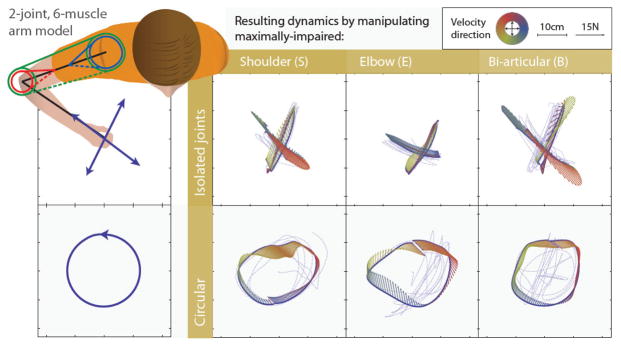
Stereotypical probing motions (isolated joints and circular motions) executed by therapists and the resulting dynamics associated with those. Small arrows represent the magnitude and direction of the force experienced by therapists during the movement (dashed lines). The arrow’s color represents the direction of the velocity during the movement.

Figure 2a shows the frequency of selected answers for the different impairments. Therapists exhibited a systematic bias towards assigning the hypertonic shoulder label when the severity of hypertonia was low (very mild and mild) and towards the hypertonic bi-articular label when the severity is higher (moderate and severe), regardless of the muscle group being impaired.

To quantify the therapists’ performance, we looked at the reliability of an assessment on an impaired arm. Using a frequentist approach this can be quantified as:

$$\mathrm{b}=\frac{1}{3}\sum _i\frac{n_{i,i}}{n_{i,i}+{\displaystyle \sum _{j\ne i}}{n}_{j,i}}i,j\in \{\mathit{shoulder},\mathit{elbow},\mathit{biarticular}\}$$ (8)

where n_a,b represents number of trials with condition a labeled as b.

Figure 2b shows therapists’ ability to correctly identify the location of the impairment. Surprisingly, for levels very mild to moderate, the reliability of the therapists’ assessment was no statistically different from the reliability of an unbiased random choice (H₀: μ_χ=1/3; p_{very mild}=0.83, p_mild=0.73, p_moderate=0.11, p_severe<0.05). However, it is worth noting that therapists’ assessments differ from a random choice in that therapists tended to select both muscle groups when the level of severity was high. This makes the therapists’ choice a safer option if an intervention needs to be planned based on this diagnosis.

IV. Discussion

In this work, we used a physical simulator to investigate how therapists are able to discriminate between similar conditions of hypertonia in three different arm muscles’ groups affected by four levels of severity. Therapists are trained to recognize the nature and severity of physical disabilities through the manipulation of patients’ limbs. This skill is acquired only after a long period of clinical practice and the evaluation of different aspects of hypertonia is expressed using largely their subjective judgment [25]. In spite of this large reliance on human perception, to our knowledge there are no studies in the scientific literature describing the perceptual identification of the nature and severity of hypertonic impairments in multi-joint systems. Some studies have tried to classify the ability of therapists to discern non-biological stimuli, such as linear stiffness [26, 27]. However, these studies have focused on the tactile sensations produced by surfaces, which scarcely relate to the perception of mechanical stimuli perceived via proprioceptive feedback, which is predominant during large movements [28]. In the attempt to understand the sensation associated to the manipulation of an hypertonic limb, other groups have tried to reproduce the haptic sensation of hypertonia via robotic prototypes [29–32]. Yet, such approaches were limited to only one degree of freedom (DOF) and focused on mimicking current assessment techniques (e.g. Ashworth test). In contrast, our approach allows us to characterize how therapists perceive different types of hypertonia in a multi-joint system through a single interaction port. While therapists do not diagnose whole arm hypertonia by manipulating only the end effector (hand) of the patient, we are interested in understanding the interaction that occurs through a single haptic port under the rationale that results derived from this study should be directly applicable to both on-site and remote scenarios [13].

We observed a rather poor performance of trained expert therapists who participated in our study in recognizing which muscle group was affected by hypertonia. This begs the question if the forces produced by a real hypertonic patient might be different from those produced by our model. There is no general consensus on what the different components of hypertonia are. However, there is general agreement that hypertonic conditions are often appearing together (e.g. rigidity, dystonia and spasticity), and produce a non-linear position dependent force with a non-linear dependence on the amount and rate of muscle stretch. Our model captures these two characteristics with assumptions based on physiologically reasonable values. Furthermore, all the participating therapists agreed that the sensation produced by the rendered hypertonic arm model was compatible with their memories of interacting with real hypertonic patients through standard manipulation. Some therapists reported the model to be “slightly more viscous than expected”. In addition, all clinicians were exposed to a familiarization phase where they reported to be able to recognize the sources of the impairment and to be able to distinguish between them.

We conclude that multi-joint abnormalities cannot be distinguished by isolating individual joints. Our current studies focus on testing if the individualization of abnormalities is possible via manipulation strategies derived from understanding the force-field produced by the different types of hypertonia. Providing a method to enable therapists to appreciate and quantify hypertonic phenomena can lead to enhanced training, improved classification, and consequently better treatment of these disorders.

We are currently using this approach to i) assess the capabilities of naïve subjects to correctly discriminate between different hypertonic impairments [33] and to ii) assess how the perception of hypertonia is affected by the impedance introduced by the virtual connection between a patient and a clinician interacting remotely [34].

Figure 3.

a) Three dimensional histograms that represent the frequency of selected answers by the therapists; they demonstrated confusion in distinguishing the location of the hypertonia. b) Mean and standard error of reliability of an assessment as defined in eq. (8).

Table I.

Inertial and geometrical parameters

Symbol	Denomination	Value
msubject	Virtual patient mass*	75 [kg ]
l1, l2	Upper and lower arm length*	0.31,0.35 [m]
r1, r2	Upper and lower arm center of mass*	0.135, 0.150 [m]
m1, m2	Upper and lower arm mass*	2.1, 1.2 [kg]
I1, I2	Upper and lower arm moment of inertia about the proximal joint*	0.0593, 0.0407 [kg m2]
ρsf, ρse	Shoulder adductors and abductors moment arm**	0.03, 0.03 [m]
ρef, ρee	Elbow flexors and extensors moment arm**	0.021, 0.021 [m]
ρbf1, ρbf2, ρbe1, ρbe2	Biarticular flexors and extensors moment arm**	0.044, 0.044, 0.0338, 0.0338 [m]

^*from equations proposed in [1];

^**as defined in [2]